Deformare

Exemplu de deformare

In fizica si inginerie , deformarea unui corp continuu (sau structură ) este orice schimbare în configurația geometrică a corpului , care conduce la o modificare a acesteia formă sau mărime în urma aplicării unui intern sau extern stres .

Studiul deformării unui corp continuu are o importanță fundamentală în mecanica continuului și în mecanica structurală , deoarece este formulată caracterizarea mecanică a comportamentului materialului care constituie corpul (și, prin urmare, modul în care acesta se deformează sub acțiunea forțelor aplicate). prin relații constitutive exprimate convenabil în termenii legăturii dintre parametrii care descriu starea de stres și deformarea corpului însuși. În acest scop, nu este atât de important să cunoaștem deformarea globală a corpului, ci să ajungem la o caracterizare locală a deformării, adică o descriere a deformării care afectează o vecinătate generică a fiecărui punct al corpului.

În general, materialele pot fi caracterizate pe baza deformărilor lor elastice și plastice . O deformare elastică este o deformare care dispare atunci când stresul încetează, altfel există o deformare plastică sau permanentă. Există materiale care au practic doar deformare plastică și materiale care sunt elastice până la o anumită valoare a stresului, după care există plasticitate până la eșec. În cele ce urmează vom defini starea de deformare a continuumului tridimensional Cauchy , referindu-ne la elementele relative pentru studiul deformării altor modele de corpuri continue ( grinzi , cochilii etc.).

Notatie si simbolologie

Operații pe vectori și tensori / matrici :

${\mathbf {a} }\,\cdot \,{\mathbf {b} }$ ${\ displaystyle {\ mathbf {a}} \, \ cdot \, {\ mathbf {b}}}$ ${\ displaystyle {\ mathbf {a}} \, \ cdot \, {\ mathbf {b}}}$ : produs scalar între vectori;
${\mathbf {a} }\,\times \,{\mathbf {b} }$ ${\ displaystyle {\ mathbf {a}} \, \ times \, {\ mathbf {b}}}$ ${\ displaystyle {\ mathbf {a}} \, \ times \, {\ mathbf {b}}}$ : produs vector între vectori;
$\mathbf {A} ^{t}$ ${\ displaystyle \ mathbf {A} ^ {t}}$ ${\ displaystyle \ mathbf {A} ^ {t}}$ : tensorul transpus al tensorului $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf {A}$ ;
$\mathbf {A} ^{-1}$ ${\ displaystyle \ mathbf {A} ^ {- 1}}$ ${\ displaystyle \ mathbf {A} ^ {- 1}}$ : tensorul invers al tensorului $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf {A}$ ;
$det({\mathbf {A} })$ ${\ displaystyle det ({\ mathbf {A}})}$ ${\ displaystyle det ({\ mathbf {A}})}$ : determinant al tensorului ${\mathbf {A} }$ ${\ displaystyle {\ mathbf {A}}}$ ${\ displaystyle {\ mathbf {A}}}$ ;
$\|{\mathbf {a} }\|$ ${\ displaystyle \ | {\ mathbf {a}} \ |}$ ${\ displaystyle \ | {\ mathbf {a}} \ |}$ : normă vectorială ${\mathbf {a} }$ ${\ displaystyle {\ mathbf {a}}}$ ${\ displaystyle {\ mathbf {a}}}$ ;
$\|{\mathbf {A} }\|$ ${\ displaystyle \ | {\ mathbf {A}} \ |}$ ${\ displaystyle \ | {\ mathbf {A}} \ |}$ : norma tensorului ${\mathbf {A} }$ ${\ displaystyle {\ mathbf {A}}}$ ${\ displaystyle {\ mathbf {A}}}$ ;
$\mathbf {rot} ({\mathbf {A} })$ ${\ displaystyle \ mathbf {rot} ({\ mathbf {A}})}$ ${\ displaystyle \ mathbf {rot} ({\ mathbf {A}})}$ este operatorul rotorului tensorului ${\mathbf {A} }$ ${\ displaystyle {\ mathbf {A}}}$ ${\ displaystyle {\ mathbf {A}}}$ ;

Istorie

Geneza conceptului de deformare înțeles în sensul modern al termenului, adică ca o variație locală a configurației corpului, se găsește între secolele XVII și XVIII , când Isaac Beeckman și Johann Bernoulli au introdus măsurarea deformării ca relație între variația lungimii unei fibre materiale și lungimea inițială a acesteia.

Ulterior, pe baza acestui concept, un număr mare de savanți importanți au dezvoltat tema deformării: printre aceștia ne amintim în principal pe Euler , care a dezvoltat modelul tridimensional al teoriei deformărilor infinitesimale , și pe Cauchy , care a dezvoltat teoria deformărilor finite. .

Modificări de configurare

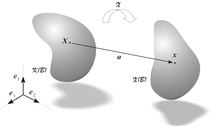
Referință și configurație deformată a continuumului Cauchy

Deformarea unui cartier din continuumul Cauchy

O configurație geometrică a continuumului Cauchy este orice regiune regulată ${\mathcal {B}}$ ${\ displaystyle {\ mathcal {B}}}$ ${\ mathcal B}$ a spațiului tridimensional euclidian ${\mathcal {E}}$ ${\ displaystyle {\ mathcal {E}}}$ ${\ displaystyle {\ mathcal {E}}}$ ( spațiul fizic ) ocupat de punctele corpului. În dezvoltarea conceptului de deformare, ne putem limita la luarea în considerare a două configurații specifice, fără a lua în considerare secvența în care se ajunge la a doua începând cu prima. Este obișnuit să apelați prima configurație nedefinită și să o identificați cu configurația de referință; a doua se numește configurație deformată . Ambii se consideră independenți de timp.

Analiza deformării constă în studiul aplicației ( transport )

{\mathbf {x} }={\boldsymbol {\chi }}({\mathbf {X} })

{\ displaystyle {\ mathbf {x}} = {\ boldsymbol {\ chi}} ({\ mathbf {X}})}

{\ displaystyle {\ mathbf {x}} = {\ boldsymbol {\ chi}} ({\ mathbf {X}})}

care aduce corpul de la configurația nedeformată la configurația deformată sau, ceea ce este același, în studiul deplasării produse măsurate de câmpul vector ${\mathbf {u} }({\mathbf {X} })$ ${\ displaystyle {\ mathbf {u}} ({\ mathbf {X}})}$ ${\ displaystyle {\ mathbf {u}} ({\ mathbf {X}})}$ definit astfel:

{\mathbf {u} }({\mathbf {X} })={\mathbf {x} }-{\mathbf {X} }={\boldsymbol {\chi }}({\mathbf {X} })-{\mathbf {X} }

{\ displaystyle {\ mathbf {u}} ({\ mathbf {X}}) = {\ mathbf {x}} - {\ mathbf {X}} = {\ boldsymbol {\ chi}} ({\ mathbf {X }}) - {\ mathbf {X}}}

{\ displaystyle {\ mathbf {u}} ({\ mathbf {X}}) = {\ mathbf {x}} - {\ mathbf {X}} = {\ boldsymbol {\ chi}} ({\ mathbf {X }}) - {\ mathbf {X}}}

În special, este important să se studieze deformarea unui vecinătate a unui punct material generic, adică a unei porțiuni mici a corpului aproape de punctul considerat. În acest scop, este utilă utilizarea tensorului gradientului (ordinul doi) al deformării

{\mathbf {F} }={\boldsymbol {\nabla }}{\boldsymbol {\chi }}({\mathbf {X} })\;\;\;[\;{\mathbf {F} }={\mathbf {1} }+{\boldsymbol {\nabla }}{\mathbf {u} }({\mathbf {X} })\;

{\ displaystyle {\ mathbf {F}} = {\ boldsymbol {\ nabla}} {\ boldsymbol {\ chi}} ({\ mathbf {X}}) \; \; \; [\; {\ mathbf {F }} = {\ mathbf {1}} + {\ boldsymbol {\ nabla}} {\ mathbf {u}} ({\ mathbf {X}}) \;}

{\ displaystyle {\ mathbf {F}} = {\ boldsymbol {\ nabla}} {\ boldsymbol {\ chi}} ({\ mathbf {X}}) \; \; \; [\; {\ mathbf {F }} = {\ mathbf {1}} + {\ boldsymbol {\ nabla}} {\ mathbf {u}} ({\ mathbf {X}}) \;}

cu referire la gradientul câmpului

{\mathbf {u} }({\mathbf {X} })\;]

{\ displaystyle {\ mathbf {u}} ({\ mathbf {X}}) \;]}

{\ displaystyle {\ mathbf {u}} ({\ mathbf {X}}) \;]}

Gradientul de deformare este o măsură a deformării unui vecinătate a unui punct generic întrucât, prin definiția unui gradient, permite reprezentarea transformării suferite de un segment orientat aparținând vecinătății configurației nedeformate $\mathbf {dX}$ ${\ displaystyle \ mathbf {dX}}$ ${\ displaystyle \ mathbf {dX}}$ la configurația deformată $\mathbf {dx} ={\boldsymbol {\chi }}(\mathbf {X+dX} )-{\boldsymbol {\chi }}({\mathbf {X} })$ ${\ displaystyle \ mathbf {dx} = {\ boldsymbol {\ chi}} (\ mathbf {X + dX}) - {\ boldsymbol {\ chi}} ({\ mathbf {X}})}$ ${\ displaystyle \ mathbf {dx} = {\ boldsymbol {\ chi}} (\ mathbf {X + dX}) - {\ boldsymbol {\ chi}} ({\ mathbf {X}})}$

\mathbf {dx} ={\mathbf {F} }\,\mathbf {dX}

{\ displaystyle \ mathbf {dx} = {\ mathbf {F}} \, \ mathbf {dX}}

{\ displaystyle \ mathbf {dx} = {\ mathbf {F}} \, \ mathbf {dX}}

De asemenea, permite reprezentarea prin intermediul formulei ( Nanson )

ds\,{\mathbf {n} }=det({\mathbf {F} })\,({\mathbf {F} }^{-1})^{t}\,(dS\,{\mathbf {N} })

{\ displaystyle ds \, {\ mathbf {n}} = det ({\ mathbf {F}}) \, ({\ mathbf {F}} ^ {- 1}) ^ {t} \, (dS \, {\ mathbf {N}})}}

{\ displaystyle ds \, {\ mathbf {n}} = det ({\ mathbf {F}}) \, ({\ mathbf {F}} ^ {- 1}) ^ {t} \, (dS \, {\ mathbf {N}})}}

transformarea suferită de un element orientat al suprafeței $d S.$ ${\ displaystyle dS}$ ${\ displaystyle dS}$ și orientare normală ${\mathbf {N} }$ ${\ displaystyle {\ mathbf {N}}}$ ${\ displaystyle {\ mathbf {N}}}$ în configurația nedeformată și a zonei $d s$ ${\ displaystyle ds}$ $ds$ și orientare ${\mathbf {n} }$ ${\ displaystyle {\ mathbf {n}}}$ ${\ displaystyle {\ mathbf {n}}}$ în configurația deformată.

În cele din urmă, raportează măsurarea unui element de volum infinitesimal în configurația nedeformată $d V.$ ${\ displaystyle dV}$ $dV$ iar în configurația deformată $d v$ ${\ displaystyle dv}$ $dv$

dv=det({\mathbf {F} })\,dV\;\;\;\;\;

{\ displaystyle dv = det ({\ mathbf {F}}) \, dV \; \; \; \; \;}

{\ displaystyle dv = det ({\ mathbf {F}}) \, dV \; \; \; \; \;}

Reprezentare în componente scalare

S-a remediat un sistem de coordonate carteziene într-o bază ortonormală $\{{\mathbf {e} }_{1},{\mathbf {e} }_{2},{\mathbf {e} }_{3}\}$ ${\ displaystyle \ {{\ mathbf {e}} _ {1}, {\ mathbf {e}} _ {2}, {\ mathbf {e}} _ {3} \}}$ ${\ displaystyle \ {{\ mathbf {e}} _ {1}, {\ mathbf {e}} _ {2}, {\ mathbf {e}} _ {3} \}}$ și indicând cu $(X_{1},X_{2},X_{3})$ ${\ displaystyle (X_ {1}, X_ {2}, X_ {3})}$ $(X_1, X_2, X_3)$ coordonatele (numite materiale sau referințe ) ale punctului din configurația de referință și cu $(x_{1},x_{2},x_{3})$ ${\ displaystyle (x_ {1}, x_ {2}, x_ {3})}$ $(x_1, x_2, x_3)$ coordonatele (numite spațiale ) ale punctului din configurația deformată, aplicarea transportului și deplasarea sunt reprezentate în componente de sistemul de relații scalare:

x_{i}=\chi _{i}(X_{1},X_{2},X_{3})\;\;,\;\;u_{i}=u_{i}(X_{1},X_{2},X_{3})\;\;,\;\;i=\{1,2,3\}

{\ displaystyle x_ {i} = \ chi _ {i} (X_ {1}, X_ {2}, X_ {3}) \; \ ;, \; \; u_ {i} = u_ {i} (X_ {1}, X_ {2}, X_ {3}) \; \ ;, \; \; i = \ {1,2,3 \}}

{\ displaystyle x_ {i} = \ chi _ {i} (X_ {1}, X_ {2}, X_ {3}) \; \ ;, \; \; u_ {i} = u_ {i} (X_ {1}, X_ {2}, X_ {3}) \; \ ;, \; \; i = \ {1,2,3 \}}

Tensorul gradientului de deformare are următoarea matrice de reprezentare în componentele scalare:

[{\mathbf {F} }]={\begin{bmatrix}{\frac {\partial x_{1}}{\partial X_{1}}}&{\frac {\partial x_{1}}{\partial X_{2}}}&{\frac {\partial x_{1}}{\partial X_{3}}}\!\\{\frac {\partial x_{2}}{\partial X_{1}}}&{\frac {\partial x_{2}}{\partial X_{2}}}&{\frac {\partial x_{2}}{\partial X_{3}}}\\{\frac {\partial x_{3}}{\partial X_{1}}}&{\frac {\partial x_{3}}{\partial X_{2}}}&{\frac {\partial x_{3}}{\partial X_{3}}}\\\end{bmatrix}}={\begin{bmatrix}1+{\frac {\partial u_{1}}{\partial X_{1}}}&{\frac {\partial u_{1}}{\partial X_{2}}}&{\frac {\partial u_{1}}{\partial X_{3}}}\\{\frac {\partial u_{2}}{\partial X_{1}}}&1+{\frac {\partial u_{2}}{\partial X_{2}}}&{\frac {\partial u_{2}}{\partial X_{3}}}\\{\frac {\partial u_{3}}{\partial X_{1}}}&{\frac {\partial u_{3}}{\partial X_{2}}}&1+{\frac {\partial u_{3}}{\partial X_{3}}}\\\end{bmatrix}}

{\ displaystyle [{\ mathbf {F}}] = {\ begin {bmatrix} {\ frac {\ partial x_ {1}} {\ partial X_ {1}}} și {\ frac {\ partial x_ {1} } {\ partial X_ {2}}} și {\ frac {\ partial x_ {1}} {\ partial X_ {3}}} \! \\ {\ frac {\ partial x_ {2}} {\ partial X_ {1}}} & {\ frac {\ partial x_ {2}} {\ partial X_ {2}}} și {\ frac {\ partial x_ {2}} {\ partial X_ {3}}} \\ { \ frac {\ partial x_ {3}} {\ partial X_ {1}}} și {\ frac {\ partial x_ {3}} {\ partial X_ {2}}} și {\ frac {\ partial x_ {3 }} {\ partial X_ {3}}} \\\ end {bmatrix}} = {\ begin {bmatrix} 1 + {\ frac {\ partial u_ {1}} {\ partial X_ {1}}} și { \ frac {\ partial u_ {1}} {\ partial X_ {2}}} și {\ frac {\ partial u_ {1}} {\ partial X_ {3}}} \\ {\ frac {\ partial u_ { 2}} {\ partial X_ {1}}} & 1 + {\ frac {\ partial u_ {2}} {\ partial X_ {2}}} și {\ frac {\ partial u_ {2}} {\ partial X_ {3}}} \\ {\ frac {\ partial u_ {3}} {\ partial X_ {1}}} și {\ frac {\ partial u_ {3}} {\ partial X_ {2}}} și 1 + {\ frac {\ partial u_ {3}} {\ partial X_ {3}}} \\\ end {bmatrix}}}

{\ displaystyle [{\ mathbf {F}}] = {\ begin {bmatrix} {\ frac {\ partial x_ {1}} {\ partial X_ {1}}} și {\ frac {\ partial x_ {1} } {\ partial X_ {2}}} și {\ frac {\ partial x_ {1}} {\ partial X_ {3}}} \! \\ {\ frac {\ partial x_ {2}} {\ partial X_ {1}}} & {\ frac {\ partial x_ {2}} {\ partial X_ {2}}} și {\ frac {\ partial x_ {2}} {\ partial X_ {3}}} \\ { \ frac {\ partial x_ {3}} {\ partial X_ {1}}} și {\ frac {\ partial x_ {3}} {\ partial X_ {2}}} și {\ frac {\ partial x_ {3 }} {\ partial X_ {3}}} \\\ end {bmatrix}} = {\ begin {bmatrix} 1 + {\ frac {\ partial u_ {1}} {\ partial X_ {1}}} și { \ frac {\ partial u_ {1}} {\ partial X_ {2}}} și {\ frac {\ partial u_ {1}} {\ partial X_ {3}}} \\ {\ frac {\ partial u_ { 2}} {\ partial X_ {1}}} & 1 + {\ frac {\ partial u_ {2}} {\ partial X_ {2}}} și {\ frac {\ partial u_ {2}} {\ partial X_ {3}}} \\ {\ frac {\ partial u_ {3}} {\ partial X_ {1}}} și {\ frac {\ partial u_ {3}} {\ partial X_ {2}}} și 1 + {\ frac {\ partial u_ {3}} {\ partial X_ {3}}} \\\ end {bmatrix}}}

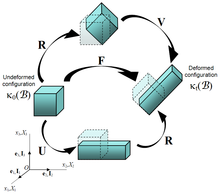
Descompunerea polară a gradientului de deformare

Deformarea alungirii

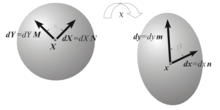
Deformație glisantă unghiulară

Variația volumului în continuumul Cauchy

Măsurători de deformare pură

În general, o deplasare generică a unui corp include atât o rată de deplasare rigidă, cât și o rată pură de deformare a corpului cu variații de formă sau dimensiune (sau ambele). În special, transformarea unui vecinătate a unui punct descris de tensor ${\mathbf {F} }$ ${\ displaystyle {\ mathbf {F}}}$ ${\ displaystyle {\ mathbf {F}}}$ este dată de compoziția unei rotații rigide a împrejurimilor cu o deformare pură a acesteia. Teorema descompunerii polare permite evaluarea ambelor contribuții, asigurându-se că există doar două descompuneri ale tensorului ${\mathbf {F} }$ ${\ displaystyle {\ mathbf {F}}}$ ${\ displaystyle {\ mathbf {F}}}$

{\mathbf {F} }={\mathbf {R} }{\mathbf {U} }={\mathbf {V} }{\mathbf {R} }

{\ displaystyle {\ mathbf {F}} = {\ mathbf {R}} {\ mathbf {U}} = {\ mathbf {V}} {\ mathbf {R}}}

{\ displaystyle {\ mathbf {F}} = {\ mathbf {R}} {\ mathbf {U}} = {\ mathbf {V}} {\ mathbf {R}}}

unde este ${\mathbf {R} }$ ${\ displaystyle {\ mathbf {R}}}$ ${\ displaystyle {\ mathbf {R}}}$ este un descriptor tensor ortogonal al rotației e $({\mathbf {U} },{\mathbf {V} })$ ${\ displaystyle ({\ mathbf {U}}, {\ mathbf {V}})}$ ${\ displaystyle ({\ mathbf {U}}, {\ mathbf {V}})}$ sunt tensori pozitivi simetrici și definitivi reprezentativi ai deformării pure supuse, numiți respectiv tensor drept și tensor stâng al deformării . Prin urmare, orice măsură posibilă a deformării pure trebuie să fie doar o funcție a tensorului ${\mathbf {U} }$ ${\ displaystyle {\ mathbf {U}}}$ ${\ displaystyle {\ mathbf {U}}}$ sau a tensorului ${\mathbf {V} }$ ${\ displaystyle {\ mathbf {V}}}$ ${\ displaystyle {\ mathbf {V}}}$ .

Măsurători locale de deformare pură

Măsurile locale de deformare pură de interes tehnic sunt dilatarea liniară , alunecarea unghiulară și dilatarea volumetrică .

Expansiune liniară

Modificarea procentuală a lungimii unui prim segment orientat $\mathbf {dX} =dL\,\mathbf {N}$ ${\ displaystyle \ mathbf {dX} = dL \, \ mathbf {N}}$ ${\ displaystyle \ mathbf {dX} = dL \, \ mathbf {N}}$ iar după deformare $\mathbf {dx} =dl\,\mathbf {n}$ ${\ displaystyle \ mathbf {dx} = dl \, \ mathbf {n}}$ ${\ displaystyle \ mathbf {dx} = dl \, \ mathbf {n}}$ se măsoară prin

\varepsilon ({\mathbf {N} })={\frac {{\mbox{d}}{l}-{\mbox{d}}{L}}{{\mbox{d}}{L}}}=\left(({\mathbf {F} }^{t}{\mathbf {F} }\,{\mathbf {N} })\,\cdot \,{\mathbf {N} }\right)^{1/2}-1=\left(({\mathbf {U} }^{2}\,{\mathbf {N} })\,\cdot \,{\mathbf {N} }\right)^{1/2}-1

{\ displaystyle \ varepsilon ({\ mathbf {N}}) = {\ frac {{\ mbox {d}} {l} - {\ mbox {d}} {L}} {{\ mbox {d}} { L}}} = \ left (({\ mathbf {F}} ^ {t} {\ mathbf {F}} \, {\ mathbf {N}}) \, \ cdot \, {\ mathbf {N}} \ right) ^ {1/2} -1 = \ left (({\ mathbf {U}} ^ {2} \, {\ mathbf {N}}) \, \ cdot \, {\ mathbf {N}} \ dreapta) ^ {1/2} -1}

{\ displaystyle \ varepsilon ({\ mathbf {N}}) = {\ frac {{\ mbox {d}} {l} - {\ mbox {d}} {L}} {{\ mbox {d}} { L}}} = \ left (({\ mathbf {F}} ^ {t} {\ mathbf {F}} \, {\ mathbf {N}}) \, \ cdot \, {\ mathbf {N}} \ right) ^ {1/2} -1 = \ left (({\ mathbf {U}} ^ {2} \, {\ mathbf {N}}) \, \ cdot \, {\ mathbf {N}} \ dreapta) ^ {1/2} -1}

Se definește astfel o măsură analogă, variația procentuală a pătratelor lungimilor

{\frac {{\mbox{d}}{l}^{2}-{\mbox{d}}{L}^{2}}{{\mbox{d}}{L}^{2}}}=({\mathbf {F} }^{t}{\mathbf {F} }-{\mathbf {1} })\,{\mathbf {N} }\,\cdot \,{\mathbf {N} }=({\mathbf {U} }^{2}-{\mathbf {1} })\,{\mathbf {N} }\,\cdot \,{\mathbf {N} }

{\ displaystyle {\ frac {{\ mbox {d}} {l} ^ {2} - {\ mbox {d}} {L} ^ {2}} {{\ mbox {d}} {L} ^ { 2}}} = ({\ mathbf {F}} ^ {t} {\ mathbf {F}} - {\ mathbf {1}}) \, {\ mathbf {N}} \, \ cdot \, {\ mathbf {N}} = ({\ mathbf {U}} ^ {2} - {\ mathbf {1}}) \, {\ mathbf {N}} \, \ cdot \, {\ mathbf {N}}}

{\ displaystyle {\ frac {{\ mbox {d}} {l} ^ {2} - {\ mbox {d}} {L} ^ {2}} {{\ mbox {d}} {L} ^ { 2}}} = ({\ mathbf {F}} ^ {t} {\ mathbf {F}} - {\ mathbf {1}}) \, {\ mathbf {N}} \, \ cdot \, {\ mathbf {N}} = ({\ mathbf {U}} ^ {2} - {\ mathbf {1}}) \, {\ mathbf {N}} \, \ cdot \, {\ mathbf {N}}}

Defilare unghiulară

Luați în considerare două segmente orientate ${\mbox{d}}{\mathbf {X} }={\mbox{d}}X\,{\mathbf {N} }$ ${\ displaystyle {\ mbox {d}} {\ mathbf {X}} = {\ mbox {d}} X \, {\ mathbf {N}}}$ ${\ displaystyle {\ mbox {d}} {\ mathbf {X}} = {\ mbox {d}} X \, {\ mathbf {N}}}$ Și ${\mbox{d}}{\mathbf {Y} }={\mbox{d}}Y\,{\mathbf {M} }$ ${\ displaystyle {\ mbox {d}} {\ mathbf {Y}} = {\ mbox {d}} Y \, {\ mathbf {M}}}$ ${\ displaystyle {\ mbox {d}} {\ mathbf {Y}} = {\ mbox {d}} Y \, {\ mathbf {M}}}$ a configurației de referință, ortogonale unele cu altele, și transformările lor ${\mbox{d}}{\mathbf {x} }={\mbox{d}}x\,{\mathbf {n} }$ ${\ displaystyle {\ mbox {d}} {\ mathbf {x}} = {\ mbox {d}} x \, {\ mathbf {n}}}$ ${\ displaystyle {\ mbox {d}} {\ mathbf {x}} = {\ mbox {d}} x \, {\ mathbf {n}}}$ Și ${\mbox{d}}{\mathbf {y} }={\mbox{d}}y\,{\mathbf {m} }$ ${\ displaystyle {\ mbox {d}} {\ mathbf {y}} = {\ mbox {d}} y \, {\ mathbf {m}}}$ ${\ displaystyle {\ mbox {d}} {\ mathbf {y}} = {\ mbox {d}} y \, {\ mathbf {m}}}$ . Alunecarea unghiulară măsoară schimbarea unghiului $\gamma ({\mathbf {N} },{\mathbf {M} })={\frac {\pi }{2}}-\vartheta$ ${\ displaystyle \ gamma ({\ mathbf {N}}, {\ mathbf {M}}) = {\ frac {\ pi} {2}} - \ vartheta}$ ${\ displaystyle \ gamma ({\ mathbf {N}}, {\ mathbf {M}}) = {\ frac {\ pi} {2}} - \ vartheta}$ subordonat între elementele liniare înainte și după deformare. Se exprimă prin:

\gamma ({\mathbf {N} },{\mathbf {M} })=\arcsin \left({\frac {{\mathbf {F} }^{t}{\mathbf {F} }\,{\mathbf {N} }\cdot {\mathbf {M} }}{\left({\mathbf {F} }^{t}{\mathbf {F} }\,{\mathbf {N} }\cdot {\mathbf {N} }\right)^{1/2}\left({\mathbf {F} }^{t}{\mathbf {F} }\,{\mathbf {M} }\cdot {\mathbf {M} }\right)^{1/2}}}\right)

{\ displaystyle \ gamma ({\ mathbf {N}}, {\ mathbf {M}}) = \ arcsin \ left ({\ frac {{\ mathbf {F}} ^ {t} {\ mathbf {F}} \, {\ mathbf {N}} \ cdot {\ mathbf {M}}} {\ left ({\ mathbf {F}} ^ {t} {\ mathbf {F}} \, {\ mathbf {N}} \ cdot {\ mathbf {N}} \ right) ^ {1/2} \ left ({\ mathbf {F}} ^ {t} {\ mathbf {F}} \, {\ mathbf {M}} \ cdot {\ mathbf {M}} \ right) ^ {1/2}}} \ right)}

{\ displaystyle \ gamma ({\ mathbf {N}}, {\ mathbf {M}}) = \ arcsin \ left ({\ frac {{\ mathbf {F}} ^ {t} {\ mathbf {F}} \, {\ mathbf {N}} \ cdot {\ mathbf {M}}} {\ left ({\ mathbf {F}} ^ {t} {\ mathbf {F}} \, {\ mathbf {N}} \ cdot {\ mathbf {N}} \ right) ^ {1/2} \ left ({\ mathbf {F}} ^ {t} {\ mathbf {F}} \, {\ mathbf {M}} \ cdot {\ mathbf {M}} \ right) ^ {1/2}}} \ right)}

=\arcsin \left({\frac {{\mathbf {U} }^{2}\,{\mathbf {N} }\cdot {\mathbf {M} }}{\left({\mathbf {U} }^{2}\,{\mathbf {N} }\cdot {\mathbf {N} }\right)^{1/2}\left({\mathbf {U} }^{2}\,{\mathbf {M} }\cdot {\mathbf {M} }\right)^{1/2}}}\right)

{\ displaystyle = \ arcsin \ left ({\ frac {{\ mathbf {U}} ^ {2} \, {\ mathbf {N}} \ cdot {\ mathbf {M}}} {\ left ({\ mathbf {U}} ^ {2} \, {\ mathbf {N}} \ cdot {\ mathbf {N}} \ right) ^ {1/2} \ left ({\ mathbf {U}} ^ {2} \ , {\ mathbf {M}} \ cdot {\ mathbf {M}} \ right) ^ {1/2}}} \ right)}

{\ displaystyle = \ arcsin \ left ({\ frac {{\ mathbf {U}} ^ {2} \, {\ mathbf {N}} \ cdot {\ mathbf {M}}} {\ left ({\ mathbf {U}} ^ {2} \, {\ mathbf {N}} \ cdot {\ mathbf {N}} \ right) ^ {1/2} \ left ({\ mathbf {U}} ^ {2} \ , {\ mathbf {M}} \ cdot {\ mathbf {M}} \ right) ^ {1/2}}} \ right)}

Expansiunea volumetrică

Mai întâi modificarea procentuală a unui element de volum $d V.$ ${\ displaystyle dV}$ $dV$ și apoi $d v$ ${\ displaystyle dv}$ $dv$ deformare:

{\frac {{\mbox{d}}v-{\mbox{d}}V}{{\mbox{d}}V}}={\mbox{det}}({\mathbf {F} })-1={\mbox{det}}({\mathbf {U} })-1

{\ displaystyle {\ frac {{\ mbox {d}} v - {\ mbox {d}} V} {{\ mbox {d}} V}} = {\ mbox {det}} ({\ mathbf {F }}) - 1 = {\ mbox {det}} ({\ mathbf {U}}) - 1}

{\ displaystyle {\ frac {{\ mbox {d}} v - {\ mbox {d}} V} {{\ mbox {d}} V}} = {\ mbox {det}} ({\ mathbf {F }}) - 1 = {\ mbox {det}} ({\ mathbf {U}}) - 1}

Măsurători tensoriale ale tulpinii pure

O descriere obiectivă a deformării pure trebuie să fie neapărat independentă de rotația rigidă și, prin urmare, de tensor ${\mathbf {R} }$ ${\ displaystyle {\ mathbf {R}}}$ ${\ displaystyle {\ mathbf {R}}}$ și funcțiile tensoarelor numai ${\mathbf {U} }$ ${\ displaystyle {\ mathbf {U}}}$ ${\ displaystyle {\ mathbf {U}}}$ sau ${\mathbf {V} }$ ${\ displaystyle {\ mathbf {V}}}$ ${\ displaystyle {\ mathbf {V}}}$ . Posibile măsurători ale tensorului hamiltonian al tensiunii termice sunt exprimate în formă

{\varepsilon }_{n}={\frac {1}{n}}({\mathbf {U} }^{n}-{\mathbf {1} })

{\ displaystyle {\ varepsilon} _ {n} = {\ frac {1} {n}} ({\ mathbf {U}} ^ {n} - {\ mathbf {1}})}

{\ displaystyle {\ varepsilon} _ {n} = {\ frac {1} {n}} ({\ mathbf {U}} ^ {n} - {\ mathbf {1}})}

unde n este un număr real (nu neapărat un număr întreg): pentru n = 1 și n = 2 vorbim respectiv despre tensorul lui Biot și tensorul lui Green .

Tensorul de deformare al lui Green

Tensorul verde este un tensor simetric definit de relația anterioară sau echivalent în termeni de gradient de deformare și gradient de deplasare:

{\varepsilon _{2}}={\mathbf {E} }={\frac {1}{2}}({\mathbf {F} }^{t}{\mathbf {F} }-{\mathbf {1} })={\frac {1}{2}}({\boldsymbol {\nabla }}{\mathbf {u} }+{\boldsymbol {\nabla }}{\mathbf {u} }^{t}+{\boldsymbol {\nabla }}{\mathbf {u} }^{t}{\boldsymbol {\nabla }}{\mathbf {u} })

{\ displaystyle {\ varepsilon _ {2}} = {\ mathbf {E}} = {\ frac {1} {2}} ({\ mathbf {F}} ^ {t} {\ mathbf {F}} - {\ mathbf {1}}) = {\ frac {1} {2}} ({\ boldsymbol {\ nabla}} {\ mathbf {u}} + {\ boldsymbol {\ nabla}} {\ mathbf {u} } ^ {t} + {\ boldsymbol {\ nabla}} {\ mathbf {u}} ^ {t} {\ boldsymbol {\ nabla}} {\ mathbf {u}})}

{\ displaystyle {\ varepsilon _ {2}} = {\ mathbf {E}} = {\ frac {1} {2}} ({\ mathbf {F}} ^ {t} {\ mathbf {F}} - {\ mathbf {1}}) = {\ frac {1} {2}} ({\ boldsymbol {\ nabla}} {\ mathbf {u}} + {\ boldsymbol {\ nabla}} {\ mathbf {u} } ^ {t} + {\ boldsymbol {\ nabla}} {\ mathbf {u}} ^ {t} {\ boldsymbol {\ nabla}} {\ mathbf {u}})}

Este o măsură a deformării, deoarece este zero în prezența unor deplasări rigide. Are un puternic interes tehnic, deoarece este ușor de determinat în ceea ce privește gradientul deformării sau al deplasării și deoarece permite o reprezentare simplă a măsurilor locale definite anterior de deformare pură:

{\begin{aligned}{\frac {{\mbox{d}}{l}^{2}-{\mbox{d}}{L}^{2}}{{\mbox{d}}{L}^{2}}}&=2{\mathbf {E} }\,{\mathbf {N} }\,\cdot \,{\mathbf {N} }\\\varepsilon ({\mathbf {N} })={\frac {{\mbox{d}}{l}-{\mbox{d}}{L}}{{\mbox{d}}{L}}}&=\left(1+2{\mathbf {E} }\,{\mathbf {N} }\,\cdot \,{\mathbf {N} }\right)^{1/2}-1\\\gamma ({\mathbf {N} },{\mathbf {M} })={\frac {\pi }{2}}-\vartheta &=\arcsin \left({\frac {2{\mathbf {E} }\,{\mathbf {N} }\cdot {\mathbf {M} }}{\left(1+2{\mathbf {E} }\,{\mathbf {N} }\cdot {\mathbf {N} }\right)^{1/2}\left(1+2{\mathbf {E} }\,{\mathbf {M} }\cdot {\mathbf {M} }\right)^{1/2}}}\right)\end{aligned}}

{\ displaystyle {\ begin {align} {\ frac {{\ mbox {d}} {l} ^ {2} - {\ mbox {d}} {L} ^ {2}} {{\ mbox {d} } {L} ^ {2}}} & = 2 {\ mathbf {E}} \, {\ mathbf {N}} \, \ cdot \, {\ mathbf {N}} \\\ varepsilon ({\ mathbf {N}}) = {\ frac {{\ mbox {d}} {l} - {\ mbox {d}} {L}} {{\ mbox {d}} {L}}} & = \ left ( 1 + 2 {\ mathbf {E}} \, {\ mathbf {N}} \, \ cdot \, {\ mathbf {N}} \ right) ^ {1/2} -1 \\\ gamma ({\ mathbf {N}}, {\ mathbf {M}}) = {\ frac {\ pi} {2}} - \ vartheta & = \ arcsin \ left ({\ frac {2 {\ mathbf {E}} \, {\ mathbf {N}} \ cdot {\ mathbf {M}}} {\ left (1 + 2 {\ mathbf {E}} \, {\ mathbf {N}} \ cdot {\ mathbf {N}} \ dreapta) ^ {1/2} \ left (1 + 2 {\ mathbf {E}} \, {\ mathbf {M}} \ cdot {\ mathbf {M}} \ right) ^ {1/2}}} \ dreapta) \ end {align}}}

{\ displaystyle {\ begin {align} {\ frac {{\ mbox {d}} {l} ^ {2} - {\ mbox {d}} {L} ^ {2}} {{\ mbox {d} } {L} ^ {2}}} & = 2 {\ mathbf {E}} \, {\ mathbf {N}} \, \ cdot \, {\ mathbf {N}} \\\ varepsilon ({\ mathbf {N}}) = {\ frac {{\ mbox {d}} {l} - {\ mbox {d}} {L}} {{\ mbox {d}} {L}}} & = \ left ( 1 + 2 {\ mathbf {E}} \, {\ mathbf {N}} \, \ cdot \, {\ mathbf {N}} \ right) ^ {1/2} -1 \\\ gamma ({\ mathbf {N}}, {\ mathbf {M}}) = {\ frac {\ pi} {2}} - \ vartheta & = \ arcsin \ left ({\ frac {2 {\ mathbf {E}} \, {\ mathbf {N}} \ cdot {\ mathbf {M}}} {\ left (1 + 2 {\ mathbf {E}} \, {\ mathbf {N}} \ cdot {\ mathbf {N}} \ dreapta) ^ {1/2} \ left (1 + 2 {\ mathbf {E}} \, {\ mathbf {M}} \ cdot {\ mathbf {M}} \ right) ^ {1/2}}} \ dreapta) \ end {align}}}

Tensorul de deformare verde are următoarea reprezentare în componentele scalare:

{\begin{bmatrix}{\mathbf {E} }\end{bmatrix}}={\begin{bmatrix}E_{11}&E_{12}&E_{13}\\E_{21}&E_{22}&E_{23}\\E_{31}&E_{32}&E_{33}\\\end{bmatrix}},\;\left\{{\begin{matrix}E_{11}&=\scriptstyle {{\frac {\partial u_{1}}{\partial X_{1}}}+{\frac {1}{2}}\left({\frac {\partial u_{1}}{\partial X_{1}}}{\frac {\partial u_{1}}{\partial X_{1}}}+{\frac {\partial u_{2}}{\partial X_{1}}}{\frac {\partial u_{2}}{\partial X_{1}}}+{\frac {\partial u_{3}}{\partial X_{1}}}{\frac {\partial u_{3}}{\partial X_{1}}}\right)}\\E_{22}&=\scriptstyle {{\frac {\partial u_{2}}{\partial X_{2}}}+{\frac {1}{2}}\left({\frac {\partial u_{1}}{\partial X_{2}}}{\frac {\partial u_{1}}{\partial X_{2}}}+{\frac {\partial u_{2}}{\partial X_{2}}}{\frac {\partial u_{2}}{\partial X_{2}}}+{\frac {\partial u_{3}}{\partial X_{2}}}{\frac {\partial u_{3}}{\partial X_{2}}}\right)}\\E_{33}&=\scriptstyle {{\frac {\partial u_{3}}{\partial X_{3}}}+{\frac {1}{2}}\left({\frac {\partial u_{1}}{\partial X_{3}}}{\frac {\partial u_{1}}{\partial X_{3}}}+{\frac {\partial u_{2}}{\partial X_{3}}}{\frac {\partial u_{2}}{\partial X_{3}}}+{\frac {\partial u_{3}}{\partial X_{3}}}{\frac {\partial u_{3}}{\partial X_{3}}}\right)}\end{matrix}}\right.,\;\left\{{\begin{matrix}E_{12}=E_{21}&=\scriptstyle {{\frac {1}{2}}\left({\frac {\partial u_{1}}{\partial X_{2}}}+{\frac {\partial u_{2}}{\partial X_{1}}}+{\frac {\partial u_{1}}{\partial X_{1}}}{\frac {\partial u_{1}}{\partial X_{2}}}+{\frac {\partial u_{2}}{\partial X_{1}}}{\frac {\partial u_{2}}{\partial X_{2}}}+{\frac {\partial u_{3}}{\partial X_{1}}}{\frac {\partial u_{3}}{\partial X_{2}}}\right)}\\E_{13}=E_{31}&=\scriptstyle {{\frac {1}{2}}\left({\frac {\partial u_{1}}{\partial X_{3}}}+{\frac {\partial u_{3}}{\partial X_{1}}}+{\frac {\partial u_{1}}{\partial X_{1}}}{\frac {\partial u_{1}}{\partial X_{3}}}+{\frac {\partial u_{2}}{\partial X_{1}}}{\frac {\partial u_{2}}{\partial X_{3}}}+{\frac {\partial u_{3}}{\partial X_{1}}}{\frac {\partial u_{3}}{\partial X_{3}}}\right)}\\E_{23}=E_{32}&=\scriptstyle {{\frac {1}{2}}\left({\frac {\partial u_{2}}{\partial X_{3}}}+{\frac {\partial u_{3}}{\partial X_{2}}}+{\frac {\partial u_{1}}{\partial X_{2}}}{\frac {\partial u_{1}}{\partial X_{3}}}+{\frac {\partial u_{2}}{\partial X_{2}}}{\frac {\partial u_{2}}{\partial X_{3}}}+{\frac {\partial u_{3}}{\partial X_{2}}}{\frac {\partial u_{3}}{\partial X_{3}}}\right)}\end{matrix}}\right.

{\ displaystyle {\ begin {bmatrix} {\ mathbf {E}} \ end {bmatrix}} = {\ begin {bmatrix} E_ {11} & E_ {12} & E_ {13} \\ E_ {21} & E_ {22} & E_ {23} \\ E_ {31} & E_ {32} & E_ {33} \\\ end {bmatrix}}, \; \ left \ {{\ begin {matrix} E_ {11} & = \ scriptstyle {{\ frac {\ partial u_ {1}} {\ partial X_ {1}}} + {\ frac {1} {2}} \ left ({\ frac {\ partial u_ {1}} {\ partial X_ {1}}} {\ frac {\ partial u_ {1}} {\ partial X_ {1}}} + {\ frac {\ partial u_ {2}} {\ partial X_ {1}}} {\ frac {\ partial u_ {2}} {\ partial X_ {1}}} + {\ frac {\ partial u_ {3}} {\ partial X_ {1}}} {\ frac {\ partial u_ {3 }} {\ partial X_ {1}}} \ right)} \\ E_ {22} & = \ scriptstyle {{\ frac {\ partial u_ {2}} {\ partial X_ {2}}} + {\ frac {1} {2}} \ left ({\ frac {\ partial u_ {1}} {\ partial X_ {2}}} {\ frac {\ partial u_ {1}} {\ partial X_ {2}}} + {\ frac {\ partial u_ {2}} {\ partial X_ {2}}} {\ frac {\ partial u_ {2}} {\ partial X_ {2}}} + {\ frac {\ partial u_ { 3}} {\ partial X_ {2}}} {\ frac {\ partial u_ {3}} {\ partial X_ {2}}} \ right)} \\ E_ {33} & = \ scriptstyle {{\ frac {\ partial u_ {3}} {\ partial X_ {3}}} + {\ frac {1} {2}} \ left ({\ frac {\ partial u_ {1}} {\ partial X_ {3}} } {\ frac {\ partial u_ {1}} {\ p artial X_ {3}}} + {\ frac {\ partial u_ {2}} {\ partial X_ {3}}} {\ frac {\ partial u_ {2}} {\ partial X_ {3}}} + { \ frac {\ partial u_ {3}} {\ partial X_ {3}}} {\ frac {\ partial u_ {3}} {\ partial X_ {3}}} \ right)} \ end {matrix}} \ dreapta., \; \ left \ {{\ begin {matrix} E_ {12} = E_ {21} & = \ scriptstyle {{\ frac {1} {2}} \ left ({\ frac {\ partial u_ { 1}} {\ partial X_ {2}}} + {\ frac {\ partial u_ {2}} {\ partial X_ {1}}} + {\ frac {\ partial u_ {1}} {\ partial X_ { 1}}} {\ frac {\ partial u_ {1}} {\ partial X_ {2}}} + {\ frac {\ partial u_ {2}} {\ partial X_ {1}}} {\ frac {\ partial u_ {2}} {\ partial X_ {2}}} + {\ frac {\ partial u_ {3}} {\ partial X_ {1}}} {\ frac {\ partial u_ {3}} {\ partial X_ {2}}} \ right)} \\ E_ {13} = E_ {31} & = \ scriptstyle {{\ frac {1} {2}} \ left ({\ frac {\ partial u_ {1}} {\ partial X_ {3}}} + {\ frac {\ partial u_ {3}} {\ partial X_ {1}}} + {\ frac {\ partial u_ {1}} {\ partial X_ {1}} } {\ frac {\ partial u_ {1}} {\ partial X_ {3}}} + {\ frac {\ partial u_ {2}} {\ partial X_ {1}}} {\ frac {\ partial u_ { 2}} {\ partial X_ {3}}} + {\ frac {\ partial u_ {3}} {\ partial X_ {1}}} {\ frac {\ partial u_ {3}} {\ partial X_ {3 }}} \ right)} \\ E_ {23 } = E_ {32} & = \ scriptstyle {{\ frac {1} {2}} \ left ({\ frac {\ partial u_ {2}} {\ partial X_ {3}}} + {\ frac {\ partial u_ {3}} {\ partial X_ {2}}} + {\ frac {\ partial u_ {1}} {\ partial X_ {2}}} {\ frac {\ partial u_ {1}} {\ partial X_ {3}}} + {\ frac {\ partial u_ {2}} {\ partial X_ {2}}} {\ frac {\ partial u_ {2}} {\ partial X_ {3}}} + {\ frac {\ partial u_ {3}} {\ partial X_ {2}}} {\ frac {\ partial u_ {3}} {\ partial X_ {3}}} \ right)} \ end {matrix}} \ right .}

{\ displaystyle {\ begin {bmatrix} {\ mathbf {E}} \ end {bmatrix}} = {\ begin {bmatrix} E_ {11} & E_ {12} & E_ {13} \\ E_ {21} & E_ {22} & E_ {23} \\ E_ {31} & E_ {32} & E_ {33} \\\ end {bmatrix}}, \; \ left \ {{\ begin {matrix} E_ {11} & = \ scriptstyle {{\ frac {\ partial u_ {1}} {\ partial X_ {1}}} + {\ frac {1} {2}} \ left ({\ frac {\ partial u_ {1}} {\ partial X_ {1}}} {\ frac {\ partial u_ {1}} {\ partial X_ {1}}} + {\ frac {\ partial u_ {2}} {\ partial X_ {1}}} {\ frac {\ partial u_ {2}} {\ partial X_ {1}}} + {\ frac {\ partial u_ {3}} {\ partial X_ {1}}} {\ frac {\ partial u_ {3 }} {\ partial X_ {1}}} \ right)} \\ E_ {22} & = \ scriptstyle {{\ frac {\ partial u_ {2}} {\ partial X_ {2}}} + {\ frac {1} {2}} \ left ({\ frac {\ partial u_ {1}} {\ partial X_ {2}}} {\ frac {\ partial u_ {1}} {\ partial X_ {2}}} + {\ frac {\ partial u_ {2}} {\ partial X_ {2}}} {\ frac {\ partial u_ {2}} {\ partial X_ {2}}} + {\ frac {\ partial u_ { 3}} {\ partial X_ {2}}} {\ frac {\ partial u_ {3}} {\ partial X_ {2}}} \ right)} \\ E_ {33} & = \ scriptstyle {{\ frac {\ partial u_ {3}} {\ partial X_ {3}}} + {\ frac {1} {2}} \ left ({\ frac {\ partial u_ {1}} {\ partial X_ {3}} } {\ frac {\ partial u_ {1}} {\ p artial X_ {3}}} + {\ frac {\ partial u_ {2}} {\ partial X_ {3}}} {\ frac {\ partial u_ {2}} {\ partial X_ {3}}} + { \ frac {\ partial u_ {3}} {\ partial X_ {3}}} {\ frac {\ partial u_ {3}} {\ partial X_ {3}}} \ right)} \ end {matrix}} \ dreapta., \; \ left \ {{\ begin {matrix} E_ {12} = E_ {21} & = \ scriptstyle {{\ frac {1} {2}} \ left ({\ frac {\ partial u_ { 1}} {\ partial X_ {2}}} + {\ frac {\ partial u_ {2}} {\ partial X_ {1}}} + {\ frac {\ partial u_ {1}} {\ partial X_ { 1}}} {\ frac {\ partial u_ {1}} {\ partial X_ {2}}} + {\ frac {\ partial u_ {2}} {\ partial X_ {1}}} {\ frac {\ partial u_ {2}} {\ partial X_ {2}}} + {\ frac {\ partial u_ {3}} {\ partial X_ {1}}} {\ frac {\ partial u_ {3}} {\ partial X_ {2}}} \ right)} \\ E_ {13} = E_ {31} & = \ scriptstyle {{\ frac {1} {2}} \ left ({\ frac {\ partial u_ {1}} {\ partial X_ {3}}} + {\ frac {\ partial u_ {3}} {\ partial X_ {1}}} + {\ frac {\ partial u_ {1}} {\ partial X_ {1}} } {\ frac {\ partial u_ {1}} {\ partial X_ {3}}} + {\ frac {\ partial u_ {2}} {\ partial X_ {1}}} {\ frac {\ partial u_ { 2}} {\ partial X_ {3}}} + {\ frac {\ partial u_ {3}} {\ partial X_ {1}}} {\ frac {\ partial u_ {3}} {\ partial X_ {3 }}} \ right)} \\ E_ {23 } = E_ {32} & = \ scriptstyle {{\ frac {1} {2}} \ left ({\ frac {\ partial u_ {2}} {\ partial X_ {3}}} + {\ frac {\ partial u_ {3}} {\ partial X_ {2}}} + {\ frac {\ partial u_ {1}} {\ partial X_ {2}}} {\ frac {\ partial u_ {1}} {\ partial X_ {3}}} + {\ frac {\ partial u_ {2}} {\ partial X_ {2}}} {\ frac {\ partial u_ {2}} {\ partial X_ {3}}} + {\ frac {\ partial u_ {3}} {\ partial X_ {2}}} {\ frac {\ partial u_ {3}} {\ partial X_ {3}}} \ right)} \ end {matrix}} \ right .}

Tensor de tulpină Biot

Tensorul de deformare Biot este un tensor simetric definit de

\varepsilon _{1}={\mathbf {U} }-{\mathbf {1} }

{\ displaystyle \ varepsilon _ {1} = {\ mathbf {U}} - {\ mathbf {1}}}

{\ displaystyle \ varepsilon _ {1} = {\ mathbf {U}} - {\ mathbf {1}}}

Determinarea tensorului Biot este mai puțin ușoară decât tensorul verde, deoarece necesită determinarea tensorului de deformare corect și acest lucru, în termeni de deformare sau gradient de deplasare, trece printr-o operațiune mai complexă a rădăcinii pătrate fiind

{\mathbf {U} }^{2}={\mathbf {F} }^{t}\,{\mathbf {F} }

{\ displaystyle {\ mathbf {U}} ^ {2} = {\ mathbf {F}} ^ {t} \, {\ mathbf {F}}}

{\ displaystyle {\ mathbf {U}} ^ {2} = {\ mathbf {F}} ^ {t} \, {\ mathbf {F}}}

Următoarea relație (neliniară) există între tensorii Green și Biot

\varepsilon _{1}={\sqrt {\varepsilon _{2}+{\mathbf {1} }}}-{\mathbf {1} }

{\ displaystyle \ varepsilon _ {1} = {\ sqrt {\ varepsilon _ {2} + {\ mathbf {1}}}} - {\ mathbf {1}}}

{\ displaystyle \ varepsilon _ {1} = {\ sqrt {\ varepsilon _ {2} + {\ mathbf {1}}}} - {\ mathbf {1}}}

Această relație poate fi astfel raportată într-o serie a seriei Taylor

\varepsilon _{1}=\varepsilon _{1}-{\tfrac {1}{2}}\,{\varepsilon _{1}}^{2}+{\tfrac {1}{2}}\,{\varepsilon _{2}}^{3}-{\tfrac {5}{8}}\,{\varepsilon _{2}}^{4}+\ldots

{\ displaystyle \ varepsilon _ {1} = \ varepsilon _ {1} - {\ tfrac {1} {2}} \, {\ varepsilon _ {1}} ^ {2} + {\ tfrac {1} {2 }} \, {\ varepsilon _ {2}} ^ {3} - {\ tfrac {5} {8}} \, {\ varepsilon _ {2}} ^ {4} + \ ldots}

{\ displaystyle \ varepsilon _ {1} = \ varepsilon _ {1} - {\ tfrac {1} {2}} \, {\ varepsilon _ {1}} ^ {2} + {\ tfrac {1} {2 }} \, {\ varepsilon _ {2}} ^ {3} - {\ tfrac {5} {8}} \, {\ varepsilon _ {2}} ^ {4} + \ ldots}

Pentru deformări foarte mici $\left(\|{\varepsilon _{2}}\|\ll 1\right)$ ${\ displaystyle \ left (\ | {\ varepsilon _ {2}} \ | \ ll 1 \ right)}$ ${\ displaystyle \ left (\ | {\ varepsilon _ {2}} \ | \ ll 1 \ right)}$ cele două măsurători tensoriale coincid practic

\varepsilon _{1}\approx \varepsilon _{2}

{\ displaystyle \ varepsilon _ {1} \ approx \ varepsilon _ {2}}

{\ displaystyle \ varepsilon _ {1} \ approx \ varepsilon _ {2}}

Teoria micilor deplasări

Deplasări rigide infinitesimale

Un corolar al ipotezei micilor deplasări și deformări este reprezentarea câmpului rigid de deplasare. În teoria liniară, deplasările punctelor $\mathbf {X+dX}$ ${\ displaystyle \ mathbf {X + dX}}$ ${\ displaystyle \ mathbf {X + dX}}$ a unui cartier al punctului $\mathbf {X}$ ${\ displaystyle \ mathbf {X}}$ ${\ mathbf {X}}$ sunt aproximate prin

{\mathbf {u} }(\mathbf {X+dX} )\approx {\mathbf {u} }({\mathbf {X} })+{\boldsymbol {\nabla }}{\mathbf {u} }({\mathbf {X} })\,\mathbf {dX}

{\ displaystyle {\ mathbf {u}} (\ mathbf {X + dX}) \ approx {\ mathbf {u}} ({\ mathbf {X}}) + {\ boldsymbol {\ nabla}} {\ mathbf { u}} ({\ mathbf {X}}) \, \ mathbf {dX}}

{\ displaystyle {\ mathbf {u}} (\ mathbf {X + dX}) \ approx {\ mathbf {u}} ({\ mathbf {X}}) + {\ boldsymbol {\ nabla}} {\ mathbf { u}} ({\ mathbf {X}}) \, \ mathbf {dX}}

Pe de altă parte, tensorul gradientului de deplasare ${\boldsymbol {\nabla }}{\mathbf {u} }$ ${\ displaystyle {\ boldsymbol {\ nabla}} {\ mathbf {u}}}$ ${\ displaystyle {\ boldsymbol {\ nabla}} {\ mathbf {u}}}$ poate fi descompus într-o parte simetrică și una antisimetrică

{\boldsymbol {\nabla }}{\mathbf {u} }={\boldsymbol {\varepsilon }}+{\boldsymbol {\Omega }}\;\;,\;\;\left\{{\begin{array}{l}{\boldsymbol {\varepsilon }}={\frac {1}{2}}\left({\boldsymbol {\nabla }}{\mathbf {u} }+{\boldsymbol {\nabla }}{\mathbf {u} }^{t}\right)\\{\boldsymbol {\Omega }}={\frac {1}{2}}\left({\boldsymbol {\nabla }}{\mathbf {u} }-{\boldsymbol {\nabla }}{\mathbf {u} }^{t}\right)\end{array}}\right.

{\ displaystyle {\ boldsymbol {\ nabla}} {\ mathbf {u}} = {\ boldsymbol {\ varepsilon}} + {\ boldsymbol {\ Omega}} \; \ ;, \; \; \ left \ {{ \ begin {array} {l} {\ boldsymbol {\ varepsilon}} = {\ frac {1} {2}} \ left ({\ boldsymbol {\ nabla}} {\ mathbf {u}} + {\ boldsymbol { \ nabla}} {\ mathbf {u}} ^ {t} \ right) \\ {\ boldsymbol {\ Omega}} = {\ frac {1} {2}} \ left ({\ boldsymbol {\ nabla}} {\ mathbf {u}} - {\ boldsymbol {\ nabla}} {\ mathbf {u}} ^ {t} \ right) \ end {array}} \ right.}

{\ displaystyle {\ boldsymbol {\ nabla}} {\ mathbf {u}} = {\ boldsymbol {\ varepsilon}} + {\ boldsymbol {\ Omega}} \; \ ;, \; \; \ left \ {{ \ begin {array} {l} {\ boldsymbol {\ varepsilon}} = {\ frac {1} {2}} \ left ({\ boldsymbol {\ nabla}} {\ mathbf {u}} + {\ boldsymbol { \ nabla}} {\ mathbf {u}} ^ {t} \ right) \\ {\ boldsymbol {\ Omega}} = {\ frac {1} {2}} \ left ({\ boldsymbol {\ nabla}} {\ mathbf {u}} - {\ boldsymbol {\ nabla}} {\ mathbf {u}} ^ {t} \ right) \ end {array}} \ right.}

Gli spostamenti dell'intorno del punto $\mathbf {X}$ $\mathbf {X}$ ${\mathbf {X}}$ sono pertanto definiti dalla somma

{\mathbf {u} }(\mathbf {X+dX} )\approx {\mathbf {u} }({\mathbf {X} })+{\boldsymbol {\Omega }}({\mathbf {X} })\,\mathbf {dX} +{\boldsymbol {\varepsilon }}({\mathbf {X} })\,\mathbf {dX}

{\mathbf {u} }(\mathbf {X+dX} )\approx {\mathbf {u} }({\mathbf {X} })+{\boldsymbol {\Omega }}({\mathbf {X} })\,\mathbf {dX} +{\boldsymbol {\varepsilon }}({\mathbf {X} })\,\mathbf {dX}

{\mathbf {u} }(\mathbf {X+dX} )\approx {\mathbf {u} }({\mathbf {X} })+{\boldsymbol {\Omega }}({\mathbf {X} })\,\mathbf {dX} +{\boldsymbol {\varepsilon }}({\mathbf {X} })\,\mathbf {dX}

di cui, essendo l'aliquota legata al tensore ${\boldsymbol {\varepsilon }}$ ${\boldsymbol {\varepsilon }}$ ${\boldsymbol {\varepsilon }}$ rappresentativa della deformazione pura dell'intorno, ne consegue che la rimanente aliquota

{\mathbf {u} }({\mathbf {X} })+{\boldsymbol {\Omega }}({\mathbf {X} })\,\mathbf {dX}

{\mathbf {u} }({\mathbf {X} })+{\boldsymbol {\Omega }}({\mathbf {X} })\,\mathbf {dX}

{\mathbf {u} }({\mathbf {X} })+{\boldsymbol {\Omega }}({\mathbf {X} })\,\mathbf {dX}

rende conto degli spostamenti rigidi (infinitesimi) dell'intorno. In particolare il termine ${\mathbf {u} }({\mathbf {X} })$ ${\mathbf {u} }({\mathbf {X} })$ ${\mathbf {u} }({\mathbf {X} })$ misura la traslazione rigida, mentre il termine ${\boldsymbol {\Omega }}({\mathbf {X} })\,\mathbf {dX}$ ${\boldsymbol {\Omega }}({\mathbf {X} })\,\mathbf {dX}$ ${\boldsymbol {\Omega }}({\mathbf {X} })\,\mathbf {dX}$ definisce la rotazione rigida. Ricorrendo al concetto di vettore assiale associato al tensore antisimmetrico della rotazione ${\boldsymbol {\Omega }}$ ${\boldsymbol {\Omega }}$ ${\boldsymbol {\Omega }}$ (il vettore velocità angolare ${\mathbf {\omega } }$ ${\mathbf {\omega } }$ ${\mathbf {\omega } }$ ), lo spostamento rigido dell'intorno può essere rappresentato dalla

{\mathbf {u} }({\mathbf {X} })+{\mathbf {\omega } }({\mathbf {X} })\,\times \,\mathbf {dX}

{\mathbf {u} }({\mathbf {X} })+{\mathbf {\omega } }({\mathbf {X} })\,\times \,\mathbf {dX}

{\mathbf {u} }({\mathbf {X} })+{\mathbf {\omega } }({\mathbf {X} })\,\times \,\mathbf {dX}

Le relazioni cinematiche (non lineari) precedentemente ottenute hanno validità generale, per qualsiasi entità degli spostamenti e delle deformazioni. Presenta un interesse fondamentale dal punto di vista applicativo l'esame dello stato di deformazione nel caso in cui risultino piccoli (in un senso che occorre rendere preciso) tanto il campo di spostamenti ${\mathbf {u} }({\mathbf {X} })$ ${\mathbf {u} }({\mathbf {X} })$ ${\mathbf {u} }({\mathbf {X} })$ che il suo gradiente ${\boldsymbol {\nabla }}{\mathbf {u} }({\mathbf {X} })$ ${\boldsymbol {\nabla }}{\mathbf {u} }({\mathbf {X} })$ ${\boldsymbol {\nabla }}{\mathbf {u} }({\mathbf {X} })$ . Si parla in tal caso di teoria lineare della deformazione (o anche, meno correttamente, di teoria delle deformazioni infinitesime ). Le relative relazioni cinematiche possono essere ottenute direttamente in maniera autonoma oppure derivate, come nel seguito, da quelle della teoria non lineare, mediante un processo al limite e trascurando i contributi infinitesimi di ordine superiore.

{\frac {\|{\mathbf {u} }({\mathbf {X} })\|}{L}}\ll 1\;\;\;,\;\;\;\|{\boldsymbol {\nabla }}{\mathbf {u} }({\mathbf {X} })\|\ll 1

{\frac {\|{\mathbf {u} }({\mathbf {X} })\|}{L}}\ll 1\;\;\;,\;\;\;\|{\boldsymbol {\nabla }}{\mathbf {u} }({\mathbf {X} })\|\ll 1

{\frac {\|{\mathbf {u} }({\mathbf {X} })\|}{L}}\ll 1\;\;\;,\;\;\;\|{\boldsymbol {\nabla }}{\mathbf {u} }({\mathbf {X} })\|\ll 1

Si dimostra che, nella teoria dei piccoli spostamenti, è lecito confondere, ai fini della scrittura delle relazioni di equilibrio , la configurazione iniziale indeformata con la configurazione corrente deformata.

Tensore della deformazione infinitesima

Nell'ipotesi di piccoli spostamenti e deformazioni, assume un ruolo fondamentale nella descrizione della deformazione il tensore della deformazione infinitesima ${\boldsymbol {\varepsilon }}$ ${\boldsymbol {\varepsilon }}$ $\boldsymbol{\varepsilon}$ , definito come la parte simmetrica del gradiente dello spostamento

{\boldsymbol {\varepsilon }}={\frac {1}{2}}\left({\boldsymbol {\nabla }}{\mathbf {u} }+{\boldsymbol {\nabla }}{\mathbf {u} }^{t}\right)

{\boldsymbol {\varepsilon }}={\frac {1}{2}}\left({\boldsymbol {\nabla }}{\mathbf {u} }+{\boldsymbol {\nabla }}{\mathbf {u} }^{t}\right)

{\boldsymbol {\varepsilon }}={\frac {1}{2}}\left({\boldsymbol {\nabla }}{\mathbf {u} }+{\boldsymbol {\nabla }}{\mathbf {u} }^{t}\right)

Valgono infatti le approssimazioni lineari per il tensore di Green

{\mathbf {E} }\approx {\boldsymbol {\varepsilon }}

{\mathbf {E} }\approx {\boldsymbol {\varepsilon }}

{\mathbf {E} }\approx {\boldsymbol {\varepsilon }}

e per le altre misure di deformazione pura:

dilatazione lineare

\varepsilon ({\mathbf {N} })={\frac {{\mbox{d}}{l}-{\mbox{d}}{L}}{{\mbox{d}}{L}}}\approx {\boldsymbol {\varepsilon }}\,{\mathbf {N} }\,\cdot \,{\mathbf {N} }

\varepsilon ({\mathbf {N} })={\frac {{\mbox{d}}{l}-{\mbox{d}}{L}}{{\mbox{d}}{L}}}\approx {\boldsymbol {\varepsilon }}\,{\mathbf {N} }\,\cdot \,{\mathbf {N} }

\varepsilon ({\mathbf {N} })={\frac {{\mbox{d}}{l}-{\mbox{d}}{L}}{{\mbox{d}}{L}}}\approx {\boldsymbol {\varepsilon }}\,{\mathbf {N} }\,\cdot \,{\mathbf {N} }

scorrimento angolare

\gamma ({\mathbf {N} },{\mathbf {M} })\approx 2\,{\boldsymbol {\varepsilon }}\,{\mathbf {N} }\,\cdot \,{\mathbf {M} }

\gamma ({\mathbf {N} },{\mathbf {M} })\approx 2\,{\boldsymbol {\varepsilon }}\,{\mathbf {N} }\,\cdot \,{\mathbf {M} }

\gamma ({\mathbf {N} },{\mathbf {M} })\approx 2\,{\boldsymbol {\varepsilon }}\,{\mathbf {N} }\,\cdot \,{\mathbf {M} }

dilatazione volumetrica

{\frac {{\mbox{d}}v-{\mbox{d}}V}{{\mbox{d}}V}}\approx {\mbox{tr}}({\boldsymbol {\varepsilon }})

{\frac {{\mbox{d}}v-{\mbox{d}}V}{{\mbox{d}}V}}\approx {\mbox{tr}}({\boldsymbol {\varepsilon }})

{\frac {{\mbox{d}}v-{\mbox{d}}V}{{\mbox{d}}V}}\approx {\mbox{tr}}({\boldsymbol {\varepsilon }})

(la traccia del tensore

{\boldsymbol {\varepsilon }}

{\boldsymbol {\varepsilon }}

{\boldsymbol {\varepsilon }}

)

Il tensore della deformazione infinitesima in componenti scalari e loro significato fisico

{\begin{bmatrix}{\boldsymbol {\varepsilon }}\end{bmatrix}}={\begin{bmatrix}\varepsilon _{11}&\varepsilon _{12}&\varepsilon _{13}\\\varepsilon _{21}&\varepsilon _{22}&\varepsilon _{23}\\\varepsilon _{31}&\varepsilon _{32}&\varepsilon _{33}\\\end{bmatrix}},\;\left\{{\begin{matrix}\varepsilon _{11}={\boldsymbol {\varepsilon }}\,{\mathbf {e} }_{1}\cdot {\mathbf {e} }_{1}=\varepsilon ({\mathbf {e} }_{1})=\scriptstyle {\frac {\partial u_{1}}{\partial X_{1}}}\\\varepsilon _{22}={\boldsymbol {\varepsilon }}\,{\mathbf {e} }_{2}\cdot {\mathbf {e} }_{2}=\varepsilon ({\mathbf {e} }_{2})=\scriptstyle {\frac {\partial u_{2}}{\partial X_{2}}}\\\varepsilon _{33}={\boldsymbol {\varepsilon }}\,{\mathbf {e} }_{3}\cdot {\mathbf {e} }_{3}=\varepsilon ({\mathbf {e} }_{3})=\scriptstyle {\frac {\partial u_{3}}{\partial X_{3}}}\end{matrix}}\right.,\;\left\{{\begin{matrix}\varepsilon _{12}=\varepsilon _{21}={\boldsymbol {\varepsilon }}\,{\mathbf {e} }_{1}\cdot {\mathbf {e} }_{2}={\tfrac {1}{2}}\,\gamma ({\mathbf {e} }_{1},{\mathbf {e} }_{2})=\scriptstyle {{\frac {1}{2}}\left({\frac {\partial u_{1}}{\partial X_{2}}}+{\frac {\partial u_{2}}{\partial X_{1}}}\right)}\\\varepsilon _{13}=\varepsilon _{31}={\boldsymbol {\varepsilon }}\,{\mathbf {e} }_{1}\cdot {\mathbf {e} }_{3}={\tfrac {1}{2}}\,\gamma ({\mathbf {e} }_{1},{\mathbf {e} }_{3})=\scriptstyle {{\frac {1}{2}}\left({\frac {\partial u_{1}}{\partial X_{3}}}+{\frac {\partial u_{3}}{\partial X_{1}}}\right)}\\\varepsilon _{23}=\varepsilon _{32}={\boldsymbol {\varepsilon }}\,{\mathbf {e} }_{2}\cdot {\mathbf {e} }_{3}={\tfrac {1}{2}}\,\gamma ({\mathbf {e} }_{2},{\mathbf {e} }_{3})=\scriptstyle {{\frac {1}{2}}\left({\frac {\partial u_{2}}{\partial X_{3}}}+{\frac {\partial u_{3}}{\partial X_{2}}}\right)}\end{matrix}}\right.

{\begin{bmatrix}{\boldsymbol {\varepsilon }}\end{bmatrix}}={\begin{bmatrix}\varepsilon _{11}&\varepsilon _{12}&\varepsilon _{13}\\\varepsilon _{21}&\varepsilon _{22}&\varepsilon _{23}\\\varepsilon _{31}&\varepsilon _{32}&\varepsilon _{33}\\\end{bmatrix}},\;\left\{{\begin{matrix}\varepsilon _{11}={\boldsymbol {\varepsilon }}\,{\mathbf {e} }_{1}\cdot {\mathbf {e} }_{1}=\varepsilon ({\mathbf {e} }_{1})=\scriptstyle {\frac {\partial u_{1}}{\partial X_{1}}}\\\varepsilon _{22}={\boldsymbol {\varepsilon }}\,{\mathbf {e} }_{2}\cdot {\mathbf {e} }_{2}=\varepsilon ({\mathbf {e} }_{2})=\scriptstyle {\frac {\partial u_{2}}{\partial X_{2}}}\\\varepsilon _{33}={\boldsymbol {\varepsilon }}\,{\mathbf {e} }_{3}\cdot {\mathbf {e} }_{3}=\varepsilon ({\mathbf {e} }_{3})=\scriptstyle {\frac {\partial u_{3}}{\partial X_{3}}}\end{matrix}}\right.,\;\left\{{\begin{matrix}\varepsilon _{12}=\varepsilon _{21}={\boldsymbol {\varepsilon }}\,{\mathbf {e} }_{1}\cdot {\mathbf {e} }_{2}={\tfrac {1}{2}}\,\gamma ({\mathbf {e} }_{1},{\mathbf {e} }_{2})=\scriptstyle {{\frac {1}{2}}\left({\frac {\partial u_{1}}{\partial X_{2}}}+{\frac {\partial u_{2}}{\partial X_{1}}}\right)}\\\varepsilon _{13}=\varepsilon _{31}={\boldsymbol {\varepsilon }}\,{\mathbf {e} }_{1}\cdot {\mathbf {e} }_{3}={\tfrac {1}{2}}\,\gamma ({\mathbf {e} }_{1},{\mathbf {e} }_{3})=\scriptstyle {{\frac {1}{2}}\left({\frac {\partial u_{1}}{\partial X_{3}}}+{\frac {\partial u_{3}}{\partial X_{1}}}\right)}\\\varepsilon _{23}=\varepsilon _{32}={\boldsymbol {\varepsilon }}\,{\mathbf {e} }_{2}\cdot {\mathbf {e} }_{3}={\tfrac {1}{2}}\,\gamma ({\mathbf {e} }_{2},{\mathbf {e} }_{3})=\scriptstyle {{\frac {1}{2}}\left({\frac {\partial u_{2}}{\partial X_{3}}}+{\frac {\partial u_{3}}{\partial X_{2}}}\right)}\end{matrix}}\right.

{\begin{bmatrix}{\boldsymbol {\varepsilon }}\end{bmatrix}}={\begin{bmatrix}\varepsilon _{11}&\varepsilon _{12}&\varepsilon _{13}\\\varepsilon _{21}&\varepsilon _{22}&\varepsilon _{23}\\\varepsilon _{31}&\varepsilon _{32}&\varepsilon _{33}\\\end{bmatrix}},\;\left\{{\begin{matrix}\varepsilon _{11}={\boldsymbol {\varepsilon }}\,{\mathbf {e} }_{1}\cdot {\mathbf {e} }_{1}=\varepsilon ({\mathbf {e} }_{1})=\scriptstyle {\frac {\partial u_{1}}{\partial X_{1}}}\\\varepsilon _{22}={\boldsymbol {\varepsilon }}\,{\mathbf {e} }_{2}\cdot {\mathbf {e} }_{2}=\varepsilon ({\mathbf {e} }_{2})=\scriptstyle {\frac {\partial u_{2}}{\partial X_{2}}}\\\varepsilon _{33}={\boldsymbol {\varepsilon }}\,{\mathbf {e} }_{3}\cdot {\mathbf {e} }_{3}=\varepsilon ({\mathbf {e} }_{3})=\scriptstyle {\frac {\partial u_{3}}{\partial X_{3}}}\end{matrix}}\right.,\;\left\{{\begin{matrix}\varepsilon _{12}=\varepsilon _{21}={\boldsymbol {\varepsilon }}\,{\mathbf {e} }_{1}\cdot {\mathbf {e} }_{2}={\tfrac {1}{2}}\,\gamma ({\mathbf {e} }_{1},{\mathbf {e} }_{2})=\scriptstyle {{\frac {1}{2}}\left({\frac {\partial u_{1}}{\partial X_{2}}}+{\frac {\partial u_{2}}{\partial X_{1}}}\right)}\\\varepsilon _{13}=\varepsilon _{31}={\boldsymbol {\varepsilon }}\,{\mathbf {e} }_{1}\cdot {\mathbf {e} }_{3}={\tfrac {1}{2}}\,\gamma ({\mathbf {e} }_{1},{\mathbf {e} }_{3})=\scriptstyle {{\frac {1}{2}}\left({\frac {\partial u_{1}}{\partial X_{3}}}+{\frac {\partial u_{3}}{\partial X_{1}}}\right)}\\\varepsilon _{23}=\varepsilon _{32}={\boldsymbol {\varepsilon }}\,{\mathbf {e} }_{2}\cdot {\mathbf {e} }_{3}={\tfrac {1}{2}}\,\gamma ({\mathbf {e} }_{2},{\mathbf {e} }_{3})=\scriptstyle {{\frac {1}{2}}\left({\frac {\partial u_{2}}{\partial X_{3}}}+{\frac {\partial u_{3}}{\partial X_{2}}}\right)}\end{matrix}}\right.

Le componenti $(\varepsilon _{11},\varepsilon _{22},\varepsilon _{33})$ $(\varepsilon _{11},\varepsilon _{22},\varepsilon _{33})$ $(\varepsilon _{11},\varepsilon _{22},\varepsilon _{33})$ misurano le variazioni percentuali di lunghezza rispettivamente nelle direzioni $\{{\mathbf {e} }_{1},{\mathbf {e} }_{2},{\mathbf {e} }_{3}\}$ $\{{\mathbf {e} }_{1},{\mathbf {e} }_{2},{\mathbf {e} }_{3}\}$ $\{{\mathbf {e} }_{1},{\mathbf {e} }_{2},{\mathbf {e} }_{3}\}$ ;
le componenti $(\varepsilon _{12},\varepsilon _{13},\varepsilon _{23})$ $(\varepsilon _{12},\varepsilon _{13},\varepsilon _{23})$ $(\varepsilon _{12},\varepsilon _{13},\varepsilon _{23})$ misurano metà degli scorrimenti angolari associati rispettivamente alle direzioni $\{{\mathbf {e} }_{1},{\mathbf {e} }_{2}\}$ $\{{\mathbf {e} }_{1},{\mathbf {e} }_{2}\}$ $\{{\mathbf {e} }_{1},{\mathbf {e} }_{2}\}$ , $\{{\mathbf {e} }_{1},{\mathbf {e} }_{3}\}$ $\{{\mathbf {e} }_{1},{\mathbf {e} }_{3}\}$ $\{{\mathbf {e} }_{1},{\mathbf {e} }_{3}\}$ ed $\{{\mathbf {e} }_{2},{\mathbf {e} }_{3}\}$ $\{{\mathbf {e} }_{2},{\mathbf {e} }_{3}\}$ $\{{\mathbf {e} }_{2},{\mathbf {e} }_{3}\}$

Parte sferica e deviatorica del tensore della deformazione

Come ogni tensore, il tensore della deformazione ${\boldsymbol {\varepsilon }}$ ${\boldsymbol {\varepsilon }}$ $\boldsymbol{\varepsilon}$ può essere decomposto in una parte sferica e una parte deviatorica

{\boldsymbol {\varepsilon }}=\langle \varepsilon \rangle \,{\mathbf {1} }+{\boldsymbol {\Delta \varepsilon }}\;\;,\;\;[{\boldsymbol {\varepsilon }}]\equiv \left[{\begin{matrix}\langle \varepsilon \rangle &0&0\\0&\langle \varepsilon \rangle &0\\0&0&\langle \varepsilon \rangle \\\end{matrix}}\right]+\left[{\begin{matrix}\varepsilon _{11}-\langle \varepsilon \rangle &\varepsilon _{12}&\varepsilon _{13}\\\varepsilon _{21}&\varepsilon _{22}-\langle \varepsilon \rangle &\varepsilon _{23}\\\varepsilon _{31}&\varepsilon _{32}&\varepsilon _{33}-\langle \varepsilon \rangle \\\end{matrix}}\right]

{\boldsymbol {\varepsilon }}=\langle \varepsilon \rangle \,{\mathbf {1} }+{\boldsymbol {\Delta \varepsilon }}\;\;,\;\;[{\boldsymbol {\varepsilon }}]\equiv \left[{\begin{matrix}\langle \varepsilon \rangle &0&0\\0&\langle \varepsilon \rangle &0\\0&0&\langle \varepsilon \rangle \\\end{matrix}}\right]+\left[{\begin{matrix}\varepsilon _{11}-\langle \varepsilon \rangle &\varepsilon _{12}&\varepsilon _{13}\\\varepsilon _{21}&\varepsilon _{22}-\langle \varepsilon \rangle &\varepsilon _{23}\\\varepsilon _{31}&\varepsilon _{32}&\varepsilon _{33}-\langle \varepsilon \rangle \\\end{matrix}}\right]

{\boldsymbol {\varepsilon }}=\langle \varepsilon \rangle \,{\mathbf {1} }+{\boldsymbol {\Delta \varepsilon }}\;\;,\;\;[{\boldsymbol {\varepsilon }}]\equiv \left[{\begin{matrix}\langle \varepsilon \rangle &0&0\\0&\langle \varepsilon \rangle &0\\0&0&\langle \varepsilon \rangle \\\end{matrix}}\right]+\left[{\begin{matrix}\varepsilon _{11}-\langle \varepsilon \rangle &\varepsilon _{12}&\varepsilon _{13}\\\varepsilon _{21}&\varepsilon _{22}-\langle \varepsilon \rangle &\varepsilon _{23}\\\varepsilon _{31}&\varepsilon _{32}&\varepsilon _{33}-\langle \varepsilon \rangle \\\end{matrix}}\right]

\

dove, indicando con ${\mathbf {1} }$ ${\mathbf {1} }$ ${\mathbf {1} }$ il tensore identità, $\langle \varepsilon \rangle$ $\langle \varepsilon \rangle$ $\langle \varepsilon \rangle$ è la deformazione di allungamento medio

\langle \varepsilon \rangle ={\frac {1}{3}}{\mbox{tr}}{\bigl (}{\boldsymbol {\varepsilon }}{\bigr )}={\frac {1}{3}}(\varepsilon _{11}+\varepsilon _{22}+\varepsilon _{33})

\langle \varepsilon \rangle ={\frac {1}{3}}{\mbox{tr}}{\bigl (}{\boldsymbol {\varepsilon }}{\bigr )}={\frac {1}{3}}(\varepsilon _{11}+\varepsilon _{22}+\varepsilon _{33})

\langle \varepsilon \rangle ={\frac {1}{3}}{\mbox{tr}}{\bigl (}{\boldsymbol {\varepsilon }}{\bigr )}={\frac {1}{3}}(\varepsilon _{11}+\varepsilon _{22}+\varepsilon _{33})

La parte sferica $\langle \varepsilon \rangle \,{\mathbf {1} }$ $\langle \varepsilon \rangle \,{\mathbf {1} }$ $\langle \varepsilon \rangle \,{\mathbf {1} }$ del tensore della deformazione è rappresentativa di uno stato di deformazione con scorrimenti angolari nulli e deformazioni estensionali uniformi in tutte le direzioni, che non producono variazioni di forma ma solo variazioni di volume.

La parte deviatorica della deformazione

\Delta {\boldsymbol {\varepsilon }}={\boldsymbol {\varepsilon }}-\langle \varepsilon \rangle \,{\mathbf {1} }

\Delta {\boldsymbol {\varepsilon }}={\boldsymbol {\varepsilon }}-\langle \varepsilon \rangle \,{\mathbf {1} }

\Delta {\boldsymbol {\varepsilon }}={\boldsymbol {\varepsilon }}-\langle \varepsilon \rangle \,{\mathbf {1} }

detta deformazione distorcente , è associata invece ad uno stato deformativo che non provoca variazione di volume, ma solo variazione di forma.

Equazioni esplicite di congruenza di S. Venant

Le relazioni

{\mathbf {E} }={\frac {1}{2}}({\boldsymbol {\nabla }}{\mathbf {u} }+{\boldsymbol {\nabla }}{\mathbf {u} }^{t}+{\boldsymbol {\nabla }}{\mathbf {u} }^{t}{\boldsymbol {\nabla }}{\mathbf {u} })\;,\;\;{\boldsymbol {\varepsilon }}={\frac {1}{2}}\left({\boldsymbol {\nabla }}{\mathbf {u} }+{\boldsymbol {\nabla }}{\mathbf {u} }^{t}\right)

{\mathbf {E} }={\frac {1}{2}}({\boldsymbol {\nabla }}{\mathbf {u} }+{\boldsymbol {\nabla }}{\mathbf {u} }^{t}+{\boldsymbol {\nabla }}{\mathbf {u} }^{t}{\boldsymbol {\nabla }}{\mathbf {u} })\;,\;\;{\boldsymbol {\varepsilon }}={\frac {1}{2}}\left({\boldsymbol {\nabla }}{\mathbf {u} }+{\boldsymbol {\nabla }}{\mathbf {u} }^{t}\right)

{\mathbf {E} }={\frac {1}{2}}({\boldsymbol {\nabla }}{\mathbf {u} }+{\boldsymbol {\nabla }}{\mathbf {u} }^{t}+{\boldsymbol {\nabla }}{\mathbf {u} }^{t}{\boldsymbol {\nabla }}{\mathbf {u} })\;,\;\;{\boldsymbol {\varepsilon }}={\frac {1}{2}}\left({\boldsymbol {\nabla }}{\mathbf {u} }+{\boldsymbol {\nabla }}{\mathbf {u} }^{t}\right)

rispettivamente per la teoria non lineare e lineare, risultano di congruenza cinematica tra quantità $({\mathbf {E} },{\boldsymbol {\varepsilon }})$ $({\mathbf {E} },{\boldsymbol {\varepsilon }})$ $({\mathbf {E} },{\boldsymbol {\varepsilon }})$ che descrivono localmente la geometria della deformazione pura, e quantità ${\mathbf {u} }$ ${\mathbf {u} }$ ${\mathbf u}$ (gli spostamenti) che rappresentano i cambiamenti di configurazione dell'intero corpo. Assegnato il campo di spostamenti ${\mathbf {u} }({\mathbf {X} })$ ${\mathbf {u} }({\mathbf {X} })$ ${\mathbf {u} }({\mathbf {X} })$ , tali relazioni determinano univocamente i campi di deformazione, sono cioè di definizione per i tensori $({\mathbf {E} }({\mathbf {X} }),{\boldsymbol {\varepsilon }}({\mathbf {X} }))$ $({\mathbf {E} }({\mathbf {X} }),{\boldsymbol {\varepsilon }}({\mathbf {X} }))$ $({\mathbf {E} }({\mathbf {X} }),{\boldsymbol {\varepsilon }}({\mathbf {X} }))$ : esse sono dette relazioni implicite di congruenza . Il problema può tuttavia essere posto in una forma inversa: assegnati generici campi tensoriali $({\mathbf {E} }({\mathbf {X} }),{\boldsymbol {\varepsilon }}({\mathbf {X} }))$ $({\mathbf {E} }({\mathbf {X} }),{\boldsymbol {\varepsilon }}({\mathbf {X} }))$ $({\mathbf {E} }({\mathbf {X} }),{\boldsymbol {\varepsilon }}({\mathbf {X} }))$ , le relazioni date sono sufficienti a definire un campo di spostamenti? O meglio, esiste un campo vettoriale ${\mathbf {u} }({\mathbf {X} })$ ${\mathbf {u} }({\mathbf {X} })$ ${\mathbf {u} }({\mathbf {X} })$ compatibile con i campi assegnati $({\mathbf {E} }({\mathbf {X} }),{\boldsymbol {\varepsilon }}({\mathbf {X} }))$ $({\mathbf {E} }({\mathbf {X} }),{\boldsymbol {\varepsilon }}({\mathbf {X} }))$ $({\mathbf {E} }({\mathbf {X} }),{\boldsymbol {\varepsilon }}({\mathbf {X} }))$ sulla base del soddisfacimento delle precedenti relazioni implicite di congruenza? In generale la risposta a tale problema è negativa.

Le precedenti relazioni cinematiche risultano pertanto anche di vincolo per le componenti dei descrittori della deformazione: queste non possono essere assegnate arbitrariamente, essendo proprio legate dalla condizione di integrabilità delle relazioni implicite di congruenza in termini del campo di spostamenti. Queste sono integrabili solo se gli assegnati campi tensoriali di deformazione soddisfano ulteriori relazioni, dette condizioni esplicite di congruenza . Nel caso lineare e per un dominio semplicemente connesso della configurazione di riferimento, tali relazioni sono dovute a S. Venant ed espresse in termini tensoriali dalla

\nabla \times \nabla \times {\boldsymbol {\varepsilon }}=\mathbf {0}

\nabla \times \nabla \times {\boldsymbol {\varepsilon }}=\mathbf {0}

\nabla \times \nabla \times {\boldsymbol {\varepsilon }}=\mathbf {0}

In termini scalari, le equazioni di S. Venant

\varepsilon _{ij,km}+\varepsilon _{km,ij}-\varepsilon _{ik,jm}-\varepsilon _{jm,ik}=0

\varepsilon _{ij,km}+\varepsilon _{km,ij}-\varepsilon _{ik,jm}-\varepsilon _{jm,ik}=0

\varepsilon_{ij,km}+\varepsilon_{km,ij}-\varepsilon_{ik,jm}-\varepsilon_{jm,ik}=0

sono rappresentate da 81 relazioni scalari nelle derivate delle componenti del campo tensoriale ${\boldsymbol {\varepsilon }}({\mathbf {X} })$ ${\boldsymbol {\varepsilon }}({\mathbf {X} })$ ${\boldsymbol {\varepsilon }}({\mathbf {X} })$ , di cui solo le 6, qui di seguito riportate per esteso, sono indipendenti

{\begin{aligned}{\varepsilon }_{11},_{22}+{\varepsilon }_{22},_{11}&=2{\varepsilon }_{12},_{12}\\{\varepsilon }_{11},_{33}+{\varepsilon }_{33},_{11}&=2{\varepsilon }_{13},_{13}\\{\varepsilon }_{22},_{33}+{\varepsilon }_{33},_{22}&=2{\varepsilon }_{23},_{23}\\{\varepsilon }_{12},_{33}+{\varepsilon }_{33},_{12}&={\varepsilon }_{13},_{23}+{\varepsilon }_{23},_{13}\\{\varepsilon }_{13},_{22}+{\varepsilon }_{22},_{13}&={\varepsilon }_{12},_{23}+{\varepsilon }_{23},_{12}\\{\varepsilon }_{23},_{11}+{\varepsilon }_{11},_{23}&={\varepsilon }_{12},_{13}+{\varepsilon }_{13},_{12}\\\end{aligned}}

{\begin{aligned}{\varepsilon }_{11},_{22}+{\varepsilon }_{22},_{11}&=2{\varepsilon }_{12},_{12}\\{\varepsilon }_{11},_{33}+{\varepsilon }_{33},_{11}&=2{\varepsilon }_{13},_{13}\\{\varepsilon }_{22},_{33}+{\varepsilon }_{33},_{22}&=2{\varepsilon }_{23},_{23}\\{\varepsilon }_{12},_{33}+{\varepsilon }_{33},_{12}&={\varepsilon }_{13},_{23}+{\varepsilon }_{23},_{13}\\{\varepsilon }_{13},_{22}+{\varepsilon }_{22},_{13}&={\varepsilon }_{12},_{23}+{\varepsilon }_{23},_{12}\\{\varepsilon }_{23},_{11}+{\varepsilon }_{11},_{23}&={\varepsilon }_{12},_{13}+{\varepsilon }_{13},_{12}\\\end{aligned}}

\begin{align} {\varepsilon}_{11},_{22}+{\varepsilon}_{22},_{11}&=2{\varepsilon}_{12},_{12} \\ {\varepsilon}_{11},_{33}+{\varepsilon}_{33},_{11}&=2{\varepsilon}_{13},_{13} \\ {\varepsilon}_{22},_{33}+{\varepsilon}_{33},_{22}&=2{\varepsilon}_{23},_{23} \\ {\varepsilon}_{12},_{33}+{\varepsilon}_{33},_{12}&={\varepsilon}_{13},_{23}+{\varepsilon}_{23},_{13} \\ {\varepsilon}_{13},_{22}+{\varepsilon}_{22},_{13}&={\varepsilon}_{12},_{23}+{\varepsilon}_{23},_{12} \\ {\varepsilon}_{23},_{11}+{\varepsilon}_{11},_{23}&={\varepsilon}_{12},_{13}+{\varepsilon}_{13},_{12} \\ \end{align}

Nel caso che il campo tensoriale ${\boldsymbol {\varepsilon }}({\mathbf {X} })$ ${\boldsymbol {\varepsilon }}({\mathbf {X} })$ ${\boldsymbol {\varepsilon }}({\mathbf {X} })$ sia dato da componenti costanti o lineari delle coordinate $\left(X_{1},X_{2},X_{3}\right)$ $\left(X_{1},X_{2},X_{3}\right)$ $\left(X_{1},X_{2},X_{3}\right)$ , allora risultano banalmente verificate le precedenti condizioni esplicite di congruenza.

Bibliografia

C. Truesdell, A First Course in Rational Continuum Mechanics , Academic Press, New York, 1977. ISBN 0-12-701301-6
ME Gurtin, An Introduction to Continuum Mechanics , Academic Press, New York, 1981. ISBN 0-12-309750-9
MA Biot-Savart, Mechanics of Incremental Deformations , John Wiley & Sons, New York, 1965. ISBN 9780471073109
L. Ascione, A. Grimaldi, Elementi di Meccanica dei Continui , Liguori Editore, Napoli, 1989. ISBN 88-207-1829-4
R. Baldacci, Scienza delle Costruzioni, vol I, Utet, Torino, 1984. ISBN 8802038376
Alfredo Sollazzo, Scienza delle Costruzioni , II, Torino, Utet, 1988, ISBN 88-02-04170-9 .

Voci correlate

Altri progetti

Wikizionario contiene il lemma di dizionario « deformazione »
Wikimedia Commons contiene immagini o altri file su deformazione

Collegamenti esterni

( EN ) free download del libro "MA Biot, Mechanics of Incremental Deformation , Wiley, 1965" ( PDF ), su olemiss.edu .

Controllo di autorità	Thesaurus BNCF 26429 · LCCN ( EN ) sh85036465

Portale Ingegneria

Portale Meccanica

V · D · M Meccanica classica e meccanica del continuo
Grandezze intensive	Densità · Velocità macroscopica · Campo medio · Tensione interna · Temperatura · Deformazione · Densità termica
Grandezze estensive	Massa · Portata · Quantità di moto · Forza esterna · Energia interna · Calore · Dissipazione · Lavoro termodinamico
Bilanci	Conservazione della massa · Bilancio della quantità di moto · Bilancio di energia interna
Approssimazioni	Equazioni di Eulero · Equazioni di Navier-Stokes · Equazioni di Burnett
Leggi	Legge di Pascal · Legge di Newton · Legge di Fourier · Legge di Stokes · Legge di Hooke
Meccanica dei solidi	Solido · Teoria dell'elasticità · Teoria della plasticità · Reologia · Viscoelasticità
Meccanica dei fluidi	Fluido · Fluidostatica · Fluidodinamica · Viscosità · Fluido newtoniano · Fluido non newtoniano