1 - 2 + 3 - 4 + · · ·

Reprezentarea pe plan a primelor mii de termeni ai calculului 1 - 2 + 3 - 4 + ...

În matematică , 1 - 2 + 3 - 4 + ... este seria infinită ai cărei termeni sunt succesiunea unor numere întregi alternante . Folosind notația de însumare , suma primilor $m$ ${\ displaystyle m}$ $m$ termenii seriei pot fi exprimați după cum urmează:

\sum _{n=0}^{m}n(-1)^{n+1}={\frac {1-{(2m+1)}{\cos({\pi }{m})}}{4}}.

{\ displaystyle \ sum _ {n = 0} ^ {m} n (-1) ^ {n + 1} = {\ frac {1 - {(2m + 1)} {\ cos ({\ pi} {m })}} {4}}.}

{\ displaystyle \ sum _ {n = 0} ^ {m} n (-1) ^ {n + 1} = {\ frac {1 - {(2m + 1)} {\ cos ({\ pi} {m })}} {4}}.}

Sumele parțiale ale acestei serii infinite (1, -1, 2, -2, ...), nu tind spre o limită , nici finită, nici infinită. În acest caz putem spune că 1 - 2 + 3 - 4 + ... este o serie nedeterminată (sau neregulată).

La mijlocul secolului al XVIII-lea , Leonhard Euler a enunțat ceea ce el a numit o ecuație paradoxală :

1-2+3-4+\cdots ={\frac {1}{4}}.

{\ displaystyle 1-2 + 3-4 + \ cdots = {\ frac {1} {4}}.}

1-2 + 3-4 + \ cdots = {\ frac {1} {4}}.

O explicație corectă a acestei ecuații a venit abia mult mai târziu. În 1890 , Ernesto Cesaro , Émile Borel și alți matematicieni au definit metodele de extindere a conceptului de sumabilitate în conformitate cu un punct de vedere care a făcut posibilă atribuirea unei limite chiar și seriilor care până acum nu erau de nerezolvat. Aceste noi metode au dat noi interpretări ecuației Euler. Multe dintre aceste metode se referă la sumele parțiale de 1 - 2 + 3 - 4 + ..., cărora le atribuie valoarea de ¹ ⁄ ₄ . Pe suma lui Cesaro , pe de altă parte, termenii succesiunii nu sunt rezumabili; acesta este un exemplu de secvență pentru care sunt necesare metode de sumabilitate ușor mai puternice, cum ar fi cele din suma Abel .

Seria 1 - 2 + 3 - 4 + ... este strâns legată de seria 1 - 1 + 1 - 1 + ..., mai cunoscută sub numele de seria Grandi . Euler a considerat aceste două secvențe ca fiind cazuri particulare din seria 1 ⁿ - 2 ⁿ + 3 ⁿ - 4 ⁿ + ..., pentru valori arbitrare de n . Aceste idei i-au extins studiul asupra problemei de la Basel cercetarea direcționată asupra ecuațiilor funcționale ale funcțiilor care sunt acum cunoscute sub numele de funcția eta a lui Dirichlet și funcția zeta a lui Riemann .

Divergenţă

Termenii secvenței (1, −2, 3, −4, ...) nu tind spre 0 ; prin urmare, neconvergența seriei relative este o simplă consecință a criteriului cel mai elementar, cel care necesită convergența secvenței la zero ca condiție necesară.

Este totuși util, pentru continuare, să constatăm comportamentul acestei serii analizând-o dintr-un punct de vedere mai fundamental. Prin definiție, convergența sau divergența unei serii infinite este determinată de convergența sau divergența succesiunii sale de sume parțiale; sumele parțiale de 1 - 2 + 3 - 4 + ... sunt: ^[1]

1 = 1,
1-2 = −1,
1 - 2 + 3 = 2,
1 - 2 + 3 - 4 = −2,
1 - 2 + 3 - 4 + 5 = 3,
1 - 2 + 3 - 4 + 5 - 6 = −3, ...

În această secvență se observă că seria își asumă toate valorile întregi, altele decât zero (putem include și 0 dacă considerăm că suma este goală ), oferind în plus o demonstrație a enumerabilității setului $\mathbb {Z}$ ${\ displaystyle \ mathbb {Z}}$ $\ mathbb {Z}$ a numerelor întregi. ^[2] În mod clar, nu se stabilizează pe un anumit număr și, prin urmare, 1 - 2 + 3 - 4 + ... este oscilant (în timp ce divergă în valoare absolută ).

Metode euristice pentru sumabilitate

Stabilitate și liniaritate

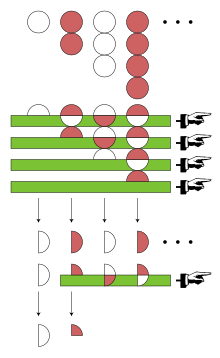
Deoarece termenii 1, −2, 3, −4, 5, −6, ... urmează o schemă simplă, seria 1 - 2 + 3 - 4 + ... poate fi manipulată cu schimbări adecvate ale termenilor din sumă pentru a obține o valoare finită. Este posibil să dai sens unei expresii precum s = 1 - 2 + 3 - 4 + ... pentru unele s întregi: de exemplu, următoarele manipulări o fac valabilă pentru s = ¹ ⁄ ₄ : ^[3]

${\begin{array}{rclllll}4s&=&&(1-2+3-4+\cdots )&+(1-2+3-4+\cdots )&+(1-2+3-4+\cdots )&+(1-2+3-4+\cdots )\\&=&&(1-2+3-4+\cdots )&+1+(-2+3-4+5+\cdots )&+1+(-2+3-4+5+\cdots )&-1+(3-4+5-6+\cdots )\\&=&1+[&(1-2-2+3)&+(-2+3+3-4)&+(3-4-4+5)&+(-4+5+5-6)+\cdots ]\\&=&1+[&0+0+0+0+\cdots ]\\4s&=&1\end{array}}$ ${\ displaystyle {\ begin {array} {rclllll} 4s & = && (1-2 + 3-4 + \ cdots) & + (1-2 + 3-4 + \ cdots) & + (1-2 + 3 - 4+ \ cdots) & + (1-2 + 3-4 + \ cdots) \\ & = && (1-2 + 3-4 + \ cdots) & + 1 + (- 2 + 3-4 + 5 + \ cdots) & + 1 + (- 2 + 3-4 + 5 + \ cdots) & - 1+ (3-4 + 5-6 + \ cdots) \\ & = & 1 + [& (1-2 -2 + 3) & + (- 2 + 3 + 3-4) & + (3-4-4 + 5) & + (- 4 + 5 + 5-6) + \ cdots] \\ & = & 1 + [& 0 + 0 + 0 + 0 + \ cdots] \\ 4s & = & 1 \ end {array}}}$ ${\ displaystyle {\ begin {array} {rclllll} 4s & = && (1-2 + 3-4 + \ cdots) & + (1-2 + 3-4 + \ cdots) & + (1-2 + 3 - 4+ \ cdots) & + (1-2 + 3-4 + \ cdots) \\ & = && (1-2 + 3-4 + \ cdots) & + 1 + (- 2 + 3-4 + 5 + \ cdots) & + 1 + (- 2 + 3-4 + 5 + \ cdots) & - 1+ (3-4 + 5-6 + \ cdots) \\ & = & 1 + [& (1-2 -2 + 3) & + (- 2 + 3 + 3-4) & + (3-4-4 + 5) & + (- 4 + 5 + 5-6) + \ cdots] \\ & = & 1 + [& 0 + 0 + 0 + 0 + \ cdots] \\ 4s & = & 1 \ end {array}}}$

Asa $s={\frac {1}{4}}.$ ${\ displaystyle s = {\ frac {1} {4}}.}$ ${\ displaystyle s = {\ frac {1} {4}}.}$

Adăugând 4 exemplare de 1 - 2 + 3 - 4 + ... folosind doar schimbarea termenilor de adunare, rezultatul este 1. S-a adăugat calculul 1 - 1 + 1 - 1 + ..., seria de Mare .

Alternativ, puteți scrie următoarele 4 egalități și puteți adăuga membru la membru:

{\begin{aligned}s=1-2+3-4+5-6+\cdots \\s=\ \ \ \ \ \ \ 1-2+3-4+5-\cdots \\s=\ \ \ \ \ \ \ 1-2+3-4+5-\cdots \\s=\ \ \ \ \ \ \ \ \ \ \ \ \ \ 1-2+3-4+\cdots \\{\text{------------------------------------------}}\\4s=1+0+0+0+0+0+\cdots \end{aligned}}

{\ displaystyle {\ begin {align} s = 1-2 + 3-4 + 5-6 + \ cdots \\ s = \ \ \ \ \ \ 1-2 + 3-4 + 5- \ cdots \\ s = \ \ \ \ \ \ \ 1-2 + 3-4 + 5- \ cdots \\ s = \ \ \ \ \ \ \ \ \ \ \ \ 1-2 + 3-4 + \ cdots \ \ {\ text {------------------------------------------}} \ \ 4s = 1 + 0 + 0 + 0 + 0 + 0 + \ cdots \ end {align}}}

{\ displaystyle {\ begin {align} s = 1-2 + 3-4 + 5-6 + \ cdots \\ s = \ \ \ \ \ \ 1-2 + 3-4 + 5- \ cdots \\ s = \ \ \ \ \ \ \ 1-2 + 3-4 + 5- \ cdots \\ s = \ \ \ \ \ \ \ \ \ \ \ \ 1-2 + 3-4 + \ cdots \ \ {\ text {------------------------------------------}} \ \ 4s = 1 + 0 + 0 + 0 + 0 + 0 + \ cdots \ end {align}}}

sau $4s=1,$ ${\ displaystyle 4s = 1,}$ ${\ displaystyle 4s = 1,}$ acesta este $s={\frac {1}{4}}.$ ${\ displaystyle s = {\ frac {1} {4}}.}$ ${\ displaystyle s = {\ frac {1} {4}}.}$

Rezultatul acestui calcul este prezentat grafic în dreapta.

Deși 1 - 2 + 3 - 4 + ... nu are o sumă în sensul obișnuit, ecuația s = 1 - 2 + 3 - 4 + ... = ¹ ⁄ ₄ poate fi un exemplu natural pentru a descrie cum o se poate defini extensia conceptului de sumă. O definiție generalizată a sumei pentru o serie care în mod obișnuit nu este convergentă se numește metodă de însumare , în care suma se face numai pe anumite subseturi ale indexului de serie posibil.

Există metode de acest tip, iar unele dintre acestea sunt indicate mai jos, fiecare dintre acestea fiind caracterizată de proprietățile pe care le împărtășește cu conceptul obișnuit de adăugare.

Ceea ce implică manipularea descrisă mai sus este că, dată fiind o metodă de însumare care este liniară și stabilă, care permite sumabilitatea seriei 1 - 2 + 3 - 4 + ..., atunci rezultatul sumei trebuie să fie ¹ ⁄ ₄ . Mai mult, din moment ce ${\begin{array}{rcllll}2s&=&&(1-2+3-4+\cdots )&+&(1-2+3-4+\cdots )\\&=&1+&(-2+3-4+\cdots )&+1-2&+(3-4+5\cdots )\\&=&0+&(-2+3)+(3-4)+(-4+5)+\cdots \\{\frac {1}{2}}&=&&1-1+1-1\cdots \\\end{array}}$ ${\ displaystyle {\ begin {array} {rcllll} 2s & = && (1-2 + 3-4 + \ cdots) & + & (1-2 + 3-4 + \ cdots) \\ & = & 1 + & (-2 + 3-4 + \ cdots) & + 1-2 & + (3-4 + 5 \ cdots) \\ & = & 0 + & (- 2 + 3) + (3-4) + ( - 4 + 5) + \ cdots \\ {\ frac {1} {2}} & = && 1-1 + 1-1 \ cdots \\\ end {array}}}$ ${\ begin {array} {rcllll} 2s & = && (1-2 + 3-4 + \ cdots) & + & (1-2 + 3-4 + \ cdots) \\ & = & 1 + & (- 2+ 3-4 + \ cdots) & + 1-2 & + (3-4 + 5 \ cdots) \\ & = & 0 + & (- 2 + 3) + (3-4) + (- 4 + 5) + \ cdots \\ {\ frac {1} {2}} & = && 1-1 + 1-1 \ cdots \\\ end {array}}$

atunci această metodă de însumare trebuie să facă și seria Grandi sumabilă, dând ca rezultat s = 1 - 1 + 1 - 1 + ... = ¹ ⁄ ₂ .

O altă metodă, care exploatează rezultatul seriei Grandi, este următoarea:

${\begin{array}{rclllll}s&=&(1-2)+3+(-4+5)-6+(7-8)+9\cdots \\&=&(-1+1-1+1\cdots )+(3-6+9-12+\cdots )\\[0.4em]&=&-{\frac {1}{2}}+3\cdot (1-2+3-4+\cdots )\\[0.4em]s&=&-{\frac {1}{2}}+3s\\[0.4em]s&=&{\frac {1}{4}}\\\end{array}}$ ${\ displaystyle {\ begin {array} {rclllll} s & = & (1-2) +3 + (- 4 + 5) -6+ (7-8) +9 \ cdots \\ & = & (- 1 + 1-1 + 1 \ cdots) + (3-6 + 9-12 + \ cdots) \\ [0.4em] & = & - {\ frac {1} {2}} + 3 \ cdot (1-2 + 3-4 + \ cdots) \\ [0.4em] s & = & - {\ frac {1} {2}} + 3s \\ [0.4em] s & = & {\ frac {1} {4} } \\ \ end {array}}}$ ${\ begin {array} {rclllll} s & = & (1-2) +3 + (- 4 + 5) -6+ (7-8) +9 \ cdots \\ & = & (- 1 + 1- 1 +1 \ cdots) + (3-6 + 9-12 + \ cdots) \\ [0.4em] & = & - {\ frac {1} {2}} + 3 \ cdot (1-2 + 3- 4 + \ cdots) \\ [0.4em] s & = & - {\ frac {1} {2}} + 3s \\ [0.4em] s & = & {\ frac {1} {4}} \\ \ end {array}}$

Succesiune cauchy

O demonstrație grafică a faptului că 1 - 2 + 3 - 4 + ... este egal cu produsul Cauchy între 1 - 1 + 1 - 1 + ... și 1 - 1 + 1 - 1 + ...

În 1891 , Ernesto Cesaro și-a exprimat speranța că seriile divergente au constituit metode importante în calculele matematice, indicând teoria în care (1 - 1 + 1 - 1 + ...) 2 = 1 - 2 + 3 - 4 + .. este echivalent cu ¹ ⁄ ₄ . ^[4] Pentru Cesaro această ecuație a fost o aplicație a teoremei pe care a publicat-o anul anterior, care a fost considerată prima din istoria seriilor divergente. Detaliile acestei metode de sumabilitate se află în ideea centrală care susține că 1 - 2 + 3 - 4 + ... este produsul Cauchy al 1 - 1 + 1 - 1 + ... și 1 - 1 + 1 - 1 + ….

Produsul Cauchy , descoperit de matematicianul francez Augustin-Louis Cauchy , este alcătuit din două serii infinite. În cazul în care Σ a _n = Σ b _n = Σ (−1) ⁿ , termenii seriei Cauchy sunt dați printr-o sumă finită:

{\begin{array}{rcl}c_{n}&=&\displaystyle \sum _{k=0}^{n}a_{k}b_{n-k}=\sum _{k=0}^{n}(-1)^{k}(-1)^{n-k}\\[1em]&=&\displaystyle \sum _{k=0}^{n}(-1)^{n}=(-1)^{n}(n+1).\end{array}}

{\ displaystyle {\ begin {array} {rcl} c_ {n} & = & \ displaystyle \ sum _ {k = 0} ^ {n} a_ {k} b_ {nk} = \ sum _ {k = 0} ^ {n} (- 1) ^ {k} (- 1) ^ {nk} \\ [1em] & = & \ displaystyle \ sum _ {k = 0} ^ {n} (- 1) ^ {n} = (- 1) ^ {n} (n + 1). \ End {array}}}

{\ begin {array} {rcl} c_ {n} & = & \ displaystyle \ sum _ {{k = 0}} ^ {n} a_ {k} b _ {{nk}} = \ sum _ {{k = 0}} ^ {n} (- 1) ^ {k} (- 1) ^ {{nk}} \\ [1em] & = & \ displaystyle \ sum _ {{k = 0}} ^ {n} (-1) ^ {n} = (- 1) ^ {n} (n + 1). \ End {array}}

Produsul seriei este, prin urmare, următorul:

\sum _{n=0}^{\infty }(-1)^{n}(n+1)=1-2+3-4+\cdots .

{\ displaystyle \ sum _ {n = 0} ^ {\ infty} (- 1) ^ {n} (n + 1) = 1-2 + 3-4 + \ cdots.}

\ sum _ {{n = 0}} ^ {\ infty} (- 1) ^ {n} (n + 1) = 1-2 + 3-4 + \ cdots.

Astfel, o sumă care respectă secvența Cauchy , adică două serii finite care se potrivesc cu 1 - 1 + 1 - 1 + ... = ¹ ⁄ ₂ și 1 - 2 + 3 - 4 + ... = ¹ ⁄ ₄ , va avea ca rezultat ¹ ⁄ ₂ și ¹ ⁄ ₄ . Cu rezultatul primei serii, există o echivalență între suma 1 - 1 + 1 - 1 + ... și cea a 1 - 2 + 3 - 4 + ..., prin urmare această metodă este liniară, stabilă și respectă secvența lui Cauchy.

Suma Cesaro este un exemplu simplu de serie divergentă. Seria 1 - 1 + 1 - 1 + ... poate fi rezumată, conform teoremei lui Cesaro, într-un mod parțial; acest tip de calcul se numește $(C,1)$ ${\ displaystyle (C, 1)}$ ${\ displaystyle (C, 1)}$ -sumabil. 1 - 2 + 3 - 4 + ... în schimb nu necesită suportul teoremei lui Cesaro, din acest motiv este definit $(C,2)$ ${\ displaystyle (C, 2)}$ ${\ displaystyle (C, 2)}$ -sumabil. ^[5] ^[6] Pentru a fi utilizată într-o serie, suma lui Cesaro trebuie, prin urmare, să îndeplinească una liniară și stabilă .

Metode specifice

Cesaro și Hölder

Date despre suma (H, 2) a ¹ ⁄ ₄ .

Pentru a găsi sumabilitatea într-o sumă de Cesaro $(C,1)$ ${\ displaystyle (C, 1)}$ ${\ displaystyle (C, 1)}$ de 1 - 2 + 3 - 4 + ..., dacă există, conceptul de medie aritmetică trebuie aplicat sumelor parțiale ale seriei, care sunt, în această serie:

1, −1, 2, −2, 3, −3, ...,

Prin urmare, mijloacele aritmetice sunt următoarele:

1, 0, ²⁄ ₃ , 0, ³⁄ ₅ , 0, ⁴ ⁄ ₇ ,….

Această secvență nu converge, în acest caz 1 - 2 + 3 - 4 + ... nu poate fi însumată cu criteriile teoremei lui Cesaro.

Există două binecunoscute generalizări ale sumei lui Cesaro : conceptul simplu care deține suma $(H,n)$ ${\ displaystyle (H, n)}$ ${\ displaystyle (H, n)}$ operează pe numere naturale $n .$ ${\ displaystyle n.}$ ${\ displaystyle n.}$ Acolo $(H,1)$ ${\ displaystyle (H, 1)}$ ${\ displaystyle (H, 1)}$ Suma lui Cesaro, care trebuie aplicată, necesită o serie în care trebuie găsite multe medii matematice. Astfel, media regulată converge la ¹ ⁄ ₂ , iar sumele impare sunt egale cu 0 . ^[7] ^[8] În acest caz, media mediei converge la 0 și ¹ ⁄ ₂ , adică ¹ ⁄ ₄ . Astfel, 1 - 2 + 3 - 4 + ... este (H, 2) sumabil cu ¹ ⁄ ₄ .

Acolo $H.$ ${\ displaystyle H}$ $H.$ este partea ecuației găsită de Otto Hölder , care a demonstrat în 1882 ce înseamnă astăzi în matematică legătura dintre suma lui Abel și metodele pentru suma $(H,n)$ ${\ displaystyle (H, n)}$ ${\ displaystyle (H, n)}$ cu 1 - 2 + 3 - 4 + ...; această succesiune a fost prima căreia i s-a aplicat această regulă. ^[9] ^[10] Faptul că ¹ ⁄ ₄ este suma $(H,2)$ ${\ displaystyle (H, 2)}$ ${\ displaystyle (H, 2)}$ din 1 - 2 + 3 - 4 + ... garantează că suma lui Abel poate fi aplicată acestei serii.

O altă generalizare a sumei Cesaro este succesiunea metodelor $(C,n).$ ${\ displaystyle (C, n).}$ ${\ displaystyle (C, n).}$ El a arătat într-adevăr că suma $(C,n)$ ${\ displaystyle (C, n)}$ ${\ displaystyle (C, n)}$ iar suma $(H,n)$ ${\ displaystyle (H, n)}$ ${\ displaystyle (H, n)}$ da același rezultat, în ciuda contextului istoric diferit. În 1887 , Cesaro a căutat o definiție pentru regula sumei $(C,n),$ ${\ displaystyle (C, n),}$ ${\ displaystyle (C, n),}$ dar a reușit să dea doar câteva exemple. În special, a adăugat 1 - 2 + 3 - 4 + ... cu ¹ ⁄ ₄ cu o metodă strâns legată de $(C,n),$ ${\ displaystyle (C, n),}$ ${\ displaystyle (C, n),}$ dar nu a justificat cum a făcut-o. El, în 1890 , a definit metodele $(C,n)$ ${\ displaystyle (C, n)}$ ${\ displaystyle (C, n)}$ în stări ordonate ale teoremei sale cu ajutorul secvenței Cauchy grație unei serii $(C,n)$ ${\ displaystyle (C, n)}$ ${\ displaystyle (C, n)}$ -sumabil și la o serie $(C,m)$ ${\ displaystyle (C, m)}$ ${\ displaystyle (C, m)}$ -sumabil, făcând totul să iasă $(C,m+n+1)$ ${\ displaystyle (C, m + n + 1)}$ ${\ displaystyle (C, m + n + 1)}$ -sumabil. ^[11]

Suma lui Abel

Sume parțiale de 1−2 x +3 x ² +…; 1 / (1 + x ) ²; rezultatul va fi întotdeauna 1.

Într-un document din 1749 , Euler admite că o serie diferă, dar nu are o sumă precisă.

( EN )

„Când se spune că suma acestei serii 1 - 2 + 3 - 4 + 5 - 6 ... este ¹ ⁄ ₄ , aceasta trebuie să pară paradoxală. Căci prin adăugarea a 100 de termeni din această serie, obținem –50, totuși, suma a 101 termeni dă +51, care este destul de diferit de ¹ ⁄ ₄ și devine și mai mare atunci când se mărește numărul de termeni. Dar am observat deja la un moment anterior că este necesar să se dea cuvântului sum un sens mai extins. "

( IT )

«Când spunem că rezultatul dintre sumele seriei 1 - 2 + 3 - 4 + 5 - 6 ... este ¹ ⁄ ₄ , acest fapt trebuie să pară paradoxal. Adăugând 100 de termeni din această serie, vom avea un rezultat de –50, totuși, adăugând rezultatul cu 101 avem +51; prin urmare, rezultatul total nu ar trebui să fie de ¹ ⁄ ₄ . Dar deja anunțasem anterior că este necesar să se dea cuvântului „sumă” o definiție mai detaliată ”.

( Euler, 1749. ^[12] )

Euler a propus noi definiții ale cuvântului sum de mai multe ori, cartea publicând Euler pe serie infinită (literalmente Euler pe serie infinită). În cazul seriei 1 - 2 + 3 - 4 + ..., ideile sale despre sumă sunt similare cu cele utilizate pentru suma lui Abel .

( EN )

„Nu mai este îndoielnic că suma acestei serii 1 - 2 + 3 - 4 + 5 + ... este ¹ ⁄ ₄ ; deoarece apare din expansiunea formulei ¹ ⁄ _{(1 + 1) ²} , a cărei valoare este incontestabil ¹ ⁄ ₄ . Ideea devine mai clară luând în considerare seria generală 1-2 x + 3 x ² - 4 x ³ + 5 x ⁴ - 6 x ⁵ ... care apare în timp ce extindeți expresia ¹ ⁄ _{(1 + x) ²} , pe care această serie este într-adevăr egal după ce am stabilit $x=1$ ${\ displaystyle x = 1}$ $x = 1$ . "

( IT )

«Nu există nicio îndoială că rezultatul adăugării 1 - 2 + 3 - 4 + 5 + ... este ¹ ⁄ ₄ ; deoarece provine din extinderea formulei ¹ ⁄ _{(1 + 1) ²} , care valoare este ¹ ⁄ ₄ . Ideea este mai clară din considerarea seriei generale 1-2 x + 3 x ² - 4 x ³ + 5 x ⁴ - 6 x ⁵ ... care este generată prin extinderea expresiei ¹ ⁄ _{(1+ x ) ²} , la care seria este evident egală prin plasare $x=1$ ${\ displaystyle x = 1}$ $x = 1$ . "

( Euler, 1749. ^[13] )

Există multe modalități de a vedea asta, cel puțin pentru valori $|x|<1,$ ${\ displaystyle | x | <1,}$ ${\ displaystyle | x | <1,}$ Euler are dreptate când cere

1-2x+3x^{2}-4x^{3}+\cdots ={\frac {1}{(1+x)^{2}}}.

{\ displaystyle 1-2x + 3x ^ {2} -4x ^ {3} + \ cdots = {\ frac {1} {(1 + x) ^ {2}}}.}

1-2x + 3x ^ {2} -4x ^ {3} + \ cdots = {\ frac {1} {(1 + x) ^ {2}}}.

O modalitate este de a utiliza expansiunea Taylor la cel de-al doilea membru.

Din punct de vedere modern, seria 1 - 2 x + 3 x ² - 4 x ³ + ... nu definește o funcție pentru $x=1,$ ${\ displaystyle x = 1,}$ ${\ displaystyle x = 1,}$ de aceea această valoare nu poate fi pur și simplu substituită în expresie. Deoarece această funcție este definită pentru $|x|<1,$ ${\ displaystyle | x | <1,}$ ${\ displaystyle | x | <1,}$ putem calcula limita pentru $x\to 1$ ${\ displaystyle x \ to 1}$ ${\ displaystyle x \ to 1}$ și aceasta este definiția sumei lui Abel :

\lim _{x\rightarrow 1^{-}}\sum _{n=1}^{\infty }n(-x)^{n-1}=\lim _{x\rightarrow 1^{-}}{\frac {1}{(1+x)^{2}}}={\frac {1}{4}}.

{\ displaystyle \ lim _ {x \ rightarrow 1 ^ {-}} \ sum _ {n = 1} ^ {\ infty} n (-x) ^ {n-1} = \ lim _ {x \ rightarrow 1 ^ {-}} {\ frac {1} {(1 + x) ^ {2}}} = {\ frac {1} {4}}.}

\ lim _ {{x \ rightarrow 1 ^ {{-}}}} \ sum _ {{n = 1}} ^ {\ infty} n (-x) ^ {{n-1}} = \ lim _ { {x \ rightarrow 1 ^ {{-}}}} {\ frac {1} {(1 + x) ^ {2}}} = {\ frac 14}.

Euler și Borel

Suma lui Euler de ¹ ⁄ ₂ - ¹ ⁄ ₄ .

Euler a aplicat o altă metodă de calcul în serie: o transformare binomială a propriei sale invenții. Pentru a calcula transformarea binomială a lui Euler , începem cu o succesiune de termeni pozitivi, care vor forma apoi seria alternativă, în acest caz avem 1, 2, 3, 4, .... Primul element al acestei secvențe este indicat cu $a_{0}.$ ${\ displaystyle a_ {0}.}$ ${\ displaystyle a_ {0}.}$

Apoi, trebuie să calculăm diferențele directe între 1, 2, 3, 4, ...; care sunt 1, 1, 1, 1,…. Primul element din această secvență este indicat cu $\Delta a_{0}.$ ${\ displaystyle \ Delta a_ {0}.}$ ${\ displaystyle \ Delta a_ {0}.}$ Numerotarea binomială depinde, de asemenea, de diferențele de diferențe, dar toate diferențele directe între 1, 1, 1, 1, ... sunt 0. Transformarea Euler a 1 - 2 + 3 - 4 + ... este de asemenea definibilă ca:

{\frac {1}{2}}a_{0}-{\frac {1}{4}}\Delta a_{0}+{\frac {1}{8}}\Delta ^{2}a_{0}-\cdots ={\frac {1}{2}}-{\frac {1}{4}}.

{\ displaystyle {\ frac {1} {2}} a_ {0} - {\ frac {1} {4}} \ Delta a_ {0} + {\ frac {1} {8}} \ Delta ^ {2 } a_ {0} - \ cdots = {\ frac {1} {2}} - {\ frac {1} {4}}.}

{\ frac 12} a_ {0} - {\ frac 14} \ Delta a_ {0} + {\ frac 18} \ Delta ^ {2} a_ {0} - \ cdots = {\ frac 12} - {\ frac 14}.

În terminologia modernă se spune că seria 1 - 2 + 3 - 4 + ... poate fi însumată prin intermediul sumei lui Euler și valorează ¹ ⁄ ₄ . Conform sumei lui Euler, în această serie este necesar să se aplice un alt tip de criteriu de sumabilitate, reprezentând 1 - 2 + 3 - 4 + ... ca

\sum _{k=0}^{\infty }a_{k}=\sum _{k=0}^{\infty }(-1)^{k}(k+1),

{\ displaystyle \ sum _ {k = 0} ^ {\ infty} a_ {k} = \ sum _ {k = 0} ^ {\ infty} (- 1) ^ {k} (k + 1),}

\ sum _ {{k = 0}} ^ {\ infty} a_ {k} = \ sum _ {{k = 0}} ^ {\ infty} (- 1) ^ {k} (k + 1),

avem seria convergentă peste tot:

a(x)=\sum _{k=0}^{\infty }{\frac {(-1)^{k}(k+1)x^{k}}{k!}}=e^{-x}(1-x).

{\ displaystyle a (x) = \ sum _ {k = 0} ^ {\ infty} {\ frac {(-1) ^ {k} (k + 1) x ^ {k}} {k!}} = și ^ {- x} (1-x).}

a (x) = \ sum _ {{k = 0}} ^ {\ infty} {\ frac {(-1) ^ {k} (k + 1) x ^ {k}} {k!}} = e ^ {{- x}} (1-x).

Suma Borel aplicată în seria 1 - 2 + 3 - 4 + ... va fi deci ^[14]

\int _{0}^{\infty }e^{-x}a(x)\,dx=\int _{0}^{\infty }e^{-2x}(1-x)\,dx={\frac {1}{2}}-{\frac {1}{4}}.

{\ displaystyle \ int _ {0} ^ {\ infty} e ^ {- x} a (x) \, dx = \ int _ {0} ^ {\ infty} e ^ {- 2x} (1-x) \, dx = {\ frac {1} {2}} - {\ frac {1} {4}}.}

\ int _ {0} ^ {\ infty} e ^ {{- x}} a (x) \, dx = \ int _ {0} ^ {\ infty} e ^ {{- 2x}} (1-x ) \, dx = {\ frac 12} - {\ frac 14}.

Separarea măsurilor

Aleksander Saičev și Wojbor Andrzej Woyczyński au ajuns la 1 - 2 + 3 - 4 + ... = ¹ ⁄ ₄ prin aplicarea a două principii fizice: relația infinitesimală și separarea măsurilor. Pentru a fi precis, aceste principii fac parte dintr-o familie lungă numită metode φ-sumabile , ale cărei sume, în această serie, sunt ¹ ⁄ ₄ : dacă $\varphi (x)$ ${\ displaystyle \ varphi (x)}$ $\ varphi (x)$ este o funcție cu prima și a doua derivată continuă și integrabilă în $(0,+\infty ),$ ${\ displaystyle (0, + \ infty),}$ ${\ displaystyle (0, + \ infty),}$ astfel încât $\varphi (0)=1$ ${\ displaystyle \ varphi (0) = 1}$ ${\ displaystyle \ varphi (0) = 1}$ și limitele $\varphi (x)$ ${\ displaystyle \ varphi (x)}$ $\ varphi (x)$ Și $x\varphi (x)$ ${\ displaystyle x \ varphi (x)}$ ${\ displaystyle x \ varphi (x)}$ la $+\infty$ ${\ displaystyle + \ infty}$ $+ \ infty$ sunt 0. ^[15]

\lim _{\delta \to 0}\sum _{m=0}^{\infty }(-1)^{m}(m+1)\varphi (\delta m)={\frac {1}{4}}.

{\ displaystyle \ lim _ {\ delta \ to 0} \ sum _ {m = 0} ^ {\ infty} (- 1) ^ {m} (m + 1) \ varphi (\ delta m) = {\ frac {1} {4}}.}

\ lim _ {{\ delta \ to 0}} \ sum _ {{m = 0}} ^ {\ infty} (- 1) ^ {m} (m + 1) \ varphi (\ delta m) = {\ frac 14}.

Acest rezultat generalizează suma lui Abel , care se obține prin aplicare $\varphi (x)=e^{-x}.$ ${\ displaystyle \ varphi (x) = e ^ {- x}.}$ ${\ displaystyle \ varphi (x) = e ^ {- x}.}$ Rezultatul general poate fi demonstrat prin asocierea termenilor seriei pe $m$ ${\ displaystyle m}$ $m$ și convertirea expresiei într-o integrală Riemann . Pentru ultimul pas, în proba corespunzătoare pentru 1 - 1 + 1 - 1 + ... se aplică teorema valorii medii , dar avem nevoie de o formă Lagrange mai puternică decât teorema lui Taylor .

Generalizări

Sume ale lui Euler în cartea sa din 1755 , Institutions .

Produsul Cauchy de 1 - 1 + 1 - 1 + ... de trei ori singur este 1 - 3 + 6 - 10 + ..., adică seria alternativă a unui număr triunghiular . După suma lui Abel și suma lui Euler rezultatul este ¹ ⁄ ₈ . ^[16] Produsul Cauchy de 1 - 1 + 1 - 1 + ... în sine de patru ori este 1 - 4 + 10 - 20 + ..., adică seria alternativă a unui număr tetraedric . Conform sumei lui Abel, rezultatul este ¹ ⁄ ₁₆ .

O altă generalizare a 1 - 2 + 3 - 4 + ... într-o direcție ușor diferită este seria 1 - 2 ⁿ + 3 ⁿ - 4 ⁿ + ... pentru alte valori ale $n .$ ${\ displaystyle n.}$ ${\ displaystyle n.}$ Pentru un întreg pozitiv $n,$ ${\ displaystyle n,}$ $n,$ aceste serii funcționează cu suma lui Abel după cum urmează: ^[5] ^[17]

1-2^{n}+3^{n}-\cdots ={\frac {2^{n+1}-1}{n+1}}B_{n+1}.

{\ displaystyle 1-2 ^ {n} + 3 ^ {n} - \ cdots = {\ frac {2 ^ {n + 1} -1} {n + 1}} B_ {n + 1}.}

1-2 ^ {{n}} + 3 ^ {{n}} - \ cdots = {\ frac {2 ^ {{n + 1}} - 1} {n + 1}} B _ {{n + 1 }}.

Aici $B_{n}$ ${\ displaystyle B_ {n}}$ $B_ {n}$ sunt numerele Bernoulli . Pentru $n$ ${\ displaystyle n}$ $n$ chiar și seria este redusă:

1-2^{2k}+3^{2k}-\cdots =0.

{\ displaystyle 1-2 ^ {2k} + 3 ^ {2k} - \ cdots = 0.}

1-2 ^ {{2k}} + 3 ^ {{2k}} - \ cdots = 0.

Ultima sumă devine obiectul deriziunii lui Niels Henrik Abel în 1826 :

( EN )

„Seriile divergente se referă la toată lucrarea diavolului și este păcat că cineva îndrăznește să găsească vreo dovadă pe ele. Se poate scoate din ele ceea ce își dorește dacă le folosește și ele au făcut atâtea nefericiri și atâtea paradoxuri. Ne putem gândi la ceva mai îngrozitor decât să spunem asta $0=1-2^{n}+3^{n}-4^{n}+\ldots$ ${\ displaystyle 0 = 1-2 ^ {n} + 3 ^ {n} -4 ^ {n} + \ ldots}$ $0 = 1-2 ^ {n} + 3 ^ {n} -4 ^ {n} + \ ldots$ unde n este un număr pozitiv. Iată ceva de care să râzi, prieteni ".

( IT )

„Seriile divergente sunt toate lucrările diavolului și este păcat să căutăm ipoteze și teorii despre ele. Puteți obține ceva din ele dacă doriți cu adevărat să le folosiți și asta le face atât de nefericite și paradoxale. Poți gândi lucruri mult mai șocante dacă spui asta $0=1-2^{n}+3^{n}-4^{n}+\ldots$ ${\ displaystyle 0 = 1-2 ^ {n} + 3 ^ {n} -4 ^ {n} + \ ldots}$ $0 = 1-2 ^ {n} + 3 ^ {n} -4 ^ {n} + \ ldots$ unde n este un număr pozitiv. Aici râde, prieteni. "

( Grattan-Giunness, p. 80. ^[18] ^[19] )

Profesorul lui Cesaro, Eugène Charles Catalan , a denigrat și el serii divergente . Sub influența catalanului, Cesaro s-a referit inițial la „formule convenționale” precum 1 - 2 ⁿ + 3 ⁿ - 4 ⁿ + ... și la „egalități absurde”, iar în 1883 a exprimat o viziune tipică a acelei perioade conform căreia formulele erau false dar oarecum util totuși. În cele din urmă, în cartea sa din 1890 Sur la multiplication des séries , Cesaro a urmat o abordare modernă pornind de la definiții.

Seriile sunt, de asemenea, studiate pentru valori non-întregi ale lui n ; acest lucru a permis descoperirea funcției Dirichlet eta . O parte din motivele studiilor lui Euler asupra seriei 1 - 2 + 3 - 4 + ... se referă la ecuația funcțională a funcției eta, care duce direct la ecuația funcțională a funcției zeta Riemann . Euler a devenit, de asemenea, celebru pentru găsirea valorilor acestor funcții pentru numere întregi pare (inclusiv problema de la Basel ) și pentru încercarea de a găsi valorile lor cu numere întregi impare (inclusiv constanta lui Apéry ). Funcția eta, în special, este ușor de studiat cu metodele lui Euler, deoarece seria sa Dirichlet poate fi însumată oriunde folosind suma Abel . Funcția zeta a seriei Dirichlet este foarte dificil de adăugat acolo unde divergă. ^[20] De exemplu, corespondentul 1 - 2 + 3 - 4 + ... în funcția zeta este seria non-alternativă 1 + 2 + 3 + 4 + ..., căreia i s-au aplicat recent metode fizice care însă necesită metode de sumă mai elaborate.

Notă

^ Hardy, p. 8.
^ Beals, p. 23.
^ Hardy, p. 6.
^ Ferraro, p. 130.
^ ^a ^b Hardy, p. 3.
^ Weidlich, pp. 52-55.
^ Hardy, p. 9.
^ Weidlich, pp. 17-18.
^ Ferraro, p. 118.
^ Trucciarone, p. 10.
^ Ferraro, pp. 123-128.
^ Euler, p. 2.
^ Euler, pp. 3, 25.
^ Wiedlich, p. 59.
^ Saičev și Woyczyński, pp. 260-264.
^ Kline, p. 313.
^ Knopp, p. 41.
^ Grattan-Giunness, p. 80.
^ Markuševič, p. 48.
^ Euler, pp. 20-25.

Bibliografie

( EN ) Richard Beals, Analiza: o introducere . Cambridge UP, 2004. ISBN 0-521-60047-2
(EN) Harry Davis, seria Fourier și funcțiile ortogonale. Dover, 1989. ISBN 0-486-65973-9
( EN ) Leonhard Euler, Remarques sur un beau rapport between les séries des puissances tant direct that réciproques . Memoires de Berlin, 1978.
Giovanni Ferraro, Prima definiție modernă a sumei seriilor divergente: un aspect al matematicii din 1900 . Arhiva pentru Istoria Științelor Exacte, 1999. DOI 7004070050036 ^{[ conexiune întreruptă ]}
( EN ) Ivor Grattan, Dezvoltarea bazelor analizei matematice de la Euler la Riemann . MIT Press, 1970. ISBN 0-262-07034-0
( EN ) Godfrey Harold Hardy, Seria divergentă . Clarendon Press, 1949. LLCN 9175377
(EN) Morris Kline, Euler și Infinite Series. Revista de matematică 56, 1983.
(EN) Shaughan Lavine, Înțelegerea infinitului. Harvard UP, 1994. ISBN 0-674-92096-1
( RU ) Aleksandr Markuševič, Seria: concepte fundamentale cu expunere istorică . Hindustan, 1961. LLCN 6817528
( RU ) Ivan Saičev, Distribuții în științele fizice și inginerești, volumul 1 . Birkhaüser, 1996. ISBN 0-8176-3924-1
John Tucciarone, Dezvoltarea teoriei sumabilității divergente în seria din 1880 până în 1925 . Arhiva pentru Istoria Științelor Exacte 10, 1973. DOI 41665708511356 ^{[ conexiune întreruptă ]}
( EN ) Anders Vretblad, Analiza Fourier și aplicațiile sale . Springer, 2003. ISBN 0-387-00836-5
( EN ) John Weidlič, Metode de sumabilitate pentru serii divergente . Stanford, 1950. OCLC 38624384

Elemente conexe

linkuri externe

( RO ) Ecuații și formule pentru 1 - 2 + 3 - 4 + ... , pe home.scarlet.be . Adus la 28 februarie 2008 (arhivat din original la 26 decembrie 2012) .

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică

[1] Hardy, p. 8.

[2] Beals, p. 23.

[3] Hardy, p. 6.

[4] Ferraro, p. 130.

[autogenerato1-5] Hardy, p. 3.

[6] Weidlich, pp. 52-55.

[7] Hardy, p. 9.

[8] Weidlich, pp. 17-18.

[9] Ferraro, p. 118.

[10] Trucciarone, p. 10.

[11] Ferraro, pp. 123-128.

[12] Euler, p. 2.

[13] Euler, pp. 3, 25.

[14] Wiedlich, p. 59.

[15] Saičev și Woyczyński, pp. 260-264.

[16] Kline, p. 313.

[17] Knopp, p. 41.

[18] Grattan-Giunness, p. 80.

[19] Markuševič, p. 48.

[20] Euler, pp. 20-25.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]