Algebră liniară
|
Algebra liniară este ramura matematicii care se ocupă cu studiul vectorilor , spațiilor vectoriale (sau spațiilor liniare), transformărilor liniare și sistemelor de ecuații liniare . Spațiile vectoriale sunt o temă centrală în matematica modernă; Algebra liniară este utilizată pe scară largă în algebra abstractă , geometrie și analiză funcțională . Algebra liniară are, de asemenea, o reprezentare concretă în geometria analitică .
Cu algebra liniară, toate fenomenele fizice „liniare” sunt complet studiate, adică cele în care distorsiunile , turbulențele și fenomenele haotice în general nu sunt implicate intuitiv. Chiar și mai complexe fenomene, nu numai în fizică , ci și în cele naturale și științele sociale , pot fi studiate și înapoi cu aproximări datorate unui model liniar trasat.
Istorie
Istoria algebrei liniare moderne începe în anii 1843 și 1844 . În 1843, William Rowan Hamilton (care a introdus termenul de vector ) a inventat cuaternionii . În 1844, Hermann Grassmann și-a publicat cartea Die lineale Ausdehnungslehre . Arthur Cayley a introdus matrici (2 × 2), una dintre ideile fundamentale ale algebrei liniare, în 1857 .
Introducere elementară
Algebra liniară își are originea în studiul vectorilor în spații carteziene bidimensionale și tridimensionale. Un vector, în acest caz, este un segment orientat, caracterizat prin lungime (sau magnitudine), direcție și direcție. Vectorii pot fi folosiți pentru a reprezenta anumite entități fizice, cum ar fi forțele , și pot fi adăugați împreună și înmulțiți cu un scalar , formând astfel primul exemplu de spațiu vectorial pe reali .
Algebra liniară modernă a fost extinsă pentru a include spații de dimensiuni arbitrare sau infinite. Un spațiu vectorial de dimensiune n se numește spațiu n . Multe dintre rezultatele utile în 2 spații și 3 spații pot fi extinse la spații cu dimensiuni mai mari. Deși mulți oameni nu pot vizualiza cu ușurință vectori în n- spații, acești vectori sau n-tupluri sunt utile pentru reprezentarea datelor. Deoarece vectori, cum ar fi tupluri n-, sunt liste ordonate de n componente, mulți oameni să înțeleagă și să manipuleze datele eficient în această structură. De exemplu, în economie , se pot crea și utiliza vectori cu 8 dimensiuni (octuple) pentru a reprezenta produsul intern brut din 8 state. Puteți decide să afișați PIB-ul a 8 state pentru un anumit an, de exemplu ( Italia , Statele Unite , Marea Britanie , Franța , Germania , Spania , Japonia , Australia ), folosind un vector (v 1 , v 2 , v 3 , v 4 , v 5 , v 6 , v 7 , v 8 ) unde PIB-ul fiecărui stat se află în poziția sa respectivă.
Un spațiu vectorial este definit deasupra unui câmp , cum ar fi câmpul numărului real sau câmpul numărului complex . Operatorii liniari mapează elemente de la un spațiu vectorial la altul (sau la sine), astfel încât să se mențină compatibilitatea cu adunarea și multiplicarea scalară definite în spațiile vectoriale. Mulțimea tuturor acestor transformări este, de asemenea, un spațiu vectorial. Dacă o bază este fixată pentru un spațiu vectorial, fiecare transformare liniară poate fi reprezentată printr-un tabel numit matrice . În algebra liniară, prin urmare, studiem proprietățile matricilor și algoritmii pentru calcularea mărimilor importante care le caracterizează, cum ar fi rangul , determinantul și setul valorilor proprii ale acestuia.
Un spațiu vectorial (sau spațiu liniar), ca un concept pur abstract pe care sunt dovedite teoremele , face parte din algebra abstractă și este bine integrat în acest câmp: unele obiecte algebrice conexe, de exemplu, sunt inelul de hartă liniară dintr-un spațiu vectorial în sine, sau grupul de hărți liniare (sau matrice ) inversabile. Algebra liniară joacă, de asemenea, un rol important în analiză , în special în descrierea derivatelor de ordin superior în analiza vectorială și în rezolvarea ecuațiilor diferențiale .
În concluzie, se poate spune pur și simplu că problemele liniare în matematică - cele care prezintă „linearitate” în comportamentul lor - sunt cele mai ușor de rezolvat și că problemele „neliniare” sunt deseori studiate prin aproximarea lor cu situații liniare. De exemplu, în analiză , derivata este o primă încercare de aproximare liniară a unei funcții. Diferența față de problemele neliniare este foarte importantă în practică: metoda generală de găsire a unei formulări liniare a unei probleme, în termeni de algebră liniară și rezolvarea acesteia, dacă este necesar cu calcule matriciale, este una dintre cele mai generale metode aplicabile în matematică.
Noțiuni de bază
Spațiu vectorial
Cea mai importantă noțiune în algebră liniară este cea a spațiului vectorial . Un spațiu vector este un set de elemente, numite vectori , având proprietăți care le fac similare vectorilor aplicați unui punct fix ( originea ) planului sau spațiului.
Mai precis, ele sunt definite pe câteva operații binare : [1]
- doi vectori Și ele pot fi adăugate, dând astfel naștere unui nou vector . Proprietățile sumei vectoriale sunt asociativitatea , comutativitatea , existența elementului neutru , existența elementului invers ;
- un vector poate fi redimensionat, adică înmulțit cu un număr , dând astfel naștere unui nou vector . proprietățile multiplicării prin scalar sunt asociativitatea, existența unui neutru;
- suma vectorială este distributivă în raport cu produsul , în timp ce produsul este distributiv în raport cu suma.
Numarul (numit scalar ) aparține unui câmp fixat de la început: acesta poate fi de exemplu câmpul a numerelor reale sau a câmpului de numere complexe .
Planul cartezian este exemplul fundamental al spațiului vectorial. Fiecare punct din plan este de fapt identificat în mod unic ca o pereche de numere reale. Originea este punctul . Ideea poate fi interpretat alternativ ca un punct al planului sau ca un vector aplicat în originea pornind de la și intră .
În mod similar, spațiul cartezian este format din tripluri de puncte . Mai general, tuplurile de numere reale
formează un spațiu vectorial care este indicat cu . Chiar mai general, poate fi înlocuit cu alt câmp și astfel obțineți spațiul vectorial .
Aplicații liniare

O hartă liniară este o funcție între două spații vectoriale
că este compatibil cu operațiile definite pe ambele. Adică trebuie să se aplice următoarele proprietăți:
pentru fiecare pereche de vectori în și la fiecare urcare . Termenii „aplicație”, „funcție”, „transformare”, „hartă” și „omomorfism” sunt sinonimi în acest context. Termenul „liniar” înseamnă compatibilitatea cu operațiile. O aplicație liniară trimite în mod necesar originea (de ) în originea (de ):
Spațiile Și pot coincide. În acest caz, aplicația este mai bine o transformare a , care este o funcție care schimbă punctele cu , numit și endomorfism . O transformare a trebuie neapărat să mențină originea O fixată.
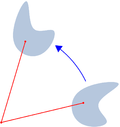
Multe transformări ale planului cartezian sau ale spațiului care mențin originea O fixă sunt liniare: printre acestea, rotațiile (în jurul lui O), reflexiile față de o linie sau un plan (care trece prin O), omotetica (centrată în O) și proiecțiile (pe o linie dreaptă sau plan care trece prin O).
Aplicațiile liniare apar în contexte foarte diferite. De exemplu, funcțional
care se asociază cu o funcție integrala sa este o aplicație liniară
din spatiu a funcțiilor continue cu valoare reală în .
Baze și dimensiuni

Un punct are dimensiunea zero, o linie are dimensiunea unu, un plan are dimensiunea doi și un spațiu are dimensiunea trei. Algebra liniară ne permite să definim riguros și să tratăm spații mai mari decât al treilea. Spațiul fundamental al dimensiunii este spațiul vectorial al tuplelor, notat cu . Pentru , acesta este planul cartezian obișnuit.
Orice spațiu vectorial are o dimensiune. Aceasta este definită algebric, ca număr de elemente dintr-o bază pentru : o bază este un set de vectori care servește ca sistem de referință pentru . Strict, o bază este o succesiune
de vectori independenți care generează spațiu . Un spațiu vectorial poate avea, de asemenea, dimensiune infinită: spațiile vectoriale de dimensiune infinită sunt adesea mai complicate și multe teoreme de algebră liniară necesită ca ipoteze că au dimensiuni finite.
Noțiunile de bază și dimensiunea se aplică (care are dimensiunea ) Și subspațiile conținute în acesta. Cu toate acestea, fiind definite într-un mod pur algebric, ele se aplică și în contexte foarte diferite: de exemplu, matrice formează un spațiu vectorial de dimensiune . Polinoamele dintr-o variabilă formează un spațiu vectorial de dimensiune infinită: totuși, prin restrângerea gradului polinoamelor la o anumită valoare maximă obținem un spațiu vectorial de dimensiune .
Produs scalar
Doi transportatori Și a unui spațiu vectorial poate fi adăugat : rezultatul este un vector . De asemenea, un vector și o urcare poate fi multiplicat : rezultatul este un vector . Cu toate acestea, în definiția spațiului vectorial, nu există nicio operațiune de produs între doi vectori.
Cu toate acestea, în unele contexte, este util să adăugați o operație binară suplimentară între vectori, care se comportă ca un produs. Rezultatul acestui produs poate fi la rândul său un vector sau un scalar. În primul caz, această operație se numește produs vector , iar în al doilea produs scalar . Cu toate acestea, funcționarea produsului vector este interesantă doar în dimensiunea a treia, în timp ce produsele scalare există (și sunt utile) în toate dimensiunile: din acest motiv, acestea din urmă sunt mult mai studiate.
Mai mult, definiția spațiului vectorial nu oferă nici măcar o noțiune de lungime (echivalent, normă ) pentru vectori și nici de unghi între doi dintre ei. Cu toate acestea, ambele noțiuni de lungime și unghi sunt definite dacă este fixat un produs scalar adecvat. [2]
Aplicații
Sisteme liniare
Un sistem de ecuații liniare este baza unui anumit număr de ecuații liniare în unele variabile . Folosind tablouri șimultiplicare rând cu coloană , un sistem poate fi scris într-un mod strict, după cum urmează:
În această expresie este o matrice , este vectorul variabilelor , ..., Și este un alt vector format din constante.
Algebra liniară oferă numeroși algoritmi pentru determinarea soluțiilor unui sistem liniar. Legătura dintre sistemele de ecuații și algebra liniară constă în faptul că matricea poate fi interpretat ca o aplicație liniară de în : conform acestei interpretări, soluțiile sunt exact contra - imaginile .
Teorema Rouché-Capelli oferă o metodă de numărare a soluțiilor, fără a le determina neapărat complet. [3] În cazul în care sistemul este pătrat și are o singură soluție, aceasta poate fi scrisă în mod explicit folosind regula lui Cramer . Cu toate acestea, această soluție teoretică este practic utilizabilă doar pentru a rezolva sisteme foarte mici. [4] În timp ce metodele de eliminare (de exemplu Gauss și cele iterative (de exemplu Gauss-Seidel ) ne permit să calculăm în mod eficient soluțiile unui sistem liniar, chiar și de dimensiuni mari.
Geometrie analitică

În geometria analitică, o linie dreaptă sau un plan sunt descrise prin sisteme de ecuații liniare: așa cum tocmai am văzut, acestea pot fi studiate cu ușurință cu instrumentele algebrei liniare. Prin urmare, ne putem confrunta cu probleme precum pozițiile reciproce a două linii (sau plane) în spațiu (care pot fi incidente, paralele sau înclinate) și modul în care acestea variază pentru transformări liniare.
Conicile din plan precum elipsa , parabola și hiperbola sunt determinate de ecuații de gradul al doilea . Aceste ecuații sunt mai complicate decât cele liniare, care sunt de gradul I. În ciuda acestui fapt, clasificarea conicelor se realizează eficient cu instrumentele algebrei liniare, datorită teoremelor non-banale precum teorema spectrală și teorema lui Sylvester . Cu aceleași instrumente clasificăm cvadricele în spațiu.
Calcul diferențial
Analiza matematică a funcțiilor într-o singură variabilă nu folosește algebră liniară. Pe de altă parte, analiza funcțiilor în mai multe variabile depinde puternic de acest sector. Noțiunea de derivată este de fapt extinsă în mai multe variabile la cea a diferențialului : în timp ce derivata este un număr real simplu care indică panta unei funcții într-un punct, diferențialul este o aplicație liniară, care indică întotdeauna „panta” lui o funcție (multi-variabilă) la un moment dat.
Noțiunea de derivată secundară se extinde și asupra mai multor variabile: rezultatul este o matrice numită matrice Hessian . Dacă această matrice este simetrică , de exemplu, atunci când ipotezele teoremei lui Schwarz sunt valabile, poate fi ușor reprezentată ca o diagonală grație teoremei spectrale .
Analiza funcțională
Multe probleme de analiză funcțională , cum ar fi căutarea unei soluții pentru o ecuație diferențială , se confruntă cu analiza unui anumit spațiu de funcții . Un spațiu de funcții este un spațiu vector ale cărui elemente sunt funcții de un anumit tip (de exemplu continuu, integrabil, diferențiat ... definit pe un domeniu fix). Spațiile de acest tip sunt în general de dimensiune infinită și sunt echipate cu unele structuri suplimentare, cum ar fi un produs scalar (în spațiile Hilbert ), o normă (în spațiile Banach ) sau o topologie mai generală (în spațiile vectoriale topologice ).
Exemple de spații funcționale includ spații Lp și spații Sobolev .
Mecanica cuantică

Mecanica cuantică utilizează pe larg cele mai avansate teoreme ale algebrei liniare. Modelul matematic utilizat în acest domeniu al fizicii (formalizat în principal de Paul Dirac și John Von Neumann ) descrie stările posibile ale unui sistem cuantic ca elemente ale unui anumit spațiu Hilbert și mărimile observabile (cum ar fi poziția, viteza etc.) ca operatori autoadjuncti . Valorile pe care aceste cantități le pot asuma atunci când sunt măsurate efectiv sunt valorile proprii ale operatorului.
Introducerea și utilizarea acestor concepte matematice non-banale în fizica cuantică a fost unul dintre stimulii majori pentru dezvoltarea algebrei liniare în secolul al XX-lea .
Instrumente
Matrici
O matrice este un tabel de numere, cum ar fi:
Matricile sunt utile în algebra liniară pentru reprezentarea hărților liniare. Acest lucru se face prinînmulțirea rând cu coloană . De exemplu, matricea descrisă reprezintă o transformare a planului cartezian in sinea lui. Această transformare trimite punctul în sens
Această transformare nu este altceva decât o rotație de 90º în sens invers acelor de ceasornic cu originea centrată.
Relația dintre matrice și hărți liniare este foarte puternică. Orice aplicație liniară între spații vectoriale de dimensiune Și poate fi descris prin intermediul unei matrici de tip asociat , cu condiția ca bazele să fie fixate în ambele spații vectoriale. Efectul unei schimbări de bază este codificat de schimbarea matricei de bază, iar compoziția funcțiilor are ca rezultat omultiplicare între matrice .
Eliminarea lui Gauss
Eliminarea lui Gauss este un algoritm care permite reducerea unei matrice într-o formă mai simplă prin mișcări oportune pe linii. Acest algoritm este utilizat în principal pentru a determina soluțiile unui sistem de ecuații liniare, dar are și mai multe aplicații interne la algebra liniară: cu eliminarea lui Gauss putem determina rangul , determinantul sau inversul unei matrice, putem extrage o bază dintr-un set de generatoare .
Determinant

Determinantul este un număr asociat cu o matrice pătrată , denumit în general . Din punct de vedere algebric, determinantul este important deoarece este zero exact atunci când matricea nu este inversabilă ; când nu este zero, oferă și o metodă pentru descrierea matricei inverse folosind regula lui Cramer .
Din punct de vedere geometric, determinantul oferă multe informații despre transformarea asociată : semnul său (pe numere reale) indică dacă transformarea menține orientarea spațiului, iar valoarea sa absolută indică modul în care zonele obiectelor se schimbă după transformare.
Valori proprii și vectori proprii

Pentru a caracteriza un endomorfism este util să studiem unii vectori, numiți vectori proprii . Geometric, un vector propriu este un vector care nu schimbă direcția. Din punct de vedere algebric, este un vector astfel încât
pentru unele alpinism , numită valoare proprie . Endomorfismul este deosebit de simplu de descris dacă este diagonalizabil : geometric, aceasta înseamnă că există o bază de vectori proprii; algebric, înseamnă că endomorfismul poate fi reprezentat printr-o matrice diagonală , cum ar fi
Valorile proprii pot fi ușor găsite calculând polinomul caracteristic al matricei asociate, definit ca
Valorile proprii ale sunt tocmai rădăcinile acestui polinom. Vectorii proprii se organizează în subespaiuri vectoriale numite spații proprii. Când spațiul vectorial este un spațiu de funcții, valoarea proprie este o funcție specială, numită funcție proprie .
Forma canonică Iordania
Un endomorfism diagonalizabil poate fi ușor reprezentat prin intermediul unei matrice diagonale. Cu toate acestea, nu toate endomorfismele sunt diagonalizabile: de exemplu, o rotație în sens invers acelor de ceasornic a planului cartezian de unghi este reprezentat de matrice
că pentru diferit de 0 e ) nu are nici valori proprii, nici vectori proprii și, prin urmare, a fortiori nu poate fi diagonalizabilă. Un alt exemplu de matrice non-diagonalizabilă este următorul
Cu toate acestea, dacă câmpul considerat este câmpul de numere complexe , este totuși posibil să se reprezinte endomorfismul printr-o matrice care seamănă pe cât posibil cu o matrice diagonală, ca în al doilea exemplu prezentat. Această reprezentare, numită forma canonică a lui Jordan , caracterizează complet endomorfismele. Există o reprezentare similară în domeniul real, puțin mai complicată.
Ortogonalizare
Similar unui endomorfism, un produs scalar poate fi reprezentat și de o matrice pătrată . Anche in questo contesto, la forma più semplice da trattare è quella in cui la matrice risulta essere diagonale, e questo accade precisamente quando si fissa una base ortogonale .
A differenza degli endomorfismi, in questo contesto è sempre possibile trovare una matrice diagonale. In altre parole, per qualsiasi prodotto scalare è possibile trovare basi ortogonali. Se il prodotto scalare è definito positivo , un algoritmo efficiente a questo scopo è l' ortogonalizzazione di Gram-Schmidt . Per prodotti scalari più generali si può usare l' algoritmo di Lagrange .
Teoremi
Teorema della dimensione
Il teorema della dimensione (o del rango ) è un teorema che mette in relazione le dimensioni del nucleo e dell' immagine di un'applicazione lineare , secondo la formula:
Qui Im e Ker denotano immagine e nucleo, mentre è la dimensione del dominio di . Questo risultato è anche chiamato teorema del rango , perché tradotto nel linguaggio delle matrici assume la forma seguente:
Qui rk e null indicano rispettivamente il rango e l' indice di nullità di una matrice del tipo .
Teorema di Rouché-Capelli
Il teorema di Rouché-Capelli dà alcune informazioni sull'insieme delle soluzioni di un generico sistema lineare:
Il teorema afferma due cose:
- il sistema ha soluzione se e solo se le matrici e hanno lo stesso rango ;
- se ci sono soluzioni, queste formano un sottospazio affine di dimensione , dove è il numero di incognite (cioè il numero di colonne di ).
In particolare, il numero di soluzioni può essere solo zero, uno o infinito (se le equazioni sono a coefficienti reali o complessi).
Il teorema è generalmente usato per determinare rapidamente se un sistema ammette una o più soluzioni: non può però essere usato per determinarle esplicitamente. Uno strumento per questo scopo è il metodo di eliminazione di Gauss .
Relazione di Grassmann
La formula di Grassmann mette in relazione le dimensioni di vari sottospazi, definiti a partire da due sottospazi e entrambi contenuti uno spazio fissato . La formula è la seguente:
Nell'espressione compaiono i sottospazi ottenuti come somma e intersezione di e .
Teorema spettrale
Il teorema spettrale fornisce una condizione forte di diagonalizzabilità per alcuni endomorfismi, detti simmetrici o autoaggiunti (a volte il termine operatore è usato come sinonimo di endomorfismo). La nozione di endomorfismo simmetrico (o operatore autoaggiunto) dipende dalla presenza di un fissato prodotto scalare definito positivo (o hermitiano se si usano spazi vettoriali complessi ). Il teorema spettrale asserisce che un tale endomorfismo ha una base ortonormale formata da autovettori .
Generalizzazione e argomenti correlati
I metodi dell'algebra lineare sono stati estesi ad altre branche della matematica, grazie al loro successo. Nella teoria dei moduli si sostituisce il campo degli scalari con un anello . L' algebra multilineare si occupa dei problemi che mappano linearmente 'molte variabili' in un numero differente di variabili, portando inevitabilmente al concetto di tensore . Nella teoria spettrale degli operatori si riescono a gestire matrici di dimensione infinita applicando l' analisi matematica in una teoria non puramente algebrica. In tutti questi casi le difficoltà tecniche sono maggiori. Inoltre, l'algebra lineare viene a essere fondamentale per ambiti riguardanti l'ottimizzazione, in particolare la ricerca operativa .
Note
- ^ Gatto, Letterio., Lezioni di algebra lineare e geometria per l'ingegneria : i veri appunti del corso , CLUT, 2013, ISBN 9788879923439 , OCLC 956082822 . URL consultato il 19 marzo 2019 .
- ^ Più precisamente, questo accade per uno spazio vettoriale reale dotato di un prodotto scalare definito positivo .
- ^ Lo spazio delle soluzioni di un sistema è uno spazio affine , ed il teorema di Rouché-Capelli fornisce un metodo per calcolarne la dimensione. Il numero di soluzioni può essere solo 0, 1 o infinito.
- ^ Problemi computazionali che limitano l'uso della Regola di Cramer
Bibliografia
- ( IT ) Ciro Ciliberto (1994): Algebra lineare , Boringhieri
- ( IT ) Serge Lang (2014): Algebra lineare , Boringhieri
- ( EN ) Steven Roman (1992): Advanced linear algebra , Springer, ISBN 0-387-97837-2
- ( EN ) de Boor, Carl, Applied Linear Algebra , (University of Wisconsin-Madison, 2002).
- ( EN ) Rife, Susan A, Matrix Algebra. [ collegamento interrotto ] (Naval Postgraduate School, Monterey, California, 1996)
- ( EN ) Delatorre, Anthony R. e Cooke, William K., Matrix Algebra. [ collegamento interrotto ] (Naval Postgraduate School, Monterey, California, 1998)
- ( EN ) Beezer, Rob, A First Course in Linear Algebra , licenza GFDL .
- ( EN ) JHM Wedderburn Lectures on Matrices (American Mathematical Society, Providence, 1934) ISBN 0-8218-3204-2
- ( EN ) Fearnley-Sander, Desmond, Hermann Grassmann and the Creation of Linear Algebra , American Mathematical Monthly 86 (1979), pp. 809 – 817.
- ( EN ) Grassmann, Hermann, Die lineale Ausdehnungslehre ein neuer Zweig der Mathematik: dargestellt und durch Anwendungen auf die übrigen Zweige der Mathematik, wie auch auf die Statik, Mechanik, die Lehre vom Magnetismus und die Krystallonomie erläutert , O. Wigand, Leipzig, 1844.
- ( EN ) Shafarevich, Igor R. , Remizov, Alexey O. Linear Algebra and Geometry , Springer, 2012, ISBN 978-3-642-30993-9
Voci correlate
- Algoritmo di Lagrange
- Autovalore e autovettore
- Base (algebra lineare)
- Determinante
- Dimensione (spazio vettoriale)
- Eliminazione di Gauss
- Forma canonica di Jordan
- Formula di Grassmann
- Matrice
- Ortogonalizzazione di Gram-Schmidt
- Prodotto scalare
- Sistema di equazioni lineari
- Spazio vettoriale
- Teorema della dimensione
- Teorema di Rouché-Capelli
- Teorema spettrale
- Trasformazione lineare
Altri progetti
-
 Wikibooks contiene testi o manuali su algebra lineare
Wikibooks contiene testi o manuali su algebra lineare -
 Wikizionario contiene il lemma di dizionario « algebra lineare »
Wikizionario contiene il lemma di dizionario « algebra lineare » -
 Wikiversità contiene risorse su algebra lineare
Wikiversità contiene risorse su algebra lineare -
 Wikimedia Commons contiene immagini o altri file su algebra lineare
Wikimedia Commons contiene immagini o altri file su algebra lineare
Collegamenti esterni
- Algebra lineare , in Enciclopedia Italiana , Istituto dell'Enciclopedia Italiana .
- Algebra lineare , su sapere.it , De Agostini .
- ( EN ) Algebra lineare , su Enciclopedia Britannica , Encyclopædia Britannica, Inc.
- ( EN ) IV Proskuryakov, Linear algebra , in Encyclopaedia of Mathematics , Springer e European Mathematical Society, 2002.
- ( EN ) Linear Algebra Toolkit .
- ( EN ) Linear Algebra Workbench : moltiplica e inverte matrici, risolve sistemi, trova autovalori, ecc.
| Controllo di autorità | Thesaurus BNCF 17729 · LCCN ( EN ) sh85003441 · GND ( DE ) 4035811-2 · BNF ( FR ) cb11937509n (data) · BNE ( ES ) XX527736 (data) · NDL ( EN , JA ) 00570681 |
|---|



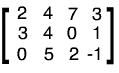


































![\ Psi: C ([0,1]) \ to \ mathbb {R}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68ed84309d7b35cb6ba83d082940007174977575)
![C ([0,1])](https://wikimedia.org/api/rest_v1/media/math/render/svg/44211c4c325ea7edb9462e7ccecda09841a41216)











































