Algoritmul lui Prim

Algoritmul lui Prim
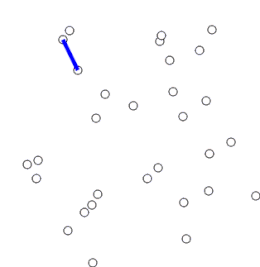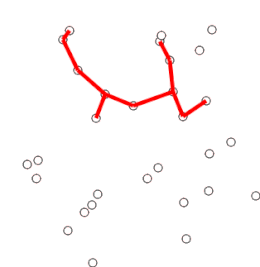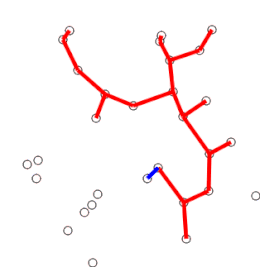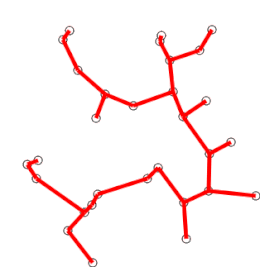
Executarea algoritmului lui Prim
Clasă	Arborele minim de acoperire
Structură de date	Grafic
Cel mai rău caz din punct de vedere temporal	$O(\|E\|+\|V\|\log \|V\|)$ ${\ displaystyle O (\| E \| + \| V \| \ log \| V \|)}$ $O (\| E \| + \| V \| \ log \| V \|)$
Manual

Algoritmul lui Prim este un algoritm optim utilizat în teoria graficelor , informatică și cercetarea operațiunilor pentru a determina copacii minimi care se întind dintr-un grafic neorientat cu greutăți non-negative.

Istorie

A fost inițial dezvoltat în 1930 de matematicianul ceh Vojtěch Jarník și mai târziu, în 1957, a fost dezvoltat independent de informaticianul Robert C. Prim . În 1959 a fost redescoperită de Edsger Dijkstra . Datorită contribuțiilor acestor cercetători, este adesea menționat ca algoritm DJP (Dijkstra, Jarnìk, Prim), algoritm Jarnik sau algoritm Prim-Jarnik.

Caracteristici

Caracteristicile algoritmului lui Prim pot fi rezumate în următoarele puncte:

Algoritm lacom : deoarece evaluează din când în când cele mai bune soluții locale fără a pune la îndoială alegerile anterioare.
Algoritm exact : deoarece oferă o soluție precisă pentru fiecare instanță a problemei fără a face rotunjiri sau alte inexactități.
Algoritm excelent : deoarece prezintă cea mai bună soluție (sau, cu aceeași calitate a soluțiilor, una dintre cele mai bune soluții).

Descriere

Pentru descrierea algoritmului, se presupune că graficul este reprezentat folosind o structură de date numită listă de adiacență, care se realizează de obicei cu o matrice căreia fiecare poziție îi corespunde un vârf. Fiecare element al matricei indică o listă generică legată care va conține toate vârfurile adiacente vârfului considerat. Mai mult, se presupune că fiecare vârf v are câmpurile de date cheie [v] și π [v] , respectiv valoarea asociată vârfului și indicatorul către părintele acestuia din urmă în cadrul MST.

Inițial, toate câmpurile cheie [v] sunt setate la + ∞ și toate câmpurile π [v] la NIL.
Luăm orice vârf ca rădăcină a copacului și setăm cheia acestuia la 0.
Toate vârfurile rămase sunt inserate într-o structură de date adecvată (de obicei o coadă prioritară ) și extrase în ordine crescătoare.
Lista adiacențelor vârfului extras ( u ) este apoi derulată luând în considerare doar vârfurile ( v ) încă în interiorul structurii auxiliare.
Pentru fiecare dintre ele astfel încât distanța sa de u este cea mai mică dintre toate cele luate în considerare, stabilim π [v] egal cu u inserând v în MST.
Ciclul se încheie prin actualizarea câmpului cheie [v] cu valoarea distanței dintre u și v .

Utilizarea unei structuri de date auxiliare este de dorit pentru a evita să verifice continuu dacă vârful considerat într-unul din pașii algoritmului a fost deja văzut anterior.

Cu alte cuvinte, având în vedere un grafic G = (V, E) (V este setul de vârfuri sau noduri, E este setul de arce) și un arbore de soluție S în care vom plasa nodurile atinse în diferiții pași ai algoritmului procedăm după cum urmează: plasez în S un nod de pornire (arbitrar) din care voi alege apoi arcul incident de greutate minimă care nu este conectat la noduri aparținând arborelui soluției S. După ce am făcut alegerea ramurii din pasul I anterior va include în S vârful conectat la vârful de pornire din ramura tocmai aleasă. La fiecare vârf pe care îl includ în S, ramurile incidente ale acelui vârf vor fi adăugate ramurilor dintre care o voi alege pe cea mai puțin costisitoare care se conectează la un vârf care nu aparține lui S. Algoritmul se termină atunci când cardinalitatea (numerozitatea) S este egal cu cel al lui V (acest lucru este valabil numai dacă graficul este conectat).

Analiza complexității

Complexitatea algoritmului lui Prim depinde de implementarea structurii de date auxiliare utilizate pentru a conține nodurile din pasul (3). Dacă este implementat cu o coadă prioritară și presupunând o complexitate constantă, testul prezenței sau absenței în coadă, timpul total de execuție al algoritmului este $O(V\cdot \log {V}+E\cdot \log {V})$ ${\ displaystyle O (V \ cdot \ log {V} + E \ cdot \ log {V})}$ ${\ displaystyle O (V \ cdot \ log {V} + E \ cdot \ log {V})}$ unde este $V\cdot \log {V}$ ${\ displaystyle V \ cdot \ log {V}}$ ${\ displaystyle V \ cdot \ log {V}}$ este timpul necesar operațiunilor de extracție din coadă și $E\cdot \log {V}$ ${\ displaystyle E \ cdot \ log {V}}$ ${\ displaystyle E \ cdot \ log {V}}$ este timpul necesar pentru a parcurge listele de adiacență și a efectua atribuirea menționată la pasul (6).

Deci timpul total de execuție al algoritmului lui Prim este $O(E\cdot \log {V})$ ${\ displaystyle O (E \ cdot \ log {V})}$ ${\ displaystyle O (E \ cdot \ log {V})}$ .

Dacă coada de prioritate se face cu Fibonacci Heap, timpul de execuție poate fi îmbunătățit în continuare. De fapt, timpul de inserare și reducere a cheii este redus $O(1)$ ${\ displaystyle O (1)}$ $O (1)$ , amortizat de deleteKeys cu cost $O(\log {V})$ ${\ displaystyle O (\ log {V})}$ ${\ displaystyle O (\ log {V})}$ .

Implementarea algoritmului lui Prim cu Fibonacci Heap este cel mai eficient care poate fi obținut, de fapt costul de execuție este $O(E+V\cdot \log {V})$ ${\ displaystyle O (E + V \ cdot \ log {V})}$ ${\ displaystyle O (E + V \ cdot \ log {V})}$ . Pentru a confirma acest lucru, luați în considerare un grafic complet conectat ( $E=O(V^{2})$ ${\ displaystyle E = O (V ^ {2})}$ ${\ displaystyle E = O (V ^ {2})}$ ) și se compară timpii de execuție.

Algoritmul lui Prim este un exemplu perfect al modului în care structurile de date eficiente vă permit să rezolvați eficient o problemă.

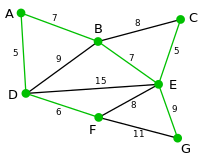
Exemplu

Noduri procesate	Partile disponibile	Noduri în coadă	Descriere
{}		{A, B, C, D, E, F, G}	Grafic direcțional original, numerele de pe laturi indică greutatea lor. Un vârf arbitrar poate fi ales ca punct de plecare și aici vom continua alegând vârful D. Note despre coloana „imagine”: nodurile și laturile care au fost alese pentru reintrarea în soluție vor fi indicate în verde. laturile care sunt evaluate vor fi indicate cu albastru alegerea curentă de adăugat soluției parțiale va fi indicată în albastru. în negru vor fi indicate laturile care nu se încadrează în soluție sau care nu sunt considerate deoarece sunt conectate la noduri care nu sunt încă accesibile de soluția actuală sau pentru că sunt conectate la noduri deja atinse din alte părți la un cost mai mic.
{D}	{D, A} = 5 V {D, B} = 9 {D, E} = 15 {D, F} = 6	{A, B, C, E, F, G}	Vârfurile A , B , E și F sunt cele conectate direct la D. A este 5, B este 9, E este 15, F este 6. Vârful cel mai apropiat de D este A și, prin urmare, este selectat împreună cu latura AD .
{LA}	{D, B} = 9 {D, E} = 15 {D, F} = 6 V {A, B} = 7	{B, C, E, F, G}	Următorul vârf de ales va fi cel mai apropiat de D sau A. B este 9 din D și 7 din A , E este 15 din D și F este 6 din D. Dintre toate vârfurile, F este cel mai apropiat și, prin urmare, este ales împreună cu partea DF care îl unește.
{A, D, F}	{D, B} = 9 {D, E} = 15 {A, B} = 7 V {F, E} = 8 {F, G} = 11	{B, C, E, G}	Algoritmul continuă ca la pașii anteriori. Partea cea mai apropiată de D , A sau F trebuie aleasă dintre B , E sau G. Observând greutățile, se dovedește a fi B, care este doar 7 din A și, prin urmare, este ales împreună cu partea de îmbinare AB .
{A, B, D, F}	{B, C} = 8 {B, E} = 7 V {D, B} = 9 cicluri {D, E} = 15 {F, E} = 8 {F, G} = 11	{C, E, G}	În acest caz, putem alege între C , E și G. Vertex C este 8 din B , E este 7 din B și G este 11 din F. Vertexul E este cel mai apropiat, așa că să alegem vârful E împreună cu latura BE .
{A, B, D, E, F}	{B, C} = 8 {D, B} = 9 cicluri {D, E} = 15 cicluri {E, C} = 5 V {E, G} = 9 {F, E} = 8 cicluri {F, G} = 11	{C, G}	Singurele vârfuri disponibile sunt C și G. C este 5 din E și G este 9 din E. C este cel mai apropiat și se alege împreună cu partea CE .
{A, B, C, D, E, F}	{B, C} = 8 cicluri {D, B} = 9 cicluri {D, E} = 15 cicluri {E, G} = 9 V {F, E} = 8 cicluri {F, G} = 11	{G}	Vertexul G este singurul vârf rămas. Este 11 din F și 9 din E. E este cel mai apropiat, așa că alegem G împreună cu partea EG .
{A, B, C, D, E, F, G}	{B, C} = 8 cicluri {D, B} = 9 cicluri {D, E} = 15 cicluri {F, E} = 8 cicluri {F, G} = 11 cicluri	{}	Toate vârfurile au fost selectate și arborele care se întinde pe cel mai mic cost este afișat în verde. În acest caz, costul este de 39.

Aplicații

În cadrul teoriei graficelor își găsește aplicarea în identificarea graficelor și a componentelor conectate. De asemenea, are multe aplicații practice care nu au legătură directă cu teoria graficelor. (de exemplu, este folosit pentru a dezvolta labirinturi).

Variat

Poate fi folosit și pe grafice orientate cu greutate non-negativă, dar în această situație își pierde caracteristica de a fi un algoritm optim. Pentru aceste tipuri de grafice, algoritmul lui Prim prezintă o soluție, dar nu este cea optimă.

Bibliografie

Thomas H. Cormen , Charles E. Leiserson , Ronald L. Rivest , Clifford Stein .Introducere în algoritmi , ediția a doua. MIT Press și McGraw-Hill, 2001. ISBN 0-262-03293-7 . Secțiunea 23.2: Algoritmii lui Kruskal și Prim, pp. 567-574. Ediție italiană de la p. 480 la p. 490.
Robert E. Tarjan, Structuri de date și algoritmi de rețea , Philadelphia, Society for Industrial and Applied Mathematics, 1983, ISBN 978-0-89871-187-5 ,OCLC 10120539 .

Elemente conexe

Alte proiecte

Wikimedia Commons conține imagini sau alte fișiere despre algoritmul lui Prim

Portal IT

Portalul de matematică