Algebra booleană

Algebra booleană (numită și algebră booleană sau rețea booleană ), în matematică și logică matematică , este ramura algebrei în care variabilele pot presupune doar valori adevărate și false ( valori de adevăr ), denotate în general respectiv ca 1 și 0.

fundal

Concepută în 1847 la University College Cork de George Boole în cartea sa Analiza matematică a logicii pentru a scrie logică propozițională în formă algebrică și dezvoltată în continuare de el în 1854 în An Investigation of the Laws of Thought , algebra booleană a fost fundamentală în domeniul digitalului. electronică , unde în proiectarea circuitelor electronice teoremele deductibile din axiomele care stau la baza algebrei au o mare importanță, cum ar fi teorema Shannon din 1940, care arată cum să descompunem o funcție booleană complexă în funcții mai simple sau să obținem o expresie canonică dintr-o tabelul adevărului . Algebra booleană joacă un rol de importanță fundamentală în informatică , atât de mult încât fiecare limbaj de programare modern definește operatorii logici din cadrul ei; este folosit și în teoria și probabilitatea mulțimilor .

Descriere

Operațiile fundamentale nu sunt adunarea și scăderea, ci operatorii logici : conjuncția sau produsul logic indicat cu ∧ sau ȘI ; disjuncția sau suma logică indicată cu ∨ sau OR ; negarea sau complementarea indicată cu ¬ sau NU . Cu acest formalism putem descrie relațiile logice într-un mod similar cu ceea ce face algebra obișnuită cu relațiile numerice: combinația dintre AND, OR și NOT permite dezvoltarea oricărei funcții booleene și, prin urmare, cei trei operatori logici formează un set funcțional complet .

Definiție formală

Matematic, algebra booleană este orice rețea dotată cu proprietăți, cum ar fi distributivitatea , existența minimului și maximului și existența complementului : algebra booleană este criptomorfă , adică asociată biunivoc și în așa fel încât să fie logic echivalentă cu o parțial ordonată ansamblu reticulat. Pe de altă parte, fiecare algebră booleană se dovedește a fi criptomorfă pentru un anumit tip de inel, numit inel boolean . Structura poate fi specificată prin grupuri și inele sau prin rețele într-un mod complet echivalent.

Mai precis, vorbim de algebră booleană cu referire la un set K pe care sunt definite operațiile de sumă logică (+, OR) și produs logic (*, ȘI), adică o triplă $(K,+,*)$ ${\ displaystyle (K, +, *)}$ $(K, +, *)$ , care constituie o rețea în care sunt satisfăcute și proprietatea distributivă, existența minimului și maximului și existența complementului .

În detaliu, avem o algebră booleană când su $(K,+,*)$ ${\ displaystyle (K, +, *)}$ $(K, +, *)$ următoarele proprietăți sunt îndeplinite:

Comutativ: $a+b=b+a\qquad a*b=b*a$ ${\ displaystyle a + b = b + a \ qquad a * b = b * a}$ $a + b = b + a \ qquad a * b = b * a$

Asociativ: $a+(b+c)=(a+b)+c\qquad a*(b*c)=(a*b)*c$ ${\ displaystyle a + (b + c) = (a + b) + c \ qquad a * (b * c) = (a * b) * c}$ $a + (b + c) = (a + b) + c \ qquad a * (b * c) = (a * b) * c$

Absorbţie: $a+(a*b)=a\qquad a*(a+b)=a$ ${\ displaystyle a + (a * b) = a \ qquad a * (a + b) = a}$ $a + (a * b) = a \ qquad a * (a + b) = a$

Distributiv: $a*(b+c)=(a*b)+(a*c)\qquad a+(b*c)=(a+b)*(a+c)$ ${\ displaystyle a * (b + c) = (a * b) + (a * c) \ qquad a + (b * c) = (a + b) * (a + c)}$ $a * (b + c) = (a * b) + (a * c) \ qquad a + (b * c) = (a + b) * (a + c)$

Idempotență

a+a=a\qquad a*a=a

{\ displaystyle a + a = a \ qquad a * a = a}

a + a = a \ qquad a * a = a

Existența minimului și maximului: $a*0=0\qquad a+1=1$ ${\ displaystyle a * 0 = 0 \ qquad a + 1 = 1}$ $a * 0 = 0 \ qquad a + 1 = 1$

Complementează existența: $a*{\overline {a}}=0\qquad a+{\overline {a}}=1$ ${\ displaystyle a * {\ overline {a}} = 0 \ qquad a + {\ overline {a}} = 1}$ ${\ displaystyle a * {\ overline {a}} = 0 \ qquad a + {\ overline {a}} = 1}$

Modul în care sunt listate proprietățile vrea să evidențieze simetria care există între cei doi operatori, care se află atunci la originea legii dualității și a altor proprietăți foarte importante. În listarea axiomelor, complementul a fost indicat cu o cratimă pe variabilă (ceea ce este tipografic dificil de realizat, chiar dacă este cea mai bună notație); complementul poate fi indicat și cu un „!” (punctul de exclamare) înainte de variabila booleană (notație tipică programării în C și C ++), cu o bară înaintea variabilei sau chiar cu un semn minus înaintea ei, atunci când nu este o notație echivocă. Complementul corespunde operației logice NU .

O observație finală se referă la faptul că primele 4 proprietăți se referă la rețele în general, în timp ce cele rămase sunt tipice algebrei booleene, care vor fi, prin urmare, indicate cu sextuple $(K,+,*,!,0,1)$ ${\ displaystyle (K, +, *,!, 0,1)}$ ${\ displaystyle (K, +, *,!, 0,1)}$ . Având în vedere formularea generală, din acest moment ne referim la algebra primordială , pe care o consideră $K=\{0,1\}$ ${\ displaystyle K = \ {0,1 \}}$ ${\ displaystyle K = \ {0,1 \}}$ , adică mulțimea pe care se bazează algebra booleană este compusă doar din minim și maxim.

Legea dualității și unele proprietăți care derivă din axiomele acum văzute cu dovezile relative sunt acum enumerate; pe lângă aceste consecințe, există două teoreme importante ale algebrei booleene, care sunt teoremele lui De Morgan și teorema lui Shannon . Teoremele pe care le dovedim acum sunt valabile pentru orice „porțiune a realității” care satisface axiomele acestei algebre abstracte și, în special, vor fi aplicabile în algebra mulțimilor , în algebra logicii propozițiilor și în algebra lui circuite.

Legea dualității

Din orice identitate booleană poate fi extrasă alta prin dualitate , adică prin înlocuirea fiecărui operator și a elementelor 0 și 1 cu dualul respectiv: dualul + este *, dualul 0 este 1 (dovada acestui lucru se află în următoarea paragraf), dualul a este , în general! a (a negată, NU a).

Datorită acestei legi, putem vedea cum cele 14 postulate date pentru a defini algebra booleană nu sunt toate independente unele de altele: în special, vedem că PX și PX '(pentru X = 1, ..., 7) sunt unul dintre dual al celuilalt.

Completele 0 și 1

0 și 1 sunt complementare unele cu altele: pentru a o demonstra, trebuie doar să verificați definiția complementului, adică aceea

a*{\overline {a}}=0\qquad a+{\overline {a}}=1

{\ displaystyle a * {\ overline {a}} = 0 \ qquad a + {\ overline {a}} = 1}

a * \ overline a = 0 \ qquad a + \ overline a = 1

Vezi imediat asta

1*0=0\qquad 1+0=1

{\ displaystyle 1 * 0 = 0 \ qquad 1 + 0 = 1}

{\ displaystyle 1 * 0 = 0 \ qquad 1 + 0 = 1}

prin aplicarea respectivă a proprietăților minimului și a celui al maximului și a teoremei menționate tocmai se dovedește.

Observăm că, datorită modului în care este structurată această algebră, această dovadă ne-a permis să demonstrăm pornind de la axiome că elementul neutru există și este unic (existența nu este deci postulată și unicitatea este inerentă existenței fiind doar 2 valorile Lucrează cu el, ceea ce nu este adevărat pentru alte tipuri de algebră și alte structuri algebrice).

Convoluţie

Negând același element de două ori, obținem același element (logică aristotelică: o dublă negație corespunde unei afirmații).

Pentru a demonstra acest lucru, este suficient să se ia în considerare axioma existenței complementului considerat pe două elemente a și b =! A :

a*{\overline {a}}=0\qquad a+{\overline {a}}=1

{\ displaystyle a * {\ overline {a}} = 0 \ qquad a + {\ overline {a}} = 1}

a * \ overline a = 0 \ qquad a + \ overline a = 1

b*{\overline {b}}={\overline {a}}*!{\overline {a}}=0\qquad b+{\overline {b}}={\overline {a}}+!{\overline {a}}=1

{\ displaystyle b * {\ overline {b}} = {\ overline {a}} *! {\ overline {a}} = 0 \ qquad b + {\ overline {b}} = {\ overline {a}} +! {\ overline {a}} = 1}

b * \ overline b = \ overline a *! \ overline a = 0 \ qquad b + \ overline b = \ overline a +! \ overline a = 1

Deoarece proprietatea comutativă este validă și deoarece complementul există unic, se poate deduce cu ușurință că $!{\overline {a}}=a$ ${\ displaystyle! {\ overline {a}} = a}$ $! \ overline a = a$ , ceea ce au vrut să demonstreze.

Elemente neutre

0 este elementul neutru al sumei (disjuncție logică, ∨, OR) și 1 este elementul neutru al produsului (conjuncție logică, ∧, ȘI).

Pentru demonstrație, este suficient să exploatăm proprietatea absorbției datorită căreia deducem că:

a+(a*0)=a\qquad a*(a+1)=a

{\ displaystyle a + (a * 0) = a \ qquad a * (a + 1) = a}

a + (a * 0) = a \ qquad a * (a + 1) = a

Acum, exploatând proprietatea maximului și minimului pentru care a * 0 = 0 și a + 1 = 1, este ușor de dedus că:

a+0=a\qquad a*1=a

{\ displaystyle a + 0 = a \ qquad a * 1 = a}

a + 0 = a \ qquad a * 1 = a

ceea ce trebuia arătat.

Absorbția complementului (a doua teoremă de absorbție)

Absorbția complementului spune că

a+{\overline {a}}*b=a+b

{\ displaystyle a + {\ overline {a}} * b = a + b}

a + \ overline a * b = a + b

Pentru a demonstra acest lucru, este suficient să se aplice proprietatea distributivă conform căreia:

a+{\overline {a}}*b=(a+{\overline {a}})*(a+b)

{\ displaystyle a + {\ overline {a}} * b = (a + {\ overline {a}}) * (a + b)}

a + \ overline a * b = (a + \ overline a) * (a + b)

apoi, observând că a +! a = 1 și că 1 este elementul neutru al produsului logic, se demonstrează teorema.

Prin legea dualității se înțelege, de asemenea, că există o teoremă dublă a ceea ce va fi:

{\overline {a}}*(a+{\overline {b}})={\overline {a}}*{\overline {b}}

{\ displaystyle {\ overline {a}} * (a + {\ overline {b}}) = {\ overline {a}} * {\ overline {b}}}

\ overline a * (a + \ overline b) = \ overline a * \ overline b

Această teoremă poate fi considerată adevărată prin acceptarea validității legii dualității sau poate fi dovedită într-un mod destul de similar cu cel anterior. Trebuie remarcat faptul că, în scrierea expresiei duale, trebuia respectată prioritatea de aplicare a operațiilor și, prin urmare, parantezele din jurul a +! B ale celei de-a doua expresii sunt necesare .

Teorema unui singur element

De sine $x+y=a$ ${\ displaystyle x + y = a}$ $x + y = a$ Și $xy=0$ ${\ displaystyle xy = 0}$ $xy = 0$ , atunci y este unic (sau chiar x este unic deoarece vedem că, din moment ce proprietatea comutativă este validă, rolul lui x și y în expresii este același).

Pentru demonstrație, se presupune absurd că există două valori distincte y și z care satisfac cele două expresii, și anume

x+y=x+z=a\qquad xy=xz=0

{\ displaystyle x + y = x + z = a \ qquad xy = xz = 0}

x + y = x + z = a \ qquad xy = xz = 0

Fiind și asta

xy=x{\overline {x}}+xy=x({\overline {x}}+y)\qquad xz={\overline {x}}x+xz=x({\overline {x}}+z)

{\ displaystyle xy = x {\ overline {x}} + xy = x ({\ overline {x}} + y) \ qquad xz = {\ overline {x}} x + xz = x ({\ overline {x }} + z)}

xy = x \ overline x + xy = x (\ overline x + y) \ qquad xz = \ overline xx + xz = x (\ overline x + z)

s-a obținut că

xy=xz=0\Rightarrow x({\overline {x}}+y)=x({\overline {x}}+z)\Rightarrow {\overline {x}}+y={\overline {x}}+z

{\ displaystyle xy = xz = 0 \ Rightarrow x ({\ overline {x}} + y) = x ({\ overline {x}} + z) \ Rightarrow {\ overline {x}} + y = {\ overline {x}} + z}

xy = xz = 0 \ Rightarrow x (\ overline x + y) = x (\ overline x + z) \ Rightarrow \ overline x + y = \ overline x + z

În ultimul pas, principiul echivalenței egalităților a fost exploatat și x nu a fost simplificat, ceea ce nu a fost dovedit și nu poate fi dovedit în această algebră. Deci, ceea ce aveți acum este că

x+y=x+z\qquad {\overline {x}}+y={\overline {x}}+z

{\ displaystyle x + y = x + z \ qquad {\ overline {x}} + y = {\ overline {x}} + z}

x + y = x + z \ qquad \ overline x + y = \ overline x + z

Înmulțind membru cu membru și folosind proprietatea distributivă, avem:

(x+y)*({\overline {x}}+y)=x{\overline {x}}+xy+{\overline {x}}y+y=0+(x+{\overline {x}})y+y=y=(x+z)*({\overline {x}}+z)=z

{\ displaystyle (x + y) * ({\ overline {x}} + y) = x {\ overline {x}} + xy + {\ overline {x}} y + y = 0 + (x + {\ overline {x}}) y + y = y = (x + z) * ({\ overline {x}} + z) = z}

(x + y) * (\ overline x + y) = x \ overline x + xy + \ overline xy + y = 0 + (x + \ overline x) y + y = y = (x + z) * (\ suprasolicitați x + z) = z

adică y = z și, prin urmare, elementul care satisface cele două relații scrise mai sus este unic.

Principiul eliminării

După cum sa menționat mai devreme, principiile eliminării nu sunt valabile în algebra booleană, adică nu este valabil ca:

x+y=x+z\Rightarrow y=z\qquad xy=xz\Rightarrow y=z

{\ displaystyle x + y = x + z \ Rightarrow y = z \ qquad xy = xz \ Rightarrow y = z}

x + y = x + z \ Rightarrow y = z \ qquad xy = xz \ Rightarrow y = z

Este adevărat că y = z numai dacă aceste două expresii scrise acum se mențin simultan.

Singurul lucru care se poate spune în schimb dacă se menține doar prima expresie este că:

x+y=x+z\Rightarrow {\overline {x}}y={\overline {x}}z

{\ displaystyle x + y = x + z \ Rightarrow {\ overline {x}} y = {\ overline {x}} z}

x + y = x + z \ Rightarrow \ overline xy = \ overline xz

Funcții booleene

Același subiect în detaliu: funcția booleană .

Algebra booleană este tratamentul algebrei universale cu două stări și modelele acestei teorii, numite algebre booleene . Algebra universală se ocupă cu studierea familiei de operații pe un set, numit setul fundamental al familiei algebrice și, în cazul structurii algebrice booleene, aceasta conține doar valorile 0 și 1. În practică, algebrele booleene se ocupă de tratamentul funcțiilor booleene ale căror noțiuni principale sunt menționate acum: studiul acestor funcții este fundamental astăzi pentru studiul circuitelor și rețelelor logice, prin urmare scopurile lor practice pot fi imediat văzute, dar importanța acestor structuri algebrice nu este limitată numai pentru aceasta, deoarece este fundamental și în studiul propozițiilor și al mulțimilor, care sunt argumente puțin mai abstracte, dar la fel de valabile și importante.

Numărul de argumente care necesită o operație definită pe setul fundamental se numește arity (o adăugare, de exemplu, este o operație a arity 2, numită și operație binară ): o operație pe {0,1} a arity n poate trebuie aplicat pentru fiecare din cele 2 valori posibile pentru ⁿ argumentele sale ( de exemplu , este suficient să se calculeze dispozițiile 2 elemente de pe n locuri), de exemplu , dacă avem o operație de aritate 3, având în vedere că K = {0 , 1}, argumentele posibile sunt 000,001,010,011,100,101,110,111 care sunt 8.

Pentru fiecare alegere de argumente operația poate produce doar rezultatele 0 și 1 și pentru aceasta există 2 ^{2 ⁿ} operații de n argumente: acest număr corespunde deci numărului total de funcții posibile ale n variabilelor din algebra booleană.

Algebra cu două stări are 2 operații fără argumente (2 ^{2 ⁰} ) care returnează valorile 0 și 1 fără a lua în considerare niciun argument și 4 operații cu un singur argument (2 ^{2 ¹} ): există două operații posibile (2 ¹ ), identitate și negație și, prin urmare, în total operațiile sunt 4 deoarece avem 0 → 0 (id.), 0 → 1 (neg.), 1 → 0 (neg.), 1 → 1 (id.). Apoi, există 16 operații binare , 256 operații ternare, 65.536 operații cuaternare și așa mai departe.

Deoarece algebra despre care vorbește se bazează pe un set finit, o funcție poate fi reprezentată la fel ca și în formă algebrică (adică compoziția lui ȘI, SAU și NU), sub formă de tabel , adică cu un tabel în care fiecare compoziție a variabile de „intrare” (folosind o terminologie mai informatică) ieșirea (sau chiar ieșirile) este potrivită: toate funcțiile, inclusiv cele ale algebrelor, pot fi reprezentate teoretic prin tabele, dar dacă setul pe care se bazează algebra este infinit (de exemplu setul de numere reale) nu este un mod convenabil de a studia funcția; pentru algebra booleană, utilizarea tabelelor este o modalitate utilă de a studia funcțiile și, de exemplu, permite cu ușurință construirea de circuite și rețele logice în aplicații electronice. Un exemplu de tabele are în vedere operațiile binare pe care le-am văzut deja 16:

LA	B.	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15
0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

O familie , numită și index , este indexată de un set de indici , care în cazul unei familii de operații care constituie o algebră se numesc simboluri de operație și constituie limbajul algebrei în cauză. Operațiunea indexată de un simbol dat se numește interpretarea acelui simbol și fiecare simbol definește numărul unic de argumente ale interpretărilor sale posibile. În cazul luat în considerare, există o corespondență unu-la-unu între simbol și interpretare. Algebra booleană are atâtea simboluri câte operații posibile numite simboluri de operație booleană , chiar dacă puține operații au simboluri convenționale, cum ar fi! pentru negare, + pentru conjuncție și * pentru disjuncție. În general, ⁿ f _{i este} al i-lea simbol al n argumentelor. În ultimul exemplu considerat, în schimb, este dat un simbol pentru fiecare dintre cele 16 funcții posibile sau este, de asemenea, posibil să se exprime fiecare funcție ca o combinație adecvată a simbolurilor convenționale fundamentale, adică ȘI (*), SAU (+) si nu (!).

Funcție dublă

Având o funcție $f(x_{1},x_{2},\dots ,x_{n})$ ${\ displaystyle f (x_ {1}, x_ {2}, \ dots, x_ {n})}$ $f (x_ {1}, x_ {2}, \ dots, x_ {n})$ sub orice formă se numește funcție duală a $f$ ${\ displaystyle f}$ $f$ și este indicat cu $\delta f$ ${\ displaystyle \ delta f}$ $\ delta f$ o funcție care are forma duală de $f$ ${\ displaystyle f}$ $f$ , de exemplu:

y={\overline {a}}+b*(c+0)\qquad duale=a*({\overline {b}}+{\overline {c}}*1)

{\ displaystyle y = {\ overline {a}} + b * (c + 0) \ qquad dual = a * ({\ overline {b}} + {\ overline {c}} * 1)}

{\ displaystyle y = {\ overline {a}} + b * (c + 0) \ qquad dual = a * ({\ overline {b}} + {\ overline {c}} * 1)}

Forma duală trebuie să respecte precedența de aplicare a operației formei de pornire, din acest motiv, în care nu au existat paranteze, deoarece AND are prioritate față de OR, când AND devine OR și OR devine AND, pot fi necesare paranteze .

O altă observație foarte importantă este că variabilele, și nu constantele 0 și 1, nu pot fi negate, deoarece în orice caz variabila trebuie să-și asume toate valorile posibile și, prin urmare, indiferent dacă există sau nu negație, funcția nu se schimbă : în cazul văzut mai sus, atunci funcția duală poate fi scrisă și ca

duale={\overline {a}}*(b+c*1)

{\ displaystyle dual = {\ overline {a}} * (b + c * 1)}

dual = \ overline a * (b + c * 1)

unde observăm că constanta a fost negată. Această observație poate fi importantă atunci când se proiectează o rețea logică, deoarece înseamnă salvarea NU a porților sau chiar în general, în expresia algebrică este întotdeauna util să aveți mai puține operațiuni de făcut.

Bazele

Un set complet funcțional este un set de operații a căror compoziție permite obținerea tuturor operațiunilor aparținând algebrei și uneori la acestea se face referire la termenul bază , utilizat într-un sens diferit de bazele spațiilor vectoriale . Cele trei baze principale utilizate în algebra booleană sunt:

Zăbrele , o bază logică introdusă în secolul al 19 - lea de către George Boole , Charles Sanders Peirce și alți matematicieni care au căutat o formalizare algebrică a proceselor logice.
Inelul boolean , o bază (non-aritmetică) introdusă în secolul al XX-lea de Ivan Ivanovič Žegalkin și Marshall Stone care provine din algebra abstractă .
Baza NAND , provenind din faptul că prin operația NAND este posibil să se obțină toate operațiunile pe set {0,1}. Această bază este utilizată în special în configurația circuitelor logice din electronica digitală .

Elementele comune rețelei și inelului sunt constantele 0 și 1 și o operație binară asociativă și comutativă, care în baza rețelei se numește întâlnire , din termenul englezesc meet și notată între două elemente x și y prin simbolul x ∧ y , în timp ce în baza inelului se numește multiplicare și se notează xy . Baza rețelei are, de asemenea, operațiile algebrice de unire x ∨ y și complement ¬ x , în timp ce baza inelului are operația de adiție suplimentară (non-aritmetică) x ⊕ y sau x + y .

Reticul

În baza zăbrelei la o algebră booleană ( A , $\wedge$ ${\ displaystyle \ wedge}$ $\ wedge$ , $\vee$ ${\ displaystyle \ vee}$ $\ vee$ ) asociază un set parțial ordonat ( A , $\leq$ ${\ displaystyle \ leq}$ $\ leq$ ), definind:

$a\leq b\Leftrightarrow a=a\wedge b$ ${\ displaystyle a \ leq b \ Leftrightarrow a = a \ wedge b}$ $a \ leq b \ Leftrightarrow a = a \ wedge b$

care echivalează și cu

b=a\vee b

{\ displaystyle b = a \ vee b}

b = a \ vee b

De asemenea, este posibil să asociați o algebră booleană cu o rețea distributivă ( A , $\leq$ ${\ displaystyle \ leq}$ $\ leq$ ), considerat ca un set parțial ordonat, cu un element minim 0 și un element maxim 1, în care fiecare element x are un element complementar $\neg x$ ${\ displaystyle \ neg x}$ $\ neg x$ astfel încât

x\wedge \neg x=0

{\ displaystyle x \ wedge \ neg x = 0}

x \ wedge \ neg x = 0

Și

x\vee \neg x=1

{\ displaystyle x \ vee \ neg x = 1}

x \ vee \ neg x = 1

Aici $\wedge$ ${\ displaystyle \ wedge}$ $\ wedge$ Și $\vee$ ${\ displaystyle \ vee}$ $\ vee$ sunt folosite pentru a indica inf și sup a două elemente. Dacă complementele există, atunci acestea sunt unice.

Inel

Baza inelară a algebrei booleene generice ( A , $\wedge$ ${\ displaystyle \ wedge}$ $\ wedge$ , $\vee$ ${\ displaystyle \ vee}$ $\ vee$ ) este definit ca ( A , +, *), definind a + b: = ( a $\wedge \neg$ ${\ displaystyle \ wedge \ neg}$ $\ wedge \ neg$ b ) $\vee$ ${\ displaystyle \ vee}$ $\ vee$ ( b $\wedge \neg$ ${\ displaystyle \ wedge \ neg}$ $\ wedge \ neg$ a ). În acest inel elementul neutru pentru sumă coincide cu 0 algebrei booleene, în timp ce elementul neutru al înmulțirii este elementul 1 al algebrei booleene. Acest inel are proprietatea că a * a = a pentru fiecare a din A ; inelele cu această proprietate se numesc inele booleene .

Dimpotrivă, având în vedere un inel boolean A , acesta poate fi transformat într-o algebră booleană definind x $\vee$ ${\ displaystyle \ vee}$ $\ vee$ y = x + y - x $\cdot$ ${\ displaystyle \ cdot}$ $\ cdot$ y și x $\wedge$ ${\ displaystyle \ wedge}$ $\ wedge$ y = x $\cdot$ ${\ displaystyle \ cdot}$ $\ cdot$ y . Întrucât aceste două operații sunt inverse reciproc, se poate spune că fiecare inel boolean este criptomorf al unei algebre booleene și invers. Mai mult, o funcție f : A $\rightarrow$ ${\ displaystyle \ rightarrow}$ $\ sageata dreapta$ B este un homomorfism între algebre booleene dacă și numai dacă este un homomorfism între inelele booleene. Categoria inelelor booleene și a algebrelor booleene sunt echivalente.

Un inel ideal al algebrei booleene A este un subset I astfel încât pentru fiecare x , y în I avem x $\vee$ ${\ displaystyle \ vee}$ $\ vee$ y în I și pentru fiecare a în A a $\wedge$ ${\ displaystyle \ wedge}$ $\ wedge$ x în I. Această noțiune de ideal coincide cu noțiunea de inel ideal în inelele booleene. Un I ideal al lui A se numește prim dacă eu $\neq$ ${\ displaystyle \ neq}$ $\ neq$ A și dacă a $\wedge$ ${\ displaystyle \ wedge}$ $\ wedge$ b în I implică întotdeauna a în I sau b în I. Se spune că un I ideal al lui A este maxim dacă eu $\neq$ ${\ displaystyle \ neq}$ $\ neq$ A și dacă singurul ideal propriu care conține I este A în sine. Această notație coincide cu notația teoretică a idealului prim și idealului maxim din inelul boolean A.

Dualul unui ideal este un filtru . Un filtru din algebra booleană A este un subset F astfel încât pentru fiecare x , y în F avem x $\wedge$ ${\ displaystyle \ wedge}$ $\ wedge$ y în F și pentru fiecare a în A dacă a $\vee$ ${\ displaystyle \ vee}$ $\ vee$ x = a atunci a este în F.

Operația de completare * aplicată subseturilor trimite, prin urmare, idealurile în filtre și invers: dacă B este o algebră booleană și $I\subseteq B$ ${\ displaystyle I \ subseteq B}$ $I \ subseteq B$ un ideal al său (propriu), atunci ${\tilde {I}}=\{x^{*}:x\in I\}$ ${\ displaystyle {\ tilde {I}} = \ {x ^ {*}: x \ in I \}}$ ${\ tilde I} = \ {x ^ {*}: x \ in I \}$ este filtrul dual (adecvat) al lui I. Dacă în schimb $F\subseteq B$ ${\ displaystyle F \ subseteq B}$ $F \ subseteq B$ este un filtru (propriu), ${\tilde {F}}=\{x^{*}:x\in F\}$ ${\ displaystyle {\ tilde {F}} = \ {x ^ {*}: x \ în F \}}$ ${\ tilde F} = \ {x ^ {*}: x \ în F \}$ idealul dual (propriu-zis) al lui F.

Accident vascular cerebral Sheffer

Lovitura de bază Sheffer sau NAND se bazează pe operațiile NOT și AND, prin care este posibil să se obțină toate operațiile booleene. O algebră booleană poate fi definită atât prin NOT și AND, cât și prin NOT și OR, fiind posibil să se definească OR prin NOT și AND precum și AND prin NOT și OR:

a~AND~b=~NOT~(~NOT~a~OR~~NOT~b)

{\ displaystyle a ~ AND ~ b = ~ NOT ~ (~ NOT ~ a ~ OR ~~ NOT ~ b)}

a ~ AND ~ b = ~ NOT ~ (~ NOT ~ a ~ OR ~~ NOT ~ b)

a~OR~b=~NOT~(~NOT~a~AND~~NOT~b)

{\ displaystyle a ~ OR ~ b = ~ NOT ~ (~ NOT ~ a ~ AND ~~ NOT ~ b)}

a ~ OR ~ b = ~ NOT ~ (~ NOT ~ a ~ AND ~~ NOT ~ b)

Colecția tuturor subseturilor unui set dat, adică setul de părți sau set de mediu , echipat cu operațiile de unire , intersecție și completare a seturilor, care joacă rolul OR, ȘI și respectiv NU, constituie o algebră booleană .

Mai formal, dacă B este un ansamblu format din cel puțin 2 elemente, algebra booleană având B drept suport este structura algebrică formată din B, prin două operații binare pe B, OR și ȘI , printr-o operație unară NU pe B și din elementul 0 din B, care se bucură de următoarele proprietăți:

Simetria AND: $\forall a,b\in B:a~AND~b=b~AND~a$ ${\ displaystyle \ forall a, b \ în B: a ~ ȘI ~ b = b ~ ȘI ~ a}$ $\ forall a, b \ in B: a ~ AND ~ b = b ~ AND ~ a$
Simetria OR: $\forall a,b\in B:a~OR~b=b~OR~a$ ${\ displaystyle \ forall a, b \ în B: a ~ OR ~ b = b ~ OR ~ a}$ $\ forall a, b \ in B: a ~ OR ~ b = b ~ OR ~ a$
Implicarea NU: $\forall a\in B:NOT(NOT(a))=a$ ${\ displaystyle \ forall a \ în B: NOT (NOT (a)) = a}$ $\ forall a \ în B: NOT (NOT (a)) = a$
Legile lui De Morgan : $\forall a,b\in B:NOT(a~OR~b)=NOT(a)~AND~NOT(b)$ ${\ displaystyle \ forall a, b \ în B: NOT (a ~ OR ~ b) = NOT (a) ~ AND ~ NOT (b)}$ $\ forall a, b \ in B: NOT (a ~ OR ~ b) = NOT (a) ~ AND ~ NOT (b)$

Mulțimea B este, de asemenea, delimitată mai jos, fiind:

\forall a\in B:a~AND~\mathbf {0} =\mathbf {0} ;~a~OR~\mathbf {0} =a

{\ displaystyle \ forall a \ în B: a ~ AND ~ \ mathbf {0} = \ mathbf {0}; ~ a ~ OR ~ \ mathbf {0} = a}

\ forall a \ in B: a ~ AND ~ {\ mathbf {0}} = {\ mathbf {0}}; ~ a ~ OR ~ {\ mathbf {0}} = a

Elementul 1 este definit ca negarea sau complementul 0: 1: = NU (0). Prin urmare, mulțimea B este delimitată mai sus, fiind:

\forall a\in B:a~OR~\mathbf {1} =\mathbf {1} ;a~AND~\mathbf {1} =a

{\ displaystyle \ forall a \ în B: a ~ OR ~ \ mathbf {1} = \ mathbf {1}; a ~ AND ~ \ mathbf {1} = a}

\ forall a \ in B: a ~ OR ~ {\ mathbf {1}} = {\ mathbf {1}}; a ~ AND ~ {\ mathbf {1}} = a

și în special

0 ȘI 1 = 0; 0 SAU 1 = 1

De asemenea, definim, ca o operație derivată din cele anterioare, operatorul OR exclusiv binar, notat XOR:

\forall a,b\in B:a~XOR~b:=(a~OR~b)~AND~(NOT(a~AND~b))

{\ displaystyle \ forall a, b \ in B: a ~ XOR ~ b: = (a ~ OR ~ b) ~ AND ~ (NOT (a ~ AND ~ b))}

\ forall a, b \ in B: a ~ XOR ~ b: = (a ~ OR ~ b) ~ AND ~ (NOT (a ~ AND ~ b))

În această algebră diferența simetrică corespunde operatorului XOR:

\forall a,b\in B:a~XOR~b=b~XOR~a

{\ displaystyle \ forall a, b \ în B: a ~ XOR ~ b = b ~ XOR ~ a}

\ forall a, b \ in B: a ~ XOR ~ b = b ~ XOR ~ a

În electronică, poarta logică NAND constă din n intrări și o ieșire care merge la nivelul 0 numai dacă n intrări merg la nivelul 1. Corespunde conexiunii în serie a unei porți ȘI și a unei porți NOT .

Operatori booleni

Același subiect în detaliu: Poarta logică .

Am văzut că operatorii algebrei booleene pot fi reprezentați în diferite moduri, dar sunt adesea scrise pur și simplu ca ȘI, SAU și NU, care este scrierea pe care o folosim acum pentru a vorbi despre operatorii booleni. În descrierea circuitelor, pot fi folosite și NAND (NOT AND), NOR (NOT OR), XOR (exclusive OR) și XNOR (exclusive NOT OR).

Diferitele simboluri pentru a reprezenta operatorii sunt alese în funcție de domeniul în care se lucrează: matematicienii folosesc adesea simbolul + pentru OR, și × sau * pentru AND, deoarece în anumite moduri acești operatori funcționează într-un mod similar cu adăugarea și multiplicare. Negarea NU este adesea reprezentată de o linie trasă deasupra argumentului negației, adică expresia de negat. Sau în informatică se folosește simbolul | sau || pentru OR, & o && pentru AND, și ~ o! pentru NU (de exemplu, A SAU B ȘI NU C este egal cu A | B & ~ C sau A + B *! C). Dacă se referă la operatori cu simbolurile adunării și multiplicării și apoi intenționează negația ca și cum ar fi o „exponențiere”, este ușor să ne amintim ordinea de aplicare a operatorilor: mai întâi se aplică negațiile, apoi AND-urile și apoi OR-urile.

În proiectarea circuitelor electronice, se folosesc și operatorii scurți NAND (ȘI negat), NOR (SAU negat) și XNOR (XOR negat): acești operatori, la fel ca XOR, sunt combinații ale celor trei operatori de bază și sunt folosiți doar pentru a reda notația mai simplă.

Operatori:

NU - simboluri alternative: x , ~, ¬ ,! (în C , C ++ , C # și JavaScript )
ȘI - simboluri alternative: *, $\wedge$ ${\ displaystyle \ wedge}$ $\ wedge$ , &, && (în C , C ++ , C # și JavaScript ), DAR (atunci când este utilizat împreună cu NOT)
SAU - simboluri alternative: +, $\vee$ ${\ displaystyle \ vee}$ $\ vee$ , |, || (în C , C ++ , C # și JavaScript )
XOR - simboluri alternative: ⊕, ${\dot {\lor }}$ ${\ displaystyle {\ dot {\ lor}}}$ ${\ dot {\ lor}}$ , ∨ , ^, EOR, orr
NAND - simbol alternativ: ↑
NOR - simbol alternativ: ↓
XNOR - simbol alternativ: ≡, EQU

Valori:

adevărat - simboluri alternative: adevărat , 1 , PORNIT , DA ( DA ), ridicat
false - simboluri alternative: false , 0 , OFF , NO , low

În electronica digitală un bit 1 este definit ca fiind adevărat, atât în intrare, cât și în ieșire, care de obicei ia valoarea de 5 V , în timp ce bitul 0 este definit ca fals, atât în intrare cât și în ieșire, care ia valoarea de 0 V.

Următorii sunt cei mai comuni operatori și porțile lor logice respective:

NU

Același subiect în detaliu: Invertor .

Operatorul NOT returnează inversul valorii primite. O concatenare de NOT poate fi simplificată cu un singur NOT dacă numărul de repetări este impar sau cu niciuna dacă numărul de repetări este par. Inoltre la porta logica NOT possiede una sola variabile binaria.

A	NOT A
0	1
1	0

Spesso, al fine di semplificare espressioni complesse, si usano operatori brevi che uniscono l'operazione di NOT ad altre: questi operatori sono NOR (OR + NOT), NAND (AND + NOT), XNOR (XOR + NOT). La negazione, in questi casi, viene applicata dopo il risultato dell'operatore principale (OR, AND, XOR).

Il simbolo di una porta NOT è

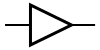
Buffer

Buffer è la negazione del risultato dell'operazione NOT; restituisce il valore uguale a quello in entrata. Il Buffer non è un vero e proprio operatore, poiché in realtà non manipola l'informazione che riceve, bensì la lascia passare invariata; il Buffer dunque è semplificabile con un collegamento privo di operatori.

A	Buffer A
0	0
1	1

Il simbolo di una porta Buffer è:

composta da un NOT in serie a un altro NOT.

La ragione per cui si parla di questo "pseudo-operatore" è data da questioni di sincronia dei segnali : quando si tratta di circuiti e reti logiche in modo più approfondito si rende necessario considerare anche il tempo in cui il segnale arriva e l'elemento buffer viene interpretato in questi casi come un ritardo applicato a un certo segnale.

AND

L'operazione AND restituisce come valore 1 se tutti gli elementi hanno valore 1, mentre restituisce 0 in tutti gli altri casi come ad esempio quando una porta è alta mentre le altre sono basse e può essere messa in serie. Tale operazione è anche detta prodotto logico. Di seguito la tabella rappresenta l'operatore AND nel caso di due entrate, ma la definizione data ora è generalizzata a n ingressi:

A	B	A AND B
0	0	0
0	1	0
1	0	0
1	1	1

Siccome questa operazione gode della proprietà associativa, è possibile realizzare un'operazione logica AND con un numero di proposizioni arbitrarie concatenando varie AND a due ingressi, per esempio:

$p_{1}\wedge (p_{2}\wedge (p_{3}\wedge p_{4}))$ $p_{1}\wedge (p_{2}\wedge (p_{3}\wedge p_{4}))$ $p_{1}\wedge (p_{2}\wedge (p_{3}\wedge p_{4}))$

Nei circuiti digitali , la porta logica AND è un meccanismo comune per avere un segnale di vero se un certo numero di altri segnali sono tutti veri.

Nella teoria degli insiemi corrisponde all' intersezione .

Il simbolo di una porta AND è:

OR

L'operazione logica OR restituisce 1 se almeno uno degli elementi è 1, mentre restituisce 0 in tutti gli altri casi. Tale operazione è anche detta somma logica. Di seguito la tabella rappresenta l'operatore OR nel caso di due entrate, ma la definizione data ora è generalizzata a n ingressi:

A	B	A OR B
0	0	0
0	1	1
1	0	1
1	1	1

Siccome questa operazione gode della proprietà associativa, è possibile realizzare un'operazione logica OR con più ingressi concatenando varie OR a due ingressi, per esempio:

$(p_{1}\vee p_{2})\vee (p_{3}\vee p_{4})$ $(p_{1}\vee p_{2})\vee (p_{3}\vee p_{4})$ $(p_{1}\vee p_{2})\vee (p_{3}\vee p_{4})$

Nei circuiti digitali , la porta logica OR è un meccanismo comune per avere un segnale alto se almeno un segnale è alto e un segnale basso se e solo se tutti i segnali sono bassi.

Nella teoria degli insiemi corrisponde all' unione .

Il simbolo di una porta OR a due ingressi è:

XOR

L'operatore XOR, detto anche EX-OR, OR esclusivo o somma modulo 2 , restituisce 1 se e solo se il numero degli operandi uguali a 1 è dispari , mentre restituisce 0 in tutti gli altri casi. La tabella rappresenta il caso in cui gli operatori siano 2, poi in generale ci si riferisce a questo operatore come operatore di disparità .

A	B	A XOR B
0	0	0
0	1	1
1	0	1
1	1	0

Nella teoria degli insiemi corrisponde alla differenza simmetrica . Per passare nella forma canonica SP (somma di prodotti) basta applicare la regola:

A⊕B $=A*!B+!A*B$ ${\displaystyle =A*!B+!A*B}$ $=A*!B+!A*B$

dove ⊕ è il simbolo di XOR.

Il simbolo di una porta XOR è:

NAND

L'operatore NAND, la negazione del risultato dell'operazione AND, restituisce 0 se e solo se tutti gli elementi sono 1, mentre restituisce 1 in tutti gli altri casi.

A	B	A NAND B
0	0	1
0	1	1
1	0	1
1	1	0

Il simbolo di una porta NAND è:

La porta NAND è composta da una porta NOT in serie ad una AND.

Utilizzando le leggi di De Morgan , è possibile convertire una porta OR in NAND. Vale, dunque, la seguente relazione: $A\lor B={\overline {{\overline {A}}\land {\overline {B}}}}={\overline {A}}\uparrow {\overline {B}}$ $A\lor B={\overline {{\overline {A}}\land {\overline {B}}}}={\overline {A}}\uparrow {\overline {B}}$ $A\lor B={\overline {{\overline {A}}\land {\overline {B}}}}={\overline {A}}\uparrow {\overline {B}}$

NOR

L'operatore NOR, la negazione del risultato dell'operazione OR, restituisce 1 se e solo se tutti gli elementi sono 0, mentre restituisce 0 in tutti gli altri casi.

A	B	A NOR B
0	0	1
0	1	0
1	0	0
1	1	0

Il simbolo di una porta NOR è:

composta da un NOT in serie a un OR.

Utilizzando le leggi di De Morgan , è possibile convertire una porta AND in NOR. Vale, dunque, la seguente relazione: $A\land B={\overline {{\overline {A}}\lor {\overline {B}}}}={\overline {A}}\downarrow {\overline {B}}$ $A\land B={\overline {{\overline {A}}\lor {\overline {B}}}}={\overline {A}}\downarrow {\overline {B}}$ $A\land B={\overline {{\overline {A}}\lor {\overline {B}}}}={\overline {A}}\downarrow {\overline {B}}$

XNOR

L'operatore XNOR, detto anche EX-NOR o EQU, è la negazione del risultato dell'operazione XOR; nella sua versione a due elementi restituisce 1 se tutti gli elementi sono uguali a 1 oppure se tutti gli elementi sono uguali a 0. Questo operatore viene generalizzato a n ingressi come operatore di parità , cioè è un'operazione che restituisce il valore 1 se il numero di 1 in ingresso è pari .

A	B	A XNOR B
0	0	1
0	1	0
1	0	0
1	1	1

Il simbolo di una porta XNOR è:

composta da un NOT in serie a un XOR.

Algebra dei circuiti

Come hanno mostrato già i primi studi pionieristici di J. Piesch ^[1] , l'Algebra di Boole si presta bene allo studio degli insiemi, delle proposizioni e dei circuiti. Ci si vuole soffermare su come quest'algebra diventa uno strumento per l'analisi e la sintesi delle reti di commutazione (in elettrotecnica il termine viene usato per indicare un cambio d'ordine della chiusura di due o più contatti elettrici, in telecomunicazioni ha un'accezione diversa).

L'algebra booleana consente di descrivere in forma algebrica le funzioni dei circuiti componenti e delle reti, fornendo altresì i metodi per la realizzazione del progetto logico: è stabilita quindi una corrispondenza biunivoca fra espressioni algebriche e reti di commutazione. La corrispondenza è facilmente realizzabile avendo già parlato di Operatori booleani : si parte ad esempio da un'espressione algebrica per realizzare un circuito, basta sostituire a ogni operatore logico la corrispondente porta logica e applicare agli ingressi di queste opportunamente le variabili booleane in gioco; inoltre, avendo visto l'esistenza di porte logiche come ad esempio la XOR, che sono combinazioni degli operatori booleani elementari AND, OR e NOT, è possibile manipolare opportunamente un'espressione algebrica in modo da utilizzare il minor numero possibile di porte nella realizzazione del circuito. Viceversa un circuito può essere espresso da una funzione y=f(x1,x2,...xn) dove y è l'uscita, le x sono le entrate e la funzione f è una combinazione di porte logiche.

Nell'algebra dei circuiti si associa il valore 0 al livello logico basso e il valore 1 al livello logico alto . In una visione semplificata il valore 0 corrisponde nella pratica a una tensione di 0 V mentre il valore 1 corrisponde a 5 V, oppure 3,5 V o addirittura 1,5 V: il motivo per cui si preferisce associare il valore alto a 5 V piuttosto che a 1,5 V è che la tensione nella pratica non è stabile e perciò il valore 0 si può "confondere" con il valore 1 causando una perdita di informazione ; d'altra parte però, una tensione di 1,5 V per indicare il valore alto significa minor dispendio di energia ed è un vantaggio molto significativo.

Volendo approfondire il discorso sui valori logici alto e basso e sulla loro realizzazione pratica, si può dire che, a seconda della tecnologia ci sono diversi range di valori possibili: per esempio, la tecnologia TTL associa il valore logico 0 a una tensione compresa tra 0 V e 0,8 V, tra 0 e 2 V c'è una banda vietata , cioè un insieme di valori che non devono essere assunti, e il valore logico 1 è associato al range di valori 1,5 V - 5 V. Come si è accennato, la tecnologia odierna spinge sull'abbassare la soglia dei 5 V cercando di stabilizzare sempre di più il potenziale.

Esempi

Questa algebra ha applicazioni nella logica , dove 0 è interpretato come "falso", 1 come "vero", $\vee$ $\vee$ $\vee$ è OR , $\wedge$ $\wedge$ $\wedge$ è AND e $\neg$ $\neg$ $\neg$ è NOT . Le espressioni che coinvolgono le variabili e le operazioni booleane rappresentano forme dichiarative; due espressioni possono essere equivalenti utilizzando i suddetti assiomi se e soltanto se le forme dichiarative corrispondenti sono logicamente equivalenti . L'algebra booleana binaria, inoltre, è usata per il disegno di circuiti nell' ingegneria elettronica ; qui 0 e 1 rappresentano le due condizioni differenti di un bit in un circuito digitale , in genere bassa e alta tensione . I circuiti sono descritti da espressioni che contengono delle variabili e due espressioni sono uguali per tutti i valori delle variabili se e soltanto se i circuiti corrispondenti hanno la stessa funzione di trasferimento . Ogni combinazione dei segnali in ingresso in uscita dal componente può essere rappresentata da un'adeguata espressione booleana

L'algebra booleana a due stati è inoltre importante nella teoria generale delle algebre booleane, perché un'equazione che coinvolge parecchie variabili è generalmente vera in ogni algebra booleana se e soltanto se è vera nell'algebra booleana a due stati. Ciò può, per esempio, essere usato per indicare che le seguenti leggi ( teorema del consenso ) sono generalmente valide in ogni algebra booleana:

$(a\vee b)\wedge (\neg a\vee c)\wedge (b\vee c)=(a\vee b)\wedge (\neg a\vee c)$ $(a\vee b)\wedge (\neg a\vee c)\wedge (b\vee c)=(a\vee b)\wedge (\neg a\vee c)$ $(a\vee b)\wedge (\neg a\vee c)\wedge (b\vee c)=(a\vee b)\wedge (\neg a\vee c)$

$(a\wedge b)\vee (\neg a\wedge c)\vee (b\wedge c)=(a\wedge b)\vee (\neg a\wedge c)$ $(a\wedge b)\vee (\neg a\wedge c)\vee (b\wedge c)=(a\wedge b)\vee (\neg a\wedge c)$ $(a\wedge b)\vee (\neg a\wedge c)\vee (b\wedge c)=(a\wedge b)\vee (\neg a\wedge c)$

Il raggruppamento di un generico insieme S , forma un'algebra booleana con le due operazioni $\vee$ $\vee$ $\vee$ = unione e $\wedge$ $\wedge$ $\wedge$ = intersezione . Il più piccolo elemento 0 è l' insieme vuoto e il più grande elemento 1 è l' insieme S stesso.
L' insieme di tutti i sottoinsiemi di un insieme S che sono limitati è un'algebra booleana.
Per ogni numero naturale n , l'insieme di tutti i divisori positivi di n forma un reticolo distributivo se scrive $a\leq b$ $a\leq b$ $a\leq b$ per a divide b . Questo reticolo è un'algebra booleana se e soltanto se per ogni n non vi sono divisori quadrati . Il più piccolo elemento, che in generale si indica con lo 0, in questa algebra booleana è il numero naturale 1; mentre l'elemento che usualmente indica con l'1 in questi insiemi è l'elemento "n".
Altri esempi di algebre booleane sono dati dagli spazi topologici : se X è uno spazio topologico, allora l'insieme di tutti i sottoinsiemi di X che siano aperti o chiusi formano un'algebra booleana con le operazioni $\vee$ $\vee$ $\vee$ = unione e $\wedge$ $\wedge$ $\wedge$ = intersezione .
Se R è un anello arbitrario dove è definito un insieme idempotente tipo:

A = { a in R : a ² = a e a $\cdot$ $\cdot$ $\cdot$ x = x $\cdot$ $\cdot$ $\cdot$ a per ogni x in R }

L'insieme A diventa un'algebra booleana con le operazioni a $\vee$ $\vee$ $\vee$ b = a + b − a $\cdot$ $\cdot$ $\cdot$ b e a $\wedge$ $\wedge$ $\wedge$ b = a $\cdot$ $\cdot$ $\cdot$ b .

Omomorfismi e isomorfismi

Un omomorfismo tra due algebre booleane A e B è una funzione f : A $\rightarrow$ $\rightarrow$ $\rightarrow$ B tale che per ogni a , b in A :

f ( a $\vee$ $\vee$ $\vee$ b ) = f ( a ) $\vee$ $\vee$ $\vee$ f ( b )
f ( a $\wedge$ $\wedge$ $\wedge$ b ) = f ( a ) $\wedge$ $\wedge$ $\wedge$ f ( b )
f (0) = 0
f (1) = 1

Da queste proprietà segue anche f ( $\neg$ $\neg$ $\neg$ a ) = $\neg$ $\neg$ $\neg$ f ( a ) per ogni a in A. Ogni algebra booleana, con la definizione di omomorfismo, forma una categoria . Un isomorfismo da A su B è un omomorfismo da A su B che è biiettivo . L'inverso di un isomorfismo è ancora un isomorfismo, e le due algebre booleane A e B si dicono isomorfe . Dal punto di vista della teoria dell'algebra booleana, due algebre booleane isomorfe non sono distinguibili, ma differiscono soltanto nella notazione dei loro elementi.

Espressioni booleane

All'interno di ciascuna algebra di Boole, dato un insieme di variabili e le operazioni correlate, è possibile definire delle espressioni che vengono ad assumere un determinato valore ottenibile anche sotto forme diverse. Possono esistere cioè delle espressioni che, pur essendo differenti, si rivelino equivalenti. Oltre al fatto che le espressioni booleane assumono una particolare importanza per quanto riguarda il calcolo proposizionale , in cui le variabili sono proposizioni legate tramite congiunzioni, disgiunzioni, negazioni e altre operazioni più complesse, possono esistere moltissime altre espressioni, accomunate sempre dalle proprietà e dagli assiomi booleani, nelle quali si sostituisce spesso l'operazione + (comunemente detta somma) con ∨ e * (comunemente detta prodotto) con ∧ e in cui la complementazione è indicata col simbolo ' .

Per poter presentare nel modo più efficiente un'espressione booleana, la si riduce in somma di prodotti fondamentali o forma normale disgiuntiva . Un prodotto fondamentale è un prodotto in cui ciascuna variabile, o il suo complemento, appaia una sola volta e rigorosamente fuori da parentesi o complementazioni complesse.
Ad esempio, date le variabili x, y, z all'interno di un'algebra di Boole, sono prodotti fondamentali

P(x,y,z) = xy
P(x,y,z) = x'yz'

Mentre non sono prodotti fondamentali

yyz
yy'z
(xy)'

È così possibile avere una somma di prodotti fondamentali, forma in cui ogni espressione può essere ridotta, ma che non è unica. Un esempio è: xy + xz + z'. Nel momento in cui ogni singola variabile, o il suo complemento, siano contenuti in tutti i prodotti fondamentali della forma normale disgiuntiva, si ha allora una somma di prodotti fondamentali completa o forma normale disgiuntiva completa . Tale scrittura è unica, pertanto se due espressioni sono equivalenti avranno la stessa forma normale disgiuntiva completa.

Se si desidera invece che un'espressione sia scritta nel modo più corto possibile, allora la si esprime in somma di implicanti prime o minimali (Minimizzazione di Quine-McQluskey). Un' implicante prima (o minimale) rispetto a un'espressione è un prodotto fondamentale che non altera l'espressione se sommato per intero a essa, cioè restituisce un risultato equivalente a quella iniziale; sommando un prodotto strettamente contenuto nell'implicante, tuttavia, non si ottiene un'equivalenza.
Per individuare tutte le implicanti prime, esistono varie tecniche, tra cui il metodo del consenso , che si basa sull'applicazione ciclica delle proprietà di assorbimento, idempotenza, involuttività e di De Morgan accompagnate a ogni passo dall'opportuna addizione di un consenso. Dati due prodotti fondamentali, se solo e solo se una variabile appare in uno di essi non negata e nell'altro negata si chiama consenso il risultato della moltiplicazione delle restanti variabili. Ad esempio:

dati P = xyz, Q = x'z il consenso sarà C = yzz = yz
dati P = xy' Q= xy il consenso sarà C = xx = x
dati P = xyz e Q = x'yz' non esiste consenso, in quanto due diverse variabili appaiono una volta negate e una volta no.

La somma di implicanti prime è unica, pertanto due espressioni equivalenti avranno la stessa. Nel momento in cui, completando ogni singola implicante prima, l'apporto all'espressione di una o più di esse è inutile in quanto contenuta nelle altre, la si può eliminare ottenendo la più essenziale delle scritture, la forma minimale . Essa, pur essendo comoda, ha l'inconveniente di non essere unica, e dunque di non consentire l'individuazione di equivalenze tra più espressioni.

Rappresentazione delle algebre booleane

Si può dimostrare che ogni reticolo booleano finito è isomorfo al reticolo booleano di tutti i sottoinsiemi di un insieme finito. Di conseguenza, il numero di elementi di ogni reticolo booleano finito ha un sostegno che contiene un numero di elementi uguale a una potenza di 2 .

Marshall Stone ha enunciato il celebre teorema di rappresentazione per le algebre booleane dimostrando che ogni algebra booleana "A" è isomorfa a tutte le algebre booleane aperte-chiuse in un certo spazio topologico compatto non connesso di Hausdorff .

Note

^ ( DE ) H. Piesch, H. Sequenz, Die Österreichischen Wegbereiter der Theorie der Elektrischen Schaltungen (I pionieri austriaci della teoria della commutazione elettrica), Elecktrotechnik & Maschinenbau, Vol. 75, pp. 241-245

Bibliografia

Giuseppe Calabrese, Le basi dell'elettronica - L'algebra di Boole , Milano, Editoriale Delfino, 1973.
Giuseppe Calabrese, L'algebra di Boole. La logica applicata agli automatismi , Milano, Editoriale Delfino, 1974.
( EN ) Steven Givant e Paul Halmos, Introduction to Boolean Algebras , Undergraduate Texts in Mathematics, Springer , 2009, ISBN 978-0-387-40293-2 .
( EN ) George Boole , An Investigation of the Laws of Thought , Prometheus Books, 2003 [1854] , ISBN 978-1-59102-089-9 .
( EN ) Steven Givant e Paul Halmos, Introduction to Boolean Algebras , Undergraduate Texts in Mathematics, Springer , 2009, ISBN 978-0-387-40293-2 .
( EN ) John A. Camara, Electrical and Electronics Reference Manual for the Electrical and Computer PE Exam , Professional Publications Inc., 2010, p. 41, ISBN 978-1-59126-166-7 .

Voci correlate

06-XX , sezione primaria dello schema di classificazione MSC 2000
Algebra di insiemi
Connettivo logico
Diagramma di Venn
Forma canonica
Funzione booleana
Mappa di Karnaugh
Operazione bit a bit
Porta logica
Sistema formale
Sistema numerico binario
Tabella della verità
Teorema dell'assorbimento
Teorema di Shannon
Teoremi di De Morgan
Teoria degli insiemi
Algebra di Robbins

Altri progetti

Wikiversità contiene risorse su algebra di Boole
Wikimedia Commons contiene immagini o altri file su algebra di Boole

Collegamenti esterni

Algebra di Boole , su sapere.it , De Agostini .
( EN ) Algebra di Boole , su Enciclopedia Britannica , Encyclopædia Britannica, Inc.
( EN ) Opere riguardanti Algebra di Boole , su Open Library , Internet Archive .
Introduzione alla logica Booleana ( PDF ), su matematicamente.it .
Panoramica sull'Algebra Booleana ( PDF ), su wwwusers.di.uniroma1.it .
Facoltà di Ingegneria Energetica - Univ. del Sannio - Elementi di Informatica: Algebra di Boole 2008/2009 ( PDF ), su ing.unisannio.it . URL consultato il 13 agosto 2012 (archiviato dall' url originale il 24 dicembre 2012) .
Corso di Laurea a distanza - Fondamenti di Informatica: Algebra di Boole, Operatori Logici, Teoremi Fondamentali ( PDF ), su corsiadistanza.polito.it .
Descrizione dell'algebra booleana su Okpedia , su okpedia.it .

Controllo di autorità	Thesaurus BNCF 17741 · LCCN ( EN ) sh85003429 · GND ( DE ) 4146280-4 · BNF ( FR ) cb119793249 (data) · BNE ( ES ) XX4576349 (data) · NDL ( EN , JA ) 00560863

Portale Elettronica

Portale Informatica

Portale Matematica

[1] ( DE ) H. Piesch, H. Sequenz, Die Österreichischen Wegbereiter der Theorie der Elektrischen Schaltungen (I pionieri austriaci della teoria della commutazione elettrica), Elecktrotechnik & Maschinenbau, Vol. 75, pp. 241-245

[1]

V · D · M Elettronica digitale
Componenti	Circuito combinatorio · Circuito integrato · Porta logica · Circuito sequenziale
Teoria	Segnale discreto · Algebra di Boole · Sintesi logica · Logica computazionale · Logica di ottimizzazione · Architettura dei calcolatori · Elaborazione numerica dei segnali
Progettazione	Register transfer level · Formal equivalence checking · Circuiti sincroni · Circuiti asincroni · Automa a stati finiti
Applicazioni	Hardware · Audio digitale · Fotografia digitale · Video digitale · Letteratura elettronica · Telecomunicazione

LA	B.	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15
0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

LA	B.	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15
0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

LA	B.	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15
0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1