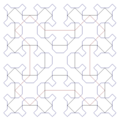
Curba Sierpiński

Curbele Sierpiński $S_{n}$ ${\ displaystyle S_ {n}}$ $S_ {n}$ pentru n = 1,2, ..., ele constituie o succesiune de curbe plane închise continue definite de recurența descoperită de Wacław Sierpiński , care în limită $n\rightarrow \infty$ ${\ displaystyle n \ rightarrow \ infty}$ ${\ displaystyle n \ rightarrow \ infty}$ umplu complet suprafața pătratului unitar: prin urmare, curba lor de graniță, cunoscută și sub numele de curba Sierpiński , este un exemplu de curbă care umple spațiul .

Deoarece curba Sierpiński acoperă planul, dimensiunea sa Hausdorff (în limită $n\rightarrow \infty$ ${\ displaystyle n \ rightarrow \ infty}$ $n \ rightarrow \ infty$ ) Și $2$ ${\ displaystyle 2}$ $2$ .

Lungimea euclidiană a $S_{n}$ ${\ displaystyle S_ {n}}$ $S_ {n}$ Și $l_{n}={2 \over 3}(1+{\sqrt {2}})2^{n}-{1 \over 3}(2-{\sqrt {2}}){1 \over 2^{n}}$ ${\ displaystyle l_ {n} = {2 \ over 3} (1 + {\ sqrt {2}}) 2 ^ {n} - {1 \ over 3} (2 - {\ sqrt {2}}) {1 \ peste 2 ^ {n}}}$ ${\ displaystyle l_ {n} = {2 \ over 3} (1 + {\ sqrt {2}}) 2 ^ {n} - {1 \ over 3} (2 - {\ sqrt {2}}) {1 \ peste 2 ^ {n}}}$ , adică crește exponențial cu $n$ ${\ displaystyle n}$ $n$ dincolo de toate limitele, în timp ce limita pentru $n\rightarrow \infty$ ${\ displaystyle n \ rightarrow \ infty}$ ${\ displaystyle n \ rightarrow \ infty}$ a zonei incluse de $S_{n}$ ${\ displaystyle S_ {n}}$ $S_ {n}$ Și $5/12$ ${\ displaystyle 5/12}$ ${\ displaystyle 5/12}$ decât cea a pătratului (în metrica euclidiană).

Curba Sierpiński de ordinul întâi
Curba Sierpiński
de ordine de la 1 la 2
Curba Sierpiński
de ordine de la 1 la 3

Utilizările curbei

Curba Sierpiński este utilă în mai multe aplicații practice, deoarece este cea mai simetrică dintre cele mai frecvent studiate curbe care acoperă planul. De exemplu, a fost folosit ca bază pentru construirea rapidă a unei soluții aproximative la problema vânzătorului călător (solicitând cea mai scurtă cale care atinge toate elementele unui set de puncte atribuit): procedura euristică constă în vizitarea punctelor din aceeași secvență cu care apar în curba Sierpiński ^[1] . Pentru a face acest lucru este necesar să efectuați doi pași: mai întâi calculați o imagine inversă pentru fiecare punct care urmează să fie vizitat; apoi reordonați valorile. Această idee a fost utilizată pentru a construi sisteme de rutare pentru vehicule comerciale, pe baza fișierelor Rolodex ^[2] .

O curbă care acoperă planul este o hartă continuă a intervalului de unitate la pătratul unității și, prin urmare, o aplicație inversă (pseudo) mapează pătratul unității la intervalul de unitate. O modalitate de a construi un pseudo invers este următoarea. Potriviți colțul din stânga jos (0,0) al pătratului unității cu punctul 0,0 (și 1,0). Deci colțul din stânga sus (0,1) trebuie să corespundă cu 0,25, colțul din dreapta sus (1,1) la 0,50 și colțul din dreapta jos (1,0) cu 0,75. Funcția inversă a punctelor interioare este calculată utilizând structura recursivă a curbei. Mai jos este o funcție codată în Java care calculează pozițiile relative ale fiecărui punct de pe curba Sierpiński (adică o valoare pseudo-inversă). Folosește ca intrare coordonatele punctului (x, y) care urmează să fie convertit și coordonatele vârfurilor unui triunghi isoscel care îl include (ax, ay), (bx, by) și (cx, cy) (Notă că unitatea pătrată este uniunea a două triunghiuri de acest tip). Restul parametrilor specifică nivelul de precizie la care trebuie calculată inversa.

 static long sierp_pt2code (ax dublu, dublu ay, dublu bx, dublu după, dublu cx, dublu cy,
       int currentLevel, int maxLevels, cod lung, dublu x, dublu y)
   {
       if (currentLevel <= maxLevel) {
           currentLevel ++;
           if ((sqr (x-ax) + sqr (y-ay)) <(sqr (x-cx) + sqr (y-cy))) {
               cod = sierp_pt2code (ax, ay, (ax + cx) /2.0, (ay + cy) /2.0, bx, by,
                   currentLevel, maxLevel, cod 2 * + 0, x, y);
           }
           altceva {
               code = sierp_pt2code (bx, by, (ax + cx) /2.0, (ay + cy) /2.0, cx, cy,
                   currentLevel, maxLevel, cod 2 * + 1, x, y);
           }
       }
       cod retur;
   }

Desenați curba

Următorul applet Java desenează o curbă Sierpiński cu patru metode care se apelează reciproc:

 import java.awt. *;
import java.applet. *;

public class SierpinskiCurve extinde Applet {
    private SimpleGraphics sg = nul;
    private int dist0 = 128, dist;

public nul init () {
        sg = new SimpleGraphics (getGraphics ());
        dist0 = 128;
        redimensionare (4 * dist0, 4 * dist0);
    }

public void paint (Grafică g) {
        nivel int = 3;
        dist = dist0;
        pentru (int i = nivel; i> 0; i--) dist / = 2;
        sg.goToXY (2 * dist, dist);
        serpA (nivel); // începe recursivitatea
        sg.lineRel (+ dist, + dist);
        sierpB (nivel); // începe recursivitatea
        sg.lineRel (-dist, + dist);
        sierpC (nivel); // începe recursivitatea
        sg.lineRel (-dist, -dist);
        sierpD (nivel); // începe recursivitatea
        sg.lineRel (+ dist, -dist);
    }

private void sierpA (nivel int) {
        dacă (nivel> 0) {
            serpA (nivel-1); sg.lineRel (+ dist, + dist);
            sierpB (nivel-1); sg.lineRel (+ 2 * dist, 0);
            sierpD (nivel-1); sg.lineRel (+ dist, -dist);
            serpA (nivel-1);
        }
    }

private void sierpB (nivel int) {
        dacă (nivel> 0) {
            sierpB (nivel-1); sg.lineRel (-dist, + dist);
            sierpC (nivel-1); sg.lineRel (0, + 2 * dist);
            serpA (nivel-1); sg.lineRel (+ dist, + dist);
            sierpB (nivel-1);
        }
    }

private void sierpC (nivel int) {
        dacă (nivel> 0) {
            sierpC (nivel-1); sg.lineRel (-dist, -dist);
            sierpD (nivel-1); sg.lineRel (-2 * dist, 0);
            sierpB (nivel-1); sg.lineRel (-dist, + dist);
            sierpC (nivel-1);
        }
    }

private void sierpD (nivel int) {
        dacă (nivel> 0) {
            sierpD (nivel-1); sg.lineRel (+ dist, -dist);
            serpA (nivel-1); sg.lineRel (0, -2 * dist);
            sierpC (nivel-1); sg.lineRel (-dist, -dist);
            sierpD (nivel-1);
        }
    }
}

clasa SimpleGraphics {
    private Graphics g = nul;
    private int x = 0, y = 0;

public SimpleGraphics (Graphics g) {this.g = g; }
    public void goToXY (int x, int y) {this.x = x; this.y = y; }

public void lineRel (int deltaX, int deltaY) {
        g.drawLine (x, y, x + deltaX, y + deltaY);
        x + = deltaX; y + = deltaY;
    }
}

Notă

^ Platzman, Loren K. și John J. Bartholdi, III (1989). „Curbele de umplere a spațiului și problema vânzătorului călător planar”, Journal of the Association of Computing Machinery 36 (4): 719-737.
^ Bartholdi, John J. III, Unele aplicații combinatorii ale curbelor de umplere a spațiului. Arhivat 3 august 2012 în Archive.is .

Elemente conexe

Curba Sierpiński în triunghiul Sierpiński
Curba Hilbert
Curba Peano
Fulgul de zăpadă al lui Koch
Lista fractalelor după dimensiunea Hausdorff

Alte proiecte

Wikimedia Commons conține imagini sau alte fișiere pe curba Sierpiński

linkuri externe

( RO ) Eric W. Weisstein, Curba Sierpiński , în MathWorld , Wolfram Research.
Giorgio Pietrocola, Curva di Peano-Sierpinski (animație didactică) , pe Maecla, Tartapelago , 2007. Adus pe 27 decembrie 2018 .

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică

[1] Platzman, Loren K. și John J. Bartholdi, III (1989). „Curbele de umplere a spațiului și problema vânzătorului călător planar”, Journal of the Association of Computing Machinery 36 (4): 719-737.

[2] Bartholdi, John J. III, Unele aplicații combinatorii ale curbelor de umplere a spațiului. Arhivat 3 august 2012 în Archive.is .

[1]

[2]

V · D · M Teoria haosului
Teoria bifurcației	Furcă de bifurcație · Nod de șa de bifurcație · Bifurcație imperfectă · Bifurcație transcritică · Bifurcație Hopf · Larva Pin (sistem dinamic)
Fractale	Arta fractală · Buddhabrot · navă de ardere · compresie fractală · Koch fulg de zăpadă · curba Peano · curba Sierpinski · Dimensiunea Hausdorff · dimensiunii fractale · Funcția Cantor · Set Cantor · Set Julia · Mandelbrot · Fractalii pentru dimensiune Hausdorff · Cantor de praf · Sterling · Sierpinski Triangle · Dimensiunea Minkowski-Bouligand
Atractorii	Sistem Lorenz · Atractorul din Hénon · Harta Poincaré · Harta logistică · Harta potcoavelor · Spațiul de fază
Teoreticienii haosului	Edward Norton Lorenz · Aleksandr Lyapunov · Benoît Mandelbrot · Edward October · Henri Poincare · David Ruelle · Stephen Wolfram · James Yorke