Dirac delta

Graficul delta Dirac

În matematică , funcția delta Dirac , numită și impuls Dirac, distribuție Dirac sau funcție δ , este o distribuție a cărei introducere formală a pregătit calea pentru studiul teoriei distribuției .

Introdusă de Paul Dirac , deși este deja prezentă în lucrările lui Oliver Heaviside , este o funcție generalizată care depinde de un parametru real în așa fel încât este nulă pentru toate valorile parametrului, cu excepția zero, și integrala sa pe parametrul dintre $-\infty$ ${\ displaystyle - \ infty}$ $- \ infty$ Și $+\infty$ ${\ displaystyle + \ infty}$ $+ \ infty$ este egal cu $1$ ${\ displaystyle 1}$ $1$ .

Este folosit pentru a reprezenta aproximativ fenomene precum vârfurile înalte și înguste ale unor funcții sau discontinuitățile lor: este același tip de abstractizare care se face pentru sarcina punctuală, masa punctului, electronul punctual. Analogul discret este delta Kronecker .

Descriere

Definiția lui Dirac

Chiar înainte de definiția formală a lui Dirac, matematicienii din trecut aveau nevoie să definească o funcție impulsivă , adică reprezentând un fenomen fizic de durată infinitesimală. Delta a fost inițial definită ca o funcție nulă pentru $t\neq 0$ ${\ displaystyle t \ neq 0}$ $t \ neq 0$ , cu integral egal cu 1 care se integrează pe întreaga axă a absciselor și, de asemenea, ca limită a secvențelor adecvate.

În mod formal, delta Dirac este definită de următoarea notație:

\int _{-\infty }^{+\infty }\delta (x)\operatorname {\phi } (x)\,\mathop {} \!\mathrm {d} x=\operatorname {\phi } (0)

{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} \ delta (x) \ operatorname {\ phi} (x) \, \ mathop {} \! \ mathrm {d} x = \ operatorname {\ phi} (0)}

{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} \ delta (x) \ operatorname {\ phi} (x) \, \ mathop {} \! \ mathrm {d} x = \ operatorname {\ phi} (0)}

valabil pentru orice funcție continuă într-un vecinătate de zero. Această definiție a fost introdusă pentru prima dată de Dirac la sfârșitul anilor 1920 în cercetările sale despre mecanica cuantică . Rețineți că, în timp ce utilizați simbolul integral , operația nu este de integrare, ci de aplicare a unui funcțional ( $\delta$ ${\ displaystyle \ delta}$ $\ delta$ tocmai) la o funcție de testare $\operatorname {\phi }$ ${\ displaystyle \ operatorname {\ phi}}$ $\ operatorname \ phi$ . Delta Dirac este deci funcția generalizată (definită cu simbolologia de mai sus) care transformă funcția de testare $\operatorname {\phi } (t)$ ${\ displaystyle \ operatorname {\ phi} (t)}$ $\ operatorname \ phi (t)$ în număr $\operatorname {\phi } (0)$ ${\ displaystyle \ operatorname {\ phi} (0)}$ $\ operatorname \ phi (0)$ .

Deși este ușor de demonstrat că nu poate exista nicio funcție cu proprietățile deltei Dirac, această definiție s-a dovedit foarte utilă din punct de vedere operațional și a fost adoptată curând în multe domenii ale fizicii și științelor aplicate. Tot pentru Dirac era clar că delta nu era o funcție în sensul obișnuit; ideea sa a fost că valoarea deltei la punctul 0 era o infinitate de grad „suficient de mare” pentru a permite proprietatea definitorie. O formalizare corectă matematic a deltei a fost posibilă numai mulți ani mai târziu în contextul teoriei distribuției .

În general, delta Dirac poate fi definită atât ca distribuție , cât și ca măsură .

Delta ca distribuție

Delta Dirac poate fi definită ca o distribuție , adică o funcționalitate liniară continuă pe un spațiu adecvat de funcții numite funcții de testare sau „dovadă”. Luați în considerare spațiul Schwartz , adică spațiul funcțiilor care scad rapid, ca spațiul funcțiilor de testare $S(\mathbb {R} ^{n})$ ${\ displaystyle S (\ mathbb {R} ^ {n})}$ $S ({\ mathbb R} ^ {n})$ infinit și infinit diferențiat, ale cărui derivate parțiale sunt încă în scădere rapidă.

Spațiul distribuțiilor temperate este definit ca spațiul dual al spațiului Schwartz. Distribuția delta Dirac asociată cu funcția de testare $\operatorname {\phi } \in S(\mathbb {R} ^{n})$ ${\ displaystyle \ operatorname {\ phi} \ în S (\ mathbb {R} ^ {n})}$ ${\ displaystyle \ operatorname {\ phi} \ în S (\ mathbb {R} ^ {n})}$ este definit ca: ^[1] ^[2]

\delta _{a}[\operatorname {\phi } ]=\operatorname {\phi } (a)

{\ displaystyle \ delta _ {a} [\ operatorname {\ phi}] = \ operatorname {\ phi} (a)}

\ delta _ {a} [\ operatorname \ phi] = \ operatorname \ phi (a)

adică delta unei funcții într-un punct $la$ ${\ displaystyle a}$ $la$ este o funcționalitate care își asociază valoarea în punct cu funcția.

Delta ca măsură

Una dintre modalitățile de a defini delta Dirac este să o considerăm o măsură care, pentru orice subset $LA$ ${\ displaystyle A}$ $LA$ de numere reale, se întoarce $\delta (A)=1$ ${\ displaystyle \ delta (A) = 1}$ $\ delta (A) = 1$ de sine $0\in A$ ${\ displaystyle 0 \ în A}$ $0 \ în A$ Și $\delta (A)=0$ ${\ displaystyle \ delta (A) = 0}$ $\ delta (A) = 0$ in caz contrar. Integrala Lebesgue permite definirea integrării în raport cu măsura $\delta$ ${\ displaystyle \ delta}$ $\ delta$ :

\int _{-\infty }^{+\infty }f(x)\,\delta \{\mathop {} \!\mathrm {d} x\}=f(0)

{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} f (x) \, \ delta \ {\ mathop {} \! \ mathrm {d} x \} = f (0)}

{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} f (x) \, \ delta \ {\ mathop {} \! \ mathrm {d} x \} = f (0)}

pentru fiecare funcție $f$ ${\ displaystyle f}$ $f$ continuați să compactați suportul. Această măsură este singulară și, prin urmare, nu este absolut continuă în ceea ce privește măsura Lebesgue . În consecință, delta Dirac nu are derivată Radon-Nikodym , adică nu există funcție $\delta$ ${\ displaystyle \ delta}$ $\ delta$ astfel încât:

\int _{-\infty }^{+\infty }f(x)\delta (x)\,\mathop {} \!\mathrm {d} x=f(0)

{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} f (x) \ delta (x) \, \ mathop {} \! \ mathrm {d} x = f (0)}

{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} f (x) \ delta (x) \, \ mathop {} \! \ mathrm {d} x = f (0)}

Utilizarea ultimei notații pentru delta este un abuz de notație , iar delta nu este o distribuție regulată.

Cu toate acestea, notația integrală este utilizată pe scară largă și fără a aduce atingere $\delta (x-x_{0})$ ${\ displaystyle \ delta (x-x_ {0})}$ $\ delta (x-x _ {{0}})$ nu este o funcție pe care o folosim pentru a scrie: ^[3]

\langle \delta _{x_{0}}|f\rangle =\int _{-\infty }^{+\infty }\delta (x-x_{0})f(x)\,\mathop {} \!\mathrm {d} x=f(x_{0})

{\ displaystyle \ langle \ delta _ {x_ {0}} | f \ rangle = \ int _ {- \ infty} ^ {+ \ infty} \ delta (x-x_ {0}) f (x) \, \ mathop {} \! \ mathrm {d} x = f (x_ {0})}

{\ displaystyle \ langle \ delta _ {x_ {0}} | f \ rangle = \ int _ {- \ infty} ^ {+ \ infty} \ delta (x-x_ {0}) f (x) \, \ mathop {} \! \ mathrm {d} x = f (x_ {0})}

Ca măsură a probabilității pe reali, delta Dirac se caracterizează prin funcția sa de distribuție care nu este alta decât funcția Heaviside :

H(x)={\begin{cases}1&{\text{se }}x\geq 0\\0&{\text{se }}x<0\end{cases}}

{\ displaystyle H (x) = {\ begin {cases} 1 & {\ text {se}} x \ geq 0 \\ 0 & {\ text {se}} x <0 \ end {cases}}}

H (x) = {\ begin {cases} 1 & {\ text {se}} x \ geq 0 \\ 0 & {\ text {se}} x <0 \ end {cases}}

Aceasta înseamnă că $H(x)$ ${\ displaystyle H (x)}$ $H (x)$ este integrala funcției indicator a $\mathbf {1} _{(-\infty ,x]}$ ${\ displaystyle \ mathbf {1} _ {(- \ infty, x]}}$ ${\ mathbf 1} _ {{(- \ infty, x]}}$ cu privire la măsură $\delta$ ${\ displaystyle \ delta}$ $\ delta$ . Adică:

H(x)=\int _{\mathbb {R} }\mathbf {1} _{(-\infty ,x]}(t)\,\delta \{\mathop {} \!\mathrm {d} t\}=\delta (-\infty ,x]

{\ displaystyle H (x) = \ int _ {\ mathbb {R}} \ mathbf {1} _ {(- \ infty, x]} (t) \, \ delta \ {\ mathop {} \! \ mathrm {d} t \} = \ delta (- \ infty, x]}

{\ displaystyle H (x) = \ int _ {\ mathbb {R}} \ mathbf {1} _ {(- \ infty, x]} (t) \, \ delta \ {\ mathop {} \! \ mathrm {d} t \} = \ delta (- \ infty, x]}

Generalizări

Funcția delta poate fi definită în spațiul euclidian $\mathbb {R} ^{n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ in marime $n$ ${\ displaystyle n}$ $n$ ca măsură astfel încât:

\int _{\mathbb {R} ^{n}}f(\mathbf {x} )\,\delta \{\mathop {} \!\mathrm {d} \mathbf {x} \}=f(\mathbf {0} )

{\ displaystyle \ int _ {\ mathbb {R} ^ {n}} f (\ mathbf {x}) \, \ delta \ {\ mathop {} \! \ mathrm {d} \ mathbf {x} \} = f (\ mathbf {0})}

{\ displaystyle \ int _ {\ mathbb {R} ^ {n}} f (\ mathbf {x}) \, \ delta \ {\ mathop {} \! \ mathrm {d} \ mathbf {x} \} = f (\ mathbf {0})}

pentru fiecare funcție continuă $f$ ${\ displaystyle f}$ $f$ suport compact. In caz $n$ ${\ displaystyle n}$ $n$ -dimensional delta este produsul deltelor unice dintr-o dimensiune, adică dacă $\mathbf {x} =(x_{1},x_{2},\dots ,x_{n})$ ${\ displaystyle \ mathbf {x} = (x_ {1}, x_ {2}, \ dots, x_ {n})}$ ${\ mathbf {x}} = (x_ {1}, x_ {2}, \ dots, x_ {n})$ , avem:

\delta (\mathbf {x} )=\delta (x_{1})\delta (x_{2})\dots \delta (x_{n})

{\ displaystyle \ delta (\ mathbf {x}) = \ delta (x_ {1}) \ delta (x_ {2}) \ dots \ delta (x_ {n})}

\ delta ({\ mathbf {x}}) = \ delta (x_ {1}) \ delta (x_ {2}) \ dots \ delta (x_ {n})

Această scriere este valabilă și în definiția deltei ca distribuție, dar acest produs poate fi definit doar în anumite ipoteze restrictive.

Conceptul de măsurare deltiformă , pe de altă parte, are sens pentru orice set. Este $X$ ${\ displaystyle X}$ $X$ un întreg, fie el $x_{0}\in X$ ${\ displaystyle x_ {0} \ în X}$ $x_0 \ în X$ Și $\Sigma$ ${\ displaystyle \ Sigma}$ $\ Sigma$ o algebră sigma a subseturilor de $X$ ${\ displaystyle X}$ $X$ , apoi măsura definită pe seturi $A\in \Sigma$ ${\ displaystyle A \ in \ Sigma}$ $A \ in \ Sigma$ din raport:

\delta _{x_{0}}(A)={\begin{cases}1&\mathrm {se\ } x_{0}\in A\\0&\mathrm {se\ } x_{0}\notin A\end{cases}}

{\ displaystyle \ delta _ {x_ {0}} (A) = {\ begin {cases} 1 & \ mathrm {if \} x_ {0} \ în A \\ 0 & \ mathrm {if \} x_ {0 } \ notin A \ end {cases}}}

\ delta _ {{x_ {0}}} (A) = {\ begin {cases} 1 & {\ mathrm {if \}} x_ {0} \ în A \\ 0 & {\ mathrm {if \}} x_ {0} \ notin A \ end {cases}}

este măsura Dirac în $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ .

În sfârșit, o altă generalizare răspândită se referă la varietăți diferențiate , în care multe dintre proprietățile deltei ca distribuție pot fi exploatate datorită structurii diferențiabile. Funcția delta pe o varietate $M.$ ${\ displaystyle M}$ $M.$ în sens $x_{0}\in M$ ${\ displaystyle x_ {0} \ în M}$ $x_ {0} \ în M$ este definit ca distribuția:

\delta _{x_{0}}[\operatorname {\phi } ]=\operatorname {\phi } (x_{0})

{\ displaystyle \ delta _ {x_ {0}} [\ operatorname {\ phi}] = \ operatorname {\ phi} (x_ {0})}

\ delta _ {{x_ {0}}} [\ operatorname \ phi] = \ operatorname \ phi (x_ {0})

pentru fiecare funcție $\operatorname {\phi }$ ${\ displaystyle \ operatorname {\ phi}}$ $\ operatorname \ phi$ suport real, neted și compact activat $M.$ ${\ displaystyle M}$ $M.$ . Un caz particular foarte utilizat este cazul în care $M.$ ${\ displaystyle M}$ $M.$ este un set deschis de $\mathbb {R} ^{n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ .

Semnificația fizică

Funcția delta poate fi gândită ca densitatea unui punct. Luați în considerare, de exemplu, un corp cu masă $M.$ ${\ displaystyle M}$ $M.$ finit, extins într-o anumită regiune $V.$ ${\ displaystyle V}$ $V.$ a spațiului tridimensional. Ne putem asocia cu orice punct $X$ ${\ displaystyle x}$ $X$ de spațiu o cantitate $\rho (x)$ ${\ displaystyle \ rho (x)}$ $\ rho (x)$ care reprezintă densitatea corpului. Functia $\rho$ ${\ displaystyle \ rho}$ $\ rho$ nu va fi nimic în afara regiunii $V.$ ${\ displaystyle V}$ $V.$ și, intern, va asuma valori astfel încât integrala:

\int _{V}\rho (x)\,\operatorname {d} x

{\ displaystyle \ int _ {V} \ rho (x) \, \ operatorname {d} x}

\ int _ {V} \ rho (x) \, \ operatorname {d} x

converg la $M.$ ${\ displaystyle M}$ $M.$ . Fiind $\rho (x)=0$ ${\ displaystyle \ rho (x) = 0}$ $\ rho (x) = 0$ in afara de $V.$ ${\ displaystyle V}$ $V.$ integralul poate fi extins la întregul spațiu și, prin urmare, poate fi scris:

\int \rho (x)\,\operatorname {d} x=M.

{\ displaystyle \ int \ rho (x) \, \ operatorname {d} x = M.}

{\ displaystyle \ int \ rho (x) \, \ operatorname {d} x = M.}

Acum, dacă ne imaginăm îngustarea regiunii $V.$ ${\ displaystyle V}$ $V.$ fără a modifica masa corpului, densitatea acestuia va trebui, prin urmare, să crească și va tinde spre infinit așa cum tinde $V.$ ${\ displaystyle V}$ $V.$ până la punctul unic: vrem, prin urmare, să găsim o expresie ca densitate limită pentru densitatea corpului punctului.

Pentru simplitate, considerăm un corp cu masă constantă și o regiune $V.$ ${\ displaystyle V}$ $V.$ sferic cu raza $R.$ ${\ displaystyle R}$ $R.$ ; volumul de $V.$ ${\ displaystyle V}$ $V.$ Sara:

{\frac {4}{3}}\pi R^{3},

{\ displaystyle {\ frac {4} {3}} \ pi R ^ {3},}

{\ displaystyle {\ frac {4} {3}} \ pi R ^ {3},}

și densitatea corespunzătoare:

\rho _{R}(x)={\frac {M}{V}}={\frac {3M}{4\pi R^{3}}},

{\ displaystyle \ rho _ {R} (x) = {\ frac {M} {V}} = {\ frac {3M} {4 \ pi R ^ {3}}},}

{\ displaystyle \ rho _ {R} (x) = {\ frac {M} {V}} = {\ frac {3M} {4 \ pi R ^ {3}}},}

și așa:

\int \rho _{R}(x)\,\mathop {} \!\mathrm {d} x=M,\quad \forall R.

{\ displaystyle \ int \ rho _ {R} (x) \, \ mathop {} \! \ mathrm {d} x = M, \ quad \ forall R.}

{\ displaystyle \ int \ rho _ {R} (x) \, \ mathop {} \! \ mathrm {d} x = M, \ quad \ forall R.}

Dacă luați în considerare limita :

\rho (x)=\lim _{R\to 0}\rho _{R}(x)

{\ displaystyle \ rho (x) = \ lim _ {R \ to 0} \ rho _ {R} (x)}

\ rho (x) = \ lim _ {{R \ to 0}} \ rho _ {R} (x)

se va întâmpla că $\rho (x)=\infty$ ${\ displaystyle \ rho (x) = \ infty}$ $\ rho (x) = \ infty$ pentru $x=0$ ${\ displaystyle x = 0}$ $x = 0$ , $\rho (x)=0$ ${\ displaystyle \ rho (x) = 0}$ $\ rho (x) = 0$ pentru $x\not =0$ ${\ displaystyle x \ not = 0}$ $x \ not = 0$ , de la care:

\int \rho (x)\,\operatorname {d} x=0,

{\ displaystyle \ int \ rho (x) \, \ operatorname {d} x = 0,}

{\ displaystyle \ int \ rho (x) \, \ operatorname {d} x = 0,}

și asta înseamnă că $\rho (x)$ ${\ displaystyle \ rho (x)}$ $\ rho (x)$ nu este comparabilă cu densitatea unui punct de masă $M.$ ${\ displaystyle M}$ $M.$ .

Să luăm apoi în considerare un alt tip de limită pentru densități $\rho _{R}$ ${\ displaystyle \ rho _ {R}}$ $\ rho _ {R}$ : așa-numita limită slabă . Cu câteva calcule se poate observa că pentru fiecare funcție continuă $h$ ${\ displaystyle h}$ $h$ :

\lim _{R\to 0}\int \rho _{R}(x)h(x)\,\operatorname {d} x=Mh(0).

{\ displaystyle \ lim _ {R \ to 0} \ int \ rho _ {R} (x) h (x) \, \ operatorname {d} x = Mh (0).}

{\ displaystyle \ lim _ {R \ to 0} \ int \ rho _ {R} (x) h (x) \, \ operatorname {d} x = Mh (0).}

Această formulă arată că limita slabă a secvenței $\rho _{R}$ ${\ displaystyle \ rho _ {R}}$ $\ rho _ {R}$ , este funcționalul care se asociază funcției $h$ ${\ displaystyle h}$ $h$ valoarea $Mh(0)$ ${\ displaystyle Mh (0)}$ $Mh (0)$ , această limită, pe care o indicăm simbolic $M\delta (x)$ ${\ displaystyle M \ delta (x)}$ $M \ delta (x)$ , este densitatea căutată; de fapt, locul $h(x)=1$ ${\ displaystyle h (x) = 1}$ $h (x) = 1$ , avem:

\int M\delta (x)\,\operatorname {d} x=\lim _{R\to 0}\int \rho _{R}(x)\,\operatorname {d} x=M,

{\ displaystyle \ int M \ delta (x) \, \ operatorname {d} x = \ lim _ {R \ to 0} \ int \ rho _ {R} (x) \, \ operatorname {d} x = M ,}

{\ displaystyle \ int M \ delta (x) \, \ operatorname {d} x = \ lim _ {R \ to 0} \ int \ rho _ {R} (x) \, \ operatorname {d} x = M ,}

unde prima integral este o expresie simbolică care implică trecerea la limită.

Aplicații

Delta Dirac poate fi utilizată pentru a exprima impulsiv orice cantitate fizică extinsă (de exemplu, înmulțind cantitatea cu această funcție). În telecomunicații, de exemplu, este folosit pentru a exprima un semnal de tip impulsiv, adică cu o durată infinitesimală de amplitudine A și pentru formalizarea așa-numitei teoreme de eșantionare .

Proprietăți și operațiuni ale deltei Dirac

Principalele proprietăți ale deltei sunt explicate mai jos.

Produs pentru un scalar

Prin definiție de distribuție avem:

\int _{-\infty }^{+\infty }a\delta (t)\operatorname {\phi } (t)\,\mathop {} \!\mathrm {d} t=a\int _{-\infty }^{+\infty }\delta (t)\operatorname {\phi } (t)\,\mathop {} \!\mathrm {d} t

{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} a \ delta (t) \ operatorname {\ phi} (t) \, \ mathop {} \! \ mathrm {d} t = a \ int _ {- \ infty} ^ {+ \ infty} \ delta (t) \ operatorname {\ phi} (t) \, \ mathop {} \! \ mathrm {d} t}

{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} a \ delta (t) \ operatorname {\ phi} (t) \, \ mathop {} \! \ mathrm {d} t = a \ int _ {- \ infty} ^ {+ \ infty} \ delta (t) \ operatorname {\ phi} (t) \, \ mathop {} \! \ mathrm {d} t}

Traducere

Din definiția distribuției, avem că delta Dirac „întârziată în timp” acționează ca:

\int _{-\infty }^{+\infty }f(t)\delta (t-T)\,\mathop {} \!\mathrm {d} t=f(T).

{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} f (t) \ delta (tT) \, \ mathop {} \! \ mathrm {d} t = f (T).}

{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} f (t) \ delta (t-T) \, \ mathop {} \! \ mathrm {d} t = f (T).}

Aceasta este convoluția unei funcții $f(t)$ ${\ displaystyle f (t)}$ $f (t)$ cu delta întârziată înseamnă evaluarea funcției la timp $T.$ ${\ displaystyle T}$ $T.$ , și din aceasta rezultă că:

(f*\delta (t-T))=\int _{-\infty }^{+\infty }f(\tau )\cdot \delta (t-T-\tau )\,\mathop {} \!\mathrm {d} \tau =\int _{-\infty }^{+\infty }f(\tau )\cdot \delta (\tau -(t-T))\,\mathop {} \!\mathrm {d} \tau =f(t-T).

{\ displaystyle (f * \ delta (tT)) = \ int _ {- \ infty} ^ {+ \ infty} f (\ tau) \ cdot \ delta (tT- \ tau) \, \ mathop {} \! \ mathrm {d} \ tau = \ int _ {- \ infty} ^ {+ \ infty} f (\ tau) \ cdot \ delta (\ tau - (tT)) \, \ mathop {} \! \ mathrm { d} \ tau = f (tT).}

{\ displaystyle (f * \ delta (tT)) = \ int _ {- \ infty} ^ {+ \ infty} f (\ tau) \ cdot \ delta (tT- \ tau) \, \ mathop {} \! \ mathrm {d} \ tau = \ int _ {- \ infty} ^ {+ \ infty} f (\ tau) \ cdot \ delta (\ tau - (tT)) \, \ mathop {} \! \ mathrm { d} \ tau = f (tT).}

Acest lucru este adevărat dacă $f(t)$ ${\ displaystyle f (t)}$ $f (t)$ este o distribuție temperată și, ca caz particular, avem:

\int _{-\infty }^{+\infty }\delta (\xi -x)\delta (x-\eta )\,\mathop {} \!\mathrm {d} x=\delta (\xi -\eta ).

{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} \ delta (\ xi -x) \ delta (x- \ eta) \, \ mathop {} \! \ mathrm {d} x = \ delta (\ xi - \ eta).}

{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} \ delta (\ xi -x) \ delta (x- \ eta) \, \ mathop {} \! \ mathrm {d} x = \ delta (\ xi - \ eta).}

Rescalare (și reflecție)

Din definiția deltei avem:

\delta (at)={1 \over |a|}\delta (t)

{\ displaystyle \ delta (at) = {1 \ over | a |} \ delta (t)}

\ delta (at) = {1 \ over | a |} \ delta (t)

Intr-adevar:

\int _{-\infty }^{+\infty }\delta (at)\operatorname {\phi } (t)\,\mathop {} \!\mathrm {d} t={1 \over |a|}\int _{-\infty }^{+\infty }\delta (t)\operatorname {\phi } \left({t \over a}\right)\mathop {} \!\mathrm {d} t={1 \over |a|}\operatorname {\phi } (0)=\int _{-\infty }^{+\infty }{1 \over |a|}\delta (t)\operatorname {\phi } (t)\,\mathop {} \!\mathrm {d} t.

{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} \ delta (at) \ operatorname {\ phi} (t) \, \ mathop {} \! \ mathrm {d} t = {1 \ over | a |} \ int _ {- \ infty} ^ {+ \ infty} \ delta (t) \ operatorname {\ phi} \ left ({t \ over a} \ right) \ mathop {} \! \ mathrm { d} t = {1 \ over | a |} \ operatorname {\ phi} (0) = \ int _ {- \ infty} ^ {+ \ infty} {1 \ over | a |} \ delta (t) \ operatorname {\ phi} (t) \, \ mathop {} \! \ mathrm {d} t.}

{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} \ delta (at) \ operatorname {\ phi} (t) \, \ mathop {} \! \ mathrm {d} t = {1 \ over | a |} \ int _ {- \ infty} ^ {+ \ infty} \ delta (t) \ operatorname {\ phi} \ left ({t \ over a} \ right) \ mathop {} \! \ mathrm { d} t = {1 \ over | a |} \ operatorname {\ phi} (0) = \ int _ {- \ infty} ^ {+ \ infty} {1 \ over | a |} \ delta (t) \ operatorname {\ phi} (t) \, \ mathop {} \! \ mathrm {d} t.}

Primul pas este permis dacă acestea sunt considerate separat $a>0$ ${\ displaystyle a> 0}$ $a> 0$ Și $a<0$ ${\ displaystyle a <0}$ $a <0$ , și constatând că rezultatul este definit până la semn $-$ ${\ displaystyle -}$ $-$ .

Rezultă ca un caz special că, văzută ca o funcție, delta este uniformă :

\operatorname {\delta } (t)=\operatorname {\delta } (-t).

{\ displaystyle \ operatorname {\ delta} (t) = \ operatorname {\ delta} (-t).}

{\ displaystyle \ operatorname {\ delta} (t) = \ operatorname {\ delta} (-t).}

Compoziție cu o funcție

De sine $f$ ${\ displaystyle f}$ $f$ este o funcție diferențiată cu derivată diferită de zero în zerouri $x_{i}$ ${\ displaystyle x_ {i}}$ $x_i$ funcției, apoi:

\delta (f(x))=\sum _{i}{\frac {\delta (x-x_{i})}{|f'(x_{i})|}}.

{\ displaystyle \ delta (f (x)) = \ sum _ {i} {\ frac {\ delta (x-x_ {i})} {| f '(x_ {i}) |}}.}

{\ displaystyle \ delta (f (x)) = \ sum _ {i} {\ frac {\ delta (x-x_ {i})} {| f '(x_ {i}) |}}.}

Produs pentru o funcție

Având o funcție $\operatorname {\alpha } (t)$ ${\ displaystyle \ operatorname {\ alpha} (t)}$ $\ operatorname \ alpha (t)$ elegant $C^{\infty }$ ${\ displaystyle C ^ {\ infty}}$ $C ^ \ infty$ , avem:

\operatorname {\alpha } (t)\operatorname {\delta } (t-t_{0})=\operatorname {\alpha } (t_{0})\operatorname {\delta } (t-t_{0}).

{\ displaystyle \ operatorname {\ alpha} (t) \ operatorname {\ delta} (t-t_ {0}) = \ operatorname {\ alpha} (t_ {0}) \ operatorname {\ delta} (t-t_ { 0}).}

{\ displaystyle \ operatorname {\ alpha} (t) \ operatorname {\ delta} (t-t_ {0}) = \ operatorname {\ alpha} (t_ {0}) \ operatorname {\ delta} (t-t_ { 0}).}

Intr-adevar:

\int _{-\infty }^{+\infty }(\alpha (t)\delta (t-t_{0}))\operatorname {\phi } (t)\,\mathop {} \!\mathrm {d} t=\int _{-\infty }^{+\infty }\delta (t-t_{0})(\alpha (t)\operatorname {\phi } (t))\,\mathop {} \!\mathrm {d} t=

{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} (\ alpha (t) \ delta (t-t_ {0})) \ operatorname {\ phi} (t) \, \ mathop {} \ ! \ mathrm {d} t = \ int _ {- \ infty} ^ {+ \ infty} \ delta (t-t_ {0}) (\ alpha (t) \ operatorname {\ phi} (t)) \, \ mathop {} \! \ mathrm {d} t =}

{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} (\ alpha (t) \ delta (t-t_ {0})) \ operatorname {\ phi} (t) \, \ mathop {} \ ! \ mathrm {d} t = \ int _ {- \ infty} ^ {+ \ infty} \ delta (t-t_ {0}) (\ alpha (t) \ operatorname {\ phi} (t)) \, \ mathop {} \! \ mathrm {d} t =}

\operatorname {\alpha } (t_{0})\operatorname {\phi } (t_{0})=\int _{-\infty }^{+\infty }(\alpha (t_{0})\delta (t-t_{0}))\operatorname {\phi } (t)\,\mathop {} \!\mathrm {d} t.

{\ displaystyle \ operatorname {\ alpha} (t_ {0}) \ operatorname {\ phi} (t_ {0}) = \ int _ {- \ infty} ^ {+ \ infty} (\ alpha (t_ {0} ) \ delta (t-t_ {0})) \ operatorname {\ phi} (t) \, \ mathop {} \! \ mathrm {d} t.}

{\ displaystyle \ operatorname {\ alpha} (t_ {0}) \ operatorname {\ phi} (t_ {0}) = \ int _ {- \ infty} ^ {+ \ infty} (\ alpha (t_ {0} ) \ delta (t-t_ {0})) \ operatorname {\ phi} (t) \, \ mathop {} \! \ mathrm {d} t.}

Derivată a funcției pas

Funcția delta este derivata funcției pas $\operatorname {u} (t)$ ${\ displaystyle \ operatorname {u} (t)}$ $\ operatorname u (t)$ (uneori indicat, cu abuz de notație, $\operatorname {1} (t)$ ${\ displaystyle \ operatorname {1} (t)}$ $\ operatorname 1 (t)$ ). Această funcție se mai numește funcția Heaviside și în acest caz este indicată cu simbolul $\operatorname {H} (x)$ ${\ displaystyle \ operatorname {H} (x)}$ $\ operatorname H (x)$ . Valoarea funcției pas este 0 pentru $x<0$ ${\ displaystyle x <0}$ $x <0$ și 1 pentru $x>0$ ${\ displaystyle x> 0}$ $x> 0$ .

Dovada se obține efectuând o integrare pe părți și aplicând proprietățile integralelor și ale funcției pas:

\int _{-\infty }^{+\infty }\operatorname {u} '(t)\operatorname {\phi } (t)\,\mathop {} \!\mathrm {d} t=-\int _{-\infty }^{+\infty }\operatorname {u} (t)\operatorname {\phi } '(t)\,\mathop {} \!\mathrm {d} t=-\int _{0}^{+\infty }\operatorname {\phi } '(t)\,\mathop {} \!\mathrm {d} t=-[\operatorname {\phi } (t)]_{0}^{+\infty }=\operatorname {\phi } (0)=\int _{-\infty }^{+\infty }\operatorname {\delta } (t)\operatorname {\phi } (t)\,\mathop {} \!\mathrm {d} t

{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} \ operatorname {u} '(t) \ operatorname {\ phi} (t) \, \ mathop {} \! \ mathrm {d} t = - \ int _ {- \ infty} ^ {+ \ infty} \ operatorname {u} (t) \ operatorname {\ phi} '(t) \, \ mathop {} \! \ mathrm {d} t = - \ int _ {0} ^ {+ \ infty} \ operatorname {\ phi} '(t) \, \ mathop {} \! \ mathrm {d} t = - [\ operatorname {\ phi} (t)] _ { 0} ^ {+ \ infty} = \ operatorname {\ phi} (0) = \ int _ {- \ infty} ^ {+ \ infty} \ operatorname {\ delta} (t) \ operatorname {\ phi} (t ) \, \ mathop {} \! \ mathrm {d} t}

{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} \ operatorname {u} '(t) \ operatorname {\ phi} (t) \, \ mathop {} \! \ mathrm {d} t = - \ int _ {- \ infty} ^ {+ \ infty} \ operatorname {u} (t) \ operatorname {\ phi} '(t) \, \ mathop {} \! \ mathrm {d} t = - \ int _ {0} ^ {+ \ infty} \ operatorname {\ phi} '(t) \, \ mathop {} \! \ mathrm {d} t = - [\ operatorname {\ phi} (t)] _ { 0} ^ {+ \ infty} = \ operatorname {\ phi} (0) = \ int _ {- \ infty} ^ {+ \ infty} \ operatorname {\ delta} (t) \ operatorname {\ phi} (t ) \, \ mathop {} \! \ mathrm {d} t}

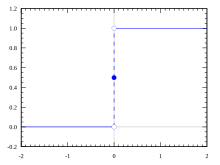
Funcția de pas a lui Heaviside, folosind convenția de jumătate din maxim

Această definiție este punctul de plecare pentru calcularea derivatei de distribuție a unei funcții, adică a derivatei acesteia în sensul distribuțiilor. Acest calcul se efectuează prin adăugarea la derivata obișnuită a funcției impulsurile concentrate în punctele de discontinuitate ale funcției, cu o zonă egală cu saltul funcției în punctele în sine. Această abordare este fundamentală în studiul semnalelor .

Putem obține dovada inversă, adică să dovedim asta $\operatorname {u} (t)$ ${\ displaystyle \ operatorname {u} (t)}$ $\ operatorname u (t)$ este primitiv de $\operatorname {\delta } (t)$ ${\ displaystyle \ operatorname {\ delta} (t)}$ $\ operatorname \ delta (t)$ , observând că:

\int _{a}^{b}\delta (t)\,\mathop {} \!\mathrm {d} t=\left\{{\begin{matrix}1,\,{\mbox{se }}a<0<b\\0,\,{\mbox{se }}0\notin [a,b]\end{matrix}}\right.

{\ displaystyle \ int _ {a} ^ {b} \ delta (t) \, \ mathop {} \! \ mathrm {d} t = \ left \ {{\ begin {matrix} 1, \, {\ mbox {se}} a <0 <b \\ 0, \, {\ mbox {se}} 0 \ notin [a, b] \ end {matrix}} \ right.}

{\ displaystyle \ int _ {a} ^ {b} \ delta (t) \, \ mathop {} \! \ mathrm {d} t = \ left \ {{\ begin {matrix} 1, \, {\ mbox {se}} a <0 <b \\ 0, \, {\ mbox {se}} 0 \ notin [a, b] \ end {matrix}} \ right.}

Din proprietățile integralei Riemann avem:

\int _{a}^{b}f'(t)\mathop {} \!\mathrm {d} t=[f(t)]_{a}^{b}=f(b)-f(a).

{\ displaystyle \ int _ {a} ^ {b} f '(t) \ mathop {} \! \ mathrm {d} t = [f (t)] _ {a} ^ {b} = f (b) -face).}

{\ displaystyle \ int _ {a} ^ {b} f '(t) \ mathop {} \! \ mathrm {d} t = [f (t)] _ {a} ^ {b} = f (b) -face).}

Singura funcție care satisface această constrângere este pasul.

Derivată de distribuție a deltei

Derivata de distribuție a deltei este distribuția $\delta '$ ${\ displaystyle \ delta '}$ $\ delta '$ definit dintr-o funcție de testare $\operatorname {\phi }$ ${\ displaystyle \ operatorname {\ phi}}$ $\ operatorname \ phi$ suport neted și compact:

\delta '[\operatorname {\phi } ]=-\delta [\operatorname {\phi } ']=-\operatorname {\phi } '(0)

{\ displaystyle \ delta '[\ operatorname {\ phi}] = - \ delta [\ operatorname {\ phi}'] = - \ operatorname {\ phi} '(0)}

\ delta '[\ operatorname \ phi] = - \ delta [\ operatorname \ phi'] = - \ operatorname \ phi '(0)

Echivalent:

\int _{-\infty }^{+\infty }\delta '(x)\operatorname {\phi } (x)\,\mathop {} \!\mathrm {d} x=-\int _{-\infty }^{+\infty }\delta (x)\operatorname {\phi } '(x)\,\mathop {} \!\mathrm {d} x

{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} \ delta '(x) \ operatorname {\ phi} (x) \, \ mathop {} \! \ mathrm {d} x = - \ int _ {- \ infty} ^ {+ \ infty} \ delta (x) \ operatorname {\ phi} '(x) \, \ mathop {} \! \ mathrm {d} x}

{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} \ delta '(x) \ operatorname {\ phi} (x) \, \ mathop {} \! \ mathrm {d} x = - \ int _ {- \ infty} ^ {+ \ infty} \ delta (x) \ operatorname {\ phi} '(x) \, \ mathop {} \! \ mathrm {d} x}

De fapt, prin integrarea pe părți:

\int _{-\infty }^{+\infty }{\frac {\mathop {} \!\mathrm {d} }{\operatorname {d} t}}\delta (t)\phi (t)\,\operatorname {d} t=\left[\delta (t)\phi (t)\right]_{-\infty }^{+\infty }-\int _{-\infty }^{+\infty }\delta (t)\;{\frac {\operatorname {d} }{\operatorname {d} t}}\phi (t)\,\operatorname {d} t

{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} {\ frac {\ mathop {} \! \ mathrm {d}} {\ operatorname {d} t}} \ delta (t) \ phi ( t) \, \ operatorname {d} t = \ left [\ delta (t) \ phi (t) \ right] _ {- \ infty} ^ {+ \ infty} - \ int _ {- \ infty} ^ { + \ infty} \ delta (t) \; {\ frac {\ operatorname {d}} {\ operatorname {d} t}} \ phi (t) \, \ operatorname {d} t}

{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} {\ frac {\ mathop {} \! \ mathrm {d}} {\ operatorname {d} t}} \ delta (t) \ phi ( t) \, \ operatorname {d} t = \ left [\ delta (t) \ phi (t) \ right] _ {- \ infty} ^ {+ \ infty} - \ int _ {- \ infty} ^ { + \ infty} \ delta (t) \; {\ frac {\ operatorname {d}} {\ operatorname {d} t}} \ phi (t) \, \ operatorname {d} t}

iar termenul evaluat dispare grație definiției deltei.

Derivatul $k$ ${\ displaystyle k}$ $k$ -th este distribuția definită în același mod:

\delta ^{(k)}[\operatorname {\phi } ]=(-1)^{k}\operatorname {\phi } ^{(k)}(0).

{\ displaystyle \ delta ^ {(k)} [\ operatorname {\ phi}] = (- 1) ^ {k} \ operatorname {\ phi} ^ {(k)} (0).}

{\ displaystyle \ delta ^ {(k)} [\ operatorname {\ phi}] = (- 1) ^ {k} \ operatorname {\ phi} ^ {(k)} (0).}

Prima derivată a deltei este limita raportului incremental:

\delta '(x)=\lim _{h\to 0}{\frac {\delta (x+h)-\delta (x)}{h}},

{\ displaystyle \ delta '(x) = \ lim _ {h \ to 0} {\ frac {\ delta (x + h) - \ delta (x)} {h}},}

{\ displaystyle \ delta '(x) = \ lim _ {h \ to 0} {\ frac {\ delta (x + h) - \ delta (x)} {h}},}

și mai exact avem:

\delta '=\lim _{h\to 0}{\frac {1}{h}}(\tau _{h}\delta -\delta ),

{\ displaystyle \ delta '= \ lim _ {h \ to 0} {\ frac {1} {h}} (\ tau _ {h} \ delta - \ delta),}

{\ displaystyle \ delta '= \ lim _ {h \ to 0} {\ frac {1} {h}} (\ tau _ {h} \ delta - \ delta),}

unde este $\tau _{h}$ ${\ displaystyle \ tau _ {h}}$ $\ tau _ {h}$ este operatorul de traducere, definit pe o funcție din $\tau _{h}\operatorname {\phi } (x)=\operatorname {\phi } (x+h)$ ${\ displaystyle \ tau _ {h} \ operatorname {\ phi} (x) = \ operatorname {\ phi} (x + h)}$ $\ tau _ {h} \ operatorname \ phi (x) = \ operatorname \ phi (x + h)$ și pe o distribuție de la:

(\tau _{h}S)[\operatorname {\phi } ]=S[\tau _{-h}\operatorname {\phi } ].

{\ displaystyle (\ tau _ {h} S) [\ operatorname {\ phi}] = S [\ tau _ {- h} \ operatorname {\ phi}].}

{\ displaystyle (\ tau _ {h} S) [\ operatorname {\ phi}] = S [\ tau _ {- h} \ operatorname {\ phi}].}

Din derivata delta, delta în sine poate fi recuperată folosind formula:

x\delta '(x)=-\delta (x).

{\ displaystyle x \ delta '(x) = - \ delta (x).}

{\ displaystyle x \ delta '(x) = - \ delta (x).}

În plus, convoluția $\delta '$ ${\ displaystyle \ delta '}$ $\ delta '$ o functie $f$ ${\ displaystyle f}$ $f$ netedă și compatibilă este:

\delta '*f=\delta *f'=f',

{\ displaystyle \ delta '* f = \ delta * f' = f ',}

{\ displaystyle \ delta '* f = \ delta * f' = f ',}

explicit:

(\delta '*f)(a)=\int _{-\infty }^{+\infty }\delta '(a-x)f(x)\,\mathop {} \!\mathrm {d} x=f'(a),

{\ displaystyle (\ delta '* f) (a) = \ int _ {- \ infty} ^ {+ \ infty} \ delta' (ax) f (x) \, \ mathop {} \! \ mathrm {d } x = f '(a),}

{\ displaystyle (\ delta '* f) (a) = \ int _ {- \ infty} ^ {+ \ infty} \ delta' (ax) f (x) \, \ mathop {} \! \ mathrm {d } x = f '(a),}

care rezultă direct din proprietățile derivatei unei convoluții în sensul distribuțiilor.

Delta ca limită a unei succesiuni

Funcția delta poate fi considerată ca limita unor secvențe particulare

\delta (x)=\lim _{\varepsilon \to 0^{+}}\eta _{\varepsilon }(x).

{\ displaystyle \ delta (x) = \ lim _ {\ varepsilon \ to 0 ^ {+}} \ eta _ {\ varepsilon} (x).}

{\ displaystyle \ delta (x) = \ lim _ {\ varepsilon \ to 0 ^ {+}} \ eta _ {\ varepsilon} (x).}

În mod echivalent, este definit utilizând convergența în sensul distribuțiilor:

\lim _{\varepsilon \to 0^{+}}\int _{-\infty }^{+\infty }\eta _{\varepsilon }(x)f(x)\,\mathop {} \!\mathrm {d} x=f(0),

{\ displaystyle \ lim _ {\ varepsilon \ to 0 ^ {+}} \ int _ {- \ infty} ^ {+ \ infty} \ eta _ {\ varepsilon} (x) f (x) \, \ mathop { } \! \ mathrm {d} x = f (0),}

{\ displaystyle \ lim _ {\ varepsilon \ to 0 ^ {+}} \ int _ {- \ infty} ^ {+ \ infty} \ eta _ {\ varepsilon} (x) f (x) \, \ mathop { } \! \ mathrm {d} x = f (0),}

pentru toate funcțiile continue $f$ ${\ displaystyle f}$ $f$ suport compact. Succesiunea $\eta _{\varepsilon }(x)$ ${\ displaystyle \ eta _ {\ varepsilon} (x)}$ $\ eta _ {{\ varepsilon}} (x)$ se numește apoi o succesiune de aproximanți ai deltei. Trebuie avut în vedere faptul că aceasta este o convergență slabă în sensul teoriei distribuției, adică valabilă în sens obișnuit doar pentru secvența integralelor. De fapt, multe dintre secvențele aproximantelor nu sunt convergente în sens obișnuit.

Este posibil să se dea un criteriu general pentru aproximanții deltei. O succesiune de funcții ${\operatorname {\delta } _{n}}$ ${\ displaystyle {\ operatorname {\ delta} _ {n}}}$ ${\ operatorname \ delta _ {n}}$ real integrabil local converge slab către delta, dacă:

$\forall \epsilon >0$ ${\ displaystyle \ forall \ epsilon> 0}$ $\ forall \ epsilon> 0$ , succesiunile:

\int _{-\infty }^{-a}\delta _{n}(x)\,\mathop {} \!\mathrm {d} x\qquad \int _{a}^{+\infty }\delta _{n}(x)\,\mathop {} \!\mathrm {d} x

{\ displaystyle \ int _ {- \ infty} ^ {- a} \ delta _ {n} (x) \, \ mathop {} \! \ mathrm {d} x \ qquad \ int _ {a} ^ {+ \ infty} \ delta _ {n} (x) \, \ mathop {} \! \ mathrm {d} x}

{\ displaystyle \ int _ {- \ infty} ^ {- a} \ delta _ {n} (x) \, \ mathop {} \! \ mathrm {d} x \ qquad \ int _ {a} ^ {+ \ infty} \ delta _ {n} (x) \, \ mathop {} \! \ mathrm {d} x}

converg uniform la 0

\forall a\in [\epsilon ,{+\infty }]

{\ displaystyle \ forall a \ in [\ epsilon, {+ \ infty}]}

\ forall a \ in [\ epsilon, {+ \ infty}]

$\lim _{n\to \infty }\,\int _{-\infty }^{+\infty }\delta _{n}(x)\,\mathop {} \!\mathrm {d} x=1$ ${\ displaystyle \ lim _ {n \ to \ infty} \, \ int _ {- \ infty} ^ {+ \ infty} \ delta _ {n} (x) \, \ mathop {} \! \ mathrm {d } x = 1}$ ${\ displaystyle \ lim _ {n \ to \ infty} \, \ int _ {- \ infty} ^ {+ \ infty} \ delta _ {n} (x) \, \ mathop {} \! \ mathrm {d } x = 1}$

$|\int _{-\infty }^{a}\delta _{n}(x)\,\mathop {} \!\mathrm {d} x|<K$ ${\ displaystyle | \ int _ {- \ infty} ^ {a} \ delta _ {n} (x) \, \ mathop {} \! \ mathrm {d} x | <K}$ ${\ displaystyle | \ int _ {- \ infty} ^ {a} \ delta _ {n} (x) \, \ mathop {} \! \ mathrm {d} x | <K}$

\forall n\in \mathbb {N}

{\ displaystyle \ forall n \ in \ mathbb {N}}

\ forall n \ in \ mathbb {N}

, unde este

K.

{\ displaystyle K}

K.

este un număr real pozitiv independent de

n

{\ displaystyle n}

n

.

Secvențe reprezentând delta Dirac

Iată câteva dintre cele mai cunoscute succesiuni care reprezintă delta Dirac:

Limita unei distribuții normale (per $n\rightarrow \infty$ ${\ displaystyle n \ rightarrow \ infty}$ $n \ rightarrow \ infty$ ):

\delta _{n}(x)={\sqrt {\frac {n}{\pi }}}e^{-nx^{2}}

{\ displaystyle \ delta _ {n} (x) = {\ sqrt {\ frac {n} {\ pi}}} e ^ {- nx ^ {2}}}

\delta _{n}(x)={\sqrt {\frac {n}{\pi }}}e^{-nx^{2}}

Limite di una distribuzione di Cauchy (per $n\to 0^{+}$ $n\to 0^{+}$ $n\to 0^{+}$ ):

\delta _{n}(x)={\frac {1}{\pi }}{\frac {n}{n^{2}+x^{2}}}={\frac {1}{2\pi }}\int _{-\infty }^{+\infty }e^{ikx-|nk|}\,\mathop {} \!\mathrm {d} k

\delta _{n}(x)={\frac {1}{\pi }}{\frac {n}{n^{2}+x^{2}}}={\frac {1}{2\pi }}\int _{-\infty }^{+\infty }e^{ikx-|nk|}\,\mathop {} \!\mathrm {d} k

\delta _{n}(x)={\frac {1}{\pi }}{\frac {n}{n^{2}+x^{2}}}={\frac {1}{2\pi }}\int _{-\infty }^{+\infty }e^{ikx-|nk|}\,\mathop {} \!\mathrm {d} k

$\varphi$ $\varphi$ $\varphi$ di Cauchy:

\delta _{n}(x)={\frac {e^{-|x/n|}}{2n}}={\frac {1}{2\pi }}\int _{-\infty }^{+\infty }{\frac {e^{ikx}}{1+n^{2}k^{2}}}\,\mathop {} \!\mathrm {d} k

\delta _{n}(x)={\frac {e^{-|x/n|}}{2n}}={\frac {1}{2\pi }}\int _{-\infty }^{+\infty }{\frac {e^{ikx}}{1+n^{2}k^{2}}}\,\mathop {} \!\mathrm {d} k

\delta _{n}(x)={\frac {e^{-|x/n|}}{2n}}={\frac {1}{2\pi }}\int _{-\infty }^{+\infty }{\frac {e^{ikx}}{1+n^{2}k^{2}}}\,\mathop {} \!\mathrm {d} k

Limite di una funzione rettangolo :

\delta _{n}(x)={\frac {\operatorname {rect} (x/n)}{n}}={\frac {1}{2\pi }}\int _{-\infty }^{+\infty }\operatorname {sinc} \left({\frac {nk}{2\pi }}\right)e^{ikx}\,\mathop {} \!\mathrm {d} k

\delta _{n}(x)={\frac {\operatorname {rect} (x/n)}{n}}={\frac {1}{2\pi }}\int _{-\infty }^{+\infty }\operatorname {sinc} \left({\frac {nk}{2\pi }}\right)e^{ikx}\,\mathop {} \!\mathrm {d} k

\delta _{n}(x)={\frac {\operatorname {rect} (x/n)}{n}}={\frac {1}{2\pi }}\int _{-\infty }^{+\infty }\operatorname {sinc} \left({\frac {nk}{2\pi }}\right)e^{ikx}\,\mathop {} \!\mathrm {d} k

Funzione rettangolare $\varphi$ $\varphi$ $\varphi$ (per $n\to 0^{+}$ $n\to 0^{+}$ $n\to 0^{+}$ ): ^[4]

\delta _{n}(x)={\frac {1}{\pi x}}\sin \left({\frac {x}{n}}\right)={\frac {1}{2\pi }}\int _{-1/n}^{1/n}\cos(kx)\,\mathop {} \!\mathrm {d} k

\delta _{n}(x)={\frac {1}{\pi x}}\sin \left({\frac {x}{n}}\right)={\frac {1}{2\pi }}\int _{-1/n}^{1/n}\cos(kx)\,\mathop {} \!\mathrm {d} k

\delta _{n}(x)={\frac {1}{\pi x}}\sin \left({\frac {x}{n}}\right)={\frac {1}{2\pi }}\int _{-1/n}^{1/n}\cos(kx)\,\mathop {} \!\mathrm {d} k

Derivata della sigmoide (o Statistica di Fermi-Dirac ):

\delta _{n}(x)=\partial _{x}{\frac {1}{1+e^{-x/n}}}=-\partial _{x}{\frac {1}{1+e^{x/n}}}

\delta _{n}(x)=\partial _{x}{\frac {1}{1+e^{-x/n}}}=-\partial _{x}{\frac {1}{1+e^{x/n}}}

\delta _{n}(x)=\partial _{x}{\frac {1}{1+e^{{-x/n}}}}=-\partial _{x}{\frac {1}{1+e^{{x/n}}}}

Limite della funzione di Airy :

\delta _{n}(x)={\frac {1}{n}}A_{i}\left({\frac {x}{n}}\right)

\delta _{n}(x)={\frac {1}{n}}A_{i}\left({\frac {x}{n}}\right)

\delta _{n}(x)={\frac {1}{n}}A_{i}\left({\frac {x}{n}}\right)

Limite della funzione di Bessel :

\delta _{n}(x)={\frac {1}{n}}J_{1/n}\left({\frac {x+1}{n}}\right)

\delta _{n}(x)={\frac {1}{n}}J_{1/n}\left({\frac {x+1}{n}}\right)

\delta _{n}(x)={\frac {1}{n}}J_{{1/n}}\left({\frac {x+1}{n}}\right)

La delta e la trasformata di Fourier

Lo stesso argomento in dettaglio: Trasformata di Fourier .

Rappresentazione di Fourier della delta

Ogni funzione appartenente ad $L^{1}(\mathbb {R} )$ $L^{1}(\mathbb {R} )$ $L^{1}(\mathbb{R} )$ può essere scritta come:

f(x)={\frac {1}{2\pi }}\int _{-\infty }^{+\infty }e^{ikx}\left(\int _{-\infty }^{+\infty }e^{-iky}f(y)\,\mathop {} \!\mathrm {d} y\right)\mathop {} \!\mathrm {d} k

f(x)={\frac {1}{2\pi }}\int _{-\infty }^{+\infty }e^{ikx}\left(\int _{-\infty }^{+\infty }e^{-iky}f(y)\,\mathop {} \!\mathrm {d} y\right)\mathop {} \!\mathrm {d} k

f(x)={\frac {1}{2\pi }}\int _{-\infty }^{+\infty }e^{ikx}\left(\int _{-\infty }^{+\infty }e^{-iky}f(y)\,\mathop {} \!\mathrm {d} y\right)\mathop {} \!\mathrm {d} k

Non è possibile scambiare l'ordine di integrazione, tuttavia è possibile scrivere:

f(x)=\lim _{N\to \infty }{\frac {1}{2\pi }}\int _{-N}^{+N}e^{ikx}\ \left(\int _{-\infty }^{+\infty }e^{-iky}f(y)\,\mathop {} \!\mathrm {d} y\right)\mathop {} \!\mathrm {d} k

f(x)=\lim _{N\to \infty }{\frac {1}{2\pi }}\int _{-N}^{+N}e^{ikx}\ \left(\int _{-\infty }^{+\infty }e^{-iky}f(y)\,\mathop {} \!\mathrm {d} y\right)\mathop {} \!\mathrm {d} k

f(x)=\lim _{N\to \infty }{\frac {1}{2\pi }}\int _{-N}^{+N}e^{ikx}\ \left(\int _{-\infty }^{+\infty }e^{-iky}f(y)\,\mathop {} \!\mathrm {d} y\right)\mathop {} \!\mathrm {d} k

Il primo termine dell'integrale equivale alla successione:

\delta _{N}(t)={\frac {1}{\pi }}{\frac {\sin Nt}{t}}={\frac {1}{2\pi }}\int _{-N}^{+N}e^{ikt}\,\mathop {} \!\mathrm {d} k

\delta _{N}(t)={\frac {1}{\pi }}{\frac {\sin Nt}{t}}={\frac {1}{2\pi }}\int _{-N}^{+N}e^{ikt}\,\mathop {} \!\mathrm {d} k

\delta _{N}(t)={\frac {1}{\pi }}{\frac {\sin Nt}{t}}={\frac {1}{2\pi }}\int _{-N}^{+N}e^{ikt}\,\mathop {} \!\mathrm {d} k

Si nota che tale successione gode delle proprietà:

\lim _{t\to {\pm \infty }}\delta _{N}(t)=0\qquad \int _{-\infty }^{+\infty }\delta _{N}(t)\,\mathop {} \!\mathrm {d} t=1

\lim _{t\to {\pm \infty }}\delta _{N}(t)=0\qquad \int _{-\infty }^{+\infty }\delta _{N}(t)\,\mathop {} \!\mathrm {d} t=1

\lim _{t\to {\pm \infty }}\delta _{N}(t)=0\qquad \int _{-\infty }^{+\infty }\delta _{N}(t)\,\mathop {} \!\mathrm {d} t=1

che sono le proprietà richieste alla delta di Dirac.

Inserendo tale rappresentazione nella precedente scrittura, e sapendo che il teorema di Fubini Tonelli permette di scambiare l'ordine di integrazione, si ottiene infatti:

f(x)=\lim _{N\to \infty }\int _{-\infty }^{+\infty }\delta _{N}(x-y)f(y)\,\mathop {} \!\mathrm {d} y

f(x)=\lim _{N\to \infty }\int _{-\infty }^{+\infty }\delta _{N}(xy)f(y)\,\mathop {} \!\mathrm {d} y

f(x)=\lim _{N\to \infty }\int _{-\infty }^{+\infty }\delta _{N}(x-y)f(y)\,\mathop {} \!\mathrm {d} y

Ovvero la delta di Dirac è definita come il limite della successione:

\delta (t)=\lim _{N\to \infty }{\frac {1}{\pi }}{\frac {\sin Nt}{t}}=\lim _{N\to \infty }{\frac {1}{2\pi }}\int _{-N}^{+N}e^{ikt}\,\mathop {} \!\mathrm {d} k

\delta (t)=\lim _{N\to \infty }{\frac {1}{\pi }}{\frac {\sin Nt}{t}}=\lim _{N\to \infty }{\frac {1}{2\pi }}\int _{-N}^{+N}e^{ikt}\,\mathop {} \!\mathrm {d} k

\delta (t)=\lim _{N\to \infty }{\frac {1}{\pi }}{\frac {\sin Nt}{t}}=\lim _{N\to \infty }{\frac {1}{2\pi }}\int _{-N}^{+N}e^{ikt}\,\mathop {} \!\mathrm {d} k

e dunque la rappresentazione di Fourier della delta è:

\delta (t)={\frac {1}{2\pi }}\int _{-\infty }^{+\infty }e^{ikt}\,\mathop {} \!\mathrm {d} k

\delta (t)={\frac {1}{2\pi }}\int _{-\infty }^{+\infty }e^{ikt}\,\mathop {} \!\mathrm {d} k

\delta (t)={\frac {1}{2\pi }}\int _{-\infty }^{+\infty }e^{ikt}\,\mathop {} \!\mathrm {d} k

La trasformata della delta

La rappresentazione di Fourier rende evidente che la delta è l'antitrasformata della funzione costante $f(x)=1$ ${\displaystyle f(x)=1}$ $f(x)=1$ :

\int _{-\infty }^{+\infty }1\cdot e^{i2\pi xk}\,\mathop {} \!\mathrm {d} k=\delta (x)

\int _{-\infty }^{+\infty }1\cdot e^{i2\pi xk}\,\mathop {} \!\mathrm {d} k=\delta (x)

\int _{-\infty }^{+\infty }1\cdot e^{i2\pi xk}\,\mathop {} \!\mathrm {d} k=\delta (x)

e dunque:

{\hat {\delta }}(k)=\int _{-\infty }^{+\infty }e^{-i2\pi xk}\delta (x)\,\mathop {} \!\mathrm {d} x=1

{\hat {\delta }}(k)=\int _{-\infty }^{+\infty }e^{-i2\pi xk}\delta (x)\,\mathop {} \!\mathrm {d} x=1

{\hat {\delta }}(k)=\int _{-\infty }^{+\infty }e^{-i2\pi xk}\delta (x)\,\mathop {} \!\mathrm {d} x=1

La dimostrazione si può ottenere anche a partire dalla definizione di trasformata di Fourier delle distribuzioni:

({\mathcal {F}}[\delta ],\phi )=\int _{-\infty }^{+\infty }{\mathcal {F}}[\delta ](\omega )\operatorname {\phi } (\omega )\,\mathop {} \!\mathrm {d} \omega =\int _{-\infty }^{+\infty }\delta (\omega ){\mathcal {F}}[\operatorname {\phi } ](\omega )\,\mathop {} \!\mathrm {d} \omega ={\mathcal {F}}[\operatorname {\phi } ](0)=

({\mathcal {F}}[\delta ],\phi )=\int _{-\infty }^{+\infty }{\mathcal {F}}[\delta ](\omega )\operatorname {\phi } (\omega )\,\mathop {} \!\mathrm {d} \omega =\int _{-\infty }^{+\infty }\delta (\omega ){\mathcal {F}}[\operatorname {\phi } ](\omega )\,\mathop {} \!\mathrm {d} \omega ={\mathcal {F}}[\operatorname {\phi } ](0)=

({\mathcal {F}}[\delta ],\phi )=\int _{-\infty }^{+\infty }{\mathcal {F}}[\delta ](\omega )\operatorname {\phi } (\omega )\,\mathop {} \!\mathrm {d} \omega =\int _{-\infty }^{+\infty }\delta (\omega ){\mathcal {F}}[\operatorname {\phi } ](\omega )\,\mathop {} \!\mathrm {d} \omega ={\mathcal {F}}[\operatorname {\phi } ](0)=

=\left[\int _{-\infty }^{+\infty }\operatorname {\phi } (t)e^{-i\omega t}\,\mathop {} \!\mathrm {d} t\right]_{\omega =0}=\int _{-\infty }^{+\infty }\operatorname {\phi } (t)\,\mathop {} \!\mathrm {d} t=(1,\phi )

=\left[\int _{-\infty }^{+\infty }\operatorname {\phi } (t)e^{-i\omega t}\,\mathop {} \!\mathrm {d} t\right]_{\omega =0}=\int _{-\infty }^{+\infty }\operatorname {\phi } (t)\,\mathop {} \!\mathrm {d} t=(1,\phi )

=\left[\int _{-\infty }^{+\infty }\operatorname {\phi } (t)e^{-i\omega t}\,\mathop {} \!\mathrm {d} t\right]_{\omega =0}=\int _{-\infty }^{+\infty }\operatorname {\phi } (t)\,\mathop {} \!\mathrm {d} t=(1,\phi )

La trasformata ${\hat {\delta }}$ ${\hat {\delta }}$ ${\hat {\delta }}$ della delta è definita come l'unica distribuzione temperata tale che:

\langle {\hat {\delta }},\phi \rangle =\langle \delta ,{\hat {\phi }}\rangle

\langle {\hat {\delta }},\phi \rangle =\langle \delta ,{\hat {\phi }}\rangle

\langle {\hat {\delta }},\phi \rangle =\langle \delta ,{\hat {\phi }}\rangle

per ogni funzione di Schwartz $\operatorname {\phi }$ $\operatorname {\phi }$ $\operatorname \phi$ .

Segue inoltre che la delta fornisce la condizione di ortogonalizzazione delle autofunzioni degli operatori di derivazione e integrazione, che costituiscono il nucleo della trasformata integrale di Fourier su $\mathbb {R}$ $\mathbb {R}$ $\mathbb R$ :

\int _{-\infty }^{+\infty }e^{i2\pi \xi _{1}t}\left[e^{i2\pi \xi _{2}t}\right]^{*}\,\mathop {} \!\mathrm {d} t=\int _{-\infty }^{+\infty }e^{-i2\pi (\xi _{2}-\xi _{1})t}\,\mathop {} \!\mathrm {d} t=\delta (\xi _{1}-\xi _{2})

\int _{-\infty }^{+\infty }e^{i2\pi \xi _{1}t}\left[e^{i2\pi \xi _{2}t}\right]^{*}\,\mathop {} \!\mathrm {d} t=\int _{-\infty }^{+\infty }e^{-i2\pi (\xi _{2}-\xi _{1})t}\,\mathop {} \!\mathrm {d} t=\delta (\xi _{1}-\xi _{2})

\int _{-\infty }^{+\infty }e^{i2\pi \xi _{1}t}\left[e^{i2\pi \xi _{2}t}\right]^{*}\,\mathop {} \!\mathrm {d} t=\int _{-\infty }^{+\infty }e^{-i2\pi (\xi _{2}-\xi _{1})t}\,\mathop {} \!\mathrm {d} t=\delta (\xi _{1}-\xi _{2})

Tramite prolungamento analitico è anche possibile definire la trasformata di Laplace della delta nel seguente modo:

\int _{0}^{+\infty }\delta (t-a)e^{-st}\,\mathop {} \!\mathrm {d} t=e^{-sa}

\int _{0}^{+\infty }\delta (ta)e^{-st}\,\mathop {} \!\mathrm {d} t=e^{-sa}

\int _{0}^{+\infty }\delta (t-a)e^{-st}\,\mathop {} \!\mathrm {d} t=e^{-sa}

Note

^ Reed, Simon , pag. 135 .
^ F. Farassat , pag. 4 .
^ Reed, Simon , pag. 136 .
^ Se $\delta (n,x)$ $\delta (n,x)$ $\delta (n,x)$ è una distribuzione di probabilità su tutto l'asse reale (es. non è negativa tra $-\infty$ $-\infty$ $-\infty$ e $+\infty$ $+\infty$ $+\infty$ ), allora un'altra $\delta _{\phi }(n,x)$ $\delta _{\phi }(n,x)$ $\delta _{\phi }(n,x)$ può essere costruita sulla sua funzione caratteristica come segue:
$\delta _{\varphi }(a,x)={\frac {1}{2\pi }}~{\frac {\varphi (1/a,x)}{\delta (1/a,0)}}$ $\delta _{\varphi }(a,x)={\frac {1}{2\pi }}~{\frac {\varphi (1/a,x)}{\delta (1/a,0)}}$ $\delta _{\varphi }(a,x)={\frac {1}{2\pi }}~{\frac {\varphi (1/a,x)}{\delta (1/a,0)}}$
dove:
$\varphi (a,k)=\int _{-\infty }^{+\infty }\delta (a,x)e^{-ikx}\,\mathop {} \!\mathrm {d} x$ $\varphi (a,k)=\int _{-\infty }^{+\infty }\delta (a,x)e^{-ikx}\,\mathop {} \!\mathrm {d} x$ $\varphi (a,k)=\int _{-\infty }^{+\infty }\delta (a,x)e^{-ikx}\,\mathop {} \!\mathrm {d} x$
è la funzione caratteristica di $\delta (n,x)$ $\delta (n,x)$ $\delta (n,x)$ . Questo risultato è collegato alla proprietà di località della trasformata di Fourier .