Densitatea unui grafic

Fie graficul G = (N, A) definit ca o pereche din cele două mulțimi N: = {1,2,3, ..., n} și A, un subset al produsului cartezian N × N. N va fi setul de n noduri care alcătuiesc graficul de mai sus și A setul de arce.

fie n cardinalitatea lui N (adică numărul de noduri ale unui dat)
fie L cardinalitatea lui A (adică numărul de muchii ale aceluiași grafic)

Dacă perechile de noduri sunt considerate ordonate, graficul se numește orientat sau digraf, altfel nu orientat sau simplu. Se spune că graficul este ponderat dacă o greutate sau un cost este asociat cu fiecare arc.

Densitatea unui grafic simplu (Δ) sau nedirecționat este definită ca:

Δ = 2L / n (n-1)

Densitatea unui grafic orientat (Δ) este definită ca:

Δ = L / n (n-1)

În cazul graficelor ponderate în L, suma greutăților fiecărui arc trebuie înlocuită.

Densitatea unui grafic presupune valori cuprinse între 0 și 1 și, prin urmare, poate fi ușor conectată la conceptul de probabilitate . Densitatea unui grafic măsoară probabilitatea ca orice pereche de noduri să fie adiacente, în timp ce conexiunea unui grafic depinde de distribuția marginilor între noduri.

Un grafic deconectat poate avea o densitate mai mare decât una conectată datorită concentrației marginilor dintre un număr mic de noduri.

Exemple

Completați grafice nedirecționate

Să avem un grafic complet nedirecționat $\,K_{n}$ ${\ displaystyle \, K_ {n}}$ ${\ displaystyle \, K_ {n}}$ cu n = 1,2,3, ..., 8.

$K_{1}$ ${\ displaystyle K_ {1}}$ ${\ displaystyle K_ {1}}$	$K_{2}$ ${\ displaystyle K_ {2}}$ $K_ {2}$	$K_{3}$ ${\ displaystyle K_ {3}}$ ${\ displaystyle K_ {3}}$	$K_{4}$ ${\ displaystyle K_ {4}}$ ${\ displaystyle K_ {4}}$
$K_{5}$ ${\ displaystyle K_ {5}}$ ${\ displaystyle K_ {5}}$	$K_{6}$ ${\ displaystyle K_ {6}}$ ${\ displaystyle K_ {6}}$	$K_{7}$ ${\ displaystyle K_ {7}}$ ${\ displaystyle K_ {7}}$	$K_{8}$ ${\ displaystyle K_ {8}}$ ${\ displaystyle K_ {8}}$

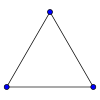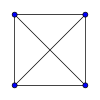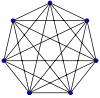Densitatea graficului complet dintr-o singură parte $K_{n}$ ${\ displaystyle K_ {n}}$ ${\ displaystyle K_ {n}}$ este întotdeauna egal cu unul.

Grafice bipartite

Să presupunem că luăm în considerare următorul grafic ciclic nedirectat (numit grafic bipartit ): . Puteți verifica cu ușurință dacă densitatea sa este aproximativ egală cu 0,28.

Aplicație la rețelele sociale

Un grup de indivizi între care există sau nu relații poate fi reprezentat matematic printr-un grafic. Chiar și mai multe grupuri de indivizi pot fi schematizate în același mod.

În general:

Diferiti actori (entități sociale) stabilesc relații între ei sau nu.
Actorii nu coincid neapărat cu indivizii, dar pot fi entități, orașe, națiuni etc.
Relațiile pot fi emoționale (prietenie, dragoste, autoritate, descendență, relații de muncă)

sau pot exprima conexiuni fizice (poduri, drumuri) sau chiar transferuri de resurse.
Densitatea din graficul care reprezintă o rețea socială poate fi un parametru care reprezintă eficiența în schimbul de informații și utilitatea pentru indivizi singuri. În lucrările lui Mark Granovetter se evidențiază și modul în care rețelele mici și dense pot fi mai puțin utile decât rețelele formate din verigi slabe, deoarece acestea din urmă sunt mai flexibile, oferindu-se astfel unui schimb mai bun de idei și oportunități.

Referințe

Paul E. Black, Grafic rar , din Dicționar de algoritmi și structuri de date, Paul E. Black (ed.), NIST . Adus la 29 septembrie 2005.
Thomas F. Coleman și Jorge J. Moré, Estimarea matricilor rare Jacobian și a problemelor de colorare a graficelor , în SIAM Journal on Numerical Analysis , vol. 20, nr. 1, 1983, pp. 187–209, DOI : 10.1137 / 0720013 .
Reinhard Diestel, Teoria graficelor , Texte postuniversitare în matematică, Springer-Verlag, 2005, ISBN 3-540-26183-4 ,OCLC 181535575 .
Bruno Preiss, Structuri de date și algoritmi cu modele de proiectare orientate pe obiecte în C ++ , John Wiley & Sons, 1998, ISBN 0-471-24134-2 .
I. Streinu și L. Theran, Hipergrafuri și algoritmi de joc cu pietricele , în European Journal of Combinatorics (ediție specială pentru Oriented Matroids '05) , 2008, arΧiv : math / 0703921 .

Elemente conexe

Portalul de matematică

Portalul de sociologie