Derivat

Linia L tangentă la P la graficul funcției are o pantă dată de derivata funcției la P

În matematică , funcția derivată $f'(x)$ ${\ displaystyle f '(x)}$ $f '(x)$ a unei funcții $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ reprezintă rata de schimbare a unei funcții față de o variabilă, adică măsura cât de mult se modifică valoarea unei funcții pe măsură ce se schimbă argumentul acesteia. Mai informal, derivatul măsoară creșterea (sau scăderea) care ar avea o funcție într-un anumit punct, deplasându-se foarte puțin din punctul luat în considerare.

Derivata unei funcții $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ intr-un loc $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ , în cazul funcțiilor cu o singură variabilă în câmpul real , corespunde pantei liniei tangente la graficul funcției $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ în sens $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ și reprezintă cea mai bună aproximare liniară . În cazul în care derivata există (adică funcția este diferențiată) în fiecare punct al domeniului , poate fi văzută la rândul ei ca o funcție care asociază derivata din acel punct la fiecare punct.

Conceptul de derivată este, împreună cu cel al integralului , una dintre pietrele de temelie ale analizei matematice și ale calculului infinitesimal . Înțelesul practic al derivatului este rata de schimbare a unei anumite cantități luate în considerare. Un exemplu bine cunoscut al unei derivate este schimbarea poziției unui obiect în raport cu timpul, numită viteză instantanee.

Descriere

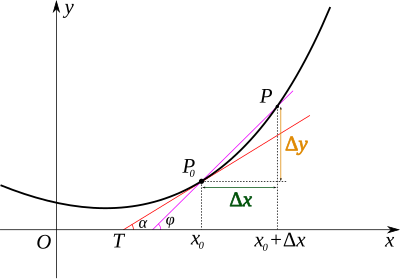
Derivata unei funcții într-un punct este coeficientul unghiular al liniei tangente la curba din punct. Prin urmare, este un număr care măsoară panta liniei tangente.

Derivata unei funcții $f$ ${\ displaystyle f}$ $f$ intr-un loc $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ este valoarea coeficientului unghiular al liniei drepte tangente la curba din punct, adică tangenta trigonometrică a unghiului format de tangentă la un punct al curbei ecuației $y=f(x)$ ${\ displaystyle y = f (x)}$ $y = f (x)$ iar axa absciselor . Dacă derivata unei funcții $f$ ${\ displaystyle f}$ $f$ intr-un loc $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ Și $f'(x)=0$ ${\ displaystyle f '(x) = 0}$ $f '(x) = 0$ , linia tangentă la graficul funcției $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ este paralel cu axa abscisei, în timp ce dacă se calculează limita cu care se calculează derivata dintr-un punct $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ linia tangentă la graficul funcției este infinită $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ este paralel cu axa ordonatelor. Funcția derivată este obținută cu o serie de operații algebrice cunoscute sub numele de reguli de derivare , aplicabile universal tuturor funcțiilor derivabile.

În cazul funcțiilor mai multor variabile, tangenta la un punct al curbei funcției nu este unică, ci variază în funcție de direcția aleasă. Prin urmare, nu mai este posibil să se definească o singură funcție a acelorași variabile independente care să țină cont de panta graficului funcției într-un punct: atunci recurgem la derivatele parțiale ale funcției, adică coeficienții unghiulari de tangente considerate de-a lungul direcțiilor paralele cu axele care reprezintă variabilele independente.

Derivatele parțiale sunt egale ca număr cu variabilele în sine și o proprietate remarcabilă a acestora este că, dacă funcția este suficient de „regulată” (adică diferențiată ) este posibil să se calculeze tangenta sa de-a lungul oricărei direcții cu o combinație liniară a derivatelor parțiale înșiși. Acest lucru este posibil deoarece operatorul de derivare este un operator liniar și, prin urmare, derivata unei combinații liniare de funcții diferențiate este combinația liniară a derivatelor funcțiilor unice, iar derivata produsului unui scalar pentru o funcție este produsul a scalarului pentru derivata funcției.

Definiție

O animație care oferă o idee intuitivă a derivatului, pe măsură ce „leagănul” unei funcții se schimbă atunci când argumentul se schimbă.

Noțiunea de derivată este introdusă, în cazul unei funcții cu o variabilă independentă în câmpul real, prin considerarea unei funcții reale $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ de variabilă reală $X$ ${\ displaystyle x}$ $X$ și un punct $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ a domeniului său. Derivatul lui $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ în $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ este definit ca numărul $f'(x_{0})$ ${\ displaystyle f '(x_ {0})}$ $f '(x_0)$ egală cu limita raportului incremental atunci când creșterea tinde la 0, sub ipoteza că această limită există și este finită. A spus explicit $h$ ${\ displaystyle h}$ $h$ creșterea, o funcție $f$ ${\ displaystyle f}$ $f$ definit într-un cartier al $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ se spune că este diferențiat la acest punct $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ dacă există și limita este finită:

f'(x_{0})=\lim _{h\to 0}{\frac {f(x_{0}+h)-f(x_{0})}{h}}

{\ displaystyle f '(x_ {0}) = \ lim _ {h \ to 0} {\ frac {f (x_ {0} + h) -f (x_ {0})} {h}}}

{\ displaystyle f '(x_ {0}) = \ lim _ {h \ to 0} {\ frac {f (x_ {0} + h) -f (x_ {0})} {h}}}

iar valoarea acestei limite este derivata funcției la punct $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ . Dacă funcția $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ este diferențiat în orice punct al unui interval dat $(a,b)$ ${\ displaystyle (a, b)}$ $(a, b)$ , Atunci se spune că este diferențiat $(a,b)$ ${\ displaystyle (a, b)}$ $(a, b)$ și funcție $f'\colon x\in (a,b)\to f'(x)$ ${\ displaystyle f '\ colon x \ in (a, b) \ to f' (x)}$ ${\ displaystyle f '\ colon x \ in (a, b) \ to f' (x)}$ care se asociază fiecărui punct $X$ ${\ displaystyle x}$ $X$ derivatul $f'(x)$ ${\ displaystyle f '(x)}$ $f '(x)$ din $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ este funcția derivată a $f$ ${\ displaystyle f}$ $f$ .

Derivată complexă

Același subiect în detaliu: Derivat complex .

Deși cel mai simplu caz este cel al funcțiilor reale, definiția derivatei își găsește locul cel mai natural în contextul analizei complexe , unde, atunci când este aplicată funcțiilor variabile complexe , ia numele de derivată complexă. ^[1] A spus $U$ ${\ displaystyle U}$ $U$ un subset deschis al planului complex , o funcție complexă $f\colon U\to \mathbb {C}$ ${\ displaystyle f \ colon U \ to \ mathbb {C}}$ ${\ displaystyle f \ colon U \ to \ mathbb {C}}$ poate fi diferențiat într-un sens complex la un moment dat $z_{0}\in U$ ${\ displaystyle z_ {0} \ în U}$ $z_0 \ în U$ dacă există limita : ^[2]

f'(z_{0})=\lim _{z\to z_{0}}{\frac {f(z)-f(z_{0})}{z-z_{0}}}.

{\ displaystyle f '(z_ {0}) = \ lim _ {z \ to z_ {0}} {\ frac {f (z) -f (z_ {0})} {z-z_ {0}}} .}

{\ displaystyle f '(z_ {0}) = \ lim _ {z \ to z_ {0}} {\ frac {f (z) -f (z_ {0})} {z-z_ {0}}} .}

Această limită trebuie înțeleasă în raport cu topologia podelei. Cu alte cuvinte, pentru fiecare succesiune de numere complexe care converge la $z_{0}$ ${\ displaystyle z_ {0}}$ $z_0$ , raportul incremental trebuie să tindă la același număr, indicat cu $f'(z_{0}).$ ${\ displaystyle f '(z_ {0}).}$ ${\ displaystyle f '(z_ {0}).}$ De sine $f$ ${\ displaystyle f}$ $f$ poate fi diferențiat în sens complex în fiecare punct $z_{0}\in U$ ${\ displaystyle z_ {0} \ în U}$ $z_0 \ în U$ , se spune că este o funcție holomorfă pe $U$ ${\ displaystyle U}$ $U$ .

Relația dintre derivată reală și complexă

Relația dintre diferențialitatea funcțiilor reale și funcțiile complexe este dată de faptul că, dacă o funcție complexă:

f(z)\equiv f(x+iy)=u(x,y)+iv(x,y)

{\ displaystyle f (z) \ equiv f (x + iy) = u (x, y) + iv (x, y)}

{\ displaystyle f (z) \ equiv f (x + iy) = u (x, y) + iv (x, y)}

atunci este holomorf $tu$ ${\ displaystyle u}$ $tu$ Și $v$ ${\ displaystyle v}$ $v$ posedă prima derivată parțială cu privire la $X$ ${\ displaystyle x}$ $X$ Și $y$ ${\ displaystyle y}$ $y$ și să satisfacă ecuațiile Cauchy-Riemann : ^[3]

{\frac {\partial u}{\partial x}}={\frac {\partial v}{\partial y}},\qquad {\frac {\partial u}{\partial y}}=-{\frac {\partial v}{\partial x}}.

{\ displaystyle {\ frac {\ partial u} {\ partial x}} = {\ frac {\ partial v} {\ partial y}}, \ qquad {\ frac {\ partial u} {\ partial y}} = - {\ frac {\ partial v} {\ partial x}}.}

{\ displaystyle {\ frac {\ partial u} {\ partial x}} = {\ frac {\ partial v} {\ partial y}}, \ qquad {\ frac {\ partial u} {\ partial y}} = - {\ frac {\ partial v} {\ partial x}}.}

În mod echivalent, derivatul Wirtinger $\partial f/\partial {\overline {z}}$ ${\ displaystyle \ partial f / \ partial {\ overline {z}}}$ $\ partial f / \ partial \ overline {z}$ din $f$ ${\ displaystyle f}$ $f$ în ceea ce privește complexul conjugat ${\overline {z}}$ ${\ displaystyle {\ overline {z}}}$ $\ overline {z}$ din $z$ ${\ displaystyle z}$ $z$ Nu-i nimic.

Derivată dreaptă și derivată stângă

Derivatul potrivit al $f$ ${\ displaystyle f}$ $f$ în $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ este numărul:

f'_{+}(x_{0})=\lim _{h\to 0^{+}}{\frac {f(x_{0}+h)-f(x_{0})}{h}}.

{\ displaystyle f '_ {+} (x_ {0}) = \ lim _ {h \ to 0 ^ {+}} {\ frac {f (x_ {0} + h) -f (x_ {0}) } {h}}.}

{\ displaystyle f '_ {+} (x_ {0}) = \ lim _ {h \ to 0 ^ {+}} {\ frac {f (x_ {0} + h) -f (x_ {0}) } {h}}.}

În mod similar, derivatul din stânga al $f$ ${\ displaystyle f}$ $f$ în $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ este numărul:

f'_{-}(x_{0})=\lim _{h\to 0^{-}}{\frac {f(x_{0}+h)-f(x_{0})}{h}}.

{\ displaystyle f '_ {-} (x_ {0}) = \ lim _ {h \ to 0 ^ {-}} {\ frac {f (x_ {0} + h) -f (x_ {0}) } {h}}.}

{\ displaystyle f '_ {-} (x_ {0}) = \ lim _ {h \ to 0 ^ {-}} {\ frac {f (x_ {0} + h) -f (x_ {0}) } {h}}.}

O funcție este diferențiată în $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ dacă și numai dacă derivatele din dreapta și din stânga există finite și egale. Acestea permit, de asemenea, să se definească diferențialitatea pe un interval nedeschis: dacă $f$ ${\ displaystyle f}$ $f$ este definit de exemplu în intervalul închis $[a,b]$ ${\ displaystyle [a, b]}$ $[a, b]$ , se spune că $f$ ${\ displaystyle f}$ $f$ este diferențiat în $[a,b]$ ${\ displaystyle [a, b]}$ $[a, b]$ dacă este diferențiat în orice punct intern $x\in (a,b)$ ${\ displaystyle x \ in (a, b)}$ $x \ in (a, b)$ iar dacă există derivate la stânga și la dreapta respectiv la extreme $x=a$ ${\ displaystyle x = a}$ $x = a$ Și $x=b$ ${\ displaystyle x = b}$ $x = b$ .

Notări

Același subiect în detaliu: Notare pentru diferențiere .

Prima notație a derivatei din punct $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ care apare istoric este:

\left({\frac {\mathrm {d} f}{\mathrm {d} x}}\right)_{(x_{0})}

{\ displaystyle \ left ({\ frac {\ mathrm {d} f} {\ mathrm {d} x}} \ right) _ {(x_ {0})}}

\ left (\ frac {\ mathrm {d} f} {\ mathrm {d} x} \ right) _ {(x_0)}

încă folosit în fizică astăzi. Alternativ, conform notației Lagrange este indicat cu:

f^{\prime }(x_{0}),

{\ displaystyle f ^ {\ prime} (x_ {0}),}

{\ displaystyle f ^ {\ prime} (x_ {0}),}

conform notației Cauchy-Euler cu:

\operatorname {D} \left[{f}({x_{0}})\right],

{\ displaystyle \ operatorname {D} \ left [{f} ({x_ {0}}) \ right],}

{\ displaystyle \ operatorname {D} \ left [{f} ({x_ {0}}) \ right],}

conform notației lui Leibniz cu:

{\frac {\mathrm {d} f(x_{0})}{\mathrm {d} x}}

{\ displaystyle {\ frac {\ mathrm {d} f (x_ {0})} {\ mathrm {d} x}}}

\ frac {\ mathrm {d} f (x_0)} {\ mathrm {d} x}

și conform notației lui Newton cu:

{\dot {f}}(x_{0}).

{\ displaystyle {\ dot {f}} (x_ {0}).}

{\ displaystyle {\ dot {f}} (x_ {0}).}

Derivată parțială

Același subiect în detaliu: Derivat parțial .

În cazul unei funcții de mai multe variabile, creșterea funcției față de o singură variabilă este derivata parțială a funcției față de acea variabilă. Având în vedere o funcție vectorială a mai multor variabile $\mathbf {F} :E\subset \mathbb {R} ^{n}\rightarrow \mathbb {R} ^{m}$ ${\ displaystyle \ mathbf {F}: E \ subset \ mathbb {R} ^ {n} \ rightarrow \ mathbb {R} ^ {m}}$ $\ mathbf {F}: E \ subset \ mathbb R ^ n \ rightarrow \ mathbb R ^ m$ definit pe un set deschis de spațiu euclidian $\mathbb {R} ^{n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb R ^ n$ , spus $\{\mathbf {e} _{i}\}_{1\leq i\leq n}$ ${\ displaystyle \ {\ mathbf {e} _ {i} \} _ {1 \ leq i \ leq n}}$ $\ {\ mathbf e_i \} _ {1 \ le i \ le n}$ Și $\{\mathbf {u} _{i}\}_{1\leq i\leq m}$ ${\ displaystyle \ {\ mathbf {u} _ {i} \} _ {1 \ leq i \ leq m}}$ $\ {\ mathbf u_i \} _ {1 \ le i \ le m}$ baza canonică a $\mathbb {R} ^{n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb R ^ n$ Și $\mathbb {R} ^{m}$ ${\ displaystyle \ mathbb {R} ^ {m}}$ $\ mathbb R ^ m$ funcția poate fi scrisă astfel:

\mathbf {F} (\mathbf {x} )=\sum _{i}^{m}F_{i}(\mathbf {x} )\mathbf {u} _{i},\quad \mathbf {x} =(x_{1},x_{2},\dots ,x_{n})\in E.

{\ displaystyle \ mathbf {F} (\ mathbf {x}) = \ sum _ {i} ^ {m} F_ {i} (\ mathbf {x}) \ mathbf {u} _ {i}, \ quad \ mathbf {x} = (x_ {1}, x_ {2}, \ dots, x_ {n}) \ în E.}

{\ displaystyle \ mathbf {F} (\ mathbf {x}) = \ sum _ {i} ^ {m} F_ {i} (\ mathbf {x}) \ mathbf {u} _ {i}, \ quad \ mathbf {x} = (x_ {1}, x_ {2}, \ dots, x_ {n}) \ în E.}

Componenta $the$ ${\ displaystyle i}$ $the$ -alea din funcție este atunci:

F_{i}(\mathbf {x} )=\mathbf {F} (\mathbf {x} )\cdot \mathbf {u} _{i},\quad 1\leq i\leq m.

{\ displaystyle F_ {i} (\ mathbf {x}) = \ mathbf {F} (\ mathbf {x}) \ cdot \ mathbf {u} _ {i}, \ quad 1 \ leq i \ leq m.}

{\ displaystyle F_ {i} (\ mathbf {x}) = \ mathbf {F} (\ mathbf {x}) \ cdot \ mathbf {u} _ {i}, \ quad 1 \ leq i \ leq m.}

Este definit ca o derivată parțială a $F_{i}$ ${\ displaystyle F_ {i}}$ $F_i$ în ceea ce privește variabila $x_{j}$ ${\ displaystyle x_ {j}}$ $x_j$ limita: ^[4]

{\begin{aligned}{\frac {\partial F_{i}(\mathbf {x} )}{\partial x_{j}}}&=\lim _{t\to 0}{\frac {F_{i}(\mathbf {x} +t\mathbf {e} _{j})-F_{i}(\mathbf {x} )}{t}}\\&=\lim _{t\to 0}{\frac {F_{i}(x_{1},x_{2},\ldots x_{j}+t,\ldots ,x_{n})-F_{i}(x_{1},x_{2},\ldots ,x_{n})}{t}}\end{aligned}}

{\ displaystyle {\ begin {align} {\ frac {\ partial F_ {i} (\ mathbf {x})} {\ partial x_ {j}}} & = \ lim _ {t \ to 0} {\ frac {F_ {i} (\ mathbf {x} + t \ mathbf {e} _ {j}) - F_ {i} (\ mathbf {x})} {t}} \\ & = \ lim _ {t \ la 0} {\ frac {F_ {i} (x_ {1}, x_ {2}, \ ldots x_ {j} + t, \ ldots, x_ {n}) - F_ {i} (x_ {1}, x_ {2}, \ ldots, x_ {n})} {t}} \ end {align}}}

{\ displaystyle {\ begin {align} {\ frac {\ partial F_ {i} (\ mathbf {x})} {\ partial x_ {j}}} & = \ lim _ {t \ to 0} {\ frac {F_ {i} (\ mathbf {x} + t \ mathbf {e} _ {j}) - F_ {i} (\ mathbf {x})} {t}} \\ & = \ lim _ {t \ la 0} {\ frac {F_ {i} (x_ {1}, x_ {2}, \ ldots x_ {j} + t, \ ldots, x_ {n}) - F_ {i} (x_ {1}, x_ {2}, \ ldots, x_ {n})} {t}} \ end {align}}}

Această limită este uneori numită limita raportului incremental al $f$ ${\ displaystyle f}$ $f$ în sens $\mathbf {x}$ ${\ displaystyle \ mathbf {x}}$ $\ mathbf {x}$ , și este, de asemenea, notat cu $D_{j}F_{i}$ ${\ displaystyle D_ {j} F_ {i}}$ $D_jF_i$ . Derivata parțială a unei funcții sau, în cazul unei funcții vectoriale a uneia dintre componentele sale, se realizează apoi luând în considerare alte variabile decât cea cu privire la care se dorește derivarea ca constante și calculând raportul lor incremental.

Derivată direcțională

Același subiect în detaliu: Derivat direcțional .

Derivata direcțională a unei funcții scalare $f(\mathbf {x} )=f(x_{1},x_{2},\ldots ,x_{n})$ ${\ displaystyle f (\ mathbf {x}) = f (x_ {1}, x_ {2}, \ ldots, x_ {n})}$ $f (\ mathbf {x}) = f (x_1, x_2, \ ldots, x_n)$ de-a lungul unui vector unitate $\mathbf {u} =(u_{1},\ldots ,u_{n})$ ${\ displaystyle \ mathbf {u} = (u_ {1}, \ ldots, u_ {n})}$ $\ mathbf {u} = (u_1, \ ldots, u_n)$ este funcția definită de limită :

D_{\mathbf {u} }{f}(\mathbf {x} )=\lim _{h\rightarrow 0^{+}}{\frac {f(\mathbf {x} +h\mathbf {u} )-f(\mathbf {x} )}{h}}.

{\ displaystyle D _ {\ mathbf {u}} {f} (\ mathbf {x}) = \ lim _ {h \ rightarrow 0 ^ {+}} {\ frac {f (\ mathbf {x} + h \ mathbf {u}) -f (\ mathbf {x})} {h}}.}

{\ displaystyle D _ {\ mathbf {u}} {f} (\ mathbf {x}) = \ lim _ {h \ rightarrow 0 ^ {+}} {\ frac {f (\ mathbf {x} + h \ mathbf {u}) -f (\ mathbf {x})} {h}}.}

Dacă funcția $f$ ${\ displaystyle f}$ $f$ este diferențiat în $\mathbf {x}$ ${\ displaystyle \ mathbf {x}}$ $\ mathbf {x}$ , atunci derivata direcțională există de-a lungul fiecărui vector unitar $\mathbf {u} ,$ ${\ displaystyle \ mathbf {u},}$ $\ mathbf {u},$ și avem: ^[5]

D_{\mathbf {u} }{f}(\mathbf {x} )=\nabla f(\mathbf {x} )\cdot \mathbf {u} ,

{\ displaystyle D _ {\ mathbf {u}} {f} (\ mathbf {x}) = \ nabla f (\ mathbf {x}) \ cdot \ mathbf {u},}

{\ displaystyle D _ {\ mathbf {u}} {f} (\ mathbf {x}) = \ nabla f (\ mathbf {x}) \ cdot \ mathbf {u},}

unde este $\nabla f$ ${\ displaystyle \ nabla f}$ $\ nabla f$ la al doilea membru reprezintă gradientul de $f$ ${\ displaystyle f}$ $f$ Și $\cdot$ ${\ displaystyle \ cdot}$ $\ cdot$ produsul scalar euclidian . În $\mathbf {x}$ ${\ displaystyle \ mathbf {x}}$ $\ mathbf {x}$ derivata direcțională a $f$ ${\ displaystyle f}$ $f$ reprezintă variația lui $f$ ${\ displaystyle f}$ $f$ lung $\mathbf {u}$ ${\ displaystyle \ mathbf {u}}$ $\ mathbf {u}$ .

Generalizări ale derivatei

Același subiect în detaliu: Generalizări ale derivatei .

Diferențialitatea unei funcții

Același subiect în detaliu: funcție diferențiată , clasa C a unei funcții și diferențial (matematică) .

O funcție din

\mathbb {R}

{\ displaystyle \ mathbb {R}}

\ R

în

\mathbb {R}

{\ displaystyle \ mathbb {R}}

\ R

Este diferențiat la un punct dacă este aproximat aproape de acel punct de la o linie. Prin urmare, această linie trebuie să fie tangentă la graficul funcției. Această noțiune se extinde la dimensiuni arbitrare și se numește o funcție diferențiată .

O funcție diferențiată la un punct este o funcție care poate fi aproximată printr-o transformare liniară în punct. Pentru ca acest lucru să se întâmple, este necesar să existe toate derivatele parțiale calculate în punct, adică există limite finite ale raporturilor direcționale incrementale (prin urmare, dacă o funcție este diferențiată într-un punct, atunci aceasta este diferențiată în punct). Proprietatea de diferențiere a unei funcții permite generalizarea conceptului de funcție diferențiată la funcțiile vectoriale ale unei variabile vectoriale și permite identificarea unui hiperplan tangent pentru fiecare punct al graficului său.

O functie $\mathbf {F} :U\rightarrow \mathbb {R} ^{m}$ ${\ displaystyle \ mathbf {F}: U \ rightarrow \ mathbb {R} ^ {m}}$ $\ mathbf {F}: U \ rightarrow \ mathbb R ^ m$ definit pe un set deschis de spațiu euclidian $\mathbb {R} ^{n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb R ^ n$ se spune că poate fi diferențiat la un moment dat $\mathbf {x} _{0}$ ${\ displaystyle \ mathbf {x} _ {0}}$ $\ mathbf {x} _0$ domeniu dacă există o aplicație liniară $\mathbf {L} :\mathbb {R} ^{n}\rightarrow \mathbb {R} ^{m}$ ${\ displaystyle \ mathbf {L}: \ mathbb {R} ^ {n} \ rightarrow \ mathbb {R} ^ {m}}$ $\ mathbf {L}: \ mathbb R ^ n \ rightarrow \ mathbb R ^ m$ astfel încât aproximarea să dețină:

\mathbf {F} (\mathbf {x} _{0}+\mathbf {h} )-\mathbf {F} (\mathbf {x} _{0})=\mathbf {L} (\mathbf {x} _{0})\mathbf {h} +\mathbf {r} (\mathbf {h} ),

{\ displaystyle \ mathbf {F} (\ mathbf {x} _ {0} + \ mathbf {h}) - \ mathbf {F} (\ mathbf {x} _ {0}) = \ mathbf {L} (\ mathbf {x} _ {0}) \ mathbf {h} + \ mathbf {r} (\ mathbf {h}),}

{\ displaystyle \ mathbf {F} (\ mathbf {x} _ {0} + \ mathbf {h}) - \ mathbf {F} (\ mathbf {x} _ {0}) = \ mathbf {L} (\ mathbf {x} _ {0}) \ mathbf {h} + \ mathbf {r} (\ mathbf {h}),}

unde este $\mathbf {r} (\mathbf {h} )$ ${\ displaystyle \ mathbf {r} (\ mathbf {h})}$ $\ mathbf r (\ mathbf {h})$ este anulat atunci când incrementul este anulat $\mathbf {h}$ ${\ displaystyle \ mathbf {h}}$ $\ mathbf {h}$ . Această condiție poate fi scrisă într-un mod echivalent:

\lim _{\mathbf {h} \to \mathbf {0} }{\frac {\mathbf {F} (\mathbf {x} _{0}+\mathbf {h} )-\mathbf {F} (\mathbf {x} _{0})-\mathbf {L} (\mathbf {x} _{0})\mathbf {h} }{\|\mathbf {h} \|}}=\mathbf {0} .

{\ displaystyle \ lim _ {\ mathbf {h} \ to \ mathbf {0}} {\ frac {\ mathbf {F} (\ mathbf {x} _ {0} + \ mathbf {h}) - \ mathbf { F} (\ mathbf {x} _ {0}) - \ mathbf {L} (\ mathbf {x} _ {0}) \ mathbf {h}} {\ | \ mathbf {h} \ |}} = \ mathbf {0}.}

{\ displaystyle \ lim _ {\ mathbf {h} \ to \ mathbf {0}} {\ frac {\ mathbf {F} (\ mathbf {x} _ {0} + \ mathbf {h}) - \ mathbf { F} (\ mathbf {x} _ {0}) - \ mathbf {L} (\ mathbf {x} _ {0}) \ mathbf {h}} {\ | \ mathbf {h} \ |}} = \ mathbf {0}.}

Dacă funcția $\mathbf {F}$ ${\ displaystyle \ mathbf {F}}$ $\ mathbf {F}$ este diferențiat în $\mathbf {x} _{0}$ ${\ displaystyle \ mathbf {x} _ {0}}$ $\ mathbf {x} _0$ , aplicația $\mathbf {L}$ ${\ displaystyle \ mathbf {L}}$ $\ mathbf {L}$ este reprezentată de matricea iacobiană $J_{F}$ ${\ displaystyle J_ {F}}$ $J_F$ .

Vectorul:

\mathbf {L} (\mathbf {x} _{0})\mathbf {h} =\mathrm {d} \mathbf {F} (\mathbf {x} _{0})=J_{F}\mathbf {h}

{\ displaystyle \ mathbf {L} (\ mathbf {x} _ {0}) \ mathbf {h} = \ mathrm {d} \ mathbf {F} (\ mathbf {x} _ {0}) = J_ {F } \ mathbf {h}}

\ mathbf {L} (\ mathbf {x} _0) \ mathbf {h} = \ mathrm {d} \ mathbf {F} (\ mathbf {x} _0) = J_F \ mathbf h

se numește diferențial de $\mathbf {F}$ ${\ displaystyle \ mathbf {F}}$ $\ mathbf {F}$ în $\mathbf {x} _{0}$ ${\ displaystyle \ mathbf {x} _ {0}}$ $\ mathbf {x} _0$ Și $\mathbf {L} (\mathbf {x_{0}} )$ ${\ displaystyle \ mathbf {L} (\ mathbf {x_ {0}})}$ $\ mathbf {L} (\ mathbf {x_0})$ este derivata totală a funcției $\mathbf {F}$ ${\ displaystyle \ mathbf {F}}$ $\ mathbf {F}$ .

Functia $\mathbf {F}$ ${\ displaystyle \ mathbf {F}}$ $\ mathbf {F}$ în cele din urmă este diferențiat dacă este așa în fiecare punct al domeniului. ^[6] În special, teorema diferențială totală afirmă că o funcție este diferențiată într-un punct dacă toate derivatele parțiale există într-un vecinătate al punctului pentru fiecare componentă a funcției și dacă sunt și funcții continue. De asemenea, dacă cererea obligatorie $\mathbf {x}$ ${\ displaystyle \ mathbf {x}}$ $\ mathbf {x}$ la $\mathbf {L} (\mathbf {x} )$ ${\ displaystyle \ mathbf {L} (\ mathbf {x})}$ $\ mathbf {L} (\ mathbf {x})$ este continuă, funcția se spune că poate fi diferențiată prin continuitate . ^[7]

Continuitate și derivabilitate

Același subiect în detaliu: funcție continuă .

Teorema continuității afirmă că dacă $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ este diferențiat în $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ asa de $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ este de asemenea continuu în $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ .

Teorema obținută prin inversarea ipotezelor cu teze nu este valabilă: de exemplu, funcția $f(x)=|x|$ ${\ displaystyle f (x) = | x |}$ $f (x) = | x |$ este continuu pe întregul domeniu, dar nu poate fi diferențiat la momentul respectiv $x_{0}=0$ ${\ displaystyle x_ {0} = 0}$ ${\ displaystyle x_ {0} = 0}$ , deoarece limitele dreapta și stânga ale raportului incremental nu coincid. Continuitatea unei funcții este deci o condiție necesară, dar nu suficientă, pentru a determina derivabilitatea acesteia. O funcție poate fi, de asemenea, diferențiată (și, prin urmare, continuă) la un moment dat $p$ ${\ displaystyle p}$ $p$ , dar fii discontinuu în fiecare punct din jur $p$ ${\ displaystyle p}$ $p$ . Acest lucru se întâmplă pentru funcții precum:

f(x)={\begin{cases}0,&{\text{ se }}x\in \mathbb {Q} ,\\x^{2},&{\text{ se }}x\in \mathbb {R} \setminus \mathbb {Q} .\end{cases}}

{\ displaystyle f (x) = {\ begin {cases} 0 și {\ text {se}} x \ in \ mathbb {Q}, \\ x ^ {2} și {\ text {se}} x \ in \ mathbb {R} \ setminus \ mathbb {Q}. \ end {cases}}}

{\ displaystyle f (x) = {\ begin {cases} 0 și {\ text {se}} x \ in \ mathbb {Q}, \\ x ^ {2} și {\ text {se}} x \ in \ mathbb {R} \ setminus \ mathbb {Q}. \ end {cases}}}

fiind $\mathbb {Q}$ ${\ displaystyle \ mathbb {Q}}$ $\ mathbb {Q}$ mulțimea numerelor raționale e $\mathbb {R}$ ${\ displaystyle \ mathbb {R}}$ $\ mathbb {R}$ mulțimea numerelor reale , în timp ce simbolul "\" denotă diferența dintre mulțimi. Funcția în cauză admite derivată în (limita raportului incremental se menține), dar nu este continuă în niciun punct, cu excepția lo. Observăm că, dacă în schimb o funcție este de două ori diferențiată într-un punct, atunci este continuă într-un vecinătate a acelui punct.

Pentru a arăta că dacă $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ este diferențiat în $x_{0},$ ${\ displaystyle x_ {0},}$ ${\ displaystyle x_ {0},}$ atunci este continuu în $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ , se consideră egalitatea anterioară:

f(x)=f(x_{0})+f^{\prime }(x_{0})(x-x_{0})+o(x-x_{0}),

{\ displaystyle f (x) = f (x_ {0}) + f ^ {\ prime} (x_ {0}) (x-x_ {0}) + o (x-x_ {0}),}

{\ displaystyle f (x) = f (x_ {0}) + f ^ {\ prime} (x_ {0}) (x-x_ {0}) + o (x-x_ {0}),}

de la care:

{\begin{aligned}\lim _{x\to x_{0}}f(x)&=\lim _{x\to x_{0}}f(x_{0})+f^{\prime }(x_{0})(x-x_{0})+o(x-x_{0})\\&=f(x_{0})\\\end{aligned}}

{\ displaystyle {\ begin {align} \ lim _ {x \ to x_ {0}} f (x) & = \ lim _ {x \ to x_ {0}} f (x_ {0}) + f ^ { \ prime} (x_ {0}) (x-x_ {0}) + o (x-x_ {0}) \\ & = f (x_ {0}) \\\ end {align}}}

{\ displaystyle {\ begin {align} \ lim _ {x \ to x_ {0}} f (x) & = \ lim _ {x \ to x_ {0}} f (x_ {0}) + f ^ { \ prime} (x_ {0}) (x-x_ {0}) + o (x-x_ {0}) \\ & = f (x_ {0}) \\\ end {align}}}

Deci funcția este continuă în $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ . Estimarea liniară a funcției din jur $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ este o aproximare mai bună decât:

f(x)=f(x_{0})+o(1)

{\ displaystyle f (x) = f (x_ {0}) + o (1)}

f (x) = f (x_0) + o (1)

garantat doar de continuitate (aici $o(1){\underset {x\to x_{0}}{\longrightarrow }}0$ ${\ displaystyle o (1) {\ underset {x \ to x_ {0}} {\ longrightarrow}} 0}$ $sau (1) \ underset {x \ to x_0} {\ longrightarrow} 0$ ). Dacă funcția este diferențiată în $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ infinitesimalul poate fi „defalcat” $o(1)$ ${\ displaystyle o (1)}$ $o (1)$ într-un termen liniar și un infinitesimal de ordin superior. Teorema lui Lagrange oferă o aproximare diferită (întotdeauna liniară) în ipoteza că funcția este diferențiată într-un vecinătate a $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ :

f(x)=f(x_{0})+f^{\prime }(\xi )(x-x_{0})

{\ displaystyle f (x) = f (x_ {0}) + f ^ {\ prime} (\ xi) (x-x_ {0})}

f (x) = f (x_0) + f ^ {\ prime} (\ xi) (x-x_0)

pentru toți $X$ ${\ displaystyle x}$ $X$ în astfel de împrejurimi și cu $\xi$ ${\ displaystyle \ xi}$ $\ xi$ un punct dat în $(x_{0},x)$ ${\ displaystyle (x_ {0}, x)}$ $(x_0, x)$ (sau $(x,x_{0})$ ${\ displaystyle (x, x_ {0})}$ $(x, x_0)$ , dacă este un cartier de stânga). Deși aproximarea este acum „exactă” (nu există termeni infinitezimali neglijați), teorema nu poate arăta pentru care $\xi$ ${\ displaystyle \ xi}$ $\ xi$ egalitatea este adevărată.

Funcții nediferențiate

Funcția de valoare absolută nu este diferențiată la origine, unde are un punct unghiular

O funcție continuă poate fi nediferențiată. De exemplu, o funcție continuă nu poate fi diferențiată la un punct izolat al domeniului, în prezența unui punct unghiular , a unei cuspide sau a unei inflexiuni tangente verticale. Există, de asemenea, funcții continue care au forme mai complexe de non-derivabilitate, cum ar fi funcția Cantor . Funcția Weierstrass este o funcție reală a unei variabile reale care are proprietatea de a fi continuă în fiecare punct, dar de a nu fi diferențiată în niciunul.

Teoreme

Câteva teoreme și rezultate semnificative sunt prezentate mai jos.

Reguli de derivare

Același subiect în detaliu: reguli de derivare .

Lasa-i sa fie $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ Și $g(x)$ ${\ displaystyle g (x)}$ $g (x)$ funcții reale ale variabilei reale $X$ ${\ displaystyle x}$ $X$ derivabil, și așa să fie $\mathrm {D}$ ${\ displaystyle \ mathrm {D}}$ $\ mathrm {D}$ operația de derivare cu privire la $X$ ${\ displaystyle x}$ $X$ :

\mathrm {D} [f(x)]=f'(x),\qquad \mathrm {D} [g(x)]=g'(x).

{\ displaystyle \ mathrm {D} [f (x)] = f '(x), \ qquad \ mathrm {D} [g (x)] = g' (x).}

{\ displaystyle \ mathrm {D} [f (x)] = f '(x), \ qquad \ mathrm {D} [g (x)] = g' (x).}

Regula sumei ( liniaritatea ):

\mathrm {D} [\alpha f(x)+\beta g(x)]=\alpha f'(x)+\beta g'(x),\qquad \alpha ,\beta \in \mathbb {R} .

{\ displaystyle \ mathrm {D} [\ alpha f (x) + \ beta g (x)] = \ alpha f '(x) + \ beta g' (x), \ qquad \ alpha, \ beta \ in \ mathbb {R}.}

{\ displaystyle \ mathrm {D} [\ alpha f (x) + \ beta g (x)] = \ alpha f '(x) + \ beta g' (x), \ qquad \ alpha, \ beta \ in \ mathbb {R}.}

Regula produsului (sau a lui Leibniz ):

\mathrm {D} [{f(x)\cdot g(x)}]=f'(x)\cdot g(x)+f(x)\cdot g'(x).

{\ displaystyle \ mathrm {D} [{f (x) \ cdot g (x)}] = f '(x) \ cdot g (x) + f (x) \ cdot g' (x).}

{\ displaystyle \ mathrm {D} [{f (x) \ cdot g (x)}] = f '(x) \ cdot g (x) + f (x) \ cdot g' (x).}

Regula cotientului :

\mathrm {D} \!\left[{f(x) \over g(x)}\right]={f'(x)\cdot g(x)-f(x)\cdot g'(x) \over g(x)^{2}}.

{\ displaystyle \ mathrm {D} \! \ left [{f (x) \ over g (x)} \ right] = {f '(x) \ cdot g (x) -f (x) \ cdot g' (x) \ peste g (x) ^ {2}}.}

{\ displaystyle \ mathrm {D} \! \ left [{f (x) \ over g (x)} \ right] = {f '(x) \ cdot g (x) -f (x) \ cdot g' (x) \ peste g (x) ^ {2}}.}

Regula funcției reciproce :

\mathrm {D} \!\left[{1 \over f(x)}\right]=-{f'(x) \over f(x)^{2}}.

{\ displaystyle \ mathrm {D} \! \ left [{1 \ over f (x)} \ right] = - {f '(x) \ over f (x) ^ {2}}.}

{\ displaystyle \ mathrm {D} \! \ left [{1 \ over f (x)} \ right] = - {f '(x) \ over f (x) ^ {2}}.}

Regula funcției inverse :

\mathrm {D} [f^{-1}(y)]={1 \over f'(x)},

{\ displaystyle \ mathrm {D} [f ^ {- 1} (y)] = {1 \ over f '(x)},}

{\ displaystyle \ mathrm {D} [f ^ {- 1} (y)] = {1 \ over f '(x)},}

cu:

y={f(x)},\qquad x={f^{-1}(y)}.

{\ displaystyle y = {f (x)}, \ qquad x = {f ^ {- 1} (y)}.}

{\ displaystyle y = {f (x)}, \ qquad x = {f ^ {- 1} (y)}.}

Regula lanțului :

\mathrm {D} \left[f\left(g(x)\right)\right]=f'\left(g(x)\right)\cdot g'(x).

{\ displaystyle \ mathrm {D} \ left [f \ left (g (x) \ right) \ right] = f '\ left (g (x) \ right) \ cdot g' (x).}

{\ displaystyle \ mathrm {D} \ left [f \ left (g (x) \ right) \ right] = f '\ left (g (x) \ right) \ cdot g' (x).}

Teorema lui Fermat

Același subiect în detaliu: teorema lui Fermat asupra punctelor staționare .

Este $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ o funcție diferențiată și, prin urmare, continuă, la un moment dat $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ în cadrul domeniului . De sine $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ este un punct maxim sau minim pentru funcție $f,$ ${\ displaystyle f,}$ $f,$ apoi derivata funcției în $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ nu este nimic, adică $f'(x_{0})=0$ ${\ displaystyle f '(x_ {0}) = 0}$ $f '(x_ {0}) = 0$ .

Nu este imperativ ca. $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ este intern domeniului, fiind suficient să fie un punct de acumulare dreapta și stânga pentru domeniu, în timp ce este esențial să presupunem că funcția este diferențiată în punctul $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ întrucât nu este posibil să se deducă derivabilitatea sa din celelalte ipoteze ale teoremei. Fiecare punct în care $f'(x)$ ${\ displaystyle f '(x)}$ $f '(x)$ dispare (adică este egal cu zero) se numește punctul staționar . Maximele și minimele relative se numesc puncte staționare ale $f'(x)$ ${\ displaystyle f '(x)}$ $f '(x)$ .

Această teoremă este utilizată pe scară largă în studiul funcțiilor, deoarece definește posibilitatea de a avea un punct maxim sau minim în care funcția derivată dispare.

Teorema lui Rolle

Același subiect în detaliu: teorema lui Rolle .

Este $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ o funcție continuă în intervalul închis $[a,b]$ ${\ displaystyle [a, b]}$ $[a, b]$ și diferențiat în intervalul deschis $(a,b)$ ${\ displaystyle (a, b)}$ $(a, b)$ . De sine $f(a)=f(b)$ ${\ displaystyle f (a) = f (b)}$ $f (a) = f (b)$ atunci există cel puțin un punct $x_{0}\in (a,b)$ ${\ displaystyle x_ {0} \ in (a, b)}$ $x_0 \ in (a, b)$ unde prima derivată $f'(x)$ ${\ displaystyle f '(x)}$ $f '(x)$ anulezi.

Teorema lui Lagrange

Același subiect în detaliu: teorema lui Lagrange .

Este $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ o funcție continuă în $[a,b]$ ${\ displaystyle [a, b]}$ $[a, b]$ și diferențiat în intervalul deschis $(a,b)$ ${\ displaystyle (a, b)}$ $(a, b)$ . Apoi, există cel puțin un punct $x_{0}\in (a,b)$ ${\ displaystyle x_ {0} \ in (a, b)}$ $x_0 \ in (a, b)$ astfel încât:

f'(x_{0})={{f(b)-f(a)} \over {b-a}}.

{\ displaystyle f '(x_ {0}) = {{f (b) -f (a)} \ over {ba}}.}

{\ displaystyle f '(x_ {0}) = {{f (b) -f (a)} \ over {b-a}}.}

Teorema afirmă că există cel puțin un punct $(x_{0},f(x_{0}))$ ${\ displaystyle (x_ {0}, f (x_ {0}))}$ $(x_0, f (x_0))$ a graficului funcției în care linia tangentă are un coeficient unghiular egal cu cel al corzii liniei care trece prin puncte $(a,f(a))$ ${\ displaystyle (a, f (a))}$ $(a, f (a))$ Și $(b,f(b))$ ${\ displaystyle (b, f (b))}$ $(b, f (b))$ . Este o generalizare a teoremei lui Rolle care analizează cazul în care $f(a)$ ${\ displaystyle f (a)}$ $face)$ este diferit de $f(b)$ ${\ displaystyle f (b)}$ $f (b)$ .

Teorema lui Cauchy

Același subiect în detaliu: teorema lui Cauchy (analiză matematică) .

Lasa-i sa fie $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ Și $g(x)$ ${\displaystyle g(x)}$ $g(x)$ funzioni continue in $[a,b]$ ${\displaystyle [a,b]}$ $[a,b]$ e derivabili in $(a,b)$ ${\displaystyle (a,b)}$ $(a,b)$ con $g'(x)$ ${\displaystyle g'(x)}$ $g'(x)$ diversa da 0 per ogni punto dell'intervallo. Allora esiste almeno un punto $x_{0}\in (a,b)$ $x_{0}\in (a,b)$ $x_0 \in (a,b)$ tale per cui:

{f'(x_{0}) \over g'(x_{0})}={{f(b)-f(a)} \over {g(b)-g(a)}}.

{f'(x_{0}) \over g'(x_{0})}={{f(b)-f(a)} \over {g(b)-g(a)}}.

{f'(x_{0}) \over g'(x_{0})}={{f(b)-f(a)} \over {g(b)-g(a)}}.

Considerando in particolare la funzione $g(t)=t$ ${\displaystyle g(t)=t}$ $g(t) = t$ , si ottiene l'affermazione del teorema di Lagrange.

Con il teorema di Cauchy è inoltre possibile dimostrare la regola di de l'Hôpital .

Monotonia a partire dalla derivata

Lo stesso argomento in dettaglio: Teorema di Lagrange .

Sia $f(x)$ ${\displaystyle f(x)}$ $f(x)$ continua in $[a,b]$ ${\displaystyle [a,b]}$ $[a,b]$ e derivabile in $(a,b)$ ${\displaystyle (a,b)}$ $(a,b)$ . Allora:

Per ogni $x\in (a,b)$ $x\in (a,b)$ $x \in (a,b)$ si ha $f'(x)\geqslant 0$ $f'(x)\geqslant 0$ $f'(x) \geqslant 0$ se e solo se la funzione è crescente in $(a,b)$ ${\displaystyle (a,b)}$ $(a,b)$ .
Per ogni $x\in (a,b)$ $x\in (a,b)$ $x \in (a,b)$ si ha $f'(x)\leqslant 0$ $f'(x)\leqslant 0$ $f'(x) \leqslant 0$ se e solo se la funzione è decrescente in $(a,b)$ ${\displaystyle (a,b)}$ $(a,b)$ .

La funzione può non essere strettamente crescente (o decrescente), e il teorema è direttamente ricavabile dall'enunciato di Lagrange.

Analogamente, valgono anche i fatti seguenti:

Se per ogni $x\in (a,b)$ $x\in (a,b)$ $x \in (a,b)$ si ha $f'(x)>0,$ ${\displaystyle f'(x)>0,}$ $f'(x)>0,$ allora la funzione è strettamente crescente in $(a,b)$ ${\displaystyle (a,b)}$ $(a,b)$ .
Se per ogni $x\in (a,b)$ $x\in (a,b)$ $x \in (a,b)$ si ha $f'(x)<0,$ ${\displaystyle f'(x)<0,}$ $f'(x)<0,$ allora la funzione è strettamente decrescente in $(a,b)$ ${\displaystyle (a,b)}$ $(a,b)$ .

Una funzione strettamente crescente non ha necessariamente derivata ovunque positiva. Ad esempio, $f(x)=x^{3}$ $f(x)=x^{3}$ $f(x)=x^{3}$ è strettamente crescente, ma ha derivata nulla nell'origine, dove c'è un punto di flesso .

Il teorema della funzione costante afferma che una funzione è costante in un intervallo $[a,b]$ ${\displaystyle [a,b]}$ $[a,b]$ se e solo se è derivabile e la derivata è ovunque nulla nell'intervallo. Mentre la condizione necessaria è conseguenza della definizione di derivata (la derivata di una costante è uguale a zero), la sufficienza segue dal teorema di Lagrange .

Derivate di ordine superiore

La derivata $n$ ${\displaystyle n}$ $n$ -esima $f^{(n)}$ $f^{(n)}$ $f^{(n)}$ di una funzione $f$ ${\displaystyle f}$ $f$ è la funzione che si ottiene derivando successivamente $n$ ${\displaystyle n}$ $n$ volte la funzione $f$ ${\displaystyle f}$ $f$ . Si definiscono così la derivata seconda, terza, e così via; e si usa generalmente una delle seguenti notazioni:

{\begin{aligned}f''=f^{(2)}&={\frac {\mathrm {d} ^{2}f}{\mathrm {d} x^{2}}}\\f'''=f^{(3)}&={\frac {\mathrm {d} ^{3}f}{\mathrm {d} x^{3}}}\\&\vdots \\f^{(n)}&={\frac {\mathrm {d} ^{n}f}{\mathrm {d} x^{n}}}.\end{aligned}}

{\begin{aligned}f''=f^{(2)}&={\frac {\mathrm {d} ^{2}f}{\mathrm {d} x^{2}}}\\f'''=f^{(3)}&={\frac {\mathrm {d} ^{3}f}{\mathrm {d} x^{3}}}\\&\vdots \\f^{(n)}&={\frac {\mathrm {d} ^{n}f}{\mathrm {d} x^{n}}}.\end{aligned}}

{\begin{aligned}f''=f^{(2)}&={\frac {\mathrm {d} ^{2}f}{\mathrm {d} x^{2}}}\\f'''=f^{(3)}&={\frac {\mathrm {d} ^{3}f}{\mathrm {d} x^{3}}}\\&\vdots \\f^{(n)}&={\frac {\mathrm {d} ^{n}f}{\mathrm {d} x^{n}}}.\end{aligned}}

Una funzione derivabile non è necessariamente derivabile $n$ ${\displaystyle n}$ $n$ volte. Ad esempio, la funzione $f(x)=x|x|$ ${\displaystyle f(x)=x|x|}$ $f(x) = x |x|$ ha una derivata prima, ma non una seconda: infatti, la derivata di $f$ ${\displaystyle f}$ $f$ è $f'(x)=2|x|$ ${\displaystyle f'(x)=2|x|}$ $f'(x)=2|x|$ , che non è a sua volta derivabile nell'origine.

La classe delle funzioni derivabili $n$ ${\displaystyle n}$ $n$ volte e la cui derivata $n$ ${\displaystyle n}$ $n$ -esima è continua si indica con $C^{n}$ $C^{n}$ $C^n$ .

Convessità

Lo stesso argomento in dettaglio: Funzione convessa .

Sia $f:[a,b]\to \mathbb {R}$ $f:[a,b]\to \mathbb {R}$ $f: [a,b] \to \mathbb{R}$ derivabile. Allora $f(x)$ ${\displaystyle f(x)}$ $f(x)$ è convessa se e solo se $f'(x)$ ${\displaystyle f'(x)}$ $f'(x)$ è crescente in $[a,b]$ ${\displaystyle [a,b]}$ $[a,b]$ . Se $f$ ${\displaystyle f}$ $f$ possiede derivata seconda, allora la convessità della funzione è data dalla disequazione:

f''(x)\geq 0.

f''(x)\geq 0.

f''(x)\geq 0.

Il cambiamento di segno della derivata seconda determina quindi un cambiamento di convessità della funzione e un relativo punto di flesso .

Significato geometrico della derivata

La retta in rosso è la tangente al grafico della f(x) nel punto (x ₀ , f(x ₀ ))

Il valore della derivata di $f(x)$ ${\displaystyle f(x)}$ $f(x)$ calcolata in $x_{0}$ $x_{0}$ $x_0$ ha un significato geometrico: è il coefficiente angolare della retta tangente alla curva rappresentata dal grafico di $f(x)$ ${\displaystyle f(x)}$ $f(x)$ nel punto di coordinate $(x_{0},f(x_{0}))$ $(x_{0},f(x_{0}))$ $(x_0,f(x_0))$ . In altre parole, la derivata è il valore della tangente trigonometrica dell'angolo (convesso) che la retta tangente in $x_{0}$ $x_{0}$ $x_0$ al grafico della funzione forma con l'asse delle ascisse (a patto che tale angolo non sia retto ).

L'equazione della retta tangente in $x_{0}$ $x_{0}$ $x_0$ risulta:

y=f(x_{0})+f'(x_{0})(x-x_{0}).

y=f(x_{0})+f'(x_{0})(x-x_{0}).

y=f(x_{0})+f'(x_{0})(x-x_{0}).

Più precisamente, se $f(x)$ ${\displaystyle f(x)}$ $f(x)$ è derivabile nel punto $x_{0}$ $x_{0}$ $x_0$ , allora esiste una funzione $o(x-x_{0})$ $o(x-x_{0})$ $o(x-x_0)$ definita in un intorno di $x_{0}$ $x_{0}$ $x_0$ tale che:

f(x)=f(x_{0})+f'(x_{0})(x-x_{0})+o(x-x_{0}),

f(x)=f(x_{0})+f'(x_{0})(x-x_{0})+o(x-x_{0}),

f(x)=f(x_{0})+f'(x_{0})(x-x_{0})+o(x-x_{0}),

con:

\lim _{x\to x_{0}}{{o(x-x_{0})} \over {x-x_{0}}}=0

\lim _{x\to x_{0}}{{o(x-x_{0})} \over {x-x_{0}}}=0

\lim_{x \to x_0}{{o(x-x_0)}\over{x-x_0}} = 0

e tale formula è l' espansione di Taylor di $f(x)$ ${\displaystyle f(x)}$ $f(x)$ troncata al termine di primo grado. Si dice che $o(x-x_{0})$ $o(x-x_{0})$ $o(x-x_0)$ è un infinitesimo di ordine superiore alla funzione $(x-x_{0})$ $(x-x_{0})$ $(x-x_0)$ , e con questo si vuole esprimere l'idea che il termine $o(x-x_{0})$ $o(x-x_{0})$ $o(x-x_0)$ fornisce un contributo che diventa trascurabile rispetto agli altri termini quando ci si avvicina a $x_{0}$ $x_{0}$ $x_0$ . Si può anche dire che una funzione derivabile in $x_{0}$ $x_{0}$ $x_0$ è approssimabile linearmente intorno a $x_{0}$ $x_{0}$ $x_0$ con la sua retta tangente in tale punto.

Se si definisce infatti $o(x-x_{0})$ $o(x-x_{0})$ $o(x-x_0)$ , avente lo stesso dominio di $f$ ${\displaystyle f}$ $f$ , come:

o(x-x_{0})=f(x)-f(x_{0})-f^{\prime }(x_{0})(x-x_{0}),

o(x-x_{0})=f(x)-f(x_{0})-f^{\prime }(x_{0})(x-x_{0}),

o(x-x_{0})=f(x)-f(x_{0})-f^{\prime }(x_{0})(x-x_{0}),

si verifica che:

\lim _{x\to x_{0}}{{o(x-x_{0})} \over {x-x_{0}}}=\lim _{x\to x_{0}}\left({\frac {f(x)-f(x_{0})}{x-x_{0}}}-f^{\prime }(x_{0})\right).

\lim _{x\to x_{0}}{{o(x-x_{0})} \over {x-x_{0}}}=\lim _{x\to x_{0}}\left({\frac {f(x)-f(x_{0})}{x-x_{0}}}-f^{\prime }(x_{0})\right).

\lim _{x\to x_{0}}{{o(x-x_{0})} \over {x-x_{0}}}=\lim _{x\to x_{0}}\left({\frac {f(x)-f(x_{0})}{x-x_{0}}}-f^{\prime }(x_{0})\right).

Ricordando che per $x\to x_{0}$ $x\to x_{0}$ $x \to x_0$ allora $x-x_{0}\to 0$ $x-x_{0}\to 0$ $x-x_0 \to 0$ , e quindi $h=x-x_{0}$ $h=x-x_{0}$ $h = x-x_0$ . Sostituendo questa ultima uguaglianza con la precedente equazione si ha:

\lim _{h\to 0}{\frac {f(x_{0}+h)-f(x_{0})}{h}}-f^{\prime }(x_{0})=0.

\lim _{h\to 0}{\frac {f(x_{0}+h)-f(x_{0})}{h}}-f^{\prime }(x_{0})=0.

\lim _{h\to 0}{\frac {f(x_{0}+h)-f(x_{0})}{h}}-f^{\prime }(x_{0})=0.

Esempio

Una funzione espressa come serie di potenze $\sum _{n=0}^{\infty }a_{n}X^{n}$ $\sum _{n=0}^{\infty }a_{n}X^{n}$ $\sum_{n=0}^\infty a_n X^n$ con raggio di convergenza $r$ ${\displaystyle r}$ $r$ è continua e derivabile su tutto l'intervallo $(-r,r)$ ${\displaystyle (-r,r)}$ $(-r, r)$ . La derivata può essere calcolata derivando termine a termine la serie nel modo seguente:

f'(x)=\sum _{n=1}^{\infty }na_{n}x^{n-1}.

f'(x)=\sum _{n=1}^{\infty }na_{n}x^{n-1}.

f'(x)=\sum _{n=1}^{\infty }na_{n}x^{n-1}.

Tuttavia, in una serie di potenze si preferisce che $n$ ${\displaystyle n}$ $n$ sia l'indice della potenza, quindi utilizzando uno shift diventa:

f'(x)=\sum _{n=0}^{\infty }{(n+1)}a_{n+1}x^{n}.

f'(x)=\sum _{n=0}^{\infty }{(n+1)}a_{n+1}x^{n}.

f'(x)=\sum _{n=0}^{\infty }{(n+1)}a_{n+1}x^{n}.

Questo tipo di derivata è importante per lo sviluppo di Taylor e Maclaurin.

Note

^ Weisstein, Eric W. Derivative. From MathWorld , su mathworld.wolfram.com . URL consultato il 25-11-2012 .
^ Rowland, Todd. Complex Differentiable. From MathWorld , su mathworld.wolfram.com . URL consultato il 25-11-2012 .
^ Weisstein, Eric W. Cauchy-Riemann Equations. From MathWorld , su mathworld.wolfram.com . URL consultato il 25-11-2012 .
^ W. Rudin , Pag. 216 .
^ W. Rudin , Pag. 219 .
^ W. Rudin , Pag. 214 .
^ W. Rudin , Pag. 220 .

Bibliografia

Paolo Marcellini , Carlo Sbordone : Analisi Matematica Uno , Liguori Editore, 1998, ISBN 9788820728199
Nicola Fusco , Paolo Marcellini , Carlo Sbordone : Lezioni di Analisi Matematica Due , Zanichelli, 2020, ISBN 9788808520203
Walter Rudin , Principi di Analisi Matematica , Milano, McGraw-Hill, 1991, ISBN 88-386-0647-1 .
( EN ) Abramowitz, M. and Stegun, IA (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing . New York: Dover, p. 11, 1972.
( EN ) Amend, B. Camp FoxTrot . Kansas City, MO: Andrews McMeel, p. 19, 1998.
( EN ) Anton, Howard, Calculus: A New Horizon, 6th ed. , New York, Wiley, 1999, ISBN 978-04-71153-06-1 .
( EN ) Beyer, WH Derivatives . CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 229–232, 19

Voci correlate

Altri progetti

Wikibooks contiene testi o manuali su derivata
Wikizionario contiene il lemma di dizionario « derivata »
Wikiversità contiene risorse su derivata

Collegamenti esterni

Derivata , su Treccani.it – Enciclopedie on line , Istituto dell'Enciclopedia Italiana .
( EN ) Derivata , su Enciclopedia Britannica , Encyclopædia Britannica, Inc.
Derivata , in Treccani.it – Enciclopedie on line , Istituto dell'Enciclopedia Italiana.
WIMS Function Calculator calcolo delle derivate online; questo sito permette anche di fare esercizi interattivi
Differenziazione calcolatrice , su easycalculation.com .
( EN ) Online Derivatives Calculator .
Limite, derivate, integrali Directory con varie risorse sulle derivate

Controllo di autorità	Thesaurus BNCF 32594 · LCCN ( EN ) sh2011005437 · NDL ( EN , JA ) 00560650

Portale Matematica : accedi alle voci di Wikipedia che trattano di matematica

[1] Weisstein, Eric W. Derivative. From MathWorld , su mathworld.wolfram.com . URL consultato il 25-11-2012 .

[2] Rowland, Todd. Complex Differentiable. From MathWorld , su mathworld.wolfram.com . URL consultato il 25-11-2012 .

[3] Weisstein, Eric W. Cauchy-Riemann Equations. From MathWorld , su mathworld.wolfram.com . URL consultato il 25-11-2012 .

[4] W. Rudin , Pag. 216 .

[5] W. Rudin , Pag. 219 .

[6] W. Rudin , Pag. 214 .

[7] W. Rudin , Pag. 220 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

V · D · M Analisi matematica
Calcolo infinitesimale	Numero reale · Infinitesimo · O-grande · Successione ( di funzioni ) · Successione di Cauchy · Teorema di Bolzano-Weierstrass · Stima asintotica · Limite ( di una funzione · di una successione · Forma indeterminata ) · Teorema dei due carabinieri · Limite notevole · Punto di accumulazione · Punto isolato · Intorno · Serie ( di funzioni ) · Criteri di convergenza ·Limite di funzioni a più variabili
Studio della continuità	Funzione continua · Punto di discontinuità · Continuità uniforme · Funzione lipschitziana · Teorema di Bolzano · Teorema di Weierstrass · Teorema dei valori intermedi · Teorema di Heine-Cantor · Modulo di continuità · Funzione semicontinua · Continuità separata · Teorema di approssimazione di Weierstrass
Calcolo differenziale	Derivata · Differenziale · Regole di derivazione · Teorema di Fermat · Teorema di Rolle · Teorema di Lagrange · Teorema di Cauchy · Teorema di Darboux · Teorema di Taylor · Serie di Taylor · Funzione differenziabile · Gradiente · Jacobiana · Hessiana · Forma differenziale · Generalizzazioni della derivata · Derivata parziale · Derivata mista
Integrale	Primitiva · Integrale di Riemann · Integrale improprio · Integrale di Lebesgue · Teorema fondamentale · Metodi di integrazione · Tavole · Integrale multiplo , di linea ( 1ª specie · 2ª specie ) e di superficie ( di volume )
Studio di funzione	Funzione · Variabile · Dominio e codominio · Funzioni pari e dispari · Funzione periodica · Funzione monotona · Funzione convessa · Massimo e minimo di una funzione · Punto angoloso · Cuspide · Punto di flesso · Asintoto · Grafico di una funzione · Funzione iniettiva
Disuguaglianze	Disuguaglianza triangolare · Disuguaglianza di Cauchy-Schwarz · Bernoulli · Jensen · Hölder · Young · Minkowski
Altro	Approssimazione di Stirling · Prodotto di Wallis · Funzione Gamma · Teorema delle funzioni implicite · Teorema della funzione inversa · Funzione hölderiana · Spazio metrico · Spazio normato · Intervallo · Insieme trascurabile · Insieme chiuso · Insieme aperto · Palla · Omeomorfismo · Omeomorfismo locale · Diffeomorfismo · Diffeomorfismo locale · Classe C di una funzione · Equazione differenziale · Problema di Cauchy