Determinant (algebră)

O transformare liniară a planului cartezian este descrisă de o matrice pătrată

2\times 2

{\ displaystyle 2 \ times 2}

2 \ ori 2

. Determinantul matricei oferă informații despre transformare: valoarea absolută descrie schimbarea zonei, în timp ce semnul descrie schimbarea orientării . În exemplul prezentat aici, matricea are determinant -1: prin urmare transformarea păstrează zonele (un pătrat al zonei 1 se transformă într-un paralelogram al zonei 1), dar inversează orientarea planului.

În algebra liniară , determinantul unei matrice pătrate $LA$ ${\ displaystyle A}$ $LA$ este un număr care descrie unele proprietăți algebrice și geometrice ale matricei .

În general este denumit $\det(A)$ ${\ displaystyle \ det (A)}$ $\ det (A)$ și, uneori, cu $|A|$ ${\ displaystyle | A |}$ $| A |$ . Ultima notație este mai compactă, dar și mai ambiguă, deoarece este uneori folosită pentru a descrie o normă a matricei. ^[1]

Determinantul este un instrument puternic utilizat în diferite domenii ale matematicii: în primul rând în studiul sistemelor de ecuații liniare , apoi în calculul multidimensional (de exemplu în Jacobian ), în calculul tensorial , în geometria diferențială , în teoria combinatorie etc. .

Volumul acestui paralelipiped este valoarea absolută a determinantului matricei

3\times 3

{\ displaystyle 3 \ times 3}

3 \ ori 3

format din vectori

r_{1},r_{2}

{\ displaystyle r_ {1}, r_ {2}}

r_1, r_2

Și

r_{3}

{\ displaystyle r_ {3}}

r_3

. Această relație între volum și determinant este valabilă în orice dimensiune.

Principala semnificație geometrică a determinantului se obține prin interpretarea matricei pătrate $LA$ ${\ displaystyle A}$ $LA$ de ordine $n$ ${\ displaystyle n}$ $n$ ca transformare liniară a unui spațiu vectorial a $n$ ${\ displaystyle n}$ $n$ mărime : cu această interpretare, valoarea absolută a $\det(A)$ ${\ displaystyle \ det (A)}$ $\ det (A)$ este factorul cu care se modifică volumele obiectelor conținute în spațiu (chiar dacă acest lucru este necorespunzător fără a lua în considerare sensul măsurării ). Dacă este diferit de zero, semnul determinantului indică, de asemenea, dacă transformarea $LA$ ${\ displaystyle A}$ $LA$ păstrează sau modifică orientarea spațiului față de axele de referință.

Definiție

Determinantul unei matrice 2 × 2 este egal cu:

\det {\begin{pmatrix}a&b\\c&d\end{pmatrix}}=ad-bc

{\ displaystyle \ det {\ begin {pmatrix} a & b \\ c & d \ end {pmatrix}} = ad-bc}

{\ displaystyle \ det {\ begin {pmatrix} a & b \\ c & d \ end {pmatrix}} = ad-bc}

Pentru a defini determinantul unei matrice pătrate generice $n\times n$ ${\ displaystyle n \ times n}$ $n \ ori n$ pot fi urmate două abordări: cea axiomatică, care definește determinantul ca singura mărime care satisface unele axiome, și cea constructivă printr-o formulă explicită. Există, de asemenea, diverse metode de calcul care sunt mai ușoare în funcție de context.

Definiție prin axiome

Este $K^{n\times n}$ ${\ displaystyle K ^ {n \ times n}}$ $K ^ {n \ ori n}$ spațiul vectorial al matricelor pătrate $n\times n$ ${\ displaystyle n \ times n}$ $n \ ori n$ la valorile din câmp $K.$ ${\ displaystyle K}$ $K.$ (de exemplu, câmpul numerelor reale sau complexe ).

Determinantul este singura funcție $\det :K^{n\times n}\to K$ ${\ displaystyle \ det: K ^ {n \ times n} \ to K}$ $\ det: K ^ {n \ times n} \ to K$ având următoarele proprietăți:

$\det I=1$ ${\ displaystyle \ det I = 1}$ $\ det I = 1$ unde matricea $THE$ ${\ displaystyle I}$ $THE$ este matricea identității .
Se comportă în felul următor în ceea ce privește algoritmul Gauss-Jordan :
- de sine $B.$ ${\ displaystyle B}$ $B.$ se obține schimbând două rânduri sau două coloane de $LA$ ${\ displaystyle A}$ $LA$ , asa de $\det B=-\det A$ ${\ displaystyle \ det B = - \ det A}$ $\ det B = - \ det A$ ,
- de sine $B.$ ${\ displaystyle B}$ $B.$ se obține înmulțind un rând sau o coloană cu $LA$ ${\ displaystyle A}$ $LA$ pentru $k$ ${\ displaystyle k}$ $k$ , asa de $\det B=k\det A$ ${\ displaystyle \ det B = k \ det A}$ $\ det B = k \ det A$ ,
- de sine $B.$ ${\ displaystyle B}$ $B.$ se obține prin adăugarea unui rând sau, respectiv, a unei coloane de $LA$ ${\ displaystyle A}$ $LA$ la altul, atunci $\det B=\det A$ ${\ displaystyle \ det B = \ det A}$ $\ det B = \ det A$

Proprietățile enumerate au o semnificație geometrică: sunt proprietățile pe care trebuie să le verifice o funcție a cărei valoare absolută este volumul poliedrului identificat de vectorii de rând ai matricei $B.$ ${\ displaystyle B}$ $B.$ și al căror semn este pozitiv dacă și numai dacă acești vectori sunt echi-orientați către baza canonică.

Definiție constructivă

Determinantul unei matrice $A_{n\times n}$ ${\ displaystyle A_ {n \ times n}}$ $A_ {n \ ori n}$ poate fi definit într-un mod mai constructiv, folosind formula Leibniz :

\det(A):=\sum _{\sigma \in S_{n}}\operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma (i)}

{\ displaystyle \ det (A): = \ sum _ {\ sigma \ in S_ {n}} \ operatorname {sgn} (\ sigma) \ prod _ {i = 1} ^ {n} a_ {i, \ sigma (the)}}

\ det (A): = \ sum _ {\ sigma \ in S_n} \ sgn (\ sigma) \ prod_ {i = 1} ^ n a_ {i, \ sigma (i)}

În formulă, $S_{n}$ ${\ displaystyle S_ {n}}$ $S_n$ este ansamblul tuturor permutațiilor $\sigma$ ${\ displaystyle \ sigma}$ $\ sigma$ a setului numeric $\{1,2,\ldots ,n\}$ ${\ displaystyle \ {1,2, \ ldots, n \}}$ $\ {1,2, \ ldots, n \}$ , $\operatorname {sgn}(\sigma )$ ${\ displaystyle \ operatorname {sgn} (\ sigma)}$ $\ sgn (\ sigma)$ denotă semnul permutării ( $+1$ ${\ displaystyle +1}$ $+1$ de sine $\sigma$ ${\ displaystyle \ sigma}$ $\ sigma$ este o permutație uniformă, $-1$ ${\ displaystyle -1}$ $-1$ dacă este ciudat ) e $\sigma (i)$ ${\ displaystyle \ sigma (i)}$ ${\ displaystyle \ sigma (i)}$ indică $the$ ${\ displaystyle i}$ $the$ -al elementul permutării.

Din această formulă vedem că numărul de elemente ale însumării este egal cu $n!$ ${\ displaystyle n!}$ $n!$ (cardinalitatea $S_{n}$ ${\ displaystyle S_ {n}}$ $S_ {n}$ ).

De exemplu, determinantul unei matrice 3 × 3 ( n = 3 ) este

{\begin{aligned}\sum _{\sigma \in S_{n}}\operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma _{i}}&=\operatorname {sgn}([1,2,3])\prod _{i=1}^{n}a_{i,[1,2,3]_{i}}+\operatorname {sgn}([1,3,2])\prod _{i=1}^{n}a_{i,[1,3,2]_{i}}+\operatorname {sgn}([2,1,3])\prod _{i=1}^{n}a_{i,[2,1,3]_{i}}\\&+\operatorname {sgn}([2,3,1])\prod _{i=1}^{n}a_{i,[2,3,1]_{i}}+\operatorname {sgn}([3,1,2])\prod _{i=1}^{n}a_{i,[3,1,2]_{i}}+\operatorname {sgn}([3,2,1])\prod _{i=1}^{n}a_{i,[3,2,1]_{i}}\\&=\prod _{i=1}^{n}a_{i,[1,2,3]_{i}}-\prod _{i=1}^{n}a_{i,[1,3,2]_{i}}-\prod _{i=1}^{n}a_{i,[2,1,3]_{i}}+\prod _{i=1}^{n}a_{i,[2,3,1]_{i}}+\prod _{i=1}^{n}a_{i,[3,1,2]_{i}}-\prod _{i=1}^{n}a_{i,[3,2,1]_{i}}\\&=a_{1,1}a_{2,2}a_{3,3}-a_{1,1}a_{2,3}a_{3,2}-a_{1,2}a_{2,1}a_{3,3}+a_{1,2}a_{2,3}a_{3,1}\\&\qquad +a_{1,3}a_{2,1}a_{3,2}-a_{1,3}a_{2,2}a_{3,1}.\end{aligned}}

{\ displaystyle {\ begin {align} \ sum _ {\ sigma \ in S_ {n}} \ operatorname {sgn} (\ sigma) \ prod _ {i = 1} ^ {n} a_ {i, \ sigma _ {i}} & = \ operatorname {sgn} ([1,2,3]) \ prod _ {i = 1} ^ {n} a_ {i, [1,2,3] _ {i}} + \ operatorname {sgn} ([1,3,2]) \ prod _ {i = 1} ^ {n} a_ {i, [1,3,2] _ {i}} + \ operatorname {sgn} ([2 , 1,3]) \ prod _ {i = 1} ^ {n} a_ {i, [2,1,3] _ {i}} \\ & + \ operatorname {sgn} ([2,3,1 ]) \ prod _ {i = 1} ^ {n} a_ {i, [2,3,1] _ {i}} + \ operatorname {sgn} ([3,1,2]) \ prod _ {i = 1} ^ {n} a_ {i, [3,1,2] _ {i}} + \ operatorname {sgn} ([3,2,1]) \ prod _ {i = 1} ^ {n} a_ {i, [3,2,1] _ {i}} \\ & = \ prod _ {i = 1} ^ {n} a_ {i, [1,2,3] _ {i}} - \ prod _ {i = 1} ^ {n} a_ {i, [1,3,2] _ {i}} - \ prod _ {i = 1} ^ {n} a_ {i, [2,1,3 ] _ {i}} + \ prod _ {i = 1} ^ {n} a_ {i, [2,3,1] _ {i}} + \ prod _ {i = 1} ^ {n} a_ { i, [3,1,2] _ {i}} - \ prod _ {i = 1} ^ {n} a_ {i, [3,2,1] _ {i}} \\ & = a_ {1 , 1} a_ {2,2} a_ {3,3} -a_ {1,1} a_ {2,3} a_ {3,2} -a_ {1,2} a_ {2,1} a_ {3 , 3} + a_ {1,2} a_ {2,3} a_ {3,1} \\ & \ qquad + a_ {1,3} a_ {2,1} a_ {3,2} -a_ {1 , 3} a_ {2,2} a_ {3,1}. \ End {align}}}

{\ displaystyle {\ begin {align} \ sum _ {\ sigma \ in S_ {n}} \ operatorname {sgn} (\ sigma) \ prod _ {i = 1} ^ {n} a_ {i, \ sigma _ {i}} & = \ operatorname {sgn} ([1,2,3]) \ prod _ {i = 1} ^ {n} a_ {i, [1,2,3] _ {i}} + \ operatorname {sgn} ([1,3,2]) \ prod _ {i = 1} ^ {n} a_ {i, [1,3,2] _ {i}} + \ operatorname {sgn} ([2 , 1,3]) \ prod _ {i = 1} ^ {n} a_ {i, [2,1,3] _ {i}} \\ & + \ operatorname {sgn} ([2,3,1 ]) \ prod _ {i = 1} ^ {n} a_ {i, [2,3,1] _ {i}} + \ operatorname {sgn} ([3,1,2]) \ prod _ {i = 1} ^ {n} a_ {i, [3,1,2] _ {i}} + \ operatorname {sgn} ([3,2,1]) \ prod _ {i = 1} ^ {n} a_ {i, [3,2,1] _ {i}} \\ & = \ prod _ {i = 1} ^ {n} a_ {i, [1,2,3] _ {i}} - \ prod _ {i = 1} ^ {n} a_ {i, [1,3,2] _ {i}} - \ prod _ {i = 1} ^ {n} a_ {i, [2,1,3 ] _ {i}} + \ prod _ {i = 1} ^ {n} a_ {i, [2,3,1] _ {i}} + \ prod _ {i = 1} ^ {n} a_ { i, [3,1,2] _ {i}} - \ prod _ {i = 1} ^ {n} a_ {i, [3,2,1] _ {i}} \\ & = a_ {1 , 1} a_ {2,2} a_ {3,3} -a_ {1,1} a_ {2,3} a_ {3,2} -a_ {1,2} a_ {2,1} a_ {3 , 3} + a_ {1,2} a_ {2,3} a_ {3,1} \\ & \ qquad + a_ {1,3} a_ {2,1} a_ {3,2} -a_ {1 , 3} a_ {2,2} a_ {3,1}. \ End {align}}}

În special:

De sine $n=1$ ${\ displaystyle n = 1}$ $n = 1$ , determinantul $LA$ ${\ displaystyle A}$ $LA$ este pur și simplu:

\det(A):=a_{1,1}

{\ displaystyle \ det (A): = a_ {1,1}}

\ det (A): = a_ {1,1}

De sine $n=2$ ${\ displaystyle n = 2}$ $n = 2$ , obținem formula deja văzută:

\det(A):=a_{1,1}a_{2,2}-a_{2,1}a_{1,2}

{\ displaystyle \ det (A): = a_ {1,1} a_ {2,2} -a_ {2,1} a_ {1,2}}

\ det (A): = a_ {1,1} a_ {2,2} -a_ {2,1} a_ {1,2}

De sine $n=3$ ${\ displaystyle n = 3}$ $n = 3$ , noi obținem:

\det(A):=a_{1,1}a_{2,2}a_{3,3}+a_{1,3}a_{2,1}a_{3,2}+a_{1,2}a_{2,3}a_{3,1}-a_{1,3}a_{2,2}a_{3,1}-a_{1,1}a_{2,3}a_{3,2}-a_{1,2}a_{2,1}a_{3,3}\

{\ displaystyle \ det (A): = a_ {1,1} a_ {2,2} a_ {3,3} + a_ {1,3} a_ {2,1} a_ {3,2} + a_ { 1,2} a_ {2,3} a_ {3,1} -a_ {1,3} a_ {2,2} a_ {3,1} -a_ {1,1} a_ {2,3} a_ { 3,2} -a_ {1,2} a_ {2,1} a_ {3,3} \}

\ det (A): = a_ {1,1} a_ {2,2} a_ {3,3} + a_ {1,3} a_ {2,1} a_ {3.2} + a_ {1,2} a_ {2,3} a_ {3,1} - a_ {1,3} a_ {2,2} a_ {3,1} - a_ {1,1} a_ {2,3} a_ {3,2} - a_ {1,2} a_ {2,1} a_ {3,3} \

Ultima formulă poate fi stocată prin regula Sarrus (care, totuși, nu poate fi extinsă la cazuri $n>3$ ${\ displaystyle n> 3}$ $n> 3$ ).

Complexitatea definiției constructive (inclusiv generarea de permutări) este ridicată:

n!\cdot (2n+1)=O(N\cdot N!)

{\ displaystyle n! \ cdot (2n + 1) = O (N \ cdot N!)}

n! \ cdot (2n + 1) = O (N \ cdot N!)

Metode de calcul

Definiția constructivă a determinantului este adesea complicată de utilizat pentru un calcul concret, deoarece se bazează pe o sumă de ben $n!$ ${\ displaystyle n!}$ $n!$ addendi. Există și alți algoritmi care vă permit să calculați determinantul mai ușor. Fiecare metodă are o eficiență variabilă, în funcție de dimensiunea matricei și de prezența zerourilor.

Matrici pătrate de ordinul 2

Zona paralelogramului este determinantul matricei

Determinantul unei matrice 2 × 2 este egal cu:

\det {\begin{pmatrix}a&b\\c&d\end{pmatrix}}:=ad-bc

{\ displaystyle \ det {\ begin {pmatrix} a & b \\ c & d \ end {pmatrix}}: = ad-bc}

\ det \ begin {pmatrix} a & b \\ c & d \ end {pmatrix}: = ad-bc

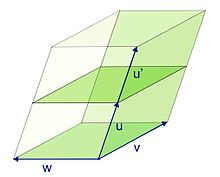
Valoarea absolută a acestei expresii este egală cu aria paralelogramului cu vârfuri în $(0,0),(a,c),(b,d)$ ${\ displaystyle (0,0), (a, c), (b, d)}$ $(0,0), (a, c), (b, d)$ Și $(a+b,c+d)$ ${\ displaystyle (a + b, c + d)}$ $(a + b, c + d)$ . Semnul determinantului (dacă acesta este diferit de zero) depinde de ordinea ciclică în care apar vârfurile paralelogramului (semnul este negativ dacă paralelogramul a fost „răsturnat” și pozitiv în caz contrar).

După cum se explică mai jos, această proprietate geometrică se extinde și în dimensiuni mai mari de 2: determinantul unei matrice $3\times 3$ ${\ displaystyle 3 \ times 3}$ $3 \ ori 3$ este de exemplu volumul poliedrului ale cărui vârfuri sunt obținute din coloanele matricei cu același procedeu văzut.

Matrici pătrate de ordinul 3

Calculul determinantului unei matrice

3\times 3

{\ displaystyle 3 \ times 3}

3 \ ori 3

folosind o metodă echivalentă cu regula lui Sarrus. Această metodă nu se extinde la matrice mai mari.

Determinantul unei matrice 3 × 3 este egal cu:

\det {\begin{pmatrix}a&b&c\\d&e&f\\g&h&i\end{pmatrix}}=aei+bfg+cdh-gec-hfa-idb

{\ displaystyle \ det {\ begin {pmatrix} a & b & c \\ d & e & f \\ g & h & i \ end {pmatrix}} = aei + bfg + cdh-gec-hfa-idb}

\ det \ begin {pmatrix} a & b & c \\ d & e & f \\ g & h & i \ end {pmatrix} = aei + bfg + cdh - gec - hfa - idb

O metodă mnemonică pentru amintirea acestei formule, exprimată prin regula lui Sarrus (această metodă nu se extinde la matrice mai mari), implică calcularea produselor termenilor pe diagonalele „continue”. Repetând primele două coloane din dreapta matricei:

{\begin{pmatrix}a&b&c\\d&e&f\\g&h&i\end{pmatrix}}{\begin{matrix}a&b\\d&e\\g&h\end{matrix}}

{\ displaystyle {\ begin {pmatrix} a & b & c \\ d & e & f \\ g & h & i \ end {pmatrix}} {\ begin {matrix} a & b \\ d & e \\ g & h \ end {matrix}}}

\ begin {pmatrix} a & b & c \\ d & e & f \\ g & h & i \ end {pmatrix} \ begin {matrix} a & b \\ d & e \\ g & h \ end { matrice}

produsele componentelor de pe cele 3 „diagonale” începând din stânga sus (diagonale principale) sunt $la Și the$ ${\ displaystyle aei}$ $aei$ , $b f g$ ${\ displaystyle bfg}$ $bfg$ Și $c d h$ ${\ displaystyle cdh}$ $cdh$ , în timp ce pe cele 3 „diagonale” începând din stânga jos (diagonale secundare) sunt situate $g Și c$ ${\ displaystyle gec}$ $gec$ , $h f la$ ${\ displaystyle hfa}$ $hfa$ , $the d b$ ${\ displaystyle idb}$ $idb$ . Determinantul matricei este exact diferența dintre suma primilor trei termeni $(aei+bfg+cdh)$ ${\ displaystyle (aei + bfg + cdh)}$ $(aei + bfg + cdh)$ iar suma ultimelor trei $(gec+hfa+idb)$ ${\ displaystyle (gec + hfa + idb)}$ $(gec + hfa + idb)$ .

Rețineți că valoarea determinantului este echivalentă în acest caz cu produsul mixt al vectorilor:

{\begin{pmatrix}a\\d\\g\end{pmatrix}}\quad ;\quad {\begin{pmatrix}b\\e\\h\end{pmatrix}}\quad ;\quad {\begin{pmatrix}c\\f\\i\end{pmatrix}}

{\ displaystyle {\ begin {pmatrix} a \\ d \\ g \ end {pmatrix}} \ quad; \ quad {\ begin {pmatrix} b \\ e \\ h \ end {pmatrix}} \ quad; \ quad {\ begin {pmatrix} c \\ f \\ i \ end {pmatrix}}}

\ begin {pmatrix} a \\ d \\ g \ end {pmatrix} \ quad; \ quad \ begin {pmatrix} b \\ e \\ h \ end {pmatrix} \ quad; \ quad \ begin {pmatrix} c \\ f \\ i \ end {pmatrix}

iar valoarea sa absolută este echivalentă cu volumul paralelipipedului care are drept margini cei trei vectori.

Dezvoltarea Laplace

Același subiect în detaliu: teorema lui Laplace .

Dezvoltarea Laplace este o metodă de calcul a determinantului, care este eficientă numai pentru matrici foarte mici sau matrice care conțin un număr mare de zerouri ^[2] . Continuăm alegând o linie, $the$ ${\ displaystyle i}$ $the$ -thth, folosind formula:

\det(A)=\sum _{j=1}^{n}\ a_{i,j}C_{i,j}

{\ displaystyle \ det (A) = \ sum _ {j = 1} ^ {n} \ a_ {i, j} C_ {i, j}}

\ det (A) = \ sum_ {j = 1} ^ n \ a_ {i, j} C_ {i, j}

unde este $C_{i,j}$ ${\ displaystyle C_ {i, j}}$ $C_ {i, j}$ este complementul algebric al cuplului $(i,j)$ ${\ displaystyle (i, j)}$ $(i, j)$ , acesta este $C_{i,j}$ ${\ displaystyle C_ {i, j}}$ $C_ {i, j}$ este dat de $(-1)^{i+j}$ ${\ displaystyle (-1) ^ {i + j}}$ $(-1) ^ {i + j}$ pentru determinantul ( minor ) al ordinii $n-1$ ${\ displaystyle n-1}$ $n-1$ obținută din matrice $LA$ ${\ displaystyle A}$ $LA$ prin ștergerea rândului $the$ ${\ displaystyle i}$ $the$ -th și coloana $j$ ${\ displaystyle j}$ $j$ -alea.

Există o dezvoltare similară de - a lungul $j$ ${\ displaystyle j}$ $j$ -a coloana.

Algoritm Gauss

Același subiect în detaliu: Metoda Gaussian Elimination .

Definiția axiomatică oferă un alt instrument util pentru calcularea determinantului, care se bazează pe aceste două principii:

Determinantul unei matrice triunghiulare este pur și simplu produsul elementelor de pe diagonală, adică:

\det(A)=\prod _{i=1}^{n}a_{ii}

{\ displaystyle \ det (A) = \ prod _ {i = 1} ^ {n} a_ {ii}}

\ det (A) = \ prod_ {i = 1} ^ n a_ {ii}

Folosind algoritmul Gauss , este posibil să se transforme fiecare matrice într-o matrice triunghiulară prin operații elementare pe rândurile și coloanele sale; al cărui efect asupra determinantului este prescris de axiome.

Exemplu

Să presupunem că vrem să calculăm determinantul:

A={\begin{pmatrix}-2&2&-3\\-1&1&3\\2&0&-1\end{pmatrix}}

{\ displaystyle A = {\ begin {pmatrix} -2 & 2 & -3 \\ - 1 & 1 & 3 \\ 2 & 0 & -1 \ end {pmatrix}}}

A = \ begin {pmatrix} -2 & 2 & -3 \\ -1 & 1 & 3 \\ 2 & 0 & -1 \ end {pmatrix}

Puteți continua direct prin definiția constructivă:

{\begin{aligned}\det(A)&=(-2)\cdot 1\cdot (-1)+(-3)\cdot 0\cdot (-1)\\&\quad +2\cdot 3\cdot 2-(-3)\cdot 1\cdot 2-(-2)\cdot 3\cdot 0-2\cdot (-1)\cdot (-1)\\&=2+0+12-(-6)-0-2=18\end{aligned}}

{\ displaystyle {\ begin {align} \ det (A) & = (- 2) \ cdot 1 \ cdot (-1) + (- 3) \ cdot 0 \ cdot (-1) \\ & \ quad +2 \ cdot 3 \ cdot 2 - (- 3) \ cdot 1 \ cdot 2 - (- 2) \ cdot 3 \ cdot 0-2 \ cdot (-1) \ cdot (-1) \\ & = 2 + 0 + 12 - (- 6) -0-2 = 18 \ end {align}}}

{\ displaystyle {\ begin {align} \ det (A) & = (- 2) \ cdot 1 \ cdot (-1) + (- 3) \ cdot 0 \ cdot (-1) \\ & \ quad +2 \ cdot 3 \ cdot 2 - (- 3) \ cdot 1 \ cdot 2 - (- 2) \ cdot 3 \ cdot 0-2 \ cdot (-1) \ cdot (-1) \\ & = 2 + 0 + 12 - (- 6) -0-2 = 18 \ end {align}}}

Alternativ, este posibil să se utilizeze dezvoltarea Laplace în funcție de un rând sau o coloană. Este mai bine să alegeți un rând sau o coloană cu multe zerouri, pentru a reduce suplimentele dezvoltării; în cazul nostru ne dezvoltăm conform celei de-a doua coloane:

\det(A)=(-1)^{1+2}\cdot 2\cdot \det {\begin{pmatrix}-1&3\\2&-1\end{pmatrix}}+(-1)^{2+2}\cdot 1\cdot \det {\begin{pmatrix}-2&-3\\2&-1\end{pmatrix}}

{\ displaystyle \ det (A) = (- 1) ^ {1 + 2} \ cdot 2 \ cdot \ det {\ begin {pmatrix} -1 & 3 \\ 2 & -1 \ end {pmatrix}} + ( - 1) ^ {2 + 2} \ cdot 1 \ cdot \ det {\ begin {pmatrix} -2 & -3 \\ 2 & -1 \ end {pmatrix}}}

\ det (A) = (- 1) ^ {1 + 2} \ cdot 2 \ cdot \ det \ begin {pmatrix} -1 & 3 \\ 2 & -1 \ end {pmatrix} + (-1) ^ { 2+ 2} \ cdot 1 \ cdot \ det \ begin {pmatrix} -2 & -3 \\ 2 & -1 \ end {pmatrix}

=(-2)\cdot ((-1)\cdot (-1)-2\cdot 3)+1\cdot ((-2)\cdot (-1)-2\cdot (-3))=(-2)(-5)+8=18

{\ displaystyle = (- 2) \ cdot ((-1) \ cdot (-1) -2 \ cdot 3) +1 \ cdot ((-2) \ cdot (-1) -2 \ cdot (-3) ) = (- 2) (- 5) + 8 = 18}

= (- 2) \ cdot ((- 1) \ cdot (-1) -2 \ cdot3) +1 \ cdot ((- 2) \ cdot (-1) -2 \ cdot (-3)) = (- 2) (- 5) +8 = 18

Dezvoltarea lui Laplace poate fi combinată cu unele mișcări gaussiene. De exemplu, aici este deosebit de avantajos să adăugați a doua coloană la prima:

{\begin{pmatrix}0&2&-3\\0&1&3\\2&0&-1\end{pmatrix}}

{\ displaystyle {\ begin {pmatrix} 0 & 2 & -3 \\ 0 & 1 & 3 \\ 2 & 0 & -1 \ end {pmatrix}}}

\ begin {pmatrix} 0 & 2 & -3 \\ 0 & 1 & 3 \\ 2 & 0 & -1 \ end {pmatrix}

Această mișcare nu schimbă determinantul. Dezvoltând de-a lungul primei coloane, obținem astfel:

\det(A)=(-1)^{3+1}\cdot 2\cdot \det {\begin{pmatrix}2&-3\\1&3\end{pmatrix}}

{\ displaystyle \ det (A) = (- 1) ^ {3 + 1} \ cdot 2 \ cdot \ det {\ begin {pmatrix} 2 & -3 \\ 1 & 3 \ end {pmatrix}}}

\ det (A) = (- 1) ^ {3 + 1} \ cdot 2 \ cdot \ det \ begin {pmatrix} 2 & -3 \\ 1 & 3 \ end {pmatrix}

=2\cdot (2\cdot 3-1\cdot (-3))=2\cdot 9=18

{\ displaystyle = 2 \ cdot (2 \ cdot 3-1 \ cdot (-3)) = 2 \ cdot 9 = 18}

= 2 \ cdot (2 \ cdot3-1 \ cdot (-3)) = 2 \ cdot 9 = 18

Proprietate

Proprietăți elementare

Din proprietățile enumerate în definiția axiomatică, este ușor de dedus că:

Dacă toate elementele unui rând (sau coloană) sunt nule, atunci $\det(A)=0$ ${\ displaystyle \ det (A) = 0}$ $\ det (A) = 0$ .
De sine $LA$ ${\ displaystyle A}$ $LA$ are două rânduri (sau coloane) egale sau proporționale, atunci $\det(A)=0$ ${\ displaystyle \ det (A) = 0}$ $\ det (A) = 0$ .
Dacă un rând (sau coloană) este o combinație liniară de două sau mai multe alte rânduri (sau coloane) paralele cu acesta, atunci $\det(A)=0$ ${\ displaystyle \ det (A) = 0}$ $\ det (A) = 0$ .
De sine $LA$ ${\ displaystyle A}$ $LA$ este modificat prin mișcări gaussiene pe coloane (în loc de pe rânduri), efectul este întotdeauna cel descris în definiția axiomatică.
În special, schimbând două rânduri sau două coloane, determinantul schimbă semnul, rămânând același în valoare absolută. Rezultă că un număr par de schimburi nu schimbă nici semnul, nici forma determinantului.
Dacă un rând (sau o coloană) este suma a două rânduri (sau coloane), $\det(A)$ ${\ displaystyle \ det (A)}$ $\ det (A)$ este suma celor doi determinanți obținuți prin înlocuirea respectivului rând (sau coloană) cu cele două rânduri (sau coloane) a căror sumă este.

Determinantul măsoară volumul paralelipipedului generat de vectorii coloanei matricei. Înmulțind un vector cu doi, volumul se înmulțește cu doi (așa cum este cerut de definiția axiomatică)

Înmulțirea matricilor

Determinantul este o funcție multiplicativă, în sensul că teorema lui Binet susține:

\det(AB)=\det(A)\det(B)

{\ displaystyle \ det (AB) = \ det (A) \ det (B)}

\ det (AB) = \ det (A) \ det (B)

O matrice pătrată $LA$ ${\ displaystyle A}$ $LA$ cu valori într-un câmp $K.$ ${\ displaystyle K}$ $K.$ este inversabil dacă și numai dacă $\det(A)\neq 0$ ${\ displaystyle \ det (A) \ neq 0}$ $\ det (A) \ neq 0$ . Dacă da, se aplică egalitatea:

\det(A^{-1})=\left(\det(A)\right)^{-1}

{\ displaystyle \ det (A ^ {- 1}) = \ left (\ det (A) \ right) ^ {- 1}}

\ det (A ^ {- 1}) = \ left (\ det (A) \ right) ^ {- 1}

Proprietățile enumerate mai sus arată că aplicația:

\det :{\textrm {GL}}_{n}(K)\to K^{*}

{\ displaystyle \ det: {\ textrm {GL}} _ {n} (K) \ to K ^ {*}}

\ det: \ textrm {GL} _n (K) \ to K ^ *

din grupul liniar general din elementele nenule ale $K.$ ${\ displaystyle K}$ $K.$ este un homomorfism al grupurilor .

Ca o consecință a teoremei lui Binet, dacă $THE$ ${\ displaystyle I}$ $THE$ este matricea de identitate de tip $n\times n$ ${\ displaystyle n \ times n}$ $n \ ori n$ Și $r$ ${\ displaystyle r}$ $r$ un scalar, este ușor să verificați asta $\det(rI)=r^{n}$ ${\ displaystyle \ det (rI) = r ^ {n}}$ $\ det (rI) = r ^ n$ . Intr-adevar:

\det(rA)=\det(rI\cdot A)=r^{n}\det(A)

{\ displaystyle \ det (rA) = \ det (rI \ cdot A) = r ^ {n} \ det (A)}

\ det (rA) = \ det (rI \ cdot A) = r ^ n \ det (A)

Matrici similare transpuse

O matrice și transpunerea ei au același determinant:

\det(A)=\det(A^{T})

{\ displaystyle \ det (A) = \ det (A ^ {T})}

\ det (A) = \ det (A ^ T)

De sine $LA$ ${\ displaystyle A}$ $LA$ Și $B.$ ${\ displaystyle B}$ $B.$ sunt similare (adică există o matrice inversabilă $X$ ${\ displaystyle X}$ $X$ astfel încât $LA$ ${\ displaystyle A}$ $LA$ = $X^{-1}BX$ ${\ displaystyle X ^ {- 1} BX}$ $X ^ {- 1} B X$ ) apoi prin teorema lui Binet $\det(A)=\det(B)$ ${\ displaystyle \ det (A) = \ det (B)}$ $\ det (A) = \ det (B)$

Aceasta înseamnă că determinantul este un invariant de similitudine . Din aceasta rezultă că determinantul unei transformări liniare $f:V\to V$ ${\ displaystyle f: V \ to V}$ $f: V \ to V$ este bine definit (nu depinde de alegerea unei baze pentru spațiul vectorial $V.$ ${\ displaystyle V}$ $V.$ ).

Pe de altă parte, există matrici cu același determinant care nu sunt similare.

În câmpul numerelor reale, semnul determinantului este, de asemenea, invariant sub congruență .

Valori proprii

Determinantul unei matrice triunghiulare este produsul elementelor din diagonală.

De sine $LA$ ${\ displaystyle A}$ $LA$ este de tip $n\times n$ ${\ displaystyle n \ times n}$ $n \ ori n$ cu valori reale sau complexe și are toate valorile proprii $\lambda _{1},\ldots ,\lambda _{n}$ ${\ displaystyle \ lambda _ {1}, \ ldots, \ lambda _ {n}}$ $\ lambda_1, \ ldots, \ lambda_n$ în câmp (numărat cu multiplicitate), apoi:

\det(A)=\lambda _{1}\lambda _{2}\cdots \lambda _{n}

{\ displaystyle \ det (A) = \ lambda _ {1} \ lambda _ {2} \ cdots \ lambda _ {n}}

\ det (A) = \ lambda_ {1} \ lambda_ {2} \ cdots \ lambda_ {n}

Această egalitate rezultă din faptul că $LA$ ${\ displaystyle A}$ $LA$ este întotdeauna similar cu forma normală Jordan , care este o matrice triunghiulară superioară cu valorile proprii pe diagonala principală.

Din legătura dintre determinant și valorile proprii putem obține o relație între funcția de urmărire , funcția exponențială și determinantul:

\det(e^{A})=e^{\operatorname {tr} (A)}

{\ displaystyle \ det (e ^ {A}) = e ^ {\ operatorname {tr} (A)}}

\ det (e ^ A) = e ^ {\ operatorname {tr} (A)}

Derivat

Determinantul poate fi considerat o funcție polinomială :

\det :\mathbb {R} ^{n\times n}\to \mathbb {R}

{\ displaystyle \ det: \ mathbb {R} ^ {n \ times n} \ to \ mathbb {R}}

{\ displaystyle \ det: \ mathbb {R} ^ {n \ times n} \ to \ mathbb {R}}

de aceea poate fi diferențiat în raport cu orice variabilă corespunzătoare valorii pe care o poate asuma într-o casetă și pentru oricare dintre valorile sale. Diferențialul său poate fi exprimat prin formula Jacobi :

d\det(A)=\operatorname {tr} (\operatorname {cof^{\top }} (A)dA)

{\ displaystyle d \ det (A) = \ operatorname {tr} (\ operatorname {cof ^ {\ top}} (A) dA)}

d \ det (A) = \ operatorname {tr} (\ operatorname {cof ^ \ top} (A) dA)

unde este $\operatorname {cof^{\top }} (A)$ ${\ displaystyle \ operatorname {cof ^ {\ top}} (A)}$ $\ operatorname {cof ^ \ top} (A)$ denotă transpunerea matricei cofactorilor (numiți și complemente algebrice ) a $LA$ ${\ displaystyle A}$ $LA$ , in timp ce $\operatorname {tr} (A)$ ${\ displaystyle \ operatorname {tr} (A)}$ $\ operatorname {tr} (A)$ denotă urmele sale. În special, dacă $LA$ ${\ displaystyle A}$ $LA$ este inversabil avem:

d\det(A)=\det(A)\,\operatorname {tr} (A^{-1}dA)

{\ displaystyle d \ det (A) = \ det (A) \, \ operatorname {tr} (A ^ {- 1} dA)}

d \ det (A) = \ det (A) \, \ operatorname {tr} (A ^ {- 1} dA)

sau, mai colocvial, dacă valorile matricei $X$ ${\ displaystyle X}$ $X$ sunt suficient de mici:

\det(A+X)-\det(A)\approx \det(A)\,\operatorname {tr} (A^{-1}X)

{\ displaystyle \ det (A + X) - \ det (A) \ approx \ det (A) \, \ operatorname {tr} (A ^ {- 1} X)}

\ det (A + X) - \ det (A) \ approx \ det (A) \, \ operatorname {tr} (A ^ {- 1} X)

Cazul special al $LA$ ${\ displaystyle A}$ $LA$ coincidând cu matricea identitară $THE$ ${\ displaystyle I}$ $THE$ Oportunitati:

\det(I+X)\approx 1+\operatorname {tr} (X)

{\ displaystyle \ det (I + X) \ approx 1+ \ operatorname {tr} (X)}

\ det (I + X) \ approx 1 + \ operatorname {tr} (X)

Aplicații

Sisteme liniare

Determinantul este util pentru a calcula rangul unei matrice și, prin urmare, pentru a determina dacă un sistem de ecuații liniare are o soluție, folosind teorema Rouché-Capelli . Când sistemul are o singură soluție, acest lucru poate fi explicat folosind determinantul, prin intermediul regulii lui Cramer .

Matrici și transformări inversabile

Se spune că o matrice este singulară dacă are un determinant nul. O matrice singulară nu este niciodată inversabilă și, dacă este definită pe un câmp , este valabilă și inversa: o matrice non-singulară este întotdeauna inversabilă.

O transformare liniară a planului , a spațiului sau mai general a unui spațiu euclidian sau vectorial (de dimensiune finită) $f:V\to V$ ${\ displaystyle f: V \ to V}$ $f: V \ to V$ este reprezentată (după alegerea unei baze ) de o matrice pătrată $LA$ ${\ displaystyle A}$ $LA$ . Determinantul este o mărime care nu depinde de baza aleasă și, prin urmare, doar de funcție $f$ ${\ displaystyle f}$ $f$ : putem vorbi deci de determinant al $f$ ${\ displaystyle f}$ $f$ , care este indicat cu $\det(f)$ ${\ displaystyle \ det (f)}$ $\ det (f)$ .

Multe pretenții despre $f$ ${\ displaystyle f}$ $f$ sunt echivalente:

f

{\ displaystyle f}

f

este o corespondență unu-la-unu

\Leftrightarrow

{\ displaystyle \ Leftrightarrow}

\ Leftrightarrow

f

{\ displaystyle f}

f

este un izomorfism

\Leftrightarrow

{\ displaystyle \ Leftrightarrow}

\ Leftrightarrow

f

{\ displaystyle f}

f

este injectiv

\Leftrightarrow

{\ displaystyle \ Leftrightarrow}

\ Leftrightarrow

f

{\ displaystyle f}

f

este surjectiv

\Leftrightarrow

{\ displaystyle \ Leftrightarrow}

\ Leftrightarrow

\det(A)=\det(f)\neq 0

{\ displaystyle \ det (A) = \ det (f) \ neq 0}

\ det (A) = \ det (f) \ neq 0

Deci, fiecare dintre aceste afirmații echivalente este adevărată dacă și numai dacă determinantul nu este zero.

Valori proprii și vectori proprii

Același subiect în detaliu: Polinom caracteristic .

Determinantul permite găsirea valorilor proprii ale unei matrice $LA$ ${\ displaystyle A}$ $LA$ prin polinomul său caracteristic :

p(x)=\det(A-xI)

{\ displaystyle p (x) = \ det (A-xI)}

p (x) = \ det (A - xI)

unde este $THE$ ${\ displaystyle I}$ $THE$ este matricea de identitate având același număr de rânduri ca $LA$ ${\ displaystyle A}$ $LA$ .

Baze, sisteme de referință

Date $n$ ${\ displaystyle n}$ $n$ vectori în spațiul euclidian $\mathbb {R} ^{n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ $\ R ^ n$ , este $LA$ ${\ displaystyle A}$ $LA$ matricea având acești vectori drept coloane. Următoarele afirmații sunt echivalente:

vectorii sunt independenți

\Leftrightarrow

{\ displaystyle \ Leftrightarrow}

\ Leftrightarrow

vectorii generează

\mathbb {R} ^{n}

{\ displaystyle \ mathbb {R} ^ {n}}

\ mathbb {R} ^ {n}

\Leftrightarrow

{\ displaystyle \ Leftrightarrow}

\ Leftrightarrow

vectorii formează o bază

\Leftrightarrow

{\ displaystyle \ Leftrightarrow}

\ Leftrightarrow

\det(A)\neq 0

{\ displaystyle \ det (A) \ neq 0}

\ det (A) \ neq 0

Dacă $n$ ${\ displaystyle n}$ $n$ vectorii formează o bază, apoi semnul lui $\det(A)$ ${\ displaystyle \ det (A)}$ $\ det (A)$ determină orientarea bazei: dacă este pozitivă, baza formează un cadru de referință pentru mâna dreaptă , în timp ce dacă este negativă, este denumită cadru de referință pentru stângaci (în analogie cu regula mâinii drepte ).

Volumele

Cub înainte de transformare, de volumul 1.

Imaginea cubului după transformare este un paralelipiped , al cărui volum este egal cu determinantul transformării.

Valoarea absolută $|\det A|$ ${\ displaystyle | \ det A |}$ $| \ det A |$ al determinantului este egal cu volumul paralelipipedului subtins de vectorii dați de coloanele din $LA$ ${\ displaystyle A}$ $LA$ (paralelipipedul este de fapt un paralelogram dacă $n=2$ ${\ displaystyle n = 2}$ $n = 2$ , și un solid de dimensiuni $n$ ${\ displaystyle n}$ $n$ în general). Mai general, având în vedere o transformare liniară :

f:\mathbb {R} ^{n}\rightarrow \mathbb {R} ^{n}

{\ displaystyle f: \ mathbb {R} ^ {n} \ rightarrow \ mathbb {R} ^ {n}}

f: \ R ^ n \ rightarrow \ R ^ n

reprezentată printr-o matrice $LA$ ${\ displaystyle A}$ $LA$ și orice subset $S.$ ${\ displaystyle S}$ $S.$ din $\mathbb {R} ^{n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ măsurabilă în funcție de Lebesgue , volumul imaginii $f(S)$ ${\ displaystyle f (S)}$ $f (S)$ este dat de:

\left|\det(A)\right|\cdot \operatorname {volume} (S)

{\ displaystyle \ left | \ det (A) \ right | \ cdot \ operatorname {volume} (S)}

\ left | \ det (A) \ right | \ cdot \ operatorname {volume} (S)

Chiar mai general, dacă transformarea liniară $f:\mathbb {R} ^{n}\rightarrow \mathbb {R} ^{m}$ ${\ displaystyle f: \ mathbb {R} ^ {n} \ rightarrow \ mathbb {R} ^ {m}}$ $f: \ R ^ n \ rightarrow \ R ^ m$ este reprezentată de o matrice $LA$ ${\ displaystyle A}$ $LA$ de tip $m\times n$ ${\ displaystyle m \ times n}$ $m \ ori n$ Și $S.$ ${\ displaystyle S}$ $S.$ este un subset de $\mathbb {R} ^{n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ $\ R ^ {n}$ măsurabilă conform lui Lebesgue, apoi volumul de $f(S)$ ${\ displaystyle f (S)}$ $f (S)$ este dat de:

{\sqrt {\det(A^{T}A)}}\cdot \operatorname {volume} (S)

{\ displaystyle {\ sqrt {\ det (A ^ {T} A)}} \ cdot \ operatorname {volume} (S)}

\ sqrt {\ det (A ^ T A)} \ cdot \ operatorname {volume} (S)

Generalizări

Pfaffiano

Pfaffian este un analog al determinantului pentru matrici de tip înclinare-simetrice $2n\times 2n$ ${\ displaystyle 2n \ times 2n}$ $2n \ times 2n$ . Este un polinom de grad $n$ ${\ displaystyle n}$ $n$ al cărui pătrat este egal cu determinantul matricei.

Dimensiuni infinite

Pentru spațiile cu dimensiuni infinite nu există o generalizare a determinanților și a noțiunii de volum. Sunt posibile mai multe abordări, inclusiv utilizarea extensiei de urmărire a unui tablou .

Determinant al unui endomorfism

De sine $V.$ ${\ displaystyle V}$ $V.$ este un spațiu vectorial de dimensiune finită $n$ ${\ displaystyle n}$ $n$ pe teren $\mathbb {K}$ ${\ displaystyle \ mathbb {K}}$ $\ mathbb {K}$ atunci este posibil să se definească determinantul unui endomorfism $f:V\to V$ ${\ displaystyle f: V \ to V}$ $f: V \ to V$ direct, fără a recurge la o bază de $V.$ ${\ displaystyle V}$ $V.$ . Este $\Lambda ^{n}(V)$ ${\ displaystyle \ Lambda ^ {n} (V)}$ $\ Lambda ^ n (V)$ spațiul vectorial al $n-$ ${\ displaystyle n-}$ $n-$ vectori ai $V.$ ${\ displaystyle V}$ $V.$ . Să luăm în considerare endomorfismul $T_{f}$ ${\ displaystyle T_ {f}}$ $T_f$ din $\Lambda ^{n}(V)$ ${\ displaystyle \ Lambda ^ {n} (V)}$ $\ Lambda ^ n (V)$ definit astfel încât:

T_{f}(x_{1}\wedge x_{2}\wedge \cdots \wedge x_{n})=f(x_{1})\wedge f(x_{2})\wedge \cdots \wedge f(x_{n})

{\ displaystyle T_ {f} (x_ {1} \ wedge x_ {2} \ wedge \ cdots \ wedge x_ {n}) = f (x_ {1}) \ wedge f (x_ {2}) \ wedge \ cdots \ wedge f (x_ {n})}

T_f (x_1 \ wedge x_2 \ wedge \ cdots \ wedge x_n) = f (x_1) \ wedge f (x_2) \ wedge \ cdots \ wedge f (x_n)

pentru fiecare $x_{1},x_{2},\ldots ,x_{n}\in V$ $x_{1},x_{2},\ldots ,x_{n}\in V$ $x_1, x_2, \ldots, x_n \in V$ , ed esteso per linearità a tutto $\Lambda ^{n}(V)$ $\Lambda ^{n}(V)$ $\Lambda^n(V)$ . Poiché $\Lambda ^{n}(V)$ $\Lambda ^{n}(V)$ $\Lambda^n(V)$ ha dimensione uguale a 1 risulta che $T_{f}$ $T_{f}$ $T_f$ altro non è che la moltiplicazione per uno scalare. Quindi possiamo definire il determinante di $f$ ${\displaystyle f}$ $f$ attraverso l'equazione:

f(x_{1})\wedge f(x_{2})\wedge \cdots \wedge f(x_{n})=\det(f)(x_{1}\wedge x_{2}\wedge \cdots \wedge x_{n})

f(x_{1})\wedge f(x_{2})\wedge \cdots \wedge f(x_{n})=\det(f)(x_{1}\wedge x_{2}\wedge \cdots \wedge x_{n})

f(x_1) \wedge f(x_2) \wedge \cdots \wedge f(x_n) = \det(f) (x_1 \wedge x_2 \wedge \cdots \wedge x_n)

per ogni $x_{1},x_{2},\ldots ,x_{n}\in V$ $x_{1},x_{2},\ldots ,x_{n}\in V$ $x_1, x_2, \ldots, x_n \in V$ . A questo punto seguono tutte le proprietà del determinante, in particolare è immediato che $\det(\operatorname {id} )=1$ $\det(\operatorname {id} )=1$ $\det(\operatorname{id}) = 1$ dove $\operatorname {id}$ $\operatorname {id}$ $\operatorname{id}$ è l'endomorfismo identità di $V$ ${\displaystyle V}$ $V$ . Se $g$ ${\displaystyle g}$ $g$ è un altro endomorfismo di $V$ ${\displaystyle V}$ $V$ allora:

\det(g\circ f)(x_{1}\wedge x_{2}\wedge \cdots \wedge x_{n})=(g\circ f)(x_{1})\wedge (g\circ f)(x_{2})\wedge \cdots \wedge (g\circ f)(x_{n})

\det(g\circ f)(x_{1}\wedge x_{2}\wedge \cdots \wedge x_{n})=(g\circ f)(x_{1})\wedge (g\circ f)(x_{2})\wedge \cdots \wedge (g\circ f)(x_{n})

\det(g \circ f) (x_1 \wedge x_2 \wedge \cdots \wedge x_n) = (g \circ f)(x_1) \wedge (g \circ f)(x_2) \wedge \cdots \wedge (g \circ f)(x_n)

=\det(g)(f(x_{1})\wedge f(x_{2})\wedge \cdots \wedge f(x_{n}))=\det(f)\det(g)(x_{1}\wedge x_{2}\wedge \cdots \wedge x_{n})

=\det(g)(f(x_{1})\wedge f(x_{2})\wedge \cdots \wedge f(x_{n}))=\det(f)\det(g)(x_{1}\wedge x_{2}\wedge \cdots \wedge x_{n})

= \det(g) (f(x_1) \wedge f(x_2) \wedge \cdots \wedge f(x_n)) = \det(f)\det(g) (x_1 \wedge x_2 \wedge \cdots \wedge x_n)

da cui $\det(g\circ f)=\det(g)\det(f)$ $\det(g\circ f)=\det(g)\det(f)$ $\det(g \circ f) = \det(g) \det(f)$ . Se $f$ ${\displaystyle f}$ $f$ non è un isomorfismo allora l'immagine di $f$ ${\displaystyle f}$ $f$ ha dimensione strettamente minore di $n$ ${\displaystyle n}$ $n$ e quindi $f(x_{1}),f(x_{2}),\ldots ,f(x_{n})$ $f(x_{1}),f(x_{2}),\ldots ,f(x_{n})$ $f(x_1), f(x_2), \ldots, f(x_n)$ sono sicuramente linearmente dipendenti, essendo che $\wedge$ $\wedge$ $\wedge$ è una forma multilineare alternante segue che $f(x_{1})\wedge f(x_{2})\wedge \cdots \wedge f(x_{n})=0$ $f(x_{1})\wedge f(x_{2})\wedge \cdots \wedge f(x_{n})=0$ $f(x_1) \wedge f(x_2) \wedge \cdots \wedge f(x_n) = 0$ e quindi $\det(f)=0$ $\det(f)=0$ $\det(f) = 0$ . Si verifica che fissata una base su $V$ ${\displaystyle V}$ $V$ il determinante della matrice associata a $f$ ${\displaystyle f}$ $f$ rispetto a tale base coincide con il determinante di $f$ ${\displaystyle f}$ $f$ .

Storia

Lo stesso argomento in dettaglio: Storia del determinante .

Note

^ La notazione $|\cdot |$ $|\cdot |$ $|\cdot |$ fu introdotta per la prima volta nel 1841 dal matematico inglese Arthur Cayley ( MacTutor ).
^ Per una matrice $n\times n$ $n\times n$ $n \times n$ piena , ossia senza elementi nulli, si dovrebbero eseguire n! moltiplicazioni.

Approfondimenti

( EN ) Andrews, GE and Burge, WH Determinant Identities. Pacific J. Math. 158, 1-14, 1993.
( EN ) Arfken, G. "Determinants." §4.1 in Mathematical Methods for Physicists , 3rd ed. Orlando, FL: Academic Press, pp. 168–176, 1985.
( EN ) Brenner, J. and Cummings, L. The Hadamard Maximum Determinant Problem. Amer. Math. Monthly 79, 626-630, 1972.
Ernesto Pascal I determinanti: teoria ed applicazioni. Con tutte le più recenti ricerche (Milano: U. Hoepli, 1897)
Francesco Calderara Trattato dei determinanti (Palermo: Virzì, 1913)
( FR ) Francesco Brioschi , Théorie des déterminants et leurs principales applications; traduit de l'italien par M. Édouard Combescure , Parigi, Mallet-Bachelier, 1856. URL consultato il 25 luglio 2021 .
( FR ) R. Baltzer, Théorie et applications des déterminants, avec l'indication des sources originales; traduit de l'allemand par J. Hoüel , Parigi, Mallet-Bachelier, 1861. URL consultato il 25 luglio 2021 .
( EN ) Charles Dodgson An elementary treatise on determinants, with their application to simultaneous linear equations and algebraical geometry (Oxford: University Press, 1867)
( EN ) RF Scott e GB Matthews The theory of determinants and their applications (Cambridge: University Press, 1904)

Voci correlate

Collegamenti esterni

( EN ) DA Suprunenko, Determinant , in Encyclopaedia of Mathematics , Springer e European Mathematical Society, 2002.
( EN ) Eric W. Weisstein, Determinant , in MathWorld , Wolfram Research.
( EN ) Storia dell'uso delle matrici e dei determinanti su MacTutor
( IT ) Calcolatrice per matrici e vettori online
( EN ) WebApp to calculate determinants and descriptively solve systems of linear equations , su sole.ooz.ie . URL consultato il 19 gennaio 2014 (archiviato dall' url originale il 21 febbraio 2014) .
( EN ) Determinant Interactive Program and Tutorial , su people.revoledu.com .
( EN ) Online Matrix Calculator , su matrixcalc.org .
( EN ) Linear algebra: determinants. Compute determinants of matrices up to order 6 using Laplace expansion you choose.
( EN ) Matrices and Linear Algebra on the Earliest Uses Pages , su economics.soton.ac.uk .
( EN ) Determinants explained in an easy fashion in the 4th chapter as a part of a Linear Algebra course. , su algebra.math.ust.hk . URL consultato il 19 gennaio 2014 (archiviato dall' url originale il 25 maggio 2009) .
( EN ) Instructional Video on taking the determinant of an nxn matrix (Khan Academy) , su khanexercises.appspot.com (archiviato dall' url originale il 25 marzo 2010) .

Controllo di autorità	Thesaurus BNCF 32649 · LCCN ( EN ) sh85037299 · BNF ( FR ) cb11975737s (data) · NDL ( EN , JA ) 00562696

Portale Matematica : accedi alle voci di Wikipedia che trattano di matematica

[mactutor1-1] La notazione $|\cdot |$ $|\cdot |$ $|\cdot |$ fu introdotta per la prima volta nel 1841 dal matematico inglese Arthur Cayley ( MacTutor ).

[2] Per una matrice $n\times n$ $n\times n$ $n \times n$ piena , ossia senza elementi nulli, si dovrebbero eseguire n! moltiplicazioni.

[1]

[2]

V · D · M Algebra lineare
Spazio vettoriale	Vettore · Sottospazio vettoriale ( Sottospazio generato ) · Applicazione lineare ( Nucleo · Immagine ) · Base · Dimensione · Teorema della dimensione · Formula di Grassmann · Sistema lineare · Algoritmo di Gauss · Teorema di Rouché-Capelli · Regola di Cramer · Spazio duale · Spazio proiettivo · Spazio affine · Teorema della dimensione per spazi vettoriali
Matrici	Identità · Nulla · Quadrata · Invertibile · Simmetrica · Antisimmetrica · Trasposta · Diagonale · Triangolare · Di cambiamento di base · Ortogonale · Normale · Simplettica · Moltiplicazione di matrici · Rango · Teorema di Kronecker · Minore · Matrice dei cofattori · Determinante · Teorema di Binet · Teorema di Laplace · Radice quadrata di una matrice
Diagonalizzabilità	Autovettore e autovalore · Spettro · Polinomio caratteristico · Polinomio minimo · Teorema di Hamilton-Cayley · Matrice a blocchi · Forma canonica di Jordan · Teorema di diagonalizzabilità
Prodotto scalare	Forma bilineare · Sottospazio ortogonale · Spazio euclideo · Base ortonormale · Algoritmo di Lagrange · Segnatura · Teorema di Sylvester · Gram-Schmidt · Forma sesquilineare · Forma hermitiana · Teorema spettrale