Funcție de stand compact

În matematică , o funcție valorică reală sau complexă definită pe un domeniu de $\mathbb {R} ^{n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ (sau, mai general, într-un spațiu topologic ) numim o funcție cu suport compact dacă are ca suport un subset compact al setului de definiții (suportul este definit ca închiderea setului de puncte ale domeniului în care funcția nu este anulat ).

Funcțiile de suport compacte, care sunt, de asemenea, continue sau infinit diferențiabile sunt de o importanță deosebită: în acest caz câmpul este limitat la o clasă foarte restrânsă de funcții, numite funcții de testare , care sunt utilizate în principal în teoria distribuțiilor .

Din teorema Heine-Borel și din definiția suportului unei funcții rezultă că o funcție are suport compact dacă este diferită de 0 într-un set închis și delimitat de puncte.

Definiție

O funcție definită pe un spațiu topologic $X$ ${\ displaystyle X}$ $X$ se spune că este un suport compact dacă suportul său:

\mathrm {supp} \,f:={\overline {\{\mathbf {x} \in X:f(\mathbf {x} )\neq \mathbf {0} \}}}

{\ displaystyle \ mathrm {supp} \, f: = {\ overline {\ {\ mathbf {x} \ în X: f (\ mathbf {x}) \ neq \ mathbf {0} \}}}}

{\ displaystyle \ mathrm {supp} \, f: = {\ overline {\ {\ mathbf {x} \ în X: f (\ mathbf {x}) \ neq \ mathbf {0} \}}}}

este un subset compact de $X$ ${\ displaystyle X}$ $X$ , adică pentru fiecare familie $\{U_{i}\}_{i\in I}$ ${\ displaystyle \ {U_ {i} \} _ {i \ în I}}$ $\ {U_ {i} \} _ {{i \ în I}}$ de subseturi deschise de $\mathrm {supp} \,f$ ${\ displaystyle \ mathrm {supp} \, f}$ ${\ displaystyle \ mathrm {supp} \, f}$ astfel încât:

\bigcup _{i\in I}U_{i}\supseteq \mathrm {supp} \,f

{\ displaystyle \ bigcup _ {i \ in I} U_ {i} \ supseteq \ mathrm {supp} \, f}

{\ displaystyle \ bigcup _ {i \ in I} U_ {i} \ supseteq \ mathrm {supp} \, f}

există un subset finit $J$ ${\ displaystyle J}$ $J$ din $THE$ ${\ displaystyle I}$ $THE$ astfel încât: ^[1]

\bigcup _{i\in J}U_{i}\supseteq \mathrm {supp} \,f

{\ displaystyle \ bigcup _ {i \ in J} U_ {i} \ supseteq \ mathrm {supp} \, f}

{\ displaystyle \ bigcup _ {i \ in J} U_ {i} \ supseteq \ mathrm {supp} \, f}

O clasă importantă de funcții de suport compacte este cea a funcțiilor de testare . Domeniul spațiului funcțiilor de testare $SAU$ ${\ displaystyle O}$ $SAU$ din $\mathbb {R} ^{n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ se numește $D(O)$ ${\ displaystyle D (O)}$ ${\ displaystyle D (O)}$ , în timp ce spațiul funcțional testează $\mathbb {R} ^{n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ se notează cu $D.$ ${\ displaystyle D}$ $D.$ , unde nu este necesar să se specifice numărul de variabile.

Rețineți că o funcție de suport compactă într-un domeniu dat de $\mathbb {R} ^{n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ poate fi extins în mod natural la o funcție de suport compactă peste toate $\mathbb {R} ^{n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ pur și simplu prin atribuirea valorii 0 tuturor punctelor din afara domeniului original. În acest fel este posibil să ne gândim la o funcție în $D(O)$ ${\ displaystyle D (O)}$ ${\ displaystyle D (O)}$ ca având stăpânire în $\mathbb {R} ^{n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ și, prin urmare, dacă $O\subset O'\subset \mathbb {R} ^{n}$ ${\ displaystyle O \ subset O '\ subset \ mathbb {R} ^ {n}}$ ${\ displaystyle O \ subset O '\ subset \ mathbb {R} ^ {n}}$ ai și tu $D(O)\subset D(O')\subset D$ ${\ displaystyle D (O) \ subset D (O ') \ subset D}$ ${\ displaystyle D (O) \ subset D (O ') \ subset D}$ .

Funcții continue cu suport compact

O clasă deosebit de importantă de funcții de suport compacte este cea a funcțiilor care sunt, de asemenea, continue . Arată acel spațiu $C_{c}(X)$ ${\ displaystyle C_ {c} (X)}$ $C_ {c} (X)$ de funcții continue cu suport compact pe un spațiu Hausdorff compact local $X$ ${\ displaystyle X}$ $X$ a cu valori complexe este dens într-un spațiu L ^p definit pe un spațiu de măsurare , cu condiția ca $1\leq p<\infty$ ${\ displaystyle 1 \ leq p <\ infty}$ ${\ displaystyle 1 \ leq p <\ infty}$ . ^[2] Această clasă de funcții are, de asemenea, proprietatea în care se află două funcții $C_{c}(\mathbb {R} ^{k})$ ${\ displaystyle C_ {c} (\ mathbb {R} ^ {k})}$ ${\ displaystyle C_ {c} (\ mathbb {R} ^ {k})}$ ele diferă numai pentru seturile de măsuri Lebesgue diferite de zero și, prin urmare, dacă sunt egale aproape peste tot, atunci sunt egale. De asemenea, făcându-l să coincidă $X$ ${\ displaystyle X}$ $X$ cu spațiu $\mathbb {R} ^{k}$ ${\ displaystyle \ mathbb {R} ^ {k}}$ ${\ mathbb {R}} ^ {k}$ , atâta timp cât $L^{p}(\mathbb {R} ^{k})$ ${\ displaystyle L ^ {p} (\ mathbb {R} ^ {k})}$ ${\ displaystyle L ^ {p} (\ mathbb {R} ^ {k})}$ este complet, este completarea spațiului obținut prin echipare $C_{c}(\mathbb {R} ^{k})$ ${\ displaystyle C_ {c} (\ mathbb {R} ^ {k})}$ ${\ displaystyle C_ {c} (\ mathbb {R} ^ {k})}$ din $L^{p}$ ${\ displaystyle L ^ {p}}$ $L ^ {p}$ - metric. În cazul în care $p=\infty$ ${\ displaystyle p = \ infty}$ ${\ displaystyle p = \ infty}$ , finalizarea $C_{c}(\mathbb {R} ^{k})$ ${\ displaystyle C_ {c} (\ mathbb {R} ^ {k})}$ ${\ displaystyle C_ {c} (\ mathbb {R} ^ {k})}$ prin $L^{\infty }$ ${\ displaystyle L ^ {\ infty}}$ $L ^ {\ infty}$ - metrica este spațiul $C_{0}(\mathbb {R} ^{k})$ ${\ displaystyle C_ {0} (\ mathbb {R} ^ {k})}$ ${\ displaystyle C_ {0} (\ mathbb {R} ^ {k})}$ a funcțiilor continue care dispar la infinit. ^[3]

Proprietate

Funcțiile de asistență compacte beneficiază de asemenea de următoarele proprietăți.

Având o funcție $f$ ${\ displaystyle f}$ $f$ local integrabil în $\mathbb {R} ^{n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ e o $\phi$ ${\ displaystyle \ phi}$ $\ phi$ în $D.$ ${\ displaystyle D}$ $D.$ , apoi integralul Lebesgue :

\int f(x)\phi (x)d^{n}x

{\ displaystyle \ int f (x) \ phi (x) d ^ {n} x}

{\ displaystyle \ int f (x) \ phi (x) d ^ {n} x}

are întotdeauna o valoare finită.

De sine $g$ ${\ displaystyle g}$ $g$ este o funcție absolut continuă activată $\mathbb {R}$ ${\ displaystyle \ mathbb {R}}$ $\ mathbb {R}$ cu derivat de Radon-Nikodym $g^{'}$ ${\ displaystyle g '}$ ${\ displaystyle g '}$ , apoi reține:

\int g'(x)\phi (x)dx=-\int g(x)\phi '(x)dx

{\ displaystyle \ int g '(x) \ phi (x) dx = - \ int g (x) \ phi' (x) dx}

{\ displaystyle \ int g '(x) \ phi (x) dx = - \ int g (x) \ phi' (x) dx}

Cu alte cuvinte, atunci când se efectuează integrarea părții cu o funcție de testare, termenii limită se anulează.

Suma sau produsul a două funcții compatibile este încă compatibilă.

Convergenţă

Spaţiu $D(O)$ ${\ displaystyle D (O)}$ ${\ displaystyle D (O)}$ Poate fi prevăzut cu o structură spațială topologică care definește un criteriu de convergență pentru succesiuni . O succesiune de funcții $\{\phi _{k}\}$ ${\ displaystyle \ {\ phi _ {k} \}}$ ${\ displaystyle \ {\ phi _ {k} \}}$ din $D(O)$ ${\ displaystyle D (O)}$ ${\ displaystyle D (O)}$ converge la o funcție $\phi \in D(O)$ ${\ displaystyle \ phi \ în D (O)}$ ${\ displaystyle \ phi \ în D (O)}$ dacă sprijinul $\phi _{k}$ ${\ displaystyle \ phi _ {k}}$ ${\ displaystyle \ phi _ {k}}$ este cuprins în sprijinul $\phi$ ${\ displaystyle \ phi}$ $\ phi$ , și dacă derivatele fiecărui ordin de $\phi _{k}$ ${\ displaystyle \ phi _ {k}}$ ${\ displaystyle \ phi _ {k}}$ converg uniform la derivatele corespunzătoare ale $\phi$ ${\ displaystyle \ phi}$ $\ phi$ .

Aceasta este o condiție foarte puternică de convergență. Într-adevăr, o secvență convergentă în $D(O)$ ${\ displaystyle D (O)}$ ${\ displaystyle D (O)}$ este, de asemenea, punctual convergent , uniform convergent și convergent în spațiul funcțiilor p-însumabile pentru fiecare $p$ ${\ displaystyle p}$ $p$ .

Exemple

Un exemplu de funcție de suport compact este funcția clopot :

\Omega (x)={\begin{cases}e^{-{\frac {1}{1-|x|^{2}}}}&|x|<1\\0&|x|\geq 1\end{cases}}

{\ displaystyle \ Omega (x) = {\ begin {cases} e ^ {- {\ frac {1} {1- | x | ^ {2}}}} & | x | <1 \\ 0 & | x | \ geq 1 \ end {cases}}}

{\ displaystyle \ Omega (x) = {\ begin {cases} e ^ {- {\ frac {1} {1- | x | ^ {2}}}} & | x | <1 \\ 0 & | x | \ geq 1 \ end {cases}}}

definit pe toate

\mathbb {R} ^{n}

{\ displaystyle \ mathbb {R} ^ {n}}

\ mathbb {R} ^ {n}

.

Functia

\operatorname {\Omega }

{\ displaystyle \ operatorname {\ Omega}}

{\ displaystyle \ operatorname {\ Omega}}

are suport în discul închis cu raza 1 centrat în 0, este infinit diferențiat și dispare cu toate derivatele sale pentru

||x||\to 1

{\ displaystyle || x || \ to 1}

{\ displaystyle || x || \ to 1}

.

Funcția Ω în dimensiunea 1

Se dă o rudă apropiată a funcției clopot, $\forall \varepsilon >0$ ${\ displaystyle \ forall \ varepsilon> 0}$ ${\ displaystyle \ forall \ varepsilon> 0}$ , de la:

\Omega _{\varepsilon }(x)={\begin{cases}K_{\varepsilon }e^{-{\frac {1}{1-{\frac {|x|^{2}}{\varepsilon ^{2}}}}}}&|x|<\varepsilon \\0&|x|\geq \varepsilon \end{cases}}

{\ displaystyle \ Omega _ {\ varepsilon} (x) = {\ begin {cases} K _ {\ varepsilon} e ^ {- {\ frac {1} {1 - {\ frac {| x | ^ {2} } {\ varepsilon ^ {2}}}}}} & | x | <\ varepsilon \\ 0 & | x | \ geq \ varepsilon \ end {cases}}}

{\ displaystyle \ Omega _ {\ varepsilon} (x) = {\ begin {cases} K _ {\ varepsilon} e ^ {- {\ frac {1} {1 - {\ frac {| x | ^ {2} } {\ varepsilon ^ {2}}}}}} & | x | <\ varepsilon \\ 0 & | x | \ geq \ varepsilon \ end {cases}}}

unde este

K_{\varepsilon }

{\ displaystyle K _ {\ varepsilon}}

{\ displaystyle K _ {\ varepsilon}}

este o constantă reală pozitivă aleasă pentru a avea:

\int \Omega _{\varepsilon }(x)d^{n}x=1

{\ displaystyle \ int \ Omega _ {\ varepsilon} (x) d ^ {n} x = 1}

{\ displaystyle \ int \ Omega _ {\ varepsilon} (x) d ^ {n} x = 1}

Functia

\operatorname {\Omega _{\varepsilon }}

{\ displaystyle \ operatorname {\ Omega _ {\ varepsilon}}}

{\ displaystyle \ operatorname {\ Omega _ {\ varepsilon}}}

se bucură de aceleași proprietăți ca clopotul, cu excepția faptului că are suport în discul cu rază închisă

\varepsilon

{\ displaystyle \ varepsilon}

\ varepsilon

. Se poate arăta că

\operatorname {\Omega _{\varepsilon }}

{\ displaystyle \ operatorname {\ Omega _ {\ varepsilon}}}

{\ displaystyle \ operatorname {\ Omega _ {\ varepsilon}}}

sunt aproximanți ai deltei , în sensul că, au luat o funcție

\operatorname {\phi }

{\ displaystyle \ operatorname {\ phi}}

{\ displaystyle \ operatorname {\ phi}}

continuă în 0, contează

\lim _{\varepsilon \to 0}\,\int \Omega _{\varepsilon }(x)\phi (x)d^{n}x=\phi (0)

{\ displaystyle \ lim _ {\ varepsilon \ to 0} \, \ int \ Omega _ {\ varepsilon} (x) \ phi (x) d ^ {n} x = \ phi (0)}

{\ displaystyle \ lim _ {\ varepsilon \ to 0} \, \ int \ Omega _ {\ varepsilon} (x) \ phi (x) d ^ {n} x = \ phi (0)}

.

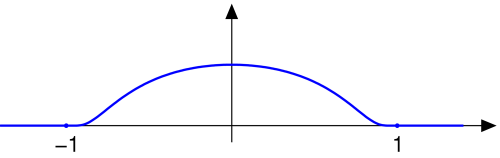
O funcție de suport compactă importantă într-o variabilă este obținută din convoluția lui $\operatorname {\Omega _{\varepsilon }}$ ${\ displaystyle \ operatorname {\ Omega _ {\ varepsilon}}}$ ${\ displaystyle \ operatorname {\ Omega _ {\ varepsilon}}}$ cu funcția caracteristică $\operatorname {\chi } _{[-1,1]}(x)$ ${\ displaystyle \ operatorname {\ chi} _ {[- 1,1]} (x)}$ ${\ displaystyle \ operatorname {\ chi} _ {[- 1,1]} (x)}$ , care este 1 pentru $-1\leq x\leq 1$ ${\ displaystyle -1 \ leq x \ leq 1}$ $-1 \ leq x \ leq 1$ și 0 în caz contrar. Prin urmare, avem, pentru fiecare $\varepsilon >0$ ${\ displaystyle \ varepsilon> 0}$ $\ varepsilon> 0$ :

\operatorname {\chi _{\varepsilon }(x)} =\int \Omega _{\varepsilon }(x-y)\chi _{[-1,1]}(y)dy

{\ displaystyle \ operatorname {\ chi _ {\ varepsilon} (x)} = \ int \ Omega _ {\ varepsilon} (xy) \ chi _ {[- 1,1]} (y) dy}

{\ displaystyle \ operatorname {\ chi _ {\ varepsilon} (x)} = \ int \ Omega _ {\ varepsilon} (x-y) \ chi _ {[- 1,1]} (y) dy}

Se poate observa că, pentru această funcție, se aplică următoarele:

\chi _{\varepsilon }(x)={\begin{cases}1&|x|<1-\varepsilon \\0&|x|>1+\varepsilon \end{cases}}

{\ displaystyle \ chi _ {\ varepsilon} (x) = {\ begin {cases} 1 & | x | <1- \ varepsilon \\ 0 & | x |> 1+ \ varepsilon \ end {cases}}}

{\ displaystyle \ chi _ {\ varepsilon} (x) = {\ begin {cases} 1 & | x | <1- \ varepsilon \\ 0 & | x |> 1+ \ varepsilon \ end {cases}}}

prin urmare

\varepsilon \to 0,\operatorname {\chi _{\varepsilon }(x)} \to \operatorname {\chi } _{[-1,1]}(x)

{\ displaystyle \ varepsilon \ to 0, \ operatorname {\ chi _ {\ varepsilon} (x)} \ to \ operatorname {\ chi} _ {[- 1,1]} (x)}

{\ displaystyle \ varepsilon \ to 0, \ operatorname {\ chi _ {\ varepsilon} (x)} \ to \ operatorname {\ chi} _ {[- 1,1]} (x)}

punctual .

Notă

^ W. Rudin , pagina 35 .
^ W. Rudin , pagina 68 .
^ W. Rudin , pagina 69 .

Bibliografie

( EN ) Walter Rudin , Analiză reală și complexă , Mladinska Knjiga, McGraw-Hill, 1970, ISBN 0-07-054234-1 .
- trad. it.: Analiză reală și complexă , trad. Maria Laura Vesentini - Edoardo Vesentini , col. Programul de matematică fizică electronică , Torino, Boringhieri , 1974, ISBN 978-88-339-5342-7 .
( EN ) K. Yosida, Analiza funcțională , Springer (1980) pp. Capitolul. 8, Sect. 4; 5

Elemente conexe

linkuri externe

( EN ) SM Nikol'skii, Function of compact support , în Enciclopedia Matematicii , Springer și European Mathematical Society, 2002.

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică

[1] W. Rudin , pagina 35 .

[2] W. Rudin , pagina 68 .

[3] W. Rudin , pagina 69 .

[1]

[2]

[3]