Geometrie hiperbolică

În geometria hiperbolică, liniile paralele în general „diverg” și unghiurile interne ale unui triunghi sunt mai mici decât în geometria euclidiană. Așa se întâmplă de exemplu pentru geodezie pe o suprafață în formă de șa ca aceasta.

Discul Poincaré este un model de geometrie hiperbolică. În figură este descrisă o teselare a discului prin triunghiuri hiperbolice : în ciuda faptului că apar diferite, în geometria hiperbolică aceste triunghiuri sunt de fapt toate congruente , adică de aceeași magnitudine. Din teselări de acest tip, Escher a construit unele dintre celebrele sale litografii.

Geometria hiperbolică, numită și geometria lui Bolyai-Lobachevsky, este o geometrie neeuclidiană obținută prin înlocuirea postulatului paralel cu așa-numitul postulat hiperbolic.

A fost studiat inițial de Saccheri în secolul al XVIII-lea , în ciuda faptului că el credea că este inconsistent , iar mai târziu de Bolyai , Gauss și Lobachevskii , ca geometrie astrală. La 150 de ani de la naștere, geometria hiperbolică este încă un subiect central al matematicii, reînviat la sfârșitul anilor șaptezeci de descoperirile lui William Thurston .

fundal

Nikolay Ivanovich Lobachevsky a contribuit la nașterea și dezvoltarea geometriei hiperbolice.

Geometria hiperbolică a fost creată în secolul al XIX-lea ca un instrument specific pentru rezolvarea unei probleme deschise de secole și cunoscut deja la același Euclid : al cincilea postulat al lui Euclid este efectiv independent de primul sau poate fi demonstrat de acestea? Geometria hiperbolică, care satisface primele 4 postulate, dar nu și a cincea, își arată independența efectivă.

Cu toate acestea, geometria hiperbolică nu este acceptată imediat ca o geometrie adevărată, cu demnitate egală cu cea euclidiană. Descoperirile lui Saccheri , Lambert , Legendre , Gauss , Schweikart , Taurinus , Lobachevsky , Bolyai au fost considerate surprinzătoare și paradoxale doar în timp și au găsit apoi o poziție naturală și o rigurozitate și raționament. Încet, s-a descoperit că geometria hiperbolică nu este doar rezultatul negării celui de-al cincilea postulat, ci este o geometrie reală cu proprietățile și definițiile sale, care poate fi considerată nouă în raport cu cea euclidiană.

Descoperirea și dezvoltarea geometriei hiperbolice sunt, prin urmare, un exemplu fundamental al unui proces de cercetare matematică care a devenit obișnuit în ultimele două secole: în matematică se poate întâmpla ca, modificând o singură axiomă, să fie construită o nouă teorie completă, unde unele proprietăți care par fundamentale, dar este posibil să descoperim noi entități geometrice (cum ar fi hiperparalele , orociclurile și orosferele etc.) având proprietăți care sunt totuși interesante.

Definiție

Două linii drepte în plan care nu se intersectează în niciun punct se numesc paralele . Cel de- al cincilea postulat al lui Euclid (sau paralel, exprimat aici într-una din numeroasele sale formulări echivalente, datorită lui Playfair ) afirmă că, dată fiind o linie dreaptă $r$ ${\ displaystyle r}$ $r$ și un punct $P.$ ${\ displaystyle P}$ $P.$ , există o singură linie paralelă cu $r$ ${\ displaystyle r}$ $r$ trecând prin $P.$ ${\ displaystyle P}$ $P.$ .

Geometria hiperbolică este geometria obținută prin modificarea acestui postulat, în modul următor:

Având o linie dreaptă $r$ ${\ displaystyle r}$ $r$ și un punct $P.$ ${\ displaystyle P}$ $P.$ disjunct de la $r$ ${\ displaystyle r}$ $r$ , trec cel puțin două linii distincte $P.$ ${\ displaystyle P}$ $P.$ și paralel cu $r$ ${\ displaystyle r}$ $r$ .

Geometria hiperbolică este o geometrie obținută prin modificarea postulatului V în direcția opusă. Un spațiu pe care este construită o geometrie hiperbolică este denumit spațiu hiperbolic . Primele patru axiome ale lui Euclid sunt următoarele.

Între două puncte orice este posibil să trasezi o singură linie dreaptă .
Puteți extinde o linie dincolo de două puncte pe termen nelimitat.
Având în vedere un punct și o lungime, este posibil să se descrie un cerc .
Toate unghiurile drepte sunt congruente .

Mai precis, primul postulat nu este complet verificat în geometria sferică : pe suprafața unei sfere există de fapt puncte , numite puncte antipodale , pentru care trec infinit drept . Cel de-al doilea postulat nu a apărut însă în geometria sferică , deoarece liniile sunt întotdeauna limitate, ca curbe închise.

Modele

Același subiect în detaliu: spațiul hiperbolic .

Existența reală a geometriilor hiperbolice este garantată prin construirea unor modele. De fapt, aceste modele se dovedesc a fi toate egale între ele: din acest motiv geometria hiperbolică este substanțial unică, la fel ca geometria euclidiană și geometria eliptică ^[1] .

Un model este un spațiu, care include noțiunile de punct, linie și unghi, pe care se aplică cele 5 axiome ale geometriei hiperbolice. Există patru modele utilizate în mod obișnuit pentru geometria hiperbolică. În fiecare dintre aceste modele, geometria hiperbolică poate fi introdusă la diferite niveluri. În sensul cel mai clasic, poate fi introdus prin definirea punctelor, a liniilor drepte, a unghiurilor și, eventual, a distanțelor.

Model de disc

Având în vedere o linie (aici în albastru închis) și un punct disjunct, există cel puțin două linii care trec prin punctul care nu traversează linia. În adevăr, există nesfârșite: trei sunt desenate aici.

Același subiect în detaliu: Disco Poincaré .

În modelul discului Poincare, spațiul hiperbolic este format din punctele interioare către un cerc $C.$ ${\ displaystyle C}$ $C.$ . Liniile sunt arcuri de circumferință care intersectează marginea cercului perpendicular. Unghiurile care formează două dintre aceste „linii” atunci când se intersectează într-un punct sunt cele formate de liniile tangente din punct. Distanța dintre două puncte este definită în așa fel încât să crească exponențial atunci când unul dintre cele două puncte este deplasat spre marginea cercului.

Cele 5 axiome ale geometriei hiperbolice sunt satisfăcute de acest model. Intr-adevar:

Având în vedere două puncte interne a $C.$ ${\ displaystyle C}$ $C.$ , există de fapt un singur arc de circumferință perpendicular pe marginea cercului care trece prin cele două puncte.
Un arc de circumferință poate fi extins la infinit: faptul că distanța tinde spre infinit ca marginea lui $C.$ ${\ displaystyle C}$ $C.$ implică faptul că această margine nu este atinsă niciodată și, prin urmare, extensia nu este niciodată întreruptă.
Puteți desena un cerc cu un centru și o rază fixe.
Unghiurile drepte sunt congruente.
Având în vedere un punct $P.$ ${\ displaystyle P}$ $P.$ și o linie dreaptă $r$ ${\ displaystyle r}$ $r$ care nu îl conține, trec cel puțin două linii drepte $P.$ ${\ displaystyle P}$ $P.$ disjunct de la $r$ ${\ displaystyle r}$ $r$ .

Modelul semiplanului

Același subiect în detaliu: modelul semi-plan Poincaré .

Modelul pe jumătate de plan este similar cu modelul discului. Spațiul hiperbolic este semiplanul planului cartezian format din I și cadranul II: axa x nu este inclusă. „Liniile” sunt arcuri de circumferință ortogonale față de axa abscisei. Unghiurile sunt cele formate de liniile tangente.

Modelul Klein

Același subiect în detaliu: modelul Klein .

V postulatul geometriei hiperbolice în modelul Klein.

În modelul Klein al spațiului hiperbolic este (ca și în modelul discului) setul de puncte din interiorul unui cerc $C.$ ${\ displaystyle C}$ $C.$ . Liniile drepte, totuși, sunt segmente reale: simplitatea mai mare în descrierea liniilor drepte este plătită în descrierea unghiurilor, care sunt distorsionate în raport cu unghiurile euclidiene: unghiul format din două linii drepte nu este cel euclidian. , dar depinde de aceasta printr-o formulă adecvată.

Spațiul hiperbolic poate fi reprezentat ca unul dintre cele două „clapete” ale unui hiperboloid, de exemplu cel superior. Liniile drepte sunt intersecțiile cu planurile care trec prin centrul hiperboloidului.

Modelul hiperboloidului

În spațiul model hiperbolic hiperboloid este descris cu ajutorul algebrei liniare sau chiar a spus liniarizat. Spațiul hiperbolic este un hiperboloid conținut în spațiul tridimensional, iar liniile sunt intersecțiile hiperboloidului cu un plan care trece prin centrul hiperboloidului. Descrierea matematică a acestui model are puternice paralele cu spațiul-timp Minkowski : distanța dintre două puncte este aceeași ca în relativitatea specială .

Acest model este ușor de realizat unele conturi, deoarece se bazează pe instrumentele algebrei liniare. Cu toate acestea, este mai puțin intuitiv și mai dificil de vizualizat, deoarece este conținut mai degrabă în spațiul tridimensional decât în plan.

Proprietate

Paralelism

Același subiect în detaliu: Paralelismul în geometria hiperbolică .

Liniile paralele cu o dată

L

{\ displaystyle l}

L

trecători pentru

P.

{\ displaystyle P}

P.

formează un unghi

\theta

{\ displaystyle \ theta}

\ theta

, Unghiul de paralelism menționat .

Noțiunea de paralelism în geometria hiperbolică diferă foarte mult de cea prezentă în geometria euclidiană.

Al cincilea postulat hiperbolic afirmă că, dată fiind o linie dreaptă $L$ ${\ displaystyle l}$ $L$ și un punct $P.$ ${\ displaystyle P}$ $P.$ disjunct de la $L$ ${\ displaystyle l}$ $L$ , există cel puțin două linii paralele a $L$ ${\ displaystyle l}$ $L$ trecători pentru $P.$ ${\ displaystyle P}$ $P.$ . Totuși, din postulat rezultă că aceste linii sunt infinite: aceasta rezultă din următoarele fapte.

Este $B.$ ${\ displaystyle B}$ $B.$ punctul de $L$ ${\ displaystyle l}$ $L$ mai aproape de $P.$ ${\ displaystyle P}$ $P.$ . Segmentul $P. B.$ ${\ displaystyle PB}$ $PB$ este perpendicular pe $L$ ${\ displaystyle l}$ $L$ (Vezi figura). Fiecare linie $s$ ${\ displaystyle s}$ $s$ trecând prin $P.$ ${\ displaystyle P}$ $P.$ acum este identificat prin unghi $\theta$ ${\ displaystyle \ theta}$ $\ theta$ care se formează cu segmentul $P. B.$ ${\ displaystyle PB}$ $PB$ . Unghiul se numește unghi de paralelism al $L$ ${\ displaystyle l}$ $L$ Și $s$ ${\ displaystyle s}$ $s$ .
Dacă două linii $s_{1}$ ${\ displaystyle s_ {1}}$ $s_ {1}$ Și $s_{2}$ ${\ displaystyle s_ {2}}$ $s_ {2}$ sunt paralele cu $L$ ${\ displaystyle l}$ $L$ , acestea formează unghiuri diferite $\theta _{1}$ ${\ displaystyle \ theta _ {1}}$ $\ theta_1$ Și $\theta _{2}$ ${\ displaystyle \ theta _ {2}}$ $\ theta_2$ : orice altă linie dreaptă cu un unghi între $\theta _{1}$ ${\ displaystyle \ theta _ {1}}$ $\ theta_1$ Și $\theta _{2}$ ${\ displaystyle \ theta _ {2}}$ $\ theta_2$ se dovedește a fi paralel cu $L$ ${\ displaystyle l}$ $L$ .

Liniile paralele a $L$ ${\ displaystyle l}$ $L$ trecători pentru $P.$ ${\ displaystyle P}$ $P.$ Acestea sunt toate și numai liniile drepte cu unghi de paralelism aparținând unui interval închis $[\theta ,\pi -\theta ]$ ${\ displaystyle [\ theta, \ pi - \ theta]}$ $[\ theta, \ pi - \ theta]$ . Liniile drepte cu un unghi de paralelism $\theta$ ${\ displaystyle \ theta}$ $\ theta$ Și $\pi -\theta$ ${\ displaystyle \ pi - \ theta}$ $\ pi - \ theta$ Ele sunt numite echivalente asimptotic $L$ ${\ displaystyle l}$ $L$ deoarece într-o direcție acestea se apropie din ce în ce mai mult $L$ ${\ displaystyle l}$ $L$ fără a o intersecta vreodată. Două linii paralele care nu sunt echivalente asimptotic sunt iperparalele: acestea sunt distanțate în ambele direcții atât de exponențial .

În geometria hiperbolică noțiunea de paralelism este deci mai complexă decât în geometria euclidiană: de exemplu, noțiunea nu este o relație de echivalență , deoarece nu merită proprietatea tranzitivă.

Un pătrat este un poligon cu 4 laturi de lungime egală și 4 unghiuri egale

\alpha

{\ displaystyle \ alpha}

\ alfa

. În geometria euclidiană

\alpha

{\ displaystyle \ alpha}

\ alfa

Trebuie să fie un unghi drept . În acest hiperbolic, poate fi orice unghi acut .

Poligoane

Același subiect în detaliu: Poligon hiperbolic .

În geometria hiperbolică, suma

\alpha +\beta +\gamma

{\ displaystyle \ alpha + \ beta + \ gamma}

\ alpha + \ beta + \ gamma

dintre unghiurile interioare ale unui triunghi este mai mic decât

\pi

{\ displaystyle \ pi}

\ pi

(sau 180º).

La fel ca în geometria euclidiană, un segment este o porțiune dreaptă delimitată de două puncte (extremele sale), iar un poligon este o figură mărginită de o succesiune de segmente, astfel încât două segmente succesive se intersectează cu extreme.

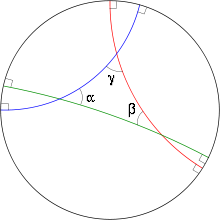
Relațiile dintre lungimile laturilor și unghiurile interne din geometria hiperbolică sunt totuși foarte diferite de cele prezente în geometria euclidiană. De exemplu, suma unghiurilor interioare ale unui triunghi hiperbolic este strict mai mică decât $\pi$ ${\ displaystyle \ pi}$ $\ pi$ : Aceasta poate lua orice valoare în „ intervalul deschis ” $(0,\pi )$ ${\ displaystyle (0, \ pi)}$ $(0, \ pi)$ . Unghiurile interne din geometria hiperbolică sunt mai mici.

Acest fapt se extinde la toate poligoanele: suma unghiurilor interioare ale unui poligon hiperbolic cu $n$ ${\ displaystyle n}$ $n$ laturile este un număr variabil în interval $(0,(n-2)\pi )$ ${\ displaystyle (0, (n-2) \ pi)}$ $(0, (n-2) \ pi)$ . De exemplu:

Există pătrate cu colțuri interne $\alpha$ ${\ displaystyle \ alpha}$ $\ alfa$ pentru fiecare $\alpha$ ${\ displaystyle \ alpha}$ $\ alfa$ astfel încât $0<\alpha <\pi /2$ ${\ displaystyle 0 <\ alpha <\ pi / 2}$ $0 <\ alpha <\ pi / 2$ : un exemplu este prezentat în figură.
Pentru fiecare $n>4$ ${\ displaystyle n> 4}$ $n> 4$ există un poligon de $n$ ${\ displaystyle n}$ $n$ laturi de aceeași lungime cu toate unghiurile drepte.

Construcție cu riglă și busolă

În geometria hiperbolică este posibil să construim cu linie și busolă segmentul având ca unghi de paralelism un unghi dat.

În unele cazuri, este posibilă pătrarea cercului , spre deosebire de ceea ce se întâmplă în geometria euclidiană , unde niciodată nu este posibil să se determine cu o riglă și busolă latura unui pătrat având aceeași zonă a unui cerc dat.

Trigonometrie

Un alt rezultat interesant este dat de formulele de trigonometrie a sferei care sunt aceleași atât în spațiul hiperbolic atât în euclidian, deoarece proprietățile geometriei sferei derivate din proprietățile angoloidelor și ale triedrelor , care sunt proprietăți ale geometriei absolute .

Acest lucru este valabil și în plan, unde planul de trigonometrie hiperbolică nu este mai mult decât trigonometria aplicată pe o sferă imaginară cu rază.

Geometria hiperbolică a spațiului

Același subiect în detaliu: geometria hiperbolică a spațiului .

Un octaedru hiperbolic .

Geometria hiperbolică se extinde de la plan la spațiu și chiar în dimensiuni arbitrare. Fiecare dintre modelele spațiului hiperbolic are, de fapt, o generalizare naturală în dimensiune $n$ ${\ displaystyle n}$ $n$ orice. Prin urmare, există o geometrie solidă a spațiului hiperbolic tridimensional $n=3$ ${\ displaystyle n = 3}$ $n = 3$ , care face obiectul studiului matematicii contemporane. De un interes deosebit sunt poliedrele hiperbolice, precum octaedrul prezentat în Fig.

Notă

^ O formulare mai riguroasă a acestor geometrii poate fi încadrată în cadrul axiomelor lui Hilbert , care le completează pe cele ale lui Euclid.

Bibliografie

Coxeter , HSM (1942) Geometrie non-euclidiană, University of Toronto Press, Toronto
Nikolai I. Lobachevsky , Pangeometrie, traducător și editor: A. Papadopoulos, Heritage of European Mathematics Series, Vol. 4, European Mathematical Society, 2010.
Milnor, John W. (1982) Geometrie hiperbolică: primii 150 de ani , Bull. Amer. Matematica. Soc. (NS) Volumul 6, Numărul 1, pp. 9 - 24.
Riccardo Benedetti , Carlo Petronio (1992) Prelegeri despre geometria hiperbolică, Universitext Springer-Verlag, ISBN 978-3-642-58158-8 .
Reynolds, William F. (1993) Geometrie hiperbolică pe un hiperboloid, lunar american matematic 100: 442-455.
Maria Dedò (1996): Transformări geometrice. Cu o introducere în modelul Poincaré, Freeman - Decibel, ISBN 9788808162601
Stillwell, John. (1996) Surse în geometrie hiperbolică, volumul 10 din seria AMS / LMS History of Mathematics.
James W. Anderson, Geometrie hiperbolică, Springer 2005, ISBN 1-85233-934-9
Samuels, David. (Martie 2006) Knit Theory Discover Magazine, volumul 27, numărul 3.