Grup (matematică)

Mișcările cubului Rubik formează un grup, numit grupul cubului Rubik .

În matematică, un grup este o structură algebrică formată prin combinarea unui set ne-gol cu o operație binară internă (cum ar fi adunarea sau multiplicarea), care satisface axiomele asociativității , existenței elementului neutru și existenței inversului fiecare element.

Aceste axiome sunt satisfăcute de numeroase structuri algebrice, cum ar fi numerele întregi cu operația de adunare , dar sunt mult mai generale și sunt independente de natura particulară a grupului considerat. În acest fel devine posibil să se lucreze flexibil cu obiecte matematice de natură și origine foarte diferite, recunoscând câteva aspecte structurale comune importante. Rolul cheie al grupurilor în numeroase domenii, atât interne, cât și externe matematicii, le face unul dintre conceptele fundamentale ale matematicii moderne.

Conceptul de grup s-a născut din studiile asupra ecuațiilor polinomiale , începute de Évariste Galois în anii treizeci ai secolului al XIX-lea . În urma contribuțiilor din alte domenii ale matematicii, cum ar fi teoria numerelor și geometria , noțiunea de grup a fost generalizată și definită ferm în jurul anului 1870 . Teoria modernă a grupurilor - o disciplină matematică foarte activă - se ocupă cu studiul abstract al grupurilor. Mathematical Reviews are 3.224 de articole de cercetare despre teoria grupurilor și generalizările sale publicate numai în 2005 .

Matematicienii au dezvoltat diverse noțiuni pentru divizarea grupurilor în părți mai mici și mai ușor de studiat, cum ar fi subgrupuri și coeficienți . Pe lângă studierea proprietăților lor abstracte, teoreticienii grupurilor se ocupă și de diferitele moduri în care un grup poate fi exprimat concret, atât din punct de vedere teoretic , cât și din punct de vedere computațional . O teorie deosebit de bogată a fost dezvoltată pentru grupurile finite , culminând cu clasificarea monumentală a grupurilor simple finite , finalizată în 1983 .

Definiție și primele proprietăți

Definiție

Un grup este un întreg $G.$ ${\ displaystyle G}$ $G.$ echipat cu o operație binară $*$ ${\ displaystyle *}$ $*$ , care pentru fiecare pereche de elemente $la$ ${\ displaystyle a}$ $la$ , $b$ ${\ displaystyle b}$ $b$ din $G.$ ${\ displaystyle G}$ $G.$ asociază un element , pe care îl indicăm cu $a*b$ ${\ displaystyle a * b}$ $a * b$ , aparținând $G.$ ${\ displaystyle G}$ $G.$ , pentru care sunt îndeplinite următoarele axiome : ^[1]

proprietate asociativă : date $la, b, c$ ${\ displaystyle a, b, c}$ $a, b, c$ aparținând $G.$ ${\ displaystyle G}$ $G.$ , merita $(a*b)*c=a*(b*c)$ ${\ displaystyle (a * b) * c = a * (b * c)}$ $(a * b) * c = a * (b * c)$ .
existența elementului neutru : există în $G.$ ${\ displaystyle G}$ $G.$ un element neutru $Și$ ${\ displaystyle e}$ $Și$ în ceea ce privește operațiunea $*$ ${\ displaystyle *}$ $*$ , adică astfel încât $a*e=e*a=a$ ${\ displaystyle a * e = e * a = a}$ $a * e = e * a = a$ pentru fiecare $la$ ${\ displaystyle a}$ $la$ aparținând $G.$ ${\ displaystyle G}$ $G.$ .
existența inversului : pentru fiecare element $la$ ${\ displaystyle a}$ $la$ din $G.$ ${\ displaystyle G}$ $G.$ există un element ${la}^{'}$ ${\ displaystyle a '}$ $la'$ , invers de $la$ ${\ displaystyle a}$ $la$ , astfel încât $a*a'=a'*a=e$ ${\ displaystyle a * a '= a' * a = e}$ $a * a '= a' * a = e$ .

Impunând doar unele dintre aceste axiome, se obțin alte structuri, cum ar fi magma , cvasigrupul , semigrupul și monoidul .

Este important să subliniem că structura grupului este formată din două obiecte: întregul $G.$ ${\ displaystyle G}$ $G.$ și operația binară $*$ ${\ displaystyle *}$ $*$ pe el. Pentru simplitate, totuși, este obișnuit să se noteze un grup cu doar simbolul întregului pe care grupul este „construit”, dacă operațiunea este clară din context și nu există riscul confuziei.

Se spune că un grup este comutativ (sau abelian ) dacă operația este comutativă, adică satisface relația $a*b=b*a$ ${\ displaystyle a * b = b * a}$ $a * b = b * a$ pentru fiecare cuplu $la$ ${\ displaystyle a}$ $la$ , $b$ ${\ displaystyle b}$ $b$ de elemente ale $G.$ ${\ displaystyle G}$ $G.$ . ^[2]

Cardinalitatea întregului $G.$ ${\ displaystyle G}$ $G.$ este indicat cu $|G|$ ${\ displaystyle | G |}$ $| G |$ și se numește ordinea grupului: dacă s-a terminat, atunci $G.$ ${\ displaystyle G}$ $G.$ este un grup finit , altfel este infinit .

Primele proprietăți

Vedem imediat că elementul neutru al unui grup este determinat în mod univoc. De fapt dacă $Și$ ${\ displaystyle e}$ $Și$ , $f$ ${\ displaystyle f}$ $f$ ambele sunt elemente neutre, da $f=e*f=e$ ${\ displaystyle f = e * f = e}$ $f = e * f = e$ , unde prima egalitate rezultă din faptul că $Și$ ${\ displaystyle e}$ $Și$ este un element neutru, iar al doilea prin faptul că este $f$ ${\ displaystyle f}$ $f$ .

La fel, inversul unui element este determinat în mod unic. De fapt dacă ${la}^{'}$ ${\ displaystyle a '}$ $la'$ , ${la}^{″}$ ${\ displaystyle a ''}$ $la''$ ambii sunt inversi ai $la$ ${\ displaystyle a}$ $la$ , da $a'=a'*e=a'*(a*a'')=(a'*a)*a''=e*a''=a''$ ${\ displaystyle a '= a' * e = a '* (a * a' ') = (a' * a) * a '' = e * a '' = a ''}$ $a '= a' * e = a '* (a * a' ') = (a' * a) * a '' = e * a '' = a ''$ , unde egalitățile decurg din definiția elementului neutru, din faptul că ${la}^{″}$ ${\ displaystyle a ''}$ $la''$ este un invers al $la$ ${\ displaystyle a}$ $la$ , din proprietatea asociativă, din faptul că ${la}^{'}$ ${\ displaystyle a '}$ $la'$ este un invers al $la$ ${\ displaystyle a}$ $la$ , și din nou din definiția elementului neutru.

Inversul elementului $la$ ${\ displaystyle a}$ $la$ este indicat adesea cu $a^{-1}$ ${\ displaystyle a ^ {- 1}}$ $a ^ {{- 1}}$ .

Puteri

Date $a\in G$ ${\ displaystyle a \ în G}$ $a \ in G$ Și $z\in \mathbb {Z}$ ${\ displaystyle z \ in \ mathbb {Z}}$ ${\ displaystyle z \ in \ mathbb {Z}}$ , puterea de bază $la$ ${\ displaystyle a}$ $la$ și exponent $z$ ${\ displaystyle z}$ $z$ , indicat cu $a^{z}$ ${\ displaystyle a ^ {z}}$ ${\ displaystyle a ^ {z}}$ , este definit de următoarele:

$\qquad a^{0}:=e$ ${\ displaystyle \ qquad a ^ {0}: = e}$ ${\ displaystyle \ qquad a ^ {0}: = e}$ ,

$\qquad a^{z}:=a\ast a^{z-1}$ ${\ displaystyle \ qquad a ^ {z}: = a \ ast a ^ {z-1}}$ ${\ displaystyle \ qquad a ^ {z}: = a \ ast a ^ {z-1}}$ de sine $z>0$ ${\ displaystyle z> 0}$ $z> 0$ ,

$\qquad a^{z}:={\left(a^{-1}\right)}^{-z}$ ${\ displaystyle \ qquad a ^ {z}: = {\ left (a ^ {- 1} \ right)} ^ {- z}}$ ${\ displaystyle \ qquad a ^ {z}: = {\ left (a ^ {- 1} \ right)} ^ {- z}}$ de sine $z<0$ ${\ displaystyle z <0}$ ${\ displaystyle z <0}$ .

Notări multiplicative și aditive

Ca și în cazul înmulțirii obișnuite între numere, este adesea adoptată o notație multiplicativă pentru operația binară a unui grup $G.$ ${\ displaystyle G}$ $G.$ : produsul a două elemente $la$ ${\ displaystyle a}$ $la$ Și $b$ ${\ displaystyle b}$ $b$ este indicat deci cu $la b$ ${\ displaystyle ab}$ $ab$ in loc de $a*b$ ${\ displaystyle a * b}$ $a * b$ . În acest caz, elementul neutru $Și$ ${\ displaystyle e}$ $Și$ este indicat în general cu $1_{G}$ ${\ displaystyle 1_ {G}}$ $1_ {G}$ (sau chiar doar $1$ ${\ displaystyle 1}$ $1$ dacă nu există riscul de ambiguitate).

Când grupul este abelian, uneori se preferă utilizarea unui aditiv, mai degrabă decât notație multiplicativă, indicând $la b$ ${\ displaystyle ab}$ $ab$ cu $a+b$ ${\ displaystyle a + b}$ $a + b$ . Cu această notație, elementul neutru devine $0_{G}$ ${\ displaystyle 0_ {G}}$ ${\ displaystyle 0_ {G}}$ (sau pur și simplu), puterea $a^{z}$ ${\ displaystyle a ^ {z}}$ ${\ displaystyle a ^ {z}}$ devine $z la$ ${\ displaystyle za}$ ${\ displaystyle za}$ și se numește multiplu $z$ ${\ displaystyle z}$ $z$ -th (o $z$ ${\ displaystyle z}$ $z$ -uple) de $la$ ${\ displaystyle a}$ $la$ , și invers $a^{-1}$ ${\ displaystyle a ^ {- 1}}$ $a ^ {{- 1}}$ este indicat cu $-a$ ${\ displaystyle -a}$ $-la$ , și se spune de obicei opus lui $la$ ${\ displaystyle a}$ $la$ .

Istorie

Conceptul modern al grupului își are originile în diferite domenii ale matematicii.

Matematicianul francez Évariste Galois este adesea menționat ca fiind fondatorul teoriei moderne a grupurilor.

În algebră , teoria grupurilor s-a născut la începutul secolului al XIX-lea în studiul ecuațiilor polinomiale . Matematicianul francez Évariste Galois , extinzând lucrările anterioare ale lui Paolo Ruffini și Joseph-Louis Lagrange , a furnizat în 1832 un criteriu pentru solvabilitatea unei ecuații polinomiale în funcție de grupul de simetrie al rădăcinilor sale (denumit ulterior grupul Galois ). Din lucrările sale derivă teorema lui Abel-Ruffini , care stabilește imposibilitatea de a găsi formule de soluție generală pentru ecuații de grad mai mare de 4.

Cu toate acestea , grupurile de permutare sunt obiecte matematice mai generale și au fost studiate într-o perspectivă mai largă de Augustin-Louis Cauchy . Prima definiție abstractă a unui grup finit a apărut în „ Despre teoria grupurilor”, de Arthur Cayley , în funcție de ecuația simbolică θ ⁿ = 1 din 1854 .

Matematicianul german Felix Klein a subliniat strânsele corelații dintre grupuri și geometrii.

În geometrie , noțiunea de grup s-a dezvoltat în mod natural în studiul simetriilor obiectelor plane și solide, cum ar fi poligoane și poliedre . În a doua jumătate a secolului al XIX-lea , matematicienii au descoperit existența geometriilor neeuclidiene și însăși noțiunea de „geometrie” a fost larg re-discutată. Matematicianul Felix Klein a propus în programul său Erlangen din 1872 să utilizeze conceptul de grup de simetrie ca element de construcție al definiției unei geometrii: în viziunea lui Klein, grupul de simetrie este elementul fundamental care determină geometria și distinge de exemplu geometria euclidiană de hiperbolică sau geometrie proiectivă . O importanță deosebită în geometrie sunt și grupurile Lie , introduse de Sophus Lie începând cu 1884 .

Un al treilea domeniu care a contribuit la dezvoltarea teoriei grupurilor este teoria numerelor . Unele structuri de grup abeliene au fost utilizate implicit în Disquisitiones Arithmeticae din 1798 ale lui Carl Friedrich Gauss și apoi, mai explicit, de Leopold Kronecker . În 1847, Ernst Kummer , încercând să demonstreze ultima teoremă a lui Fermat , a început studiul grupurilor de clase ideale ale unui câmp numeric.

Unirea tuturor acestor concepte dezvoltate în diferite domenii ale matematicii într-o singură teorie a grupurilor a început cu Traité des substitutions et des équations algébriques din 1870 a lui Camille Jordan . În 1882 Walther von Dyck a formulat prima dată definiția modernă a unui grup abstract. În secolul al XX-lea , grupurile au obținut o largă recunoaștere datorită lucrărilor lui Ferdinand Georg Frobenius și William Burnside , care s-au ocupat de teoria reprezentării grupurilor finite, grație teoriei reprezentărilor modulare și articolelor lui Issai Schur de Richard Brauer . Teoria grupurilor Lie și, mai general, a grupurilor compacte la nivel local a fost avansată de Hermann Weyl , Élie Joseph Cartan și mulți alții. Omologul algebric, adică teoria grupurilor algebrice a fost dezvoltat de Claude Chevalley (începând cu anii 1930 ) și mai târziu de Armand Borel și Jacques Tits .

Anul universitar 1960 - 61 a fost dedicat de Universitatea din Chicago teoriei grupurilor. La inițiativă au participat teoreticieni de la Daniel Gorenstein , John G. Thompson și Walter Feit , care au început o colaborare fructuoasă, culminând cu clasificarea grupurilor simple terminate în 1982 , un proiect care a implicat mulți matematicieni. Chiar și astăzi, teoria grupurilor este o ramură foarte activă a matematicii cu impact crucial în numeroase alte sectoare.

Exemple

Numere

Ansamblul numerelor întregi

\mathbb {Z} =\{\ldots ,-4,-3,-2,-1,0,1,2,3,4,\ldots \}

{\ displaystyle \ mathbb {Z} = \ {\ ldots, -4, -3, -2, -1,0,1,2,3,4, \ ldots \}}

{\ mathbb Z} = \ {\ ldots, -4, -3, -2, -1,0,1,2,3,4, \ ldots \}

și funcționarea sa de sumă $+$ ${\ displaystyle +}$ $+$ formează un grup abelian . Grupul este apoi identificat de cuplu $(\mathbb {Z} ,+)$ ${\ displaystyle (\ mathbb {Z}, +)}$ ${\ displaystyle (\ mathbb {Z}, +)}$ . Cu toate acestea, numere întregi nu formează un grup cu multiplicarea operației: multiplicare este asociativă și are ca element neutru numărul $1$ ${\ displaystyle 1}$ $1$ (sau $(\mathbb {Z} ,\cdot \,)$ ${\ displaystyle (\ mathbb {Z}, \ cdot \,)}$ ${\ displaystyle (\ mathbb {Z}, \ cdot \,)}$ este un monoid comutativ), dar majoritatea elementelor din $\mathbb {Z}$ ${\ displaystyle \ mathbb {Z}}$ $\ mathbb {Z}$ nu are invers cu privire la multiplicare. De exemplu, nu există un număr întreg care să se înmulțească cu $2$ ${\ displaystyle 2}$ $2$ da drept urmare $1$ ${\ displaystyle 1}$ $1$ , asa de $2$ ${\ displaystyle 2}$ $2$ nu admite invers în $\mathbb {Z}$ ${\ displaystyle \ mathbb {Z}}$ $\ mathbb {Z}$ cu privire la multiplicare; mai exact, singurele numere întregi care admit multiplicativ invers în $\mathbb {Z}$ ${\ displaystyle \ mathbb {Z}}$ $\ mathbb {Z}$ Sunt $1$ ${\ displaystyle 1}$ $1$ Și $-1$ ${\ displaystyle -1}$ $-1$ .

Numerele raționale , numerele reale și numerele complexe formează, de asemenea , un grup cu operația de adunare. Se obțin astfel alte trei grupuri: $(\mathbb {Q} ,+),\,(\mathbb {R} ,+),\,(\mathbb {C} ,+).$ ${\ displaystyle (\ mathbb {Q}, +), \, (\ mathbb {R}, +), \, (\ mathbb {C}, +).}$ ${\ displaystyle (\ mathbb {Q}, +), \, (\ mathbb {R}, +), \, (\ mathbb {C}, +).}$

Numerele raționale, private de zero, formează un grup cu multiplicare. Un număr rațional, altul decât zero, este de fapt identificat printr-o fracție $a/b$ ${\ displaystyle a / b}$ $a / b$ cu $a\neq 0$ ${\ displaystyle a \ neq 0}$ $a \ neq 0$ , a cărei inversă (în ceea ce privește multiplicarea) este fracția $b/a$ ${\ displaystyle b / a}$ $b / a$ . În mod similar, numerele reale (sau complexe) nenule formează un grup cu multiplicare. Prin urmare, sunt și grupuri $(\mathbb {Q} \setminus \left\{0\right\},\cdot \,),\,(\mathbb {R} \setminus \left\{0\right\},\cdot \,),\,(\mathbb {C} \setminus \left\{0\right\},\cdot \,)$ ${\ displaystyle (\ mathbb {Q} \ setminus \ left \ {0 \ right \}, \ cdot \,), \, (\ mathbb {R} \ setminus \ left \ {0 \ right \}, \ cdot \ ,), \, (\ mathbb {C} \ setminus \ left \ {0 \ right \}, \ cdot \,)}$ ${\ displaystyle (\ mathbb {Q} \ setminus \ left \ {0 \ right \}, \ cdot \,), \, (\ mathbb {R} \ setminus \ left \ {0 \ right \}, \ cdot \ ,), \, (\ mathbb {C} \ setminus \ left \ {0 \ right \}, \ cdot \,)}$ . (Această construcție nu funcționează cu numere întregi, adică $(\mathbb {Z} \setminus \left\{0\right\},\cdot \,)$ ${\ displaystyle (\ mathbb {Z} \ setminus \ left \ {0 \ right \}, \ cdot \,)}$ ${\ displaystyle (\ mathbb {Z} \ setminus \ left \ {0 \ right \}, \ cdot \,)}$ nu este un grup: aceasta este legată de faptul că raționalele, reale sau complexe, formează un câmp cu operațiile de sumă și produs, în timp ce numerele întregi formează doar un inel .)

Toate aceste grupuri de număr sunt abelieni.

Permutări

Același subiect în detaliu: Permutare și grup simetric .

Permutările unui set fix $X$ ${\ displaystyle X}$ $X$ formează un grup împreună cu operația de compunere a funcției . Acest grup este cunoscut sub numele de grup simetric și este în general notat cu $S(X)$ ${\ displaystyle S (X)}$ $S X)$ (sau ${\textrm {Sym}}(X)$ ${\ displaystyle {\ textrm {Sym}} (X)}$ ${\ displaystyle {\ textrm {Sym}} (X)}$ ). De exemplu, dacă $X=\{A,B,C\}$ ${\ displaystyle X = \ {A, B, C \}}$ $X = \ {A, B, C \}$ , o permutare poate fi descrisă printr-un cuvânt din cele trei litere $LA, B., C.$ ${\ displaystyle A, B, C}$ $A, B, C$ , fără repetări: de exemplu, cuvântul ACB indică o permutare a ultimelor două litere (numită transpunere ), în timp ce cuvântul BAC indică o transpunere a primelor două. Grupul $S(X)$ ${\ displaystyle S (X)}$ $S X)$ deci constă din șase elemente: ABC, ACB, BAC, BCA, CAB, CBA.

Grupul simetric pe 3 elemente $S_{3}$ ${\ displaystyle S_ {3}}$ $S_ {3}$ este cel mai mic exemplu de grup non-abelian: prin compunerea celor două permutări ACB și BAC în cele două moduri posibile, de fapt, se obțin permutări diferite.

Grupuri de simetrie

Același subiect în detaliu: Simetrie (matematică) .

Simetriile unui obiect geometric formează întotdeauna un grup. De exemplu, simetriile unui poligon regulat formează un grup finit numit grup diedru . Simetriile unui pătrat sunt prezentate mai jos.

identitate (nu mișcă nimic)	Rotație la 90 ° în sensul acelor de ceasornic	Rotire la 180 ° în sensul acelor de ceasornic	Rotire 270 ° în sensul acelor de ceasornic
simetrie verticală	simetrie orizontală	simetrie diagonală	altă simetrie diagonală
Elementele grupului de simetrie al pătratului.

Simetriile unui tetraedru sunt 24: pe lângă identitate, există 11 rotații în jurul unei axe, 6 reflecții față de un plan și alte 6 operații obținute prin compunerea rotațiilor și reflecțiilor.

Simetriile unui poliedru formează, de asemenea , un grup finit. O importanță deosebită sunt grupurile de simetrie ale solidelor platonice . De exemplu, grupul de simetrie al tetraedrului este format din 24 de elemente.

Algebră liniară

Algebra liniară oferă multe grupuri, de obicei infinite. În primul rând, un spațiu vector, cum ar fi spațiul euclidian R ⁿ de dimensiunea n este un grup abelian cu suma obișnuită între vectori.

Tablourile cu m rânduri și n coloane sunt, de asemenea, un grup abelian cu suma. În ceea ce privește seturile numerice, în unele cazuri este posibilă și construirea de seturi de matrice care formează un grup cu produsul matricilor . Între acestea,

Grupul liniar general format din toate matricile pătrate inversabile .
Grupul ortogonal format din matricele pătrate ortogonale .

Noțiuni de bază

Același subiect în detaliu: Glosar al teoriei grupurilor .

Pentru a înțelege mai profund structura unui grup, au fost introduse câteva concepte importante. Caracteristica fundamentală care îi unește este „compatibilitatea” lor cu funcționarea grupului.

Homomorfisme

Același subiect în detaliu: Homomorfismul grupurilor .

Harta care trimite un întreg

X

{\ displaystyle x}

X

în opusul său

-x

{\ displaystyle -x}

-X

este un homomorfism din grup

\mathbb {Z}

{\ displaystyle \ mathbb {Z}}

\ mathbb Z

in sinea lui. Este, de asemenea, un izomorfism, deoarece este o corespondență unu-la-unu. Mai general, orice omomorfism dă

\mathbb {Z}

{\ displaystyle \ mathbb {Z}}

\ mathbb Z

în sine trimite

X

{\ displaystyle x}

X

în

k X

{\ displaystyle kx}

kx

, unde este

k

{\ displaystyle k}

k

este un număr întreg fix. Izomorfismul arătat este, prin urmare, singurul izomorfism, în plus față de identitate (obținut cu

k=1

{\ displaystyle k = 1}

k = 1

).

De sine $(G,\ast )$ ${\ displaystyle (G, \ ast)}$ ${\ displaystyle (G, \ ast)}$ Și $(H,\cdot )$ ${\ displaystyle (H, \ cdot)}$ ${\ displaystyle (H, \ cdot)}$ sunt două grupuri, un omomorfism al grupurilor este o funcție

f:G\to H

{\ displaystyle f: G \ to H}

f: G \ to H

că este „compatibilă” cu structurile de grup ale $G.$ ${\ displaystyle G}$ $G.$ Și $H.$ ${\ displaystyle H}$ $H.$ , adică că „păstrează” operațiunile celor două grupuri: mai precis, trebuie să aibă

f(a\ast b)=f(a)\cdot f(b)

{\ displaystyle f (a \ ast b) = f (a) \ cdot f (b)}

{\ displaystyle f (a \ ast b) = f (a) \ cdot f (b)}

pentru fiecare pereche de elemente $la$ ${\ displaystyle a}$ $la$ Și $b$ ${\ displaystyle b}$ $b$ în $G.$ ${\ displaystyle G}$ $G.$ . Omiind, ca de obicei, simbolurile operațiilor de grup, condiția anterioară este scrisă ca $f(ab)=f(a)f(b)$ ${\ displaystyle f (ab) = f (a) f (b)}$ ${\ displaystyle f (ab) = f (a) f (b)}$ (pentru fiecare $a,b\in G$ ${\ displaystyle a, b \ în G}$ ${\ displaystyle a, b \ în G}$ ). În special, această cerere asigură că $f$ ${\ displaystyle f}$ $f$ automat „păstrează” chiar și elementele neutre și inverse, adică

f(1_{G})=1_{H}

{\ displaystyle f (1_ {G}) = 1_ {H}}

{\ displaystyle f (1_ {G}) = 1_ {H}}

,

f(a^{-1})={\left(f(a)\right)}^{-1}\quad \forall a\in G.

{\ displaystyle f (a ^ {- 1}) = {\ left (f (a) \ right)} ^ {- 1} \ quad \ forall a \ in G.}

{\ displaystyle f (a ^ {- 1}) = {\ left (f (a) \ right)} ^ {- 1} \ quad \ forall a \ in G.}

De exemplu, funcția

{\begin{array}{ccccc}f&:&\mathbb {Z} &\to &\mathbb {Z} \\&&z&\mapsto &2z\end{array}}

{\ displaystyle {\ begin {array} {ccccc} f &: & \ mathbb {Z} & \ to & \ mathbb {Z} \\ && z & \ mapsto & 2z \ end {array}}}

{\ displaystyle {\ begin {array} {ccccc} f &: & \ mathbb {Z} & \ to & \ mathbb {Z} \\ && z & \ mapsto & 2z \ end {array}}}

este un homomorfism al grupurilor.

Dacă omomorfismul $f$ ${\ displaystyle f}$ $f$ este o funcție bijectivă (respectiv injectivă , surjectivă ), se spune că este un izomorfism (respectiv monomorfism, epimorfism). ^[3]

Ca și în cazul altor structuri algebrice , două grupuri izomorfe $G.$ ${\ displaystyle G}$ $G.$ Și $H.$ ${\ displaystyle H}$ $H.$ au aceleași proprietăți „intrinseci” și pot fi considerați (cu un minim de precauție) „același grup”. Acest lucru se datorează faptului că toate relațiile algebrice sunt transferate din $G.$ ${\ displaystyle G}$ $G.$ în $H.$ ${\ displaystyle H}$ $H.$ și invers: de exemplu, arată că $g^{2}=gg=e$ ${\ displaystyle g ^ {2} = dd = e}$ $g ^ {2} = dd = e$ pentru o vreme $g$ ${\ displaystyle g}$ $g$ în $G.$ ${\ displaystyle G}$ $G.$ echivalează cu a demonstra că $f(g)^{2}=f(g)f(g)=e$ ${\ displaystyle f (g) ^ {2} = f (g) f (g) = e}$ $f (g) ^ {2} = f (g) f (g) = e$ în $H.$ ${\ displaystyle H}$ $H.$ .

Subgrupuri

Același subiect în detaliu: Subgrup .

După cum se vede mai sus, simetriile unui pătrat formează un grup de ordine 8. Acest grup conține 1 subgrup de ordine 8 (el însuși), 3 subgrupuri de ordine 4, 5 subgrupuri de ordine 2 și 1 subgrup de ordine 1 (subgrupul trivial) . Subgrupurile sunt descrise aici în figura care arată efectele simetriilor simple asupra unei figuri nesimetrice (litera F).

Un subgrup este un subset $H.$ ${\ displaystyle H}$ $H.$ a unui grup $G.$ ${\ displaystyle G}$ $G.$ care se dovedește a fi el însuși un grup în ceea ce privește operațiunea moștenită de la aceea a $G.$ ${\ displaystyle G}$ $G.$ . Cu alte cuvinte, un subset $H.$ ${\ displaystyle H}$ $H.$ din $G.$ ${\ displaystyle G}$ $G.$ se numește subgrup de $(G,\ast )$ ${\ displaystyle (G, \ ast)}$ ${\ displaystyle (G, \ ast)}$ de sine $(H,\ast _{|H\times H})$ ${\ displaystyle (H, \ ast _ {| H \ times H})}$ ${\ displaystyle (H, \ ast _ {| H \ times H})}$ este un grup, în care elementul neutru este același cu $G.$ ${\ displaystyle G}$ $G.$ , sau $1_{H}=1_{G}$ ${\ displaystyle 1_ {H} = 1_ {G}}$ ${\ displaystyle 1_ {H} = 1_ {G}}$ . În acest caz, este obișnuit să scrieți $H\leq G$ ${\ displaystyle H \ leq G}$ ${\ displaystyle H \ leq G}$ (respectiv, $H<G$ ${\ displaystyle H <G}$ ${\ displaystyle H <G}$ ) pentru a indica asta $H.$ ${\ displaystyle H}$ $H.$ este un subgrup (respectiv, un subgrup propriu ) al lui $G.$ ${\ displaystyle G}$ $G.$ .

Are asta $H.$ ${\ displaystyle H}$ $H.$ este un subgrup de $G.$ ${\ displaystyle G}$ $G.$ dacă și numai dacă ambele fapte sunt valabile:

$1_{G}$ ${\ displaystyle 1_ {G}}$ $1_ {G}$ aparține lui $H.$ ${\ displaystyle H}$ $H.$ ,
$H.$ ${\ displaystyle H}$ $H.$ este închisă în ceea ce privește funcționarea $G.$ ${\ displaystyle G}$ $G.$ , adică: dacă $la$ ${\ displaystyle a}$ $la$ Și $b$ ${\ displaystyle b}$ $b$ sunt elemente ale $H.$ ${\ displaystyle H}$ $H.$ , de asemenea $la b$ ${\ displaystyle ab}$ $ab$ aparține lui $H.$ ${\ displaystyle H}$ $H.$ .

Echivalent, $H\leq G$ ${\ displaystyle H \ leq G}$ ${\ displaystyle H \ leq G}$ dacă și numai dacă este valabil

de sine $h_{1}$ ${\ displaystyle h_ {1}}$ $h_ {1}$ Și $h_{2}$ ${\ displaystyle h_ {2}}$ $h_ {2}$ sunt elemente ale $H.$ ${\ displaystyle H}$ $H.$ , asa de ${\left(h_{1}\right)}^{-1}{h_{2}}$ ${\ displaystyle {\ left (h_ {1} \ right)} ^ {- 1} {h_ {2}}}$ ${\ displaystyle {\ left (h_ {1} \ right)} ^ {- 1} {h_ {2}}}$ aparține lui $H.$ ${\ displaystyle H}$ $H.$ .

Printre subgrupurile unui grup $G.$ ${\ displaystyle G}$ $G.$ , sunt mereu acolo $G.$ ${\ displaystyle G}$ $G.$ ea însăși și subgrupul banal $\{1_{G}\}$ ${\ displaystyle \ {1_ {G} \}}$ ${\ displaystyle \ {1_ {G} \}}$ , care constă doar din elementul neutru.

Studiul subgrupurilor este foarte important în înțelegerea structurii generale a unui grup.

De exemplu, numerele pare formează un subgrup (corect) de numere întregi. Mai general, numere întregi divizibile cu un număr natural fix $n$ ${\ displaystyle n}$ $n$ (adică numerele întregi exprimabile ca produs al $n$ ${\ displaystyle n}$ $n$ și un întreg potrivit) formează un subgrup de $\mathbb {Z}$ ${\ displaystyle \ mathbb {Z}}$ $\ mathbb {Z}$ , care este indicat cu $n\mathbb {Z}$ ${\ displaystyle n \ mathbb {Z}}$ $n {\ mathbb Z}$ : de aceea $n\mathbb {Z} \leq \mathbb {Z}$ ${\ displaystyle n \ mathbb {Z} \ leq \ mathbb {Z}}$ ${\ displaystyle n \ mathbb {Z} \ leq \ mathbb {Z}}$ pentru fiecare $n\in \mathbb {N}$ ${\ displaystyle n \ in \ mathbb {N}}$ $n \ in \ mathbb {N}$ (Rețineți că $0\mathbb {Z} =\left\{0\right\}$ ${\ displaystyle 0 \ mathbb {Z} = \ left \ {0 \ right \}}$ ${\ displaystyle 0 \ mathbb {Z} = \ left \ {0 \ right \}}$ ). În schimb, se poate dovedi că orice subgrup de $\mathbb {Z}$ ${\ displaystyle \ mathbb {Z}}$ $\ mathbb {Z}$ este de această formă: de fapt, luați un subgrup $H\leq \mathbb {Z}$ ${\ displaystyle H \ leq \ mathbb {Z}}$ ${\ displaystyle H \ leq \ mathbb {Z}}$ ; de sine $H=\left\{0\right\}$ ${\ displaystyle H = \ left \ {0 \ right \}}$ ${\ displaystyle H = \ left \ {0 \ right \}}$ , ia în considerare $n=0$ ${\ displaystyle n = 0}$ $n = 0$ . Să presupunem că $H\neq \left\{0\right\}$ ${\ displaystyle H \ neq \ left \ {0 \ right \}}$ ${\ displaystyle H \ neq \ left \ {0 \ right \}}$ : așa să fie $n$ ${\ displaystyle n}$ $n$ cel mai mic întreg pozitiv aparținând $H.$ ${\ displaystyle H}$ $H.$ ; din definiția multiplului unui element și din faptul că $H.$ ${\ displaystyle H}$ $H.$ este închis în ceea ce privește adăugarea, avem în primul rând asta $n\mathbb {Z}$ ${\ displaystyle n \ mathbb {Z}}$ ${\ displaystyle n \ mathbb {Z}}$ este un subset (subgrup) al $H.$ ${\ displaystyle H}$ $H.$ . De asemenea, dacă $h$ ${\ displaystyle h}$ $h$ este un element al $H.$ ${\ displaystyle H}$ $H.$ , efectuarea împărțirii lui $h$ ${\ displaystyle h}$ $h$ pentru $n$ ${\ displaystyle n}$ $n$ există două numere întregi (determinate în mod unic) $q$ ${\ displaystyle q}$ $q$ (coeficient) ed $r$ ${\ displaystyle r}$ $r$ (odihnă) relații satisfăcătoare $h=nq+r$ ${\ displaystyle h = nq + r}$ ${\ displaystyle h = nq + r}$ , $0\leq r<n$ ${\ displaystyle 0 \ leq r <n}$ ${\ displaystyle 0 \ leq r <n}$ . Dacă ar fi $r>0$ ${\ displaystyle r> 0}$ $r> 0$ , fiind asta $h$ ${\ displaystyle h}$ $h$ Și $n q$ ${\ displaystyle nq}$ ${\ displaystyle nq}$ apartine $H.$ ${\ displaystyle H}$ $H.$ , s-ar deduce că $r=h-nq$ ${\ displaystyle r = h-nq}$ ${\ displaystyle r = h-nq}$ aparține lui $H.$ ${\ displaystyle H}$ $H.$ (subgrup de $\mathbb {Z}$ ${\ displaystyle \ mathbb {Z}}$ $\ mathbb {Z}$ ipotetic), ceea ce generează o contradicție, deoarece pe de o parte există $r<n$ ${\ displaystyle r <n}$ ${\ displaystyle r <n}$ , dar pe de altă parte $n$ ${\ displaystyle n}$ $n$ este cel mai mic întreg pozitiv aparținând $H.$ ${\ displaystyle H}$ $H.$ . Prin urmare, nu poate fi avut decât $r=0$ ${\ displaystyle r = 0}$ $r = 0$ , adică $h=nq\in n\mathbb {Z}$ ${\ displaystyle h = nq \ in n \ mathbb {Z}}$ ${\ displaystyle h = nq \ in n \ mathbb {Z}}$ : rezultă că fiecare element al $H.$ ${\ displaystyle H}$ $H.$ este cuprins în $n\mathbb {Z}$ ${\ displaystyle n \ mathbb {Z}}$ ${\ displaystyle n \ mathbb {Z}}$ , asta este ceea ce $H.$ ${\ displaystyle H}$ $H.$ este un subset (subgrup) al $n\mathbb {Z}$ ${\ displaystyle n \ mathbb {Z}}$ ${\ displaystyle n \ mathbb {Z}}$ ; asa de $H=n\mathbb {Z}$ ${\ displaystyle H = n \ mathbb {Z}}$ ${\ displaystyle H = n \ mathbb {Z}}$ .

Generatoare

Același subiect în detaliu: Generatorii unui grup .

Un subset $S.$ ${\ displaystyle S}$ $S.$ din $G.$ ${\ displaystyle G}$ $G.$ este posibil să nu fie un subgrup: generează totuși un subgrup $H.$ ${\ displaystyle H}$ $H.$ , format din toate produsele elementelor din $S.$ ${\ displaystyle S}$ $S.$ și inversele lor. Acesta este cel mai mic subgrup al $G.$ ${\ displaystyle G}$ $G.$ conținând $S.$ ${\ displaystyle S}$ $S.$ .

De exemplu, setul $\{2\}$ ${\ displaystyle \ {2 \}}$ $\ {2 \}$ este setul $\{4,6\}$ ${\ displaystyle \ {4,6 \}}$ $\ {4,6 \}$ ambii sunt generatori ai subgrupului $2\mathbb {Z}$ ${\ displaystyle 2 \ mathbb {Z}}$ $2 {\ mathbb Z}$ din $\mathbb {Z}$ ${\ displaystyle \ mathbb {Z}}$ $\ mathbb Z$ format din toate numerele pare.

Ordinea unui articol

Un element $la$ ${\ displaystyle a}$ $la$ a unui grup multiplicativ $G.$ ${\ displaystyle G}$ $G.$ generează un subgrup, format din toate puterile sale întregi: $\ldots ,a^{-2},a^{-1},1_{G},a,a^{2},\ldots$ ${\ displaystyle \ ldots, a ^ {- 2}, a ^ {- 1}, 1_ {G}, a, a ^ {2}, \ ldots}$ ${\ displaystyle \ ldots, a ^ {- 2}, a ^ {- 1}, 1_ {G}, a, a ^ {2}, \ ldots}$ . Ordinea acestui grup este cel mai mic număr natural $n$ ${\ displaystyle n}$ $n$ pentru care cineva are $a^{n}=1_{G}$ ${\ displaystyle a ^ {n} = 1_ {G}}$ ${\ displaystyle a ^ {n} = 1_ {G}}$ (astfel de $n$ ${\ displaystyle n}$ $n$ poate fi și infinit, pentru orice eventualitate $a^{n}$ ${\ displaystyle a ^ {n}}$ $a ^ {n}$ este diferit de $1_{G}$ ${\ displaystyle 1_ {G}}$ $1_ {G}$ pentru fiecare $n$ ${\ displaystyle n}$ $n$ ), și este (prin definiție) ordinea elementului $la$ ${\ displaystyle a}$ $la$ . Rețineți că în grupurile aditive ordinea unui element $la$ ${\ displaystyle a}$ $la$ este definit ca cel mai mic întreg pozitiv $k$ ${\ displaystyle k}$ $k$ pe care o verifici $ka=0_{G}$ ${\ displaystyle ka = 0_ {G}}$ ${\ displaystyle ka = 0_ {G}}$ .

Cursuri secundare

Același subiect în detaliu: Clasa laterală .

Uneori poate fi util să identificați două elemente ale unui grup care diferă pentru un element al unui anumit subgrup. Această idee este formalizată în conceptul unei clase laterale : un subgrup $H.$ ${\ displaystyle H}$ $H.$ definește clasele din stânga și din dreapta, care pot fi gândite ca traduceri ale $H.$ ${\ displaystyle H}$ $H.$ pentru un element arbitrar $g$ ${\ displaystyle g}$ $g$ . Mai exact, clasele din stânga și din dreapta $H.$ ${\ displaystyle H}$ $H.$ conținând $g$ ${\ displaystyle g}$ $g$ sunt respectiv

gH={\big \{}gh\ |\ h\in H{\big \}},\quad Hg={\big \{}hg\ |\ h\in H{\big \}}.

gH={\big \{}gh\ |\ h\in H{\big \}},\quad Hg={\big \{}hg\ |\ h\in H{\big \}}.

gH={\big \{}gh\ |\ h\in H{\big \}},\quad Hg={\big \{}hg\ |\ h\in H{\big \}}.

Le classi laterali sinistre hanno tutte la stessa cardinalità e formano una partizione di $G$ ${\displaystyle G}$ $G$ . In altre parole, due classi laterali sinistre $g_{1}H$ $g_{1}H$ $g_{1}H$ e $g_{2}H$ $g_{2}H$ $g_{2}H$ coincidono oppure hanno intersezione vuota . Le classi coincidono se e solo se

g_{1}^{-1}g_{2}\in H

g_{1}^{-1}g_{2}\in H

g_{1}^{{-1}}g_{2}\in H

cioè se i due elementi "differiscono" per un elemento di $H$ ${\displaystyle H}$ $H$ . Analoghe considerazioni valgono per le classi laterali destre.

Ad esempio, il sottogruppo $3\mathbb {Z}$ $3\mathbb {Z}$ $3{\mathbb Z}$ di $\mathbb {Z}$ $\mathbb {Z}$ $\mathbb Z$ formato dagli elementi divisibili per $3$ ${\displaystyle 3}$ $3$ ha tre classi laterali, ovvero

3\mathbb {Z} ,\;3\mathbb {Z} +1,\;3\mathbb {Z} +2

3\mathbb {Z} ,\;3\mathbb {Z} +1,\;3\mathbb {Z} +2

3\mathbb {Z} ,\;3\mathbb {Z} +1,\;3\mathbb {Z} +2

,

che consistono, rispettivamente, negli interi congrui a , $1$ ${\displaystyle 1}$ $1$ , $2$ ${\displaystyle 2}$ $2$ modulo $3$ ${\displaystyle 3}$ $3$ . Più in generale, per ogni $n\in \mathbb {N}$ $n\in \mathbb {N}$ $n\in \mathbb{N}$ con $n\geq 1$ $n\geq 1$ $n\geq 1$ , il sottogruppo $n\mathbb {Z}$ $n\mathbb {Z}$ $n{\mathbb Z}$ ha $n$ ${\displaystyle n}$ $n$ classi laterali: $\quad n\mathbb {Z} +0,\,\ldots ,\,n\mathbb {Z} +(n-1)$ $\quad n\mathbb {Z} +0,\,\ldots ,\,n\mathbb {Z} +(n-1)$ $\quad n\mathbb {Z} +0,\,\ldots ,\,n\mathbb {Z} +(n-1)$ .

La cardinalità dell'insieme delle classi laterali destre e quella dell'insieme delle classi laterali sinistre di un sottogruppo $H$ ${\displaystyle H}$ $H$ di $G$ ${\displaystyle G}$ $G$ coincidono: tale cardinalità è l' indice di $H$ ${\displaystyle H}$ $H$ in $G$ ${\displaystyle G}$ $G$ .

Sottogruppo normale

Lo stesso argomento in dettaglio: Sottogruppo normale .

Le 16 simmetrie di un ottagono regolare formano un gruppo diedrale di ordine 16. Sono 8 rotazioni (prima riga) e 8 riflessioni (seconda riga). Le rotazioni formano un sottogruppo (ciclico)

H

{\displaystyle H}

H

di ordine 8. Le riflessioni non formano un sottogruppo, ma possono essere descritte come classe laterale

sH=Hs

{\displaystyle sH=Hs}

sH=Hs

di

H

{\displaystyle H}

H

, dove

s

{\displaystyle s}

s

è una qualsiasi riflessione. Il sottogruppo

H

{\displaystyle H}

H

ha due classi laterali

H

{\displaystyle H}

H

e

s H

{\displaystyle sH}

sH

ed è normale perché

sH=Hs

{\displaystyle sH=Hs}

sH=Hs

. ^[4] Questo sottogruppo ha solo due classi laterali:

H

{\displaystyle H}

H

stesso e

r H

{\displaystyle rH}

rH

, dove

r

{\displaystyle r}

r

è una qualsiasi riflessione.

In un gruppo non abeliano, le classi laterali destre e sinistre di $H$ ${\displaystyle H}$ $H$ possono non coincidere: è possibile cioè che esista $g\in G$ $g\in G$ $g\in G$ tale che si abbia

gH\neq Hg.

gH\neq Hg.

gH\neq Hg.

Quando $gH=Hg$ ${\displaystyle gH=Hg}$ $gH=Hg$ per ogni $g\in G$ $g\in G$ $g\in G$ , diciamo che $H$ ${\displaystyle H}$ $H$ è un sottogruppo normale di $G$ ${\displaystyle G}$ $G$ , e scriviamo

H\trianglelefteq G.

H\trianglelefteq G.

H\trianglelefteq G.

In tale caso si parla semplicemente di classi laterali.

In un gruppo abeliano tutti i sottogruppi sono normali.

Gruppi quoziente

Lo stesso argomento in dettaglio: Gruppo quoziente .

Le classi laterali di

N

{\displaystyle N}

N

formano una partizione del gruppo

G

{\displaystyle G}

G

. Considerando ciascuna classe come un singolo elemento, e moltiplicando due classi

a N

{\displaystyle aN}

aN

e

b N

{\displaystyle bN}

bN

come suggerito in figura, si ottiene il gruppo quoziente. Per fare ciò è necessario che il sottogruppo

N

{\displaystyle N}

N

sia normale.

I sottogruppi normali hanno molte buone proprietà: la più importante è la possibilità di definire una struttura di gruppo sull'insieme delle classi laterali, e quindi una nozione di gruppo quoziente .

Il gruppo quoziente di un sottogruppo normale $N$ ${\displaystyle N}$ $N$ in $G$ ${\displaystyle G}$ $G$ è l'insieme delle classi laterali

G/_{N}=\{gN\ |\ g\in G\}

G/_{N}=\{gN\ |\ g\in G\}

G/_{N}=\{gN\ |\ g\in G\}

con un'operazione ereditata da $G$ ${\displaystyle G}$ $G$ :

g_{1}N\cdot g_{2}N=(g_{1}\cdot g_{2})N.

g_{1}N\cdot g_{2}N=(g_{1}\cdot g_{2})N.

g_{1}N\cdot g_{2}N=(g_{1}\cdot g_{2})N.

Questa definizione risulta ben posta grazie all'ipotesi di normalità. La proiezione

\pi :G\to G/_{N}

\pi :G\to G/_{N}

\pi :G\to G/_{N}

che associa ad un elemento $g$ ${\displaystyle g}$ $g$ la sua classe laterale $g N$ ${\displaystyle gN}$ $gN$ risulta essere un omomorfismo. La classe $eN=N$ ${\displaystyle eN=N}$ $eN=N$ è l'identità del gruppo quoziente e l'inverso di $g N$ ${\displaystyle gN}$ $gN$ è semplicemente $g^{-1}N$ $g^{-1}N$ $g^{{-1}}N$ .

Ad esempio, il sottogruppo $n\mathbb {Z}$ $n\mathbb {Z}$ $n{\mathbb Z}$ di $\mathbb {Z}$ $\mathbb {Z}$ ${\mathbb Z}$ definisce un quoziente

\mathbb {Z} /_{n\mathbb {Z} }=\{n\mathbb {Z} ,n\mathbb {Z} +1,\ldots ,n\mathbb {Z} +n-1\}.

\mathbb {Z} /_{n\mathbb {Z} }=\{n\mathbb {Z} ,n\mathbb {Z} +1,\ldots ,n\mathbb {Z} +n-1\}.

{\mathbb Z}/_{{n{\mathbb {Z}}}}=\{n{\mathbb Z},n{\mathbb Z}+1,\ldots ,n{\mathbb Z}+n-1\}.

Questo quoziente ha $n$ ${\displaystyle n}$ $n$ elementi ed è il prototipo di gruppo ciclico . Usando il linguaggio dell' aritmetica modulare , questo gruppo può essere pensato come l'insieme delle classi di resto modulo $n$ ${\displaystyle n}$ $n$ :

\mathbb {Z} /_{n\mathbb {Z} }=\{0,1,\ldots ,n-1\}

\mathbb {Z} /_{n\mathbb {Z} }=\{0,1,\ldots ,n-1\}

{\mathbb Z}/_{{n{\mathbb {Z}}}}=\{0,1,\ldots ,n-1\}

e la proiezione

\pi :\mathbb {Z} \to \mathbb {Z} /_{n\mathbb {Z} }

\pi :\mathbb {Z} \to \mathbb {Z} /_{n\mathbb {Z} }

\pi :{\mathbb Z}\to {\mathbb Z}/_{{n{\mathbb {Z}}}}

è la mappa che manda l'intero $i$ ${\displaystyle i}$ $i$ nel resto della divisione di $i$ ${\displaystyle i}$ $i$ per $n$ ${\displaystyle n}$ $n$ .

Tipologie

Gruppi ciclici

Lo stesso argomento in dettaglio: Gruppo ciclico .

Le radici seste complesse dell'unità , ovvero i numeri complessi

z

{\displaystyle z}

z

tali che

z^{6}=1

z^{6}=1

z^{6}=1

, formano (con la moltiplicazione) un gruppo ciclico di ordine 6.

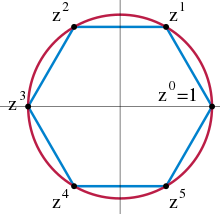
Un gruppo ciclico è un gruppo generato da un solo elemento $g$ ${\displaystyle g}$ $g$ . Il gruppo è determinato dall'ordine dell'elemento: se $g$ ${\displaystyle g}$ $g$ ha ordine finito $n$ ${\displaystyle n}$ $n$ , il gruppo consta solo degli elementi $e=g^{0},g^{1},\ldots ,g^{n-1}$ $e=g^{0},g^{1},\ldots ,g^{n-1}$ $e=g^{0},g^{1},\ldots ,g^{{n-1}}$ ed è quindi isomorfo a

\mathbb {Z} /_{n\mathbb {Z} }.

\mathbb {Z} /_{n\mathbb {Z} }.

{\mathbb Z}/_{{n{\mathbb Z}}}.

Questo gruppo è a volte indicato con il simbolo $C_{n}$ $C_{n}$ $C_n$ . Se l'elemento $g$ ${\displaystyle g}$ $g$ ha ordine infinito, il gruppo è invece isomorfo a $\mathbb {Z}$ $\mathbb {Z}$ $\mathbb Z$ .

I gruppi ciclici compaiono in moltissimi contesti. Un elemento $g$ ${\displaystyle g}$ $g$ di un gruppo arbitrario $G$ ${\displaystyle G}$ $G$ genera sempre un sottogruppo ciclico: per questo motivo, ogni gruppo contiene numerosi sottogruppi ciclici.

Gruppi abeliani

Lo stesso argomento in dettaglio: Gruppo abeliano .

Un gruppo abeliano è un gruppo la cui operazione è commutativa . Sono gruppi abeliani tutti i gruppi numerici considerati sopra e anche tutti i gruppi ciclici. Il più piccolo gruppo abeliano che non fa parte di queste categorie è il gruppo di Klein , che contiene 4 elementi.

Gruppi diedrali

Lo stesso argomento in dettaglio: Gruppo diedrale .

Il gruppo diedrale $D_{2n}$ $D_{2n}$ $D_{{2n}}$ è il gruppo di simmetria di un poligono regolare con $n$ ${\displaystyle n}$ $n$ lati. Il gruppo contiene $2n$ ${\displaystyle 2n}$ $2n$ elementi e non è abeliano (se $n>1$ ${\displaystyle n>1}$ $n>1$ ): infatti se $s$ ${\displaystyle s}$ $s$ indica una riflessione rispetto ad un asse e $r$ ${\displaystyle r}$ $r$ una rotazione di $2\pi /n$ $2\pi /n$ $2\pi /n$ gradi vale la relazione $r^{k}s=sr^{n-k}$ $r^{k}s=sr^{nk}$ $r^{k}s=sr^{{n-k}}$ .

Gruppi simmetrici

Lo stesso argomento in dettaglio: Gruppo simmetrico .

Il gruppo simmetrico $S(X)$ ${\displaystyle S(X)}$ $S(X)$ di un insieme è definito come l'insieme delle permutazioni dell'insieme $X$ ${\displaystyle X}$ $X$ . Quando $X$ ${\displaystyle X}$ $X$ consta di $n$ ${\displaystyle n}$ $n$ elementi, il gruppo simmetrico ne contiene $n!$ ${\displaystyle n!}$ $n!$ ed è generalmente indicato con il simbolo $S_{n}$ $S_{n}$ $S_{n}$ . Questo gruppo non è mai abeliano per $n>2$ ${\displaystyle n>2}$ $n>2$ .

Gruppi finiti

Lo stesso argomento in dettaglio: Gruppo finito .

Un gruppo finito è un gruppo che ha ordine $n$ ${\displaystyle n}$ $n$ finito. Vi sono svariati tipi di gruppi finiti: tra questi, i gruppi ciclici $C_{n}$ $C_{n}$ $C_n$ , i diedrali $D_{2n}$ $D_{2n}$ $D_{{2n}}$ ed i simmetrici $S_{n}$ $S_{n}$ $S_{n}$ .

Gruppi semplici

Lo stesso argomento in dettaglio: Gruppo semplice .

Un gruppo semplice è un gruppo $G$ ${\displaystyle G}$ $G$ che non contiene sottogruppi normali, eccetto il sottogruppo banale $\{e\}$ $\{e\}$ $\{e\}$ e se stesso $G$ ${\displaystyle G}$ $G$ . Un gruppo semplice non ha quozienti (perché i quozienti si fanno solo con i sottogruppi normali!) ed è quindi in un certo senso un "blocco primario" con cui poter costruire gruppi più complessi.

Ad esempio, il gruppo ciclico $C_{n}$ $C_{n}$ $C_n$ è semplice se e solo se $n$ ${\displaystyle n}$ $n$ è primo .

Costruzioni

Prodotto diretto

Lo stesso argomento in dettaglio: Prodotto diretto .

Il prodotto diretto di due gruppi $G$ ${\displaystyle G}$ $G$ e $H$ ${\displaystyle H}$ $H$ è il prodotto cartesiano

G\times H

G\times H

G\times H

munito di un'operazione che riprende indipendentemente le due operazioni di $G$ ${\displaystyle G}$ $G$ e $H$ ${\displaystyle H}$ $H$ .

I vettori del piano centrati in un punto fissato, muniti dell'usuale somma fra vettori, formano un gruppo. Dopo aver fissato un sistema di coordinate nel piano, tale gruppo risulta essere

\mathbb {R} ^{2}=\mathbb {R} \times \mathbb {R}

\mathbb {R} ^{2}=\mathbb {R} \times \mathbb {R}

{\mathbb R}^{2}={\mathbb R}\times {\mathbb R}

. Analogamente, i vettori nello spazio centrati nell'origine formano il gruppo

\mathbb {R} ^{3}

\mathbb {R} ^{3}

\mathbb {R} ^{3}

.

L'ordine del prodotto è il prodotto degli ordini, quindi il prodotto di due gruppi finiti è anch'esso finito. Inoltre, il prodotto di due gruppi abeliani è abeliano. Quindi un prodotto di gruppi ciclici come ad esempio

\mathbb {Z} /_{2\mathbb {Z} }\times \mathbb {Z} /_{2\mathbb {Z} }

\mathbb {Z} /_{2\mathbb {Z} }\times \mathbb {Z} /_{2\mathbb {Z} }

{\mathbb Z}/_{{2{\mathbb Z}}}\times {\mathbb Z}/_{{2{\mathbb Z}}}

è abeliano di ordine 4. Questo gruppo, noto come gruppo di Klein , è il più piccolo gruppo abeliano non ciclico.

Il prodotto di $n$ ${\displaystyle n}$ $n$ copie di $\mathbb {R}$ $\mathbb {R}$ $\mathbb R$

\mathbb {R} ^{n}=\mathbb {R} \times \ldots \times \mathbb {R}

\mathbb {R} ^{n}=\mathbb {R} \times \ldots \times \mathbb {R}

{\mathbb R}^{n}={\mathbb R}\times \ldots \times {\mathbb R}

è l'usuale spazio euclideo con $n$ ${\displaystyle n}$ $n$ coordinate, munito della somma fra vettori.

Prodotto libero

Il prodotto libero di due gruppi $G$ ${\displaystyle G}$ $G$ e $H$ ${\displaystyle H}$ $H$ è il gruppo

G*H

{\displaystyle G*H}

G*H

ottenuto prendendo tutte le parole con lettere in $G$ ${\displaystyle G}$ $G$ e $H$ ${\displaystyle H}$ $H$ a meno di una semplice relazione di equivalenza che permette l'inserimento (o l'eliminazione) di sottoparole del tipo $u^{-1}u$ $u^{-1}u$ $u^{{-1}}u$ .

A differenza del prodotto diretto, il prodotto libero di due gruppi non banali non è mai finito, né abeliano. Il prodotto libero di $n$ ${\displaystyle n}$ $n$ copie di $\mathbb {Z}$ $\mathbb {Z}$ $\mathbb Z$ :

\mathbb {Z} *\ldots *\mathbb {Z}

\mathbb {Z} *\ldots *\mathbb {Z}

{\mathbb Z}*\ldots *{\mathbb Z}

è detto gruppo libero .

Prodotto semidiretto

Lo stesso argomento in dettaglio: Prodotto semidiretto .

Il prodotto semidiretto di due gruppi $G$ ${\displaystyle G}$ $G$ e $H$ ${\displaystyle H}$ $H$ è un'operazione che generalizza il prodotto diretto: l'insieme è sempre il prodotto cartesiano $G\times H$ $G\times H$ $G\times H$ , ma l'operazione di gruppo è definita in modo diverso. Ad esempio, il gruppo diedrale $D_{2n}$ $D_{2n}$ $D_{{2n}}$ , che consta di $2n$ ${\displaystyle 2n}$ $2n$ elementi, può essere descritto come prodotto semidiretto di due gruppi ciclici di ordine 2 e $n$ ${\displaystyle n}$ $n$ . Si scrive:

\mathbb {Z} _{n}\rtimes _{\psi }\mathbb {Z} _{2}.

\mathbb {Z} _{n}\rtimes _{\psi }\mathbb {Z} _{2}.

{\mathbb {Z}}_{n}\rtimes _{\psi }{\mathbb {Z}}_{2}.

Il simbolo $\psi$ $\psi$ $\psi$ indica un particolare omomorfismo utile a definire di quale prodotto semidiretto si tratta.

Presentazioni

Lo stesso argomento in dettaglio: Presentazione di un gruppo .

Combinando le nozioni di generatore e di gruppo quoziente è possibile ottenere una descrizione di un generico gruppo tramite una sua presentazione . Una presentazione è una scrittura del tipo

\langle a,b,c\ |\ a^{2}b,ab^{2}c,ac^{2}b\rangle .

\langle a,b,c\ |\ a^{2}b,ab^{2}c,ac^{2}b\rangle .

\langle a,b,c\ |\ a^{2}b,ab^{2}c,ac^{2}b\rangle .

I termini a sinistra della sbarretta sono i generatori , mentre le parole a destra sono le relazioni . Una permutazione determina effettivamente un gruppo, ottenuto come quoziente del gruppo libero su tre elementi $a, b, c$ ${\displaystyle a,b,c}$ $a,b,c$ per il più piccolo sottogruppo normale che contiene le relazioni. Ad esempio, le presentazioni seguenti indicano rispettivamente un gruppo ciclico, diedrale, ed il gruppo di Klein:

\langle a\ |\ a^{n}\rangle ,\quad \langle r,s\ |\ r^{n},s^{2},srsr\rangle ,\quad \langle a,b\ |\ a^{2},b^{2},aba^{-1}b^{-1}\rangle .

\langle a\ |\ a^{n}\rangle ,\quad \langle r,s\ |\ r^{n},s^{2},srsr\rangle ,\quad \langle a,b\ |\ a^{2},b^{2},aba^{-1}b^{-1}\rangle .

\langle a\ |\ a^{n}\rangle ,\quad \langle r,s\ |\ r^{n},s^{2},srsr\rangle ,\quad \langle a,b\ |\ a^{2},b^{2},aba^{{-1}}b^{{-1}}\rangle .

La prima presentazione indica che il gruppo ha un solo generatore di ordine $n$ ${\displaystyle n}$ $n$ , cioè vale $a^{n}=1$ $a^{n}=1$ $a^{n}=1$ . Nell'ultima presentazione, la parola $aba^{-1}b^{-1}$ $aba^{-1}b^{-1}$ $aba^{{-1}}b^{{-1}}$ fornisce la relazione $aba^{-1}b^{-1}=1$ $aba^{-1}b^{-1}=1$ $aba^{{-1}}b^{{-1}}=1$ ; altrimenti detto, i due elementi commutano: $ab=ba$ ${\displaystyle ab=ba}$ $ab=ba$ . Questa parola è detta commutatore e viene spesso indicata con il simbolo $[a,b]$ ${\displaystyle [a,b]}$ $[a,b]$ .

Teoremi

Teorema di Lagrange

Lo stesso argomento in dettaglio: Teorema di Lagrange (teoria dei gruppi) .

In presenza di un gruppo finito $G$ ${\displaystyle G}$ $G$ , l'ordine $o(g)$ ${\displaystyle o(g)}$ $o(g)$ di un qualsiasi elemento $g$ ${\displaystyle g}$ $g$ è un numero finito che divide l'ordine $|G|$ ${\displaystyle |G|}$ $|G|$ di $G$ ${\displaystyle G}$ $G$ . Questo fatto, noto come teorema di Lagrange , pur essendo di immediata dimostrazione, ha come conseguenza vari fatti non ovvi.

Una delle prime conseguenze è il fatto che un gruppo di ordine primo $p$ ${\displaystyle p}$ $p$ è necessariamente un gruppo ciclico.

Questo risultato può inoltre essere usato per dimostrare agevolmente il piccolo teorema di Fermat .

Teoremi di isomorfismo

Lo stesso argomento in dettaglio: Teoremi di isomorfismo .

Vi sono tre teoremi di isomorfismo che asseriscono che, in condizioni molto generali, alcuni gruppi costruiti in modo diverso risultano in realtà isomorfi. Tutti e tre i teoremi fanno uso della nozione di gruppo quoziente. Il primo, ampiamente usato anche in algebra lineare per gli spazi vettoriali , asserisce che in presenza di un omomorfismo di gruppi

f:G\to H

f:G\to H

f:G\to H

il nucleo

\operatorname {Ker} f=\{g\in G\ |f(g)=e\}

\operatorname {Ker} f=\{g\in G\ |f(g)=e\}

\operatorname {Ker}f=\{g\in G\ |f(g)=e\}

è sempre un sottogruppo normale e l'omomorfismo $f$ ${\displaystyle f}$ $f$ induce un isomorfismo

G/\operatorname {Ker} f\cong \operatorname {Im} f

G/\operatorname {Ker} f\cong \operatorname {Im} f

G/\operatorname {Ker}f\cong \operatorname {Im}f

dove il termine a destra è l' immagine di $f$ ${\displaystyle f}$ $f$ . ^[5]

Teorema di Cayley

Lo stesso argomento in dettaglio: Teorema di Cayley .

Il teorema di Cayley asserisce che qualsiasi gruppo può essere visto sottogruppo di un gruppo simmetrico . Se il gruppo è finito, anche il gruppo simmetrico in questione lo è. Ad esempio, un gruppo ciclico può essere interpretato come un gruppo di permutazioni cicliche, un gruppo diedrale come un gruppo di particolari permutazioni dei vertici di un poligono, etc.

Teoremi di Sylow

Lo stesso argomento in dettaglio: Teoremi di Sylow .

Sia $G$ ${\displaystyle G}$ $G$ un gruppo finito. Il teorema fornisce una condizione necessaria per l'esistenza di sottogruppi di ordine fissato in $G$ ${\displaystyle G}$ $G$ : ad esempio, se $G$ ${\displaystyle G}$ $G$ ha ordine 20 allora non ci sono sottogruppi di ordine 3, perché 3 non divide 20.

I teoremi di Sylow forniscono delle condizioni sufficienti per l'esistenza di sottogruppi di ordine fissato. Il primo teorema di Sylow asserisce che per ogni potenza $p^{r}$ $p^{r}$ $p^{r}$ di un numero primo $p$ ${\displaystyle p}$ $p$ che divida l'ordine di $G$ ${\displaystyle G}$ $G$ esiste almeno un sottogruppo di $G$ ${\displaystyle G}$ $G$ con questo ordine. Gli altri teoremi di Sylow forniscono delle informazioni più dettagliate nel caso in cui l'esponente $r$ ${\displaystyle r}$ $r$ sia il più grande possibile.

Come conseguenza, se $G$ ${\displaystyle G}$ $G$ ha ordine 20 allora contiene sicuramente dei sottogruppi di ordine 2, 4 e 5. Il teorema non si estende però a tutti i divisori: ad esempio, un tale gruppo $G$ ${\displaystyle G}$ $G$ potrebbe non contenere un sottogruppo di ordine 10.

Classificazioni

Non esistono tabelle generali che descrivano in modo esaustivo tutti i gruppi possibili. Usando strumenti semplici, quali ad esempio le presentazioni , è estremamente facile costruire gruppi molto complicati, la maggior parte dei quali non ha un "nome" come $D_{2n}$ $D_{2n}$ $D_{{2n}}$ o $S_{n}$ $S_{n}$ $S_{n}$ . Esistono però delle classificazioni parziali in alcuni ambiti.

Gruppi abeliani finitamente generati

I gruppi abeliani finitamente generati sono classificati. Ciascun gruppo è del tipo

\mathbb {Z} ^{n}\times \mathbb {Z} /_{k_{1}\mathbb {Z} }\times \cdots \times \mathbb {Z} _{k_{u}\mathbb {Z} }.

\mathbb {Z} ^{n}\times \mathbb {Z} /_{k_{1}\mathbb {Z} }\times \cdots \times \mathbb {Z} _{k_{u}\mathbb {Z} }.

{\mathbb {Z}}^{n}\times {\mathbb {Z}}/_{{k_{1}{\mathbb Z}}}\times \cdots \times {\mathbb {Z}}_{{k_{u}{\mathbb Z}}}.

Un gruppo abeliano finitamente generato è quindi un prodotto di gruppi ciclici. Questa scrittura non è però unica: ad esempio, i gruppi seguenti sono isomorfi

\mathbb {Z} /_{2\mathbb {Z} }\times \mathbb {Z} /_{3\mathbb {Z} }\cong \mathbb {Z} /_{6\mathbb {Z} }.

\mathbb {Z} /_{2\mathbb {Z} }\times \mathbb {Z} /_{3\mathbb {Z} }\cong \mathbb {Z} /_{6\mathbb {Z} }.

{\mathbb Z}/_{{2{\mathbb Z}}}\times {\mathbb Z}/_{{3{\mathbb Z}}}\cong {\mathbb Z}/_{{6{\mathbb Z}}}.

La scrittura è però unica se si richiede che ciascun $k_{i}$ $k_{i}$ $k_{i}$ divida il successivo $k_{i+1}$ $k_{i+1}$ $k_{{i+1}}$ . Si noti che $\mathbb {Q}$ $\mathbb {Q}$ ${\mathbb Q}$ e $\mathbb {R}$ $\mathbb {R}$ $\mathbb R$ non sono finitamente generati.

Gruppi semplici finiti

Lo stesso argomento in dettaglio: Classificazione dei gruppi semplici finiti .

Non esiste una classificazione di tutti i gruppi finiti. D'altra parte, ogni gruppo finito può essere "decomposto" (in un certo senso) in gruppi semplici , e tali gruppi sono stati effettivamente classificati.

Ci sono 4 classi infinite di gruppi semplici finiti ( ciclici , alternanti , lineari , di tipo Lie ) più 26 gruppi sporadici . Il più grosso di questi contiene circa $8\times 10^{53}$ $8\times 10^{53}$ $8\times 10^{{53}}$ elementi!

Gruppi piccoli

Lo stesso argomento in dettaglio: Tavola dei gruppi piccoli .

Esistono tavole che mostrano tutti i gruppi aventi ordine $i=1,2,3,$ ${\displaystyle i=1,2,3,}$ $i=1,2,3,$ ... fino ad un certo $n$ ${\displaystyle n}$ $n$ . Per ogni $i$ ${\displaystyle i}$ $i$ vi è almeno un gruppo di ordine $i$ ${\displaystyle i}$ $i$ , il gruppo ciclico $C_{i}$ $C_{i}$ $C_{i}$ . Il primo gruppo non ciclico è il gruppo di Klein $C_{2}\times C_{2}$ $C_{2}\times C_{2}$ $C_{2}\times C_{2}$ , che ha ordine 4. Il primo gruppo non abeliano è $S_{3}$ $S_{3}$ $S_{3}$ , che ha ordine 6, seguito da $D_{8}$ $D_{8}$ $D_{8}$ ed il gruppo dei quaternioni $Q_{8}$ $Q_{8}$ $Q_{8}$ , aventi ordine 8.

Applicazioni

Teoria di Galois

Lo stesso argomento in dettaglio: Teoria di Galois .

La teoria di Galois nasce come strumento per studiare le radici di un polinomio . Le radici, anche complesse, di un polinomio di secondo grado $ax^{2}+bx+c$ $ax^{2}+bx+c$ $ax^{2}+bx+c$ sono individuate dalla nota formula

x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.

x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.

x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.

Analoghe formule per risolvere le equazioni di terzo e quarto grado erano già note nel Cinquecento. Secondo il teorema di Abel-Ruffini , non ci sono però formule di questo tipo per equazioni di grado 5 o superiore. Usando il linguaggio della teoria di Galois, questo problema può essere affrontato nel modo seguente: le soluzioni di un dato polinomio possono essere espresse con formule di questo tipo (che usano le quattro operazioni ei radicali) se e solo se il relativo gruppo di Galois è un gruppo risolubile . I gruppi simmetrici $S_{2},S_{3},S_{4}$ $S_{2},S_{3},S_{4}$ $S_{2},S_{3},S_{4}$ sono risolubili, ma $S_{5}$ $S_{5}$ $S_{5}$ no: questo implica che non vi sia una formula generale per le equazioni di quinto grado.

La teoria di Galois si applica anche a problemi di costruzione con riga e compasso . Ad esempio, può essere usata per capire quali poligoni regolari possono essere costruiti e per dimostrare l'impossibilità della quadratura del cerchio o della trisezione di un angolo .

Aritmetica modulare

Lo stesso argomento in dettaglio: Aritmetica modulare .

L' aritmetica modulare è strettamente connessa con la teoria dei gruppi ciclici. Tramite questa connessione, è possibile dimostrare vari fatti aritmetici non banali usando semplici strumenti della teoria dei gruppi. Il collegamento fra le due teorie è sancito dal fatto seguente: i numeri interi considerati a meno di congruenza rispetto ad un intero fissato $n$ ${\displaystyle n}$ $n$ formano con l'addizione un gruppo ciclico $C_{n}$ $C_{n}$ $C_n$ di ordine $n$ ${\displaystyle n}$ $n$ .

Ad esempio, tramite questa corrispondenza il piccolo teorema di Fermat può essere dedotto dal fatto che, similmente a quanto accade per i numeri razionali o reali, se $n$ ${\displaystyle n}$ $n$ è primo si può togliere lo zero da $C_{n}$ $C_{n}$ $C_n$ e ottenere un gruppo anche con la moltiplicazione. ^[6]

Analogamente il fatto che il prodotto di $C_{a}$ $C_{a}$ $C_{a}$ e $C_{b}$ $C_{b}$ $C_{b}$ sia isomorfo a $C_{ab}$ $C_{ab}$ $C_{{ab}}$ se e solo $a$ ${\displaystyle a}$ $a$ e $b$ ${\displaystyle b}$ $b$ sono coprimi è un enunciato moderno equivalente al teorema cinese del resto , già noto nel III secolo .

Gruppi di simmetria

Lo stesso argomento in dettaglio: Gruppo di simmetria .

L' ottaedro ha 24 simmetrie rotatorie: queste formano il gruppo

S_{4}

S_{4}

S_{4}

. Il cubo , duale dell'ottaedro, ha lo stesso gruppo di simmetria.

Il dodecaedro ha 60 simmetrie rotatorie: queste formano il gruppo alternante

A_{5}

A_{5}

A_{5}

. Idem per il suo duale, l' icosaedro .

Le simmetrie di un oggetto geometrico formano sempre un gruppo. Ad esempio, le simmetrie di un poligono regolare formano un gruppo diedrale $D_{2n}$ $D_{2n}$ $D_{{2n}}$ ; le simmetrie di un tetraedro regolare formano invece un gruppo isomorfo al gruppo simmetrico $S_{4}$ $S_{4}$ $S_{4}$ su quattro elementi: ogni permutazione dei suoi 4 vertici è realizzata da una simmetria.

Per un oggetto nel piano e nello spazio, le simmetrie possono essere di vario tipo: traslazioni , rotazioni , riflessioni e operazioni più complicate ottenute componendo queste, come ad esempio le glissoriflessioni . Alcune di queste simmetrie (come le rotazioni e le traslazioni) preservano l' orientazione del piano (o dello spazio), mentre altre (come le riflessioni) la invertono. Se sono presenti simmetrie di entrambi i tipi, quelle che preservano l'orientazione formano sempre un sottogruppo di indice 2. Ad esempio, per un poligono regolare questo sottogruppo è un gruppo ciclico $C_{n}$ $C_{n}$ $C_n$ dentro $D_{2n}$ $D_{2n}$ $D_{{2n}}$ , mentre per il tetraedro è il gruppo alternante $A_{4}$ $A_{4}$ $A_{4}$ dentro $S_{4}$ $S_{4}$ $S_{4}$ .

Il gruppo di simmetria di un poliedro è sempre finito. Le simmetrie di un poliedro che preservano l'orientazione sono tutte rotazioni intorno a qualche asse. Nonostante la grande varietà di poliedri esistenti, vi sono però pochi gruppi di simmetria possibili. I gruppi di rotazioni possibili sono i seguenti:

C_{n},D_{n},A_{4},S_{4},A_{5}\,\!

C_{n},D_{n},A_{4},S_{4},A_{5}\,\!

C_{n},D_{n},A_{4},S_{4},A_{5}\,\!

I primi due tipi di gruppi sono realizzati da piramidi e prismi (e più generalmente dei prismatoidi ). I tre gruppi $A_{4},S_{4}$ $A_{4},S_{4}$ $A_{4},S_{4}$ e $A_{5}$ $A_{5}$ $A_{5}$ sono realizzati dai solidi platonici .

Gruppo fondamentale

Lo stesso argomento in dettaglio: Gruppo fondamentale .

Il gruppo fondamentale dello spazio ottenuto rimuovendo un punto dal piano è isomorfo a

\mathbb {Z}

\mathbb {Z}

\mathbb Z

. La curva che fa due giri mostrata in figura corrisponde al valore intero "2".

Il gruppo fondamentale di un toro è

\mathbb {Z} \times \mathbb {Z}

\mathbb {Z} \times \mathbb {Z}

{\mathbb Z}\times {\mathbb Z}

: i due generatori sono mostrati in figura.

In topologia , il "numero di buchi" di uno spazio topologico $X$ ${\displaystyle X}$ $X$ è codificato efficientemente dal suo gruppo fondamentale , generalmente indicato con il simbolo $\pi _{1}(X)$ $\pi _{1}(X)$ $\pi _{1}(X)$ . Il gruppo fondamentale è costruito prendendo tutte le curve chiuse contenute nello spazio (che partono e arrivano da un fissato punto base ). Due curve che possono essere ottenute l'una dall'altra tramite uno spostamento continuo (detto omotopia ) sono considerate equivalenti. Due curve possono essere composte tramite concatenamento ed il risultato è effettivamente un gruppo.

Il gruppo fondamentale è uno dei concetti più importanti in topologia, ed è uno dei primi strumenti usati per distinguere spazi topologici distinti (ovvero non omeomorfi ). Ad uno spazio topologico possono essere associati vari altri gruppi, come i più generali gruppi di omotopia o di omologia .

La circonferenza unitaria nel piano complesso con l'operazione di moltiplicazione (fra numeri complessi) forma un gruppo di Lie e quindi in particolare un gruppo topologico . Si tratta di una varietà differenziabile : ogni punto ha un intorno (qui disegnato in rosso) omeomorfo ad un intervallo aperto della retta reale.

Estensioni

Anelli, campi, spazi vettoriali

Lo stesso argomento in dettaglio: Anello (algebra) , Campo (matematica) e Spazio vettoriale .

La nozione di gruppo può essere estesa aggiungendo all'operazione di gruppo un'altra operazione che soddisfi dei nuovi assiomi. Ad esempio, un anello è un insieme $A$ ${\displaystyle A}$ $A$ dotato di due operazioni, generalmente indicate con i simboli $+$ ${\displaystyle +}$ $+$ e $\times$ $\times$ $\times$ , che soddisfano alcune proprietà. Queste proprietà richiedono in particolare che $(A,+)$ ${\displaystyle (A,+)}$ $(A,+)$ sia un gruppo abeliano. L'esempio fondamentale di anello è $\mathbb {Z}$ $\mathbb {Z}$ $\mathbb Z$ con le usuali operazioni di addizione e moltiplicazione.

Quando la moltiplicazione è commutativa e ammette un'inversa per tutti gli elementi diversi da zero, l'anello è detto campo . Gli esempi fondamentali di campo sono $\mathbb {Q}$ $\mathbb {Q}$ ${\mathbb Q}$ , $\mathbb {R}$ $\mathbb {R}$ $\mathbb {R}$ e $\mathbb {C}$ $\mathbb {C}$ $\mathbb C$ . Gli interi non formano però un campo.

Una struttura un po' più complessa è quella di spazio vettoriale . Uno spazio vettoriale $V$ ${\displaystyle V}$ $V$ è un gruppo abeliano dotato di un'altra operazione chiamata "prodotto per scalare". Gli spazi vettoriali vengono studiati nell'ambito dell' algebra lineare .

Gruppi topologici e di Lie

Lo stesso argomento in dettaglio: Gruppo topologico e Gruppo di Lie .

La nozione di gruppo può essere arricchita anche usando alcuni strumenti propri della topologia . Un gruppo topologico è un gruppo che è anche uno spazio topologico , che soddisfi delle naturali relazioni di compatibilità fra le due nozioni (l'operazione interna e la topologia). Ad esempio, $\mathbb {Z}$ $\mathbb {Z}$ $\mathbb Z$ , $\mathbb {Q}$ $\mathbb {Q}$ ${\mathbb Q}$ , $\mathbb {R}$ $\mathbb {R}$ $\mathbb {R}$ e $\mathbb {C}$ $\mathbb {C}$ $\mathbb C$ muniti dell'usuale topologia euclidea sono gruppi topologici. ^[7]

Se il gruppo topologico ha anche una struttura di varietà differenziabile (sempre compatibile con l'operazione del gruppo), allora è un gruppo di Lie . I gruppi di Lie hanno un ruolo molto importante nella geometria del XX secolo. Esempi di gruppi di Lie sono:

\mathbb {R} ^{n},\mathbb {C} ^{n},S^{1},\operatorname {O} (n),\operatorname {GL} (n,\mathbb {R} )

\mathbb {R} ^{n},\mathbb {C} ^{n},S^{1},\operatorname {O} (n),\operatorname {GL} (n,\mathbb {R} )

{\mathbb R}^{n},{\mathbb C}^{n},S^{1},\operatorname O(n),\operatorname {GL}(n,{\mathbb R})

dove $S^{1}$ $S^{1}$ $S^{1}$ è la circonferenza unitaria del piano complesso , O è il gruppo ortogonale e GL è il gruppo generale lineare .

Semigruppi, monoidi

Eliminando alcuni dei tre assiomi è possibile definire varie strutture algebriche che generalizzano la nozione di gruppo. Tali strutture, riassunte nella tabella a fianco, sono però molto meno utilizzate. Ad esempio, i numeri naturali $\mathbb {N}$ $\mathbb {N}$ $\mathbb N$ formano un monoide ei numeri pari $2\mathbb {Z}$ $2\mathbb {Z}$ $2{\mathbb Z}$ formano un semigruppo , entrambi con la somma. Le nozioni di loop , quasigruppo e magma sono meno frequenti perché è poco usuale trovare operazioni non associative.

Si può inoltre sostituire l'operazione di gruppo con una funzione parziale , definita solo per alcune coppie di elementi. Ad esempio, le matrici invertibili (di grandezza arbitraria) con lamoltiplicazione formano un gruppoide : quando possono essere moltiplicate fra loro, tutte e tre gli assiomi di gruppo sono soddisfatti.

Note

^ Hoffman, Kunze , Pag. 82 .
^ Hoffman, Kunze , Pag. 83 .
^ Una condizione equivalente consiste nel richiedere che esista un'inversa $g:H\to G$ $g:H\to G$ $g:H\to G$ , tale che componendo le due funzioni (in entrambi i modi possibili) si ottenga l' identità di $G$ ${\displaystyle G}$ $G$ o $H$ ${\displaystyle H}$ $H$ , rispettivamente.
^ Più in generale, ogni sottogruppo di indice 2 è normale. Un sottogruppo di indice 3 può però essere non normale!
^ Si noti che l'immagine, a differenza del nucleo, non è necessariamente un sottogruppo normale.
^ In altre parole, $C_{n}$ $C_{n}$ $C_n$ in questo caso è un campo . Quando $n$ ${\displaystyle n}$ $n$ non è primo le classi di resto formano soltanto un anello .
^ La topologia su $\mathbb {Z}$ $\mathbb {Z}$ ${\mathbb Z}$ risulta essere discreta . Quella su $\mathbb {Q}$ $\mathbb {Q}$ ${\mathbb Q}$ no.

Bibliografia

Michael Artin , Algebra , Bollati Boringhieri, 1997, ISBN 88-339-5586-9 .
Israel Nathan Herstein , Algebra , Editori Riuniti, 2003, ISBN 88-359-5479-7 .
Serge Lang , Algebra lineare , Bollati Boringhieri, 1970, ISBN 88-339-5035-2 .
( EN ) Kenneth Hoffman, Ray Kunze, Linear Algebra , 2ª ed., Englewood Cliffs, New Jersey, Prentice - Hall, inc., 1971, ISBN 0-13-536821-9 .
George W. Mackey , Gruppi , Enciclopedia del Novecento (1978), Istituto dell'Enciclopedia italiana Treccani

Voci correlate

Altri progetti

Wikizionario contiene il lemma di dizionario « gruppo »
Wikimedia Commons contiene immagini o altri file su gruppo

Collegamenti esterni

( EN ) Gruppo , su Enciclopedia Britannica , Encyclopædia Britannica, Inc.

Controllo di autorità	Thesaurus BNCF 5497 · GND ( DE ) 4022379-6

Portale Matematica : accedi alle voci di Wikipedia che trattano di matematica

[1] Hoffman, Kunze , Pag. 82 .

[2] Hoffman, Kunze , Pag. 83 .

[3] Una condizione equivalente consiste nel richiedere che esista un'inversa $g:H\to G$ $g:H\to G$ $g:H\to G$ , tale che componendo le due funzioni (in entrambi i modi possibili) si ottenga l' identità di $G$ ${\displaystyle G}$ $G$ o $H$ ${\displaystyle H}$ $H$ , rispettivamente.

[4] Più in generale, ogni sottogruppo di indice 2 è normale. Un sottogruppo di indice 3 può però essere non normale!

[5] Si noti che l'immagine, a differenza del nucleo, non è necessariamente un sottogruppo normale.

[6] In altre parole, $C_{n}$ $C_{n}$ $C_n$ in questo caso è un campo . Quando $n$ ${\displaystyle n}$ $n$ non è primo le classi di resto formano soltanto un anello .

[7] La topologia su $\mathbb {Z}$ $\mathbb {Z}$ ${\mathbb Z}$ risulta essere discreta . Quella su $\mathbb {Q}$ $\mathbb {Q}$ ${\mathbb Q}$ no.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

	Totalità	Associatività	Neutro	Inverso
Generalizzazioni della nozione di gruppo
Gruppo	sì	sì	sì	sì
Monoide	sì	sì	sì	no
Semigruppo	sì	sì	no	no
Loop	sì	no	sì	sì
Quasigruppo	sì	no	no	sì
Magma	sì	no	no	no
Gruppoide	no	sì	sì	sì
Categoria	no	sì	sì	no