Strângere de mână (matematică)
În teoria graficelor, o ramură a matematicii, lema strângerii de mână este afirmația că fiecare grafic nedirecționat a terminat un număr par de vârfuri cu grad impar (numărul de muchii care ating vârful). În termeni mai colocviali, într-un grup de oameni dintre care unii dau din mână, un număr par de oameni trebuie să fi dat mâna unui număr impar de alte persoane. Vârfurile de grad impar dintr-un grafic sunt uneori numite noduri vârfuri impare sau impare; în această terminologie, lema de strângere de mână poate fi reformulată ca afirmația că fiecare grafic are un număr par de noduri impare.
Lema de strângere de mână este o consecință a formulei sumei de grade (uneori numită la rândul ei lema de strângere de mână),
pentru un grafic cu set de vârfuri V și set de margini E. Ambele rezultate au fost dovedite de Leonhard Euler (1736) în celebrul său articol despre cele șapte poduri din Königsberg, care a început studiul teoriei graficelor.
Alte aplicații includ demonstrația că pentru unele structuri combinatorii, numărul structurilor este întotdeauna egal și asistență cu dovezile lemei Sperner și „problema alpinismului” (în italiană „alpinism”). Clasa de complexitate PPA încapsulează dificultatea de a găsi un al doilea vârf impar, dat fiind unul dintre acești vârfuri într-un grafic larg definit implicit.
Proces
Demonstrarea lui Euler a sumei formei de grade folosește tehnica dublei numărări: numără numărul de perechi de accidente (v, e) unde e este o margine și vârful v este unul dintre capetele sale, în două moduri diferite. Vârful v aparține perechilor deg (v), unde deg (v) (gradul lui v) este numărul de muchii care îi sunt incidente. Prin urmare, numărul de perechi incidente este suma gradelor. Cu toate acestea, fiecare arc din grafic aparține exact a două perechi incidente, una pentru fiecare dintre punctele sale finale; prin urmare, numărul de perechi de accidente este de 2 | E |. Deoarece aceste două formule contează același set de obiecte, acestea trebuie să aibă valori egale.
Într-o sumă de numere întregi, paritatea sumei nu este afectată de termenii pari din sumă; suma agregată este pară atunci când există un număr par de termeni impari și impar când există un număr impar de termeni impari. Deoarece o parte a formei sumei de grade este numărul par 2 | E |, suma de pe cealaltă parte trebuie să aibă un număr par de termeni impari; adică trebuie să existe un număr par de vârfuri de grad impar.
Alternativ, inducția matematică poate fi utilizată pentru a demonstra că numărul vârfurilor de grad impar este egal, prin îndepărtarea unei margini la un moment dat dintr-un grafic dat și folosirea unei analize de caz pe gradele punctelor sale finale pentru a determina efectul acestei îndepărtări asupra paritatea numărului de vârfuri de grad impar.
În clase speciale de grafice
Grafice regulate
Formula sumei gradelor implică faptul că fiecare r - grafic regulat cu n vârfuri are nr / 2 arcuri. În special, dacă r este impar, numărul de arce trebuie să fie divizibil cu r, iar numărul de vârfuri trebuie să fie egal.
Grafică infinită
Un grafic infinit care nu respectă lema strângerii de mână. Lema strângerii de mână nu se aplică graficelor infinite, chiar și atunci când acestea au doar un număr finit de vârfuri de grad impar. De exemplu, un grafic de cale infinită cu un punct final are doar un singur vârf de grad impar mai degrabă decât să aibă un număr par de astfel de vârfuri.
Aplicații
Traseele și tururile lui Euler
Leonhard Euler a demonstrat pentru prima dată lema strângerii de mână în lucrarea sa de pe cele Șapte Poduri din Königsberg, solicitând un tur pe jos al orașului Königsberg (acum Kaliningrad), traversând fiecare dintre cele șapte poduri ale sale o dată. Acest lucru poate fi tradus în termeni de teorie a graficului ca solicitând o cale Euler sau un tur Euler al unui grafic conectat care reprezintă orașul și podurile acestuia: o plimbare prin graficul care traversează fiecare margine o dată, care se termină la un vârf altul decât cel care începe în cazul unui tur Euler sau revenirea la punctul de plecare în cazul unui tur Euler. Euler a afirmat rezultatele fundamentale ale acestei probleme în ceea ce privește numărul de vârfuri impare din grafic, pe care lema de strângere a mâinii o limitează la a fi un număr par. Dacă acest număr este zero, există o cale Euler și dacă este două, există o cale Euler . Dacă nu, problema nu poate fi rezolvată. În cazul celor șapte poduri Königsberg, graficul care reprezintă problema are patru vârfuri impare și nu are nici o cale Euler, nici un viraj Euler.
În algoritmul Christofides - Serdyukov pentru aproximarea problemei vânzătorului călător, faptul că numărul de vârfuri impare joacă, de asemenea, un rol cheie, permițând algoritmului să conecteze astfel de vârfuri în perechi pentru a construi un grafic în care un viraj Euler constituie un tur TSP aproximativ. [1] .
În enumerarea combinatorie
Se poate arăta că mai multe structuri combinatorii sunt pare ca număr, conectându-le la vârfurile impare într-un „grafic swap” adecvat.
De exemplu, după cum arată CAB Smith, în orice grafic cub G trebuie să existe un număr egal de cicluri hamiltoniene printr-un arc fix uv; Thomason (1978) a folosit o demonstrație bazată pe lema strângerii de mână pentru a extinde acest rezultat la graficele G în care toate vârfurile au grade impare. Thomason definește un grafic de schimb H , ale cărui vârfuri sunt unul la unu cu căile hamiltoniene care încep și continuă în u până la v. Două astfel de căi p 1 și p 2 sunt conectate printr-o margine în H dacă puteți obține p 2 adăugând o nouă margine la sfârșitul lui p 1 și îndepărtând o altă margine din mijlocul lui p 1; aceasta este o relație simetrică, atunci H este un grafic nedirecționat. Dacă calea p se termină la vârful w, atunci p-ul corespunzător din vârful H are un grad egal cu numărul de moduri în care p poate fi extins de un arc care nu are legătură cu u; adică, gradul acestui vârf în H este fie deg (w) - 1 (un număr par) dacă p nu face parte dintr-un ciclu hamiltonian prin UV, fie deg (w) - 2 (un număr impar) dacă p este parte a unui ciclu hamiltonian prin uv. Deoarece H are un număr par de vârfuri impare, G trebuie să aibă un număr egal de cicluri hamiltoniene prin uv.
Alte aplicații
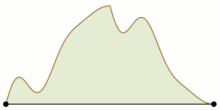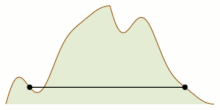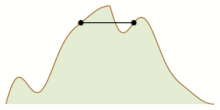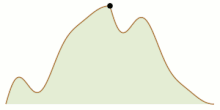
Lema de strângere de mână este, de asemenea, utilizată în dovezile lemei lui Sperner și în cazul liniar în bucăți al problemei „alpinismului”. Este vorba de găsirea condițiilor care trebuie să îndeplinească două funcții care formează profilurile unui munte bidimensional, astfel încât doi alpiniști (alpiniști în italiană) să poată începe de jos pe laturile opuse ale muntelui și să își coordoneze mișcările pentru a se întâlni (posibil în partea de sus) rămânând mereu la aceeași înălțime.
Complexitatea computațională
În legătură cu metoda graficului de schimb care demonstrează existența structurilor combinatorii, este interesant să ne întrebăm cât de eficient pot fi găsite aceste structuri. De exemplu, să presupunem că furnizăm un ciclu hamiltonian într-un grafic cub ca intrare; rezultă din teorema lui Smith că există un al doilea ciclu. Cât de repede poate fi găsit acest al doilea ciclu? Papadimitriou (1994) a studiat complexitatea de calcul a unor astfel de întrebări sau, mai general, a căutării unui al doilea summit de grad impar când vi se dă un singur summit impar într-un grafic mare definit implicit. El a definit clasa de complexitate PPA pentru a încapsula astfel de probleme; o clasă strâns legată definită pe grafice directe, PPAD, a atras o atenție semnificativă în teoria jocurilor algoritmice, deoarece calculul unui echilibru Nash este echivalent din punct de vedere computeric cu problemele mai dificile din această clasă.
Notă
- ^ Nicos Christofides, analiza celui mai rău caz al unei noi euristici pentru problema vânzătorului călător (PDF) Raport 388, 1976. Lema strângerii de mână este citată în partea de sus a paginii 2.