Martingale (matematică)

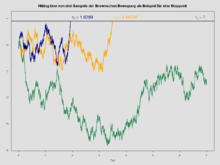
Simulări ale mișcării browniene : un exemplu clasic de martingală continuă .

În teoria probabilității , martingala este un proces stocastic $X_{t}$ ${\ displaystyle X_ {t}}$ $X_ {t}$ , indexat de un parametru în creștere $t$ ${\ displaystyle t}$ $t$ (deseori interpretat ca timp ), cu următoarea proprietate: pentru fiecare $s\leq t$ ${\ displaystyle s \ leq t}$ $s \ leq t$ , așteptarea de $X_{t}$ ${\ displaystyle X_ {t}}$ $X_ {t}$ condiționată de valorile $X_{r},r\leq s$ ${\ displaystyle X_ {r}, r \ leq s}$ $X_ {r}, r \ leq s$ , este egal cu $X_{s}$ ${\ displaystyle X_ {s}}$ $X_ {s}$ . Cel mai cunoscut exemplu de martingală, în care parametrul $s$ ${\ displaystyle s}$ $s$ este continuu , este fără îndoială mișcarea browniană .

Exemplu

Înainte de a da o definiție precisă, să ilustrăm un exemplu. Să luăm în considerare un om care joacă capete sau cozi cu o monedă: cu fiecare aruncare a monedei câștigă un euro în cazul capetelor, în timp ce pierde un euro în cazul cozilor. Este $X_{0},X_{1},X_{2},\ldots$ ${\ displaystyle X_ {0}, X_ {1}, X_ {2}, \ ldots}$ $X_ {0}, X_ {1}, X_ {2}, \ ldots$ banii (exprimați în euro) deținut de bărbat, respectiv înainte de prima aruncare ( $X_{0}$ ${\ displaystyle X_ {0}}$ $X_ {0}$ ), după prima lansare ( $X_{1}$ ${\ displaystyle X_ {1}}$ $X_ {1}$ ), după a doua lansare ( $X_{2}$ ${\ displaystyle X_ {2}}$ $X_ {2}$ ) si asa mai departe.

Dacă moneda este nedreaptă (adică dacă șansele de a câștiga și a pierde pe fiecare flip sunt egale), valoarea așteptată de $X_{n}$ ${\ displaystyle X_ {n}}$ $X_ {n}$ , adică din banii deținuți ulterior $n$ ${\ displaystyle n}$ $n$ lansare, va fi pur și simplu $X_{0}$ ${\ displaystyle X_ {0}}$ $X_ {0}$ , sau numărul de euro deținut inițial. Dar dacă vom afla asta mai târziu $m$ ${\ displaystyle m}$ $m$ distribuția pe care o are acest domn ${\bar {x}}$ ${\ displaystyle {\ bar {x}}}$ ${\ bar {x}}$ €, cea mai rezonabilă așteptare în ceea ce privește euro câștigat ulterior $n$ ${\ displaystyle n}$ $n$ lansează (cu $n>m$ ${\ displaystyle n> m}$ $n> m$ ) va fi în schimb ${\bar {x}}$ ${\ displaystyle {\ bar {x}}}$ ${\ bar {x}}$ . Aceasta este tocmai proprietatea martingalei .

Istorie

Paul Pierre Lévy a propus noțiunea de martingală

În matematică, termenul martingale se referea inițial la o serie de strategii folosite de pariorii francezi în secolul al XVIII-lea . Cea mai simplă dintre aceste strategii a fost folosită în jocuri similare cu capetele sau cozile de astăzi: pariorul a ales o parte a unei monede. Acest lucru a fost aruncat, iar jucătorul a câștigat sau a pierdut o sumă fixă de bani, în funcție de faptul că a ghicit sau nu fața arătată de monedă după cădere. Strategia martingalei a constat în dublarea pariului după fiecare aruncare pierdută. Această tehnică, care aparent duce la o anumită victorie finală, a fost de fapt cauza pierderilor mari din partea pariorilor. O analiză mai atentă arată că miza care trebuie pariată crește exponențial odată cu rolurile pierdute și este ușor convins că, pentru a asigura victoria, ar trebui să existe un capital infinit pentru a putea paria, iar dealerul ar trebui să fie, de asemenea, dispus să accepte mail de orice dimensiune. Câștigul net este doar miza inițială. În mod ironic, unul dintre rezultatele elementare demonstrate de teoria martingalei de astăzi este inexistența unui sistem de pariuri câștigător.

Conceptul de martingală a fost introdus în teoria probabilităților de Paul Pierre Lévy . O mare parte din rezultatele avansate cu privire la martingale au fost produse de Joseph Leo Doob , cu contribuții importante ale lui Kiyoshi Itō la aplicații analitice. Din anii 1970 , teoria martingalei a găsit aplicații largi în multe domenii ale matematicii pure și aplicate . În special, în teoria probabilității , în fizica matematică și în finanța matematică . Succesul acestei teorii este de așa natură încât este una dintre puținele ramuri ale matematicii cunoscute și de către cercetătorii din alte discipline, în special de cei implicați în tehnici de finanțare și bursă. De asemenea, datorită contribuțiilor aduse acestei teorii, Lévy, Itō și Doob sunt considerați printre cei mai mari matematicieni ai secolului XX .

Definiție

Martingala în timp discret

O martingală în timp discret este un proces stocastic în timp discret $X_{1},\ldots ,X_{n},\ldots$ ${\ displaystyle X_ {1}, \ ldots, X_ {n}, \ ldots}$ $X_ {1}, \ ldots, X_ {n}, \ ldots$ la valori în $\mathbb {R}$ ${\ displaystyle \ mathbb {R}}$ $\ mathbb {R}$ astfel încât

\mathbf {E} (\vert X_{n}\vert )<\infty ,

{\ displaystyle \ mathbf {E} (\ vert X_ {n} \ vert) <\ infty,}

\ mathbf {E} (\ vert X_ {n} \ vert) <\ infty,

\mathbf {E} (X_{n+1}|X_{1}\dots X_{n})=X_{n},\quad n\in \mathbb {N} .

{\ displaystyle \ mathbf {E} (X_ {n + 1} | X_ {1} \ dots X_ {n}) = X_ {n}, \ quad n \ in \ mathbb {N}.}

\ mathbf {E} (X_ {n + 1} | X_ {1} \ dots X_ {n}) = X_ {n}, \ quad n \ in \ mathbb {N}.

Martingala în timp continuu

Un proces stochastic $X_{t},t\geq 0$ ${\ displaystyle X_ {t}, t \ geq 0}$ $X_ {t}, t \ geq 0$ este totuși o martingală

\mathbf {E} (\vert X_{t}\vert )<\infty ,

{\ displaystyle \ mathbf {E} (\ vert X_ {t} \ vert) <\ infty,}

\ mathbf {E} (\ vert X_ {t} \ vert) <\ infty,

\mathbf {E} (X_{t}|\{X_{u}\}_{u\leq s})=X_{s},\quad \forall \ s\leq t,

{\ displaystyle \ mathbf {E} (X_ {t} | \ {X_ {u} \} _ {u \ leq s}) = X_ {s}, \ quad \ forall \ s \ leq t,}

\ mathbf {E} (X_ {t} | \ {X_ {u} \} _ {u \ leq s}) = X_ {s}, \ quad \ forall \ s \ leq t,

Mai general, un proces stochastic $Y:T\times \Omega \rightarrow S$ ${\ displaystyle Y: T \ times \ Omega \ rightarrow S}$ $Y: T \ times \ Omega \ rightarrow S$ se spune martingale cu privire la o filtrare ${\mathcal {F}}$ ${\ displaystyle {\ mathcal {F}}}$ ${\ mathcal {F}}$ și o măsură de probabilitate $\mathbb {P}$ ${\ displaystyle \ mathbb {P}}$ $\ mathbb {P}$ de sine:

${\mathcal {F}}$ ${\ displaystyle {\ mathcal {F}}}$ ${\ mathcal {F}}$ este o filtrare a spațiului de probabilitate $(\Omega ,\Sigma ,\mathbb {P} )$ ${\ displaystyle (\ Omega, \ Sigma, \ mathbb {P})}$ $(\ Omega, \ Sigma, \ mathbb {P})$ că studiem
$Da$ ${\ displaystyle Y}$ $Da$ este adaptat la filtrare , adică pentru fiecare $t\in T$ ${\ displaystyle t \ in T}$ $t \ in T$ variabila aleatorie $Y_{t}$ ${\ displaystyle Y_ {t}}$ $YT}$ este măsurabilă conform ${\mathcal {F}}_{t}$ ${\ displaystyle {\ mathcal {F}} _ {t}}$ ${\ mathcal {F}} _ {t}$
$\mathbf {E} _{P}(\vert Y_{t}\vert )<\infty \quad \forall t$ ${\ displaystyle \ mathbf {E} _ {P} (\ vert Y_ {t} \ vert) <\ infty \ quad \ forall t}$ $\ mathbf {E} _ {P} (\ vert Y_ {t} \ vert) <\ infty \ quad \ forall t$
$\mathbf {E} _{P}([Y_{t}-Y_{s}]\chi _{F})=0\quad \forall s,t:s<t,\ \forall F\in {\mathcal {F}}_{s}$ ${\ displaystyle \ mathbf {E} _ {P} ([Y_ {t} -Y_ {s}] \ chi _ {F}) = 0 \ quad \ forall s, t: s <t, \ \ forall F \ în {\ mathcal {F}} _ {s}}$ $\ mathbf {E} _ {P} ([Y_ {t} -Y_ {s}] \ chi _ {F}) = 0 \ quad \ forall s, t: s <t, \ \ forall F \ in {\ mathcal {F}} _ {s}$

Submartingale

Procesul stochastic $(X_{n})_{n\in \mathbb {R} _{+}}$ ${\ displaystyle (X_ {n}) _ {n \ in \ mathbb {R} _ {+}}}$ ${\ displaystyle (X_ {n}) _ {n \ in \ mathbb {R} _ {+}}}$ este o submartială (sau submartială) dacă primele patru puncte ale definiției martingalei și predicția condiționată a $X_{t}$ ${\ displaystyle X_ {t}}$ $X_t$ , cunoscând valorile conținute în filtrare ${\mathcal {F}}$ ${\ displaystyle {\ mathcal {F}}}$ ${\ mathcal {F}}$ este mai mare sau egal cu $X_{s}$ ${\ displaystyle X_ {s}}$ $X_s$ , pentru fiecare $s<t$ ${\ displaystyle s <t}$ ${\ displaystyle s <t}$ , sau

$\mathbf {E} _{P}([Y_{t}]\chi _{F})\geqslant Y_{s}\quad \forall s,t:s<t,\ \forall F\in {\mathcal {F}}_{s}$ ${\ displaystyle \ mathbf {E} _ {P} ([Y_ {t}] \ chi _ {F}) \ geqslant Y_ {s} \ quad \ forall s, t: s <t, \ \ forall F \ in {\ mathcal {F}} _ {s}}$ ${\ displaystyle \ mathbf {E} _ {P} ([Y_ {t}] \ chi _ {F}) \ geqslant Y_ {s} \ quad \ forall s, t: s <t, \ \ forall F \ in {\ mathcal {F}} _ {s}}$

Supermartingale

Procesul stochastic $(X_{n})_{n\in \mathbb {R} _{+}}$ ${\ displaystyle (X_ {n}) _ {n \ in \ mathbb {R} _ {+}}}$ ${\ displaystyle (X_ {n}) _ {n \ in \ mathbb {R} _ {+}}}$ este o supermartingală dacă primele patru puncte ale definiției martingalei și predicția condiționată a $X_{t}$ ${\ displaystyle X_ {t}}$ $X_t$ , cunoscând valorile conținute în filtrare ${\mathcal {F}}$ ${\ displaystyle {\ mathcal {F}}}$ ${\ mathcal {F}}$ este mai mic sau egal cu $X_{s}$ ${\ displaystyle X_ {s}}$ $X_s$ , pentru fiecare $s<t$ ${\ displaystyle s <t}$ ${\ displaystyle s <t}$ , sau

$\mathbf {E} _{P}([Y_{t}]\chi _{F})\leqslant Y_{s}\quad \forall s,t:s<t,\ \forall F\in {\mathcal {F}}_{s}$ ${\ displaystyle \ mathbf {E} _ {P} ([Y_ {t}] \ chi _ {F}) \ leqslant Y_ {s} \ quad \ forall s, t: s <t, \ \ forall F \ in {\ mathcal {F}} _ {s}}$ ${\ displaystyle \ mathbf {E} _ {P} ([Y_ {t}] \ chi _ {F}) \ leqslant Y_ {s} \ quad \ forall s, t: s <t, \ \ forall F \ in {\ mathcal {F}} _ {s}}$

Note Martingale

Urna Poliei

Luați în considerare o urnă care conține inițial două bile, una albă și una neagră. La fiecare extragere se extrage o minge din urnă, se verifică culoarea și apoi se reintroduce în urnă împreună cu o altă minge de aceeași culoare. De exemplu, dacă o minge neagră este prinsă la prima remiză, minge tocmai prinsă și o altă minge neagră sunt plasate în urnă. Prin urmare, la a doua remiză vor fi două bile negre și una albă.

Este $(Y_{n})_{n\geqslant 0}$ ${\ displaystyle (Y_ {n}) _ {n \ geqslant 0}}$ ${\ displaystyle (Y_ {n}) _ {n \ geqslant 0}}$ un proces stochastic care numără numărul de bile negre la fiecare moment $n,\forall {n\geqslant 0}$ ${\ displaystyle n, \ forall {n \ geqslant 0}}$ ${\ displaystyle n, \ forall {n \ geqslant 0}}$ . Se ridică $X_{n}={\dfrac {Y_{n}}{n+2}}$ ${\ displaystyle X_ {n} = {\ dfrac {Y_ {n}} {n + 2}}}$ ${\ displaystyle X_ {n} = {\ dfrac {Y_ {n}} {n + 2}}}$ proporția de bile negre instantaneu $n$ ${\ displaystyle n}$ $n$ . Rețineți că în primul moment, când $n=0$ ${\ displaystyle n = 0}$ $n = 0$ , sunt două bile în urnă, una neagră și una albă. Se definește pe sine $U_{k}=\mathrm {I} _{\{{\text{estraggo pallina nera all'istante }}k\}}$ ${\ displaystyle U_ {k} = \ mathrm {I} _ {\ {\ text {I draw instant black ball}} k \}}}$ ${\ displaystyle U_ {k} = \ mathrm {I} _ {\ {\ text {I draw instant black ball}} k \}}}$ funcția care indică extragerea instantaneu a unei bile negre $k$ ${\ displaystyle k}$ $k$ . Acolo $\sigma$ ${\ displaystyle \ sigma}$ $\ sigma$ - algebra generată de $(U_{1},\ldots ,U_{k})$ ${\ displaystyle (U_ {1}, \ ldots, U_ {k})}$ ${\ displaystyle (U_ {1}, \ ldots, U_ {k})}$ este o filtrare ${\mathcal {F}}^{U}=({\mathcal {F}}_{i}^{U})_{i\geqslant 1}$ ${\ displaystyle {\ mathcal {F}} ^ {U} = ({\ mathcal {F}} _ {i} ^ {U}) _ {i \ geqslant 1}}$ ${\ displaystyle {\ mathcal {F}} ^ {U} = ({\ mathcal {F}} _ {i} ^ {U}) _ {i \ geqslant 1}}$ de spațiu $(\Omega ,{\mathcal {A}},P)$ ${\ displaystyle (\ Omega, {\ mathcal {A}}, P)}$ ${\ displaystyle (\ Omega, {\ mathcal {A}}, P)}$ .

Predicția numărului de bile negre instantaneu $n+1$ ${\ displaystyle n + 1}$ $n + 1$ cunoscând numărul de bile negre trase instantaneu $n$ ${\ displaystyle n}$ $n$ Și $E[Y_{n+1}|{\mathcal {F}}_{n}^{U}]={\dfrac {n+3}{n+2}}Y_{n}$ ${\ displaystyle E [Y_ {n + 1} | {\ mathcal {F}} _ {n} ^ {U}] = {\ dfrac {n + 3} {n + 2}} Y_ {n}}$ ${\ displaystyle E [Y_ {n + 1} | {\ mathcal {F}} _ {n} ^ {U}] = {\ dfrac {n + 3} {n + 2}} Y_ {n}}$ . Predicția proporției de bile negre prezente în urnă instantaneu $n+1$ ${\ displaystyle n + 1}$ $n + 1$ Și $E[X_{n+1}|{\mathcal {F}}_{n}^{U}]=E{\biggl [}{\dfrac {Y_{n+1}}{n+3}}|{\mathcal {F}}_{n}^{U}{\biggr ]}={\dfrac {1}{n+3}}E[Y_{n+1}|{\mathcal {F}}_{n}^{U}]={\dfrac {Y_{n}}{n+2}}=X_{n}$ ${\ displaystyle E [X_ {n + 1} | {\ mathcal {F}} _ {n} ^ {U}] = E {\ biggl [} {\ dfrac {Y_ {n + 1}} {n + 3 }} | {\ mathcal {F}} _ {n} ^ {U} {\ biggr]} = {\ dfrac {1} {n + 3}} E [Y_ {n + 1} | {\ mathcal {F }} _ {n} ^ {U}] = {\ dfrac {Y_ {n}} {n + 2}} = X_ {n}}$ ${\ displaystyle E [X_ {n + 1} | {\ mathcal {F}} _ {n} ^ {U}] = E {\ biggl [} {\ dfrac {Y_ {n + 1}} {n + 3 }} | {\ mathcal {F}} _ {n} ^ {U} {\ biggr]} = {\ dfrac {1} {n + 3}} E [Y_ {n + 1} | {\ mathcal {F }} _ {n} ^ {U}] = {\ dfrac {Y_ {n}} {n + 2}} = X_ {n}}$ .

După cum se dovedește $E[X_{n+1}|{\mathcal {F}}_{n}^{U}]=X_{n}$ ${\ displaystyle E [X_ {n + 1} | {\ mathcal {F}} _ {n} ^ {U}] = X_ {n}}$ ${\ displaystyle E [X_ {n + 1} | {\ mathcal {F}} _ {n} ^ {U}] = X_ {n}}$ , se poate concluziona că $(X_{n})_{n\geqslant 0}$ ${\ displaystyle (X_ {n}) _ {n \ geqslant 0}}$ ${\ displaystyle (X_ {n}) _ {n \ geqslant 0}}$ este o martingală în comparație cu ${\mathcal {F}}^{U}$ ${\ displaystyle {\ mathcal {F}} ^ {U}}$ ${\ displaystyle {\ mathcal {F}} ^ {U}}$ .

Bibliografie

Daniel Revuz, Marc Yor (1999): Continuous Martingales and Brownian motion , ediția a III-a Springer, ISBN 3-540-64325-7

Elemente conexe

linkuri externe

( EN ) Martingala , în Encyclopedia Britannica , Encyclopædia Britannica, Inc.
Pagina principală a SRS Varadhan , cu material introductiv la teoria martingalei.