Metru

De la Wikipedia, enciclopedia liberă.
Salt la navigare Salt la căutare
Notă despre dezambiguizare.svg Dezambiguizare - Dacă sunteți în căutarea altor semnificații, consultați Metro (dezambiguizare) .
Metru
US National Length Meter.JPG
Detaliu al barului nr. 27 , construit în 1889 și păstrat la Bureau international des poids et mesures ; a reprezentat prototipul standard internațional de 1 metru lungime
Informații generale
Sistem DA
mărimea lungime
Simbol m
Conversii
1 min ... ...echivalentă cu...
Unitate CGS 100 cm
Unitate SUA / Imp ≈ 39,3701 in
≈ 3.28084 ft
≈ 1,09361 m
≈ 6,21371 × 10 −4 mi
Unitatea Planck ≈ 6,25 × 10 34 l P.
Unități atomice ≈ 1,89 × 10 10 la 0
Unitate SA ≈ 6,68459 × 10 −12 AU
Editați datele pe Wikidata · Manual

Contorul ( simbol : m [1] , uneori indicat eronat ca mt ) este unitatea de bază a lungimii SI (International System of Measurement Units). [1]

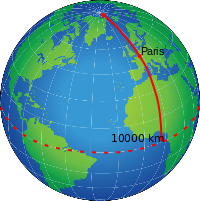
Inițial Adunarea Națională Franceză a aprobat la 26 martie 1791 propunerea pentru o definiție teoretică a contorului ca 1/10 000 000 a arcului meridianului terestru dintre polul nord și ecuatorul care a trecut prin Paris (așa-numitul Paris meridian ). Cu toate acestea, studiile ulterioare au stabilit că lungimea cartierului terestru a fost de 10 001 957 metri în loc de 10 000 000 așteptate. În 1799 a fost creat primul eșantion standard de platină cu iridiu . [2]

Odată cu progresul științei au existat evoluții ulterioare până în 1983 , în timpul celei de-a XVII-a Conférence générale des poids et mesures (Conferința generală a greutăților și măsurilor) din Paris, contorul a fost redefinit ca distanță parcursă de lumină în vid într-un interval egal la 1/299 792 458 de secundă [1] [3] , presupunând că viteza luminii în vid, prin definiție, este egală cu c = 299 792 458 m / s . [4] Această definiție și valoarea constantei fizice au fost confirmate în 2018 de cea de-a 26-a CGPM. [5]

Istorie

Distanța de la Polul Nord la Ecuator prin Paris

Termenul "metru" provine din grecescul "metron" care înseamnă măsură. A fost reînviat în 1675 de Tito Livio Burattini , care a propus una dintre primele definiții bazate pe lungimea unui pendul care o bate pe a doua . Perioada de jumătate a unui pendul actual de un metru este de aproximativ o secundă și variază în funcție de latitudine fiind influențată în primul rând de rotația pământului . [6]

Definiția inițială a contorului bazată pe dimensiunea Pământului este urmărită în 1791 , stabilită de Academia Franceză de Științe ca 1/10 000 000 din distanța dintre polul nord și ecuator , de-a lungul suprafeței pământului, calculată pe meridianul parizian . La 7 aprilie 1795 , Franța a adoptat contorul ca unitate oficială de măsură, urmată de alte țări europene. În Italia, metroul a fost introdus pentru prima dată de Napoleon în timpul campaniei italiene din 1796 . De atunci, în ciuda diferitelor rezistențe politice, exacerbate în timpul Congresului de la Viena , metroul nu a părăsit niciodată peninsula italiană, chiar dacă a fost adoptat de statele italiene în momente diferite și pe căi diferite. [7]

Incertitudinea în definirea contorului a determinat Biroul internațional de măsuri și măsuri (BIPM) să redefinească contorul în 1889 ca distanță între două linii gravate pe un eșantion de bară de platină - iridiu păstrat în Sèvres lângă Paris . [8]

Bara de platină-iridiu utilizată ca probă de metru în perioada 1889-1960

În 1960 , odată cu disponibilitatea laserelor , cea de-a unsprezecea Conferință generală de greutăți și măsuri a schimbat definiția contorului în: lungimea egală cu 1 650 763,73 lungimi de undă în vidul radiației corespunzător tranziției dintre nivelurile 2p 10 și 5d 5 din atomul de cripton-86 .

În 1983, cea de-a XVII-a Conferință Generală a Greutăților și Măsurilor a definit metrul ca distanța pe care o parcurge lumina în vid în 1/299 792 458 de secundă (adică viteza luminii în vid a fost definită ca fiind 299 792 458 metri pe al doilea). Deoarece viteza luminii în vid este considerată aceeași peste tot, această definiție este mai universală decât definiția bazată pe măsurarea circumferinței Pământului sau a lungimii unei bare specifice din aliaj metalic, iar contorul de testare poate fi reprodus fidel în orice laborator. special echipat. Celălalt avantaj este că poate fi (teoretic) măsurat cu o precizie mai mare decât circumferința Pământului sau distanța dintre două puncte.

Din nou, datorită experimentelor de laborator, de la sfârșitul anului 1997 este posibil să se atingă un ordin de precizie de ordinul a 10 −10 m. Acest rezultat poate fi obținut prin exploatarea relației λ = c / ν ( λ lungime de undă, c viteza luminii, ν frecvența radiației) utilizând oscilatoare laser stabilizate la frecvență cunoscută (inexactitate Δ ν / ν mai bună decât 10 −10 ) a cărei radiație este utilizat în sistemele de măsurare interferometrică.

Multiple și submultiple

Pictogramă lupă mgx2.svg Același subiect în detaliu: ordine de mărime (lungime) .

Folosind prefixele SI , se obțin următorii multipli și submultipli (în italice multiplii și submultiplii care nu sunt obținuți folosind prefixe sau care nu aparțin Sistemului Internațional de Unități ):

Nume Simbol Corespondenţă Exemplu
yotameter Da 10 24 m 1 000 000 000 000 000 000 000 000 000 m 1 000 000 000 000 000 000 000 000 000 000 000/1 m Distanțe intergalactice
zetameter Zm 10 21 m 1 000 000 000 000 000 000 000 000 m 1 000 000 000 000 000 000 000 000/1 m Dimensiunea unei galaxii
exametro Em 10 18 m 1 000 000 000 000 000 000 000 m 1 000 000 000 000 000 000 000 000/1 m Distanțele interstelare
petameter P.m 10 15 m 1 000 000 000 000 000 m 1 000 000 000 000 000 000 000/1 m
termometru Tm 10 12 m 1 000 000 000 000 m 1 000 000 000 000/1 m Despre distanța dintre Soare și Saturn
gigametru Gm 10 9 m 1 000 000 000 m 1 000 000 000/1 m De aproximativ 3 ori distanța dintre Pământ și Lună
megametru Mm 10 6 m 1 000 000 m 1 000 000/1 m Ruta de la Milano la Brindisi
miriametru mam 10 4 m 10 000 m 10 000/1 m Diametrul unui oraș mare
kilometru (sau kilometru) km 10 3 m 1 000 m 1000/1 m Dimensiunea unei țări
hectometru hm 10 2 m 100 m 100/1 m Aproximativ înălțimea zgârie-nori Pirelli
decametru baraj 10 1 m 10 m 10/1 m Dimensiunea unei case
metru m 10 0 m 1 m 1/1 m Distanța aproximativă între doi inci, brațele întinse
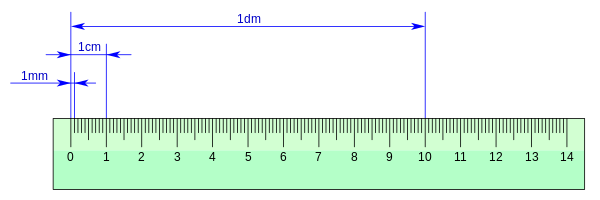
decimetru dm 10 −1 m 0,1 m 1/10 m Dimensiunea palmei unei mâini
centimetru cm 10 −2 m 0,01 m 1/100 m Grosimea unui deget
milimetru mm 10 −3 m 0,001 m 1/1 000 m Grosimea unui cui
micrometru (sau micron) μm 10 −6 m 0,000001 m 1/1 000 000 m Diametrul unui microb
nanometru marja nr 10 −9 m 0,000000001 m 1/1 000 000 000 m Dimensiunea elementelor microprocesorului
ångström LA 10 −10 m 0,0000000001 m 1/10 000 000 000 m Diametrul unui atom de oxigen
picometru p.m 10 −12 m 0,000000000001 m 1/1 000 000 000 000 m Lungimea de undă a razelor gamma
femtometru (sau oprire) fm 10 −15 m 0,000000000000001 m 1/1 000 000 000 000 000 000 000 m Raza protonului sau neutronului
actometru a.m 10 −18 m 0,000000000000000001 m 1/1 000 000 000 000 000 000 000 m Dimensiunea quarkului
zeptometru zm 10 −21 m 0,00000000000000000000001 m 1/1 000 000 000 000 000 000 000 000 m
yoctometru ym 10 −24 m 0,00000000000000000000000001 m 1/1 000 000 000 000 000 000 000 000 000 000 000 m Magnitudinea neutrino

ReglaMedida.svg

Picometrul este utilizat în mod obișnuit la măsurarea distanțelor pe scara atomică ; diametrul unui atom este între aproximativ 30 și 600 µm. Este egal cu o milionime de microni și a fost numit micromicron, stigmat sau bicron. Simbolul µµ a fost folosit odată.

Yottameterul ar putea fi folosit pentru a măsura distanțele intergalactice , dar astronomii sunt de multă vreme obișnuiți să folosească ani-lumină și parsecs și continuă să le prefere.

Notă

  1. ^ a b c ( EN ) IUPAC Gold Book, „metru” , la goldbook.iupac.org .
  2. ^ Anand K. Bewoor, Metrology & Measurement , Tata McGraw-Hill Education, 2009, p. 15, ISBN 978-0-07-014000-4 .
  3. ^ Meridianul și măsura Pământului , pe torinoscienza.it . Adus la 17 octombrie 2010 (arhivat din original la 19 ianuarie 2012) .
  4. ^ Lecții ale cursului Fundamentelor de metrologie mecanică ( PDF ), pe docente.unicas.it . Adus pe 9 septembrie 2013 .
  5. ^ (EN) BIPM - Rezoluția 1 a 26-a CGPM , pe bipm.org. Adus la 22 martie 2019 (arhivat din original la 4 februarie 2021) .
  6. ^ De ce bate contorul pe al doilea? , pe roma1.infn.it . Adus la 22 octombrie 2010 .
  7. ^ Emanuele Lugli, Unitatea de măsură. O scurtă istorie a metroului în Italia , Bologna, Il Mulino, 2014.
  8. ^ O copie a acestui eșantion, în Italia, este păstrată la Institutul Național de Cercetări Metrologice din Torino , născut din uniunea fostului Institut Metrologic Gustavo Colonnetti (IMGC-CNR) și fostul Institut Național Electrotehnic Galileo Ferraris (IEN).

Bibliografie

  • Ken Adler, Măsura tuturor lucrurilor. Povestea aventuroasă a invenției sistemului metric , Rizzoli, 2002, ISBN 9788817870672 . Istoria măsurării arcului meridian dintre Dunkerque și Barcelona de Jean-Baptiste Delambre și Pierre Méchain .
  • Emanuele Lugli, Unități de măsură: o scurtă istorie a contorului în Italia , Il Mulino, 2014, ISBN 9788815252739 .

Elemente conexe

Alte proiecte

linkuri externe

  • Metro , în Treccani.it - Vocabularul Treccani online , Institutul Enciclopediei Italiene.
Controlul autorității LCCN (EN) sh85084371 · GND (DE) 4518579-7 · BNF (FR) cb11967077c (data)
Adus de la „ https://it.wikipedia.org/w/index.php?title=Metro&oldid=120395630#Multipli_e_sottomultipli ”