număr prim

Distribuția numerelor prime (linii albastre) până la 400

În matematică , un număr prim (de asemenea, prim pentru scurt) este un întreg pozitiv care are exact doi divizori distincti. Într-un mod echivalent poate fi definit ca un număr natural mai mare de 1 care este divizibil numai cu 1 și prin el însuși; dimpotrivă, un număr mai mare de 1 care are mai mult de doi divizori se numește compozit . De exemplu 2, 3 și 5 sunt prime, în timp ce 4 și 6 nu sunt deoarece sunt, de asemenea, divizibile, respectiv, cu 2 și cu 2 și 3. Singurul număr prim par este 2, deoarece toate celelalte numere pare sunt divizibile cu 2.

Succesiunea numerelor prime începând cu 2 , 3 , 5 , 7 , 11 , 13 , 17 , 19 , 23 , 29 , 31 , 37 ... ^[1]

Numărul primar este unul dintre conceptele de bază ale teoriei numerelor , partea matematicii care studiază numerele întregi : importanța stă în posibilitatea de a construi cu ele, prin multiplicare, toate celelalte numere întregi, precum și unicitatea unui astfel de factorizare . Primele sunt, de asemenea, infinite, iar distribuția lor este încă obiectul multor cercetări.

Numerele prime au fost studiate din cele mai vechi timpuri: primele rezultate datează de la vechii greci și, în special, de elementele lui Euclid , scrise în jurul anului 300 î.Hr. Cu toate acestea, multe conjecturi care le privesc nu au fost încă demonstrate ; printre cele mai cunoscute se numără ipoteza Riemann , conjectura Goldbach și cea a primilor gemeni , care nu sunt dovedite la mai mult de un secol după formularea lor.

Ele sunt, de asemenea, relevante în multe alte domenii ale matematicii pure, cum ar fi algebra sau geometria ; recent, aceștia și-au asumat o importanță crucială în matematica aplicată și, în special, în criptografie .

Istorie

Nu se știe când a fost definit conceptul de număr prim, totuși un semnal care sugerează o anumită conștientizare a diversității acestor numere este mărturisit de Ishango Bone , o descoperire osoasă datată din paleoliticul superior , în care semnele reprezentând numerele prime dintre 10 și 20. Pentru a găsi un alt semn al acestei conștientizări, trebuie să mergi în Mesopotamia și să aștepți mileniul al II-lea î.Hr .; de fapt, acestei perioade aparțin niște tablete care conțin soluțiile unor probleme aritmetice care, pentru a fi realizate, necesită o bună cunoaștere a factorizării prime. ^[2] Papirusul Rhind (transcris în jurul anului 1650 î.Hr. ) aparține, de asemenea, aceluiași mileniu, care conține unele expansiuni în fracțiuni egiptene ale numerelor sub forma ² ⁄ _n . Extinderile numerelor care au cel mai mic dintre factorii lor în comun sunt similare, sugerând că egiptenii au fost cel puțin conștienți de diferența dintre primii și compușii lor. ^[3]

Un fragment din Elementele lui Euclid descoperite la Oxyrhynchus .

Primul semn incontestabil al unui studiu real al numerelor prime constă în Elementele lui Euclid , o carte scrisă între secolele IV și III î.Hr. , care oferă o imagine completă a cunoștințelor matematice ale timpului. Această lucrare conține câteva rezultate fundamentale, inclusiv teorema infinitului primelor ^[4] și lema lui Euclid , ^[5] care dovedește o caracterizare importantă a numerelor prime. ^[6] Euclid demonstrează , de asemenea , posibilitatea de factoring fiecare întreg pozitiv ca produs al amorse. ^[7] De asemenea, datorită site-ului lui Eratostene Greciei antice, un algoritm simplu pentru a determina care sunt numerele prime.

Pierre de Fermat

Secolele următoare au înregistrat o anumită lipsă de interes în studiul numerelor prime ^[8] și de ceva timp nu au fost prezentate rezultate deosebit de relevante pe această temă. Interesul pentru ele a reînviat în secolul al XVII-lea , cu dovezile unor rezultate noi și importante, dintre care unele se datorau lui Pierre de Fermat : în special el a dovedit o teoremă despre congruențe modulo a prima , cunoscută sub numele de „ mica teoremă a lui Fermat ”, și teorema asupra sumelor a două pătrate care afirmă că toate primele de o anumită formă pot fi scrise ca suma a două pătrate. De asemenea, el a conjecturat că toate numerele sub forma 2 ^{2 ⁿ} + 1 (numite acum numere Fermat în onoarea sa) erau prime; Fermat însuși își verificase conjectura până la n = 4, dar Euler a arătat că pentru n = 5 s-a obținut un număr compus. Până în prezent, nu se cunosc alte numere de acest tip care să fie prime. În aceeași perioadă, călugărul francez Marin Mersenne s-a concentrat asupra primului sub forma 2 ^p - 1, cu p prime, care astăzi sunt numite în onoarea sa primii Mersenne .

Alte rezultate au fost obținute de Euler în secolul al XVIII-lea : printre acestea se numără divergența seriei infinite ¹ ⁄ ₂ + ¹ ⁄ ₃ + ¹ ⁄ ₅ + ¹ ⁄ ₇ + ¹ ⁄ ₁₁ + ..., în care sunt adăugate inversele primelor și așa-numitul produs Euler , o formulă care evidențiază legătura dintre primele și seria armonică . ^[9] În corespondența lui Euler cu Christian Goldbach , acesta din urmă a formulat și celebra conjectură Goldbach , încă nedovedită astăzi, care se referă la reprezentarea numerelor pare naturale ca suma numerelor prime. ^[10]

De la începutul secolului al XIX-lea , atenția multor matematicieni s-a îndreptat spre studiul distribuției asimptotice a primului, adică spre studiul tendinței funcției care numără primii mai mici sau egali cu x . ^[11] Legendre și Gauss au presupus independent că această funcție tinde , pe măsură ce x crește, la x / ln ( x ), unde ln ( x ) indică logaritmul natural al lui x . ^[12] În 1859 ^[13] Bernhard Riemann a conectat această problemă cu poziționarea zerourilor funcției zeta Riemann , o funcție variabilă complexă ; această abordare a condus la dovada conjecturii, realizată independent de Hadamard și de la Vallée Poussin în 1896 . Acest rezultat este acum cunoscut sub numele de teorema numărului prim .

Numerele prime au rămas limitate la matematica pură până în anii 1970 , când a fost dezvoltat conceptul de criptografie cu cheie publică ; primul algoritm de acest tip, RSA , exploatează dificultatea de a lua în calcul numere mari formate doar din doi factori primi. Din acest motiv, căutarea numerelor prime din ce în ce mai mari și-a asumat, de asemenea, o importanță considerabilă. Din 1951 , această cercetare a fost efectuată prin utilizarea computerelor .

Primele proprietăți

Aplicarea sitei Eratostene pentru a găsi numere prime mai mici sau egale cu 120.

Cel mai mic prim este 2; toate celelalte sunt impare , deoarece fiecare număr par este divizibil cu 2. În trecut, 1 a fost uneori considerat un număr prim: de exemplu, Derrick Norman Lehmer l-a inclus în tabelul său de numere prime publicat în 1914 . ^[14] Astăzi, cu toate acestea, se preferă excluderea acestuia, întrucât includerea sa printre primele ar obliga să reformuleze într-un mod mai complex diferite teoreme (cum ar fi teorema fundamentală a aritmeticii ) pentru a ține cont de acest caz special. ^[15]

O metodă de verificare dacă un număr n este prim se numește test de primărie . O metodă care rezultă direct din definiție este de a verifica dacă nu este împărțită la niciun număr mai mic decât n sau, mai eficient, la niciun prim mai mic decât n . De exemplu, pentru a demonstra că 11 este prim, observați doar că nu este împărțit la 2, 3, 5 și 7 (care sunt numere prime mai mici de 11).

Reprezentarea lui 12 ca dreptunghi și încearcă să reprezinte 11 în acest fel.

Un algoritm antic care evită diviziunile este sita (adică sită ) a lui Eratostene care, mai precis, determină mulțimea primilor mai mică sau egală cu X. Pentru a face acest lucru, algoritmul începe de la mulțimea numerelor naturale cuprinse între 2 și X și elimină multiplii primilor identificați anterior (deoarece nu sunt multipli ai numerelor mai mici). ^[16] Într-adevăr, este posibil să se îmbunătățească acest algoritm oprindu-se pentru a elimina multiplii primilor mai mici sau egali cu partea întreagă a rădăcinii lui X : de fapt, dacă un număr compus c are toți factorii mai mari decât rădăcina lui X , atunci este mai mare decât X , deoarece, având să aibă cel puțin doi factori,

c>{\sqrt {X}}{\sqrt {X}}=X.

{\ displaystyle c> {\ sqrt {X}} {\ sqrt {X}} = X.}

c> \ sqrt {X} \ sqrt {X} = X.

Figura din dreapta arată cum funcționează algoritmul pentru X = 120. În mod similar, dacă utilizați metoda împărțirii pentru a demonstra primalitatea unui număr X, puteți evita verificarea divizibilității lui X cu numere mai mari decât rădăcina pătrată a lui X.

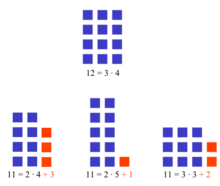
Într-o interpretare geometrică simplă a conceptului de număr prim, numerele n care nu sunt prime sunt exact acele numere care pot fi reprezentate ca dreptunghiuri compuse din n pătrate ale căror laturi sunt mai mari de 1. De exemplu 12 nu este prim, deoarece poate să fie reprezentat ca un dreptunghi cu laturile 3 și 4, în timp ce 11 este prim, deoarece nu admite nicio reprezentare de acest tip. Cu toate acestea, fiecare reprezentare a unui număr compus admite una simetrică în funcție de faptul dacă partea lungă este orizontală sau verticală; oprirea sitei (sau diviziunilor) odată atinsă rădăcina lui X înseamnă luarea în considerare a unui singur dreptunghi pentru fiecare pereche de dreptunghiuri simetrice.

factorizare primara

Același subiect în detaliu: Teorema fundamentală a aritmeticii .

Importanța numerelor prime în matematică este enormă și derivă în esență din teorema fundamentală a aritmeticii , care afirmă că orice număr întreg pozitiv, altul decât 1, poate fi factorizat prim și această descompunere este unică până la ordinea factorilor.

De exemplu, 23244 este considerat ca

23244=2^{2}\times 3\times 13\times 149

{\ displaystyle 23244 = 2 ^ {2} \ times 3 \ times 13 \ times 149}

23244 = 2 ^ 2 \ ori 3 \ ori 13 \ ori 149

și orice altă factorizare primă se obține din aceasta permutând factorii. De exemplu, factoring ulterior

23244=13\times 3\times 2\times 149\times 2

{\ displaystyle 23244 = 13 \ ori 3 \ ori 2 \ ori 149 \ ori 2}

23244 = 13 \ ori 3 \ ori 2 \ ori 149 \ ori 2

nu este altul decât precedentul cu factorii scrisi într-o ordine diferită. Din cauza acestei proprietăți, primii sunt uneori denumiți „ atomi aritmetici”. ^[17]

Acesta este, printre altele, principalul motiv pentru care 1 este exclus din setul primilor. De fapt, dacă multiplicați o factorizare a unui număr cu unul, de câte ori doriți, obțineți întotdeauna numărul inițial, creând astfel factorizări distincte.

O proprietate strâns legată de factorizarea unică este lema lui Euclid : dacă un p prim împarte produsul ab , atunci împarte a sau b . Aceasta este considerată chiar definiția elementului prim într-un domeniu de integritate , ^[18] și este evident pornind de la teorema fundamentală a aritmeticii: factorizarea lui ab trebuie să conțină de fapt p prim și, din moment ce p nu poate fi „divizat” în doi factori, trebuie să fie în mod necesar în factorizarea a cel puțin unuia dintre cele două numere.

Infinit

Același subiect în detaliu: Teorema infinitului numerelor prime .

Numerele prime sunt infinite. Cea mai veche dovadă care a supraviețuit este cea a lui Euclid , care o prezintă în cartea IX a Elementelor , ca propoziție 20, cu cuvintele:

"Numerele prime sunt mai mult decât orice multitudine dată de numere prime."

Dovada continuă în mod absurd . De fapt, presupunând că există doar un număr finit de numere prime p ₁ , p ₂ , ..., p _n , putem considera numărul q = p ₁ p ₂ ··· p _n + 1: acest număr este evident mai mare de 1 și diferită de toate numerele prime p _i . Acum, există două posibilități pentru q : poate fi prim sau compozit. Dacă ar fi prim, am avea însă o contradicție, pentru că am presupus că p _i sunt toate numere prime; dacă ar fi compus, ar avea un factor prim d , care trebuie să fie unul dintre numerele prime p _i . Dar apoi d împarte atât q cât și produsul p ₁ p ₂ p _n (fiind unul dintre numerele prime) și, prin urmare, trebuie să împartă diferența lor q - p ₁ p ₂ p _n = 1, ceea ce este imposibil. Prin urmare, q nu poate fi nici primă, nici compusă: dar acest lucru este absurd, iar numerele prime sunt infinite.

O întrebare care apare din dovadă este dacă numerele sub forma p ₁ p ₂ ··· p _n + 1, adică produsul primelor n prime plus 1 (numite numerele lui Euclid ), sunt prime sau nu. Acest lucru se întâmplă în primele cazuri (2 · 3 + 1 = 7 este prim, precum și 2 · 3 · 5 + 1 = 31), dar este fals în general: cel mai mic dintre aceste numere care trebuie compus este

2\cdot 3\cdot 5\cdot 7\cdot 11\cdot 13+1=30031=59\cdot 509.

{\ displaystyle 2 \ cdot 3 \ cdot 5 \ cdot 7 \ cdot 11 \ cdot 13 + 1 = 30031 = 59 \ cdot 509.}

2 \ cdot 3 \ cdot 5 \ cdot 7 \ cdot 11 \ cdot 13 + 1 = 30 031 = 59 \ cdot 509.

Nu se știe dacă există numere prime infinite în această succesiune, deși s-a presupus că acesta este cazul. ^[19]

Multe alte dovezi au fost create de-a lungul secolelor: Euler a dovedit această teoremă pornind de la divergența seriei armonice , Goldbach prin numerele Fermat , în timp ce Harry Furstenberg a conceput una folosind metode de topologie . ^[20]

O teoremă mai puternică, care poate fi obținută cu ușurință din infinitul numerelor prime, este cea care stabilește că seria ^{_{^{_{1/2 + 1/3 +}}}} 1/5 + 1/7 + 1/11 + ..., formată prin suma de inversele numerelor prime, divergente , ^[21] și în special, folosind notația mare -O :

\sum _{p\leq n}{\frac {1}{p}}=\ln \ln n+O(1).

{\ displaystyle \ sum _ {p \ leq n} {\ frac {1} {p}} = \ ln \ ln n + O (1).}

\ sum_ {p \ leq n} \ frac {1} {p} = \ ln \ ln n + O (1).

^[22]

Această teoremă se datorează lui Euler, care a dovedit-o în secolul al XVIII-lea.

Din dovada lui Euclid rezultă, de asemenea, că

p_{n+1}<p_{1}p_{2}\cdots p_{n}.

{\ displaystyle p_ {n + 1} <p_ {1} p_ {2} \ cdots p_ {n}.}

p_ {n + 1} <p_1p_2 \ cdots p_n.

Această inegalitate poate fi îmbunătățită: H. Bonse a dovedit în 1907 ( inegalitatea Bonse ) că ^[23]

p_{n+1}^{2}<p_{1}p_{2}...p_{n}

{\ displaystyle p_ {n + 1} ^ {2} <p_ {1} p_ {2} ... p_ {n}}

p_ {n + 1} ^ 2 <p_1 p_2 ... p_n

pentru n > 3. Pe această cale, s-a arătat că inegalitatea

p_{n+1}^{k}<p_{1}p_{2}...p_{n}

{\ displaystyle p_ {n + 1} ^ {k} <p_ {1} p_ {2} ... p_ {n}}

p_ {n + 1} ^ k <p_1 p_2 ... p_n

este verificat pentru fiecare n > 2 k - 1. ^[24]

Distribuția numerelor prime

Același subiect în detaliu: teorema numărului prim .

Comparația dintre funcțiile π ( x ) (albastru), x / ln x (verde) și Li ( x ) (roșu), se poate observa că aproximarea lui π ( x ) cu Li ( x ) se dovedește a fi de mult mai bine decât x / ln x

Odată ce s-a demonstrat că numerele prime sunt infinite, se întreabă în mod firesc cum sunt distribuite în secvența numerelor naturale, adică cât de frecvente sunt acestea și când ne putem aștepta să găsim al n - lea număr prim. Acest studiu a fost început spre sfârșitul secolului al XVIII-lea, independent de Gauss și Legendre , care au introdus funcția $\pi (x)$ ${\ displaystyle \ pi (x)}$ $\ pi (x)$ (numită funcția enumerativă a celei dintâi ) și a presupus că era aproximativ

\pi (x)\sim {\frac {x}{\ln x}}.

{\ displaystyle \ pi (x) \ sim {\ frac {x} {\ ln x}}.}

\ pi (x) \ sim \ frac {x} {\ ln x}.

^[25]

Încercarea de a demonstra această conjectură s-a întins pe tot parcursul secolului al XIX-lea; primele rezultate au fost obținute între 1848 și 1859 de Čebyšëv , care a dovedit folosind metode pur aritmetice că există două constante A și B astfel încât

A\leq {\frac {\pi (x)}{\frac {x}{\ln x}}}\leq B

{\ displaystyle A \ leq {\ frac {\ pi (x)} {\ frac {x} {\ ln x}}} \ leq B}

A \ leq \ frac {\ pi (x)} {\ frac {x} {\ ln x}} \ leq B

pentru x suficient de mare. ^[26] El a putut, de asemenea, să demonstreze că, dacă există limita relației, atunci trebuie să fie 1. ^[27]

O dovadă a fost găsită în 1896 de Hadamard și de la Vallée-Poussin , care, în timp ce lucrau independent unul de celălalt, au folosit metode similare, bazate pe utilizarea funcției zeta Riemann , care fusese introdusă de Bernhard Riemann în 1859 . Pentru o demonstrație care folosea doar metode elementare (adică fără a utiliza metode complexe de analiză ) a trebuit să aștepte până în 1949 , când a fost concepută de Selberg și Erdős . Teorema este acum cunoscută sub numele de teorema numărului prim .

Comparație între al doilea număr prim (în albastru) și n · ln n (în roșu), pentru n între 0 și 10000.

Gauss a introdus, de asemenea, o estimare mai precisă, folosind funcția de logaritm integral :

\pi (x)\sim {\frac {}{}}\mathrm {Li} (x)=\int _{2}^{x}{\frac {1}{\ln u}}\mathrm {d} u.

{\ displaystyle \ pi (x) \ sim {\ frac {} {}} \ mathrm {Li} (x) = \ int _ {2} ^ {x} {\ frac {1} {\ ln u}} \ mathrm {d} u.}

\ pi (x) \ sim \ frac {} {} \ mathrm {Li} (x) = \ int_2 ^ x \ frac {1} {\ ln u} \ mathrm {d} u.

^[28]

În 1899 de la Vallée-Poussin a dovedit că eroarea comisă prin aproximare $\pi (x)$ ${\ displaystyle \ pi (x)}$ $\ pi (x)$ așa este

\pi (x)-\mathrm {Li} (x)=O\left(x\mathrm {e} ^{-a{\sqrt {\ln x}}}\right)=O\left({\frac {x}{(\ln x)^{m}}}\right)

{\ displaystyle \ pi (x) - \ mathrm {Li} (x) = O \ left (x \ mathrm {e} ^ {- a {\ sqrt {\ ln x}}} \ right) = O \ left ( {\ frac {x} {(\ ln x) ^ {m}}} \ right)}

\ pi (x) - \ mathrm {Li} (x) = O \ left (x \ mathrm {e} ^ {- a \ sqrt {\ ln x}} \ right) = O \ left (\ frac {x} {(\ ln x) ^ m} \ dreapta)

pentru o constantă pozitivă a și orice număr întreg m ; acest rezultat a fost ușor îmbunătățit de-a lungul anilor. ^[29] Mai mult, în 1901 von Koch a arătat că, dacă ipoteza Riemann este adevărată, atunci se are o estimare mult mai precisă:

\pi (x)-\mathrm {Li} (x)=O\left({\sqrt {x}}\ln x\right).

{\ displaystyle \ pi (x) - \ mathrm {Li} (x) = O \ left ({\ sqrt {x}} \ ln x \ right).}

\ pi (x) - \ mathrm {Li} (x) = O \ left (\ sqrt x \ ln x \ right).

^[30]

O formă echivalentă teoremei numărului prim este că p _n , al n - lea număr prim, este bine aproximat de n ln ( n ). De fapt, p _n este strict mai mare decât această valoare, după cum a demonstrat J. Barkley Rosser în 1938 ; ^[31] această inegalitate a fost îmbunătățită până la atingerea, în 1995, a

p_{n}>n(\ln n+\ln \ln n-1),~

{\ displaystyle p_ {n}> n (\ ln n + \ ln \ ln n-1), ~}

p_n> n (\ ln n + \ ln \ ln n -1), ~

pentru n ≥ 2. ^[32] ^[33]

Intervalele între numere prime

Distribuția primelor gemene pentru n ≤100.000

Legat de distribuția numerelor prime este studiul intervalelor dintre două prime consecutive. Acesta, în afară de perechea formată din 2 și 3, trebuie să fie în mod necesar un număr par mai mare sau egal cu 2, deoarece între două numere consecutive cel puțin unul este par și, prin urmare, nu este prim. Dacă două numere prime au diferența 2, acestea se numesc gemeni : cu excepția „tripletului” format din 3, 5 și 7, primii gemeni apar în perechi și este ușor de verificat că, cu excepția cazului 3 și 5, numărul plasat între ele este întotdeauna un multiplu de 6. Cele mai mici perechi de gemeni gemeni sunt (3, 5), (5, 7), (11, 13), (17, 19) și (29, 31 ). S-a presupus că există perechi infinite de gemeni gemeni, deși nimeni nu a reușit încă să o demonstreze; o extensie a acestei idei este de a întreba dacă, având în vedere un număr par k , diferența dintre două numere prime consecutive este egală cu k un număr infinit de ori. Ultima problemă se numește conjectura Polignac .

Pe de altă parte, este ușor să arătăm că această diferență poate fi la fel de mare pe cât ne place: dat un număr întreg N și notând cu N! factorialul său (adică produsul tuturor numerelor cuprinse între 1 și N ), numerele

(N+1)!+2,~(N+1)!+3,\cdots ,(N+1)!+N+1

{\ displaystyle (N + 1)! + 2, ~ (N + 1)! + 3, \ cdots, (N + 1)! + N + 1}

(N + 1)! + 2, ~ (N + 1)! + 3, \ cdots, (N + 1)! + N + 1

toate sunt compozite: de fapt, dacă m este mai mic decât N , atunci ( N + 1)! + m este divizibil cu m și, prin urmare, nu este prim. Secvența, care include N numere consecutive, este deci lipsită de numere prime. De exemplu, dacă N = 5, aceste valori corespund

6!+2=722=2\times 361

{\ displaystyle 6! + 2 = 722 = 2 \ ori 361}

6! + 2 = 722 = 2 \ ori 361

6!+3=723=3\times 241

{\ displaystyle 6! + 3 = 723 = 3 \ ori 241}

6! + 3 = 723 = 3 \ ori 241

6!+4=724=4\times 181

{\ displaystyle 6! + 4 = 724 = 4 \ ori 181}

6! + 4 = 724 = 4 \ ori 181

6!+5=725=5\times 145

{\ displaystyle 6! + 5 = 725 = 5 \ ori 145}

6! + 5 = 725 = 5 \ ori 145

6!+6=726=6\times 121

{\ displaystyle 6! + 6 = 726 = 6 \ ori 121}

6! + 6 = 726 = 6 \ ori 121

în timp ce următoarea valoare, 6! + 7 = 727, este primă. ^[34] Rețineți, totuși, că există modalități mai „eficiente” de a construi intervale fără numere prime; de exemplu în loc de ( N + 1)! + 1 poate fi considerat produsul numerelor prime mai mici decât N + 2.

Din teorema numărului prim rezultă cu ușurință că intervalul așteptat între două numere prime consecutive p _n și p _{n +1} are lungimea ln ( p _n ); cu toate acestea, aceste intervale sunt uneori mult mai mari și alteori mult mai mici. La intervale scurte, conjectura primă twin precizează exact că intervalul este timpul infinit minim posibil. Această presupunere este încă deschisă, dar datorită muncii lui Zhang Yitang (anunțată în 2013 și bazată pe abordarea Goldston , Pintz și Yıldırım ^[35] ) și a contribuțiilor ulterioare ale lui James Maynard și a unui proiect Polymath , se știe că acolo sunt numere prime consecutive consecutive a căror diferență este mai mică de 246. ^[36] ^[37] ^[38] ^[39]

La problema opusă, a intervalelor lungi, se așteaptă ca astfel de intervale să fie de ordinul ln ² p _n sau, mai exact, că

0<\limsup _{n\rightarrow \infty }{\frac {p_{n+1}-p_{n}}{\ln ^{2}n}}\ll 1,

{\ displaystyle 0 <\ limsup _ {n \ rightarrow \ infty} {\ frac {p_ {n + 1} -p_ {n}} {\ ln ^ {2} n}} \ ll 1,}

0 <\ limsup_ {n \ rightarrow \ infty} \ frac {p_ {n + 1} -p_ {n}} {\ ln ^ 2n} \ ll1,

^[40]

în timp ce cele mai bune rezultate dovedite sunt

\limsup _{n\rightarrow \infty }{\frac {p_{n+1}-p_{n}}{\ln p_{n}(\ln \ln p_{n})(\ln \ln \ln \ln p_{n})/\ln \ln \ln p_{n}}}>0

{\ displaystyle \ limsup _ {n \ rightarrow \ infty} {\ frac {p_ {n + 1} -p_ {n}} {\ ln p_ {n} (\ ln \ ln p_ {n}) (\ ln \ ln \ ln \ ln p_ {n}) / \ ln \ ln \ ln p_ {n}}}> 0}

\ limsup _ {{n \ rightarrow \ infty}} {\ frac {p _ {{n + 1}} - p _ {{n}}} {\ ln p_ {n} (\ ln \ ln p_ {n} ) (\ ln \ ln \ ln \ ln p_ {n}) / \ ln \ ln \ ln p_ {n}}}> 0

^[41]

Și

p_{n+1}-p_{n}=O\left(p_{n}^{\frac {21}{40}}\right),

{\ displaystyle p_ {n + 1} -p_ {n} = O \ left (p_ {n} ^ {\ frac {21} {40}} \ right),}

p_ {n + 1} -p_n = O \ left (p_n ^ {\ frac {21} {40}} \ right),

^[42]

datorate respectiv Ford , Green , Konjagin , Maynard și Tao și lui Pintz.

Un alt rezultat clasic, deși mai slab decât cel care tocmai a fost raportat, este postulatul lui Bertrand (care este de fapt o teoremă, fiind demonstrat de Čebyšëv în 1850 ). Se afirmă că pentru fiecare n există întotdeauna un prim între n și 2 n . O consecință interesantă a acestui rezultat este că p _{n +1} <2 p _n ; având în vedere, de asemenea, că p ₁ = 2 este ușor de dedus că pentru fiecare n se menține inegalitatea

p_{n}<2^{n}.

{\ displaystyle p_ {n} <2 ^ {n}.}

p_n <2 ^ n.

De-a lungul secolelor, s-au propus multe presupuneri despre intervalele dintre primele consecutive. Cele mai faimoase sunt conjectura Legendre , care afirmă că între două pătrate consecutive există întotdeauna o primă, conjectura Brocard care afirmă că între pătratele a două prime impare consecutive există întotdeauna patru numere prime și conjectura Andrica care presupune că

{\sqrt {p_{n+1}}}-{\sqrt {p_{n}}}<1.

{\ displaystyle {\ sqrt {p_ {n + 1}}} - {\ sqrt {p_ {n}}} <1.}

\ sqrt {p_ {n + 1}} - \ sqrt {p_n} <1.

Aceste presupuneri sunt toate mult mai slabe decât se crede că sunt adevărate, dar sunt încă nedovedite. Cele mai bune rezultate în această direcție sunt demonstrarea faptului că între n ² și (n + 1) ² minciuni ^există întotdeauna cel puțin un prim sau un semi prim, datorită Chen Jingrun , ^[43] și rezultatul Baker, Harman și Pintz raportate mai sus.

Relațiile cu alte domenii ale matematicii

Fiind fundamentul aritmeticii , numerele prime sunt ingrediente fundamentale într-un număr mare de domenii ale matematicii.

Funcții aritmetice

Funcțiile aritmetice , adică funcțiile definite pe numere întregi și pe valori în numere complexe , joacă un rol crucial în teoria numerelor . În special, dintre acestea cele mai importante sunt funcțiile multiplicative , adică acele funcții f în care, pentru fiecare pereche ( a , b ) de numere coprimă , avem

f(ab)=f(a)f(b).

{\ displaystyle f (ab) = f (a) f (b).}

f (ab) = f (a) f (b).

Exemple de funcții multiplicative sunt φ ale funcției Euler , care în n asociază numărul de numere întregi care sunt în același timp mai mici și coprimă cu n și divizorul de funcții și sigma , care în n au asociat respectiv numărul divizorilor săi și suma lor . Valoarea acestor funcții în puterile celei dintâi este

Funcția lui Euler φ: $\operatorname {\varphi } (p^{m})=p^{m}-p^{m-1},$ ${\ displaystyle \ operatorname {\ varphi} (p ^ {m}) = p ^ {m} -p ^ {m-1},}$ $\ operatorname {\ varphi} (p ^ m) = p ^ m-p ^ {m-1},$
funcție divizor: $d(p^{m})=m+1,$ ${\ displaystyle d (p ^ {m}) = m + 1,}$ $d (p ^ m) = m + 1,$
funcția sigma: $\operatorname {\sigma } (p^{m})=1+p^{1}+p^{2}+p^{3}+\cdots +p^{m}.$ ${\ displaystyle \ operatorname {\ sigma} (p ^ {m}) = 1 + p ^ {1} + p ^ {2} + p ^ {3} + \ cdots + p ^ {m}.}$ $\ operatorname {\ sigma} (p ^ {m}) = 1 + p ^ {1} + p ^ {2} + p ^ {3} + \ cdots + p ^ {m}.$

Datorită proprietății care le definește, funcțiile aritmetice pot fi ușor calculate cunoscând valoarea pe care și-o asumă în puterile celei dintâi. De fapt, având în vedere un număr întreg de factorizare n

n=p_{1}^{q_{1}}\cdots p_{a}^{q_{a}},

{\ displaystyle n = p_ {1} ^ {q_ {1}} \ cdots p_ {a} ^ {q_ {a}},}

n = p_1 ^ {q_1} \ cdots p_a ^ {q_a},

avem asta

f(n)=f(p_{1}^{q_{1}})\cdots f(p_{a}^{q_{a}})

{\ displaystyle f (n) = f (p_ {1} ^ {q_ {1}}) \ cdots f (p_ {a} ^ {q_ {a}})}

f (n) = f (p_1 ^ {q_1}) \ cdots f (p_a ^ {q_a})

și, prin urmare, problema calculării f ( n ) a fost readusă la cea a calculării f pe puterile primilor care împart n , valori care sunt în general mai ușor de obținut decât o formulă generală. De exemplu, pentru a cunoaște valoarea funcției lui Euler φ pe n = 450 = 2 × 3 ² × 5 ² este suficient să se calculeze

\operatorname {\varphi } (450)=\operatorname {\varphi } (2)\cdot \operatorname {\varphi } (3^{2})\cdot \operatorname {\varphi } (5^{2})=(2-1)\cdot (9-3)\cdot (25-5)=120.

{\ displaystyle \ operatorname {\ varphi} (450) = \ operatorname {\ varphi} (2) \ cdot \ operatorname {\ varphi} (3 ^ {2}) \ cdot \ operatorname {\ varphi} (5 ^ {2 }) = (2-1) \ cdot (9-3) \ cdot (25-5) = 120.}

\ operatorname {\ varphi} (450) = \ operatorname {\ varphi} (2) \ cdot \ operatorname {\ varphi} (3 ^ 2) \ cdot \ operatorname {\ varphi} (5 ^ 2) = (2-1 ) \ cdot (9-3) \ cdot (25-5) = 120.

Faptul că o funcție multiplicativă este identificată prin valorile asumate în corespondență cu puterile numerelor prime se află la originea utilizării seriei Bell , care sunt anumite serii formale de putere formale . Având o funcție multiplicativă f și un p prim, seria Bell a lui f față de p este:

f_{p}(x)=\sum _{n=0}^{\infty }f(p^{n})x^{n}.

{\ displaystyle f_ {p} (x) = \ sum _ {n = 0} ^ {\ infty} f (p ^ {n}) x ^ {n}.}

f_p (x) = \ sum_ {n = 0} ^ \ infty f (p ^ n) x ^ n.

În special, dacă f este complet multiplicativ (adică dacă f ( ab ) = f ( a ) f ( b ) pentru fiecare a și b ), atunci f este identificat prin valorile lui f ( p ), pentru p prime, iar seria Bell este:

f_{p}(x)=\sum _{n=0}^{\infty }f(p)^{n}x^{n}={\frac {1}{1-f(p)x}}.

{\ displaystyle f_ {p} (x) = \ sum _ {n = 0} ^ {\ infty} f (p) ^ {n} x ^ {n} = {\ frac {1} {1-f (p ) X}}.}

f_p (x) = \ sum_ {n = 0} ^ \ infty f (p) ^ n x ^ n = \ frac {1} {1-f (p) x}.

Aritmetica modulară

În aritmetica modulară , numerele prime joacă un rol foarte important: inelul $\mathbb {Z} /n\mathbb {Z}$ ${\ displaystyle \ mathbb {Z} / n \ mathbb {Z}}$ $\ mathbb {Z} / n \ mathbb {Z}$ din restul claselor este de fapt un câmp dacă și numai dacă n este prim. În acest caz, studiul claselor rămase este mai simplu decât cazul general și oferă un punct de plecare util pentru analiza claselor rămase cu orice n .

De asemenea, existența unei rădăcini primitive a inelului $\mathbb {Z} /n\mathbb {Z}$ $\mathbb {Z} /n\mathbb {Z}$ $\mathbb{Z}/n\mathbb{Z}$ è legata ai numeri primi: questa infatti esiste solamente se n è un numero primo, 1, 2, 4 oppure un numero nella forma $p^{n}$ $p^{n}$ $p^n$ o $2p^{n}$ $2p^{n}$ $2p^n$ , dove p è un primo dispari. ^[44]

Uno dei teoremi più importanti dell'aritmetica modulare è costituito dal piccolo teorema di Fermat . Tale teorema afferma che, per ogni primo p e ogni numero naturale a si ha

a^{p}\equiv a\mod p.

a^{p}\equiv a\mod p.

a^p\equiv a\mod p.

Equivalentemente, per ogni primo p e ogni intero a coprimo con p , si ha

a^{p-1}\equiv 1\mod p.

a^{p-1}\equiv 1\mod p.

a^{p-1}\equiv 1\mod p.

Questa proprietà può essere usata per verificare se un numero non è primo, infatti se n è tale che

a^{n}\not \equiv a\mod n

a^{n}\not \equiv a\mod n

a^{n}\not\equiv a\mod n

per qualche intero a , allora n non può essere primo. Tuttavia questa proprietà non può essere usata per controllare se un numero è primo: esistono infatti alcuni numeri, detti numeri di Carmichael (il più piccolo dei quali è 561), che verificano questa proprietà per ogni a pur non essendo primi. Nel 1994 , William Robert Alford , Andrew Granville e Carl Pomerance hanno dimostrato che vi sono infiniti numeri di tale tipo. ^[45]

Numeri p -adici

Lo stesso argomento in dettaglio: Numero p-adico .

Un altro degli argomenti principali della teoria dei numeri è costituito dallo studio dei numeri p -adici e delle loro proprietà. Tali numeri sono definiti nel modo seguente: per ogni primo p si considera una norma sui numeri razionali $\mathbb {Q}$ $\mathbb {Q}$ $\mathbb{Q}$ che, valutata su un numero razionale q , assume valori che si avvicinano allo 0 al crescere della massima potenza di p che divide q . Tale norma è detta "norma p -adica". Completando il campo dei numeri razionali rispetto alla metrica indotta da tale norma, si ottiene un campo, indicato con $\mathbb {Q} _{p}$ $\mathbb {Q} _{p}$ $\mathbb{Q}_p$ , che "estende" i numeri razionali in un modo diverso dai numeri reali . Gli elementi di tale campo sono detti numeri p -adici . Tali numeri si possono anche costruire come limite proiettivo degli anelli $\mathbb {Z} /p\mathbb {Z} ,~\mathbb {Z} /p^{2}\mathbb {Z} ,~\mathbb {Z} /p^{3}\mathbb {Z} \ldots$ $\mathbb {Z} /p\mathbb {Z} ,~\mathbb {Z} /p^{2}\mathbb {Z} ,~\mathbb {Z} /p^{3}\mathbb {Z} \ldots$ $\mathbb{Z}/p\mathbb{Z},~\mathbb{Z}/p^2\mathbb{Z},~ \mathbb{Z}/p^3\mathbb{Z}\ldots$ .

Teoria dei gruppi

I numeri primi hanno un ruolo centrale anche nell' algebra . Nella teoria dei gruppi , un gruppo in cui ogni elemento ha ordine la potenza di un primo p è detto p-gruppo o gruppo primario . Tra i gruppi finiti , i p -gruppi sono tutti e soli i gruppi la cui cardinalità è la potenza di un primo; un esempio di p -gruppo infinito è il p -gruppo di Prüfer .

È noto che i p -gruppi hanno un centro non banale, e di conseguenza non possono essere semplici (a parte il gruppo con p elementi); se il gruppo è finito, inoltre, tutti i sottogruppi normali intersecano il centro in modo non banale.

Tutti i gruppi con un numero primo di elementi sono ciclici e dunque abeliani ; anche ogni gruppo di ordine p ² è abeliano. Inoltre, ogni gruppo abeliano finito è isomorfo al prodotto diretto di un numero finito di p -gruppi ciclici.

Ilteorema di Cauchy afferma che, dato un gruppo di ordine n e un primo p che lo divide, esiste un elemento di ordine p , e quindi un sottogruppo con p elementi. Tale teorema è generalizzato dai teoremi di Sylow , che garantiscono che in ogni gruppo di ordine n esiste almeno un sottogruppo di ordine p ^m , per ogni p ^m che divide n .

Teoria degli anelli e teoria dei campi

Nella teoria degli anelli , la caratteristica di un dominio d'integrità D è 0 oppure un numero primo. Per un campo F , che è un particolare tipo di dominio di integrità, la caratteristica determina il sottocampo fondamentale di F : se essa è diversa da 0, e dunque è un numero primo, allora tale sottocampo è isomorfo al campo delle classi di resto $\mathbb {Z} /p\mathbb {Z}$ $\mathbb {Z} /p\mathbb {Z}$ $\mathbb{Z}/p\mathbb{Z}$ .

Si mostra poi che tutti i campi finiti formano uno spazio vettoriale sul campo $\mathbb {Z} /p\mathbb {Z}$ $\mathbb {Z} /p\mathbb {Z}$ $\mathbb{Z}/p\mathbb{Z}$ , e di conseguenza hanno un numero di elementi che è primo o è una potenza di un primo. Inoltre, due campi con lo stesso numero di elementi sono isomorfi ; in particolare, ogni campo con un numero primo p di elementi coincide con $\mathbb {Z} /p\mathbb {Z}$ $\mathbb {Z} /p\mathbb {Z}$ $\mathbb{Z}/p\mathbb{Z}$ , mentre ogni campo con p ⁿ elementi è un' estensione di Galois di un campo con p elementi.

Tra le estensioni dei numeri razionali, un ruolo importante è svolto dalle estensioni ciclotomiche , ossia da quei campi che si possono ottenere aggiungendo a $\mathbb {Q}$ $\mathbb {Q}$ $\mathbb{Q}$ le radici n -esime dell'unità , per un qualche numero naturale n . Il grado di queste estensioni è strettamente legato alla primalità di n . Infatti esso è n − 1 se e solo se n è primo: tale proprietà è equivalente al fatto che il polinomio

P(x)=x^{n-1}+x^{n-2}+\cdots +x^{2}+x+1

P(x)=x^{n-1}+x^{n-2}+\cdots +x^{2}+x+1

P(x)=x^{n-1}+x^{n-2}+\cdots+x^2+x+1

è irriducibile tra i polinomi a coefficienti razionali se e solo se n è primo. Per una dimostrazione si può procedere come segue: se n è composto (ad esempio n = ab , con a e b interi maggiori di 1), lo si può dividere in a gruppi di b addendi, arrivando a una scomposizione. Ad esempio, se n = 10, prendendo a = 2 e b = 5, P ( x ) si può scomporre come

x^{9}+x^{8}+\cdots +x^{2}+x+1=x^{8}(x+1)+x^{6}(x+1)+x^{4}(x+1)+x^{2}(x+1)+(x+1)=(x^{8}+x^{6}+x^{4}+x^{2}+1)(x+1).

x^{9}+x^{8}+\cdots +x^{2}+x+1=x^{8}(x+1)+x^{6}(x+1)+x^{4}(x+1)+x^{2}(x+1)+(x+1)=(x^{8}+x^{6}+x^{4}+x^{2}+1)(x+1).

x^9+x^8+\cdots+x^2+x+1=x^8(x+1)+x^6(x+1)+x^4(x+1)+x^2(x+1)+(x+1)=(x^8+x^6+x^4+x^2+1)(x+1).

Per dimostrare l'inverso, si può usare l'invece il criterio di Eisenstein . Grazie a questa proprietà risulta inoltre che se n è primo, allora questo polinomio coincide con l' n -esimo polinomio ciclotomico .

Polinomi e progressioni aritmetiche

È stato dimostrato da Legendre alla fine del Settecento ^[46] che nessun polinomio a coefficienti interi può assumere valori soltanto primi: infatti, se esistesse un polinomio P ( n ) di questo tipo, si avrebbe P (1) = p per qualche primo p e quindi P (1) ≡ 0 mod p . Ma P (1) ≡ P (1+ kp ) mod p per ogni intero k , e quindi P (1+ kp ) dovrebbe assumere infinite volte il valore p (perché i multipli di p non possono essere primi). Tuttavia questo è assurdo, perché nessun polinomio può assumere uno stesso valore un numero di volte maggiore del proprio grado. ^[47]

Alcuni polinomi sembrano assumere valori primi "più spesso" degli altri: ad esempio Eulero notò che il polinomio di secondo grado $n^{2}+n+41$ $n^{2}+n+41$ $n^2+n+41$ produce numeri primi per ogni valore di n compreso tra 0 e 39; tuttavia, sebbene circa un terzo dei valori che questa funzione assume nei primi 10 milioni siano primi, ^[48] non è stato ancora dimostrato che ne esistano infiniti. Più in generale, non c'è alcun polinomio in una sola variabile e di grado maggiore di uno di cui sia stato dimostrato che assume infiniti valori primi. Diversa è la situazione per i polinomi in due variabili: Dirichlet dimostrò che questo avviene per ogni forma quadratica $ax^{2}+bxy+cy^{2}$ $ax^{2}+bxy+cy^{2}$ $ax^2+bxy+cy^2$ (a patto che a , b e c siano coprimi e che la forma non sia il quadrato di un polinomio di primo grado), ^[49] mentre nel 1998 John Friedlander e Henryk Iwaniec lo provarono per il polinomio di quarto grado $x^{2}+y^{4}$ $x^{2}+y^{4}$ $x^2+y^4$ . ^[50]

Frazione dei numeri primi congrui a 3 modulo 4.

A differenza di quanto accade per i polinomi di grado più alto, Dirichlet dimostrò nel 1837 che ogni polinomio di primo grado ax + b assume infiniti valori primi se e solo se a e b sono numeri naturali coprimi. Equivalentemente, una progressione aritmetica contiene infiniti numeri primi se e solo se la sua ragione e il suo primo valore sono coprimi. La prima dimostrazione di questo teorema, detto teorema di Dirichlet , viene considerata la nascita dellaTeoria dei numeri analitica . ^[51]

È noto inoltre che, se n e k sono coprimi, il rapporto tra M ei primi minori di M che sono congrui a k modulo n tende a $1/\phi (n)$ $1/\phi (n)$ $1/\phi(n)$ per M che tende all'infinito, ovvero i primi tendono a dividersi equamente tra le $\phi (n)$ $\phi (n)$ $\phi(n)$ progressioni di ragione n che contengono più di un primo. ^[52]

Sebbene non esistano progressioni aritmetiche i cui valori siano soltanto numeri primi, nel 2004 è stato dimostrato che esistono progressioni che contengono un numero arbitrariamente grande di termini consecutivi che sono primi ( teorema di Green-Tao ). ^[53] Tale risultato è stato migliorato nel 2006 per includere anche le progressioni polinomiali; più precisamente è stato dimostrato che, dati dei polinomi P ₁ , ..., P _m a coefficienti interi, esistono infiniti interi a e m tali che a + P ₁ ( n ), ..., a + P _m ( n ) sono contemporaneamente primi per 1 ≤ n ≤ m . ^[54]

Tali teoremi non sono tuttavia costruttivi , ovvero non permettono di determinare esplicitamente delle progressioni arbitrariamente lunghe; la più lunga sequenza di primi (attualmente conosciuta) che sono termini consecutivi di una progressione aritmetica è composta da 26 numeri. ^[55] È stato anche congetturato che esistano sequenze arbitrariamente lunghe di questo tipo tali che tra due termini della progressione non ci siano altri numeri primi, e la più lunga sequenza di primi di questo tipo finora trovata comprende 10 termini. ^[56] ^[57]

Una progressione aritmetica di interesse particolare per la teoria dei numeri primi è quella di ragione 4: si possono infatti separare i primi (a parte 2) in due gruppi, quelli nella forma 4 k +1 e quelli nella forma 4 k +3. Il teorema di Fermat sulle somme di due quadrati asserisce che i primi che possono essere scritti come somma di due quadrati sono tutti e soli quelli del primo gruppo. Un'importante riformulazione di questo teorema è che un primo è scomponibile nell' anello degli interi di Gauss se e solo se è della forma 4 k +1.

Problemi additivi

Il numero di modi con cui un numero n si può scrivere come somma di due primi per n ≤1 000 000

Per la loro definizione, i numeri primi sono intrinsecamente legati all' operazione di moltiplicazione. Tuttavia, sono di grande interesse anche alcuni problemi riguardanti loro proprietà additive .

Il più famoso di questi è senza dubbio la congettura proposta da Christian Goldbach nel Settecento , che afferma che ogni numero pari maggiore di 2 può essere espresso come somma di due primi. La congettura è tuttora indimostrata, ma è facilmente verificabile per gli interi “piccoli”, come ad esempio

4 = 2 + 2

6 = 3 + 3

8 = 3 + 5

10 = 3 + 7 = 5 + 5

12 = 5 + 7

14 = 3 + 11 = 7 + 7,

e tramite l'uso di computer è stata controllata anche per tutti gli n minori di 2×10 ¹⁸ . ^[58]

Alla congettura di Goldbach ne è legata un'altra, più debole e ora dimostrata, che afferma che ogni numero dispari è la somma di tre numeri primi. Questa ex -congettura è comunemente nota con il nome di congettura debole di Goldbach .

Mentre la congettura di Goldbach sembra molto lontana dall'essere risolta, la seconda ha conosciuto diversi progressi nel corso degli anni, culminati nella dimostrazione completa data da Harald Helfgott nel 2013 . In precedenza, risultati significativi erano stati ottenuti da Hardy e Littlewood , che nel 1923 provarono che l' ipotesi di Riemann generalizzata implica che ogni numero dispari sufficientemente grande è la somma di tre primi, ^[59] e da Ivan Vinogradov che nel 1937 dimostrò che l'assunzione dell'ipotesi di Riemann non è necessaria. ^[60] Per completare la dimostrazione mancavano quindi solo un numero finito di numeri dispari da controllare ^[61] , ma tale numero era ben al di là delle capacità computazionali dei moderni computer. Nel 2013, Helfgott introdusse diverse innovazioni all'interno della dimostrazione di Vinogradov, riuscendo ad abbassare notevolmente il numero di potenziali eccezioni a un numero effettivamente controllabile da un computer e quindi a completare la dimostrazione.

Sono noti anche altri risultati, sebbene molto più deboli. Usando il postulato di Bertrand si può dimostrare che ogni intero maggiore di 6 può essere scritto come somma di primi distinti. Inoltre, se p _n è l' n -esimo numero primo, allora almeno uno tra p _n , p _n − 1 e p _n + 1 può essere scritto come

\pm 2\pm 3\pm 5\cdots \pm p_{n-1}

\pm 2\pm 3\pm 5\cdots \pm p_{n-1}

\pm 2\pm 3\pm 5\cdots\pm p_{n-1}

scegliendo opportunamente i segni "più" e "meno".

Problemi additivi sono considerati anche i già citati teorema di Green-Tao sulle progressioni aritmetiche, la congettura dei primi gemelli e la congettura di Levy , che afferma che ogni intero dispari è la somma di un primo e di un semiprimo pari.

Principali problemi aperti

Molte congetture riguardanti i numeri primi non sono ancora state dimostrate. La più importante tra queste è senza dubbio l' ipotesi di Riemann , uno dei problemi aperti più importanti di tutta la matematica: ^[62] ^[63] era uno dei ventitré problemi di Hilbert , enunciati nel 1900 , ed è stato inserito tra i problemi per il millennio nel 2000 . Nella sua formulazione originale, tale ipotesi riguarda il posizionamento degli zeri complessi della funzione zeta di Riemann : nonostante il suo legame con i numeri primi non sia immediatamente chiaro, è stato provato che la sua dimostrazione avrebbe come conseguenza un notevole miglioramento della comprensione dei numeri primi. In particolare, se l'ipotesi di Riemann fosse vera, i primi sarebbero distribuiti nel modo più regolare possibile. ^[64]

Altri problemi aperti molto famosi sono le già citate congetture di Goldbach , dei primi gemelli e di Legendre .

Altre congetture riguardano l'esistenza o meno di infiniti numeri primi in una certa forma. Ad esempio si pensa che esistano infiniti numeri primi nelle sequenze n ² + 1 ^[65] , 2 ⁿ - 1 ( primi di Mersenne , OEIS:A000043 ), n ! + 1 e n ! - 1 ( primi fattoriali , sequenze OEIS:A002981 e OEIS:A117141 ), o che esistano infiniti primi nella successione di Fibonacci . ^[66] Si congettura invece che vi siano solo un numero finito di primi di Fermat , i numeri primi nella forma 2 ^{2 ⁿ} + 1. ^[67] Al momento, gli unici primi di Fermat noti sono in corrispondenza di n = 0, 1, 2, 3 e 4.

Formule per i numeri primi

Lo stesso argomento in dettaglio: Formula per i numeri primi .

Una formula per i numeri primi è un'espressione che genera solamente numeri primi. Non sono note formule chiuse (che cioè non fanno ricorso né a limiti né a serie né a sommatorie la cui lunghezza dipenda dal dato iniziale) per trovare tutti i numeri primi fino a n , o anche solo l' n -esimo primo; sono state invece trovate alcune formule che generano solo numeri primi, seppure fondamentalmente inutili dal punto di vista pratico. Un esempio è dato dal teorema di Mills che afferma che esiste una costante θ tale che

\lfloor \theta ^{3^{n}}\rfloor

\lfloor \theta ^{3^{n}}\rfloor

\lfloor \theta^{3^n}\rfloor

è sempre un numero primo. Tuttavia non si conosce nessuna formula chiusa per calcolare la costante di Mills: le approssimazioni attualmente utilizzate si basano sulla sequenza dei cosiddetti primi di Mills (i numeri primi generati tramite questa formula), che non possono essere ricavati rigorosamente, ma solamente in maniera probabilistica, assumendo per vera l' ipotesi di Riemann . ^[68]

A seguito della dimostrazione del teorema di Matiyasevich , sono stati trovati vari polinomi i cui valori positivi sono sempre numeri primi. Matijasevič dimostrò l'esistenza di un polinomio di 37º grado in 24 incognite, ma senza esplicitarlo; in seguito alcuni di questi sono stati determinati, ma rimangono poco utili per la ricerca di nuovi primi perché hanno diverse variabili e un grado molto elevato, e inoltre assumono spesso valori negativi. ^[69]

Altre formule si possono costruire attraverso il teorema di Wilson con l'uso della funzione parte intera , ma anche queste sono sostanzialmente inutilizzabili a causa della loro elevata complessità computazionale .

Aspetti computazionali

Test di primalità

Lo stesso argomento in dettaglio: Test di primalità .

Un test di primalità è un algoritmo che permette di stabilire se un dato numero è primo oppure no. Nella teoria della complessità computazionale , questo problema è a volte denotato come PRIMES, ed è stato recentemente dimostrato appartenere alla classe di complessità P . ^[70]

Il più antico e semplice test di primalità è quello di "divisione per tentativi", che consiste nell'applicare direttamente la definizione di numero primo: si prova a dividere il numero N per tutti i numeri minori di N : se nessuno di questi lo divide, allora il numero è primo. Un semplice miglioramento di questo metodo si ottiene limitando i tentativi di divisione ai numeri primi minori di ${\sqrt {N}}$ ${\sqrt {N}}$ $\sqrt{N}$ . Sebbene molto semplice da descrivere e da implementare su un calcolatore, tale metodo è poco usato nella pratica, perché richiede tempi di calcolo che aumentano esponenzialmente rispetto al numero delle cifre di N . Esso tuttavia fornisce anche i suoi fattori primi (ed è quindi un algoritmo di fattorizzazione ): questo non succede nel caso di algoritmi più sofisticati, che riescono a stabilire se un numero non è primo anche senza determinare alcun divisore non banale.

Altri algoritmi di primalità piuttosto semplici, ma poco utili dal punto di vista pratico, sono il test che si può ricavare dal crivello di Eratostene ei test di Fermat e di Wilson , che si basano rispettivamente sul piccolo teorema di Fermat e sul teorema di Wilson .

Diversi altri algoritmi sono stati sviluppati nel corso del tempo: alcuni di essi si applicano solo a classi particolari di numeri, come ad esempio i test di Lucas-Lehmer e di Proth , che si applicano solo ai numeri di Mersenne e di Proth rispettivamente. Altri, come il test di Miller-Rabin , sono probabilistici , ovvero danno una risposta certa solo se affermano che il numero non è primo, mentre se si ottiene come risultato che il numero è primo, allora c'è solo un'alta probabilità che il numero effettivamente lo sia. I numeri che passano uno di questi test, pur senza essere primi, sono detti " pseudoprimi ". La classe più famosa di pseudoprimi è quella dei numeri di Carmichael , che verificano il piccolo teorema di Fermat pur essendo composti.

Tra i test di primalità di uso generale il più usato attualmente è l' ECPP , basato sulle curve ellittiche ; ^[71] sebbene la sua complessità computazionale non sia nota, sperimentalmente si osserva che esso è un algoritmo polinomiale nel numero delle cifre di n . ^[72] Nel 2002 , i tre matematici indiani Manindra Agrawal, Neeraj Kayal e Nitin Saxena hanno sviluppato l' algoritmo AKS , il primo test di primalità deterministico con complessità polinomiale, provando dunque che il problema di stabilire se un numero è primo o no sta nella classe di complessità P . ^[73]

Algoritmi di fattorizzazione

Un programma che ha lo scopo di individuare i fattori primi di un numero è detto algoritmo di fattorizzazione ; gli algoritmi di questo tipo possono funzionare anche da test di primalità, ma sono quasi sempre più lenti da eseguire rispetto a programmi ideati solo per quest'ultimo scopo. Dopo il metodo di divisione per tentativi, i più antichi algoritmi di questo tipo sono il metodo di Fermat , che si basa sulle differenze tra il numero da fattorizzare N e alcuni quadrati, efficace in particolare quando N è il prodotto di due numeri primi vicini tra loro, e il metodo di Eulero , che si basa invece sulla rappresentazione di N come somma di due quadrati in due modi diversi.

Più recentemente, gli algoritmi per la fattorizzazione sono stati basati su una gran varietà di tecniche diverse, come le frazioni continue o le curve ellittiche , mentre altri, come ad esempio il crivello quadratico , sono basati su miglioramenti del metodo di Fermat. Altri ancora, come il metodo rho di Pollard , sono probabilistici, e non offrono la garanzia che, dato un numero non primo, ne trovino i divisori.

A oggi il più veloce algoritmo deterministico di impiego generale, ovvero senza necessità di numeri in forma particolare, è il general number field sieve , che ha complessità esponenziale sul numero di cifre di N ; ^[74] è stato proposto un algoritmo che ha tempo di esecuzione polinomiale nel numero di cifre di N ( algoritmo di Shor ), ma esso richiede di essere eseguito su un computer quantistico , la cui simulazione su un normale calcolatore richiede un tempo esponenziale. ^[75]

Impiego nella crittografia

Lo stesso argomento in dettaglio: RSA (crittografia) .

Proprio la difficoltà di fattorizzare grandi numeri ha portato allo sviluppo del primo metodo efficace di crittografia a chiave pubblica , l' RSA . In questo sistema crittografico, la persona che deve ricevere un messaggio cifrato genera una chiave formata da tre numeri: uno ( n ) è il prodotto di due numeri primi di grandi dimensioni (generalmente si usano numeri di 1024 o 2048 bit ), mentre gli altri due ( e ed f ) sono l'uno l' inverso dell'altro modulo φ( n ) (dove φ indica la funzione di Eulero ). Uno tra questi ultimi due numeri deve essere tenuto segreto (e dunque prende il nome di chiave privata ), mentre l'altro deve essere reso noto insieme al numero n (andando a formare la "chiave pubblica").

Dopo aver trasformato il messaggio in un numero m (secondo un codice stabilito in precedenza), la procedura di criptazione e decriptazione consiste nell'elevamento a potenza di m per il numero tra e ed f reso pubblico, prendendone poi il resto nella divisione per n ; il teorema di Eulero garantisce che dopo quest'operazione si possa ritornare allo stesso numero di partenza conoscendo sia e sia f .

È possibile, in teoria, ricavare la chiave privata dalle informazioni pubbliche: attualmente questo richiede la fattorizzazione del numero n , rendendo quindi la trasmissione del messaggio sicura se i due primi scelti soddisfano alcune condizioni e sono "sufficientemente" grandi. Non è ancora noto se vi siano metodi efficienti per decriptare il messaggio che non prevedano l'attacco diretto alla fattorizzazione di n , ma è stato mostrato che una cattiva scelta della chiave pubblica potrebbe rendere il sistema più vulnerabile ad attacchi di questo tipo. ^[76]

Nel 1991 la RSA Security (l'azienda che ha sfruttato commercialmente l'RSA) ha pubblicato una lista di semiprimi , offrendo dei premi in denaro per la fattorizzazione di alcuni di essi, con lo scopo di provare la sicurezza del metodo e di incoraggiare la ricerca in questo ambito: l'iniziativa è stata chiamata RSA Factoring Challenge . Nel corso degli anni, diversi di questi numeri sono stati fattorizzati, mentre per altri il problema è ancora aperto; il concorso si è comunque concluso nel 2007 . ^[77] ^[78] ^[79]

Numeri primi grandi

Lo stesso argomento in dettaglio: Il più grande numero primo conosciuto .

Il numero di cifre (in base 10 ) del più grande numero primo conosciuto, dal 1900 al 2018 . La scala sull'asse delle ordinate è logaritmica.

Già da molti secoli la ricerca di numeri primi "grandi" ha destato l'interesse dei matematici; tuttavia questa ricerca ha assunto una particolare importanza negli ultimi decenni, a causa del bisogno di tali numeri che caratterizza algoritmi quali l'RSA.

Il metodo più efficace per ottenere numeri primi grandi risale al diciassettesimo secolo, quando Marin Mersenne congetturò che $M_{n}=2^{n}-1$ $M_{n}=2^{n}-1$ $M_n=2^n-1$ sarebbe stato primo (quando n ≤ 257) solo per n uguale a 2, 3, 5, 7, 13, 19, 31, 67, 127 e 257. ^[80] La verifica della primalità di tali numeri era molto al di sopra delle possibilità dell'epoca, e infatti soltanto nel Novecento si scoprì che la congettura era falsa e probabilmente fatta "alla cieca", in quanto Mersenne tralasciò tre casi (per n = 61, 89 e 107) e non si accorse che i numeri corrispondenti a n = 67 e n = 257 erano in realtà composti.

M ₁₂₇ (un numero di 39 cifre) fu dimostrato essere primo da Édouard Lucas nel 1876, e rimase il numero primo più grande conosciuto fino al 1951 , quando vennero trovati (2 ¹⁴⁸ +1)/17 (di 44 cifre) e, poco più tardi, 180 · (2 ¹²⁷ − 1) ² + 1 (di 79 cifre), quest'ultimo tramite un calcolatore elettronico. Da allora tutti i successivi primi più grandi sono stati scoperti con l'aiuto del computer: dal 1952 (quando lo SWAC dimostrò che M ₅₂₁ è primo) al 1996 essi sono stati trovati da supercomputer , e furono tutti primi di Mersenne (trovati usando il test di Lucas-Lehmer , un algoritmo specifico per questi numeri) con l'eccezione di 391581 · 2 ²¹⁶¹⁹³ − 1, che detenne il record tra il 1989 e il 1992 . ^[81] ^[82]

In seguito, i quattordici nuovi numeri primi più grandi sono stati scoperti attraverso il GIMPS , un progetto di calcolo distribuito basato anch'esso sul test di Lucas-Lehmer. A oggi (dicembre 2018) il più grande numero primo, scoperto nel dicembre del 2018 , è 2 ^{82 589 933} − 1, composto da oltre 24 milioni di cifre decimali. ^[83] ^[84] I numeri primi noti più grandi sono numeri primi di Mersenne o altri numeri primi particolari, per i quali si dispone di un test molto efficiente in termini computazionali.

La Electronic Frontier Foundation ha offerto dei premi in denaro ai primi che riusciranno a trovare numeri primi di oltre un certo numero di cifre. I primi due di questi premi, di 50 000 e 100 000 dollari , sono stati assegnati nel 2000 e nel 2008 per il raggiungimento, rispettivamente, di un milione e di dieci milioni di cifre; il più alto premio attualmente in palio è di 250 000 dollari, per l'arrivo al miliardo di cifre. ^[85]

Generalizzazioni

Rappresentazione dei primi di Gauss di norma minore o uguale a 500. I primi di Gauss sono, per definizione, gli elementi tra gli interi di Gauss che sono primi.

Il concetto di numero primo viene esteso anche in altri campi della matematica.

Teoria degli anelli

La definizione di numero primo può essere estesa a qualunque dominio d'integrità ; vi sono due modi di estendere la definizione, in generale non equivalenti fra loro:

un elemento è irriducibile se non è invertibile e non può essere scritto come il prodotto di due elementi anch'essi non invertibili; ^[86]
un elemento è primo se non è invertibile e ogni volta che divide il prodotto ab , allora divide a oppure b . ^[87]

Un elemento primo è sempre irriducibile, ma non viceversa: tuttavia nell'anello degli interi le due definizioni sono equivalenti (come garantito dal lemma di Euclide ), e più in generale sono equivalenti in tutti gli anelli a fattorizzazione unica .

Inoltre, dato un anello A , un ideale I di A è detto "primo" se per ogni coppia a , b di elementi di A tali che a · b ∈ I almeno uno tra a e b appartiene a I .

Questa definizione è molto vicina a quella degli ordinari numeri primi, tanto che nell'anello $\mathbb {Z}$ $\mathbb {Z}$ $\mathbb{Z}$ gli ideali primi non nulli sono esattamente (2), (3), (5), ..., ovvero quelli generati dai numeri primi (più in generale, ciò avviene in ogni dominio ad ideali principali ). Lo studio degli ideali primi è un punto centrale nella geometria algebrica e nella teoria algebrica dei numeri . Un'importante analogia tra numeri primi e ideali primi è dato dal fatto che nei domini di Dedekind per gli ideali vale l'analogo delteorema fondamentale dell'aritmetica . ^[88]

Teoria dei gruppi

Nella teoria dei gruppi , un ruolo simile a quello dei numeri primi è rivestito dai gruppi semplici . Si può dimostrare infatti che ogni gruppo finito G ammette una serie di composizione , cioè una serie del tipo

1=H_{0}\triangleleft H_{1}\triangleleft \cdots \triangleleft H_{m}=G,

1=H_{0}\triangleleft H_{1}\triangleleft \cdots \triangleleft H_{m}=G,

1 = H_0\triangleleft H_1\triangleleft \cdots \triangleleft H_m = G,

ove ogni H _i è un sottogruppo normale di H _{i +1} tale che il gruppo H _{i +1} / H _i (detto gruppo fattore della serie) sia un gruppo semplice. Ilteorema di Jordan-Hölder assicura che tutte le serie di composizione per G hanno la stessa lunghezza m e gli stessi fattori di composizione, a meno di permutazioni e isomorfismi . È tuttavia da notare che gruppi diversi possono avere la stessa serie di composizione: ad esempio il gruppo ciclico $\mathbb {Z} _{2p}$ $\mathbb {Z} _{2p}$ $\mathbb{Z}_{2p}$ e il gruppo diedrale D _p , per ogni primo p , hanno entrambi la serie di composizione

1\triangleleft \mathbb {Z} _{p}\triangleleft G,

1\triangleleft \mathbb {Z} _{p}\triangleleft G,

1\triangleleft\mathbb{Z}_p\triangleleft G,

corrispondente ai fattori $\mathbb {Z} _{2}$ $\mathbb {Z} _{2}$ $\mathbb{Z}_2$ e $\mathbb {Z} _{p}$ $\mathbb {Z} _{p}$ $\mathbb{Z}_p$ .

Teoria dei nodi


Alcuni nodi primi

In teoria dei nodi , un nodo primo è un nodo non banale che non può essere "scomposto" in due nodi più piccoli. In maniera più precisa, è un nodo che non può essere scritto come somma connessa di due nodi non banali.

Nel 1949 Horst Schubert dimostrò un teorema di fattorizzazione analogo al teorema fondamentale dell'aritmetica, che asserisce che ogni nodo è ottenibile in modo unico come somma connessa di alcuni nodi primi. ^[89] Per questo motivo, i nodi primi hanno un ruolo centrale nella teoria dei nodi: una loro classificazione è stato da sempre il tema centrale della teoria fin dalla fine del XIX secolo .

Numeri primi in natura

Una Magicicada con periodo di 17 anni

In natura compaiono molti numeri, ed è quindi inevitabile che alcuni di essi siano primi. Sono tuttavia relativamente pochi gli esempi di numeri la cui presenza in natura si spieghi con la loro primalità.

Per la maggior parte, le stelle marine hanno 5 braccia, e 5 è un numero primo; tuttavia non è nota alcuna connessione tra questo numero di braccia e la primalità di 5. ^[90] Il motivo della simmetria a 5 braccia che caratterizza la maggior parte delle stelle marine e molti altri echinodermi rimane un mistero.

In entomologia si trova uno dei casi in cui si suppone che un numero compaia proprio in quanto primo. Si è infatti notato che alcune specie di cicale del genere Magicicada , che trascorrono la maggior parte delle loro vite come larve , emergono come pupe solo a intervalli di 13 o 17 anni, dopo di che si riproducono e infine muoiono dopo poche settimane. Si pensa che il motivo per cui l'intervallo di tempo è un numero primo di anni sia la difficoltà per un predatore di evolversi specializzandosi nella predazione delle Magicicada : se infatti questi insetti apparissero dopo un numero non primo di anni, allora tutti i predatori il cui ciclo vitale fosse un divisore di quel numero avrebbero una elevata probabilità di trovare le Magicicada . Sebbene esile, questo vantaggio evolutivo sembra essere stato sufficiente a selezionare cicale il cui periodo è di 13 o 17 anni. ^[91] ^[92]

Numeri primi nell'arte e nella letteratura

I numeri primi hanno influenzato molti artisti e scrittori. Il compositore francese Olivier Messiaen era ossessionato da tali numeri ^[93] e li utilizzò per creare musica non metrica: in opere come La Nativité du Seigneur (1935) o Quatre études de rythme (1949-50) impiegò simultaneamente motivi la cui lunghezza è un numero primo per creare ritmi imprevedibili. Secondo Messiaen questo modo di comporre era "ispirato dai movimenti dalla natura, movimenti di durate libere e disuguali". ^[94] Anche nel movimento di apertura di un'altra composizione, Quatuor pour la fin du temps , Messiaen utilizzò i numeri primi. Con l'obiettivo di dare l'idea dell'eternità, accostò infatti un tema di 17 note a un tema di 29 note. Essendo primi entrambi i numeri, i temi si ripetono insieme solo dopo 17 · 29 = 493 note. La stessa idea è stata utilizzata da Jem Finer che ha ideato un'installazione sonora che sino al 31 dicembre 2999 suonerà motivi sempre diversi. ^[93]

I numeri primi svolgono un ruolo anche in alcuni libri. Ad esempio, nel romanzo di fantascienza Contact di Carl Sagan (così come nella sua versione cinematografica ), i numeri primi vengono utilizzati dagli alieni per comunicare; un caso reale di uso dei primi come mezzo di comunicazione è presente nel saggio L'uomo che scambiò sua moglie per un cappello , del neurologo Oliver Sacks , dove sono descritti due gemelli autistici che per parlarsi si scambiano primi molto elevati. Vi sono riferimenti ai numeri primi anche nel romanzo di Mark Haddon Lo strano caso del cane ucciso a mezzanotte , in cui la numerazione dei capitoli segue la successione dei primi, e nel romanzo di Paolo Giordano La solitudine dei numeri primi , vincitore del premio Strega nel 2008. Il romanzo Lo zio Petros e la congettura di Goldbach di Apostolos Doxiadis (pubblicato in italiano nel 2001) è stato trasposto per le scene da Angelo Savelli . ^[95]

Molti film riflettono la fascinazione popolare verso i misteri dei numeri primi e della crittografia, come ad esempio Cube - Il cubo , ^[96] I signori della truffa , L'amore ha due facce ^[97] , A Beautiful Mind ^[98] e La solitudine dei numeri primi .

Note

^ ( EN ) The on-line encyclopedia of integer sequences , su oeis.org , The OEIS Foundation. URL consultato il 28 dicembre 2018 ( archiviato il 29 gennaio 2018) .
^ Otto Neugebauer , Capitolo 2 , in Le scienze esatte nell'antichità , Milano, Feltrinelli, 1974, ISBN 88-07-22281-7 .
^ Egyptian Unit Fractions , su Mathpages . URL consultato il 14 gennaio 2011 .
^ Libro IX, Proposizione 20.
^ Libro VII, Proposizione 30.
^ Questa proprietà è usata per generalizzare la definizione di numero primo agli anelli .
^ Libro VII, Proposizioni 31 e 32. Il primo a dimostrare esplicitamente che tale fattorizzazione è unica (cioè a dimostrare ilteorema fondamentale dell'aritmetica nella sua completezza) fu Gauss nelle Disquisitiones Arithmeticae . ( Boyer , p. 582 )
^ ( EN ) John J. O'Connor e Edmund F. Robertson, Prime numbers , su MacTutor . URL consultato il 14 gennaio 2011 .
^ Du Sautoy , p. 149 .
^ Apostol , p. 9 .
^ Apostol , p. 8 .
^ Du Sautoy , capitolo 2 .
^ Riemann's 1859 Manuscript , su claymath.org . URL consultato il 14 gennaio 2011 (archiviato dall' url originale il 23 maggio 2013) .
^ Conway e Guy , p. 111 .
^ Cosa sono i numeri primi , su matematica-old.unibocconi.it . URL consultato il 14 gennaio 2011 .
^ Si noti che se si considera che 1 sia primo anche il crivello di Eratostene andrebbe leggermente modificato: se si cominciasse con l'eliminare tutti i multipli di 1 si sarebbe costretti ad eliminare qualsiasi altro numero.
^ Ad esempio in Du Sautoy
^ vedi il paragrafo sulle generalizzazioni .
^ ( EN ) Eric W. Weisstein, Euclid Number , su MathWorld . URL consultato il 14 gennaio 2011 .
^ ( EN ) Harry Furstenberg, On the infinitude of primes , in Amer. Math. Monthly , vol. 62, n. 5, 1955, p. 353, DOI : 10.2307/2307043 .
^ Vedi la dimostrazione .
^ Vedi ad esempio in Moser , p. 24
^ H. Bonse, Üer eine bekannte Eigenschaft der Zahl 30 und ihre Verallgemeinerung , in Arch. Math. Phys , vol. 12, 1907, pp. 292-295.
^ L. Panaitopol, An inequality involving prime numbers , in Univ. Beograd. Publ. Elektrotehn. Fak. Ser. Mat. , vol. 11, 2000, pp. 3-35.
^ Con questa espressione si intende che il limite del rapporto tra queste due espressioni tende a 1 quando x tende a infinito.
^ Ingham , p. 4 e 14 .
^ Ingham , p. 4 e 20 .
^ Ingham , p. 3 .
^ Ingham , p. xi .
^ Ingham , p. 83 e 84 .
^ JB Rosser, The nth Prime is Greater than n ln n , in Proceedings of the London Mathematical Society , vol. 45, 1938, pp. 21-44.
^ P. Dusart, The k^(th) Prime is Greater than k(lnk+lnlnk-1) for k>=2. , in Math. Comput , vol. 68, 1999, pp. 411-415.
^ ( EN ) Eric W. Weisstein, Rosser's Theorem , su MathWorld . URL consultato il 14 gennaio 2011 .
^ Si noti tuttavia che in generale non è vero che il numero successivo è primo: ad esempio, se n è dispari, allora N!+( N +1) è divisibile per 2.
^ DA Goldston, J. Pintz e Y. Yilidrim, Primes in tuples. II. ( PDF ), in Acta. Math. , to appear. URL consultato il 14 gennaio 2011 .
^ Maggie McKee, First proof that infinitely many prime numbers come in pairs , in Nature , 14 maggio 2013, ISSN 0028-0836 ( WC · ACNP ) .
^ Yitang Zhang, Bounded gaps between primes ( PDF ), in Annals of Mathematics , Princeton University and the Institute for Advanced Study. URL consultato il 21 maggio 2013 .
^ Terence Tao , The prime tuples conjecture, sieve theory, and the work of Goldston-Pintz-Yildirim, Motohashi-Pintz, and Zhang , su terrytao.wordpress.com , 4 giugno 2013.
^ DHJ Polymath, Variants of the Selberg sieve, and bounded intervals containing many primes , in Research in the Mathematical Sciences , Springer International Publishing. URL consultato il 13 febbraio 2015 .
^ J. Pintz, Landau's problems on primes. ( PDF ), su renyi.hu . URL consultato il 14 gennaio 2011 .
^ K. Ford, B. Green, S. Konyagin, J. Maynard e T. Tao, Long gaps between consecutive prime numbers , su https://arxiv.org/abs/1412.5029 , 2015.
^ RC Baker, G. Harman e J. Pintz, The diﬀerence between consecutive primes, II., in Proc. London Math. Soc. , vol. 83, n. 3, 2001.
^ JR Chen, On the Distribution of Almost Primes in an Interval. , in Sci. Sinica , vol. 18, 1975, pp. 611-627.
^ Apostol , capitolo 10 .
^ WR Alford, A. Granville e C. Pomerance, There are Infinitely Many Carmichael Numbers. , in Annals of Mathematics , vol. 139, 1994, pp. 703-722.
^ Boyer , p. 565 .
^ Harold Stark, An introduction to number theory , 10ª ed., Cambridge, The MIT Press, 1998, p. 61, ISBN 0-262-69060-8 .
^ Devlin , p. 73 .
^ Davenport , p. 33 .
^ ( EN ) John Friedlander e Henryk Iwaniec , The polynomial X ² + Y ⁴ captures its primes ( PDF ), in Annals of Mathematics , vol. 148, 1998, pp. 945–1040, DOI : 10.2307/121034 . URL consultato il 14 gennaio 2011 (archiviato dall' url originale l'8 agosto 2017) .
^ Apostol , p. 7 .
^ Apostol , p. 149 .
^ Ben Green e Terence Tao , The primes contain arbitrarily long arithmetic progressions ( PDF ), in Annals of Mathematics , vol. 167, 2008, pp. 481-547. URL consultato il 23 febbraio 2009 (archiviato dall' url originale il 20 giugno 2010) . Su Arxiv
^ ( EN ) Terence Tao e Tamar Ziegler , The primes contain arbitrarily long polynomial progressions , su arXiv.org . URL consultato il 4 settembre 2009 .
^ ( EN ) Jens Kruse Andersen , Primes in Arithmetic Progression Records , su primerecords.dk . URL consultato il 28 giugno 2014 .
^ H. Dubner, T. Forbes, N. Lygeros, M. Mizony, H. Nelson e P. Zimmermann, Ten consecutive primes in arithmetic progression , in Mathematics of Computation , vol. 71, 2002, pp. 1323-1328. URL consultato il 14 gennaio 2011 .
^ Jens Kruse Andersen , The Largest Known CPAP's , su primerecords.dk . URL consultato il 28 giugno 2014 .
^ ( EN ) Tomás Oliveira e Silva, Goldbach conjecture verification , su ieeta.pt . URL consultato il 14 gennaio 2011 .
^ GH Hardy e JE Littlewood, Some problems of 'Partitio numerorum'; III: On the expression of a number as a sum of primes , in Acta Math. , vol. 44, 1923.
^ H. Davenport , 26. Sums of three primes , in Multiplicative Number Theory , 3ª ed., Berlino, Springer, 2000, ISBN 978-0-387-95097-6 .
^ Nel lavoro originale di Vinogradov tale numero non era effettivamente calcolabile ma questo problema è stato superato qualche anno dopo dal suo studente K. Borozdin. Si veda Terence Tao , Structure and Randomness in the Prime Numbers , in Dierk Schleicher e Malte Lackmann (a cura di), An Invitation to Mathematics: From Competitions to Research , Springer, 2011, pp. 1–7, DOI : 10.1007/978-3-642-19533-4_1 .
^ Enrico Bombieri , Problems of the Millennium: The Riemann Hypothesis ( PDF ), su claymath.org . URL consultato il 14 gennaio 2011 (archiviato dall' url originale l'11 gennaio 2011) .
^ Devlin , p. 211 .
^ SJ Patterson, An introduction to the theory of the Riemann zeta-function , Cambridge University Press , 1988, p. 75, ISBN 978-0-521-33535-5 .
^ ( EN ) Sequenza A002496 , su On-Line Encyclopedia of Integer Sequences , The OEIS Foundation.
^ ( EN ) Chris Caldwell, Fibonacci prime , su primes.utm.edu . URL consultato il 14 gennaio 2011 .
^ Hardy e Wright , p. 15 .
^ Chris Caldwell e Yuanyou Cheng, Determining Mills' Constant and a Note on Honaker's Problem ( PDF ), in Journal of Integer Sequences , vol. 8, 2005. URL consultato il 14 gennaio 2011 .
^ Paulo Ribenboim, The little book of big primes , Springer-Verlag, 1996, p. 116, ISBN 3-540-97042-8 . URL consultato il 14 gennaio 2011 .
^ ( EN ) PRIMES is in P little FAQ , su instantlogic.net , 14 gennaio 2011. URL consultato il 4 settembre 2008 .
^ Eric W. Weisstein, Elliptic Curve Primality Proving , su MathWorld . URL consultato il 3 settembre 2009 .
^ ( EN ) Elliptic curves and ECPP test , su primes.utm.edu , The Prime Pages. URL consultato il 14 gennaio 2011 . , da Lenstra Jr. K., Lenstra e Jr. HW, Algorithms in number theory. , in Handbook of Theoretical Computer Science Vol A: Algorithms and Complexity , Amsterdam and New York, The MIT Press, 1990, pp. 673-715, ISBN 0-444-88071-2 .
^ ( EN ) Manindra Agrawal, Neeraj Kayal e Nitin Saxena, PRIMES is in P ( PDF ), su cse.iitk.ac.in . URL consultato il 14 gennaio 2011 .
^ ( EN ) Eric W. Weisstein, Number Field Sieve , su mathworld.wolfram.com . URL consultato il 14 gennaio 2011 .
^ Samuel J. Lomonaco jr., Shor's Quantum Factoring Algorithm, in Quantum Computation - A Grand Mathematical Challenge for the Twenty-First Century and the Millennium ( PDF ), AMS, 2002, ISBN 0-8218-2084-2 . URL consultato il 14 gennaio 2011 .
^ Ron Rivest e Burt Kaliski, RSA Problem ( PDF ), su people.csail.mit.edu , 10 dicembre 2003. URL consultato il 14 gennaio 2011 .
^ ( EN ) Burt Kaliski, Announcement of "RSA Factoring Challenge" , su groups.google.com , 18 marzo 1991. URL consultato il 14 gennaio 2011 .
^ ( EN ) RSA Challenge - FAQ , su rsa.com , RSA Laboratories. URL consultato il 14 gennaio 2011 (archiviato dall' url originale il 13 febbraio 2010) .
^ ( EN ) Eric W. Weisstein, RSA Number , su mathworld.wolfram.com . URL consultato il 14 gennaio 2011 .
^ Du Sautoy , p. 78 .
^ ( EN ) Chris Caldwell, The Largest Known Prime by Year: A Brief History , su The Prime Pages . URL consultato il 14 gennaio 2011 .
^ Du Sautoy , capitolo 9 .
^ ( EN ) The Top Twenty: Largest Known Primes , su primes.utm.edu . URL consultato il 21 dicembre 2018 .
^ ( EN ) GIMPS Discovers Largest Known Prime Number: 2 ^82,589,933 -1 , su mersenne.org , 21 dicembre 2018. URL consultato il 21 dicembre 2018 .
^ ( EN ) EFF Cooperative Computing Awards , su eff.org . URL consultato il 14 gennaio 2011 .
^ definizione corrispondente a quella data sopra.
^ Ad esempio 5 divide 45 = 15 × 3 e divide 15, mentre 4, che non è primo, divide 84 = 14 × 6, ma non divide né 14 né 6.
^ Nei domini di Dedekind ogni ideale proprio non nullo si può scrivere come prodotto di ideali primi e tale scrittura è unica a meno del riordino dei fattori.
^ Eric W. Weisstein, Prime knot , su MathWorld . URL consultato il 14 gennaio 2011 .
^ Alcune stelle marine hanno un diverso numero di braccia: l' Echinaster luzonicus , ad esempio, ha normalmente sei braccia, mentre la Luidia senegalensis ha nove braccia e la Solaster endeca può avere anche 20 braccia.
^ ( EN ) Paulo RA Campos, Viviane M. de Oliveira, Ronaldo Giro e Douglas S. Galvão, Emergence of Prime Numbers as the Result of Evolutionary Strategy , in Phys. Rev. Lett. , vol. 93, 2004, DOI : 10.1103/PhysRevLett.93.098107 . URL consultato il 14 gennaio 2011 .
^ ( EN ) Prime number selection of cycles in a predator-prey model , in Complexity , vol. 6, n. 4, pp. 33-38.
^ ^a ^b Marcus Du Sautoy , Un divertissement in prima serata , in Michael Emmer (a cura di), Matematica e cultura 2006 , Springer, 2006, pp. 201-207, ISBN 978-88-470-0464-1 . URL consultato il 4 settembre 2008 .
^ Peter Hill, The Messiaen companion , Amadeus Press, 1994, ISBN 0-931340-95-0 .
^ Angelo Savelli, Zio Petros tra scienza, letteratura e teatro , in Mirella Manaresi (a cura di), Matematica e cultura in Europa , Milano, Springer, 2005, pp. 305-312. ISBN 88-470-0346-6 ; ISBN 978-88-470-0346-0 .
^ Alberto Perelli, in Mirella Manaresi, op. cit. , pp. 230-244 .
^ Michele Emmer, ibidem , pp. 245-253 .
^ Marco Li Calzi, ibidem , pp. 187-206 .

Bibliografia

( EN ) Tom M. Apostol , Introduction to Analytic Number Theory , 2ª ed., New York, Springer-Verlag, 1976, ISBN 0-387-90163-9 .
Michael Artin, Algebra , Torino, Bollati Boringhieri, 1997, ISBN 88-339-5586-9 .
Carl B. Boyer , Storia della matematica , Milano, Mondadori, 1990, ISBN 978-88-04-33431-6 .
John H. Conway e Richard K. Guy , Il libro dei numeri , Milano, Hoepli, 1999, ISBN 88-203-2519-5 .
Harold Davenport , Aritmetica superiore , Bologna, Zanichelli, 1994, ISBN 88-08-09154-6 .
Keith Devlin , Dove va la matematica , Torino, Bollati Boringhieri, 1994, ISBN 88-339-1182-9 .
Marcus du Sautoy , L'enigma dei numeri primi , Milano, Rizzoli, 2004, ISBN 88-17-00843-5 .
Euclide , Elementi
( EN ) Richard K. Guy, Unsolved problems in number theory , 3ª ed., New York, Springer-Verlag, 2004, ISBN 0-387-20860-7 .
( EN ) Godfrey Harold Hardy e Edward M. Wright , An Introduction to the Theory of Numbers , 6ª ed., Oxford, Oxford University Press, 2008, ISBN 978-0-19-921986-5 .
( EN ) Albert Edward Ingham , The Distribution of Prime Numbers , Cambridge, Cambridge University Press, 1932, ISBN 0-521-39789-8 .
( EN ) 2004 Leo Moser, An Introduction to the Theory of Numbers , West Lafayette (Indiana, USA), The Trillia Group, ISBN 978-1-931705-01-1 . URL consultato il 1º settembre 2009 .
Giulia Maria Piacentini Cattaneo, Algebra - un approccio algoritmico , Padova, Decibel-Zanichelli, 1996, ISBN 978-88-08-16270-0 .
Simon Singh , Codici & segreti , Milano, Rizzoli, 1999, ISBN 88-17-86213-4 .
( EN ) Ian Stewart e David Tall, Algebraic number theory and Fermat's last theorem , 3ª ed., Natick, Massachusetts, AK Peters, 2002, ISBN 1-56881-119-5 .
( EN ) Terence Tao e Van Vu, Additive combinatorics , Cambridge, Cambridge University Press, 2006, ISBN 978-0-521-85386-6 .
( EN ) Song Y. Yan, Primality testing and integer factorization in public-key cryptography , Boston, Kluwer Academic Publishers, 2004, ISBN 1-4020-7649-5 .

Voci correlate

Principali teoremi e congetture sui numeri primi

Numeri primi

Altre

Altri progetti

Wikiquote contiene citazioni sui numeri primi
Wikimedia Commons contiene immagini o altri file su numeri primi

Wikinotizie contiene l'articolo Scoperti i due nuovi numeri primi più grandi a distanza di pochi giorni , 18 settembre 2008

Wikinotizie contiene l'articolo Intervista a Marcus du Sautoy , 4 ottobre 2007

Collegamenti esterni

( EN ) Numero primo , su Enciclopedia Britannica , Encyclopædia Britannica, Inc.
( EN ) Eric W. Weisstein, Numero primo , in MathWorld , Wolfram Research.
( EN ) Chris Caldwell, The Prime Pages , su utm.edu . URL consultato l'11 settembre 2009 .
Laura Listanti, Il mistero dei numeri primi e la sicurezza informatica ( PDF ), su ulisse.sissa.it . URL consultato l'11 settembre 2009 (archiviato dall' url originale il 22 luglio 2011) .
( EN ) Fast Online primality test with factorization , su alpertron.com.ar . URL consultato il 28 aprile 2014 . java aplet che implementa il Metodo delle curve ellittiche , capace di testare la primalità di numeri con migliaia di cifre.
( EN ) Paolo Ardoino, Random prime numbers using OpenSSL bignum , su ardoino.com . URL consultato l'11 settembre 2009 (archiviato dall' url originale il 20 dicembre 2009) .
( EN ) Mark Chamness, Prime number generator , su alumnus.caltech.edu . URL consultato l'11 settembre 2009 (archiviato dall' url originale il 4 settembre 2009) .

Controllo di autorità	Thesaurus BNCF 16686 · LCCN ( EN ) sh85093218 · GND ( DE ) 4047263-2 · BNF ( FR ) cb11932592t (data) · NDL ( EN , JA ) 00571462

Portale Matematica : accedi alle voci di Wikipedia che trattano di matematica

Questa è una voce in vetrina , identificata come una delle migliori voci prodotte dalla comunità .
È stata riconosciuta come tale il giorno 21 settembre 2009 — vai alla segnalazione .
Naturalmente sono ben accetti suggerimenti e modifiche che migliorino ulteriormente il lavoro svolto.

Segnalazioni · Criteri di ammissione · Voci in vetrina in altre lingue · Voci in vetrina in altre lingue senza equivalente su it.wiki

[1] ( EN ) The on-line encyclopedia of integer sequences , su oeis.org , The OEIS Foundation. URL consultato il 28 dicembre 2018 ( archiviato il 29 gennaio 2018) .

[2] Otto Neugebauer , Capitolo 2 , in Le scienze esatte nell'antichità , Milano, Feltrinelli, 1974, ISBN 88-07-22281-7 .

[3] Egyptian Unit Fractions , su Mathpages . URL consultato il 14 gennaio 2011 .

[4] Libro IX, Proposizione 20.

[5] Libro VII, Proposizione 30.

[6] Questa proprietà è usata per generalizzare la definizione di numero primo agli anelli .

[7] Libro VII, Proposizioni 31 e 32. Il primo a dimostrare esplicitamente che tale fattorizzazione è unica (cioè a dimostrare ilteorema fondamentale dell'aritmetica nella sua completezza) fu Gauss nelle Disquisitiones Arithmeticae . ( Boyer , p. 582 )

[8] ( EN ) John J. O'Connor e Edmund F. Robertson, Prime numbers , su MacTutor . URL consultato il 14 gennaio 2011 .

[9] Du Sautoy , p. 149 .

[10] Apostol , p. 9 .

[11] Apostol , p. 8 .

[12] Du Sautoy , capitolo 2 .

[13] Riemann's 1859 Manuscript , su claymath.org . URL consultato il 14 gennaio 2011 (archiviato dall' url originale il 23 maggio 2013) .

[14] Conway e Guy , p. 111 .

[15] Cosa sono i numeri primi , su matematica-old.unibocconi.it . URL consultato il 14 gennaio 2011 .

[16] Si noti che se si considera che 1 sia primo anche il crivello di Eratostene andrebbe leggermente modificato: se si cominciasse con l'eliminare tutti i multipli di 1 si sarebbe costretti ad eliminare qualsiasi altro numero.

[17] Ad esempio in Du Sautoy

[18] vedi il paragrafo sulle generalizzazioni .

[19] ( EN ) Eric W. Weisstein, Euclid Number , su MathWorld . URL consultato il 14 gennaio 2011 .

[20] ( EN ) Harry Furstenberg, On the infinitude of primes , in Amer. Math. Monthly , vol. 62, n. 5, 1955, p. 353, DOI : 10.2307/2307043 .

[21] Vedi la dimostrazione .

[22] Vedi ad esempio in Moser , p. 24

[23] H. Bonse, Üer eine bekannte Eigenschaft der Zahl 30 und ihre Verallgemeinerung , in Arch. Math. Phys , vol. 12, 1907, pp. 292-295.

[24] L. Panaitopol, An inequality involving prime numbers , in Univ. Beograd. Publ. Elektrotehn. Fak. Ser. Mat. , vol. 11, 2000, pp. 3-35.

[25] Con questa espressione si intende che il limite del rapporto tra queste due espressioni tende a 1 quando x tende a infinito.

[26] Ingham , p. 4 e 14 .

[27] Ingham , p. 4 e 20 .

[28] Ingham , p. 3 .

[29] Ingham , p. xi .

[30] Ingham , p. 83 e 84 .

[31] JB Rosser, The nth Prime is Greater than n ln n , in Proceedings of the London Mathematical Society , vol. 45, 1938, pp. 21-44.

[32] P. Dusart, The k^(th) Prime is Greater than k(lnk+lnlnk-1) for k>=2. , in Math. Comput , vol. 68, 1999, pp. 411-415.

[33] ( EN ) Eric W. Weisstein, Rosser's Theorem , su MathWorld . URL consultato il 14 gennaio 2011 .

[34] Si noti tuttavia che in generale non è vero che il numero successivo è primo: ad esempio, se n è dispari, allora N!+( N +1) è divisibile per 2.

[35] DA Goldston, J. Pintz e Y. Yilidrim, Primes in tuples. II. ( PDF ), in Acta. Math. , to appear. URL consultato il 14 gennaio 2011 .

[36] Maggie McKee, First proof that infinitely many prime numbers come in pairs , in Nature , 14 maggio 2013, ISSN 0028-0836 ( WC · ACNP ) .

[37] Yitang Zhang, Bounded gaps between primes ( PDF ), in Annals of Mathematics , Princeton University and the Institute for Advanced Study. URL consultato il 21 maggio 2013 .

[38] Terence Tao , The prime tuples conjecture, sieve theory, and the work of Goldston-Pintz-Yildirim, Motohashi-Pintz, and Zhang , su terrytao.wordpress.com , 4 giugno 2013.

[39] DHJ Polymath, Variants of the Selberg sieve, and bounded intervals containing many primes , in Research in the Mathematical Sciences , Springer International Publishing. URL consultato il 13 febbraio 2015 .

[Pintz-40] J. Pintz, Landau's problems on primes. ( PDF ), su renyi.hu . URL consultato il 14 gennaio 2011 .

[41] K. Ford, B. Green, S. Konyagin, J. Maynard e T. Tao, Long gaps between consecutive prime numbers , su https://arxiv.org/abs/1412.5029 , 2015.

[42] RC Baker, G. Harman e J. Pintz, The diﬀerence between consecutive primes, II., in Proc. London Math. Soc. , vol. 83, n. 3, 2001.

[43] JR Chen, On the Distribution of Almost Primes in an Interval. , in Sci. Sinica , vol. 18, 1975, pp. 611-627.

[44] Apostol , capitolo 10 .

[45] WR Alford, A. Granville e C. Pomerance, There are Infinitely Many Carmichael Numbers. , in Annals of Mathematics , vol. 139, 1994, pp. 703-722.

[46] Boyer , p. 565 .

[47] Harold Stark, An introduction to number theory , 10ª ed., Cambridge, The MIT Press, 1998, p. 61, ISBN 0-262-69060-8 .

[48] Devlin , p. 73 .

[49] Davenport , p. 33 .

[50] ( EN ) John Friedlander e Henryk Iwaniec , The polynomial X ² + Y ⁴ captures its primes ( PDF ), in Annals of Mathematics , vol. 148, 1998, pp. 945–1040, DOI : 10.2307/121034 . URL consultato il 14 gennaio 2011 (archiviato dall' url originale l'8 agosto 2017) .

[51] Apostol , p. 7 .

[52] Apostol , p. 149 .

[53] Ben Green e Terence Tao , The primes contain arbitrarily long arithmetic progressions ( PDF ), in Annals of Mathematics , vol. 167, 2008, pp. 481-547. URL consultato il 23 febbraio 2009 (archiviato dall' url originale il 20 giugno 2010) . Su Arxiv

[54] ( EN ) Terence Tao e Tamar Ziegler , The primes contain arbitrarily long polynomial progressions , su arXiv.org . URL consultato il 4 settembre 2009 .

[55] ( EN ) Jens Kruse Andersen , Primes in Arithmetic Progression Records , su primerecords.dk . URL consultato il 28 giugno 2014 .

[56] H. Dubner, T. Forbes, N. Lygeros, M. Mizony, H. Nelson e P. Zimmermann, Ten consecutive primes in arithmetic progression , in Mathematics of Computation , vol. 71, 2002, pp. 1323-1328. URL consultato il 14 gennaio 2011 .

[57] Jens Kruse Andersen , The Largest Known CPAP's , su primerecords.dk . URL consultato il 28 giugno 2014 .

[58] ( EN ) Tomás Oliveira e Silva, Goldbach conjecture verification , su ieeta.pt . URL consultato il 14 gennaio 2011 .

[59] GH Hardy e JE Littlewood, Some problems of 'Partitio numerorum'; III: On the expression of a number as a sum of primes , in Acta Math. , vol. 44, 1923.

[60] H. Davenport , 26. Sums of three primes , in Multiplicative Number Theory , 3ª ed., Berlino, Springer, 2000, ISBN 978-0-387-95097-6 .

[61] Nel lavoro originale di Vinogradov tale numero non era effettivamente calcolabile ma questo problema è stato superato qualche anno dopo dal suo studente K. Borozdin. Si veda Terence Tao , Structure and Randomness in the Prime Numbers , in Dierk Schleicher e Malte Lackmann (a cura di), An Invitation to Mathematics: From Competitions to Research , Springer, 2011, pp. 1–7, DOI : 10.1007/978-3-642-19533-4_1 .

[62] Enrico Bombieri , Problems of the Millennium: The Riemann Hypothesis ( PDF ), su claymath.org . URL consultato il 14 gennaio 2011 (archiviato dall' url originale l'11 gennaio 2011) .

[63] Devlin , p. 211 .

[64] SJ Patterson, An introduction to the theory of the Riemann zeta-function , Cambridge University Press , 1988, p. 75, ISBN 978-0-521-33535-5 .

[65] ( EN ) Sequenza A002496 , su On-Line Encyclopedia of Integer Sequences , The OEIS Foundation.

[66] ( EN ) Chris Caldwell, Fibonacci prime , su primes.utm.edu . URL consultato il 14 gennaio 2011 .

[67] Hardy e Wright , p. 15 .

[68] Chris Caldwell e Yuanyou Cheng, Determining Mills' Constant and a Note on Honaker's Problem ( PDF ), in Journal of Integer Sequences , vol. 8, 2005. URL consultato il 14 gennaio 2011 .

[littlebook-69] Paulo Ribenboim, The little book of big primes , Springer-Verlag, 1996, p. 116, ISBN 3-540-97042-8 . URL consultato il 14 gennaio 2011 .

[70] ( EN ) PRIMES is in P little FAQ , su instantlogic.net , 14 gennaio 2011. URL consultato il 4 settembre 2008 .

[71] Eric W. Weisstein, Elliptic Curve Primality Proving , su MathWorld . URL consultato il 3 settembre 2009 .

[72] ( EN ) Elliptic curves and ECPP test , su primes.utm.edu , The Prime Pages. URL consultato il 14 gennaio 2011 . , da Lenstra Jr. K., Lenstra e Jr. HW, Algorithms in number theory. , in Handbook of Theoretical Computer Science Vol A: Algorithms and Complexity , Amsterdam and New York, The MIT Press, 1990, pp. 673-715, ISBN 0-444-88071-2 .

[73] ( EN ) Manindra Agrawal, Neeraj Kayal e Nitin Saxena, PRIMES is in P ( PDF ), su cse.iitk.ac.in . URL consultato il 14 gennaio 2011 .

[74] ( EN ) Eric W. Weisstein, Number Field Sieve , su mathworld.wolfram.com . URL consultato il 14 gennaio 2011 .

[75] Samuel J. Lomonaco jr., Shor's Quantum Factoring Algorithm, in Quantum Computation - A Grand Mathematical Challenge for the Twenty-First Century and the Millennium ( PDF ), AMS, 2002, ISBN 0-8218-2084-2 . URL consultato il 14 gennaio 2011 .

[76] Ron Rivest e Burt Kaliski, RSA Problem ( PDF ), su people.csail.mit.edu , 10 dicembre 2003. URL consultato il 14 gennaio 2011 .

[77] ( EN ) Burt Kaliski, Announcement of "RSA Factoring Challenge" , su groups.google.com , 18 marzo 1991. URL consultato il 14 gennaio 2011 .

[78] ( EN ) RSA Challenge - FAQ , su rsa.com , RSA Laboratories. URL consultato il 14 gennaio 2011 (archiviato dall' url originale il 13 febbraio 2010) .

[79] ( EN ) Eric W. Weisstein, RSA Number , su mathworld.wolfram.com . URL consultato il 14 gennaio 2011 .

[80] Du Sautoy , p. 78 .

[largestbyyear-81] ( EN ) Chris Caldwell, The Largest Known Prime by Year: A Brief History , su The Prime Pages . URL consultato il 14 gennaio 2011 .

[82] Du Sautoy , capitolo 9 .

[83] ( EN ) The Top Twenty: Largest Known Primes , su primes.utm.edu . URL consultato il 21 dicembre 2018 .

[84] ( EN ) GIMPS Discovers Largest Known Prime Number: 2 ^82,589,933 -1 , su mersenne.org , 21 dicembre 2018. URL consultato il 21 dicembre 2018 .

[85] ( EN ) EFF Cooperative Computing Awards , su eff.org . URL consultato il 14 gennaio 2011 .

[86] zione corrispondente a quella data sopra.

[87] Ad esempio 5 divide 45 = 15 × 3 e divide 15, mentre 4, che non è primo, divide 84 = 14 × 6, ma non divide né 14 né 6.

[88] Nei domini di Dedekind ogni ideale proprio non nullo si può scrivere come prodotto di ideali primi e tale scrittura è unica a meno del riordino dei fattori.

[89] Eric W. Weisstein, Prime knot , su MathWorld . URL consultato il 14 gennaio 2011 .

[90] Alcune stelle marine hanno un diverso numero di braccia: l' Echinaster luzonicus , ad esempio, ha normalmente sei braccia, mentre la Luidia senegalensis ha nove braccia e la Solaster endeca può avere anche 20 braccia.

[91] ( EN ) Paulo RA Campos, Viviane M. de Oliveira, Ronaldo Giro e Douglas S. Galvão, Emergence of Prime Numbers as the Result of Evolutionary Strategy , in Phys. Rev. Lett. , vol. 93, 2004, DOI : 10.1103/PhysRevLett.93.098107 . URL consultato il 14 gennaio 2011 .

[92] ( EN ) Prime number selection of cycles in a predator-prey model , in Complexity , vol. 6, n. 4, pp. 33-38.

[Du_Sautoy-93] Marcus Du Sautoy , Un divertissement in prima serata , in Michael Emmer (a cura di), Matematica e cultura 2006 , Springer, 2006, pp. 201-207, ISBN 978-88-470-0464-1 . URL consultato il 4 settembre 2008 .

[94] Peter Hill, The Messiaen companion , Amadeus Press, 1994, ISBN 0-931340-95-0 .

[95] Angelo Savelli, Zio Petros tra scienza, letteratura e teatro , in Mirella Manaresi (a cura di), Matematica e cultura in Europa , Milano, Springer, 2005, pp. 305-312. ISBN 88-470-0346-6 ; ISBN 978-88-470-0346-0 .

[96] Alberto Perelli, in Mirella Manaresi, op. cit. , pp. 230-244 .

[97] Michele Emmer, ibidem , pp. 245-253 .

[98] Marco Li Calzi, ibidem , pp. 187-206 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[58]

[59]

[60]

[61]

[62]

[63]

[64]

[65]

[66]

[67]

[68]

[69]

[70]

[71]

[72]

[73]

[74]

[75]

[76]

[77]

[78]

[79]

[80]

[81]

[82]

[83]

[84]

[85]

[86]

[87]

[88]

[89]

[90]

[91]

[92]

[93]

[94]

[95]

[96]

[97]

[98]

V · D · M Teoria dei numeri
Numeri più usati	Naturali · Interi · Pari e dispari
Principi generali	Principio d'induzione · Principio del buon ordinamento · Relazione di equivalenza
Successioni di interi	Fattoriale · Successione di Fibonacci · Numero di Catalan · Numero di Perrin · Numero di Eulero · Successione di Mian-Chowla · Successione di Thue-Morse
Caratteristiche dei numeri primi	Numero primo · Lemma di Euclide · Teorema dell'infinità dei numeri primi · Crivello di Eratostene · Test di primalità ·Teorema fondamentale dell'aritmetica · Interi coprimi · Identità di Bézout · MCD · mcm · Algoritmo di Euclide · Teorema dei numeri primi
Funzioni aritmetiche	Funzione moltiplicativa · Funzione additiva · Convoluzione di Dirichlet · Funzione φ di Eulero · Funzione di Möbius · Funzione tau sui positivi · Funzione sigma · Funzione di Liouville · Funzione di Mertens
Aritmetica modulare	Teorema cinese del resto · Piccolo teorema di Fermat · Teorema di Eulero · Criteri di divisibilità · Teorema di Fermat sulle somme di due quadrati · Teorema di Wilson · Legge di reciprocità quadratica
Congetture	Congettura di Goldbach · Congettura di Polignac · Congettura abc · Congettura dei numeri primi gemelli · Congettura di Legendre · Nuova congettura di Mersenne · Congettura di Collatz · Ipotesi di Riemann
Altro	Problema di Waring
Principali teorici	Fibonacci · Fermat · Gauss · Eulero · Legendre · Riemann · Dirichlet
Discipline connesse	Teoria algebrica dei numeri · Teoria analitica dei numeri · Crittografia · Teoria computazionale dei numeri