Poliedru

Unele poliedre
Dodecaedru ( Poliedru platonic )	Dodecaedru mic stelat ( Poliedru Kepler-Poinsot )
Icosidodecaedru ( Poliedru arhimedian )	Prisma înstelată ( Poliedru înstelat uniform )
Triacontahedron rombic ( Poliedru catalan )	Ebesfenomegacorona ( Poliedru Johnson )

În matematică și în special în geometria solidă și teoria graficelor , un poliedru este un solid delimitat de un număr finit de fețe plane poligonale . Ca primele poliedre care trebuie luate în considerare, pentru simplitatea lor, există cuburi , paralelipipede , piramide și prisme . Printre cele mai complexe poliedre, cele cinci solide platonice , cunoscute încă din Grecia antică, ocupă un rol central.

În derivă termenul poliedru din greacă πολύεδρον (πολύς, polys = "mulți" și ἔδρον, édron = "față"). Multe obiecte microscopice naturale ( molecule , protozoare , viruși etc.) au forme sau simetrii poliedrice. Cristalele pot apărea și sub această formă la nivel macroscopic.

Noțiuni de bază

Definiție

În matematică, nu există o definiție unică a poliedrului. ^[1] În cele mai studiate cazuri, poligoanele formează o suprafață care delimitează o zonă solidă a spațiului: în acest caz, poliedru înseamnă acest solid și nu numai poligoanele care îi delimitează suprafața. În manuale, definiția formală a „poliedrului” este adesea însoțită de ipoteze tehnice suplimentare, care vizează excluderea unor cazuri considerate „patologice”. De exemplu, în Dedò (1999, p. 65) o suprafață poliedrică este definită ca un număr finit de poligoane din spațiu astfel încât:

intersecția a două fețe este goală sau o margine sau vârf,
fiecare margine aparține exact a două fețe,
două fețe adiacente nu sunt coplanare,
a fixat un summit $v$ ${\ displaystyle v}$ $v$ și două fețe $f, g$ ${\ displaystyle f, g}$ $f, g$ accidente pe $v$ ${\ displaystyle v}$ $v$ , există un lanț de fețe $f_{1},\ldots ,f_{n}$ ${\ displaystyle f_ {1}, \ ldots, f_ {n}}$ $f_1, \ ldots, f_n$ conținând $v$ ${\ displaystyle v}$ $v$ astfel încât $f=f_{1}$ ${\ displaystyle f = f_ {1}}$ $f = f_1$ , $g=f_{n}$ ${\ displaystyle g = f_ {n}}$ $g = f_n$ Și $f_{i}$ ${\ displaystyle f_ {i}}$ $f_ {i}$ este adiacent la $f_{i+1}$ ${\ displaystyle f_ {i + 1}}$ $f_ {i + 1}$ pentru fiecare $the$ ${\ displaystyle i}$ $the$ .

Cu toate acestea, alegerea unor ipoteze tehnice suplimentare nu este univocă și depinde în mare măsură de alegerea autorului. Ipotezele enumerate aici vizează, respectiv, prevenirea:

două fețe se intersectează în interiorul lor (ceea ce, totuși, trebuie admis dacă vrem să luăm în considerare și poliedrele Kepler-Poinsot , prezente în această intrare),
o margine aparține 4, 6 sau mai multe fețe, ca în uniunea a două poliedre care se intersectează doar într-o margine,
două fețe se suprapun sau că există margini „false” cu un unghi diedru de 180 °,
un vârf $V.$ ${\ displaystyle V}$ $V.$ local aparține a 2 sau mai multe piese distincte, ca în uniunea a două poliedre care se intersectează doar la un vârf.

Fețe

Un cub are 6 fețe pătrate , 12 margini și 8 vârfuri.

Poligoanele sunt fețele poliedrului. Fetele pot avea cele mai variate forme: toate pot fi congruente ca în cub , pot avea întotdeauna același număr de laturi fără a fi congruente ca într-un paralelipiped mai generic sau pot avea un număr variabil de laturi ca într-un prisma sau o piramidă .

Margini

Laturile fețelor sunt marginile poliedrului; prin definiție, o margine aparține simultan două fețe distincte și cantitatea sa cea mai reprezentativă este lungimea sa. Un poliedru poate avea muchii de lungime constantă (ca în cub ) sau variabilă.

Cele două fețe care ating o margine formează un unghi, numit unghi diedru , care variază în general de la margine la margine, dar care poate lua o valoare constantă în unele poliedre: de exemplu, în cub este întotdeauna un unghi drept , în timp ce în tetraedrul este de aproximativ 70 ° 32 '.

Piramida pătrată are un valent 4 vârf și patru valențe 3 vârfuri.

Vârfuri

Vârfurile fețelor (adică capetele marginilor) sunt vârfurile poliedrului. Fiecare vârf aparține cel puțin 3 fețe distincte. Numarul $n$ ${\ displaystyle n}$ $n$ de fețe căreia îi aparține este, de asemenea, egal cu numărul de muchii pe care le atinge: acest număr este valența vârfului.

Cuspidul unui vârf este structura locală a poliedrului din jurul său.

Adiacențe și incidențe

În tetraedru, oricare două fețe sunt întotdeauna adiacente.

Vârfurile adiacente ale poliedrului sunt două vârfuri care sunt capete ale aceleiași margini; marginile adiacente ale poliedrului sunt două muchii care au un vârf în comun; fețele adiacente ale poliedrului sunt două fețe care au o margine comună. Fiecare dintre cele trei relații de adiacență dintre vârfuri, margini și fețe ale unui poliedru este în mod clar o relație simetrică .

De exemplu, într-un tetraedru două vârfuri și două fețe sunt întotdeauna adiacente, în timp ce o margine este adiacentă tuturor celorlalte margini, cu excepția uneia (numită opusă ).

Pentru a stabili o terminologie, sunt introduse și trei relații de incidență ; se spun accidente : un vârf și o margine ale căror vârf este o extremitate; un vârf și o față din care face parte vârful; o margine și o față a cărei margine este o latură.

Cantitate

Un hexaedru .

Pentru fiecare $F.$ ${\ displaystyle F}$ $F.$ mai mare sau egal cu 4 există un poliedru cu $F.$ ${\ displaystyle F}$ $F.$ fețe. O primă clasificare a poliedrelor se referă la numărul fețelor lor: un poliedru de 4, 5, 6, 7, 8, ... 12, ... 20, ... fețele pot fi numite respectiv tetraedru , pentaedru , hexaedru , hectaredru , octaedru , ... dodecaedru , ... icosaedru , ... conform prefixelor numerice grecești folosite și pentru poligoane . Cu toate acestea, numele octaedru , dodecaedru și icosaedru sunt rezervate în general pentru trei poliedre foarte specifice și nu pentru un poliedru generic cu 8, 12 și 20 de fețe: acestea sunt trei dintre cele 5 solide platonice .

Numărul fețelor, muchiilor și vârfurilor unui poliedru formează un triplet de numere indicate cu $(F,S,V)$ ${\ displaystyle (F, S, V)}$ $(F, S, V)$ . Tetraedrul este cel mai mic poliedru, în sensul că are 4 fețe, 6 muchii și 4 vârfuri, în timp ce pentru toate poliedrele rămase relațiile $F>4$ ${\ displaystyle F> 4}$ $F> 4$ , $S>6$ ${\ displaystyle S> 6}$ $S> 6$ , $V>4.$ ${\ displaystyle V> 4.}$ $V> 4.$

Alte noțiuni

Convexitate

Steaua octangulă este un poliedru neconvex.

Un poliedru convex este un poliedru care identifică un solid convex . Această condiție poate fi exprimată în diferite moduri echivalente.

Pentru fiecare pereche de puncte ale solidului, segmentul care le unește este conținut în întregime în solid (aceasta este definiția obișnuită a unui set convex în spațiu);
Pentru fiecare pereche de vârfuri, segmentul care le unește este conținut în întregime în solid; ^[2]
Planul care conține fiecare față împarte spațiul în două jumătăți de spații, iar poliedrul este în întregime conținut în fiecare dintre acestea.

Un poliedru neconvex se numește uneori concav .

Cele mai cunoscute poliedre sunt convexe. În timp ce definiția generală a unui poliedru variază în funcție de autor, există o definiție universal acceptată de matematicieni a unui poliedru convex, descrisă mai jos. O jumătate de spațiu este una dintre cele două porțiuni de spațiu delimitate de un plan.

Un poliedru convex este o zonă limitată de spațiu obținută ca intersecție a unui număr finit de jumătăți de spații.

Pornind de la această definiție, este posibil să se definească fețele ca poligoane obținute prin intersecția poliedrului cu planurile care delimitează aceste jumătăți de spații. De exemplu, cubul este un poliedru convex cu 6 fețe și poate fi obținut ca o intersecție de 6 jumătăți de spații, delimitate de planurile care conțin fețele.

Scheletul tetraedrului, proiectat în plan.

Schelet

Modelul unui schelet în spațiu.

Vârfurile și muchiile unui poliedru formează un grafic , numit scheletul poliedrului. De exemplu, scheletul tetraedrului este un grafic complet cu 4 vârfuri.

Scheletul unui poliedru convex este un grafic plan : de fapt este posibil să se proiecteze graficul dintr-un punct intern al poliedrului pe orice sferă centrată în punct și apoi ulterior în plan prin intermediul unei proiecții stereografice . Graficul unui poliedru mai complex poate să nu fie plan.

Planificarea dezvoltării

Același subiect în detaliu: Planificarea dezvoltării unui poliedru .

Dodecaedrul ...

... și dezvoltarea sa.

Dezvoltarea plană a unui poliedru este o figură plană formată dintr-un anumit număr de poligoane împerecheate de-a lungul unor părți, care pot fi pliate în spațiu pentru a închide și a forma un poliedru. Dezvoltarea plană este un instrument practic pentru construirea poliedrelor de hârtie.

Orice poliedru convex poate fi construit dintr-o dezvoltare plană. Același poliedru poate fi construit pornind de la diferite dezvoltări plane: setul de poligoane prezente este întotdeauna același (ele sunt fețele poliedrului), dar calea pe care o formează poate fi diferită. ^[3]

Structura combinatorie și metrică

Un paralelipiped are întotdeauna aceeași structură combinatorie, indiferent de lungimile laturilor și unghiurile pe care le formează.

Structura combinatorie a unui poliedru este ansamblul vârfurilor, muchiilor și fețelor sale și relațiile de incidență dintre ele. Structura metrică a unui poliedru este în schimb structura poliedrului ca spațiu metric , adică ca un spațiu cu o distanță între puncte.

O rotație în jurul unei axe sau a unei translații lasă neschimbate structurile metrice și combinatorii ale poliedrului. O omotomie transformă structura metrică (deoarece schimbă, de exemplu, distanțele dintre vârfuri), dar lasă structura combinatorie neschimbată. Mai general, structura combinatorie este mai flexibilă: de exemplu, doi paralelipipedi au întotdeauna aceeași structură combinatorie, dar nu neapărat metrică.

Buldoexcavatorul $(F,S,V)$ ${\ displaystyle (F, S, V)}$ $(F, S, V)$ oferă o descriere bună a structurii combinatorii a poliedrului: totuși, descrierea nu este completă, deoarece nu conține toate informațiile despre adiacențe. Informații suplimentare sunt valoarea managementului superior.

Proprietăți topologice

Proprietățile topologice ale unui poliedru sunt cele care descriu doar forma sa globală. Cele mai studiate poliedre (de exemplu, cele convexe) au toate aceeași formă topologică: sunt „echivalente topologic” cu o minge ; aceste poliedre se numesc simple . Pentru poliedre simple există o formulă importantă, numită relația lui Euler .

Topologia suprafeței

Icosaedrul mare are 20 de fețe triunghiulare care se intersectează între ele.

Suprafața unui poliedru este uniunea fețelor sale. În unele cazuri, cum ar fi în icosaedrul mare prezentat în figură, aceste fețe se pot intersecta și astfel pot forma o figură complicată. Când se întâmplă acest lucru, este posibil să nu fie clar ce porțiune solidă de spațiu trebuie considerată de fapt „cuprinsă” de fețe. Acest fenomen este similar cu cel care apare în dimensiunea 2 în poligoane stelare .

În cele mai studiate cazuri, însă, fețele nu se intersectează și formează de fapt o suprafață care poate fi studiată din punct de vedere topologic : adică este descrisă forma sa globală, ignorând unghiurile formate local de diferitele margini și vârfuri. O suprafață definește întotdeauna o porțiune de spațiu. ^[4]

Un poliedru cu o gaură, având topologia unui tor .

Din punct de vedere topologic, o suprafață în spațiu este caracterizată mai ales de „numărul de piese disjuncte” și „numărul de găuri”. Când aceasta este alcătuită dintr-o singură bucată și nu are găuri, este echivalentă cu o sferă . Piesele disjuncte și numărul de găuri din matematică sunt formalizate, respectiv, cu noțiunile de componentă conectată și gen . Un poliedru cu o gaură are o suprafață în formă de tor .

Un poliedru ale cărui fețe formează o suprafață dintr-o singură bucată, fără găuri, se numește simplu . Poliedrele convexe și majoritatea poliedrelor studiate sunt simple.

Relația lui Euler

Același subiect în detaliu: relația lui Euler .

Nu este posibil să se construiască un poliedru ale cărui vârfuri au valența 3 și ale căror fețe sunt toate hexagonale. Mingea de fotbal utilizată în mod normal este un icosaedru trunchiat , ale cărui fețe sunt 20 de hexagone și 12 pentagone.

Relația lui Euler conectează numerele $F.$ ${\ displaystyle F}$ $F.$ , $S.$ ${\ displaystyle S}$ $S.$ Și $V.$ ${\ displaystyle V}$ $V.$ a fețelor, muchiilor și vârfurilor unui poliedru simplu, după cum urmează:

F+V-S=2.

{\ displaystyle F + VS = 2.}

F + V-S = 2.

De exemplu:

pentru cub : $F=6$ ${\ displaystyle F = 6}$ $F = 6$ , $V=8$ ${\ displaystyle V = 8}$ $V = 8$ , $S=12$ ${\ displaystyle S = 12}$ $S = 12$ , de la care $F-S+V=6-12+8=2$ ${\ displaystyle F-S + V = 6-12 + 8 = 2}$ $F-S + V = 6-12 + 8 = 2$ .
pentru tetraedru : $F=4$ ${\ displaystyle F = 4}$ $F = 4$ , $V=4$ ${\ displaystyle V = 4}$ $V = 4$ , $S=6$ ${\ displaystyle S = 6}$ $S = 6$ , de la care $F-S+V=4-6+4=2$ ${\ displaystyle F-S + V = 4-6 + 4 = 2}$ $F-S + V = 4-6 + 4 = 2$ .
baza pentagonală a prismei : $F=7$ ${\ displaystyle F = 7}$ $F = 7$ , $V=10$ ${\ displaystyle V = 10}$ $V = 10$ , $S=15$ ${\ displaystyle S = 15}$ $S = 15$ , de la care $F-S+V=7-15+10=2$ ${\ displaystyle F-S + V = 7-15 + 10 = 2}$ $F-S + V = 7-15 + 10 = 2$ .
pentru dodecaedru : $F=12$ ${\ displaystyle F = 12}$ $F = 12$ , $V=20$ ${\ displaystyle V = 20}$ $V = 20$ , $S=30$ ${\ displaystyle S = 30}$ $S = 30$ , de la care $F-S+V=12-30+20=2$ ${\ displaystyle F-S + V = 12-30 + 20 = 2}$ $F-S + V = 12-30 + 20 = 2$ .

Relația lui Euler poate fi utilizată pentru a demonstra, de exemplu, că nu este posibil să construiești o minge de fotbal similară cu cea din figură, dar cu toate fețele hexagonale.

Relația lui Euler nu se poate menține în poliedre non-simple. De exemplu, într-un poliedru în formă de toro precum cel prezentat în figură, relația se menține $V-S+F=0$ ${\ displaystyle V-S + F = 0}$ $V-S + F = 0$ . Cantitatea $\chi =V-S+F$ ${\ displaystyle \ chi = V-S + F}$ $\ chi = V-S + F$ de fapt depinde doar de topologia poliedrului și se numește caracteristica Euler-Poincaré : aceasta este o cantitate foarte importantă în topologie .

Simetriile

Cele mai studiate poliedre sunt cele cu numeroase simetrii . O simetrie a unui poliedru este o izometrie a spațiului care transformă poliedrul în sine. Simetriile unui poliedru formează un grup , numit grup de simetrie .

Tipuri de simetrie

Simetriile tetraedrului: rotații în jurul unei axe sau reflexie față de un plan.

Există două clase de izometrie a spațiului euclidian tridimensional: cele care păstrează orientarea spațiului (adică transformă o mână dreaptă într-o mână dreaptă) și cele care o inversează (care transformă o mână dreaptă într-o mână stângă) . Aceeași clasificare se reflectă în simetriile unui poliedru.

O simetrie a poliedrului care păstrează orientarea trebuie să fie neapărat o rotație în jurul unei axe ^[5] indicată de literă $c_{n}$ ${\ displaystyle c_ {n}}$ $c_ {n}$ , unde n este numărul de rotații „unitare” care aduc poliedrul înapoi la configurația de pornire (e ${\frac {2\pi }{n}}={\frac {360^{\circ }}{n}}$ ${\ displaystyle {\ frac {2 \ pi} {n}} = {\ frac {360 ^ {\ circ}} {n}}}$ ${\ displaystyle {\ frac {2 \ pi} {n}} = {\ frac {360 ^ {\ circ}} {n}}}$ este unghiul corespunzător).
O simetrie care nu păstrează orientarea poate fi:
- inversiunea față de un punct, numit centrul de simetrie , indicat de literă $the$ ${\ displaystyle i}$ $the$ ;
- o reflecție de -a lungul unui plan, numit planul de simetrie $\sigma$ ${\ displaystyle \ sigma}$ $\ sigma$ ;
- compoziția unei reflexii de-a lungul unui plan și a unei rotații cu o axă perpendiculară pe plan ( rotație necorespunzătoare $s_{n}$ ${\ displaystyle s_ {n}}$ ${\ displaystyle s_ {n}}$ ).

De exemplu, tetraedrul are 7 axe de simetrie: patru pentru fiecare vârf și trei pentru fiecare pereche de margini opuse (vezi figura). De asemenea, are 6 planuri de simetrie (unul pentru fiecare margine). Cu toate acestea, simetriile sunt de fapt 24. Dintre acestea, 12 mențin orientarea și sunt: identitate , 2 rotații în jurul fiecărei axe de primul tip (de 120 ° și 240 °) și o rotație de 180 ° în jurul unei axe a celui de-al doilea tip (deci $1+2\times 4+3=12$ ${\ displaystyle 1 + 2 \ times 4 + 3 = 12}$ $1 + 2 \ ori 4 + 3 = 12$ ). Există, de asemenea, 12 simetrii care nu mențin orientarea: 6 sunt reflecții de-a lungul planurilor așa cum se arată în figură, iar alte 6 sunt compoziții de reflecții și rotații.

Avioane, axe și centrul de simetrie

Planurile și axele de simetrie sunt rezultatul prezenței simetriilor reflexive și rotative. Intersecția tuturor axelor și planurilor de simetrie poate fi un plan, o linie, un punct sau gol. Intersecția poate fi goală numai dacă nu există simetrii. ^[6] Dacă intersecția este un punct, acesta se numește centrul poliedrului. Dacă intersecția este o linie dreaptă, aceasta este axa poliedrului.

De exemplu, tetraedrul și cubul au un centru. O piramidă pătrată nu are un centru, ^[7] dar are o axă.

Chiralitate

Cubul este chiral; adică nu este echivalent ...

... la reflectarea sa.

Un poliedru este chiral dacă nu este echivalent cu imaginea sa reflectată. Mai precis, un poliedru este chiral dacă toate simetriile sale sunt rotaționale: adică nu are simetrii care să inverseze orientarea. Mai concret, un poliedru chiral se comportă ca o mână: se prezintă în două forme (una „stângă” și una „dreaptă”) care se oglindesc reciproc.

Regularitate

O simetrie mișcă un vârf pe un vârf, care poate fi același sau diferit de cel de pornire. În mod similar, mutați o margine pe o margine și o față pe o față. Prin urmare, simetria determină o permutare a vârfurilor, marginilor și fețelor.

Dodecaedrul rombic este regulat pe margini și fețe, dar nu pe vârfuri: unele au valența 3 și altele valența 4.

Simetriile unui poliedru induc o relație de echivalență pe mulțimea vârfurilor sale (și în mod similar pe mulțimea marginilor și fețelor sale): două vârfuri (sau muchii sau fețe) sunt echivalente dacă există o simetrie care mișcă primul în la. ^[8] Două vârfuri echivalente (sau margini sau fețe) trebuie să aibă neapărat același aspect: de exemplu, două vârfuri echivalente trebuie să aibă același tip de cuspid (în special, aceeași valență), două margini de aceeași lungime și același unghi diedru și două fețe echivalente trebuie să fie congruente . Toate aceste condiții necesare nu sunt în general suficiente : pot exista fețe non-echivalente congruente, margini neechivalente de aceeași lungime și cu același unghi diedru etc.

Dacă vârfurile unui poliedru sunt echivalente, se spune că acesta este regulat pe vârfuri . În mod similar, dacă toate muchiile sau toate fețele sunt echivalente, se spune că este regulat pe margini sau fețe . Termenii omogen și tranzitiv pot fi folosiți ca sinonim pentru regulat . ^[9]

Se spune că un poliedru care este regulat pe vârfuri, margini și fețe este regulat . Există doar 5 poliedre regulate simple - acestea sunt solidele platonice .

Grup de simetrie

Simetriile unui poliedru formează un grup cu operația de compunere . Acest grup este întotdeauna un grup finit .

De exemplu, grupul de simetrie al tetraedrului este grupul de permutare $S_{4}$ ${\ displaystyle S_ {4}}$ $S_ {4}$ a 4 elemente: de fapt fiecare permutare a celor 4 vârfuri se face exact printr-o simetrie. Simetriile sunt de fapt 4! = 24.

Simetriile care păstrează orientarea formează un subgrup , numit grup de rotație . Acest lucru poate coincide cu întregul grup (dacă poliedrul este chiral) sau poate avea un indice 2 (dacă nu este chiral). Tetraedrul nu este chiral: grupul de rotații este grupul alternativ $A_{4}$ ${\ displaystyle A_ {4}}$ $A_ {4}$ , având 12 elemente.

Octaedrul are 24 de simetrii rotative: acestea formează grupul

S_{4}

{\ displaystyle S_ {4}}

S_ {4}

.

Icosaedrul are 60 de simetrii de rotație: acestea formează grupul

A_{5}

{\ displaystyle A_ {5}}

A_ {5}

.

În ciuda marii varietăți de poliedre care există, există puține clase de grupuri de simetrie posibile. De exemplu, singurele grupuri care pot fi grupuri de rotație ale unor poliedri sunt

C_{n},D_{n},A_{4},S_{4},A_{5}\,\!

{\ displaystyle C_ {n}, D_ {n}, A_ {4}, S_ {4}, A_ {5} \, \!}

C_ {n}, D_ {n}, A_ {4}, S_ {4}, A_ {5} \, \!

unde este $C_{n}$ ${\ displaystyle C_ {n}}$ $C_ {n}$ este grupul ciclic de ordine $n$ ${\ displaystyle n}$ $n$ , $D_{n}$ ${\ displaystyle D_ {n}}$ $D_n$ este grupul diedric al ordinii $2n$ ${\ displaystyle 2n}$ $2n$ , $S_{n}$ ${\ displaystyle S_ {n}}$ $S_ {n}$ este grupul simetric al ordinii $n!$ ${\ displaystyle n!}$ $n!$ Și $A_{n}$ ${\ displaystyle A_ {n}}$ $A_ {n}$ este grupul alternativ de ordine $n!/2$ ${\ displaystyle n! / 2}$ $n! / 2$ . Grupurile $C_{n}$ ${\ displaystyle C_ {n}}$ $C_n$ Și $D_{n}$ ${\ displaystyle D_ {n}}$ $D_n$ se obțin și ca grupuri de rotație și simetrie ale unui poligon regulat cu $n$ ${\ displaystyle n}$ $n$ laturi: sunt, prin urmare, grupuri care se obțin și în plan, iar prezența lor nu este deci surprinzătoare. ^[10]

Grupurile $A_{4},S_{4}$ ${\ displaystyle A_ {4}, S_ {4}}$ $A_ {4}, S_ {4}$ Și $A_{5}$ ${\ displaystyle A_ {5}}$ $A_ {5}$ sunt deci singurele grupuri de rotații esențial tridimensionale. Acestea sunt grupurile de rotații ale celor 5 solide platonice: $A_{4}$ ${\ displaystyle A_ {4}}$ $A_ {4}$ pentru tetraedru, $S_{4}$ ${\ displaystyle S_ {4}}$ $S_ {4}$ pentru cub și octaedru , $A_{5}$ ${\ displaystyle A_ {5}}$ $A_5$ pentru icosaedru și dodecaedru . Solidele platonice joacă un rol central aici (ca în multe alte contexte).

Dualitate

Același subiect în detaliu: Poliedru dual .

Dualitatea dintre cub și octaedru .

Două poliedre $P.$ ${\ displaystyle P}$ $P.$ Și $Î$ ${\ displaystyle Q}$ $Î$ sunt duble dacă au rolurile de vârfuri și fețe schimbate. Mai precis, la fiecare vârf, margine sau față a $P.$ ${\ displaystyle P}$ $P.$ se potrivește cu o față, o margine sau un vârf respectiv $Î$ ${\ displaystyle Q}$ $Î$ , astfel încât adiacențele și incidențele să fie păstrate. De exemplu, dacă un vârf de $P.$ ${\ displaystyle P}$ $P.$ este adiacent la o margine de $P.$ ${\ displaystyle P}$ $P.$ , fața corespunzătoare a $Î$ ${\ displaystyle Q}$ $Î$ este adiacent marginii corespunzătoare a $Î$ ${\ displaystyle Q}$ $Î$ .

În special, tripletele numerelor $(V,S,F)$ ${\ displaystyle (V, S, F)}$ $(V, S, F)$ dintre cele două poliedre sunt opuse unul altuia. De exemplu, cubul , având $(V,S,F)=(8,12,6)$ ${\ displaystyle (V, S, F) = (8,12,6)}$ $(V, S, F) = (8, 12, 6)$ este dual al octaedrului , având $(V,S,F)=(6,12,8)$ ${\ displaystyle (V, S, F) = (6,12,8)}$ $(V, S, F) = (6,12,8)$ . În multe cazuri (ca acesta) dualitatea se realizează în așa fel încât vârfurile $Î$ ${\ displaystyle Q}$ $Î$ sunt puncte interne ale fețelor corespunzătoare ale $P.$ ${\ displaystyle P}$ $P.$ (vezi un exemplu în figură).

Fiecare poliedru convex are un poliedru dual, care poate fi definit ca rezultatul unei inversiuni față de o sferă. Când poliedrul are un centru, este firesc să luăm o sferă centrată în acest punct ca o sferă. Construcția dualului poliedrelor neconvexe este mai problematică.

Clase de poliedre

Prismatoizi

Același subiect în detaliu: Prismatoid .

Un prismatoid este un poliedru ale cărui vârfuri se află în două planuri paralele. Cu rare excepții, ^[11] prismatoidele au în general cel mult o axă de simetrie ( ortogonală la planurile paralele), iar grupul lor de simetrii este ciclic ( $C_{n}$ ${\ displaystyle C_ {n}}$ $C_n$ ) sau diedru ( $D_{n}$ ${\ displaystyle D_ {n}}$ $D_n$ ), adică similar cu grupul de simetrii ale unui poligon din plan.

Există diverse familii infinite de prismatoide. Cele mai utilizate sunt listate aici.

Piramidă	Prisma	Antiprism	Prisma înstelată	Dom	Trunchiul piramidei

O piramidă are o față numită bază și un alt vârf conectat la aceasta prin fețe triunghiulare.
O prismă are două fețe congruente care se află în două planuri paralele, conectate cu paralelogramele laterale.
Un antiprism este similar cu o prismă: are două fețe congruente pe două planuri paralele, conectate totuși cu triunghiuri.
O prismă înstelată sau o antiprismă înstelată este definită în mod analog: cele două fețe, totuși, sunt poligoane înstelate .
O cupolă are două fețe necongruente conectate prin dreptunghiuri și triunghiuri.
O piramidă trunchiată are două fețe necongruente, dar similare, conectate prin trapezoide .

Solidele platonice

Același subiect în detaliu: solid platonic .

Există exact 5 poliedre regulate simple pe fețe, margini și vârfuri. Acestea sunt solidele platonice . Aceste poliedre se mai numesc regulate .

Tetraedru (4,6,4) (3.3)	cub (6.12.8) (4.3)	Octaedru (8.12.6) (3.4)	Dodecaedru (12.30.20) (5.3)	Icosaedru (20,30,12) (3,5)

Tabelul indică triada pentru fiecare solid platonic $(F,S,V)$ ${\ displaystyle (F, S, V)}$ $(F, S, V)$ și un cuplu $(N,M)$ ${\ displaystyle (N, M)}$ $(N, M)$ , cu $Nu.$ ${\ displaystyle N}$ $Nu.$ egal cu numărul laturilor fiecărei fețe e $M.$ ${\ displaystyle M}$ $M.$ egal cu numărul de muchii de pe fiecare vârf (adică valența acestuia). Cubul și octaedrul sunt duale, dodecaedrul și icosaedrul sunt duale. Tetraedrul este dual pentru sine (dualitatea inversează triplele și perechile de numere din tabele).

Centrul fiecărui solid platonic este și centrul unei sfere inscripționate (interne și tangente la toate fețele) și a unei sfere circumscrise (externe și care conține toate vârfurile).

Pentru a fi obișnuiți , pe lângă faptul că au poligoane regulate ca fețe care sunt la fel, trebuie să aibă și toate muchiile și vârfurile echivalente.

Solidele platonice joacă un rol central în geometria solidelor : sunt solidele care au cea mai mare regularitate posibilă și cel mai mare număr de simetrii. Grupurile lor de simetrie au legături cu cele mai disparate secțiuni ale matematicii. De asemenea, au un loc proeminent în istoria gândirii grecești , arabe și renascentiste . Platon , în Timeu , a asociat câte un element fiecăruia dintre ei: foc la tetraedru, pământ la cub, aer la octaedru, apă la icosaedru, în timp ce el credea că dodecaedrul era forma universului .

Poliedre Kepler-Poinsot

Același subiect în detaliu: Poliedrul Kepler-Poinsot .

În plus față de cele 5 poliedre platonice, există și alte 4 poliedre regulate non-simple. Fețele acestor poliedre se intersectează: două dintre acestea, descoperite de Kepler , au ca fețe poligoane regulate în formă de stea ; alte două, descoperite de Louis Poinsot , au fețe regulate, care nu sunt înstelate, dar totuși împletite.

Dodecaedru mic stelat (12,30,12) (5,5)	Mare dodecaedru (12,30,12) (5,5)	Mare dodecaedru stelat (12.30.20) (5.3)	Mare icosaedru (20,30,12) (3,5)

Cele două poliedre înstelate au 12 fețe pentagone stele ( doage ). Valori $(F,S,V)$ ${\ displaystyle (F, S, V)}$ $(F, S, V)$ Și $(N,M)$ ${\displaystyle (N,M)}$ $(N,M)$ hanno lo stesso significato descritto precedentemente. I primi due poliedri sono uno duale dell'altro, come lo sono anche gli ultimi due.

Poliedri uniformi

Lo stesso argomento in dettaglio: Poliedro uniforme .

Il cubottaedro è un solido archimedeo.

Un poliedro uniforme è un poliedro

regolare sui vertici,
le cui facce sono poligoni regolari .

Il poliedro non è necessariamente semplice. I poliedri uniformi sono catalogati nel modo seguente:

Famiglie infinite di prismatoidi : prismi , antiprismi , prismi stellati e antiprismi stellati regolari.
I 5 solidi platonici ei 4 solidi di Keplero-Poinsot , che sono regolari anche su spigoli e facce.
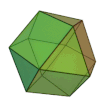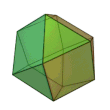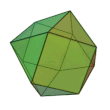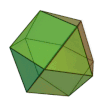
13 altri solidi convessi, detti solidi archimedei .
54 altri solidi non convessi (con facce convesse o stellate).

I poliedri duali dei poliedri uniformi sono regolari sulle facce e hanno cuspidi regolari. Tra questi, i 13 solidi duali dei solidi archimedei sono detti poliedri di Catalan dal nome del matematico belga Eugène Charles Catalan .

Solidi di Johnson

Lo stesso argomento in dettaglio: Solido di Johnson .

L' ortobicupola triangolare è un solido di Johnson.

Un solido di Johnson è un poliedro convesso

non regolare sui vertici,
le cui facce sono poligoni regolari.

In altre parole, i solidi di Johnson sono i solidi convessi con facce regolari che non sono uniformi.

I solidi di Johnson sono 92, e vengono generalmente indicati con una sigla che va da $J_{1}$ $J_{1}$ $J_{1}$ fino a $J_{92}$ $J_{92}$ $J_{92}$ .

I solidi convessi aventi facce regolari sono quindi: prismi e antiprismi regolari (in quantità infinita), i solidi platonici (5), i solidi archimedei (13) e quelli di Johnson (92).

Poliedri composti

Lo stesso argomento in dettaglio: Poliedro composto .

Questo poliedro è unione di cinque tetraedri!

Un poliedro composto è un poliedro ottenuto come unione di più poliedri distinti aventi lo stesso centro. Un poliedro di questo tipo generalmente non è convesso.

Ad esempio, la stella octangula mostrata precedentemente può essere descritta come poliedro composto, formato da due tetraedri, aventi lo stesso centro ma posizionati in modo differente.

I poliedri composti più importanti sono quelli che presentano molte simmetrie. Ad esempio il poliedro mostrato accanto in figura, denominato cinque tetraedri nel dodecaedro , è effettivamente l'unione di 5 tetraedri concentrici: ha $5\times 4=20$ $5\times 4=20$ $5\times 4 =20$ vertici, i quali sono anche i vertici di un dodecaedro regolare .

Operazioni con i poliedri

Alcune operazioni permettono di trasformare un poliedro in un altro, o di affiancare più poliedri in modo da ricoprire lo spazio.

Troncamento

Il troncamento di un vertice $v$ ${\displaystyle v}$ $v$ di un poliedro consiste nell'eliminazione di una porzione di poliedro (una cuspide ) tramite un taglio vicino a $v$ ${\displaystyle v}$ $v$ . Il pezzo da rimuovere è una piramide con vertice in $v$ ${\displaystyle v}$ $v$ e base determinata dal piano lungo cui viene fatto il taglio. La base è un poligono con $n$ ${\displaystyle n}$ $n$ lati, dove $n$ ${\displaystyle n}$ $n$ è la valenza di $v$ ${\displaystyle v}$ $v$ .

Il nuovo poliedro ha una faccia in più del precedente. Troncando un vertice alla volta, è quindi possibile, partendo dal tetraedro, costruire poliedri con un numero arbitrario 4, 5, 6... di facce.

Molti solidi archimedei sono ottenuti troncando opportunamente tutti i vertici di un solido platonico. Una troncatura variabile può essere usata in alcuni casi per passare da un poliedro al suo duale, come in questa sequenza che collega il cubo all'ottaedro:

Cubo	Cubo troncato	Cubottaedro	Ottaedro troncato	Ottaedro

Stellazione

La stellazione è un'operazione definita da Keplero nel 1619 : consiste nell'estendere alcune facce del poliedro fino ad un punto in cui queste si incontrano nuovamente. Con questa operazione Keplero costruì, partendo dal dodecaedro regolare , due dei quattro poliedri noti oggi come solidi di Keplero-Poinsot . La stella octangula è una stellazione dell' ottaedro regolare .

Qui sotto sono elencate alcune stellazioni: una dell'ottaedro regolare (la stella octangula), tre del dodecaedro regolare (le prime due sono i solidi di Keplero), e una dell'icosaedro.

Ottaedro	Dodecaedro (1)	Dodecaedro (2)	Dodecaedro (3)	Icosaedro

Tassellazione

Lo stesso argomento in dettaglio: Tassellazione dello spazio .

Alcuni poliedri possono essere usati come mattoni per riempire lo spazio senza lasciare buchi, similmente a quanto accade nelle arnie : una tale operazione è detta tassellazione dello spazio (o pavimentazione dello spazio). I poliedri in una tassellazione sono adiacenti lungo le loro facce. Fra i solidi platonici, l'unico in grado di tassellare lo spazio è il cubo; fra i solidi archimedei, vi sono il dodecaedro rombico e l' ottaedro troncato . Ottaedri e tetraedri regolari possono essere usati a coppie per tassellare lo spazio.

Cubi	Dodecaedri rombici	Ottaedri troncati	Ottaedri e tetraedri

Poliedri nel mondo reale

Naturali

Minerali

Molti minerali cristallizzano con una forma, detta abito , che corrisponde ad un poliedro. La pirite si può presentare con tre abiti diversi: con cristalli cubici, ottaedrici o aventi la forma di un dodecaedro non regolare (detto pentadodecaedro o piritoedro ). Nessun minerale ha però la forma di un icosaedro o dodecaedro regolare .

Cubo	Ottaedro	Dodecaedro

La leucite può avere la forma di un icositetraedro trapezoidale (un solido di Catalan ). Il piropo può avere la forma di un dodecaedro rombico (un poliedro di Catalan ) e l' aragonite la forma di un prisma esagonale.

Icositetraedro trapezoidale	Dodecaedro rombico	Prisma esagonale

Radiolari

Molti organismi microscopici hanno forme o simmetrie poliedrali. Tra questi, i radiolari possono avere la forma di un icosaedro regolare o di un geode . Nella forma geodale, è possibile verificare una delle conseguenze della relazione di Eulero descritta sopra: non è possibile costruire un solido i cui vertici hanno valenza 3 e le cui facce sono tutte esagonali. Nella figura sono infatti presenti alcuni pentagoni. ^[12] Le regolari geometrie degli scheletri di questi microorganismi hanno affascinato dalla fine del secolo XIX molti naturalisti, tra cui Ernst Haeckel ^[13] e Thompson D'Arcy , ^[14] che hanno anche cercato una interpretazione integrata fra biologia e geometria sul significato di queste strutture:

Icosaedro ^[15]	Geode

Artificiali

Piramidi

Il solido artificiale più antico di cui è rimasta traccia è sicuramente la piramide.

Piramidi egizie	Piramide del Louvre

Dadi

Il dado da gioco classico ha la forma di un cubo. Alcuni giochi di ruolo fanno però uso di tutti e 5 i solidi platonici: la regolarità del solido infatti garantisce che ogni faccia abbia la stessa probabilità di uscire dopo un lancio (naturalmente la densità del solido dev'essere uniforme).

I solidi platonici e due trapezoedri usati come dadi.

Per mantenere la stessa probabilità è sufficiente che il solido sia regolare sulle facce: per questo motivo vengono usati anche i trapezoedri . Ad esempio, due trapezoedri con 10 facce come in figura usati simultaneamente permettono di sorteggiare un numero da 0 a 99.

Cupole geodetiche

Una cupola geodetica è un solido con molte facce, la cui forma è molto simile a quella di una sfera (o di una porzione di questa). Come nei radiolari mostrati sopra, nelle cupole geodetiche è spesso facile verificare gli effetti della relazione di Eulero .

Disneyworld	Montréal	Museo Dalí a Figueres

Note

^ Il problema è affrontato da un punto di vista storico e matematico in ( EN ) B. Grünbaum, Are your polyhedra the same as my polyhedra? ( PDF ), in Discrete and comput. geom: the Goodman-Pollack festschrift , Aronov et al. Springer, 2003, pp. 461-488. URL consultato l'11 febbraio 2007 .
^ Un tale segmento talora viene detto diametro del poliedro ; altri definiscono diametro di un poliedro un qualsiasi segmento aventi gli estremi su vertici, spigoli o facce, e gli altri punti all'interno del solido.
^ Uno sviluppo è infatti determinato dall' albero massimale nel grafo poliedrale formato dagli spigoli che vengono incollati alla chiusura. Alberi massimali diversi possono dare luogo a sviluppi diversi.
^ Questo fatto, benché intuitivo, non è di banale dimostrazione: si tratta dell'analogo tridimensionale del teorema della curva di Jordan . Il fatto che la superficie sia un'unione di poligoni rende comunque più facile la dimostrazione: senza questa ipotesi si possono creare superfici come la sfera cornuta di Alexander , che si comportano in modo più bizzarro.
^ Questo fatto non banale può essere dimostrato con l'ausilio dell' algebra lineare : innanzitutto, il fatto che il poliedro sia un insieme limitato , implica che devono essere escluse isometrie come le traslazioni , e che c'è un punto fisso . Fissata l'origine in questo punto, lo spazio diventa uno spazio vettoriale e (fissata una base ) una isometria è descritta da una matrice ortogonale . Usando il polinomio caratteristico e gli autovalori si mostra che effettivamente questa è una rotazione intorno ad un asse.
^ La dimostrazione di quest'altro fatto non banale sfrutta la proprietà che un poliedro è un insieme limitato . Questo fatto implica, ad esempio, che più assi di simmetria si incontrano sempre in un punto.
^ La piramide quadrata ha un asse di simmetria rotatoria (passante per il vertice e ortogonale alla base) e alcuni piani di riflessione contenenti questo asse. L'intersezione di questi oggetti è una retta e non un punto.
^ Oppure il secondo nel primo: la cosa non fa differenza, basta sostituire una simmetria con la sua simmetria inversa .
^ Il termine omogeneo si riferisce al fatto che i vertici formano con le simmetrie uno spazio omogeneo , mentre il termine transitivo si riferisce al fatto che l' azione del gruppo di simmetria è transitiva : entrambe queste nozioni sono equivalenti al fatto che i vertici sono tutti equivalenti.
^ Nello spazio, questi sono i gruppi delle rotazioni di piramidi e prismi (e più generalmente dei prismatoidi ).
^ Ad esempio il tetraedro e il cubo.
^ Per la formula di Eulero, questi devono essere necessariamente 12, come nel pallone da calcio .
^ Ernst Haeckel, Kunstformen der Natur 1904 : oltre 100 illustrazioni a colori con accurata descrizione di animali e creature marine.
^ D'Arcy Wentworth Thompson, On Growth and Form (1917) 2nd ed. 1942. ISBN 0-486-67135-6 .
^ Tavola di Haeckel: Circogonia Icosahedra, "Kunstformen der Natur", 1904

Bibliografia

Maria Dedò, Forme, simmetria e topologia , Bologna, Decibel & Zanichelli, 1999, ISBN 88-08-09615-7 .
Gino Loria , Poliedri, curve e superficie secondo i metodi della geometria descrittiva , Milano, Hoepli, 1912.
Francesco Severi , Cenno sulla teoria e costruzione degli orologi solari, poliedri e loro rappresentazione , Padova, La Litotipo, 1915.
Nicoletta Sala e Gabriele Cappellato, Viaggio matematico nell'arte e nell'architettura , 2ª ed., FrancoAngeli, 2008.
( EN ) P. Cromwell, Polyhedra , 1997.
( EN ) HM Cundy e AP Rollett, Mathematical models , 3ª ed., 1981.
( EN ) HSM Coxeter ,Regular Polytopes , 3ª ed., 1973.

Voci correlate

Altri progetti

Wikizionario contiene il lemma di dizionario « poliedro »
Wikimedia Commons contiene immagini o altri file su poliedro

Collegamenti esterni

( EN ) Poliedro , su Enciclopedia Britannica , Encyclopædia Britannica, Inc.
( EN ) Virtual Polyhedra , su georgehart.com . URL consultato il 7 marzo 2008 . Sito dedicato ai poliedri con una ampia bibliografia .
( EN )The puzzling world of polyhedral dissections , su johnrausch.com . URL consultato l'11 febbraio 2008 . Libro dedicato ai puzzle tridimensionali.
( EN ) Guy's polyhedra pages , su steelpillow.com . URL consultato l'11 febbraio 2008 . Sito orientato alla ricerca attuale sui poliedri.
( EN ) Stella , su software3d.com . URL consultato l'11 febbraio 2008 . Programma dedicato alla visualizzazione di poliedri.
( EN ) The Uniform Polyhedra , su mathconsult.ch . URL consultato l'11 febbraio 2008 . Sito dedicato ai poliedri uniformi .
( EN ) Paper Models of Polyhedra , su korthalsaltes.com . URL consultato l'11 febbraio 2008 . Sviluppi di poliedri in formato PDF stampabili.
( EN ) Interactive 3D polyhedra , su ibiblio.org . URL consultato l'11 febbraio 2008 (archiviato dall' url originale il 3 aprile 2005) . Visualizzazione tridimensionale con trascinamento in Java .
( FR ) Polyèdres , su xavier.hubaut.info . URL consultato l'11 febbraio 2008 . Visualizzazione tridimensionale con trascinamento.
( FR ) Polygones, polyèdres et polytopes , su mathcurve.com . URL consultato l'11 febbraio 2008 . Informazioni metriche dettagliate su molti poliedri.
( DE , EN , FR ) Polyedergarten , su polyedergarten.de . URL consultato l'11 febbraio 2008 . Modelli di carta.

Controllo di autorità	Thesaurus BNCF 22328 · LCCN ( EN ) sh85104647 · GND ( DE ) 4132101-7 · BNF ( FR ) cb119796991 (data) · NDL ( EN , JA ) 01136723

Portale Matematica : accedi alle voci di Wikipedia che trattano di matematica

Questa è una voce in vetrina , identificata come una delle migliori voci prodotte dalla comunità .
È stata riconosciuta come tale il giorno 28 marzo 2008 — vai alla segnalazione .
Naturalmente sono ben accetti suggerimenti e modifiche che migliorino ulteriormente il lavoro svolto.

Segnalazioni · Criteri di ammissione · Voci in vetrina in altre lingue · Voci in vetrina in altre lingue senza equivalente su it.wiki

[1] Il problema è affrontato da un punto di vista storico e matematico in ( EN ) B. Grünbaum, Are your polyhedra the same as my polyhedra? ( PDF ), in Discrete and comput. geom: the Goodman-Pollack festschrift , Aronov et al. Springer, 2003, pp. 461-488. URL consultato l'11 febbraio 2007 .

[2] Un tale segmento talora viene detto diametro del poliedro ; altri definiscono diametro di un poliedro un qualsiasi segmento aventi gli estremi su vertici, spigoli o facce, e gli altri punti all'interno del solido.

[3] Uno sviluppo è infatti determinato dall' albero massimale nel grafo poliedrale formato dagli spigoli che vengono incollati alla chiusura. Alberi massimali diversi possono dare luogo a sviluppi diversi.

[4] Questo fatto, benché intuitivo, non è di banale dimostrazione: si tratta dell'analogo tridimensionale del teorema della curva di Jordan . Il fatto che la superficie sia un'unione di poligoni rende comunque più facile la dimostrazione: senza questa ipotesi si possono creare superfici come la sfera cornuta di Alexander , che si comportano in modo più bizzarro.

[5] Questo fatto non banale può essere dimostrato con l'ausilio dell' algebra lineare : innanzitutto, il fatto che il poliedro sia un insieme limitato , implica che devono essere escluse isometrie come le traslazioni , e che c'è un punto fisso . Fissata l'origine in questo punto, lo spazio diventa uno spazio vettoriale e (fissata una base ) una isometria è descritta da una matrice ortogonale . Usando il polinomio caratteristico e gli autovalori si mostra che effettivamente questa è una rotazione intorno ad un asse.

[6] La dimostrazione di quest'altro fatto non banale sfrutta la proprietà che un poliedro è un insieme limitato . Questo fatto implica, ad esempio, che più assi di simmetria si incontrano sempre in un punto.

[7] La piramide quadrata ha un asse di simmetria rotatoria (passante per il vertice e ortogonale alla base) e alcuni piani di riflessione contenenti questo asse. L'intersezione di questi oggetti è una retta e non un punto.

[8] Oppure il secondo nel primo: la cosa non fa differenza, basta sostituire una simmetria con la sua simmetria inversa .

[9] Il termine omogeneo si riferisce al fatto che i vertici formano con le simmetrie uno spazio omogeneo , mentre il termine transitivo si riferisce al fatto che l' azione del gruppo di simmetria è transitiva : entrambe queste nozioni sono equivalenti al fatto che i vertici sono tutti equivalenti.

[10] Nello spazio, questi sono i gruppi delle rotazioni di piramidi e prismi (e più generalmente dei prismatoidi ).

[11] Ad esempio il tetraedro e il cubo.

[12] Per la formula di Eulero, questi devono essere necessariamente 12, come nel pallone da calcio .

[13] Ernst Haeckel, Kunstformen der Natur 1904 : oltre 100 illustrazioni a colori con accurata descrizione di animali e creature marine.

[14] D'Arcy Wentworth Thompson, On Growth and Form (1917) 2nd ed. 1942. ISBN 0-486-67135-6 .

[15] Tavola di Haeckel: Circogonia Icosahedra, "Kunstformen der Natur", 1904

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]