Puterea (matematica)

În matematică , puterea este o operație care se asociază cu o pereche de numere $la$ ${\ displaystyle a}$ $la$ Și $n,$ ${\ displaystyle n,}$ $n,$ numit bază și respectiv exponent , numărul dat de produsul lui $n$ ${\ displaystyle n}$ $n$ factori egali cu $la$ ${\ displaystyle a}$ $la$ :

{\begin{matrix}a^{n}:=&\underbrace {a\cdot a\cdot a\cdots a} \\&n{\mbox{ volte}}\end{matrix}}

{\ displaystyle {\ begin {matrix} a ^ {n}: = & \ underbrace {a \ cdot a \ cdot a \ cdots a} \\ & n {\ mbox {times}} \ end {matrix}}}

\ begin {matrix} a ^ n: = & \ underbrace {a \ cdot a \ cdot a \ cdots a} \\ & n \ mbox {times} \ end {matrix}

în acest context $la$ ${\ displaystyle a}$ $la$ poate fi un timp întreg , rațional sau real $n$ ${\ displaystyle n}$ $n$ este un număr întreg pozitiv. Cu ipoteze adecvate asupra $la$ ${\ displaystyle a}$ $la$ este, de asemenea, posibil să se ia în considerare alte valori numerice pentru exponenți, de exemplu exponenți întregi (chiar dacă nu pozitivi), raționali sau reali.

Puterile scrise în formă $a^{n}$ ${\ displaystyle a ^ {n}}$ $a ^ {n}$ citesc ca $la$ ${\ displaystyle a}$ $la$ ridicat la $n$ ${\ displaystyle n}$ $n$ sau mai simplu $la$ ${\ displaystyle a}$ $la$ la $n$ ${\ displaystyle n}$ $n$ . Exponentul este de obicei reprezentat ca un supercript imediat în dreapta bazei.

Particularități și exemple

Unii exponenți au propriul lor nume. Exponentul doi este adesea denumit pătrat (un al doilea număr reprezintă aria unui pătrat care are acea valoare pe partea sa) și exponentul $3$ ${\ displaystyle 3}$ $3$ în ceea ce privește cubul (un număr din al treilea reprezintă volumul unui cub care are acea valoare pentru margine).

Exemple:

$3^{2}=3\cdot 3=9$ ${\ displaystyle 3 ^ {2} = 3 \ cdot 3 = 9}$ $3 ^ 2 = 3 \ cdot3 = 9$ se citește trei până la al doilea sau trei pătrate
$2^{3}=2\cdot 2\cdot 2=4\cdot 2=8$ ${\ displaystyle 2 ^ {3} = 2 \ cdot 2 \ cdot 2 = 4 \ cdot 2 = 8}$ $2 ^ 3 = 2 \ cdot2 \ cdot2 = 4 \ cdot2 = 8$ citești două la al treilea sau două la cub
$3^{4}=3\cdot 3\cdot 3\cdot 3=9\cdot 9=81$ ${\ displaystyle 3 ^ {4} = 3 \ cdot 3 \ cdot 3 \ cdot 3 = 9 \ cdot 9 = 81}$ $3 ^ 4 = 3 \ cdot3 \ cdot3 \ cdot3 = 9 \ cdot9 = 81$ se citește trei până la al patrulea sau trei la al patrulea
$\left({\frac {1}{2}}\right)^{3}={\frac {1}{2}}\cdot {\frac {1}{2}}\cdot {\frac {1}{2}}={\frac {1}{8}}$ ${\ displaystyle \ left ({\ frac {1} {2}} \ right) ^ {3} = {\ frac {1} {2}} \ cdot {\ frac {1} {2}} \ cdot {\ frac {1} {2}} = {\ frac {1} {8}}}$ $\ left (\ frac 1 2 \ right) ^ 3 = \ frac 1 2 \ cdot \ frac 1 2 \ cdot \ frac 1 2 = \ frac 1 8$ citiți o jumătate până la a treia sau o jumătate la cub

Operațiunea se extinde până la $n=0$ ${\ displaystyle n = 0}$ $n = 0$ plasarea pentru fiecare $a\neq 0$ ${\ displaystyle a \ neq 0}$ $a \ neq 0$

a^{0}=1,

{\ displaystyle a ^ {0} = 1,}

{\ displaystyle a ^ {0} = 1,}

(În cazul în care $n=0$ ${\ displaystyle n = 0}$ $n = 0$ Și $a=0$ ${\ displaystyle a = 0}$ $a = 0$ operația nu este definită: nu există $0^{0}$ ${\ displaystyle 0 ^ {0}}$ ${\ displaystyle 0 ^ {0}}$ )

este la $n$ ${\ displaystyle n}$ $n$ negative prin plasare

a^{-k}={\frac {1}{a^{k}}}.

{\ displaystyle a ^ {- k} = {\ frac {1} {a ^ {k}}}.}

{\ displaystyle a ^ {- k} = {\ frac {1} {a ^ {k}}}.}

De exemplu,

10^{-3}={\frac {1}{10^{3}}}=0,001.

{\ displaystyle 10 ^ {- 3} = {\ frac {1} {10 ^ {3}}} = 0,001.}

{\ displaystyle 10 ^ {- 3} = {\ frac {1} {10 ^ {3}}} = 0,001.}

Proprietate

Următoarele proprietăți sunt verificabile imediat dacă exponenții sunt numere întregi pozitive:

Produsul a două sau mai multe puteri care au aceeași bază, este o putere care are aceeași bază ca baza sa și suma exponenților ca exponent:

a^{n}\cdot a^{m}=a^{n+m}.

{\ displaystyle a ^ {n} \ cdot a ^ {m} = a ^ {n + m}.}

{\ displaystyle a ^ {n} \ cdot a ^ {m} = a ^ {n + m}.}

Demonstrație

$a^{n+m}=\prod _{k=1}^{n+m}a=\prod _{k=1}^{n}a\cdot \prod _{k=n+1}^{n+m}a$ ${\ displaystyle a ^ {n + m} = \ prod _ {k = 1} ^ {n + m} a = \ prod _ {k = 1} ^ {n} a \ cdot \ prod _ {k = n + 1} ^ {n + m} a}$ $a ^ {n + m} = \ prod_ {k = 1} ^ {n + m} a = \ prod_ {k = 1} ^ {n} a \ cdot \ prod_ {k = n + 1} ^ {n + dar$

dar ține minte asta

$\prod _{k=n+1}^{n+m}a=\prod _{k=1}^{m}a$ ${\ displaystyle \ prod _ {k = n + 1} ^ {n + m} a = \ prod _ {k = 1} ^ {m} a}$ $\ prod_ {k = n + 1} ^ {n + m} a = \ prod_ {k = 1} ^ {m} a$

asa de

$a^{n+m}=\prod _{k=1}^{n+m}a=\prod _{k=1}^{n}a\cdot \prod _{k=1}^{m}a=a^{n}a^{m}$ ${\ displaystyle a ^ {n + m} = \ prod _ {k = 1} ^ {n + m} a = \ prod _ {k = 1} ^ {n} a \ cdot \ prod _ {k = 1} ^ {m} a = a ^ {n} a ^ {m}}$ $a ^ {n + m} = \ prod_ {k = 1} ^ {n + m} a = \ prod_ {k = 1} ^ {n} a \ cdot \ prod_ {k = 1} ^ {m} a = a ^ {n} a ^ {m}$

Coeficientul puterilor care au aceeași bază este o putere care are aceeași bază ca baza sa și diferența exponenților ca exponent:

{\frac {a^{n}}{a^{m}}}=a^{n-m}.

{\ displaystyle {\ frac {a ^ {n}} {a ^ {m}}} = a ^ {nm}.}

{\ displaystyle {\ frac {a ^ {n}} {a ^ {m}}} = a ^ {n-m}.}

Demonstrație

${\frac {a^{n}}{a^{m}}}={\frac {a\cdot a^{n-1}}{a\cdot a^{m-1}}}={\frac {a\cdot a\cdot a^{n-2}}{a\cdot a\cdot a^{m-2}}}$ ${\ displaystyle {\ frac {a ^ {n}} {a ^ {m}}} = {\ frac {a \ cdot a ^ {n-1}} {a \ cdot a ^ {m-1}}} = {\ frac {a \ cdot a \ cdot a ^ {n-2}} {a \ cdot a \ cdot a ^ {m-2}}}}$ $\ frac {a ^ n} {a ^ m} = \ frac {a \ cdot a ^ {n-1}} {a \ cdot a ^ {m-1}} = \ frac {a \ cdot a \ cdot a ^ {n-2}} {a \ cdot a \ cdot a ^ {m-2}}$

Tragând până când ai $a^{m}$ ${\ displaystyle a ^ {m}}$ $a ^ m$ obținem următorul rezultat: ${\frac {a^{m}\cdot a^{n-m}}{a^{m}\cdot a^{m-m}}}={\frac {a^{n-m}}{a^{0}}}=a^{n-m}$ ${\ displaystyle {\ frac {a ^ {m} \ cdot a ^ {nm}} {a ^ {m} \ cdot a ^ {mm}}} = {\ frac {a ^ {nm}} {a ^ { 0}}} = a ^ {nm}}$ ${\ displaystyle {\ frac {a ^ {m} \ cdot a ^ {nm}} {a ^ {m} \ cdot a ^ {mm}}} = {\ frac {a ^ {nm}} {a ^ { 0}}} = a ^ {nm}}$

Puterea unei puteri este o putere în care baza rămâne aceeași și exponentul este dat de produsul exponenților:

\left(a^{n}\right)^{m}=a^{n\cdot m}=\left(a^{m}\right)^{n}.

{\ displaystyle \ left (a ^ {n} \ right) ^ {m} = a ^ {n \ cdot m} = \ left (a ^ {m} \ right) ^ {n}.}

{\ displaystyle \ left (a ^ {n} \ right) ^ {m} = a ^ {n \ cdot m} = \ left (a ^ {m} \ right) ^ {n}.}

NB:

(a^{m})^{n}\neq a^{m^{n}}=a^{(m^{n})};

{\ displaystyle (a ^ {m}) ^ {n} \ neq a ^ {m ^ {n}} = a ^ {(m ^ {n})};}

{\ displaystyle (a ^ {m}) ^ {n} \ neq a ^ {m ^ {n}} = a ^ {(m ^ {n})};}

de fapt, de exemplu,

(10^{10})^{100}=10^{1000}

{\ displaystyle (10 ^ {10}) ^ {100} = 10 ^ {1000}}

{\ displaystyle (10 ^ {10}) ^ {100} = 10 ^ {1000}}

este format de un 1 urmat de 1000 de zerouri, în timp ce

10^{10^{100}}=10^{(10^{100})}

{\ displaystyle 10 ^ {10 ^ {100}} = 10 ^ {(10 ^ {100})}}

{\ displaystyle 10 ^ {10 ^ {100}} = 10 ^ {(10 ^ {100})}}

este alcătuit dintr-un 1 urmat de

10^{100}

{\ displaystyle 10 ^ {100}}

10 ^ {{100}}

zerouri.

Produsul puterilor cu același exponent este o putere care are același exponent ca exponentul său și produsul bazelor ca bază:

a^{n}\cdot b^{n}=(a\cdot b)^{n}.

{\ displaystyle a ^ {n} \ cdot b ^ {n} = (a \ cdot b) ^ {n}.}

{\ displaystyle a ^ {n} \ cdot b ^ {n} = (a \ cdot b) ^ {n}.}

Demonstrație

Extindem puterile ca produse și aplicăm proprietatea comutativă pentru $la$ ${\ displaystyle a}$ $la$ Și $b$ ${\ displaystyle b}$ $b$

$a\cdot a\cdot \ldots \cdot a\cdot b\cdot b\cdot \ldots \cdot b=a\cdot b\cdot a\cdot b\cdot \ldots \cdot a\cdot b.$ ${\ displaystyle a \ cdot a \ cdot \ ldots \ cdot a \ cdot b \ cdot b \ cdot \ ldots \ cdot b = a \ cdot b \ cdot a \ cdot b \ cdot \ ldots \ cdot a \ cdot b.}$ ${\ displaystyle a \ cdot a \ cdot \ ldots \ cdot a \ cdot b \ cdot b \ cdot \ ldots \ cdot b = a \ cdot b \ cdot a \ cdot b \ cdot \ ldots \ cdot a \ cdot b.}$

Obținem întotdeauna un produs din $la$ ${\ displaystyle a}$ $la$ Și $b$ ${\ displaystyle b}$ $b$ pentru $n$ ${\ displaystyle n}$ $n$ ori este

$a^{n}\cdot b^{n}={\begin{matrix}\underbrace {a\cdot b\cdot a\cdot b\cdot \ldots \cdot a\cdot b} _{nvolte}\end{matrix}}=\left(a\cdot b\right)^{n}.$ ${\ displaystyle a ^ {n} \ cdot b ^ {n} = {\ begin {matrix} \ underbrace {a \ cdot b \ cdot a \ cdot b \ cdot \ ldots \ cdot a \ cdot b} _ {ntimes} \ end {matrix}} = \ left (a \ cdot b \ right) ^ {n}.}$ ${\ displaystyle a ^ {n} \ cdot b ^ {n} = {\ begin {matrix} \ underbrace {a \ cdot b \ cdot a \ cdot b \ cdot \ ldots \ cdot a \ cdot b} _ {ntimes} \ end {matrix}} = \ left (a \ cdot b \ right) ^ {n}.}$

Coeficientul de puteri cu același exponent este o putere care are același exponent ca exponentul său și coeficientul bazelor ca bază:

{\frac {a^{n}}{b^{n}}}=\left({\frac {a}{b}}\right)^{n}

{\ displaystyle {\ frac {a ^ {n}} {b ^ {n}}} = \ left ({\ frac {a} {b}} \ right) ^ {n}}

\ frac {a ^ n} {b ^ n} = \ left (\ frac {a} {b} \ right) ^ n

Demonstrație

Extindem puterile ca produse și separăm fracțiile

${\frac {a\cdot a\cdot a\cdot \dots \cdot a}{b\cdot b\cdot b\cdot \dots \cdot b}}={\frac {a}{b}}\cdot {\frac {a}{b}}\cdot {\frac {a}{b}}\cdot \dots \cdot {\frac {a}{b}}=\left({\frac {a}{b}}\right)^{n}.$ ${\ displaystyle {\ frac {a \ cdot a \ cdot a \ cdot \ dots \ cdot a} {b \ cdot b \ cdot b \ cdot \ dots \ cdot b}} = {\ frac {a} {b}} \ cdot {\ frac {a} {b}} \ cdot {\ frac {a} {b}} \ cdot \ dots \ cdot {\ frac {a} {b}} = \ left ({\ frac {a} {b}} \ right) ^ {n}.}$ ${\ displaystyle {\ frac {a \ cdot a \ cdot a \ cdot \ dots \ cdot a} {b \ cdot b \ cdot b \ cdot \ dots \ cdot b}} = {\ frac {a} {b}} \ cdot {\ frac {a} {b}} \ cdot {\ frac {a} {b}} \ cdot \ dots \ cdot {\ frac {a} {b}} = \ left ({\ frac {a} {b}} \ right) ^ {n}.}$

Observăm că definiția $a^{0}=1$ ${\ displaystyle a ^ {0} = 1}$ $a ^ {0} = 1$ acum este mai ușor de înțeles, deoarece este în concordanță cu proprietățile abia văzute, de fapt:

{\frac {a^{n}}{a^{n}}}=a^{n-n}=a^{0}=1.

{\ displaystyle {\ frac {a ^ {n}} {a ^ {n}}} = a ^ {nn} = a ^ {0} = 1.}

{\ displaystyle {\ frac {a ^ {n}} {a ^ {n}}} = a ^ {n-n} = a ^ {0} = 1.}

Rețineți că $a^{0}$ ${\ displaystyle a ^ {0}}$ $a ^ 0$ este un produs gol și, prin urmare, este egal cu $1.$ ${\ displaystyle 1.}$ ${\ displaystyle 1.}$

Și același lucru este valabil și pentru definiția $a^{-x}$ ${\ displaystyle a ^ {- x}}$ $a ^ {- x}$ , intr-adevar:

a^{-x}=a^{0-x}={\frac {a^{0}}{a^{x}}}={\frac {1}{a^{x}}}.

{\ displaystyle a ^ {- x} = a ^ {0-x} = {\ frac {a ^ {0}} {a ^ {x}}} = {\ frac {1} {a ^ {x}} }.}

{\ displaystyle a ^ {- x} = a ^ {0-x} = {\ frac {a ^ {0}} {a ^ {x}}} = {\ frac {1} {a ^ {x}} }.}

Rădăcini și exponenți fracționari

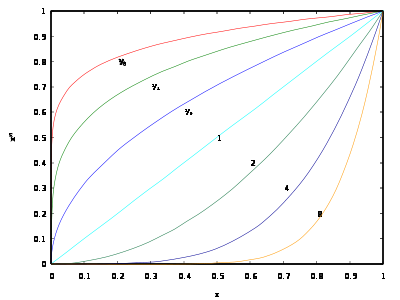
Graficul funcțiilor x ^a pentru exponenții mai mari de 1 (sub bisectoarea axelor) și mai puțin de 1 (deasupra bisectoarei)

Dat fiind un număr real non-negativ $la$ ${\ displaystyle a}$ $la$ și un număr întreg pozitiv $n,$ ${\ displaystyle n,}$ $n,$ se numește rădăcină $n$ ${\ displaystyle n}$ $n$ -thth din $la$ ${\ displaystyle a}$ $la$ acel număr real negativ $b$ ${\ displaystyle b}$ $b$ astfel încât $b^{n}=a$ ${\ displaystyle b ^ {n} = a}$ $b ^ {n} = a$ , acest număr este indicat cu ${\sqrt[{n}]{a}}$ ${\ displaystyle {\ sqrt [{n}] {a}}}$ $\ sqrt [n] a$ .

Din această definiție este imediat clar că

\left({\sqrt[{n}]{a}}\right)^{n}=a,

{\ displaystyle \ left ({\ sqrt [{n}] {a}} \ right) ^ {n} = a,}

{\ displaystyle \ left ({\ sqrt [{n}] {a}} \ right) ^ {n} = a,}

pentru orice număr real non-negativ $la$ ${\ displaystyle a}$ $la$ . Prin urmare, este rezonabil (în virtutea proprietăților puterilor) să întrebi

a^{\frac {1}{n}}:={\sqrt[{n}]{a}}.

{\ displaystyle a ^ {\ frac {1} {n}}: = {\ sqrt [{n}] {a}}.}

{\ displaystyle a ^ {\ frac {1} {n}}: = {\ sqrt [{n}] {a}}.}

În acest fel, proprietățile puterilor sunt încă respectate, de fapt

\left(a^{\frac {1}{n}}\right)^{n}:=a^{{\frac {1}{n}}\cdot n}=a^{1}=a,

{\ displaystyle \ left (a ^ {\ frac {1} {n}} \ right) ^ {n}: = a ^ {{\ frac {1} {n}} \ cdot n} = a ^ {1} = a,}

{\ displaystyle \ left (a ^ {\ frac {1} {n}} \ right) ^ {n}: = a ^ {{\ frac {1} {n}} \ cdot n} = a ^ {1} = a,}

așa cum se întâmplă pentru rădăcină $n$ ${\ displaystyle n}$ $n$ -alea.

Mai general, definiția puterii poate fi extinsă și mai mult, cu unele restricții, permițând exponentului să fie un număr rațional ${\frac {x}{y}}$ ${\ displaystyle {\ frac {x} {y}}}$ $\ frac x y$ , cu $X$ ${\ displaystyle x}$ $X$ Și $y$ ${\ displaystyle y}$ $y$ numerele întregi primează între ele e $y\neq 0$ ${\ displaystyle y \ neq 0}$ ${\ displaystyle y \ neq 0}$ , dacă apare:

a^{\frac {x}{y}}:={\sqrt[{y}]{a^{x}}}.

{\ displaystyle a ^ {\ frac {x} {y}}: = {\ sqrt [{y}] {a ^ {x}}}.}

{\ displaystyle a ^ {\ frac {x} {y}}: = {\ sqrt [{y}] {a ^ {x}}}.}

În acest caz:

de sine $y$ ${\ displaystyle y}$ $y$ este egal, puterea este definită de $la$ ${\ displaystyle a}$ $la$ real nu negativ;
de sine $y$ {\ displaystyle y} $y$ este ciudat:
- de sine $X$ ${\ displaystyle x}$ $X$ este pozitiv, puterea este definită pentru oricare $la$ ${\ displaystyle a}$ $la$ ;
- de sine $X$ ${\ displaystyle x}$ $X$ nu este pozitiv, puterea este definită pentru oricare $la$ ${\ displaystyle a}$ $la$ nu nul.

Ignorând aceste restricții și ipoteză $X$ ${\ displaystyle x}$ $X$ Și $y$ ${\ displaystyle y}$ $y$ primul dintre ei cădem în absurde precum:

-1={\sqrt[{3}]{-1}}=(-1)^{\frac {1}{3}}=(-1)^{\frac {2}{6}}={\sqrt[{6}]{(-1)^{2}}}={\sqrt[{6}]{1}}=1

{\ displaystyle -1 = {\ sqrt [{3}] {- 1}} = (- 1) ^ {\ frac {1} {3}} = (- 1) ^ {\ frac {2} {6} } = {\ sqrt [{6}] {(- 1) ^ {2}}} = {\ sqrt [{6}] {1}} = 1}

-1 = \ sqrt [3] {- 1} = (- 1) ^ {\ frac {1} {3}} = (- 1) ^ {\ frac {2} {6}} = \ sqrt [6] {(-1) ^ 2} = \ sqrt [6] {1} = 1

Pasul greșit este al treilea, în acest sens $(-1)^{\frac {2}{6}}$ ${\ displaystyle (-1) ^ {\ frac {2} {6}}}$ $(-1) ^ {\ frac {2} {6}}$ nu este definit în $\mathbb {R}$ ${\ displaystyle \ mathbb {R}}$ $\ R$ .

Puteri cu exponent real

Puteți extinde definiția operației de exponențiere și la cazurile în care baza și exponentul sunt numere reale generice (dar cu baza întotdeauna pozitivă) asigurându-vă că păstrați regulile de funcționare între putere și că funcția de putere rezultată este o funcție continuă , iar această extensie este unică. În acest fel se poate da sens unor expresii precum $3^{\sqrt {2}}$ ${\ displaystyle 3 ^ {\ sqrt {2}}}$ $3 ^ {\ sqrt {2}}$ o și ^π .

Să definim inițial $a^{b}$ ${\ displaystyle a ^ {b}}$ $a ^ b$ cu baza $a>1$ ${\ displaystyle a> 1}$ $a> 1$ iar exponentul $b>0$ ${\ displaystyle b> 0}$ $b> 0$ , ambele numere reale .

Putem scrie $b$ ${\ displaystyle b}$ $b$ în reprezentarea sa în bază $10$ ${\ displaystyle 10}$ $10$ cu scris:

b=b_{0},b_{1}b_{2}b_{3}b_{4}\ldots

{\ displaystyle b = b_ {0}, b_ {1} b_ {2} b_ {3} b_ {4} \ ldots}

{\ displaystyle b = b_ {0}, b_ {1} b_ {2} b_ {3} b_ {4} \ ldots}

Succesiunea $\beta _{n}$ ${\ displaystyle \ beta _ {n}}$ $\ beta_n$ numere

\beta _{0}=b_{0}

{\ displaystyle \ beta _ {0} = b_ {0}}

\ beta_0 = b_0

\beta _{1}=b_{0},b_{1}

{\ displaystyle \ beta _ {1} = b_ {0}, b_ {1}}

\ beta_1 = b_0, b_1

\beta _{2}=b_{0},b_{1}b_{2}

{\ displaystyle \ beta _ {2} = b_ {0}, b_ {1} b_ {2}}

\ beta_2 = b_0, b_1 b_2

\beta _{3}=b_{0},b_{1}b_{2}b_{3}

{\ displaystyle \ beta _ {3} = b_ {0}, b_ {1} b_ {2} b_ {3}}

\ beta_3 = b_0, b_1 b_2 b_3

\dots

{\ displaystyle \ dots}

\ dots

este o succesiune de numere raționale în creștere care tinde spre $b$ ${\ displaystyle b}$ $b$ .

Puterea $a^{\beta _{n}}$ ${\ displaystyle a ^ {\ beta _ {n}}}$ $a ^ {\ beta_n}$ are exponent rațional, deci a fost definit. Succesiunea numerelor reale

a^{\beta _{0}}

{\ displaystyle a ^ {\ beta _ {0}}}

a ^ {\ beta_0}

a^{\beta _{1}}

{\ displaystyle a ^ {\ beta _ {1}}}

a ^ {\ beta_1}

a^{\beta _{2}}

{\ displaystyle a ^ {\ beta _ {2}}}

a ^ {\ beta_2}

\dots

{\ displaystyle \ dots}

\ dots

este, de asemenea, o succesiune din ce în ce mai mare (din moment ce $a>1$ ${\ displaystyle a> 1}$ $a> 1$ ), este deci firesc să se definească valoarea lui $a^{b}$ ${\ displaystyle a ^ {b}}$ $a ^ b$ ca extremă superioară a acestei secvențe:

a^{b}:={\mbox{sup}}_{n}\{a^{\beta _{n}}\}.

{\ displaystyle a ^ {b}: = {\ mbox {sup}} _ {n} \ {a ^ {\ beta _ {n}} \}.}

{\ displaystyle a ^ {b}: = {\ mbox {sup}} _ {n} \ {a ^ {\ beta _ {n}} \}.}

Dacă baza este un număr între și $1$ ${\ displaystyle 1}$ $1$ poate fi definit:

a^{b}:=((a^{-1})^{b})^{-1},

{\ displaystyle a ^ {b}: = ((a ^ {- 1}) ^ {b}) ^ {- 1},}

{\ displaystyle a ^ {b}: = ((a ^ {- 1}) ^ {b}) ^ {- 1},}

atâta timp cât $a^{-1}$ ${\ displaystyle a ^ {- 1}}$ $a ^ {{- 1}}$ în acest caz este mai mare decât $1$ ${\ displaystyle 1}$ $1$ și apoi este definit al doilea membru.

De fapt, fiind $a^{b}=((a^{-1})^{b})^{-1}=((a^{-1})^{-b})$ ${\ displaystyle a ^ {b} = ((a ^ {- 1}) ^ {b}) ^ {- 1} = ((a ^ {- 1}) ^ {- b})}$ $a ^ b = ((a ^ {- 1}) ^ b) ^ {- 1} = ((a ^ {- 1}) ^ {- b})$ , avem următoarea succesiune de numere reale (luând în considerare $\beta _{n}$ ${\ displaystyle \ beta _ {n}}$ $\ beta_n$ Ca inainte):

(a^{-1})^{-\beta _{0}}

{\ displaystyle (a ^ {- 1}) ^ {- \ beta _ {0}}}

(a ^ {- 1}) ^ {- \ beta_0}

(a^{-1})^{-\beta _{1}}

{\ displaystyle (a ^ {- 1}) ^ {- \ beta _ {1}}}

(a ^ {- 1}) ^ {- \ beta_1}

(a^{-1})^{-\beta _{2}}

{\ displaystyle (a ^ {- 1}) ^ {- \ beta _ {2}}}

(a ^ {- 1}) ^ {- \ beta_2}

\dots

{\ displaystyle \ dots}

\ dots

care este o secvență descrescătoare și, prin urmare, putem pune, în acest caz, $a^{b}:={\mbox{inf}}_{n}\{(a^{-1})^{-\beta _{n}}\}$ ${\ displaystyle a ^ {b}: = {\ mbox {inf}} _ {n} \ {(a ^ {- 1}) ^ {- \ beta _ {n}} \}}$ $a ^ b: = \ mbox {inf} _n \ {(a ^ {- 1}) ^ {- \ beta_n} \}$ .