Produs scalar

În matematică , în special în calculul vectorial , produsul scalar este o operație binară care asociază un element al câmpului la fiecare pereche de vectori aparținând unui spațiu vectorial definit pe câmpul real . ^[1] Este un produs intern pe câmpul real, adică o formă bilineară biliniară definită pozitivă cu valori reale. Fiind un produs pur algebric, nu poate fi reprezentat grafic ca un vector unitate.

Noțiunea de produs scalar este generalizată în algebră liniară din spațiul euclidian către orice spațiu vectorial : acest spațiu poate avea dimensiune infinită și poate fi definit pe un câmp arbitrar (nu neapărat cel real). Această generalizare are o importanță fundamentală, de exemplu în geometria diferențială și mecanica rațională . Adăugarea unei alte proprietăți, completitudinea , conduce, de asemenea, la conceptul de spațiu Hilbert , pentru care teoria este îmbogățită cu instrumente mai sofisticate, de bază în modelarea mecanicii cuantice și în multe domenii ale analizei funcționale .

Definiție

Este definit ca un produs scalar pe spațiul vectorial $V.$ ${\ displaystyle V}$ $V.$ o formă biliniară simetrică care se asociază cu doi vectori $\mathbf {v}$ ${\ displaystyle \ mathbf {v}}$ $\ mathbf v$ Și $\mathbf {w}$ ${\ displaystyle \ mathbf {w}}$ $\ mathbf w$ din $V.$ ${\ displaystyle V}$ $V.$ un scalar în câmpul real $\mathbb {R}$ ${\ displaystyle \ mathbb {R}}$ $\ R$ , indicat în general cu $\langle \mathbf {v} ,\mathbf {w} \rangle$ ${\ displaystyle \ langle \ mathbf {v}, \ mathbf {w} \ rangle}$ $\ langle {\ mathbf v}, {\ mathbf w} \ rangle$ sau $\mathbf {v} \cdot \mathbf {w}$ ${\ displaystyle \ mathbf {v} \ cdot \ mathbf {w}}$ ${\ mathbf v} \ cdot {\ mathbf w}$ . ^[2]

Este un operator binar care testează următoarele condiții pentru $\mathbf {v}$ ${\ displaystyle \ mathbf {v}}$ $\ mathbf v$ , $\mathbf {w}$ ${\ displaystyle \ mathbf {w}}$ $\ mathbf w$ , $\mathbf {u}$ ${\ displaystyle \ mathbf {u}}$ ${\ mathbf u}$ vectori arbitrari e $k$ ${\ displaystyle k}$ $k$ element de câmp:

Simetrie:

\langle \mathbf {v} ,\mathbf {w} \rangle =\langle \mathbf {w} ,\mathbf {v} \rangle

{\ displaystyle \ langle \ mathbf {v}, \ mathbf {w} \ rangle = \ langle \ mathbf {w}, \ mathbf {v} \ rangle}

\ langle {\ mathbf v}, {\ mathbf w} \ rangle = \ langle {\ mathbf w}, {\ mathbf v} \ rangle

Liniaritatea față de primul termen:

\langle \mathbf {v} +\mathbf {w} ,\mathbf {u} \rangle =\langle \mathbf {v} ,\mathbf {u} \rangle +\langle \mathbf {w} ,\mathbf {u} \rangle

{\ displaystyle \ langle \ mathbf {v} + \ mathbf {w}, \ mathbf {u} \ rangle = \ langle \ mathbf {v}, \ mathbf {u} \ rangle + \ langle \ mathbf {w}, \ mathbf {u} \ rangle}

\ langle {\ mathbf v} + {\ mathbf w}, {\ mathbf u} \ rangle = \ langle {\ mathbf v}, {\ mathbf u} \ rangle + \ langle {\ mathbf w}, {\ mathbf u } \ rangle

\langle k\mathbf {v} ,\mathbf {w} \rangle =k\langle \mathbf {v} ,\mathbf {w} \rangle

{\ displaystyle \ langle k \ mathbf {v}, \ mathbf {w} \ rangle = k \ langle \ mathbf {v}, \ mathbf {w} \ rangle}

\ langle k {\ mathbf v}, {\ mathbf w} \ rangle = k \ langle {\ mathbf v}, {\ mathbf w} \ rangle

Mai mulți autori cer, de asemenea, ca forma să fie pozitivă definită , adică: ^[1]

\langle \mathbf {v} ,\mathbf {v} \rangle >0

{\ displaystyle \ langle \ mathbf {v}, \ mathbf {v} \ rangle> 0}

\ langle {\ mathbf v}, {\ mathbf v} \ rangle> 0

pentru fiecare $\mathbf {v}$ ${\ displaystyle \ mathbf {v}}$ $\ mathbf v$ non-zero.

Revendicările anterioare implică, de asemenea, următoarele proprietăți:

Liniaritate față de al doilea termen:

\langle \mathbf {v} ,\mathbf {w} +\mathbf {u} \rangle =\langle \mathbf {v} ,\mathbf {w} \rangle +\langle \mathbf {v} ,\mathbf {u} \rangle

{\ displaystyle \ langle \ mathbf {v}, \ mathbf {w} + \ mathbf {u} \ rangle = \ langle \ mathbf {v}, \ mathbf {w} \ rangle + \ langle \ mathbf {v}, \ mathbf {u} \ rangle}

\ langle {\ mathbf v}, {\ mathbf w} + {\ mathbf u} \ rangle = \ langle {\ mathbf v}, {\ mathbf w} \ rangle + \ langle {\ mathbf v}, {\ mathbf u } \ rangle

\langle \mathbf {v} ,k\mathbf {w} \rangle =k\langle \mathbf {v} ,\mathbf {w} \rangle

{\ displaystyle \ langle \ mathbf {v}, k \ mathbf {w} \ rangle = k \ langle \ mathbf {v}, \ mathbf {w} \ rangle}

\ langle {\ mathbf v}, k {\ mathbf w} \ rangle = k \ langle {\ mathbf v}, {\ mathbf w} \ rangle

și întrucât un vector înmulțit cu 0 returnează vectorul nul, rezultă că:

\langle \mathbf {0} ,\mathbf {0} \rangle =0

{\ displaystyle \ langle \ mathbf {0}, \ mathbf {0} \ rangle = 0}

\ langle {\ mathbf 0}, {\ mathbf 0} \ rangle = 0

.

Produs scalar degenerat

Produsul punct este degenerat dacă există un vector $\mathbf {v}$ ${\ displaystyle \ mathbf {v}}$ $\ mathbf v$ non-zero ortogonal la toți vectorii, adică astfel încât:

\langle \mathbf {v} ,\mathbf {w} \rangle =0

{\ displaystyle \ langle \ mathbf {v}, \ mathbf {w} \ rangle = 0}

\ langle {\ mathbf v}, {\ mathbf w} \ rangle = 0

pentru fiecare vector $\mathbf {w}$ ${\ displaystyle \ mathbf {w}}$ $\ mathbf w$ de spațiu.

Produs scalar definit pozitiv și negativ

Un produs cu puncte pe un spațiu vectorial $V.$ ${\ displaystyle V}$ $V.$ este definit pozitiv dacă: ^[3]

\langle \mathbf {v} ,\mathbf {v} \rangle >0\qquad \forall \mathbf {v} \neq 0

{\ displaystyle \ langle \ mathbf {v}, \ mathbf {v} \ rangle> 0 \ qquad \ forall \ mathbf {v} \ neq 0}

\ langle {\ mathbf v}, {\ mathbf v} \ rangle> 0 \ qquad \ forall {\ mathbf v} \ neq 0

negativ definit dacă:

\langle \mathbf {v} ,\mathbf {v} \rangle <0\qquad \forall \mathbf {v} \neq 0

{\ displaystyle \ langle \ mathbf {v}, \ mathbf {v} \ rangle <0 \ qquad \ forall \ mathbf {v} \ neq 0}

\ langle {\ mathbf v}, {\ mathbf v} \ rangle <0 \ qquad \ forall {\ mathbf v} \ neq 0

semidefinit pozitiv:

\langle \mathbf {v} ,\mathbf {v} \rangle \geq 0\qquad \forall \mathbf {v}

{\ displaystyle \ langle \ mathbf {v}, \ mathbf {v} \ rangle \ geq 0 \ qquad \ forall \ mathbf {v}}

\ langle {\ mathbf v}, {\ mathbf v} \ rangle \ geq 0 \ qquad \ forall {\ mathbf v}

semidefinit negativ dacă:

\langle \mathbf {v} ,\mathbf {v} \rangle \leq 0\qquad \forall \mathbf {v}

{\ displaystyle \ langle \ mathbf {v}, \ mathbf {v} \ rangle \ leq 0 \ qquad \ forall \ mathbf {v}}

\ langle {\ mathbf v}, {\ mathbf v} \ rangle \ leq 0 \ qquad \ forall {\ mathbf v}

Un produs cu punct semi-definit pozitiv este (rar) numit și un produs pseudoscalar .

Produs scalar în spațiul euclidian

Același subiect în detaliu: spațiul euclidian .

Interpretarea geometrică a produsului punct (când B are lungimea unității)

{\overrightarrow {AB}}\cdot {\overrightarrow {AC}}=|AB|\times |AH|>0

{\ displaystyle {\ overrightarrow {AB}} \ cdot {\ overrightarrow {AC}} = | AB | \ times | AH |> 0}

\ overrightarrow {AB} \ cdot \ overrightarrow {AC} = | AB | \ times | AH |> 0

{\overrightarrow {AB}}\cdot {\overrightarrow {AC}}=-|AB|\times |AH|<0

{\ displaystyle {\ overrightarrow {AB}} \ cdot {\ overrightarrow {AC}} = - | AB | \ times | AH | <0}

\ overrightarrow {AB} \ cdot \ overrightarrow {AC} = - | AB | \ times | AH | <0

Produsul scalar al a doi vectori $\mathbf {a}$ ${\ displaystyle \ mathbf {a}}$ $\ mathbf a$ Și $\mathbf {b}$ ${\ displaystyle \ mathbf {b}}$ $\ mathbf b$ a planului , aplicat pe același punct, este definit ca:

\mathbf {a} \cdot \mathbf {b} =|\mathbf {a} |\,|\mathbf {b} |\cos \theta

{\ displaystyle \ mathbf {a} \ cdot \ mathbf {b} = | \ mathbf {a} | \, | \ mathbf {b} | \ cos \ theta}

{\ mathbf {a}} \ cdot {\ mathbf {b}} = | {\ mathbf a} | \, | {\ mathbf b} | \ cos \ theta

unde este $|\mathbf {a} |$ ${\ displaystyle | \ mathbf {a} |}$ $| {\ mathbf a} |$ Și $|\mathbf {b} |$ ${\ displaystyle | \ mathbf {b} |}$ $| {\ mathbf b} |$ sunt lungimile de $\mathbf {a}$ ${\ displaystyle \ mathbf {a}}$ $\ mathbf a$ Și $\mathbf {b}$ ${\ displaystyle \ mathbf {b}}$ $\ mathbf b$ , Și $\theta$ ${\ displaystyle \ theta}$ $\ theta$ este unghiul dintre cei doi vectori. Produsul dot este indicat ca $\mathbf {a} \cdot \mathbf {b}$ ${\ displaystyle \ mathbf {a} \ cdot \ mathbf {b}}$ ${\ mathbf a} \ cdot {\ mathbf b}$ , și satisface proprietățile algebrice ale simetriei:

\mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a}

{\ displaystyle \ mathbf {a} \ cdot \ mathbf {b} = \ mathbf {b} \ cdot \ mathbf {a}}

{\ mathbf a} \ cdot {\ mathbf b} = {\ mathbf b} \ cdot {\ mathbf a}

pentru fiecare pereche de vectori $\mathbf {a}$ ${\ displaystyle \ mathbf {a}}$ $\ mathbf a$ Și $\mathbf {b}$ ${\ displaystyle \ mathbf {b}}$ $\ mathbf b$ și bilinearitate:

\mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c}

{\ displaystyle \ mathbf {a} \ cdot (\ mathbf {b} + \ mathbf {c}) = \ mathbf {a} \ cdot \ mathbf {b} + \ mathbf {a} \ cdot \ mathbf {c}}

{\ mathbf a} \ cdot ({\ mathbf b} + {\ mathbf c}) = {\ mathbf a} \ cdot {\ mathbf b} + {\ mathbf a} \ cdot {\ mathbf c}

\mathbf {a} \cdot (\lambda \mathbf {b} )=\lambda (\mathbf {a} \cdot \mathbf {b} )

{\ displaystyle \ mathbf {a} \ cdot (\ lambda \ mathbf {b}) = \ lambda (\ mathbf {a} \ cdot \ mathbf {b})}

{\ mathbf a} \ cdot (\ lambda {\ mathbf b}) = \ lambda ({\ mathbf a} \ cdot {\ mathbf b})

(\mathbf {a} +\mathbf {b} )\cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {c} +\mathbf {b} \cdot \mathbf {c}

{\ displaystyle (\ mathbf {a} + \ mathbf {b}) \ cdot \ mathbf {c} = \ mathbf {a} \ cdot \ mathbf {c} + \ mathbf {b} \ cdot \ mathbf {c}}

({\ mathbf a} + {\ mathbf b}) \ cdot {\ mathbf c} = {\ mathbf a} \ cdot {\ mathbf c} + {\ mathbf b} \ cdot {\ mathbf c}

(\lambda \mathbf {a} )\cdot \mathbf {b} =\lambda (\mathbf {a} \cdot \mathbf {b} )

{\ displaystyle (\ lambda \ mathbf {a}) \ cdot \ mathbf {b} = \ lambda (\ mathbf {a} \ cdot \ mathbf {b})}

(\ lambda {\ mathbf a}) \ cdot {\ mathbf b} = \ lambda ({\ mathbf a} \ cdot {\ mathbf b})

pentru fiecare triplet de vectori $\mathbf {a}$ ${\ displaystyle \ mathbf {a}}$ $\ mathbf a$ , $\mathbf {b}$ ${\ displaystyle \ mathbf {b}}$ $\ mathbf b$ , $\mathbf {c}$ ${\ displaystyle \ mathbf {c}}$ $\ mathbf c$ și pentru orice număr real $\lambda$ ${\ displaystyle \ lambda}$ $\ lambda$ . Primele două relații exprimă „liniaritatea spre dreapta” și celelalte două „spre stânga”.

Produsul punct al unui vector cu el însuși este întotdeauna mai mare sau egal cu zero:

\mathbf {a} \cdot \mathbf {a} =|\mathbf {a} |^{2}\geqslant 0

{\ displaystyle \ mathbf {a} \ cdot \ mathbf {a} = | \ mathbf {a} | ^ {2} \ geqslant 0}

{\ mathbf a} \ cdot {\ mathbf a} = | {\ mathbf a} | ^ {2} \ geqslant 0

În plus, acesta este zero dacă și numai dacă vectorul este zero (proprietate nulă a produsului punct):

\mathbf {a} \cdot \mathbf {a} =|\mathbf {a} |^{2}=0\Leftrightarrow \mathbf {a} =0

{\ displaystyle \ mathbf {a} \ cdot \ mathbf {a} = | \ mathbf {a} | ^ {2} = 0 \ Leftrightarrow \ mathbf {a} = 0}

{\ mathbf a} \ cdot {\ mathbf a} = | {\ mathbf a} | ^ {2} = 0 \ Leftrightarrow {\ mathbf a} = 0

Această proprietate poate fi exprimată afirmând că produsul punct este pozitiv.

Interpretarea geometrică

Atâta timp cât $|\mathbf {a} |\cos \theta$ ${\ displaystyle | \ mathbf {a} | \ cos \ theta}$ $| {\ mathbf a} | \ cos \ theta$ este lungimea proiecției ortogonale a $\mathbf {a}$ ${\ displaystyle \ mathbf {a}}$ $\ mathbf a$ pe $\mathbf {b}$ ${\ displaystyle \ mathbf {b}}$ $\ mathbf b$ dacă vectorii de proiecție ortogonală a $\mathbf {a}$ ${\ displaystyle \ mathbf {a}}$ $\ mathbf a$ pe $\mathbf {b}$ ${\ displaystyle \ mathbf {b}}$ $\ mathbf b$ Și $\mathbf {b}$ ${\ displaystyle \ mathbf {b}}$ $\ mathbf b$ au aceeași direcție, altfel este opusul lungimii, produsul scalar poate fi interpretat geometric ca produsul lungimilor acestei proiecții și a $\mathbf {b}$ ${\ displaystyle \ mathbf {b}}$ $\ mathbf b$ , înmulțit cu -1 dacă proiecția ortogonală a lui $\mathbf {a}$ ${\ displaystyle \ mathbf {a}}$ $\ mathbf a$ pe $\mathbf {b}$ ${\ displaystyle \ mathbf {b}}$ $\ mathbf b$ Și $\mathbf {b}$ ${\ displaystyle \ mathbf {b}}$ $\ mathbf b$ au direcție opusă. De asemenea, puteți schimba rolurile $\mathbf {a}$ ${\ displaystyle \ mathbf {a}}$ $\ mathbf a$ Și $\mathbf {b}$ ${\ displaystyle \ mathbf {b}}$ $\ mathbf b$ , să interpreteze $|\mathbf {b} |\cos \theta$ ${\ displaystyle | \ mathbf {b} | \ cos \ theta}$ $| {\ mathbf b} | \ cos \ theta$ ca lungime (semnată ca înainte) proiecției de $\mathbf {b}$ ${\ displaystyle \ mathbf {b}}$ $\ mathbf b$ pe $\mathbf {a}$ ${\ displaystyle \ mathbf {a}}$ $\ mathbf a$ iar produsul scalar ca produs al lungimilor acestei proiecții și al lungimii $\mathbf {a}$ ${\ displaystyle \ mathbf {a}}$ $\ mathbf a$ .

Produs scalar pozitiv, nul și negativ

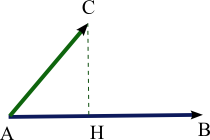
Cosinusul unui unghi $\theta$ ${\ displaystyle \ theta}$ $\ theta$ este pozitiv dacă $\theta$ ${\ displaystyle \ theta}$ $\ theta$ este un unghi acut (adică între -90 ° și 90 °), nul dacă $\theta$ ${\ displaystyle \ theta}$ $\ theta$ este un unghi drept și un unghi negativ dacă este un unghi obtuz . Rezultă că produsul dot $\mathbf {a} \cdot \mathbf {b}$ ${\ displaystyle \ mathbf {a} \ cdot \ mathbf {b}}$ ${\ mathbf a} \ cdot {\ mathbf b}$ Și:

Pozitiv dacă $|\mathbf {a} |>0$ ${\ displaystyle | \ mathbf {a} |> 0}$ $| {\ mathbf a} |> 0$ , $|\mathbf {b} |>0$ ${\ displaystyle | \ mathbf {b} |> 0}$ $| {\ mathbf b} |> 0$ și unghiul $\theta$ ${\ displaystyle \ theta}$ $\ theta$ este acută.
Nimic dacă $|\mathbf {a} |=0$ ${\ displaystyle | \ mathbf {a} | = 0}$ $| {\ mathbf a} | = 0$ , $|\mathbf {b} |=0$ ${\ displaystyle | \ mathbf {b} | = 0}$ $| {\ mathbf b} | = 0$ sau $\theta$ ${\ displaystyle \ theta}$ $\ theta$ este corect.
Negativ dacă $|\mathbf {a} |>0$ ${\ displaystyle | \ mathbf {a} |> 0}$ $| {\ mathbf a} |> 0$ , $|\mathbf {b} |>0$ ${\ displaystyle | \ mathbf {b} |> 0}$ $| {\ mathbf b} |> 0$ și unghiul $\theta$ ${\ displaystyle \ theta}$ $\ theta$ este plictisitor.

Cazurile în care $\theta$ ${\ displaystyle \ theta}$ $\ theta$ este acută și obtuză sunt prezentate în imagine. În ambele cazuri, produsul punct este calculat utilizând interpretarea geometrică, dar semnul este diferit.

În special, se aplică și următoarele proprietăți:

De sine $\theta =0$ ${\ displaystyle \ theta = 0}$ $\ theta = 0$ vectorii sunt paraleli și $\mathbf {a} \cdot \mathbf {b} =|\mathbf {a} |\cdot |\mathbf {b} |$ ${\ displaystyle \ mathbf {a} \ cdot \ mathbf {b} = | \ mathbf {a} | \ cdot | \ mathbf {b} |}$ ${\ mathbf a} \ cdot {\ mathbf b} = | {\ mathbf a} | \ cdot | {\ mathbf b} |$ .
De sine $\theta =\pi /2$ ${\ displaystyle \ theta = \ pi / 2}$ $\ theta = \ pi / 2$ vectorii sunt ortogonali și $\mathbf {a} \cdot \mathbf {b} =0$ ${\ displaystyle \ mathbf {a} \ cdot \ mathbf {b} = 0}$ ${\ mathbf a} \ cdot {\ mathbf b} = 0$ .
De sine $\theta =\pi$ ${\ displaystyle \ theta = \ pi}$ $\ theta = \ pi$ vectorii sunt paraleli, dar orientați în direcția opusă și $\mathbf {a} \cdot \mathbf {b} =-|\mathbf {a} |\cdot |\mathbf {b} |$ ${\ displaystyle \ mathbf {a} \ cdot \ mathbf {b} = - | \ mathbf {a} | \ cdot | \ mathbf {b} |}$ ${\ mathbf a} \ cdot {\ mathbf b} = - | {\ mathbf a} | \ cdot | {\ mathbf b} |$ .

De sine $\mathbf {a}$ ${\ displaystyle \ mathbf {a}}$ $\ mathbf a$ Și $\mathbf {b}$ ${\ displaystyle \ mathbf {b}}$ $\ mathbf b$ sunt versori , adică vectori de lungime 1, produsul lor scalar este pur și simplu cosinusul unghiului inclus.

Produsul scalar al unui vector $\mathbf {a}$ ${\ displaystyle \ mathbf {a}}$ $\ mathbf a$ cu sine $\mathbf {a} \cdot \mathbf {a} =|\mathbf {a} |^{2}$ ${\ displaystyle \ mathbf {a} \ cdot \ mathbf {a} = | \ mathbf {a} | ^ {2}}$ ${\ mathbf a} \ cdot {\ mathbf a} = | {\ mathbf a} | ^ {2}$ este pătratul lungimii $|\mathbf {a} |$ ${\ displaystyle | \ mathbf {a} |}$ $| {\ mathbf a} |$ vector.

Aplicații în fizică

Munca este produsul punct al vectorilor

F.

{\ displaystyle F}

F.

Și

tu

{\ displaystyle u}

tu

.

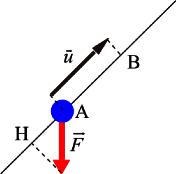
În fizica clasică , produsul scalar este utilizat în contexte în care este necesar să se calculeze proiecția unui vector de-a lungul unei componente date. De exemplu, munca $L$ ${\ displaystyle L}$ $L$ realizată de o forță constantă $\mathbf {F}$ ${\ displaystyle \ mathbf {F}}$ $\ mathbf F$ pe un corp care se mișcă în direcție $\mathbf {u}$ ${\ displaystyle \ mathbf {u}}$ ${\ mathbf u}$ este produsul dot:

L=\mathbf {F} \cdot \mathbf {u}

{\ displaystyle L = \ mathbf {F} \ cdot \ mathbf {u}}

L = {\ mathbf F} \ cdot {\ mathbf u}

dintre cei doi vectori.

Aplicații în geometrie

Teorema cosinusului poate fi ușor formulată folosind produsul punct. Având în vedere trei puncte $LA$ ${\ displaystyle A}$ $LA$ , $B.$ ${\ displaystyle B}$ $B.$ , $C.$ ${\ displaystyle C}$ $C.$ oricare dintre planuri, are următoarea relație:

{\overrightarrow {AB}}\cdot {\overrightarrow {AC}}={\frac {1}{2}}{\Big (}|AB|^{2}+|AC|^{2}-|BC|^{2}{\Big )}

{\ displaystyle {\ overrightarrow {AB}} \ cdot {\ overrightarrow {AC}} = {\ frac {1} {2}} {\ Big (} | AB | ^ {2} + | AC | ^ {2} - | BC | ^ {2} {\ Big)}}

\ overrightarrow {AB} \ cdot \ overrightarrow {AC} = {\ frac 12} {\ Big (} | AB | ^ {2} + | AC | ^ {2} - | BC | ^ {2} {\ Big) }

Expresie analitică

Produsul scalar este definit în geometrie analitică într-un mod diferit: este funcția care, în orice spațiu euclidian, se asociază la doi vectori $\mathbf {a} =[a_{1},a_{2},\dots ,a_{n}]$ ${\ displaystyle \ mathbf {a} = [a_ {1}, a_ {2}, \ dots, a_ {n}]}$ ${\ mathbf a} = [a_ {1}, a_ {2}, \ dots, a_ {n}]$ Și $\mathbf {b} =[b_{1},b_{2},\dots ,b_{n}]$ ${\ displaystyle \ mathbf {b} = [b_ {1}, b_ {2}, \ dots, b_ {n}]}$ ${\ mathbf b} = [b_ {1}, b_ {2}, \ dots, b_ {n}]$ numarul:

\mathbf {a} \cdot \mathbf {b} =a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}=\sum _{i=1}^{n}a_{i}b_{i}

{\ displaystyle \ mathbf {a} \ cdot \ mathbf {b} = a_ {1} b_ {1} + a_ {2} b_ {2} + \ cdots + a_ {n} b_ {n} = \ sum _ { i = 1} ^ {n} a_ {i} b_ {i}}

{\ mathbf {a}} \ cdot {\ mathbf {b}} = a_ {1} b_ {1} + a_ {2} b_ {2} + \ cdots + a_ {n} b_ {n} = \ sum _ {{i = 1}} ^ {n} a_ {i} b_ {i}

unde este $\sum$ ${\ displaystyle \ sum}$ $\ sum$ denotă o însumare .

De exemplu, produsul scalar a doi vectori tridimensionali [1, 3, −2] și [4, −2, −1] este [1, 3, −2] [4, −2, −1] = 1 × 4 + 3 × (−2) + (−2) × (−1) = 0.

În acest fel puteți defini unghiul $\theta$ ${\ displaystyle \ theta}$ $\ theta$ între doi vectori în orice spațiu euclidian, inversând formula dată mai sus, adică făcând unghiul să depindă de produsul scalar și nu invers:

\theta =\arccos {\frac {\mathbf {a} \cdot \mathbf {b} }{|\mathbf {a} ||\mathbf {b} |}}

{\ displaystyle \ theta = \ arccos {\ frac {\ mathbf {a} \ cdot \ mathbf {b}} {| \ mathbf {a} || \ mathbf {b} |}}}

\ theta = \ arccos {\ frac {{\ mathbf {a}} \ cdot {\ mathbf {b}}} {| {\ mathbf a} || {\ mathbf b} |}}

Notări

Adesea produsul punct între $\mathbf {a}$ ${\ displaystyle \ mathbf {a}}$ $\ mathbf a$ Și $\mathbf {b}$ ${\ displaystyle \ mathbf {b}}$ $\ mathbf b$ este indicat și ca $\langle \mathbf {a} ,\mathbf {b} \rangle$ ${\ displaystyle \ langle \ mathbf {a}, \ mathbf {b} \ rangle}$ $\ langle {\ mathbf a}, {\ mathbf b} \ rangle$ sau cum $\left(\mathbf {a} ,\mathbf {b} \right)$ ${\ displaystyle \ left (\ mathbf {a}, \ mathbf {b} \ right)}$ $\ left ({\ mathbf a}, {\ mathbf b} \ right)$ . Utilizarea produsului între matrice și considerarea vectorilor ca matrice $n\times 1$ ${\ displaystyle n \ times 1}$ $n \ ori 1$ , produsul scalar canonic este, de asemenea, scris ca:

\mathbf {a} \cdot \mathbf {b} =\mathbf {a} ^{T}\mathbf {b}

{\ displaystyle \ mathbf {a} \ cdot \ mathbf {b} = \ mathbf {a} ^ {T} \ mathbf {b}}

{\ mathbf {a}} \ cdot {\ mathbf {b}} = {\ mathbf {a}} ^ {T} {\ mathbf {b}}

unde este $\mathbf {a} ^{T}$ ${\ displaystyle \ mathbf {a} ^ {T}}$ ${\ mathbf {a}} ^ {T}$ este transpunerea $\mathbf {a}$ ${\ displaystyle \ mathbf {a}}$ $\ mathbf {a}$ . Prin urmare, exemplul văzut mai sus este scris în notație matricială după cum urmează:

{\begin{bmatrix}1&3&-2\end{bmatrix}}{\begin{bmatrix}4\\-2\\-1\end{bmatrix}}={\begin{bmatrix}0\end{bmatrix}}

{\ displaystyle {\ begin {bmatrix} 1 & 3 & -2 \ end {bmatrix}} {\ begin {bmatrix} 4 \\ - 2 \\ - 1 \ end {bmatrix}} = {\ begin {bmatrix} 0 \ end {bmatrix}}}

{\ begin {bmatrix} 1 & 3 & -2 \ end {bmatrix}} {\ begin {bmatrix} 4 \\ - 2 \\ - 1 \ end {bmatrix}} = {\ begin {bmatrix} 0 \ end { bmatrix}}

Echivalența dintre cele două definiții

Echivalența dintre cele două definiții poate fi verificată folosind teorema cosinusului . În forma descrisă mai sus, teorema afirmă că produsul scalar al doi vectori $\mathbf {a}$ ${\ displaystyle \ mathbf {a}}$ $\ mathbf a$ Și $\mathbf {b}$ ${\ displaystyle \ mathbf {b}}$ $\ mathbf b$ în plan, definit geometric, este egal cu:

\mathbf {a} \cdot \mathbf {b} ={\frac {1}{2}}{\big (}|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-|\mathbf {a} -\mathbf {b} |^{2}{\big )}

{\ displaystyle \ mathbf {a} \ cdot \ mathbf {b} = {\ frac {1} {2}} {\ big (} | \ mathbf {a} | ^ {2} + | \ mathbf {b} | ^ {2} - | \ mathbf {a} - \ mathbf {b} | ^ {2} {\ big)}}

{\ mathbf a} \ cdot {\ mathbf b} = {\ frac 12} {\ big (} | {\ mathbf a} | ^ {2} + | {\ mathbf b} | ^ {2} - | {\ mathbf a} - {\ mathbf b} | ^ {2} {\ big)}

Prin plasare $\mathbf {a} =[a_{1},a_{2}]$ ${\ displaystyle \ mathbf {a} = [a_ {1}, a_ {2}]}$ ${\ mathbf a} = [a_ {1}, a_ {2}]$ Și $\mathbf {b} =[b_{1},b_{2}]$ ${\ displaystyle \ mathbf {b} = [b_ {1}, b_ {2}]}$ ${\ mathbf b} = [b_ {1}, b_ {2}]$ și folosind teorema lui Pitagora obținem:

\mathbf {a} \cdot \mathbf {b} ={\frac {1}{2}}{\bigg (}a_{1}^{2}+a_{2}^{2}+b_{1}^{2}+b_{2}^{2}-{\big (}(a_{1}-b_{1})^{2}+(a_{2}-b_{2})^{2}{\big )}{\bigg )}={\frac {1}{2}}(2a_{1}b_{1}+2a_{2}b_{2})=a_{1}b_{1}+a_{2}b_{2}

{\ displaystyle \ mathbf {a} \ cdot \ mathbf {b} = {\ frac {1} {2}} {\ bigg (} a_ {1} ^ {2} + a_ {2} ^ {2} + b_ {1} ^ {2} + b_ {2} ^ {2} - {\ big (} (a_ {1} -b_ {1}) ^ {2} + (a_ {2} -b_ {2}) ^ {2} {\ big)} {\ bigg)} = {\ frac {1} {2}} (2a_ {1} b_ {1} + 2a_ {2} b_ {2}) = a_ {1} b_ { 1} + a_ {2} b_ {2}}

{\ mathbf a} \ cdot {\ mathbf b} = {\ frac 12} {\ bigg (} a_ {1} ^ {2} + a_ {2} ^ {2} + b_ {1} ^ {2} + b_ {2} ^ {2} - {\ big (} (a_ {1} -b_ {1}) ^ {2} + (a_ {2} -b_ {2}) ^ {2} {\ big)} {\ bigg)} = {\ frac 12} (2a_ {1} b_ {1} + 2a_ {2} b_ {2}) = a_ {1} b_ {1} + a_ {2} b_ {2}

Echivalența într-un spațiu euclidian de dimensiuni arbitrare poate fi verificată într-un mod analog.

Aplicații

Produsul scalar are o importanță fundamentală atât în fizică, cât și în diverse domenii ale matematicii , de exemplu în clasificarea conicelor , în studiul unei funcții diferențiate în jurul unui punct staționar , în transformări plane sau în soluția unor ecuații diferențiale . Adesea, în aceste contexte, se folosește teorema spectrală , un rezultat important legat de produsul scalar.

Norma unui vector

Același subiect în detaliu: Norma (matematică) .

În plan cartezian , produsul scalar permite definirea și tratarea noțiunii geometrice de lungime a unui vector. Acest concept poate fi extins la un spațiu vectorial de dimensiuni arbitrare prin introducerea unui concept analog: norma . În mod formal, dacă $K=\mathbb {R}$ ${\ displaystyle K = \ mathbb {R}}$ $K = \ R$ iar produsul scalar este definit pozitiv, este posibil să se asigure spațiul vectorial cu o normă. Mai exact, funcția:

\|\mathbf {x} \|:={\sqrt {\langle \mathbf {x} ,\mathbf {x} \rangle }}

{\ displaystyle \ | \ mathbf {x} \ |: = {\ sqrt {\ langle \ mathbf {x}, \ mathbf {x} \ rangle}}}

\ | {\ mathbf x} \ |: = {\ sqrt {\ langle {\ mathbf x}, {\ mathbf x} \ rangle}}

satisface pentru fiecare transportator $\mathbf {x}$ ${\ displaystyle \ mathbf {x}}$ $\ mathbf x$ , $\mathbf {y}$ ${\ displaystyle \ mathbf {y}}$ ${\ mathbf y}$ iar pentru fiecare urcare $\lambda$ ${\ displaystyle \ lambda}$ $\ lambda$ proprietatea:

$\|\mathbf {x} \|=0$ ${\ displaystyle \ | \ mathbf {x} \ | = 0}$ $\ | {\ mathbf x} \ | = 0$ dacă și numai dacă $\mathbf {x} =0$ ${\ displaystyle \ mathbf {x} = 0}$ ${\ mathbf x} = 0$
$\|\lambda \mathbf {x} \|=|\lambda |\|\mathbf {x} \|$ ${\ displaystyle \ | \ lambda \ mathbf {x} \ | = | \ lambda | \ | \ mathbf {x} \ |}$ $\ | \ lambda {\ mathbf x} \ | = | \ lambda | \ | {\ mathbf x} \ |$
$\|\mathbf {x} +\mathbf {y} \|\leq \|\mathbf {x} \|+\|\mathbf {y} \|$ ${\ displaystyle \ | \ mathbf {x} + \ mathbf {y} \ | \ leq \ | \ mathbf {x} \ | + \ | \ mathbf {y} \ |}$ $\ | {\ mathbf x} + {\ mathbf y} \ | \ leq \ | {\ mathbf x} \ | + \ | {\ mathbf y} \ |$

și, prin urmare, face din spațiul vectorial un spațiu normat .

Matricea asociată

Similar cu matricea asociată cu o aplicație liniară , o bază este fixă $\mathbf {v} _{1},\ldots ,\mathbf {v} _{n}$ ${\ displaystyle \ mathbf {v} _ {1}, \ ldots, \ mathbf {v} _ {n}}$ ${\ mathbf v} _ {1}, \ ldots, {\ mathbf v} _ {n}$ , un produs scalar $\phi$ ${\ displaystyle \ phi}$ $\ phi$ este identificat prin matricea simetrică asociată $M.$ ${\ displaystyle M}$ $M.$ , definit după cum urmează:

$M_{i,j}=\phi (\mathbf {v} _{i},\mathbf {v} _{j})\$ ${\ displaystyle M_ {i, j} = \ phi (\ mathbf {v} _ {i}, \ mathbf {v} _ {j}) \}$ $M _ {{i, j}} = \ phi ({\ mathbf v} _ {i}, {\ mathbf v} _ {j}) \$ ^[4]

Pe de altă parte, fiecare matrice simetrică dă naștere unui produs scalar. ^[5] Multe proprietăți ale produsului punct și ale bazei pot fi citite pe matricea asociată.

Matrice fixată $M.$ ${\ displaystyle M}$ $M.$ , pentru orice pereche de vectori de coloană $(\mathbf {x} ,\mathbf {y} )$ ${\ displaystyle (\ mathbf {x}, \ mathbf {y})}$ ${\ displaystyle (\ mathbf {x}, \ mathbf {y})}$ produsul scalar este definit de lege

$\mathbf {x} \cdot \mathbf {y} =\mathbf {x} ^{T}M\mathbf {y}$ ${\ displaystyle \ mathbf {x} \ cdot \ mathbf {y} = \ mathbf {x} ^ {T} M \ mathbf {y}}$ ${\ displaystyle \ mathbf {x} \ cdot \ mathbf {y} = \ mathbf {x} ^ {T} M \ mathbf {y}}$

Unde este $\mathbf {x} ^{T}$ ${\ displaystyle \ mathbf {x} ^ {T}}$ ${\ displaystyle \ mathbf {x} ^ {T}}$ este vectorul rând $\mathbf {x}$ ${\ displaystyle \ mathbf {x}}$ $\ mathbf {x}$ transpuse.

Matricea scrisă în raport cu o bază ortonormală a unui anumit produs scalar este matricea identității; dacă baza este ortogonală, dar nu este normalizată, matricea va fi pur și simplu diagonală.

Radical

Radicalul unui produs dot este setul de vectori $\mathbf {v} \in V$ ${\ displaystyle \ mathbf {v} \ în V}$ $\ mathbf v \ în V$ pentru care:

\langle \mathbf {v} ,\mathbf {w} \rangle =0

{\ displaystyle \ langle \ mathbf {v}, \ mathbf {w} \ rangle = 0}

\ langle {\ mathbf v}, {\ mathbf w} \ rangle = 0

pentru fiecare $\mathbf {w} \in V$ ${\ displaystyle \ mathbf {w} \ în V}$ $\ mathbf w \ în V$ . Radicalul este un subspatiu vectorial al $V.$ ${\ displaystyle V}$ $V.$ . Se spune că produsul scalar este degenerat dacă radicalul are o dimensiune mai mare decât zero.

De sine $V.$ ${\ displaystyle V}$ $V.$ are dimensiune finită e $M.$ ${\ displaystyle M}$ $M.$ este matricea asociată cu $\phi$ ${\ displaystyle \ phi}$ $\ phi$ în ceea ce privește orice bază, prin aplicarea teoremei dimensiunii este ușor de constatat că:

\operatorname {rank} (M)+\dim(\operatorname {rad} (V))=\dim V

{\ displaystyle \ operatorname {rank} (M) + \ dim (\ operatorname {rad} (V)) = \ dim V}

\ operatorname {rank} (M) + \ dim (\ operatorname {rad} (V)) = \ dim V

unde este $\operatorname {rank} (M)$ ${\ displaystyle \ operatorname {rank} (M)}$ $\ operatorname {rank} (M)$ este rangul de $M.$ ${\ displaystyle M}$ $M.$ Și $\operatorname {rad} (V)$ ${\ displaystyle \ operatorname {rad} (V)}$ $\ operatorname {rad} (V)$ este radicalul. Prin urmare, un produs scalar nu este degenerat dacă și numai dacă matricea asociată este inversabilă . Rangul produsului punct este definit ca $\operatorname {rank} (M)$ ${\ displaystyle \ operatorname {rank} (M)}$ $\ operatorname {rank} (M)$ .

Un produs scalar definitiv pozitiv sau negativ este neapărat nedegenerat. Opusul nu este adevărat, de fapt produsul scalar asociat cu baza canonică a matricei:

A={\begin{bmatrix}1&0\\0&-1\\\end{bmatrix}}

{\ displaystyle A = {\ begin {bmatrix} 1 & 0 \\ 0 & -1 \\\ end {bmatrix}}}

A = {\ begin {bmatrix} 1 & 0 \\ 0 & -1 \\\ end {bmatrix}}

nu este degenerat, dar nu este nici definit pozitiv, nici definit negativ.

Vectorii izotropi

Un vector $\mathbf {v}$ ${\ displaystyle \ mathbf {v}}$ $\ mathbf v$ este izotrop dacă $\langle \mathbf {v} ,\mathbf {v} \rangle$ ${\ displaystyle \ langle \ mathbf {v}, \ mathbf {v} \ rangle}$ $\ langle {\ mathbf v}, {\ mathbf v} \ rangle$ = 0. Toți vectorii radicalului sunt izotropi, dar pot exista vectori izotropi care nu aparțin radicalului. De exemplu, pentru produsul punct asociat cu matricea $LA$ ${\ displaystyle A}$ $LA$ descris mai sus vectorul $[1,1]$ ${\ displaystyle [1,1]}$ $[1.1]$ este izotrop, dar nu este conținut în radical, care are dimensiune zero.

Ortogonalitate

Doi transportatori $\mathbf {v}$ ${\ displaystyle \ mathbf {v}}$ $\ mathbf v$ Și $\mathbf {w}$ ${\ displaystyle \ mathbf {w}}$ $\ mathbf w$ se numesc ortogonali dacă $\langle \mathbf {v} ,\mathbf {w} \rangle =0$ ${\ displaystyle \ langle \ mathbf {v}, \ mathbf {w} \ rangle = 0}$ $\ langle {\ mathbf v}, {\ mathbf w} \ rangle = 0$ . Subspatiul ortogonal a $W$ ${\ displaystyle W}$ $W$ (subspatiu vectorial de $V.$ ${\ displaystyle V}$ $V.$ ) este definit ca:

W^{\perp }=\{\mathbf {w} \in V\ |\langle \mathbf {w} ,\mathbf {w} '\rangle =0\ \forall \mathbf {w} '\in W\}

{\ displaystyle W ^ {\ perp} = \ {\ mathbf {w} \ in V \ | \ langle \ mathbf {w}, \ mathbf {w} '\ rangle = 0 \ \ forall \ mathbf {w}' \ în W \}}

W ^ {\ perp} = \ {{\ mathbf w} \ in V \ | \ langle {\ mathbf w}, {\ mathbf w} '\ rangle = 0 \ \ forall {\ mathbf w}' \ in W \ }

Subspatiul ortogonal este tocmai un subspatiu vectorial al $V.$ ${\ displaystyle V}$ $V.$ . Spre deosebire de ceea ce se întâmplă cu produsul canonic în spațiul euclidian, un subspațiu și ortogonalul său nu se intersectează în general într-un singur punct (pot chiar să coincidă). În ceea ce privește mărimea lor, se menține următoarea inegalitate:

\dim W+\dim W^{\perp }\geq \dim V

{\ displaystyle \ dim W + \ dim W ^ {\ perp} \ geq \ dim V}

\ dim W + \ dim W ^ {\ perp} \ geq \ dim V

Dacă produsul punct nu este degenerat, atunci egalitatea se menține

\dim W+\dim W^{\perp }=\dim V

{\ displaystyle \ dim W + \ dim W ^ {\ perp} = \ dim V}

\ dim W + \ dim W ^ {\ perp} = \ dim V

În cele din urmă, dacă produsul scalar este definit pozitiv sau negativ, de fapt un spațiu și ortogonalul său se intersectează numai la origine și sunt în sumă directă . Primesti:

W\oplus W^{\perp }=V

{\ displaystyle W \ oplus W ^ {\ perp} = V}

W \ oplus W ^ {\ perp} = V

O bază ortogonală a vectorilor de $V.$ ${\ displaystyle V}$ $V.$ este o bază a doi-la-doi vectori ortogonali. O bază este ortogonală dacă și numai dacă matricea asociată cu produsul scalar față de această bază este diagonală .

Transformarea ortogonală

Același subiect în detaliu: Transformarea ortogonală .

O transformare ortogonală este o aplicație liniară inversabilă $T:V\to V$ ${\ displaystyle T: V \ to V}$ $T: V \ to V$ în sine, care păstrează produsul punct, adică astfel încât:

\langle \mathbf {v} ,\mathbf {w} \rangle =\langle T(\mathbf {v} ),T(\mathbf {w} )\rangle

{\ displaystyle \ langle \ mathbf {v}, \ mathbf {w} \ rangle = \ langle T (\ mathbf {v}), T (\ mathbf {w}) \ rangle}

\ langle {\ mathbf v}, {\ mathbf w} \ rangle = \ langle T ({\ mathbf v}), T ({\ mathbf w}) \ rangle

Teorema lui Sylvester

Același subiect în detaliu: teorema lui Sylvester .

De sine $K=\mathbb {R}$ ${\ displaystyle K = \ mathbb {R}}$ $K = \ R$ este câmpul numerelor reale și $V.$ ${\ displaystyle V}$ $V.$ are dimensiunea n , teorema reală a lui Sylvester afirmă că dat un produs scalar $\phi$ ${\ displaystyle \ phi}$ $\ phi$ pe $V.$ ${\ displaystyle V}$ $V.$ , avem asta:

Există o bază ortogonală a $V.$ ${\ displaystyle V}$ $V.$ în comparație cu $\phi$ ${\ displaystyle \ phi}$ $\ phi$ .
Două baze ortogonale pentru $V.$ ${\ displaystyle V}$ $V.$ au aceeași semnătură, de aceea depinde doar de $\phi$ ${\ displaystyle \ phi}$ $\ phi$ .
Două produse scalare cu aceeași semnătură sunt izomorfe.

Prin urmare, matricea asociată este o matrice diagonală care are pe diagonală doar numerele 0, 1 și -1, în nici o ordine specială. Lasa-i sa fie $i_{0}$ ${\ displaystyle i_ {0}}$ $i_ {0}$ , $i_{+}$ ${\ displaystyle i _ {+}}$ $eu _ {+}$ Și $i_{-}$ ${\ displaystyle i _ {-}}$ $_ {-}$ respectiv de câte ori apar numerele 0, 1 și -1 pe diagonală: triada $(i_{0},i_{+},i_{-})$ ${\ displaystyle (i_ {0}, i _ {+}, i _ {-})}$ $(i_ {0}, i _ {+}, i _ {-})$ este semnătura produsului dot .

Semnătura este un invariant complet pentru izometrie: două spații vectoriale cu produs scalar sunt izometrice dacă și numai dacă au aceeași semnătură.

Teorema complexă a lui Sylvester, pe de altă parte, spune că există întotdeauna o bază ortogonală $\mathbf {v} _{1},\dots ,\mathbf {v} _{n}$ ${\ displaystyle \ mathbf {v} _ {1}, \ dots, \ mathbf {v} _ {n}}$ ${\ mathbf v} _ {1}, \ dots, {\ mathbf v} _ {n}$ astfel încât pentru fiecare $the$ ${\ displaystyle i}$ $the$ numarul $\langle \mathbf {v} _{i},\mathbf {v} _{i}\rangle$ ${\ displaystyle \ langle \ mathbf {v} _ {i}, \ mathbf {v} _ {i} \ rangle}$ $\ langle {\ mathbf v} _ {i}, {\ mathbf v} _ {i} \ rangle$ este egal cu 0 sau 1. În acest caz, rangul este un invariant complet pentru izometrie: două spații vectoriale complexe cu produs scalar sunt izometrice dacă și numai dacă au același rang.

Endomorfism simetric

Același subiect în detaliu: teorema spectrală .

Un endomorfism $T:V\to V$ ${\ displaystyle T: V \ to V}$ $T: V \ to V$ este simetric sau autoadjunct în raport cu produsul punct dacă:

\langle T(\mathbf {v} ),\mathbf {w} \rangle =\langle \mathbf {v} ,T(\mathbf {w} )\rangle

{\ displaystyle \ langle T (\ mathbf {v}), \ mathbf {w} \ rangle = \ langle \ mathbf {v}, T (\ mathbf {w}) \ rangle}

\ langle T ({\ mathbf v}), {\ mathbf w} \ rangle = \ langle {\ mathbf v}, T ({\ mathbf w}) \ rangle

pentru fiecare pereche de vectori $\mathbf {v} ,\mathbf {w} \in V$ ${\ displaystyle \ mathbf {v}, \ mathbf {w} \ în V}$ ${\ mathbf v}, {\ mathbf w} \ în V$ . Un endomorfism este simetric dacă și numai dacă matricea asociată față de orice bază ortonormală este simetrică .

Exemple

Produsul scalar canonic dintre vectorii planului sau spațiului euclidian este un produs scalar pozitiv definit.
Este $C([0,1])$ ${\ displaystyle C ([0,1])}$ $C ([0,1])$ spațiul vectorial al funcțiilor continue pe intervalul [0,1], cu valori reale . Putem defini un produs dot $C([0,1])$ ${\ displaystyle C ([0,1])}$ $C ([0,1])$ punând:

\langle f,g\rangle =\int _{0}^{1}f(x)g(x)dx

{\ displaystyle \ langle f, g \ rangle = \ int _ {0} ^ {1} f (x) g (x) dx}

\ langle f, g \ rangle = \ int _ {0} ^ {1} f (x) g (x) dx

Acest produs dot se numește pozitiv, deoarece integrala lui

f^{2}

{\ displaystyle f ^ {2}}

f ^ {2}

este strict pozitiv dacă

f

{\ displaystyle f}

f

în mod constant nu este nimic.

Poate fi definit pe spațiul vectorial $M([0,1])$ ${\ displaystyle M ([0,1])}$ $M ([0,1])$ a funcțiilor măsurabile cu valoare reală, același produs scalar al punctului anterior. Aici produsul scalar este doar semidefinit pozitiv: de fapt dacă $f$ ${\ displaystyle f}$ $f$ este funcția care este 1 peste 1/2 și 0 peste orice altceva, integralul lui $f^{2}$ ${\ displaystyle f ^ {2}}$ $f ^ {2}$ este zero ( $f$ ${\ displaystyle f}$ $f$ este izotrop).

Notă

^ ^a ^b Hoffman, Kunze , p . 271 .
^ S. Lang , pagina 185 .
^ S. Lang , pagina 151 .
^ Acest lucru este valabil pentru o formă biliniară generică, din care produsele scalare sunt doar un anumit tip.
^ Ciò è vero solo se si considerano prodotti scalari validi anche quelli degeneri e che non sono definiti positivi per ogni coppia di vettori non nulli.

Bibliografia

Serge Lang , Algebra lineare , Torino, Bollati Boringhieri , 1992, ISBN 88-339-5035-2 .
( EN ) Kenneth Hoffman, Ray Kunze, Linear Algebra , 2ª ed., Englewood Cliffs, New Jersey, Prentice - Hall, inc., 1971, ISBN 0-13-536821-9 .
( EN ) Arfken, G. "Scalar or Dot Product." §1.3 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 13–18, 1985.
( EN ) Jeffreys, H. and Jeffreys, BS "Scalar Product." §2.06 in Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, pp. 65–67, 1988.

Voci correlate

Altri progetti

Wikibooks contiene testi o manuali sul prodotto scalare
Wikimedia Commons contiene immagini o altri file sul prodotto scalare

Collegamenti esterni

( EN ) AB Ivanov, Inner product , in Encyclopaedia of Mathematics , Springer e European Mathematical Society, 2002.
( EN ) Weisstein, Eric W. Dot product . From MathWorld
( EN ) Explanation of dot product including with complex vectors , su mathreference.com .
( EN ) "Dot Product" by Bruce Torrence, Wolfram Demonstrations Project , 2007.

Portale Matematica : accedi alle voci di Wikipedia che trattano di matematica

[inner-1] Hoffman, Kunze , p . 271 .

[2] S. Lang , pagina 185 .

[3] S. Lang , pagina 151 .

[4] Acest lucru este valabil pentru o formă biliniară generică, din care produsele scalare sunt doar un anumit tip.

[5] Ciò è vero solo se si considerano prodotti scalari validi anche quelli degeneri e che non sono definiti positivi per ogni coppia di vettori non nulli.

[1]

[2]

[3]

[4]

[5]

V · D · M Algebra lineare
Spazio vettoriale	Vettore · Sottospazio vettoriale ( Sottospazio generato ) · Applicazione lineare ( Nucleo · Immagine ) · Base · Dimensione · Teorema della dimensione · Formula di Grassmann · Sistema lineare · Algoritmo di Gauss · Teorema di Rouché-Capelli · Regola di Cramer · Spazio duale · Spazio proiettivo · Spazio affine · Teorema della dimensione per spazi vettoriali
Matrici	Identità · Nulla · Quadrata · Invertibile · Simmetrica · Antisimmetrica · Trasposta · Diagonale · Triangolare · Di cambiamento di base · Ortogonale · Normale · Simplettica · Moltiplicazione di matrici · Rango · Teorema di Kronecker · Minore · Matrice dei cofattori · Determinante · Teorema di Binet · Teorema di Laplace · Radice quadrata di una matrice
Diagonalizzabilità	Autovettore e autovalore · Spettro · Polinomio caratteristico · Polinomio minimo · Teorema di Hamilton-Cayley · Matrice a blocchi · Forma canonica di Jordan · Teorema di diagonalizzabilità
Prodotto scalare	Forma bilineare · Sottospazio ortogonale · Spazio euclideo · Base ortonormale · Algoritmo di Lagrange · Segnatura · Teorema di Sylvester · Gram-Schmidt · Forma sesquilineare · Forma hermitiana · Teorema spettrale