RB-Ax

Un copac roșu-negru (sau chiar un copac roșu-negru, copac în italiană roșu-negru) este un tip de arbore binar echilibrat de cercetare , o structură de date utilizată în IT , utilizată de obicei pentru a implementa seturi sau tablouri asociative . Structura originală a fost inventată în 1972 de Rudolf Bayer, care a numit-o „arbori binari simetrici”, dar și-a dobândit numele actual dintr-un articol din 1978 al lui Leo J. Guibas și Robert Sedgewick . Este complex, dar are un timp de execuție excelent în cel mai rău caz și este foarte eficient: efectuează căutări, inserții și ștergeri într-un timp de $O(\log n)$ ${\ displaystyle O (\ log n)}$ $O (\ log n)$ , unde este $n$ ${\ displaystyle n}$ $n$ este numărul de articole din copac.

Concepte de bază și terminologie

Un copac roșu-negru este un tip special de copac binar , care este o structură utilizată în informatică pentru a organiza date comparabile, cum ar fi numerele. Fiecare unitate de date este stocată într-un nod . Unul dintre noduri acționează întotdeauna ca punct de plecare și nu este copilul niciunui nod; de obicei se numește nod rădăcină sau pur și simplu rădăcină. Acest nod are cel mult doi copii , care sunt alte noduri la care este conectat. La rândul lor, fiecare dintre acești copii are maximum doi copii și așa mai departe. Nodul rădăcină are, de asemenea, o cale care îl conectează la orice alt nod din copac.

Dacă un nod nu are copii, acesta se numește nod de frunze , deoarece face parte intuitiv din „periferia” arborelui. Un subarbore este o porțiune a copacului care se extinde de la un anumit nod. La copacii roșu-negri, se presupune că frunzele sunt nule , ceea ce înseamnă că nu conțin date.

Deoarece copacii roșu-negri sunt, de asemenea, copaci binari de căutare, satisfac constrângerea că fiecare nod conține o valoare mai mică sau egală cu cea a tuturor nodurilor din subarborele său drept și mai mare sau egală cu cea a tuturor nodurilor din subarborele său drept. subarborele stâng. Acest lucru face rapidă găsirea unei valori date în arbore și permite sortarea eficientă a articolelor.

Utilizări și beneficii

Arborii roșu-negri, împreună cu arborii AVL , oferă cele mai bune performanțe în cel mai rău caz de căutare, inserare și ștergere. Acest lucru le face nu numai importante în aplicațiile de sistem în timp real , ci și „elemente de bază” ale altor structuri de date care oferă garanții în cel mai rău caz; de exemplu, multe structuri de date utilizate în geometria de calcul se bazează pe copaci roșu-negru.

Copacii roșu-negri sunt, de asemenea, importanți în programarea funcțională , unde sunt una dintre cele mai frecvente structuri de date persistente , utilizate pentru a construi matrice asociative și seturi capabile să mențină stări de pre-schimbare. Versiunea persistentă a copacilor roșu-negri necesită un spațiu de O (jurnal n ) pentru fiecare inserare sau ștergere, în plus față de timp.

Copacii roșu-negri sunt o izometrie de 2-3-4 copaci . Cu alte cuvinte, pentru fiecare 2-3-4 copaci, există cel puțin un copac roșu-negru cu elementele în aceeași ordine. Operațiile de inserare și ștergere pe 2-3-4 copaci sunt echivalente cu operațiile de recolorare și rotație pe copaci roșu-negri. Prin urmare, 2-3-4 copaci sunt un instrument important pentru înțelegerea logicii din spatele copacilor roșu-negri, motiv pentru care multe texte algoritmice introduc 2-3-4 copaci chiar înainte de cei roșii. 4 nu sunt aproape niciodată utilizate în practică.

Proprietate

Un copac roșu-negru este un copac binar de căutare în care fiecare nod are un atribut de culoare , a cărui valoare poate fi roșie sau neagră . În plus față de cerințele obișnuite pentru un copac de căutare binar, un copac roșu-negru îndeplinește următoarele proprietăți:

Fiecare nod are culoarea roșie sau neagră.
Nodul rădăcină este inițial negru.
Fiecare frunză este neagră și conține element nul ;
Ambii copii ai fiecărui nod roșu sunt negri;
Fiecare cale de la un nod la o frunză din subarborele său conține același număr de noduri negre.

Aceste constrângeri întăresc o proprietate critică a copacilor roșu-negri: că cea mai lungă cale de la nodul rădăcinii la o frunză este cel mult de două ori cea mai scurtă cale. Rezultatul este, prin urmare, un copac puternic echilibrat. Deoarece operațiunile de căutare, inserare și ștergere a valorii necesită un timp de execuție în cel mai rău caz proporțional cu înălțimea arborelui, această limită teoretică superioară a înălțimii face copacii roșu-negri foarte eficienți în cel mai rău caz, spre deosebire de ceea ce se întâmplă cu arborii de căutare binari obișnuiți. .

Pentru a vedea cum sunt garantate aceste proprietăți, este suficient să rețineți că nici o cale nu poate avea două noduri roșii la rând, după proprietatea 4. Cea mai scurtă cale posibilă are toate nodurile negre, iar cea mai lungă alternează între nodurile roșii și nodurile negre. Deoarece toate căile maxime au același număr de noduri negre, după proprietatea 5, aceasta arată că nici o cale nu este mai mult de două ori mai lungă decât oricare altă cale.

În multe structuri de date „copac”, este posibil ca un nod să aibă un singur copil, iar nodurile frunze să conțină date. De asemenea, este posibil să se prezinte copaci roșii-negri conform acestei paradigme, dar acest lucru ar schimba unele dintre proprietăți și ar complica algoritmul. Din acest motiv, în acest articol vorbim despre „frunze nule”, care nu conțin date și servesc pur și simplu pentru a indica unde se termină arborele. Aceste noduri sunt adesea omise în reprezentarea grafică, iar arborele reprezentat pare să contrazică principiile expuse, dar de fapt nu este cazul. Consecința este că toți nodurile interne (fără frunze) au doi copii, deși unul sau ambii dintre acești copii pot fi o frunză nulă.

Unele discuții ilustrează copacii roșu-negri ca arbori binari de căutare ale căror margini (în loc de noduri) sunt colorate în roșu sau negru; dar asta nu face nicio diferență. În terminologia noastră, culoarea unui nod corespunde cu culoarea arcului care leagă nodul de părinte, excluzând nodul rădăcină care este întotdeauna negru (proprietatea 2), având în vedere faptul că arcul corespunzător nu există.

Operațiuni

Operațiile de citire pe un copac roșu-negru nu necesită modificări la cele utilizate pentru copacii binari de căutare, deoarece copacii roșu-negri sunt specializarea lor. Dimpotrivă, rezultatul imediat al inserării sau ștergerii poate încălca proprietățile arborelui roșu-negru, iar restaurarea acelor proprietăți necesită un număr mic ( O (log n ) sau O (1) amortizat ) de recolorări (care sunt foarte rapide în practică) și nu mai mult de trei rotații ale arborelui (două pentru inserare). Deși inserarea și ștergerea sunt operațiuni complicate, timpii lor de execuție rămân în ordinea lui O (log n ).

Inserare

Începem prin a adăuga un nod ca și cum ar fi un arbore clasic de căutare binară și îl colorăm în roșu. Următorul pas depinde de culoarea celorlalte noduri adiacente. Vom folosi termenul nod unchi pentru a ne referi la fratele nodului părinte. Rețineți că:

proprietatea 3 (toate frunzele, inclusiv cele nule, sunt negre) persistă;
proprietatea 4 (ambii copii ai fiecărui nod roșu sunt negri) este amenințată numai de inserarea unui nod roșu, de recolorarea unui nod negru în roșu sau de o rotație;
proprietatea 5 (toate căile de la un nod dat la frunzele sale conțin același număr de noduri negre) este amenințată numai de inserarea unui nod negru, recolorarea unui nod roșu spre negru sau o rotație.

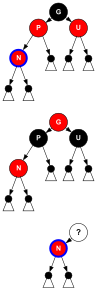
Notă : vom folosi următoarea simbolologie: N pentru nodul inserat, P pentru nodul părinte al lui N , G pentru nodul părinte al lui P și U pentru „nodul unchiului” al lui N. Rețineți că, în unele cazuri, este posibil ca rolurile și simbolurile nodurilor să fie schimbate; în orice caz, fiecare simbol continuă să reprezinte același nod pe care l-a reprezentat la începutul cazului.

Fiecare caz este demonstrat cu un exemplu de cod în limbajul C , nodurile „unchiul” și „bunicul” se găsesc prin următoarele funcții:

 nod bunic ( nod n ) {
     returnează n -> părinte -> părinte ;
 }

 nod unchiul ( nodul n ) {
     if ( n -> părinte == bunic ( n ) -> stânga )
         return bunic ( n ) -> dreapta ;
     altceva
         return bunic ( n ) -> stânga ;
 }

Cazul 1: noul nod N se află la rădăcina arborelui. În acest caz, este colorat în negru pentru a satisface proprietatea 2 (rădăcina este neagră). Deoarece această inserție adaugă un nod negru la fiecare cale, proprietatea 5 (toate căile de la un nod dat la frunzele sale conțin același număr de noduri negre) nu este încălcată.

 void insert_case1 ( nod n ) {
     if ( n -> părinte == NULL )
         n -> culoare = BLACK ;
     altceva
         insert_case2 ( n );
 }

Cazul 2: tatăl P al noului nod este negru, deci proprietatea 4 (ambii copii ai fiecărui nod roșu sunt negri) nu este invalidată. În acest caz, arborele este încă valabil. Proprietatea 5 (toate căile de la un nod dat la frunzele sale conțin același număr de noduri negre) ar părea amenințată, deoarece noul nod N are două frunze negre, dar din moment ce N este roșu, căile prin fiecare dintre copiii săi au același lucru numărul de noduri negre, deoarece acestea sunt căi separate, astfel încât proprietatea rămâne satisfăcută.

 void insert_case2 ( nod n ) {
     if ( n -> părinte -> culoare == NEGRU )
         întoarcere ; / * Arborele este încă valabil * /
     altceva
         insert_case3 ( n );
 }

Notă: În următoarele cazuri se presupune că N are un nod „bunic” G , deoarece tatăl P este roșu, iar dacă ar fi fost rădăcină ar fi fost negru. Mai mult, N are și un nod "unchi" U , deși poate fi o frunză în cazurile 4 și 5.

Cazul 3: dacă atât tatăl P, cât și unchiul U sunt roșii, atunci este posibil să recolorați atât negru, cât și bunicul G roșu pentru a păstra proprietatea 5 (toate căile de la un nod dat la frunzele sale conțin același număr de noduri negre). Acum noul nod N are un tată negru. Deoarece orice cale prin tată sau unchi trebuie să treacă prin bunic, numărul nodurilor negre de pe aceste căi nu se schimbă. Dar bunicul G ar putea încălca acum proprietatea 2 (nodul rădăcină este negru) sau proprietatea 4 (ambii copii ai fiecărui nod roșu sunt negri), deoarece ar putea avea un tată roșu. Pentru a rezolva problema, procedura trebuie repetată recursiv pe G pornind de la cazul 1. Rețineți că acesta este singurul apel recursiv și că se întâmplă înainte de orice rotație, ceea ce dovedește că va exista un număr constant de rotații.

 void insert_case3 ( nod n ) {
     if ( uncle ( n ) ! = NULL && uncle ( n ) -> color == RED ) {
         n -> părinte -> culoare = NEGRU ;
         uncle ( n ) -> culoare = BLACK ;
         bunic ( n ) -> culoare = RED ;
         insert_case1 ( bunicul ( n ));
     }
     altceva
         insert_case4 ( n );
 }

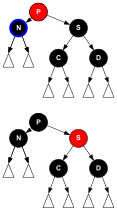
Notă: În următoarele cazuri, se presupune că nodul părinte P este copilul stâng al părintelui său. Dacă ar fi un copil drept, stânga și dreapta ar trebui inversate în cazurile 4 și 5.

Cazul 4: tatăl P este roșu, dar unchiul U este negru; noul nod N este copilul potrivit al lui P , iar P la rândul său este copilul stâng al lui G. În acest caz, se efectuează o rotație la stânga care schimbă rolurile noului nod N și al tatălui P ; apoi ne ocupăm de fostul nod părinte P folosind cazul 5 (schimbând numele N și P ). Acest lucru face ca unele căi (cele etichetate „1” în grafic) să treacă acum prin noul nod fără ca acest lucru să se întâmple mai întâi; dar ambele noduri sunt roșii, deci proprietatea 5 (toate căile de la un nod dat la frunzele sale conțin același număr de noduri negre) nu este încălcată. Proprietatea 4 (ambii copii ai fiecărui nod roșu sunt negri) este încă încălcată, dar poate fi rezolvată continuând cu cazul 5.

 void insert_case4 ( nod n ) {
     if ( n == n -> părinte -> dreapta && n -> părinte == bunic ( n ) -> stânga ) {
         rotate_left ( n -> parent );
         n = n -> stânga ;
     } else if ( n == n -> părinte -> stânga && n -> părinte == bunic ( n ) -> dreapta ) {
         rotate_right ( n -> parent );
         n = n -> dreapta ;
     }
         insert_case5 ( n );
 }

Cazul 5: tatăl P este roșu, dar bunicul G și unchiul U sunt negri, noul nod N este copilul stâng al lui P , iar P este copilul stâng al lui G. În acest caz, se efectuează o rotație dreaptă pe G ; rezultatul este un copac în care fostul tată P este acum tatăl noului nod N și al fostului bunic G. Știm că G este negru, pentru că altfel fostul său fiu P nu ar fi putut fi roșu. Culorile lui P și G sunt apoi schimbate, iar arborele rezultat îndeplinește proprietatea 4 (ambii copii ai fiecărui nod roșu sunt negri). Proprietatea 5 (toate căile care încep de la un nod dat spre frunzele sale conțin același număr de noduri negre) rămâne satisfăcută la rândul său, deoarece toate căile care treceau anterior printr-unul dintre aceste trei noduri treceau mai întâi prin G , acum prin P. În orice caz, este singurul nod negru dintre cele trei.

 void insert_case5 ( nod n ) {
     n -> părinte -> culoare = NEGRU ;
     bunic ( n ) -> culoare = RED ;
     if ( n == n -> părinte -> stânga && n -> părinte == bunic ( n ) -> stânga ) {
         rotate_right ( bunicul ( n ));
     } altceva {
         / * Aici, n == n-> părinte-> dreapta && n-> părinte == bunic (n) -> dreapta * /
         rotate_left ( bunic ( n ));
     }
 }

Rețineți că toate apelurile din cod utilizează recursivitate în coadă.

Anulare

Într-un arbore de căutare binar normal, atunci când ștergeți un nod care are doi copii non-frunze, vă puteți regăsi în două situații: fie valoarea maximă se află în subarborele din stânga, fie valoarea minimă se află în subarborele din dreapta, atunci această valoare este mutat la nod pentru a fi șters. În acest moment ștergem nodul din care am copiat valoarea, din care trebuie să avem mai puțin de doi copii non-frunze. Deoarece simpla copiere a unei valori nu încalcă nici o proprietate roșu-negru, problema se rezumă la ștergerea unui nod cu cel mult un copil. Nu contează dacă nodul este cel pe care ați dorit inițial să îl ștergeți sau nodul a cărui valoare ați copiat-o.

Dacă ștergeți un nod roșu, pur și simplu îl înlocuiți cu copilul său, care trebuie să fie negru. Toate căile care au trecut prin nodul șters vor trece acum printr-un nod roșu mai puțin și atât părintele, cât și copilul nodului șters trebuie să fie negre, deci proprietățile 3 (toate frunzele, inclusiv cele nule, sunt negre) și 4 (ambii copii din fiecare nod roșu sunt negre) sunt încă valabile. Un alt caz simplu este atunci când nodul șters este negru și copilul său este roșu. Ștergerea unui nod negru ar putea încălca proprietățile 4 (ambii copii ai fiecărui nod roșu sunt negri) și 5 (toate căile de la un nod dat la frunzele sale conțin același număr de noduri negre), dar dacă da colorează fiul negru, ambele proprietăți sunt retinut.

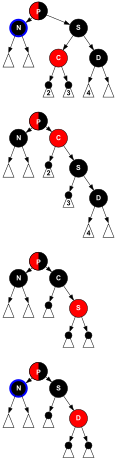
Cazul complex este atunci când atât nodul de șters cât și copilul sunt negre. Primul pas este de a înlocui nodul care trebuie șters cu copilul. Apoi îl vom numi pe N fiul din noua poziție și pe S fratele său (celălalt fiu al noului său tată). În diagrama de mai jos, vom folosi și P pentru a indica noul tată al lui N , iar si N este copilul stâng, C ca copilul stâng al lui S și D pentru copilul drept; si N este copilul potrivit, C ca copilul potrivit al lui S și D pentru copilul stâng. (Este clar că S nu poate fi o frunză.)

Atenție : între cele două cazuri, schimbăm roluri și etichete ale nodurilor, dar în orice caz, fiecare etichetă continuă să reprezinte același nod pe care îl reprezenta la începutul cazului. Orice culoare prezentată în diagramă este presupusă sau implicată de ipotezele de mai sus. Albul reprezintă o culoare necunoscută (roșu sau negru indiferent).

Vom găsi frații folosind această funcție:

 nod frate ( nod n ) {
      if ( n == n -> părinte -> stânga )
          returnează n -> părinte -> dreapta ;
      altceva
          returnează n -> părinte -> stânga ;
 }

Putem efectua pașii descriși mai sus folosind următorul cod, unde funcția replace_node înlocuiește child în poziția n a arborelui. Pentru comoditate, codul prezentat în această secțiune va presupune că frunzele nule sunt reprezentate de obiecte nod, mai degrabă decât NULL (codul din secțiunea Insert funcționează în ambele cazuri).

 void delete_one_child ( nod n ) {
     / * Se presupune că n are cel mult un copil non-nul * /
     nod copil = ( is_leaf ( n -> right )) ? n -> stânga : n -> dreapta ;
     substitut_node ( n , copil );
     if ( n -> culoare == NEGRU ) {
         if ( copil -> culoare == RED )
             copil -> culoare = NEGRU ;
         altceva
             delete_case1 ( copil );
     }
     gratuit ( n );
 }

Atenție : dacă N este o frunză nulă și nu vrem să o reprezentăm ca obiect nod, putem modifica algoritmul apelând mai întâi delete_case1 () pe părinte (nodul pe care dorim să îl ștergem, n în codul de mai sus) și ștergeți-l ulterior. Putem face acest lucru deoarece tatăl este negru, deci se comportă la fel ca o frunză nulă (uneori numită frunză „fantomă”). Și îl putem șterge în siguranță în cele din urmă, deoarece n va rămâne o frunză după toate operațiunile, așa cum se arată mai sus.

Dacă atât N, cât și tatăl original sunt negre, ștergerea tatălui va face ca traseele prin N să aibă un nod negru mai puțin decât căile care nu trec. Deoarece acest lucru ar încălca proprietatea 5 (Toate căile de la orice nod la frunzele subiacente conțin același număr de noduri negre), arborele trebuie reechilibrat. Există multe cazuri de luat în considerare.

Cazul 1: N este noua rădăcină. În acest caz, am terminat. Am eliminat un nod negru din fiecare cale, iar noua rădăcină este neagră, astfel încât toate proprietățile sunt satisfăcute.

 void delete_case1 ( nod n ) {
     if ( n -> părinte == NULL )
         întoarcere ;
     altceva
         delete_case2 ( n );
 }

Atenție : În cazurile 2, 5 și 6, să presupunem că N este copilul stâng al tatălui său P. Dacă ar fi copilul potrivit, stânga și dreapta ar fi inversate mai târziu în discuție. Din nou, codul eșantion ia în considerare ambele cazuri.

Cazul 2: S este roșu. În acest caz, inversăm culorile lui P și S și efectuăm o rotație la stânga pe P , rotind S în bunicul lui N. Rețineți că P trebuie să fie neagră, deoarece are un copil roșu. Deși toate căile au același număr de noduri negre, acum N are un frate negru și un tată roșu, deci putem continua cu pașii 4, 5 sau 6 (noul frate este negru pentru că a fost odată fiul lui S roșu) . În acest din urmă caz, îl redenumim pe S ca noul frate al lui N.

 void delete_case2 ( nod n ) {
     if ( frate ( n ) -> culoare == RED ) {
         n -> părinte -> culoare = RED ;
         frate ( n ) -> culoare = NEGRU ;
         if ( n == n -> părinte -> stânga )
             rotate_left ( n -> parent );
         altceva
             rotate_right ( n -> parent );
     }
     delete_case3 ( n );
 }

Cazul 3: P, S și S este fiul negrilor. În acest caz, pur și simplu recolorăm S roșu. Rezultatul este că toate căile care trec prin S , adică toate cele care nu trec prin N , au un nod negru mai puțin. Deoarece ștergerea părintelui inițial al lui N elimină un nod negru de pe căile care trec prin N , lucrurile sunt fixate. Cu toate acestea, toate căile care trec prin P au acum mai puțin negru decât cele care nu, deci proprietatea 5 (Toate căile de la orice nod până la frunzele subiacente conțin același număr de noduri negre) este încă încălcată. Pentru a corecta această problemă, efectuăm din nou echilibrarea pe P , începând de la cazul 1.

 void delete_case3 ( nod n ) {
     if ( n -> părinte -> culoare == NEGRU &&
         frate ( n ) -> culoare == NEGRU &&
         frate ( n ) -> stânga -> culoare == NEGRU &&
         frate ( n ) -> dreapta -> culoare == NEGRU )
     {
         frate ( n ) -> culoare = RED ;
         delete_case1 ( n -> părinte );
     }
     altceva
         delete_case4 ( n );
 }

Cazul 4: S și fiul ei sunt negri, dar P este roșu. În acest caz schimbăm culorile S și P. Această mișcare nu schimbă numărul de negri din căile care nu trec prin N , ci adaugă unul celor care trec prin ea, permițând ștergerea unui nod negru în acele căi.

 void delete_case4 ( nod n ) {
     if ( n -> părinte -> culoare == RED &&
         frate ( n ) -> culoare == NEGRU &&
         frate ( n ) -> stânga -> culoare == NEGRU &&
         frate ( n ) -> dreapta -> culoare == NEGRU )
     {
         frate ( n ) -> culoare = RED ;
         n -> părinte -> culoare = NEGRU ;
     }
     altceva
         delete_case5 ( n );
 }

Cazul 5: S este negru, copilul stâng al lui S este roșu, copilul drept este negru, iar N este copilul stâng al tatălui său. În acest caz, ne rotim dreapta pe S , astfel încât fiul stâng al lui S devine tatăl său, iar N noul frate. Schimbăm culorile lui S și ale noului ei tată. Toate căile au încă același număr de noduri negre, dar acum N are un frate negru al cărui copil drept este roșu, așa că ne întoarcem la cazul 6. Nici N, nici tatăl ei nu sunt afectați de această transformare.

(Din nou, pentru cazul 6, îl redenumim pe S ca noul frate al lui N ).

 void delete_case5 ( nod n ) {
     if ( n == n -> părinte -> stânga &&
         frate ( n ) -> culoare == NEGRU &&
         frate ( n ) -> stânga -> culoare == RED &&
         frate ( n ) -> dreapta -> culoare == NEGRU )
     {
         frate ( n ) -> culoare = RED ;
         frate ( n ) -> stânga -> culoare = NEGRU ;
         rotate_right ( frate ( n ));
     }
     altfel dacă ( n == n -> părinte -> dreapta &&
              frate ( n ) -> culoare == NEGRU &&
              frate ( n ) -> dreapta -> culoare == RED &&
              frate ( n ) -> stânga -> culoare == NEGRU )
     {
         frate ( n ) -> culoare = RED ;
         frate ( n ) -> dreapta -> culoare = NEGRU ;
         rotate_left ( frate ( n ));
     }
     delete_case6 ( n );
 }

Cazul 6: S este negru, fiul său drept este roșu, iar N este fiul stâng al tatălui său . În acest caz, ne rotim spre stânga pe P , astfel încât S devine tatăl lui P și copilul drept al lui S. Să schimbăm culorile lui P și S , iar culoarea dreaptă a copilului lui S este neagră. Subarborele va avea aceeași culoare ca și rădăcina sa, astfel încât proprietățile 4 (ambii copii ai unui nod roșu sunt negri) și 5 (Toate căile de la orice nod la frunzele subiacente conțin același număr de noduri negre) nu sunt încălcate. Cu toate acestea, N are un strămoș negru suplimentar: dacă P a devenit negru, dacă P a fost negru și S a fost adăugat ca bunic negru. Deci, cărările care traversează N întâlnesc un negru suplimentar.

În același timp, dacă o cale nu traversează N , există două posibilități:

Crucea noului frate al lui N. Deci, trebuie să treacă prin S și P , atât înainte, cât și după modificări, care au schimbat pur și simplu culoarea (adică numărul de negri nu s-a schimbat).
Treceți prin noul unchi al lui N , fiul din dreapta al lui S. În acest caz, înainte de a-l traversa pe S, tatăl lui S și fiul drept al lui S, dar acum doar prin S, care a luat culoarea fostului părinte și fiul drept al lui S, s-au schimbat de la roșu la negru. Rezultatul este că numărul de negri nu sa schimbat.

Cu toate acestea, numărul de noduri negre pe aceste căi nu se modifică. Așa că am restabilit proprietățile 4 (Ambii copii ai unui nod roșu sunt negri) și 5 (Toate căile de la orice nod la frunzele subiacente conțin același număr de noduri negre). Nodul alb, în diagramă, poate fi roșu sau negru, important este că are aceeași culoare înainte și după transformare.

 void delete_case6 ( nod n ) {
     frate ( n ) -> culoare = n -> părinte -> culoare ;
     n -> părinte -> culoare = NEGRU ;
     if ( n == n -> părinte -> stânga ) {
         / * Aici, frate (n) -> dreapta-> culoare == RED * /
         frate ( n ) -> dreapta -> culoare = NEGRU ;
         rotate_left ( n -> parent );
     }
     altceva
     {
         / * Aici, frate (n) -> stânga-> culoare == RED * /
         frate ( n ) -> stânga -> culoare = NEGRU ;
         rotate_right ( n -> parent );
     }
 }

Din nou, funcția folosește o recursie a cozii ( recursie a cozii), astfel încât algoritmul să fie încă la locul său. De asemenea, nu se efectuează apeluri recursive după o rotație, ceea ce face ca numărul de rotație să fie constant (maxim 3).

Dovada limitelor asimptotice

Un copac roșu-negru care are $n$ ${\ displaystyle n}$ $n$ nodurile interne au o înălțime $O(\lg(n))$ ${\ displaystyle O (\ lg (n))}$ $O (\ lg (n))$ .

Definiții:

$h(v)$ ${\ displaystyle h (v)}$ $h (v)$ = înălțimea subarborelui înrădăcinat în $v$ ${\ displaystyle v}$ $v$ .
$bh(v)$ ${\ displaystyle bh (v)}$ $bh (v)$ = numărul de noduri negre (fără numărare $v$ ${\ displaystyle v}$ $v$ dacă este negru) din $v$ ${\ displaystyle v}$ $v$ la orice frunză din subarborele (numită înălțime neagră).

Lemă: Un subarborel înrădăcinat în v are cel puțin $2^{bh(v)}-1$ ${\ displaystyle 2 ^ {bh (v)} - 1}$ $2 ^ {{bh (v)}} - 1$ noduri interne.

Dovada lemei (prin inducție):

Angajat: $h(v)=0$ ${\ displaystyle h (v) = 0}$ $h (v) = 0$

De sine $v$ ${\ displaystyle v}$ $v$ are înălțimea zero trebuie să fie goală, prin urmare $bh(v)=0$ ${\ displaystyle bh (v) = 0}$ $bh (v) = 0$ . Prin urmare:

$2^{bh(v)}-1=2^{0}-1=1-1=0$ ${\ displaystyle 2 ^ {bh (v)} - 1 = 2 ^ {0} -1 = 1-1 = 0}$ $2 ^ {{bh (v)}} - 1 = 2 ^ {{0}} - 1 = 1-1 = 0$

Ipoteză inductivă: $v$ ${\ displaystyle v}$ $v$ astfel încât $h(v)=k$ ${\ displaystyle h (v) = k}$ $h (v) = k$ , are $2^{bh(v)}-1$ ${\ displaystyle 2 ^ {bh (v)} - 1}$ $2 ^ {{bh (v)}} - 1$ nodurile interne implică faptul că $v^{'}$ ${\ displaystyle v '}$ $v '$ astfel încât $h(v')=k+1$ ${\ displaystyle h (v ') = k + 1}$ $h (v ') = k + 1$ are $2^{bh(v')}-1$ ${\ displaystyle 2 ^ {bh (v ')} - 1}$ $2 ^ {{bh (v ')}} - 1$ noduri interne.

De cand $v^{'}$ ${\ displaystyle v '}$ $v '$ are $h(v')>0$ ${\ displaystyle h (v ')> 0}$ $h (v ')> 0$ este un nod intern. Are doi fii a căror înălțime neagră este bh ( $v^{'}$ ${\ displaystyle v '}$ $v '$ ) sau $bh(v')-1$ ${\ displaystyle bh (v ') - 1}$ $bh (v ') - 1$ (în funcție de care $v^{'}$ ${\ displaystyle v '}$ $v '$ fie roșu, fie negru). Prin ipoteză inductivă, fiecare copil are cel puțin $2^{bh(v')-1}-1$ ${\ displaystyle 2 ^ {bh (v ') - 1} -1}$ $2 ^ {{bh (v ') - 1}} - 1$ noduri interne, deci $v^{'}$ ${\ displaystyle v '}$ $v '$ are:

$2^{bh(v')-1}-1+2^{bh(v')-1}-1+1=2^{bh(v')}-1$ ${\ displaystyle 2 ^ {bh (v ') - 1} -1 + 2 ^ {bh (v') - 1} -1 + 1 = 2 ^ {bh (v ')} - 1}$ $2 ^ {{bh (v ') - 1}} - 1 + 2 ^ {{bh (v') - 1}} - 1 + 1 = 2 ^ {{bh (v ')}} - 1$

noduri interne.

Folosind această lemă putem demonstra că înălțimea copacului este logaritmică. Deoarece cel puțin jumătate din nodurile oricărei căi de la rădăcină la frunză sunt negre (proprietatea 4 a unui copac roșu-negru), înălțimea neagră a rădăcinii este de cel puțin h (rădăcină) / 2. Din lemă obținem:

$n\geq 2^{h(root) \over 2}-1\leftrightarrow \;\lg {(n+1)}\geq {h(root) \over 2}\leftrightarrow \;h(root)\leq 2\lg {(n+1)}$ ${\ displaystyle n \ geq 2 ^ {h (root) \ over 2} -1 \ leftrightarrow \; \ lg {(n + 1)} \ geq {h (root) \ over 2} \ leftrightarrow \; h (root ) \ leq 2 \ lg {(n + 1)}}$ $n \ geq 2 ^ {{{h (root) \ over 2}}} - 1 \ leftrightarrow \; \ lg {(n + 1)} \ geq {h (root) \ over 2} \ leftrightarrow \; h ( rădăcină) \ leq 2 \ lg {(n + 1)}$

Deci înălțimea rădăcinii este $O(\lg(n))$ ${\ displaystyle O (\ lg (n))}$ $O (\ lg (n))$ .

Extinderea RB-Alberi

Extensia unui RB-Tree este o practică care constă în adăugarea de informații suplimentare la noduri, care permit susținerea eficientă a altor operațiuni în afară de cele standard.

Arborii de selecție T (sau arborii statistici de comandă ), de exemplu, sunt arbori roșu-negri care stochează în fiecare nod x dimensiunea subarborelui înrădăcinat în x în sine (cu excepția frunzelor). Ca rezultat, ei sunt capabili să caute un element cu un rang dat sau să determine rangul unui element dat, cu o complexitate O (log n ) în cel mai rău caz ^[1] .

Copiii roșii-negri înțelepți, pe de altă parte, garantează o mai mare eficiență în tratarea blocurilor de elemente adiacente. Au o structură similară cu arborii de selecție T, dar nodurile stochează doar dimensiunea subarborelui din stânga. Acestea se disting mai mult prin modul în care se desfășoară operațiunile principale ^[2] .

Notă

^ Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford, Introducere în algoritmi , ediția a III-a, MIT Press, 2009 [1990] , ISBN 978-0-262-03384-8 .
^ Alberto Boffi, O modalitate eficientă de a gestiona blocuri de date cu Wise Red-Black Trees , iunie 2021.

Alte proiecte

Wikimedia Commons conține imagini sau alte fișiere despre RB-Albero

linkuri externe

Surse

( RO ) Mathworld: Red-Black Tree , la mathworld.wolfram.com .
( EN ) San Diego State University: CS 660: Note on Red-Black Trees , de Roger Whitney
(EN) Thomas H. Cormen , Charles E. Leiserson , Ronald L. Rivest și Clifford Stein .Introducere în algoritmi , ediția a doua. MIT Press și McGraw-Hill, 2001. ISBN 0-262-03293-7 . Capitolul 13: Copaci roșii-negri, pp. 273 - 301.

Demonstrații

Animație a copacului roșu-negru , demonstrație a cazului rău de inserție
aiSee: Algoritm de sortare , GIF animat care arată inserția (200KB)

Implementări

RBT: Biblioteca Arborelui Roșu-Negru , la efsa.sourceforge.net .
libredblack: bibliotecă C pentru copaci roșu-negri , la libredblack.sourceforge.net .
Alte implementări C , pe web.mit.edu . Adus la 10 septembrie 2006 (arhivat din original la 14 februarie 2008) .
Implementare cu cod Java în java.util.TreeMap , la javaresearch.org . URL consultato il 10 settembre 2006 (archiviato dall' url originale il 20 ottobre 2007) .

Portale Informatica : accedi alle voci di Wikipedia che trattano di Informatica

[1] Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford, Introducere în algoritmi , ediția a III-a, MIT Press, 2009 [1990] , ISBN 978-0-262-03384-8 .

[2] Alberto Boffi, O modalitate eficientă de a gestiona blocuri de date cu Wise Red-Black Trees , iunie 2021.

[1]

[2]

V · D · M Strutture dati
Tipi	Collezione · Container
Astratte	Array associativo ( Multimap ) · Lista · Pila · Coda ( Deque ) · Coda di priorità · Set ( Multiset · Mfset )
Array	Bit array · Buffer circolare · Array dinamico · Hash table · Array sparso
Collegate	Lista di associazioni · Lista concatenata · Skip list · Unrolled linked list · XOR linked list
Alberi	B-albero · Albero binario di ricerca ( Albero AA · Albero AVL · RB-Albero · Albero binario di ricerca bilanciato · Albero splay ) · Heap ( Heap binario · Heap binomiale · Heap di Fibonacci ) · Albero di Merkle · Albero SPQR · Albero PQ · Albero indicizzato binario
Grafi	Diagramma binario di decisione · Digrafo aciclico · Automa a stati finiti deterministico aciclico
Alberi di partizionamento dei dati spaziali	Albero quadramentale · M-tree · R-tree ( R* tree · R+ tree ) · X-tree
Lista di strutture dati