Solid platonic

În matematică , în special în geometria solidă , termenul solid platonic este sinonim cu solid regulat și cu poliedru regulat convex și indică un poliedru convex care are poligoane regulate congruente pentru fețe (adică exact superpozabile) și care are toate muchiile și vârfurile echivalente . Rezultă că sale unghiuri , de asemenea , au aceeași amplitudine.

Cele cinci poliedre regulate convexe (solide platonice)
tetraedru	hexaedru sau cub	octaedru	dodecaedru	icosaedru
( Modelul 3D )	( Modelul 3D )	( Modelul 3D )	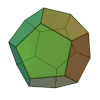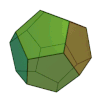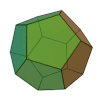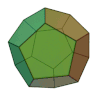( Modelul 3D )	( Modelul 3D )

Numele fiecărei figuri este derivat din numărul fețelor sale, respectiv 4, 6, 8, 12 și 20.

fundal

Modelul lui Kepler a sistemului solar cu ajutorul solidelor platonice

Regularitățile solidele platonice sunt extrem de sugestive: acest lucru a însemnat că acestea au fost studiate inca din cele mai vechi timpuri, de multe ori în căutarea sensuri ascunse în ele și atribuindu-le ezoterice valori.

Ei au fost studiate de Pitagora și Platon . Acestea din urmă, în Timeu , asociat fiecăruia dintre ei unul dintre cele patru elemente : a tetraedrul focul , la cubul supraterană , toate „ octaedru l“ aer , toate „ icosaedru l“ apă , ^[1] în timp ce în Phaedon credea că dodecaedru au forma universului : ^[2]

„Pământul adevărat pentru cei care îl privesc de sus prezintă figura acelor bile de piele cu doisprezece pene, pestrițe, deosebite în culoare”.

Platon a găsit în aceste solide prezența unei raționalități superioare ascunse în realitatea comună, atribuindu-le funcția de intermediari între perfecțiunea lumii hiperuranice și mutabilitatea fenomenelor naturale, ^[3] putând astfel afirma că „Dumnezeu geometrizează întotdeauna ". ^[4]

Demonstrarea și construirea cinci poliedre regulate și descoperirea a două dintre ele: octaedru și icosaedru ^[5] ^[6] este atribuită Teeteto , discipol al matematicianului Teodor și un elev al lui Platon .

Poliedrele regulate au fost apoi studiate de geometrii greco-alexandrieni. Construcția acestor solide sunt cuprinse în cartea a treisprezecea a elementelor de Euclid . ^[7] Propunerea 13 descrie construcția tetraedru regulat, propoziția 14 este dedicat octaedru regulat, propoziția 15 la cub, propoziția 16 la icosaedru regulată și propoziția 17 la dodecaedru regulat.

Interesul pentru solide platonice a fost , de asemenea , plin de viață , printre matematicieni și artiști renascentiști: Piero della Francesca (în tratat De corporibus regularibus), Luca Pacioli (care le -a inclus în De Divinei Proportione) și , ulterior , Niccolò Tartaglia și Rafael a studiat proprietățile lor metrice. Bombelli .

Kepler pur, în lucrarea sa Mysterium cosmographicum , a reluat, în termeni diferiți, investigația lui Platon asupra semnificației poliedrelor regulate în structura lumii: el a argumentat, de fapt, că poliedrele platonice erau strâns legate de proporțiile armonioase care îl caracterizează. . ^[8]

«Pământul este sfera care măsoară pe toate celelalte. Circumscrieți-i un dodecaedru: sfera care îl include va fi Marte [în sensul că conține orbita, care la acea vreme se credea încă circulară, a mișcării sale în jurul soarelui]. Circumscrieți un tetraedru către Marte: sfera care îl include va fi Jupiter. Circumscrieți un cub lui Jupiter: sfera care îl include va fi Saturn. Înscrie acum un icosaedru pe Pământ: sfera înscrisă pe el va fi Venus. Înscrieți un octaedru la Venus: sfera înscrisă la acesta va fi Mercur. Ai motivul numărului de planete "

Chiar și arta are numeroase referințe la solidele platonice: printre cele mai faimoase exemple, se numără Salvador Dalí (care a folosit-o în Corpus Hypercubus și în Ultima Sa cină , așezat într-un dodecaedru ) și Maurits Cornelis Escher , care a exploatat proprietățile sale geometrice pentru a realiza unele a teselelor sale.

De ce sunt doar cinci?

Poliedrele regulate nu pot fi mai mari de cinci.

Dovadă cu unghiul

{3.3} Defect de 180 °	{3.4} Defect de 120 °	{3.5} Defect de 60 °	{3.6} Defect de 0 °
{4.3} Defect de 90 °	{4.4} Defect de 0 °	{5.3} Defect de 36 °	{6.3} Defect de 0 °

Numai echilateral triunghiul, pătrat și regulate pentagon poate fi fețele de poliedre regulate. Explicația este dată nouă de Euclid în Elemente :

În fiecare vârf trebuie să convergă cel puțin trei fețe (de fapt, nu există colțuri formate din unul sau doi poligoane).
În orice angoloide suma unghiurilor fețelor care delimitează aceasta trebuie să fie mai mic decât un unghi rotund, altfel cifra este plat; cantitatea care lipsește pentru a forma 360 ° este definit ca un defect .
Deoarece sunt necesare cel puțin trei fețe pentru fiecare unghi și deoarece sunt poligoane regulate, fiecare vârf al fiecărei fețe poate contribui la unghiul cu maxim 360 ° ÷ 3 = 120 °.
Poligoanele cu șase sau mai multe laturi au unghiuri mai mari sau egale cu 120 °, prin urmare numai triunghiul, pătratul și pentagonul pot forma solide platonice. Fiecare dintre aceste figuri se comportă diferit:
1. Fețele triunghiulare: unghiurile unui triunghi echilateral au o lățime de 60 °, deci 3, 4 sau 5 triunghiuri pot insista asupra unui vârf al solidului; se formează tetraedrul, octaedrul și respectiv icosaedrul.
2. Fețe pătrate: unghiurile unui pătrat sunt de 90 ° larg, prin urmare , este posibil să se facă 3 fețe întâlnesc într - un nod (3 x 90 = 270) , pentru a obține un cub .
3. Fețele pentagonale: fiecare colț al unui pentagon obișnuit măsoară 108 °. Prin urmare, este posibil să se facă 3 fețe întâlnesc într - un nod (3 x 108 = 324) obținerea unui dodecaedru regulat .

Astfel se obțin cele cinci solide platonice posibile. ^[9]

Dovadă geometrică

Este posibil să se arate că nu există mai mult de cinci poliedre regulate , chiar pornind de la relația Euler . Având în vedere un poliedru cu fețe F, fiecare dintre care este un poligon regulat cu n laturi și în care, la fiecare nod, r muchiile se întâlnesc, care sunt , în total S.

Înmulțind numărul laturilor fiecărei fețe cu numărul fețelor poliedrului obținem dublul totalității muchiilor (fiecare margine este numărată de două ori, o dată pe prima față și o dată pe fața atașată la prima pentru acea margine):

nF=2S

{\ displaystyle nF = 2S}

nF = 2S

mai mult decât atât, totalitatea marginilor , înmulțită cu doi este egal cu numărul de vârfuri V în înmulțit cu numărul r de margini care se întâlnesc în ele, pentru că fiecare muchie unește două noduri unul de altul:

rV=2S

{\ displaystyle rV = 2S}

rV = 2S

așa că primești

F={\frac {2S}{n}}

{\ displaystyle F = {\ frac {2S} {n}}}

F = {\ frac {2S} {n}}

V={\frac {2S}{r}}

{\ displaystyle V = {\ frac {2S} {r}}}

V = {\ frac {2S} {r}}

și înlocuind aceste valori în caracteristica Euler-Poincare :

V+F-S=2

{\ displaystyle V + FS = 2}

V + F-S = 2

{\frac {2S}{r}}+{\frac {2S}{n}}-S=2

{\ displaystyle {\ frac {2S} {r}} + {\ frac {2S} {n}} - S = 2}

{\ frac {2S} {r}} + {\ frac {2S} {n}} - S = 2

și, prin împărțirea 2S, vom ajunge la

{\frac {1}{r}}+{\frac {1}{n}}-{\frac {1}{2}}={\frac {1}{S}}

{\ displaystyle {\ frac {1} {r}} + {\ frac {1} {n}} - {\ frac {1} {2}} = {\ frac {1} {S}}}

{\ frac {1} {r}} + {\ frac {1} {n}} - {\ frac {1} {2}} = {\ frac {1} {S}}

Ambele n și r trebuie să fie mai mare sau egal cu trei, deoarece un poligon trebuie să aibă cel puțin trei laturi și cel puțin trei părți trebuie să îndeplinească la vârful fiecăruia dintre colțurile unui poliedru.

Mai mult, n și r nu poate fi atât egal cu patru, deoarece , în acest caz , primul membru al ecuației ar fi egal cu 0, în timp ce 1 / S este pozitiv. Dacă n și r au fost apoi simultan mai mare de trei, S trebuie să fie negativ; această posibilitate este deci exclusă și cel puțin una trebuie să fie trei.

În cazul în care n = 3, avem

{\frac {1}{3}}+{\frac {1}{r}}-{\frac {1}{2}}={\frac {1}{S}}

{\ displaystyle {\ frac {1} {3}} + {\ frac {1} {r}} - {\ frac {1} {2}} = {\ frac {1} {S}}}

{\ frac {1} {3}} + {\ frac {1} {r}} - {\ frac {1} {2}} = {\ frac {1} {S}}

{\frac {1}{r}}-{\frac {1}{6}}={\frac {1}{S}}

{\ displaystyle {\ frac {1} {r}} - {\ frac {1} {6}} = {\ frac {1} {S}}}

{\ frac {1} {r}} - {\ frac {1} {6}} = {\ frac {1} {S}}

și , prin urmare , r poate fi egal cu 3, 4 sau 5, cazuri care corespund , respectiv , la numai tetraedru , octaedru și icosaedru .

În mod similar, în cazul în care r = 3, atunci n poate lua numai valorile 3, 4 sau 5. Putem renunța la 3 pentru că l - am luat în considerare în cazul precedent; cazuri 4 și 5 rămân, care corespund cubul si dodecaedrul .

Nu există alte cazuri posibile și, prin urmare, există cel mult cinci poliedre regulate.

Proprietăți combinatorii

Un poliedru convex este un solid platonic dacă:

toate fețele sale sunt congruente convexe regulate poligoane;
niciuna dintre fețele sale nu se intersectează cu celelalte, cu excepția marginilor;
același număr de fețe se întâlnesc la fiecare vârf.

Fiecare cutie solid platonic fi caracterizat printr - o {p, q} unde notație

p = numărul de laturi ale fiecărei fețe (sau numărul de noduri ale fiecărei fețe) e

q = numărul fețelor întâlnite la fiecare nod (sau numărul de muchii întâlnite la fiecare nod).

Acronimul {p, q}, numita notatie Schläfli , dă o combinatorie descriere a poliedrului. Notarea lui Schläfli este explicată în tabelul de mai jos.

Poliedru	Vârfuri	Margini	Fețe	Notare Schläfli	Poziţie a vârfurilor
tetraedru	4	6	4	{3, 3}	3.3.3
cub	8	12	6	{4, 3}	4.4.4
octaedru	6	12	8	{3, 4}	3.3.3.3
dodecaedru	20	30	12	{5, 3}	5.5.5
icosaedru	12	30	20	{3, 5}	3.3.3.3.3

Proprietăți metrice ale solidelor platonice

Următorul tabel grupează unele dintre principalele proprietăți metrice ale solidelor platonice, măsura marginii unui poliedru fiind setată egală cu $d$ ${\ displaystyle d}$ $d$ .

Nume	Raza sferei			Suprafaţă	Volum
Nume	Înscris	Circumscris	Tangente marginile	Suprafaţă	Volum
Tetraedru	${\frac {\sqrt {6}}{12}}d$ ${\ displaystyle {\ frac {\ sqrt {6}} {12}} d}$ ${\ frac {{\ sqrt {6}}} {12}} d$	${\frac {\sqrt {6}}{4}}d$ ${\ displaystyle {\ frac {\ sqrt {6}} {4}} d}$ ${\ frac {{\ sqrt {6}}} {4}} d$	${\frac {\sqrt {2}}{4}}d$ ${\ displaystyle {\ frac {\ sqrt {2}} {4}} d}$ ${\ frac {{\ sqrt {2}}} {4}} d$	${\sqrt {3}}d^{2}$ ${\ displaystyle {\ sqrt {3}} d ^ {2}}$ ${\ sqrt {3}} d ^ {2}$	${\frac {\sqrt {2}}{12}}d^{3}$ ${\ displaystyle {\ frac {\ sqrt {2}} {12}} d ^ {3}}$ ${\ frac {{\ sqrt {2}}} {12}} d ^ {3}$
cub	${\frac {1}{2}}d$ ${\ displaystyle {\ frac {1} {2}} d}$ ${\ frac {1} {2}} d$	${\frac {\sqrt {3}}{2}}d$ ${\ displaystyle {\ frac {\ sqrt {3}} {2}} d}$ ${\ frac {{\ sqrt {3}}} {2}} d$	${\frac {\sqrt {2}}{2}}d$ ${\ displaystyle {\ frac {\ sqrt {2}} {2}} d}$ ${\ frac {{\ sqrt {2}}} {2}} d$	$6d^{2}$ ${\ displaystyle 6d ^ {2}}$ $6d ^ {2}$	$d^{3}$ ${\ displaystyle d ^ {3}}$ $d ^ {3}$
Octaedru	${\frac {\sqrt {6}}{6}}d$ ${\ displaystyle {\ frac {\ sqrt {6}} {6}} d}$ ${\ frac {{\ sqrt {6}}} {6}} d$	${\frac {\sqrt {2}}{2}}d$ ${\ displaystyle {\ frac {\ sqrt {2}} {2}} d}$ ${\ frac {{\ sqrt {2}}} {2}} d$	${\frac {1}{2}}d$ ${\ displaystyle {\ frac {1} {2}} d}$ ${\ frac {1} {2}} d$	$2{\sqrt {3}}d^{2}$ ${\ displaystyle 2 {\ sqrt {3}} d ^ {2}}$ $2 {\ sqrt {3}} d ^ {2}$	${\frac {\sqrt {2}}{3}}d^{3}$ ${\ displaystyle {\ frac {\ sqrt {2}} {3}} d ^ {3}}$ ${\ frac {{\ sqrt {2}}} {3}} d ^ {3}$
Dodecaedru	${\frac {1}{20}}{\sqrt {(10(25+11{\sqrt {5}})}}d$ ${\ displaystyle {\ frac {1} {20}} {\ sqrt {(10 (25 + 11 {\ sqrt {5}})}} d}$ ${\ frac {1} {20}} {\ sqrt {(10 (25 + 11 {\ sqrt {5}})}} d$	${\frac {\sqrt {3}}{4}}(1+{\sqrt {5}})d$ ${\ displaystyle {\ frac {\ sqrt {3}} {4}} (1 + {\ sqrt {5}}) d}$ ${\ frac {{\ sqrt {3}}} {4}} (1 + {\ sqrt {5}}) d$	${\frac {1}{4}}(3+{\sqrt {5}})d$ ${\ displaystyle {\ frac {1} {4}} (3 + {\ sqrt {5}}) d}$ ${\ frac {1} {4}} (3 + {\ sqrt {5}}) d$	$3{\sqrt {25+10{\sqrt {5}}}}d^{2}$ ${\ displaystyle 3 {\ sqrt {25 + 10 {\ sqrt {5}}}} d ^ {2}}$ $3 {\ sqrt {25 + 10 {\ sqrt {5}}}} d ^ {2}$	${\frac {1}{4}}(15+7{\sqrt {5}})d^{3}$ ${\ displaystyle {\ frac {1} {4}} (15 + 7 {\ sqrt {5}}) d ^ {3}}$ ${\ frac {1} {4}} (15 + 7 {\ sqrt {5}}) d ^ {3}$
Icosaedru	${\frac {\sqrt {3}}{12}}(3+{\sqrt {5}})d$ ${\ displaystyle {\ frac {\ sqrt {3}} {12}} (3 + {\ sqrt {5}}) d}$ ${\ frac {{\ sqrt {3}}} {12}} (3 + {\ sqrt {5}}) d$	${\frac {1}{4}}{\sqrt {(10+2{\sqrt {5}})}}d$ ${\ displaystyle {\ frac {1} {4}} {\ sqrt {(10 + 2 {\ sqrt {5}})}}} d}$ ${\ frac {1} {4}} {\ sqrt {(10 + 2 {\ sqrt {5}})}} d$	${\frac {1}{4}}(1+{\sqrt {5}})d$ ${\ displaystyle {\ frac {1} {4}} (1 + {\ sqrt {5}}) d}$ ${\ frac {1} {4}} (1 + {\ sqrt {5}}) d$	$5{\sqrt {3}}d^{2}$ ${\ displaystyle 5 {\ sqrt {3}} d ^ {2}}$ $5 {\ sqrt {3}} d ^ {2}$	${\frac {5}{12}}(3+{\sqrt {5}})d^{3}$ ${\ displaystyle {\ frac {5} {12}} (3 + {\ sqrt {5}}) d ^ {3}}$ ${\ frac {5} {12}} (3 + {\ sqrt {5}}) d ^ {3}$

Unghiuri între fețele de poliedru obișnuite (utile pentru construirea de modele cu materiale cu grosime deloc neglijabilă)

Pentru cub - soluție banală - unghi de 90 °

Pentru celelalte poliedre, soluția poate fi obținută considerând unul dintre vârfuri ca fiind cuspida unei piramide drepte regulate care are ca bază poligonul obținut prin îmbinarea vârfurilor adiacente cu cel ales anterior și evaluarea unghiului β dintre înălțimi conduse către aceeași margine laterală a acestei piramide.

Tetraedru: → β ≈ 70 °, 53 ≈ 70 ° 32 '

Octahedron: → β ≈ 109 °, 47 ≈ 109 ° 28 '

Dodecaedru: → β ≈ 116 °, 57 ≈ 116 ° 34 '

Icosaedru: → β ≈ 138 °, 19 ≈ 138 ° 11 '

Dualitatea și simetriile solidelor platonice

Dualitatea poliedrică , adică transfigurarea unui poliedru într-un al doilea poliedru care prezintă respectiv vârfurile, muchiile și fețele corespunzătoare fețelor, muchiilor și vârfurilor primului și care prezintă relațiile de incidență consecvente între aceste trei tipuri de obiecte, este o involuție care transformă tetraedrele în tetraedre și schimbă cuburi cu octaedre și dodecaedre cu icosaedre.

Ridicată regularitatea solide platonice se reflectă în faptul că fiecare dintre ele are un asociat extins grup de simetrie . Aceste grupuri pot fi considerate subgrupuri ale grupurilor de simetrie de vârf sau grupurile de simetrie de margine sau grupurile de simetrie a feței. Grupurile de simetrie a două solide platonice duale sunt izomorfe: de fapt prin dualitate permutările vârfurilor unui poliedru devin permutări ale fețelor poliedrului dual (în timp ce permutările marginilor unui poliedru devin permutări ale marginilor dualului ).

Grupul de simetrie al tetraedrului este indicat cu T _d, grupul de simetrie al cubului și octaedru cu O _h, grupul de simetrie al icosaedru și dodecaedru cu I _h.

Solidele și cristalele platonice

Unele cristale iau forma unor solide regulate: de exemplu, clorura de sodiu , comună sare de masă, este aranjată în cristale cubice, în timp ce fluorură de calciu , adică fluorina , apare sub forma de octoedre regulate. Există, de asemenea, multe cristale care sunt aranjate după compoziții și variante ale solidelor platonice; acest lucru este echivalent cu a spune că rețelele cristaline respective prezintă de marcate simetrie proprietăți. Aceste proprietăți joacă un rol fundamental în clasificarea lor.

Notă

^ Giovanni Reale, Pentru o nouă interpretare a lui Platon, 2003, p. 678, ISBN 88-343-1036-5 .
^ Platon, Fedon, 110b.
^ Vincenzo Schettino, Știință și Artă: Chimie, arte și literatură figurative, pag. 15 , Firenze University Press, 2014.
^ Citat atribuit Platon de Plutarh în convivales Quaestiones, VIII 2 ( Moralia 718c-720c).
^ Teeteto www.treccani.it pe 20-02-2012 Adus
^(RO) George Johnston Allman , greacă Geometrie de la Thales la Euclid, Hodges, Figgis, & Company, 1889, p. 206.
^ Quadrivium. Numărul, geometrie, muzică, astronomie, Sironi Editore, 2011, p. 144, ISBN 88-518-0169-X .
^ Massimo Corradi, cele patru elemente: aer, apă, pământ și foc, 2008, p. 64, ISBN 1-4092-2642-5 .
^ Platonic Solide , pe gpmeneghin.com. Adus pe 21 mai 2016 .

Elemente conexe

Alte proiecte

Wikimedia Commons conține imagini sau alte fișiere pe solide platonice

linkuri externe

Solid platonic , în dicționar de Filosofie , Institutul Enciclopediei Italiene , 2009.
(EN) platonica solid , în Enciclopedia Britanică , Encyclopædia Britannica, Inc.
Construcția 5 solide platonice prin utilizarea software - ului numeric
Stella: Polihedron Navigator instrument pentru explorarea polihedre
Modele de hârtie poliedre pagină plină de link - uri
Sugestii de istorie despre poliedre regulate (PDF), pe mathematics.unito.it.
Unele imagini ale poliedre regulate , pe mathematita.it.
( RO ) Poliedrele uniforme , pe mathconsult.ch .
(RO) Virtual Reality poliedre în Enciclopedia poliedrelor
(RO) London South Bank University Structura și comportamentul de apă
(RO) XIII Rezervă a lui Euclid Elemente

Controlul autorității	Thesaurus BNCF 22329 · GND (DE) 4046302-3

Portalul de filosofie

Portalul de matematică

[1] Giovanni Reale, Pentru o nouă interpretare a lui Platon, 2003, p. 678, ISBN 88-343-1036-5 .

[2] Platon, Fedon, 110b.

[3] Vincenzo Schettino, Știință și Artă: Chimie, arte și literatură figurative, pag. 15 , Firenze University Press, 2014.

[4] Citat atribuit Platon de Plutarh în convivales Quaestiones, VIII 2 ( Moralia 718c-720c).

[5] Teeteto www.treccani.it pe 20-02-2012 Adus

[allen-6] (RO) George Johnston Allman , greacă Geometrie de la Thales la Euclid, Hodges, Figgis, & Company, 1889, p. 206.

[7] Quadrivium. Numărul, geometrie, muzică, astronomie, Sironi Editore, 2011, p. 144, ISBN 88-518-0169-X .

[8] Massimo Corradi, cele patru elemente: aer, apă, pământ și foc, 2008, p. 64, ISBN 1-4092-2642-5 .

[9] Platonic Solide , pe gpmeneghin.com. Adus pe 21 mai 2016 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]