Suprafaţă
 Podea | 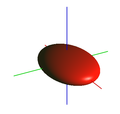 Elipsoid ( Quadric ) |
 Şa ( Graficul unei funcții ) |  Hiperboloid ( Suprafață guvernată ) |
 Helicoid ( Suprafata minima ) |  Taur |
 Benzi Mobius (Suprafață neorientabilă ) |  Suprafața de rotație |
În matematică , o suprafață este o formă geometrică fără grosime, având doar două dimensiuni. O suprafață poate fi plană (ca un plan ) sau curbată (cum ar fi marginea unei sfere sau a unui cilindru ). Poate fi limitat sau nelimitat, închis sau deschis.
Există mai multe definiții matematice ale suprafeței: toate acestea sunt conținute în noțiunea de „suprafață abstractă” și de varietate diferențiată . În cele mai frecvente cazuri termenul este folosit pentru a se referi la suprafețe dintr-un spațiu tridimensional.
Definiție
În mod informal, o suprafață este un obiect geometric ideal, fără grosime, având două dimensiuni. Unele obiecte reale se apropie de această noțiune abstractă: de exemplu o folie foarte subțire.
În mod formal, definirea unei suprafețe în spațiu necesită noțiuni matematice non-banale tipice geometriei diferențiale
Un subset a spațiului euclidian tridimensional este o suprafață dacă pentru fiecare punct cuprins în există împrejurimi deschise și o funcție de clasă
astfel încât se intersectează tocmai în punctele în care anulezi:
și având un gradient diferit de zero peste tot:
Cu alte cuvinte, întregul este o suprafață dacă este local exprimabilă ca locus al zerourilor unei funcții. Condiția ca gradientul să fie diferit de zero garantează, prin teorema lui Dini , că suprafața este un obiect neted în fiecare punct.
Clădiri

sau sub formă implicită ca locus al zerourilor funcției:
.
O suprafață poate fi construită în diferite moduri.
Forma parametrică
O suprafață poate fi construită ca o imagine a unei funcții injectabile diferențiabile a două variabile reale în spațiul euclidian tridimensional
unde este este un set de plan deschis . Pentru a obține un obiect neted, este necesar diferențialul din este, de asemenea, injectiv în fiecare punct : cu alte cuvinte trebuie să fie o scufundare .
Cu această construcție, coordonatele punctelor suprafeței sunt ușor exprimate prin ecuațiile parametrice :
deoarece cei doi parametri variază în aer liber .
Aceasta este definiția în general mai utilă în scopuri practice, deoarece permite calcularea suprafețelor și a integralelor de suprafață într-un mod ușor.
Formă implicită globală
O suprafață poate fi construit la nivel global ca locus al zerourilor cu o singură funcție diferențiată
numită ecuație cartesiană . Pentru a obține un obiect neted, gradientul de trebuie să fie diferit de zero în fiecare punct al . Rețineți că definiția generală a unei suprafețe necesită ca o astfel de funcție să existe doar local.
Graficul unei funcții
Graficul unei funcții diferențiat
definit pe un deschis a planului cartezian este o suprafata. [1] Suprafața poate fi indicată implicit prin ecuație
În cazul în care domeniul atât întregul etaj , suprafața este așadar locusul zerourilor funcției implicite globale
Suprafața poate fi descrisă și în formă parametrică prin luarea
Cu toate acestea, multe suprafețe nu reprezintă un grafic de funcții, cum ar fi suprafața sferică .
Suprafața de rotație
O suprafață de rotație (sau rotație ) este obținută prin rotirea unei curbe în jurul unei axe. Axa poate fi una dintre cele trei axe carteziene sau orice linie dreaptă.
Noțiuni de bază
Zonă
Zona a unei suprafețe exprimate în formă parametrică printr-o funcție condominiu este definit folosind instrumentele de calcul integrale după cum urmează:
În formulă există o integrală multiplă , derivatele parțiale ale funcției și produsul vector . În mod similar, este definită integralul unei funcții care are suprafața ca domeniu: această operație se numește integrală a suprafeței .
Normal
În fiecare moment a unei suprafețe se definește un plan tangent . Planul tangent este descris cu instrumentele furnizate de algebra liniară și de calcul în mai multe variabile.
Un normal în este un vector perpendicular pe planul tangent, având lungimea unității. În fiecare moment are două normale, în direcții opuse.
Curbură

Curbura este o proprietate fundamentală a suprafețelor din spațiu. În fiecare punct de pe suprafață există două curburi principale, iar curbura Gauss este definită ca produsul acestor două cantități.
Curbura Gaussiană poate fi pozitivă, zero sau negativă. Într-un plan, curbura este zero și se menține geometria euclidiană obișnuită; pe suprafețe cu curbură pozitivă sau negativă este posibilă definirea geometriilor neeuclidiene , numite respectiv eliptice și hiperbolice . În aceste geometrii, liniile euclidiene obișnuite sunt înlocuite cu geodezice , curbe la suprafață care minimizează (local) distanța dintre două puncte.
Proprietăți topologice
Topologia este o ramură a geometriei care studiază proprietățile obiectelor geometrice care rămân neschimbate atunci când deformarea este efectuată fără „smucitură”.
Tip
Genul unei suprafețe este informal „numărul de mânere” pe care le conține.
Reglabilitate

O suprafață este orientabilă dacă are două fețe (un „deasupra” și un „dedesubt”), altfel nu poate fi orientat . Contrar a ceea ce sugerează intuiția, există de fapt suprafețe cu o singură față: prototipul este banda Möbius .
Tipologie
Suprafețe algebrice
O ecuație polinomială în cele trei variabile , De exemplu
definește o suprafață algebrică . Pentru ca locusul zerourilor să fie de fapt o suprafață netedă, diferențialul ecuației trebuie să fie diferit de zero în fiecare punct. În general, totuși, se vorbește despre o „suprafață algebrică” chiar și atunci când această condiție nu este satisfăcută: în acest caz, pot apărea puncte non-netede numite singularități .
Dacă polinomul este de gradul I, suprafața este un plan. Suprafețele care pot fi descrise cu ecuații de gradul 2, 3, 4, 5 se numesc cvadrici , cubice , quartice , chintice și așa mai departe. Sexticul prezentat în figură are unele singularități.
Cvadrici
Un cvadric este o suprafață algebrică de gradul doi. Quadricele sunt clasificate cu instrumentele algebrei liniare (în esență teorema spectrală ). Cadrele nedegenerate sunt împărțite în cinci tipuri:



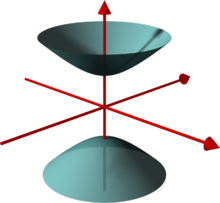
 Hiperboloid cu o singură clapă
Hiperboloid cu o singură clapă Hiperboloid cu două clape
Hiperboloid cu două clape
Suprafețe guvernate
O suprafață este guvernată dacă este o uniune de linii (infinite).
Suprafețe minime
O suprafață este minimă dacă are o suprafață (locală) minimă dintre toate cele care au o margine fixă. Din punct de vedere matematic, această condiție este echivalentă cu necesitatea ca suprafața să aibă curbura medie zero peste tot. În natură, unele structuri tind să se aranjeze în așa fel încât să minimizeze zona și, prin urmare, să formeze suprafețe minime.
Suprafețe închise
O suprafață este închisă dacă este limitată și fără margini, ca într-o sferă . Cu limbajul strict al topologiei , o suprafață este închisă dacă este compactă . [2]


 Marginea unui
Marginea unui
corp cu mânere Taur înnodat
Taur înnodat
Generalizări
Suprafață abstractă
În topologie , o ramură importantă a geometriei , se studiază o noțiune mai generală de suprafață. Suprafața studiată în acest context este un obiect mai abstract, care „are o viață proprie”, nu neapărat conținut în spațiul tridimensional.
În mod formal, o suprafață abstractă este o varietate topologică Hausdorff cu dimensiunea 2. Multe suprafețe abstracte pot fi reprezentate în spațiu, dar nu toate: de exemplu, sticla Klein nu este vizibilă în interiorul spațiului tridimensional (poate fi totuși reprezentabilă în patru - spațiul euclidian dimensional).
În multe contexte este mai util să se definească o suprafață mai degrabă ca o varietate diferențială decât una topologică. Cu toate acestea, diferența nu este substanțială.
Un alt exemplu de suprafață abstractă (sau algebrică) este suprafața Veronese , care poate fi reprezentată doar într-un spațiu proiectiv de cel puțin cinci dimensiuni, în timp ce Trompeta lui Torricelli este o altă suprafață paradoxală care poate fi desenată în trei dimensiuni.
Suprafețe imersate
O suprafață scufundată este o suprafață care se poate intersecta. Mai exact, este imaginea unei scufundări
a unei suprafețe abstracte . Prin urmare, necesită acest lucru are diferențial injectiv peste tot: această ipoteză garantează că este injectiv local, dar nu la nivel global.

De exemplu, sticla Klein este prezentată în general în spațiul tridimensional printr-o imersiune: suprafața se intersectează de-a lungul unei circumferințe. O altă suprafață scufundată este suprafața Boy : în acest caz este un plan proiectiv real , o suprafață neorientabilă care, la fel ca sticla Klein, nu poate fi conținută în spațiu.
Suprafețe complexe
În contextul geometriei complexe , o suprafață complexă este o varietate complexă de dimensiunea 2. Este un obiect complet diferit de suprafața obișnuită, deoarece are dimensiunea topologică reală 4.
În cele din urmă, în funcție de contexte, termenul de suprafață poate fi folosit pentru a indica structuri cu caracteristici diferite de cele menționate mai sus; de exemplu, o suprafață într-un spațiu euclidian (sau într-o varietate diferențiată ) poate fi numită pe scurt o suprafață, adică o varietate cu o dimensiune mai mică decât cea a spațiului ambiental (dar nu neapărat 2), uneori vorbim și despre suprafețe fractale , indicând structuri fractale construite dintr-o suprafață, dar care, în cele din urmă, nu păstrează nicio caracteristică specifică.
Teoreme
Teorema lui Gauss-Bonnet
Teorema lui Stokes
Clasificarea topologică a suprafețelor
Suprafețele compacte sunt clasificate în topologie până la homeomorfism după trei parametri: sex , numărul componentelor muchiei și ajustabilitate .
Suprafețele de tip finit sunt, de asemenea, adesea luate în considerare în topologie, obținute pornind de la suprafețe compacte prin îndepărtarea unui număr finit de puncte și astfel creând puncții . O suprafață înțepată nu este niciodată compactă. Similar suprafețelor compacte, cele de tip finit sunt clasificate după patru parametri: tipul, numărul componentelor muchiei, orientabilitatea și numărul de puncții.
Teorema uniformizării
Notă
Elemente conexe
Alte proiecte
-
 Wikționarul conține dicționarul lema « suprafață »
Wikționarul conține dicționarul lema « suprafață » -
 Wikimedia Commons conține imagini sau alte fișiere de suprafață
Wikimedia Commons conține imagini sau alte fișiere de suprafață
linkuri externe
- ( EN ) Surface , în Encyclopedia Britannica , Encyclopædia Britannica, Inc.
- ( FR ) Exemple de suprafețe din Mathcurve , Encyclopédie des formes mathématiques remarquables
| Controlul autorității | Thesaurus BNCF 21329 · NDL (EN, JA) 00.567.234 |
|---|





























































