teorema lui Pitagora

Într-un triunghi dreptunghic suma ariilor pătratelor construite pe picioare (albastru și roșu) este egală cu aria pătratului construit pe ipotenuză (violet).

Dovada de animație a teoremei lui Pitagora

Teorema lui Pitagora este o teoremă a geometriei euclidiene care stabilește o relație fundamentală între laturile unui triunghi dreptunghiular .

Se poate lua în considerare un caz special, pentru triunghiurile unghiulare, ale teoremei cosinusului .

Origine

Vizualizarea cazului triunghiului (3,4,5) cuprins în textul chinezesc Chou Pei Suan Ching (scris între 200 î.Hr. și 200 d.Hr.)

Ceea ce știm modern ca teorema lui Pitagora este de obicei atribuit filosofului și matematicianului Pitagora . În realitate afirmația sa (dar nu demonstrația sa) era deja cunoscută de babilonieni ^[1] . Uneori se susține că teorema lui Pitagora a fost cunoscută de vechii egipteni: Carl Boyer exclude această ipoteză, pe baza absenței teoremei din papirusurile matematice găsite. ^[2] A fost cunoscută și în China și cu siguranță în India , după cum demonstrează multe scripturi, inclusiv Yuktibhāṣā și Śulbasūtra . Nu există dovezi cunoscute ale teoremei care să fie considerate valabile și astăzi și antecedente sau contemporane lui Pitagora.

Afirmație

În fiecare triunghi dreptunghiular pătratul construit pe ipotenuză este echivalent cu unirea pătratelor construite pe picioare.

sau:

În fiecare triunghi dreptunghic aria pătratului construit pe ipotenuză este egală cu suma ariilor pătratelor construite pe picioare.

Utilizarea adjectivului egal în loc de echivalent necesită să se refere fie la suprafețele pătratelor „construite” pe picioare și pe ipotenuză (suprafață destinată ca măsură a extinderii unei suprafețe), fie la pătratele lungimilor a picioarelor / pătratului lungimii hipotenuzei. Posibila ambivalență a limbii italiene derivă din faptul că, în absența termenului construit , cuvântul pătrat poate defini atât suprafața figurii geometrice ca atare, cât și operația generică de ridicare la a doua putere.

În alte limbi, în special engleză, franceză și spaniolă, în enunțul teoremei pitagoreice preferăm să vorbim despre pătrate (de lungimi) ale catetelor și despre hipotenuză, ceea ce permite utilizarea simplă a termenilor egali (în engleză) , égal (în franceză), igual (în spaniolă). De exemplu, în spaniolă, el cuadrado de la hipotenusa înseamnă fără echivoc „pătratul (măsurii) hipotenuzei”.

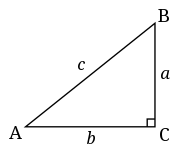
Dat fiind un triunghi dreptunghiular al laturilor $la$ ${\ displaystyle a}$ $la$ , $b$ ${\ displaystyle b}$ $b$ Și $c$ ${\ displaystyle c}$ $c$ , și denotând cu $c$ ${\ displaystyle c}$ $c$ ipotenuza ei și cu $la$ ${\ displaystyle a}$ $la$ Și $b$ ${\ displaystyle b}$ $b$ picioarele sale, teorema este exprimată prin ecuația:

a^{2}+b^{2}=c^{2},

{\ displaystyle a ^ {2} + b ^ {2} = c ^ {2},}

{\ displaystyle a ^ {2} + b ^ {2} = c ^ {2},}

sau, făcându-l explicit $c$ ${\ displaystyle c}$ $c$ :

{\sqrt {a^{2}+b^{2}}}=c.

{\ displaystyle {\ sqrt {a ^ {2} + b ^ {2}}} = c.}

{\ displaystyle {\ sqrt {a ^ {2} + b ^ {2}}} = c.}

Măsurătorile catetelor sunt, prin urmare:

{\sqrt {c^{2}-b^{2}}}=a,

{\ displaystyle {\ sqrt {c ^ {2} -b ^ {2}}} = a,}

{\ displaystyle {\ sqrt {c ^ {2} -b ^ {2}}} = a,}

Și

{\sqrt {c^{2}-a^{2}}}=b.

{\ displaystyle {\ sqrt {c ^ {2} -a ^ {2}}} = b.}

{\ displaystyle {\ sqrt {c ^ {2} -a ^ {2}}} = b.}

Un triplet de numere întregi pozitive ${a,b,c}$ ${\ displaystyle {a, b, c}}$ ${a, b, c}$ care satisface teorema lui Pitagora se numește triplă pitagorică .

În schimb, fiecare triunghi în care cele trei laturi verifică această proprietate este un dreptunghi: această teoremă, cu dovada sa, apare în ultima afirmație a primei cărți a elementelor .

Demonstrații

Animația unei demonstrații

Demonstrația clasică a teoremei lui Pitagora completează prima carte a Elementelor lui Euclid și constituie tema principală. Deoarece necesită postulatul paralel , nu se menține în geometrie neeuclidiană și neutră . În textul lui Euclid, dovada teoremei este imediat precedată de dovada constructibilității pătratelor. Într-adevăr, însăși existența pătratelor depinde de postulatul paralelelor și eșuează în geometriile neeuclidiene. Acest aspect al problemei este, în general, neglijat în predarea contemporană, care deseori tinde să presupună existența pătratelor ca fiind evidentă.

Dovada teoremei lui Pitagora constă în umplerea aceluiași pătrat cu o latură egală cu suma picioarelor mai întâi cu patru copii ale triunghiului dreptunghiular plus pătratul construit pe ipotenuză și apoi cu patru copii ale triunghiului dreptunghiular plus pătratele construite pe picioare, ca în figură.

Deoarece teorema este una dintre cele mai cunoscute din istoria matematicii , există multe dovezi ale acesteia, în total câteva sute, lucrarea matematicienilor, astronomilor, agenților de bursă, de exemplu un președinte american James A. Garfield și Leonardo da Vinci . Pentru această teoremă, 371 de dovezi diferite au fost clasificate de către omul de știință american Elisha Scott Loomis , care au fost publicate în 1927 în cartea sa The Pythagorean Proposition .

Demonstrație Abu'l-Wafa

Demonstrație Abu'l-Wafa 'i Perigal

Dovada atribuită matematicianului și astronomului persan Abu'l-Wafa spre sfârșitul secolului al X-lea d.Hr. ^[3] ^[4] și redescoperită de agentul de bursă Henry Perigal (găsită în 1835-1840 ^[5] , publicată în 1872 și mai târziu în 1891 ^[6] ) se bazează pe descompunerea pătratului construit pe catetul mai mare, în galben în imagine: de fapt, prin tăierea acestuia cu două linii drepte care trec prin centrul său, una perpendiculară și una paralelă cu hipotenuza, poate fi recompus în așa fel încât să încorporeze celălalt pătrat și formând pătratul pe hipotenuză, ca în figură. Această procedură este legată de problema trisecției pătratului .

Demonstrație aerisită

Există, de asemenea, o demonstrație poetică , realizată de astronomul Sir George Airy , în limba engleză :

„ Sunt, după cum puteți vedea,
a² + b² - ab
Când stau doi triunghiuri pe mine,
Se planifică pătratul ipotezei
Dar dacă stau pe ele în schimb
Se citesc pătratele ambelor părți. "

din care este o traducere literală

„ După cum puteți vedea, sunt
a² + b² - ab
Când sunt două triunghiuri deasupra mea
Este reprezentat pătratul hipotenuzei
Dar dacă sunt deasupra lor
Puteți citi pătratele de ambele părți "

Versetele se referă la partea albă: primele două triunghiuri sunt cele roșii, al doilea cele albastre.

Atât cea a lui Perigal, cât și cea din urmă sunt pur geometrice, adică nu necesită nicio definiție a operațiilor aritmetice, ci doar congruențe de zone și segmente.

Patratele concentrice ale lui Pomi

Dovadă cu pătrate concentrice

Dovadă geometrică bazată pe două pătrate concentrice, cu laturi egale cu ipotenuza ( $c$ ${\ displaystyle c}$ $c$ ) și suma celor două picioare ( $a+b$ ${\ displaystyle a + b}$ $a + b$ ).

După cum puteți vedea din figură, după îndepărtarea celor patru triunghiuri dreptunghiulare (în zona galbenă $(ab)/2$ ${\ displaystyle (ab) / 2}$ ${\ displaystyle (ab) / 2}$ ) la cel mai mare pătrat, care corespunde suprafeței $(a+b)^{2}$ ${\ displaystyle (a + b) ^ {2}}$ $(a + b) ^ {2}$ , veți obține cel mai mic pătrat, reprezentat în alb, care în schimb este echivalent cu suprafața $c^{2}$ ${\ displaystyle c ^ {2}}$ $c ^ {2}$ .

Prin urmare

(a+b)^{2}-4(ab)/2=c^{2},

{\ displaystyle (a + b) ^ {2} -4 (ab) / 2 = c ^ {2},}

{\ displaystyle (a + b) ^ {2} -4 (ab) / 2 = c ^ {2},}

din care se obține rezolvarea

a^{2}+b^{2}=c^{2}.

{\ displaystyle a ^ {2} + b ^ {2} = c ^ {2}.}

{\ displaystyle a ^ {2} + b ^ {2} = c ^ {2}.}

Această dovadă, folosind pasajul algebric al pătratului sumei a două numere, are o reprezentare vizuală simplă și directă, care nu necesită deplasarea și suprapunerea formelor ca celelalte dovezi geometrice formulate.

Demonstrația lui Garfield

O altă dovadă geometrică, în a cărei construcție nu apare niciun pătrat, a fost găsită în 1876 de James Abraham Garfield , care a devenit ulterior cel de-al douăzecilea președinte al Statelor Unite ale Americii . Înapoi în armată, Garfield a comentat rezultatul său: „Credem că, prin această dovadă matematică, putem determina toți parlamentarii să fie de acord, indiferent de credințele lor politice”. Garfield începuse o nemiloasă campanie anticorupție care îi provocase ura numeroșilor colegi parlamentari, atât de mult încât a fost ucis la câteva luni după ce a fost ales președinte. ^[7]

Dovada urmează practic metoda utilizată în demonstrația lui Pomi, dar aplicată la jumătate din cifră, adică luând în considerare trapezul în locul pătratului:

Să luăm în considerare o copie a triunghiului drept în cauză, rotit cu 90 de grade pentru a alinia cele două fețe diferite (în figura din lateral, roșu și albastru ). Apoi se unesc extremele hipotenuselor, obținându-se un trapez . Prin echivalarea ariei trapezului cu suma celor trei triunghiuri unghiulare, se demonstrează teorema.

În formule, a spus $la$ ${\ displaystyle a}$ $la$ catetul roșu, $b$ ${\ displaystyle b}$ $b$ albastrul și $c$ ${\ displaystyle c}$ $c$ hipotenuza și amintindu-ne de puterea binomului

{\frac {(a+b)^{2}}{2}}={\frac {ab}{2}}+{\frac {ab}{2}}+{\frac {c^{2}}{2}}\,\,\Rightarrow \,\,a^{2}+b^{2}=c^{2}.

{\ displaystyle {\ frac {(a + b) ^ {2}} {2}} = {\ frac {ab} {2}} + {\ frac {ab} {2}} + {\ frac {c ^ {2}} {2}} \, \, \ Rightarrow \, \, a ^ {2} + b ^ {2} = c ^ {2}.}

{\ displaystyle {\ frac {(a + b) ^ {2}} {2}} = {\ frac {ab} {2}} + {\ frac {ab} {2}} + {\ frac {c ^ {2}} {2}} \, \, \ Rightarrow \, \, a ^ {2} + b ^ {2} = c ^ {2}.}

Cu teoremele lui Euclid

Dovadă cu Euclid

O altă dovadă folosește prima teoremă a lui Euclid . Înălțimea este reprezentată pe ipotenuză. Aceasta împarte hipotenuza în două segmente, în lungime $p$ ${\ displaystyle p}$ $p$ Și $q$ ${\ displaystyle q}$ $q$ . Teorema lui Euclid oferă relațiile

{\frac {a}{p}}={\frac {c}{a}},\ {\frac {b}{q}}={\frac {c}{b}},

{\ displaystyle {\ frac {a} {p}} = {\ frac {c} {a}}, \ {\ frac {b} {q}} = {\ frac {c} {b}},}

{\ displaystyle {\ frac {a} {p}} = {\ frac {c} {a}}, \ {\ frac {b} {q}} = {\ frac {c} {b}},}

de la care

a^{2}=cp,\ b^{2}=cq

{\ displaystyle a ^ {2} = cp, \ b ^ {2} = cq}

a ^ {2} = cp, \ b ^ {2} = cq

prin urmare

a^{2}+b^{2}=c(p+q)=c^{2}.

{\ displaystyle a ^ {2} + b ^ {2} = c (p + q) = c ^ {2}.}

{\ displaystyle a ^ {2} + b ^ {2} = c (p + q) = c ^ {2}.}

Verso

Este, de asemenea, inversul teoremei lui Pitagora (Propunerea 48 din prima carte a Elementelor lui Euclid ): „Dacă într-un triunghi de laturi $la$ ${\ displaystyle a}$ $la$ , $b$ ${\ displaystyle b}$ $b$ Și $c$ ${\ displaystyle c}$ $c$ relația merită $a^{2}+b^{2}=c^{2}$ ${\ displaystyle a ^ {2} + b ^ {2} = c ^ {2}}$ $a ^ {2} + b ^ {2} = c ^ {2}$ , atunci triunghiul este dreptunghi ".

Demonstrație . Este $T.$ ${\ displaystyle T}$ $T.$ un triunghi de laturi $la$ ${\ displaystyle a}$ $la$ , $b$ ${\ displaystyle b}$ $b$ Și $c$ ${\ displaystyle c}$ $c$ astfel încât $a^{2}+b^{2}=c^{2}$ ${\ displaystyle a ^ {2} + b ^ {2} = c ^ {2}}$ $a ^ {2} + b ^ {2} = c ^ {2}$ . Să luăm în considerare un al doilea triunghi dreptunghiular ${T.}^{'}$ ${\ displaystyle T '}$ $T '$ care are picioare egale cu $la$ ${\ displaystyle a}$ $la$ Și $b$ ${\ displaystyle b}$ $b$ (este întotdeauna posibil să se construiască un triunghi dreptunghi având în vedere cele două laturi). Prin teorema (directă) a lui Pitagora hipotenuza triunghiului ${T.}^{'}$ ${\ displaystyle T '}$ $T '$ va fi egal cu ${\sqrt {a^{2}+b^{2}}}$ ${\ displaystyle {\ sqrt {a ^ {2} + b ^ {2}}}}$ ${\ sqrt {a ^ {2} + b ^ {2}}}$ , adică va fi egal cu partea $c$ ${\ displaystyle c}$ $c$ a triunghiului $T.$ ${\ displaystyle T}$ $T.$ . Cele două triunghiuri $T.$ ${\ displaystyle T}$ $T.$ Și ${T.}^{'}$ ${\ displaystyle T '}$ $T '$ vor fi, prin urmare, congruenți pentru al treilea criteriu de congruență , având toate cele trei laturi net egale. Dar apoi și triunghiul $T.$ ${\ displaystyle T}$ $T.$ va fi dreptunghi (CVD) .

Un corolar al teoremei lui Pitagora ne permite să stabilim dacă un triunghi este sau nu dreptunghi, acut sau obtuz. Erau $c$ ${\ displaystyle c}$ $c$ este ales ca hipotenuză, cea mai lungă parte dintre cele trei și $a+b>c$ ${\ displaystyle a + b> c}$ ${\ displaystyle a + b> c}$ (altfel nu vom avea un triunghi), se țin următoarele relații:

de sine $a^{2}+b^{2}=c^{2},$ ${\ displaystyle a ^ {2} + b ^ {2} = c ^ {2},}$ ${\ displaystyle a ^ {2} + b ^ {2} = c ^ {2},}$ atunci triunghiul este dreptunghi;
de sine $a^{2}+b^{2}>c^{2},$ ${\ displaystyle a ^ {2} + b ^ {2}> c ^ {2},}$ ${\ displaystyle a ^ {2} + b ^ {2}> c ^ {2},}$ atunci triunghiul este unghi acut;
de sine $a^{2}+b^{2}<c^{2},$ ${\ displaystyle a ^ {2} + b ^ {2} <c ^ {2},}$ ${\ displaystyle a ^ {2} + b ^ {2} <c ^ {2},}$ atunci triunghiul este obtuz.

Aplicații practice ale enunțului invers

Afirmația inversă oferă, de asemenea, un sistem pentru construirea unui unghi drept (sau pentru verificarea pătratului unui unghi deja existent) în situații practice, cum ar fi topografia sau topografia .

De exemplu, cu o frânghie de lungime egală cu suma unui triplu pitagoric (să zicem 12, suma de 5, 4 și 3, într-o anumită unitate de măsură ) ar fi suficient să aranjăm cele două porțiuni minore ale șirului (cele de măsură 4 și 3) la un anumit unghi între ele; dacă capetele coardei, aranjate în cele din urmă într-o formă triunghiulară, se închid, se va ști că unghiul dintre cele două porțiuni minore ale coardei (în acest moment cele două picioare) este cu siguranță corect.

Generalizări

Teorema lui Pitagora poate fi generalizată în diferite moduri. De obicei, o generalizare este o relație care se aplică tuturor triunghiurilor și care, atunci când este aplicată triunghiurilor dreptunghiulare, se dovedește a fi echivalentă cu teorema lui Pitagora.

Teorema cosinusului

Orice triunghi.

Același subiect în detaliu: teorema cosinusului .

O generalizare a teoremei lui Pitagora este teorema cosinusului , care se aplică oricărui triunghi (nu neapărat drept). Într-un triunghi cu vârfuri și unghiuri indicate ca în figură, egalitatea deține:

{\overline {AB}}^{2}={\overline {AC}}^{2}+{\overline {BC}}^{2}-2{\overline {AC}}\cdot {\overline {BC}}\cos \gamma .

{\ displaystyle {\ overline {AB}} ^ {2} = {\ overline {AC}} ^ {2} + {\ overline {BC}} ^ {2} -2 {\ overline {AC}} \ cdot { \ overline {BC}} \ cos \ gamma.}

\ overline {AB} ^ {2} = \ overline {AC} ^ {2} + \ overline {BC} ^ {2} -2 \ overline {AC} \ cdot \ overline {BC} \ cos \ gamma.

În cazul în care $\gamma$ ${\ displaystyle \ gamma}$ $\gamă$ fii drept, este adevărat $\cos \gamma =0$ ${\ displaystyle \ cos \ gamma = 0}$ $\ cos \ gamma = 0$ și, prin urmare, afirmația este echivalentă cu teorema lui Pitagora. Termenul suplimentar poate fi interpretat ca produsul punct al vectorilor $C. LA$ ${\ displaystyle CA}$ $CA$ Și $C. B.$ ${\ displaystyle CB}$ $CB$ .

Teorema sinusului

Același subiect în detaliu: Teorema sinelor .

Teorema sinusului se referă la lungimi și unghiuri laterale opuse.

Teorema sinusului raportează lungimile laturilor unui triunghi la sinele unghiurilor opuse. Această relație se aplică și oricărui triunghi și, dacă acesta este un dreptunghi, poate fi considerat echivalent teoremei pitagoreice (deși într-un mod mai puțin imediat decât teorema cosinusului).

Teorema sinusului afirmă că în orice triunghi, cu notațiile ca în figură, se țin următoarele relații:

{\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}=2R.

{\ displaystyle {\ frac {a} {\ sin \ alpha}} = {\ frac {b} {\ sin \ beta}} = {\ frac {c} {\ sin \ gamma}} = 2R.}

{\ frac a {\ sin \ alpha}} = {\ frac b {\ sin \ beta}} = {\ frac c {\ sin \ gamma}} = 2R.

Pătrat:

c^{2}=a^{2}{\frac {\sin ^{2}\gamma }{\sin ^{2}\alpha }},\quad b^{2}=a^{2}{\frac {\sin ^{2}\beta }{\sin ^{2}\alpha }}.

{\ displaystyle c ^ {2} = a ^ {2} {\ frac {\ sin ^ {2} \ gamma} {\ sin ^ {2} \ alpha}}, \ quad b ^ {2} = a ^ { 2} {\ frac {\ sin ^ {2} \ beta} {\ sin ^ {2} \ alpha}}.}

{\ displaystyle c ^ {2} = a ^ {2} {\ frac {\ sin ^ {2} \ gamma} {\ sin ^ {2} \ alpha}}, \ quad b ^ {2} = a ^ { 2} {\ frac {\ sin ^ {2} \ beta} {\ sin ^ {2} \ alpha}}.}

Adăugând termenii pe care îi obținem:

c^{2}+b^{2}=a^{2}{\frac {\sin ^{2}\gamma +\sin ^{2}\beta }{\sin ^{2}\alpha }}.

{\ displaystyle c ^ {2} + b ^ {2} = a ^ {2} {\ frac {\ sin ^ {2} \ gamma + \ sin ^ {2} \ beta} {\ sin ^ {2} \ alfa}}.}

{\ displaystyle c ^ {2} + b ^ {2} = a ^ {2} {\ frac {\ sin ^ {2} \ gamma + \ sin ^ {2} \ beta} {\ sin ^ {2} \ alfa}}.}

Cand $\alpha$ ${\ displaystyle \ alpha}$ $\ alfa$ este un unghi drept, obții $\beta =\pi /2-\gamma$ ${\ displaystyle \ beta = \ pi / 2- \ gamma}$ ${\ displaystyle \ beta = \ pi / 2- \ gamma}$ prin urmare

{\frac {\sin ^{2}\gamma +\sin ^{2}\beta }{\sin ^{2}\alpha }}=\sin ^{2}(\pi /2-\beta )+\sin ^{2}\beta =\cos ^{2}\beta +\sin ^{2}\beta =1.

{\ displaystyle {\ frac {\ sin ^ {2} \ gamma + \ sin ^ {2} \ beta} {\ sin ^ {2} \ alpha}} = \ sin ^ {2} (\ pi / 2- \ beta) + \ sin ^ {2} \ beta = \ cos ^ {2} \ beta + \ sin ^ {2} \ beta = 1.}

{\ displaystyle {\ frac {\ sin ^ {2} \ gamma + \ sin ^ {2} \ beta} {\ sin ^ {2} \ alpha}} = \ sin ^ {2} (\ pi / 2- \ beta) + \ sin ^ {2} \ beta = \ cos ^ {2} \ beta + \ sin ^ {2} \ beta = 1.}

Obținem astfel în acest caz teorema lui Pitagora

c^{2}+b^{2}=a^{2}.

{\ displaystyle c ^ {2} + b ^ {2} = a ^ {2}.}

c ^ {2} + b ^ {2} = a ^ {2}.

Generalizare care nu utilizează trigonometrie

Generalizarea teoremei lui Pitagora.

Este posibil să se extindă teorema lui Pitagora la orice triunghi fără a utiliza funcții trigonometrice precum sinus și cosinus. Având în vedere un triunghi $LA B. C.$ ${\ displaystyle ABC}$ $ABC$ ca și în figură, sunt trasate două segmente care leagă vârful $LA$ ${\ displaystyle A}$ $LA$ cu două puncte $g$ ${\ displaystyle g}$ $g$ Și $h$ ${\ displaystyle h}$ $h$ cuprinse în segmentul opus $B. C.$ ${\ displaystyle BC}$ $Î.Hr.$ (sau într-o extensie a acestuia), astfel încât colțurile $LA g B.$ ${\ displaystyle AgB}$ $AgB$ Și $LA h C.$ ${\ displaystyle AhC}$ $AhC$ sunt ambele egale cu unghiul $\alpha$ ${\ displaystyle \ alpha}$ $\ alfa$ a summitului $LA$ ${\ displaystyle A}$ $LA$ . Figura arată un caz în care unghiul $\alpha$ ${\ displaystyle \ alpha}$ $\ alfa$ este obtuz : dacă este acut, colonul $g$ ${\ displaystyle g}$ $g$ Și $h$ ${\ displaystyle h}$ $h$ sunt în ordine inversă (primul în dreapta și al doilea în stânga) și pot ieși din segment $B. C.$ ${\ displaystyle BC}$ $Î.Hr.$ .

Se aplică următoarea relație:

{\overline {AB}}^{2}+{\overline {AC}}^{2}={\overline {BC}}\cdot ({\overline {Bg}}+{\overline {hC}}).

{\ displaystyle {\ overline {AB}} ^ {2} + {\ overline {AC}} ^ {2} = {\ overline {BC}} \ cdot ({\ overline {Bg}} + {\ overline {hC }}).}

{\ displaystyle {\ overline {AB}} ^ {2} + {\ overline {AC}} ^ {2} = {\ overline {BC}} \ cdot ({\ overline {Bg}} + {\ overline {hC }}).}

Cand $\alpha$ ${\ displaystyle \ alpha}$ $\ alfa$ este un unghi drept, punctele $g$ ${\ displaystyle g}$ $g$ Și $h$ ${\ displaystyle h}$ $h$ coincid și obținem teorema lui Pitagora

{\overline {AB}}^{2}+{\overline {AC}}^{2}={\overline {BC}}\cdot ({\overline {Bg}}+{\overline {hC}})={\overline {BC}}^{2}.

{\ displaystyle {\ overline {AB}} ^ {2} + {\ overline {AC}} ^ {2} = {\ overline {BC}} \ cdot ({\ overline {Bg}} + {\ overline {hC }}) = {\ overline {BC}} ^ {2}.}

{\ displaystyle {\ overline {AB}} ^ {2} + {\ overline {AC}} ^ {2} = {\ overline {BC}} \ cdot ({\ overline {Bg}} + {\ overline {hC }}) = {\ overline {BC}} ^ {2}.}

Relația generală poate fi demonstrată prin exploatarea asemănării dintre triunghiuri $LA B. C.$ ${\ displaystyle ABC}$ $ABC$ , $g B. LA$ ${\ displaystyle gBA}$ $gBA$ Și $h LA C.$ ${\ displaystyle hAC}$ $are C$ , ceea ce duce la relații

{\frac {\overline {AB}}{\overline {BC}}}={\frac {\overline {Bg}}{\overline {AB}}},\quad {\frac {\overline {AC}}{\overline {BC}}}={\frac {\overline {hC}}{\overline {AC}}}.

{\ displaystyle {\ frac {\ overline {AB}} {\ overline {BC}}} = {\ frac {\ overline {Bg}} {\ overline {AB}}}, \ quad {\ frac {\ overline { AC}} {\ overline {BC}}} = {\ frac {\ overline {hC}} {\ overline {AC}}}.}

{\ frac {\ overline {AB}} {\ overline {BC}}} = {\ frac {\ overline {Bg}} {\ overline {AB}}}, \ quad {\ frac {\ overline {AC}} {\ overline {BC}}} = {\ frac {\ overline {hC}} {\ overline {AC}}}.

Se obține astfel

{\overline {AB}}^{2}={\overline {BC}}\cdot {\overline {Bg}},\quad {\overline {AC}}^{2}={\overline {BC}}\cdot {\overline {hC}}.

{\ displaystyle {\ overline {AB}} ^ {2} = {\ overline {BC}} \ cdot {\ overline {Bg}}, \ quad {\ overline {AC}} ^ {2} = {\ overline { BC}} \ cdot {\ overline {hC}}.}

{\ displaystyle {\ overline {AB}} ^ {2} = {\ overline {BC}} \ cdot {\ overline {Bg}}, \ quad {\ overline {AC}} ^ {2} = {\ overline { BC}} \ cdot {\ overline {hC}}.}

Prin adăugarea celor două egalități se obține relația inițială.

Generalizare la toate cifrele similare

Teorema lui Pitagora continuă să fie valabilă atunci când de fiecare parte a unui triunghi dreptunghiular sunt construite figuri similare, chiar dacă nu sunt regulate. Afirmația sa devine:

În fiecare triunghi dreptunghiular, aria oricărui poligon, chiar curbiliniar, construită pe hipotenuză este egală cu suma ariilor poligoanelor, similară cu cea construită pe hipotenuză, construită pe picioare.

Demonstrație

Sunt:

la

{\ displaystyle a}

la

Și

b

{\ displaystyle b}

b

catheti

c

{\ displaystyle c}

c

ipotenuza

A_{1}

{\ displaystyle A_ {1}}

{\ displaystyle A_ {1}}

zona poligonului construită pe

la

{\ displaystyle a}

la

A_{2}

{\ displaystyle A_ {2}}

{\ displaystyle A_ {2}}

zona poligonului construit pe

b

{\ displaystyle b}

b

A_{3}

{\ displaystyle A_ {3}}

{\ displaystyle A_ {3}}

zona poligonului construit pe

c .

{\ displaystyle c.}

{\ displaystyle c.}

Și

k=a/b

{\ displaystyle k = a / b}

{\ displaystyle k = a / b}

relația dintre picioare

h=c/b

{\ displaystyle h = c / b}

{\ displaystyle h = c / b}

relația dintre hipotenuză și catet

b .

{\ displaystyle b.}

{\ displaystyle b.}

Prin teorema lui Pitagora în formă clasică rezultă:

c^{2}=a^{2}+b^{2}=k^{2}b^{2}+b^{2}=b^{2}(1+k^{2}),

{\ displaystyle c ^ {2} = a ^ {2} + b ^ {2} = k ^ {2} b ^ {2} + b ^ {2} = b ^ {2} (1 + k ^ {2 }),}

{\ displaystyle c ^ {2} = a ^ {2} + b ^ {2} = k ^ {2} b ^ {2} + b ^ {2} = b ^ {2} (1 + k ^ {2 }),}

prin urmare

c^{2}/b^{2}=1+k^{2}.

{\ displaystyle c ^ {2} / b ^ {2} = 1 + k ^ {2}.}

{\ displaystyle c ^ {2} / b ^ {2} = 1 + k ^ {2}.}

Amintindu-ne că dacă două poligoane similare au 2 laturi corespunzătoare în relație $h$ ${\ displaystyle h}$ $h$ atunci suprafețele lor sunt legate $h^{2}$ ${\ displaystyle h ^ {2}}$ $h ^ 2$ , după ce am definit $h=c/b$ ${\ displaystyle h = c / b}$ $h = c / b$ , se pare

A_{3}=A_{2}h^{2}=A_{2}c^{2}/b^{2}=A_{2}(1+k^{2}).

{\ displaystyle A_ {3} = A_ {2} h ^ {2} = A_ {2} c ^ {2} / b ^ {2} = A_ {2} (1 + k ^ {2}).}

{\ displaystyle A_ {3} = A_ {2} h ^ {2} = A_ {2} c ^ {2} / b ^ {2} = A_ {2} (1 + k ^ {2}).}

După ce a definit, de asemenea, egal cu $k$ ${\ displaystyle k}$ $k$ raportul dintre cele două picioare, din motivul anterior, este egal cu $k^{2}$ ${\ displaystyle k ^ {2}}$ $k ^ 2$ raportul dintre zonele poligoanelor similare construite pe ele, adică:

A_{1}=k^{2}A_{2}.

{\ displaystyle A_ {1} = k ^ {2} A_ {2}.}

{\ displaystyle A_ {1} = k ^ {2} A_ {2}.}

Prin urmare:

A_{1}+A_{2}=k^{2}A_{2}+A_{2}=(1+k^{2})A_{2}.

{\ displaystyle A_ {1} + A_ {2} = k ^ {2} A_ {2} + A_ {2} = (1 + k ^ {2}) A_ {2}.}

{\ displaystyle A_ {1} + A_ {2} = k ^ {2} A_ {2} + A_ {2} = (1 + k ^ {2}) A_ {2}.}

Prin urmare

A_{1}+A_{2}=A_{3}.

{\ displaystyle A_ {1} + A_ {2} = A_ {3}.}

{\ displaystyle A_ {1} + A_ {2} = A_ {3}.}

Așa cum a fost menit să demonstreze.

În spațiile preilbertiene

Teorema lui Pitagora poate fi „generalizată” la spații vectoriale de orice dimensiune, cum ar fi spațiul euclidian de dimensiunea 3 sau mai mare sau un spațiu vectorial pe un corp complex, continuând să se aplice și funcțiilor văzute ca sume infinite de vectori ca în analiză funcțional, atâta timp cât este posibil să se definească un produs scalar, făcând din spațiul vectorial un spațiu preilbertian.

Dovada este simplă, iar enunțul teoremei este: „Suma pătratelor normelor a doi vectori ortogonali este egală cu pătratul normei vectorului lor de sumă”, adică $v\perp u\Rightarrow \lVert v\rVert ^{2}+\lVert u\rVert ^{2}=\lVert v+u\rVert ^{2}.$ ${\ displaystyle v \ perp u \ Rightarrow \ lVert v \ rVert ^ {2} + \ lVert u \ rVert ^ {2} = \ lVert v + u \ rVert ^ {2}.}$ ${\ displaystyle v \ perp u \ Rightarrow \ lVert v \ rVert ^ {2} + \ lVert u \ rVert ^ {2} = \ lVert v + u \ rVert ^ {2}.}$

Demonstrație

Prin definiția ortogonalității, produsul scalar dintre $v$ ${\ displaystyle v}$ $v$ Și $tu$ ${\ displaystyle u}$ $tu$ este nul și face naveta. Afirmația teoremei este echivalentă, pentru definiția normei euclidiene, cu $\langle u,u\rangle +\langle v,v\rangle =\langle u+v,u+v\rangle$ ${\ displaystyle \ langle u, u \ rangle + \ langle v, v \ rangle = \ langle u + v, u + v \ rangle}$ ${\ displaystyle \ langle u, u \ rangle + \ langle v, v \ rangle = \ langle u + v, u + v \ rangle}$ . De fapt, prin dezvoltarea produsului scalar către al doilea membru, prin biliniaritate $\langle u+v,u+v\rangle =\langle u,u+v\rangle +\langle v,u+v\rangle =\langle u,u\rangle +\langle u,v\rangle +\langle v,u\rangle +\langle v,v\rangle$ ${\ displaystyle \ langle u + v, u + v \ rangle = \ langle u, u + v \ rangle + \ langle v, u + v \ rangle = \ langle u, u \ rangle + \ langle u, v \ rangle + \ langle v, u \ rangle + \ langle v, v \ rangle}$ ${\ displaystyle \ langle u + v, u + v \ rangle = \ langle u, u + v \ rangle + \ langle v, u + v \ rangle = \ langle u, u \ rangle + \ langle u, v \ rangle + \ langle v, u \ rangle + \ langle v, v \ rangle}$ dar $u\perp v$ ${\ displaystyle u \ perp v}$ ${\ displaystyle u \ perp v}$ asa de $\langle u,v\rangle =0=\langle v,u\rangle$ ${\ displaystyle \ langle u, v \ rangle = 0 = \ langle v, u \ rangle}$ ${\ displaystyle \ langle u, v \ rangle = 0 = \ langle v, u \ rangle}$ Pentru definire. Prin urmare, teorema este dovedită.

Legenda lui Pitagora și plăci

Reprezentarea grafică a teoremei.

O legendă spune că Pitagora și-a formulat teorema în timp ce aștepta o audiență cu Policrate . Așezat într-o sală mare a palatului Samos , Pitagora a început să observe plăcile pătrate ale podelei, se crede că a văzut una perfect ruptă pe o diagonală, astfel încât să formeze doi triunghiuri egale cu unghi drept, dar în plus pentru a fi 2 triunghiuri unghiulare, ele erau, de asemenea, isoscele, având cele două laturi egale. Pitagora și-a imaginat un pătrat construit pe diagonala de rupere a plăcii, un pătrat având ca laturi diagonalele plăcilor din jur.

Dovada este următoarea:

aria fiecărei plăci adiacente laterale a fost: 2 jumătăți de plăci (= 1 placă);
suma celor două zone a fost deci: 4 jumătăți de dale (= 2 dale);
aria pătratului construit pe ipotenuză (diagonala plăcii) era: 4 jumătăți plăci. ^[8]

Sensul ezoteric al teoremei

Inscripție grafică similară teoremei lui Pitagora de către maeștrii constructori pe portalul Baugewerkeschule („Școala de construcții”) din Zittau , în sud-estul Saxoniei (Germania)

În realitate, teorema lui Pitagora nu a fost considerată doar o lege matematică a gândirii , ci și o lege ontologică , adică a ființei , referitoare la realitatea omului și a lumii. Semnificația concretă a cunoașterii este făcută actuală de obiectele înseși, de linia de tăiere și de raportor, inscripționate într-o formă pătrilobată care reprezintă forul ecleziastic după August, Constantin și mai ales Sf. Augustin pentru care momentul istoric este definit în durata sa eternă , cu toate acestea cu o referire corală la cruce.

Una dintre posibilele interpretări ale teoremei care a fost pronunțată până astăzi în cadrul francmasoneriei , ^[9] unde emblema pătratelor construite pe laturile unui triunghi dreptunghiular apare în bijuteria purtată de bătrânii ex-venerabili maeștri (numit trecut Masters ), ^[10] relatează voința Raiului , adică Providența , reprezentată de catetul vertical, cu voința individualității umane unice, simbolizată de catetul orizontal. Cu cât individul, în loc să își extindă în mod arbitrar propria voință, încearcă să o adapteze la cea a Raiului, cu atât va suferi mai puțin greutatea Destinului , adică a hipotenuzei și, prin urmare, cu atât mai mult va fi capabil să domine forțe ale necesității care cântăresc asupra vieții sale. ^[11]

„Echilibrul dintre Voință și Providență, pe de o parte, și Destin, pe de altă parte, a fost simbolizat geometric de triunghiul dreptunghiular, ale cărui laturi sunt proporționale, respectiv, cu numerele 3, 4 și 5, un triunghi căruia pitagoreismul i-a acordat o mare importanță și care , printr-o coincidență care este, de asemenea, foarte demn de remarcat, are la fel de mult în tradiția Orientului Îndepărtat. Dacă Providența este reprezentată de 3, Voința umană de 4 și Destinul de 5, în acest triunghi avem: 3 ² + 4 ² = 5 ² ; pătratul numerelor indică faptul că aceasta se referă la domeniul forțelor universale, adică la domeniul sufletesc , ceea ce corespunde Omului în „ macrocosmos ” și în centrul căruia, ca termen median, voința este situat în „ microcosmos ”. ”

( René Guénon , La Grande Triade , cap. XXI, Revue de la Table Ronde, Paris / Nancy, 1946, trad. It. În „Letter and Spirit. Review of traditional studies”, nr. 36 )

Notă

^ Umberto Eco și Riccardo Fedriga (editat de), Filosofia și poveștile sale - Antichitate și Evul Mediu , Bari-Roma, Laterza, 2014, p. 30, ISBN 978-88-581-2831-2 .
^ Boyer, History of Mathematics , cit., P. 20.
^(EN) Alpay Özdural (1995). Omar Khayyam, matematicieni și „conversații” cu artizani. Jurnalul Societății de Arhitectură Vol. 54, nr. 1, martie, 1995
^(EN) Alpay Özdural, Mathematics and Arts: Connections between Theory and Practice in the Medieval Islamic World, Historia Mathematica, Volume 27, Issue 2, May 2000, Pages 171-201 .
^(EN) A se vedea apendicele LJ Rogers din 1897. Biografia lui Henry Perigal: pe anumite poligoane regulate din rețeaua modulară . Proceedings London Mathematical Society. Volumul s1-29, Anexa pp. 732-735.
^(EN) Disecții geometrice și transpuneri
^ Paolo Calicchio, formula principală a teoremei lui Pitagora și formule inverse , pe Exercizimatematica.com , 29 martie 2018. Accesat 25 martie 2021 .
^ Legenda lui Pitagora și a plăcilor Policrates
^ René Guénon , Considerații despre inițiere , cap. XIV, Paris, 1946.
^ Arturo Reghini , Numere sacre și geometrie pitagorică , Genova, Il Basilisco, 1931.
^ Interpretare simbolică a teoremei lui Pitagora , pe acam.it.

Bibliografie

Carl B. Boyer , Istoria matematicii , Mondadori, Milano, 1990. ISBN 978-88-04-33431-6
Gino Loria , Științele exacte în Grecia antică , ediția a II-a, Milano 1914

Elemente conexe

Alte proiecte

Wikicitatul conține citate din sau despre teorema lui Pitagora
Wikimedia Commons conține imagini sau alte fișiere despre teorema lui Pitagora

linkuri externe

( EN )Teorema lui Pitagora , pe Encyclopedia Britannica , Encyclopædia Britannica, Inc.
( EN ) 54 de dovezi ale teoremei lui Pitagora , pe facultate.umb.edu .
Unele animații grafice ale diferitelor dovezi ale teoremei lui Pitagora , pe demonstrations.wolfram.com .
Animația dovezii lui Euclid , pe walter-fendt.de . Adus la 16 decembrie 2004 (arhivat din original la 4 decembrie 2004) .

Controlul autorității	Thesaurus BNCF 23251 · LCCN ( EN ) sh85109374 · GND ( DE ) 4176546-1 · BNF ( FR ) cb11946942j (data) · BNE ( ES ) XX4809534 (data) · NDL ( EN , JA ) 00934581

Portale Filosofia

Portale Matematica

[1] Umberto Eco și Riccardo Fedriga (editat de), Filosofia și poveștile sale - Antichitate și Evul Mediu , Bari-Roma, Laterza, 2014, p. 30, ISBN 978-88-581-2831-2 .

[2] Boyer, History of Mathematics , cit., P. 20.

[3] (EN) Alpay Özdural (1995). Omar Khayyam, matematicieni și „conversații” cu artizani. Jurnalul Societății de Arhitectură Vol. 54, nr. 1, martie, 1995

[4] (EN) Alpay Özdural, Mathematics and Arts: Connections between Theory and Practice in the Medieval Islamic World, Historia Mathematica, Volume 27, Issue 2, May 2000, Pages 171-201 .

[5] (EN) A se vedea apendicele LJ Rogers din 1897. Biografia lui Henry Perigal: pe anumite poligoane regulate din rețeaua modulară . Proceedings London Mathematical Society. Volumul s1-29, Anexa pp. 732-735.

[6] (EN) Disecții geometrice și transpuneri

[7] Paolo Calicchio, formula principală a teoremei lui Pitagora și formule inverse , pe Exercizimatematica.com , 29 martie 2018. Accesat 25 martie 2021 .

[8] Legenda lui Pitagora și a plăcilor Policrates

[9] René Guénon , Considerații despre inițiere , cap. XIV, Paris, 1946.

[10] Arturo Reghini , Numere sacre și geometrie pitagorică , Genova, Il Basilisco, 1931.

[11] Interpretare simbolică a teoremei lui Pitagora , pe acam.it.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]