Transformarea Lorentz

Hendrik Antoon Lorentz într-un portret de Menso Kamerlingh Onnes

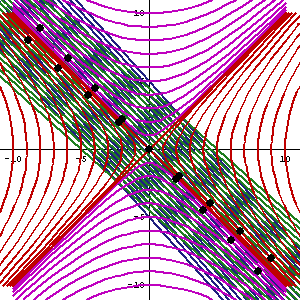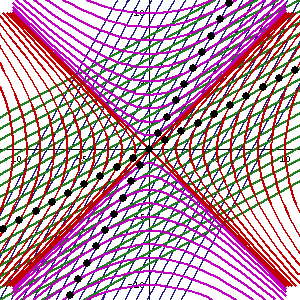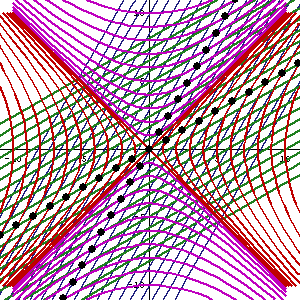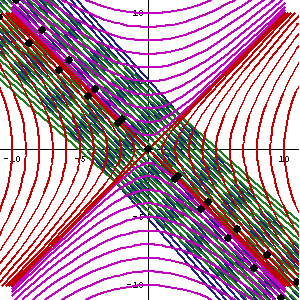
O vizualizare a transformării Lorentz. Doar una dintre coordonatele spațiale este luată în considerare. Liniile subțiri cu caractere aldine care se încrucișează cu unghiuri drepte indică coordonatele de timp și distanța unui observator în repaus cu privire la acea referință; liniile drepte oblice continue indică grila de coordonate a unui observator care se deplasează în raport cu aceeași referință.

În fizică , transformările Lorentz , formulate de fizicianul Hendrik Antoon Lorentz , sunt transformări liniare ale coordonatelor care permit descrierea modului în care măsurarea timpului și spațiului variază între două sisteme de referință inerțiale , adică sisteme în care obiectul măsurării este în mișcare rectilinie uniformă. cu privire la observator.

La rândul său, Albert Einstein a derivat transformările Lorentz în articolul din 1905 despre relativitatea specială, postulând constanța vitezei luminii în fiecare cadru de referință și validitatea relativității galileene . Faptul că ecuația undei este conservată sub transformarea Lorentz permite să scrie ecuațiile Maxwell ale electromagnetismului într-o formă invariantă în trecerea dintre două sisteme de referință în mișcare relativă. Aceasta a eliminat contradicțiile existente între electromagnetism și mecanica clasică și a explicat rezultatele nule ale experimentului Michelson-Morley .

Grupul transformărilor Lorentz , deși include și rotațiile clasice ale axelor spațiale, se caracterizează prin prezența amplificărilor (literalmente în italiană „thrust”), adică transformările dintre două sisteme inerțiale în mișcare relativă. Aceste transformări constau în esență din rotații care implică și orientarea axei timpului.

Istorie

Transformările Lorentz au fost descoperite și publicate pentru prima dată de Joseph Larmor în 1897 . ^[1] Cu toate acestea, deja cu zece ani mai devreme ( 1887 ), Woldemar Voigt publicase transformări care difereau doar într-un factor Lorentz , dar care prezentau toate caracteristicile principale ale relativității speciale, cu singurul defect de a nu forma un grup. ^[2] ^[3] ^[4] În 1905 , Henri Poincaré , celebrul matematician francez, a numit aceste transformări în cinstea fizicianului și matematicianului olandez Hendrik Antoon Lorentz , care își publicase versiunea finală în 1904 . Poincarè însuși a fost cel care a revizuit formalismul transformărilor pentru a le converti în forma coerentă și complet solidă pe care o cunoaștem astăzi.

Lorentz credea în ipoteza eterului luminifer ; numai Albert Einstein , dezvoltând teoria specială a relativității , a dat o bază adecvată pentru aplicarea ei.

Transformări între sisteme în configurație standard

O transformare Lorentz este o transformare liniară astfel încât, pornind de la coordonatele unui eveniment în spațiu-timp în sistemul de referință cartesian inerțial $S(t,x,y,z)$ ${\ displaystyle S (t, x, y, z)}$ $S (t, x, y, z)$ , coordonatele sunt obținute în raport cu un sistem de referință analog $S'(t',x',y',z')$ ${\ displaystyle S '(t', x ', y', z ')}$ $S '(t', x ', y', z ')$ care se mișcă uniform față de primul.

Mulțimea tuturor transformărilor Lorentz formează un grup , grupul Lorentz , numit și grupul omogen Lorentz . Este un subgrup al grupului Poincaré . Din legile transformării Lorentz este posibil să se demonstreze că intervalul:

ds^{2}=c^{2}dt^{2}-dx^{2}-dy^{2}-dz^{2}

{\ displaystyle ds ^ {2} = c ^ {2} dt ^ {2} -dx ^ {2} -dy ^ {2} -dz ^ {2}}

ds ^ 2 = c ^ 2dt ^ 2 - dx ^ 2 - dy ^ 2 - dz ^ 2

rămâne neschimbată în urma unei transformări Lorentz. ^[5] O cantitate care se păstrează în acest fel se numește invariant Lorentz și setul de transformări care rămân neschimbate $ds^{2}$ ${\ displaystyle ds ^ {2}}$ $ds ^ 2$ este grupul Lorentz.

Grupul Poincaré, numit și grupul Lorentz neomogen , corespunde setului de transformări care lasă intervalul neschimbat:

ds^{2}(x,y)=(x_{0}-y_{0})^{2}-(x_{1}-y_{1})^{2}-(x_{2}-y_{2})^{2}-(x_{3}-y_{3})^{2}

{\ displaystyle ds ^ {2} (x, y) = (x_ {0} -y_ {0}) ^ {2} - (x_ {1} -y_ {1}) ^ {2} - (x_ {2 } -y_ {2}) ^ {2} - (x_ {3} -y_ {3}) ^ {2}}

ds ^ 2 (x, y) = (x_0 - y_0) ^ 2 - (x_1 - y_1) ^ 2 - (x_2 - y_2) ^ 2 - (x_3 - y_3) ^ 2

Cantitățile care sunt conservate în urma transformărilor grupului Lorentz se numesc covarianți . Ecuațiile care descriu fenomenele naturale sunt covariante. ^[6]

Un observator O situat la originea unui sistem de referință local F folosește coordonatele ( x, y, z, t ) pentru a descrie un eveniment în spațiu-timp.

Transformări în direcția x

În configurație, această configurație standard presupune că ${S.}^{'}$ ${\ displaystyle S '}$ $da$ are cele trei axe spațiale paralele cu cele ale $S.$ ${\ displaystyle S}$ $S.$ , că sistemul ${S.}^{'}$ ${\ displaystyle S '}$ $da$ deplasează-te cu viteză $\mathbf {v}$ ${\ displaystyle \ mathbf {v}}$ $\ mathbf {v}$ de-a lungul axei $X$ ${\ displaystyle x}$ $X$ din $S.$ ${\ displaystyle S}$ $S.$ și că originile celor două sisteme de referință coincid pentru $t'=t=0$ ${\ displaystyle t '= t = 0}$ $t '= t = 0$ . În acest context, transformările Lorentz iau forma: ^[7]

{\begin{cases}t'=\displaystyle \gamma \left(t-{\frac {v}{c^{2}}}x\right)\\x'=\gamma \left(x-vt\right)\\y'=y\\z'=z\end{cases}}

{\ displaystyle {\ begin {cases} t '= \ displaystyle \ gamma \ left (t - {\ frac {v} {c ^ {2}}} x \ right) \\ x' = \ gamma \ left (x -vt \ right) \\ y '= y \\ z' = z \ end {cases}}}

{\ displaystyle {\ begin {cases} t '= \ displaystyle \ gamma \ left (t - {\ frac {v} {c ^ {2}}} x \ right) \\ x' = \ gamma \ left (x -vt \ right) \\ y '= y \\ z' = z \ end {cases}}}

unde este:

\gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}

{\ displaystyle \ gamma = {\ frac {1} {\ sqrt {1 - {\ frac {v ^ {2}} {c ^ {2}}}}}}

\ gamma = \ frac {1} {\ sqrt {1 - \ frac {v ^ 2} {c ^ 2}}}

se numește factorul Lorentz , în timp ce $c$ ${\ displaystyle c}$ $c$ este viteza luminii în vid. Prezentarea celor patru vectori:

x^{\mu }={\begin{bmatrix}ct\\x\\y\\z\end{bmatrix}}

{\ displaystyle x ^ {\ mu} = {\ begin {bmatrix} ct \\ x \\ y \\ z \ end {bmatrix}}}

x ^ \ mu = \ begin {bmatrix} ct \\ x \\ y \\ z \ end {bmatrix}

cele patru ecuații de mai sus pot fi exprimate printr-o relație matricială:

x'^{\nu }=\Lambda ^{\nu }{}_{\mu }x^{\mu }

{\ displaystyle x '^ {\ nu} = \ Lambda ^ {\ nu} {} _ {\ mu} x ^ {\ mu}}

{\ displaystyle x '^ {\ nu} = \ Lambda ^ {\ nu} {} _ {\ mu} x ^ {\ mu}}

unde este $\Lambda$ ${\ displaystyle \ Lambda}$ $\ Lambda$ este matricea de transformare legată de transformări într-o configurație standard lungă $X$ ${\ displaystyle x}$ $X$ :

{\begin{bmatrix}ct'\\x'\\y'\\z'\end{bmatrix}}={\begin{bmatrix}\gamma &-{\frac {v}{c}}\gamma &0&0\\-{\frac {v}{c}}\gamma &\gamma &0&0\\0&0&1&0\\0&0&0&1\\\end{bmatrix}}{\begin{bmatrix}ct\\x\\y\\z\end{bmatrix}}

{\ displaystyle {\ begin {bmatrix} ct '\\ x' \\ y '\\ z' \ end {bmatrix}} = {\ begin {bmatrix} \ gamma & - {\ frac {v} {c}} \ gamma & 0 & 0 \\ - {\ frac {v} {c}} \ gamma & \ gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\\ end {bmatrix}} {\ begin {bmatrix} ct \\ x \\ y \ \ z \ end {bmatrix}}}

\ begin {bmatrix} ct '\\ x' \\ y '\\ z' \ end {bmatrix} = \ begin {bmatrix} \ gamma & - \ frac {v} {c} \ gamma & 0 & 0 \\ - \ frac {v} {c} \ gamma & \ gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \ end {bmatrix} \ begin {bmatrix} ct \ \ x \\ y \\ z \ end {bmatrix}

Transformările $\Lambda$ ${\ displaystyle \ Lambda}$ $\ Lambda$ cu $\det(\Lambda ^{a}{}_{b})\,=+1$ ${\ displaystyle \ det (\ Lambda ^ {a} {} _ {b}) \, = + 1}$ $\ det (\ Lambda ^ a {} _ b) \, = + 1$ aparțin propriului grup al lui Lorentz , care este format din amplificări și rotații spațiale, în timp ce cei cu $\det(\Lambda ^{a}{}_{b})\,=-1$ ${\ displaystyle \ det (\ Lambda ^ {a} {} _ {b}) \, = - 1}$ $\ det (\ Lambda ^ a {} _ b) \, = - 1$ sunt numite transformări improprii Lorentz și nu formează un grup. Acestea din urmă includ reflecții spațiale și / sau temporale, astfel încât să modifice paritatea sistemului celor patru axe de referință. În programul lui Erlangen , spațiul Minkowski poate fi văzut ca geometria definită de grupul Poincarè care combină transformările Lorentz cu traduceri.

Transformări în direcția y sau z

Transformările dintre două sisteme care se traduc de-a lungul axelor $y$ ${\ displaystyle y}$ $y$ sau $z$ ${\ displaystyle z}$ $z$ sunt analogi cu cazul standard. Către $y$ ${\ displaystyle y}$ $y$ :

{\begin{aligned}t'&=\gamma \left(t-{\tfrac {v}{c^{2}}}y\right)\\x'&=x\\y'&=\gamma \left(y-vt\right)\\z'&=z\end{aligned}}

{\ displaystyle {\ begin {align} t '& = \ gamma \ left (t - {\ tfrac {v} {c ^ {2}}} y \ right) \\ x' & = x \\ y '& = \ gamma \ left (y-vt \ right) \\ z '& = z \ end {align}}}

{\ displaystyle {\ begin {align} t '& = \ gamma \ left (t - {\ tfrac {v} {c ^ {2}}} y \ right) \\ x' & = x \\ y '& = \ gamma \ left (y-vt \ right) \\ z '& = z \ end {align}}}

care poate fi scris sintetic:

{\begin{bmatrix}ct'\\x'\\y'\\z'\end{bmatrix}}={\begin{bmatrix}\gamma &0&-\beta \gamma &0\\0&1&0&0\\-\beta \gamma &0&\gamma &0\\0&0&0&1\\\end{bmatrix}}{\begin{bmatrix}c\,t\\x\\y\\z\end{bmatrix}}\qquad \mathbf {\beta } ={\frac {\mathbf {v} }{c}}

{\ displaystyle {\ begin {bmatrix} ct '\\ x' \\ y '\\ z' \ end {bmatrix}} = {\ begin {bmatrix} \ gamma & 0 & - \ beta \ gamma & 0 \\ 0 & 1 & 0 & 0 \\ - \ beta \ gamma & 0 & \ gamma & 0 \\ 0 & 0 & 0 & 1 \\\ end {bmatrix}} {\ begin {bmatrix} c \, t \\ x \\ y \\ z \ end {bmatrix}} \ qquad \ mathbf {\ beta} = {\ frac {\ mathbf {v}} {c}}}

\ begin {bmatrix} ct '\\ x' \\ y '\\ z' \ end {bmatrix} = \ begin {bmatrix} \ gamma & 0 & - \ beta \ gamma & 0 \\ 0 & 1 & 0 & 0 \\ - \ beta \ gamma & 0 & \ gamma & 0 \ \ 0 & 0 & 0 & 1 \\ \ end {bmatrix} \ begin {bmatrix} c \, t \\ x \\ y \\ z \ end {bmatrix} \ qquad \ mathbf \ beta = \ frac {\ mathbf v} {c}

unde este $\mathbf {v}$ ${\ displaystyle \ mathbf {v}}$ $\ mathbf v$ este în direcția $y$ ${\ displaystyle y}$ $y$ . Către $z$ ${\ displaystyle z}$ $z$ avem, în mod similar:

{\begin{aligned}t'&=\gamma \left(t-{\tfrac {v}{c^{2}}}z\right)\\x'&=x\\y'&=y\\z'&=\gamma \left(z-vt\right)\\\end{aligned}}

{\ displaystyle {\ begin {align} t '& = \ gamma \ left (t - {\ tfrac {v} {c ^ {2}}} z \ right) \\ x' & = x \\ y '& = y \\ z '& = \ gamma \ left (z-vt \ right) \\\ end {align}}}

{\ displaystyle {\ begin {align} t '& = \ gamma \ left (t - {\ tfrac {v} {c ^ {2}}} z \ right) \\ x' & = x \\ y '& = y \\ z '& = \ gamma \ left (z-vt \ right) \\\ end {align}}}

care poate fi scris sintetic:

{\begin{bmatrix}ct'\\x'\\y'\\z'\end{bmatrix}}={\begin{bmatrix}\gamma &0&0&-\beta \gamma \\0&1&0&0\\0&0&1&0\\-\beta \gamma &0&0&\gamma \\\end{bmatrix}}{\begin{bmatrix}c\,t\\x\\y\\z\end{bmatrix}}

{\ displaystyle {\ begin {bmatrix} ct '\\ x' \\ y '\\ z' \ end {bmatrix}} = {\ begin {bmatrix} \ gamma & 0 & 0 & - \ beta \ gamma \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ - \ beta \ gamma & 0 & 0 & \ gamma \\\ end {bmatrix}} {\ begin {bmatrix} c \, t \\ x \\ y \\ z \ end {bmatrix}}}

\ begin {bmatrix} ct '\\ x' \\ y '\\ z' \ end {bmatrix} = \ begin {bmatrix} \ gamma & 0 & 0 & - \ beta \ gamma \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ - \ beta \ gamma & 0 & 0 & \ gamma \\ \ end {bmatrix} \ begin {bmatrix} c \, t \\ x \\ y \\ z \ end {bmatrix}

unde este $\mathbf {v}$ ${\ displaystyle \ mathbf {v}}$ $\ mathbf v$ Și $\mathbf {\beta }$ ${\ displaystyle \ mathbf {\ beta}}$ $\ mathbf \ beta$ Sunt în direcție $z$ ${\ displaystyle z}$ $z$ .

Transformările Lorentz sunt adesea notate cu $\mathbf {\Lambda }$ ${\ displaystyle \ mathbf {\ Lambda}}$ $\ mathbf \ Lambda$ și sunt valabile pentru orice patru-generic generic $\mathbf {X}$ ${\ displaystyle \ mathbf {X}}$ $\ mathbf X$ : ^[8]

\mathbf {X} '={\boldsymbol {\Lambda }}(v)\mathbf {X}

{\ displaystyle \ mathbf {X} '= {\ boldsymbol {\ Lambda}} (v) \ mathbf {X}}

\ mathbf {X} '= \ boldsymbol {\ Lambda} (v) \ mathbf {X}

Transformări într-o direcție generică

Pentru o transformare într-o direcție arbitrară între două sisteme cu axe paralele și origini coincidente în spațiu-timp este convenabil să se descompună vectorul spațial $\mathbf {r}$ ${\ displaystyle \ mathbf {r}}$ $\ mathbf {r}$ în două componente, respectiv perpendiculare și paralele cu viteza $\mathbf {v}$ ${\ displaystyle \ mathbf {v}}$ $\ mathbf {v}$ :

\mathbf {r} =\mathbf {r} _{\perp }+\mathbf {r} _{\|}

{\ displaystyle \ mathbf {r} = \ mathbf {r} _ {\ perp} + \ mathbf {r} _ {\ |}}

\ mathbf {r} = \ mathbf {r} _ \ perp + \ mathbf {r} _ \ |

Se observă că doar componenta $\mathbf {r} _{\|}$ ${\ displaystyle \ mathbf {r} _ {\ |}}$ $\ mathbf {r} _ \ |$ in directia $\mathbf {v}$ ${\ displaystyle \ mathbf {v}}$ $\ mathbf {v}$ este deformat de factor $\gamma$ ${\ displaystyle \ gamma}$ $\gamă$ :

{\begin{cases}t'=\gamma \left(t-{\frac {\mathbf {v} \cdot \mathbf {r} }{c^{2}}}\right)\\\mathbf {r'} =\mathbf {r} _{\perp }+\gamma (\mathbf {r} _{\|}-\mathbf {v} t)\end{cases}}

{\ displaystyle {\ begin {cases} t '= \ gamma \ left (t - {\ frac {\ mathbf {v} \ cdot \ mathbf {r}} {c ^ {2}}} \ right) \\\ mathbf {r '} = \ mathbf {r} _ {\ perp} + \ gamma (\ mathbf {r} _ {\ |} - \ mathbf {v} t) \ end {cases}}}

\ begin {cases} t '= \ gamma \ left (t - \ frac {\ mathbf {v} \ cdot \ mathbf {r}} {c ^ {2}} \ right) \\ \ mathbf {r'} = \ mathbf {r} _ \ perp + \ gamma (\ mathbf {r} _ \ | - \ mathbf {v} t) \ end {cases}

A doua expresie poate fi rescrisă ca:

\mathbf {r'} =\mathbf {r} +\left({\frac {\gamma -1}{v^{2}}}(\mathbf {r} \cdot \mathbf {v} )-\gamma t\right)\mathbf {v}

{\ displaystyle \ mathbf {r '} = \ mathbf {r} + \ left ({\ frac {\ gamma -1} {v ^ {2}}} (\ mathbf {r} \ cdot \ mathbf {v}) - \ gamma t \ right) \ mathbf {v}}

\ mathbf {r '} = \ mathbf {r} + \ left (\ frac {\ gamma -1} {v ^ 2} (\ mathbf {r} \ cdot \ mathbf {v}) - \ gamma t \ right) \ mathbf {v}

Această expresie nu are în vedere rotația axelor și, prin urmare, nu identifică transformarea Lorentz mai generală.

Forma matricei

Această transformare poate fi exprimată folosind o matrice de blocuri :

{\begin{bmatrix}ct'\\\mathbf {r'} \end{bmatrix}}={\begin{bmatrix}\gamma &-\gamma {\boldsymbol {\beta }}^{\mathrm {T} }\\-\gamma {\boldsymbol {\beta }}&\mathbf {I} +(\gamma -1){\boldsymbol {\beta }}{\boldsymbol {\beta }}^{\mathrm {T} }/\beta ^{2}\\\end{bmatrix}}{\begin{bmatrix}ct\\\mathbf {r} \end{bmatrix}}

{\ displaystyle {\ begin {bmatrix} ct '\\\ mathbf {r'} \ end {bmatrix}} = {\ begin {bmatrix} \ gamma & - \ gamma {\ boldsymbol {\ beta}} ^ {\ mathrm {T}} \\ - \ gamma {\ boldsymbol {\ beta}} & \ mathbf {I} + (\ gamma -1) {\ boldsymbol {\ beta}} {\ boldsymbol {\ beta}} ^ {\ mathrm {T}} / \ beta ^ {2} \\\ end {bmatrix}} {\ begin {bmatrix} ct \\\ mathbf {r} \ end {bmatrix}}}

\ begin {bmatrix} ct '\\ \ mathbf {r'} \ end {bmatrix} = \ begin {bmatrix} \ gamma & - \ gamma \ boldsymbol {\ beta} ^ \ mathrm {T} \\ - \ gamma \ boldsymbol {\ beta} & \ mathbf {I} + (\ gamma-1) \ boldsymbol {\ beta} \ boldsymbol {\ beta} ^ \ mathrm {T} / \ beta ^ 2 \\ \ end {bmatrix} \ begin {bmatrix} ct \\ \ mathbf {r} \ end {bmatrix}

unde este $\mathbf {I}$ ${\ displaystyle \ mathbf {I}}$ $\ mathbf {I}$ este matricea identică, $\mathbf {\beta } ={\frac {\mathbf {v} }{c}}$ ${\ displaystyle \ mathbf {\ beta} = {\ frac {\ mathbf {v}} {c}}}$ $\ mathbf \ beta = \ frac {\ mathbf v} {c}$ este viteza relativă în unități de c exprimată ca vector coloană:

{\boldsymbol {\beta }}={\frac {\mathbf {v} }{c}}\equiv {\begin{bmatrix}\beta _{x}\\\beta _{y}\\\beta _{z}\end{bmatrix}}={\frac {1}{c}}{\begin{bmatrix}v_{x}\\v_{y}\\v_{z}\end{bmatrix}}\equiv {\begin{bmatrix}\beta _{1}\\\beta _{2}\\\beta _{3}\end{bmatrix}}={\frac {1}{c}}{\begin{bmatrix}v_{1}\\v_{2}\\v_{3}\end{bmatrix}}

{\ displaystyle {\ boldsymbol {\ beta}} = {\ frac {\ mathbf {v}} {c}} \ equiv {\ begin {bmatrix} \ beta _ {x} \\\ beta _ {y} \\ \ beta _ {z} \ end {bmatrix}} = {\ frac {1} {c}} {\ begin {bmatrix} v_ {x} \\ v_ {y} \\ v_ {z} \ end {bmatrix} } \ equiv {\ begin {bmatrix} \ beta _ {1} \\\ beta _ {2} \\\ beta _ {3} \ end {bmatrix}} = {\ frac {1} {c}} {\ începe {bmatrix} v_ {1} \\ v_ {2} \\ v_ {3} \ end {bmatrix}}}

{\ displaystyle {\ boldsymbol {\ beta}} = {\ frac {\ mathbf {v}} {c}} \ equiv {\ begin {bmatrix} \ beta _ {x} \\\ beta _ {y} \\ \ beta _ {z} \ end {bmatrix}} = {\ frac {1} {c}} {\ begin {bmatrix} v_ {x} \\ v_ {y} \\ v_ {z} \ end {bmatrix} } \ equiv {\ begin {bmatrix} \ beta _ {1} \\\ beta _ {2} \\\ beta _ {3} \ end {bmatrix}} = {\ frac {1} {c}} {\ începe {bmatrix} v_ {1} \\ v_ {2} \\ v_ {3} \ end {bmatrix}}}

in timp ce $\mathbf {\beta } ^{T}={\frac {\mathbf {v} ^{T}}{c}}$ ${\ displaystyle \ mathbf {\ beta} ^ {T} = {\ frac {\ mathbf {v} ^ {T}} {c}}}$ $\ mathbf \ beta ^ T = \ frac {\ mathbf v ^ T} {c}$ este transpunerea sa, un vector linie:

{\boldsymbol {\beta }}^{\mathrm {T} }={\frac {\mathbf {v} ^{\mathrm {T} }}{c}}\equiv {\begin{bmatrix}\beta _{x}&\beta _{y}&\beta _{z}\end{bmatrix}}={\frac {1}{c}}{\begin{bmatrix}v_{x}&v_{y}&v_{z}\end{bmatrix}}\equiv {\begin{bmatrix}\beta _{1}&\beta _{2}&\beta _{3}\end{bmatrix}}={\frac {1}{c}}{\begin{bmatrix}v_{1}&v_{2}&v_{3}\\\end{bmatrix}}

{\ displaystyle {\ boldsymbol {\ beta}} ^ {\ mathrm {T}} = {\ frac {\ mathbf {v} ^ {\ mathrm {T}}} {c}} \ equiv {\ begin {bmatrix} \ beta _ {x} & \ beta _ {y} & \ beta _ {z} \ end {bmatrix}} = {\ frac {1} {c}} {\ begin {bmatrix} v_ {x} & v_ { y} & v_ {z} \ end {bmatrix}} \ equiv {\ begin {bmatrix} \ beta _ {1} & \ beta _ {2} & \ beta _ {3} \ end {bmatrix}} = {\ frac {1} {c}} {\ begin {bmatrix} v_ {1} & v_ {2} & v_ {3} \\\ end {bmatrix}}}

{\ displaystyle {\ boldsymbol {\ beta}} ^ {\ mathrm {T}} = {\ frac {\ mathbf {v} ^ {\ mathrm {T}}} {c}} \ equiv {\ begin {bmatrix} \ beta _ {x} & \ beta _ {y} & \ beta _ {z} \ end {bmatrix}} = {\ frac {1} {c}} {\ begin {bmatrix} v_ {x} & v_ { y} & v_ {z} \ end {bmatrix}} \ equiv {\ begin {bmatrix} \ beta _ {1} & \ beta _ {2} & \ beta _ {3} \ end {bmatrix}} = {\ frac {1} {c}} {\ begin {bmatrix} v_ {1} & v_ {2} & v_ {3} \\\ end {bmatrix}}}

cu $\beta$ ${\ displaystyle \ beta}$ $\ beta$ forma de $\mathbf {\beta }$ ${\ displaystyle \ mathbf {\ beta}}$ $\ mathbf {\ beta}$ :

\beta =|{\boldsymbol {\beta }}|={\sqrt {\beta _{x}^{2}+\beta _{y}^{2}+\beta _{z}^{2}}}

{\ displaystyle \ beta = | {\ boldsymbol {\ beta}} | = {\ sqrt {\ beta _ {x} ^ {2} + \ beta _ {y} ^ {2} + \ beta _ {z} ^ {2}}}}

\ beta = | \ boldsymbol {\ beta} | = \ sqrt {\ beta_x ^ 2 + \ beta_y ^ 2 + \ beta_z ^ 2}

Explicit:

{\begin{bmatrix}c\,t'\\x'\\y'\\z'\end{bmatrix}}={\begin{bmatrix}\gamma &-\gamma \,\beta _{x}&-\gamma \,\beta _{y}&-\gamma \,\beta _{z}\\-\gamma \,\beta _{x}&1+(\gamma -1){\dfrac {\beta _{x}^{2}}{\beta ^{2}}}&(\gamma -1){\dfrac {\beta _{x}\beta _{y}}{\beta ^{2}}}&(\gamma -1){\dfrac {\beta _{x}\beta _{z}}{\beta ^{2}}}\\-\gamma \,\beta _{y}&(\gamma -1){\dfrac {\beta _{y}\beta _{x}}{\beta ^{2}}}&1+(\gamma -1){\dfrac {\beta _{y}^{2}}{\beta ^{2}}}&(\gamma -1){\dfrac {\beta _{y}\beta _{z}}{\beta ^{2}}}\\-\gamma \,\beta _{z}&(\gamma -1){\dfrac {\beta _{z}\beta _{x}}{\beta ^{2}}}&(\gamma -1){\dfrac {\beta _{z}\beta _{y}}{\beta ^{2}}}&1+(\gamma -1){\dfrac {\beta _{z}^{2}}{\beta ^{2}}}\\\end{bmatrix}}{\begin{bmatrix}c\,t\\x\\y\\z\end{bmatrix}}

{\ displaystyle {\ begin {bmatrix} c \, t '\\ x' \\ y '\\ z' \ end {bmatrix}} = {\ begin {bmatrix} \ gamma & - \ gamma \, \ beta _ {x} & - \ gamma \, \ beta _ {y} & - \ gamma \, \ beta _ {z} \\ - \ gamma \, \ beta _ {x} & 1 + (\ gamma -1) { \ dfrac {\ beta _ {x} ^ {2}} {\ beta ^ {2}}} & (\ gamma -1) {\ dfrac {\ beta _ {x} \ beta _ {y}} {\ beta ^ {2}}} & (\ gamma -1) {\ dfrac {\ beta _ {x} \ beta _ {z}} {\ beta ^ {2}}} \\ - \ gamma \, \ beta _ { y} & (\ gamma -1) {\ dfrac {\ beta _ {y} \ beta _ {x}} {\ beta ^ {2}}} & 1 + (\ gamma -1) {\ dfrac {\ beta _ {y} ^ {2}} {\ beta ^ {2}}} și (\ gamma -1) {\ dfrac {\ beta _ {y} \ beta _ {z}} {\ beta ^ {2}} } \\ - \ gamma \, \ beta _ {z} & (\ gamma -1) {\ dfrac {\ beta _ {z} \ beta _ {x}} {\ beta ^ {2}}} & (\ gamma -1) {\ dfrac {\ beta _ {z} \ beta _ {y}} {\ beta ^ {2}}} & 1 + (\ gamma -1) {\ dfrac {\ beta _ {z} ^ {2}} {\ beta ^ {2}}} \\\ end {bmatrix}} {\ begin {bmatrix} c \, t \\ x \\ y \\ z \ end {bmatrix}}}

\ begin {bmatrix} c \, t '\\ x' \\ y '\\ z' \ end {bmatrix} = \ begin {bmatrix} \ gamma & - \ gamma \, \ beta_x & - \ gamma \, \ beta_y & - \ gamma \, \ beta_z \\ - \ gamma \, \ beta_x & 1 + (\ gamma-1) \ dfrac {\ beta_x ^ 2} {\ beta ^ 2} & (\ gamma-1) \ dfrac {\ beta_x \ beta_y} {\ beta ^ 2} & (\ gamma-1) \ dfrac {\ beta_x \ beta_z} {\ beta ^ 2} \\ - \ gamma \, \ beta_y & (\ gamma-1) \ dfrac {\ beta_y \ beta_x} {\ beta ^ 2} & 1 + (\ gamma-1) \ dfrac {\ beta_y ^ 2} {\ beta ^ 2} & (\ gamma-1) \ dfrac {\ beta_y \ beta_z } {\ beta ^ 2} \\ - \ gamma \, \ beta_z & (\ gamma-1) \ dfrac {\ beta_z \ beta_x} {\ beta ^ 2} & (\ gamma-1) \ dfrac {\ beta_z \ beta_y} {\ beta ^ 2} & 1 + (\ gamma-1) \ dfrac {\ beta_z ^ 2} {\ beta ^ 2} \\ \ end {bmatrix} \ begin {bmatrix} c \, t \\ x \\ y \\ z \ end {bmatrix}

Transformarea poate fi scrisă într-un mod similar cu precedentul:

\mathbf {X} '={\boldsymbol {\Lambda }}(\mathbf {v} )\mathbf {X}

{\ displaystyle \ mathbf {X} '= {\ boldsymbol {\ Lambda}} (\ mathbf {v}) \ mathbf {X}}

\ mathbf {X} '= \ boldsymbol {\ Lambda} (\ mathbf {v}) \ mathbf {X}

și are următoarea structură matricială:

{\begin{bmatrix}c\,t'\\x'\\y'\\z'\end{bmatrix}}={\begin{bmatrix}\Lambda _{00}&\Lambda _{01}&\Lambda _{02}&\Lambda _{03}\\\Lambda _{10}&\Lambda _{11}&\Lambda _{12}&\Lambda _{13}\\\Lambda _{20}&\Lambda _{21}&\Lambda _{22}&\Lambda _{23}\\\Lambda _{30}&\Lambda _{31}&\Lambda _{32}&\Lambda _{33}\\\end{bmatrix}}{\begin{bmatrix}c\,t\\x\\y\\z\end{bmatrix}}

{\ displaystyle {\ begin {bmatrix} c \, t '\\ x' \\ y '\\ z' \ end {bmatrix}} = {\ begin {bmatrix} \ Lambda _ {00} & \ Lambda _ { 01} & \ Lambda _ {02} & \ Lambda _ {03} \\\ Lambda _ {10} & \ Lambda _ {11} & \ Lambda _ {12} & \ Lambda _ {13} \\\ Lambda _ {20} & \ Lambda _ {21} & \ Lambda _ {22} & \ Lambda _ {23} \\\ Lambda _ {30} & \ Lambda _ {31} & \ Lambda _ {32} & \ Lambda _ {33} \\\ end {bmatrix}} {\ begin {bmatrix} c \, t \\ x \\ y \\ z \ end {bmatrix}}}

\ begin {bmatrix} c \, t '\\ x' \\ y '\\ z' \ end {bmatrix} = \ begin {bmatrix} \ Lambda_ {00} & \ Lambda_ {01} & \ Lambda_ {02} & \ Lambda_ {03} \\ \ Lambda_ {10} & \ Lambda_ {11} & \ Lambda_ {12} & \ Lambda_ {13} \\ \ Lambda_ {20} & \ Lambda_ {21} & \ Lambda_ {22} & \ Lambda_ {23} \\ \ Lambda_ {30} & \ Lambda_ {31} & \ Lambda_ {32} & \ Lambda_ {33} \\ \ end {bmatrix} \ begin {bmatrix} c \, t \\ x \\ y \\ z \ end {bmatrix}

ale cărei componente sunt:

{\begin{aligned}\Lambda _{00}&=\gamma \\\Lambda _{0i}&=\Lambda _{i0}=-\gamma \beta _{i}\\\Lambda _{ij}&=\Lambda _{ji}=(\gamma -1){\dfrac {\beta _{i}\beta _{j}}{\beta ^{2}}}+\delta _{ij}=(\gamma -1){\dfrac {v_{i}v_{j}}{v^{2}}}+\delta _{ij}\\\end{aligned}}

{\ displaystyle {\ begin {align} \ Lambda _ {00} & = \ gamma \\\ Lambda _ {0i} & = \ Lambda _ {i0} = - \ gamma \ beta _ {i} \\\ Lambda _ {ij} & = \ Lambda _ {ji} = (\ gamma -1) {\ dfrac {\ beta _ {i} \ beta _ {j}} {\ beta ^ {2}}} + \ delta _ {ij } = (\ gamma -1) {\ dfrac {v_ {i} v_ {j}} {v ^ {2}}} + \ delta _ {ij} \\\ end {align}}}

\ begin {align} \ Lambda_ {00} & = \ gamma \\ \ Lambda_ {0i} & = \ Lambda_ {i0} = - \ gamma \ beta_ {i} \\ \ Lambda_ {ij} & = \ Lambda_ {ji } = (\ gamma - 1) \ dfrac {\ beta_ {i} \ beta_ {j}} {\ beta ^ {2}} + \ delta_ {ij} = (\ gamma - 1) \ dfrac {v_i v_j} { v ^ 2} + \ delta_ {ij} \\ \ end {align}

unde este $\delta _{ij}$ ${\ displaystyle \ delta _ {ij}}$ $\ delta_ {ij}$ este delta Kronecker .

Relația dintre componentele paralele și perpendiculare

Pentru a relaționa componentele paralele și perpendiculare ale $\mathbf {r}$ ${\ displaystyle \ mathbf {r}}$ $\ mathbf {r}$ în ceea ce privește viteza de traducere a sistemelor de referință, considerăm transformarea pentru $\mathbf {r}$ ${\ displaystyle \ mathbf {r}}$ $\ mathbf {r}$ :

\mathbf {r} '=\mathbf {r} _{\parallel }'+\mathbf {r} _{\bot }'=\gamma \left(\mathbf {r} _{\parallel }-\mathbf {v} t\right)+\mathbf {r} _{\bot }

{\ displaystyle \ mathbf {r} '= \ mathbf {r} _ {\ parallel}' + \ mathbf {r} _ {\ bot} '= \ gamma \ left (\ mathbf {r} _ {\ parallel} - \ mathbf {v} t \ right) + \ mathbf {r} _ {\ bot}}

\ mathbf {r} '= \ mathbf {r} _ \ parallel' + \ mathbf {r} _ \ bot '= \ gamma \ left (\ mathbf {r} _ \ parallel - \ mathbf {v} t \ right) + \ mathbf {r} _ \ bot

adăugând $\scriptstyle 0=\gamma \mathbf {r} _{\bot }-\gamma \mathbf {r} _{\bot }$ ${\ displaystyle \ scriptstyle 0 = \ gamma \ mathbf {r} _ {\ bot} - \ gamma \ mathbf {r} _ {\ bot}}$ $\ scriptstyle 0 = \ gamma \ mathbf {r} _ \ bot- \ gamma \ mathbf {r} _ \ bot$ a sterge $\scriptstyle \gamma \mathbf {r} _{\parallel }$ ${\ displaystyle \ scriptstyle \ gamma \ mathbf {r} _ {\ parallel}}$ $\ scriptstyle \ gamma \ mathbf {r} _ \ parallel$ primesti:

{\begin{aligned}\mathbf {r} '&=(\gamma \mathbf {r} _{\parallel }{\color {Violet}+\gamma \mathbf {r} _{\bot }})-\gamma \mathbf {v} t+\mathbf {r} _{\bot }{\color {Violet}-\gamma \mathbf {r} _{\bot }}\\&=\gamma \mathbf {r} -\gamma \mathbf {v} t+(1-\gamma )\mathbf {r} _{\bot }\\\end{aligned}}

{\ displaystyle {\ begin {align} \ mathbf {r} '& = (\ gamma \ mathbf {r} _ {\ parallel} {\ color {Violet} + \ gamma \ mathbf {r} _ {\ bot}} ) - \ gamma \ mathbf {v} t + \ mathbf {r} _ {\ bot} {\ color {Violet} - \ gamma \ mathbf {r} _ {\ bot}} \\ & = \ gamma \ mathbf { r} - \ gamma \ mathbf {v} t + (1- \ gamma) \ mathbf {r} _ {\ bot} \\\ end {align}}}

\ begin {align} \ mathbf {r} '& = (\ gamma \ mathbf {r} _ \ parallel {\ color {Violet} + \ gamma \ mathbf {r} _ \ bot}) - \ gamma \ mathbf {v } t + \ mathbf {r} _ \ bot {\ color {Violet} - \ gamma \ mathbf {r} _ \ bot} \\ & = \ gamma \ mathbf {r} - \ gamma \ mathbf {v} t + (1- \ gamma) \ mathbf {r} _ \ bot \\ \ end {align}

Apoi adăugând $\scriptstyle 0=(1-\gamma )\mathbf {r} _{\parallel }-(1-\gamma )\mathbf {r} _{\parallel }$ ${\ displaystyle \ scriptstyle 0 = (1- \ gamma) \ mathbf {r} _ {\ parallel} - (1- \ gamma) \ mathbf {r} _ {\ parallel}}$ $\ scriptstyle 0 = (1- \ gamma) \ mathbf {r} _ \ parallel - (1- \ gamma) \ mathbf {r} _ \ parallel$ a sterge $\scriptstyle (1-\gamma )\mathbf {r} _{\bot }$ ${\ displaystyle \ scriptstyle (1- \ gamma) \ mathbf {r} _ {\ bot}}$ $\ scriptstyle (1- \ gamma) \ mathbf {r} _ \ bot$ :

{\begin{aligned}\mathbf {r} '&=\gamma \mathbf {r} -\gamma \mathbf {v} t+[(1-\gamma )\mathbf {r} _{\bot }{\color {Violet}+(1-\gamma )\mathbf {r} _{\parallel }}]{\color {Violet}-(1-\gamma )\mathbf {r} _{\parallel }}\\&=\gamma \mathbf {r} -\gamma \mathbf {v} t+(1-\gamma )\mathbf {r} +(\gamma -1)\mathbf {r} _{\parallel }\\\end{aligned}}

{\ displaystyle {\ begin {align} \ mathbf {r} '& = \ gamma \ mathbf {r} - \ gamma \ mathbf {v} t + [(1- \ gamma) \ mathbf {r} _ {\ bot } {\ color {Violet} + (1- \ gamma) \ mathbf {r} _ {\ parallel}}] {\ color {Violet} - (1- \ gamma) \ mathbf {r} _ {\ parallel}} \ \ & = \ gamma \ mathbf {r} - \ gamma \ mathbf {v} t + (1- \ gamma) \ mathbf {r} + (\ gamma -1) \ mathbf {r} _ {\ parallel} \ \\ end {align}}}

\ begin {align} \ mathbf {r} '& = \ gamma \ mathbf {r} - \ gamma \ mathbf {v} t + [(1- \ gamma) \ mathbf {r} _ \ bot {\ color {Violet } + (1- \ gamma) \ mathbf {r} _ \ parallel}] {\ color {Violet} - (1- \ gamma) \ mathbf {r} _ \ parallel} \\ & = \ gamma \ mathbf {r } - \ gamma \ mathbf {v} t + (1- \ gamma) \ mathbf {r} + (\ gamma-1) \ mathbf {r} _ \ parallel \\ \ end {align}

și de atunci $\scriptstyle \mathbf {r} _{\parallel }$ ${\ displaystyle \ scriptstyle \ mathbf {r} _ {\ parallel}}$ $\ scriptstyle \ mathbf {r} _ \ parallel$ Și $\mathbf {r}$ ${\ displaystyle \ mathbf {r}}$ $\ mathbf {r}$ sunt paralele avem:

\mathbf {r} _{\parallel }=r_{\parallel }{\dfrac {\mathbf {v} }{v}}=\left({\dfrac {\mathbf {r} \cdot \mathbf {v} }{v}}\right){\frac {\mathbf {v} }{v}}

{\ displaystyle \ mathbf {r} _ {\ parallel} = r _ {\ parallel} {\ dfrac {\ mathbf {v}} {v}} = \ left ({\ dfrac {\ mathbf {r} \ cdot \ mathbf {v}} {v}} \ right) {\ frac {\ mathbf {v}} {v}}}

\ mathbf {r} _ \ parallel = r_ \ parallel \ dfrac {\ mathbf {v}} {v} = \ left (\ dfrac {\ mathbf {r} \ cdot \ mathbf {v}} {v} \ right) \ frac {\ mathbf {v}} {v}

În acea relație $\mathbf {v} \over v$ ${\ displaystyle \ mathbf {v} \ over v}$ $\ mathbf {v} \ peste v$ este un vector unitate adimensional care are aceeași direcție ca $\scriptstyle \mathbf {r} _{\parallel }$ ${\ displaystyle \ scriptstyle \ mathbf {r} _ {\ parallel}}$ $\ scriptstyle \ mathbf {r} _ \ parallel$ , prin urmare:

{\begin{aligned}\mathbf {r} '&=\mathbf {r} -\gamma \mathbf {v} t+{\frac {(\gamma -1)\mathbf {r} \cdot \mathbf {v} }{v^{2}}}\mathbf {v} \\&=\mathbf {r} +\left({\frac {\gamma -1}{v^{2}}}\mathbf {r} \cdot \mathbf {v} -\gamma t\right)\mathbf {v} \\\end{aligned}}

{\ displaystyle {\ begin {align} \ mathbf {r} '& = \ mathbf {r} - \ gamma \ mathbf {v} t + {\ frac {(\ gamma -1) \ mathbf {r} \ cdot \ mathbf {v}} {v ^ {2}}} \ mathbf {v} \\ & = \ mathbf {r} + \ left ({\ frac {\ gamma -1} {v ^ {2}}} \ mathbf {r} \ cdot \ mathbf {v} - \ gamma t \ right) \ mathbf {v} \\\ end {align}}}

\ begin {align} \ mathbf {r} '& = \ mathbf {r} - \ gamma \ mathbf {v} t + \ frac {(\ gamma-1) \ mathbf {r} \ cdot \ mathbf {v}} {v ^ 2} \ mathbf {v} \\ & = \ mathbf {r} + \ left (\ frac {\ gamma-1} {v ^ 2} \ mathbf {r} \ cdot \ mathbf {v} - \ gamma t \ right) \ mathbf {v} \\ \ end {align}

Această metodă este valabilă pentru orice transformare Lorentz scrisă în același mod.

Transformări Poincaré (generale neomogene)

În cele din urmă, dacă impunem că axele nu sunt paralele și că în timp $t=t'=0$ ${\ displaystyle t = t '= 0}$ ${\ displaystyle t = t '= 0}$ originile celor două sisteme nu sunt coincidente, obținem transformările mai generale neomogene ale Lorentz (numite transformări Poincaré ):

{\begin{cases}\displaystyle {\vec {r}}'={\bar {\bar {R}}}{\vec {r}}+\left[\left(\gamma -1\right){\frac {{\vec {v}}\cdot {\bar {\bar {R}}}{\vec {r}}}{v^{2}}}-\gamma t\right]{\vec {v}}+{\vec {r}}_{0}\\\displaystyle t'=\gamma \left(t-{\frac {{\vec {v}}\cdot {\bar {\bar {R}}}{\vec {r}}}{c^{2}}}\right)+t_{0}\end{cases}}

{\ displaystyle {\ begin {cases} \ displaystyle {\ vec {r}} '= {\ bar {\ bar {R}}} {\ vec {r}} + \ left [\ left (\ gamma -1 \ dreapta) {\ frac {{\ vec {v}} \ cdot {\ bar {\ bar {R}}} {\ vec {r}}} {v ^ {2}}} - \ gamma t \ right] { \ vec {v}} + {\ vec {r}} _ {0} \\\ displaystyle t '= \ gamma \ left (t - {\ frac {{\ vec {v}} \ cdot {\ bar {\ bara {R}}} {\ vec {r}}} {c ^ {2}}} \ right) + t_ {0} \ end {cases}}}

{\ displaystyle {\ begin {cases} \ displaystyle {\ vec {r}} '= {\ bar {\ bar {R}}} {\ vec {r}} + \ left [\ left (\ gamma -1 \ dreapta) {\ frac {{\ vec {v}} \ cdot {\ bar {\ bar {R}}} {\ vec {r}}} {v ^ {2}}} - \ gamma t \ right] { \ vec {v}} + {\ vec {r}} _ {0} \\\ displaystyle t '= \ gamma \ left (t - {\ frac {{\ vec {v}} \ cdot {\ bar {\ bara {R}}} {\ vec {r}}} {c ^ {2}}} \ right) + t_ {0} \ end {cases}}}

unde este

{\bar {\bar {R}}}={\begin{pmatrix}{\hat {i}}\cdot {\hat {i}}'&{\hat {j}}\cdot {\hat {i}}'&{\hat {k}}\cdot {\hat {i}}'\\{\hat {i}}\cdot {\hat {j}}'&{\hat {j}}\cdot {\hat {j}}'&{\hat {k}}\cdot {\hat {j}}'\\{\hat {i}}\cdot {\hat {k}}'&{\hat {j}}\cdot {\hat {k}}'&{\hat {k}}\cdot {\hat {k}}'\end{pmatrix}}

{\ displaystyle {\ bar {\ bar {R}}} = {\ begin {pmatrix} {\ hat {i}} \ cdot {\ hat {i}} '& {\ hat {j}} \ cdot {\ hat {i}} '& {\ hat {k}} \ cdot {\ hat {i}}' \\ {\ hat {i}} \ cdot {\ hat {j}} '& {\ hat {j} } \ cdot {\ hat {j}} '& {\ hat {k}} \ cdot {\ hat {j}}' \\ {\ hat {i}} \ cdot {\ hat {k}} '& { \ hat {j}} \ cdot {\ hat {k}} '& {\ hat {k}} \ cdot {\ hat {k}}' \ end {pmatrix}}}

{\ displaystyle {\ bar {\ bar {R}}} = {\ begin {pmatrix} {\ hat {i}} \ cdot {\ hat {i}} '& {\ hat {j}} \ cdot {\ hat {i}} '& {\ hat {k}} \ cdot {\ hat {i}}' \\ {\ hat {i}} \ cdot {\ hat {j}} '& {\ hat {j} } \ cdot {\ hat {j}} '& {\ hat {k}} \ cdot {\ hat {j}}' \\ {\ hat {i}} \ cdot {\ hat {k}} '& { \ hat {j}} \ cdot {\ hat {k}} '& {\ hat {k}} \ cdot {\ hat {k}}' \ end {pmatrix}}}

este matricea rotației sistemului.

Compoziția a două amplificări și rotații

Viziunea spațiului-timp de-a lungul liniei mondiale a unui observator care accelerează deplasarea rapidă într-o dimensiune. Direcția verticală este relativă la axa temporală, cea orizontală la axa spațială. Linia punctată este linia lumii urmată de observator, în timp ce punctele sunt evenimente în spațiu-timp.

Compoziția mai multor impulsuri sau compoziția a două transformări între două sisteme inerțiale în mișcare relativă uniformă, produce nu numai un impuls, ci și o rotație. Prin urmare, transformarea Lorentz mai generală conține posibilitatea unei rotații a axelor, numită rotație Thomas . Dacă o succesiune de impuls permite originea unei succesiuni de sisteme inerțiale să revină la punctul de plecare, atunci setul de rotații Thomas produce o rotație generală numită precesie Thomas . ^[9]

Compoziția a două impulsuri $B(\mathbf {u} )$ ${\ displaystyle B (\ mathbf {u})}$ $B (\ mathbf {u})$ Și $B(\mathbf {v} )$ ${\ displaystyle B (\ mathbf {v})}$ $B (\ mathbf {v})$ respectiv caracterizate prin viteze $\mathbf {u}$ ${\ displaystyle \ mathbf {u}}$ $\ mathbf {u}$ Și $\mathbf {v}$ ${\ displaystyle \ mathbf {v}}$ $\ mathbf {v}$ , este dat de: ^[10] ^[11]

B(\mathbf {u} )B(\mathbf {v} )=B\left(\mathbf {u} \oplus \mathbf {v} \right)\mathrm {Gyr} \left[\mathbf {u} ,\mathbf {v} \right]=\mathrm {Gyr} \left[\mathbf {u} ,\mathbf {v} \right]B\left(\mathbf {v} \oplus \mathbf {u} \right)

{\ displaystyle B (\ mathbf {u}) B (\ mathbf {v}) = B \ left (\ mathbf {u} \ oplus \ mathbf {v} \ right) \ mathrm {Gyr} \ left [\ mathbf { u}, \ mathbf {v} \ right] = \ mathrm {Gyr} \ left [\ mathbf {u}, \ mathbf {v} \ right] B \ left (\ mathbf {v} \ oplus \ mathbf {u} \ dreapta)}

B (\ mathbf {u}) B (\ mathbf {v}) = B \ left (\ mathbf {u} \ oplus \ mathbf {v} \ right) \ mathrm {Gyr} \ left [\ mathbf {u}, \ mathbf {v} \ right] = \ mathrm {Gyr} \ left [\ mathbf {u}, \ mathbf {v} \ right] B \ left (\ mathbf {v} \ oplus \ mathbf {u} \ right)

unde este $\mathbf {u} \oplus \mathbf {v}$ ${\ displaystyle \ mathbf {u} \ oplus \ mathbf {v}}$ $\ mathbf {u} \ oplus \ mathbf {v}$ este compoziția vitezei și $\mathrm {Gyr}$ ${\ displaystyle \ mathrm {Gyr}}$ $\ mathrm {Gyr}$ rotația rezultată din această compoziție. De sine $\mathrm {Gyr}$ ${\ displaystyle \ mathrm {Gyr}}$ $\ mathrm {Gyr}$ este matricea 3 × 3 asociată cu rotația coordonatelor spațiale, apoi matricea de rotație pentru cele patru coordonate este dată de:

\mathrm {Gyr} [\mathbf {u} ,\mathbf {v} ]={\begin{pmatrix}1&0\\0&\mathrm {gyr} [\mathbf {u} ,\mathbf {v} ]\end{pmatrix}}

{\ displaystyle \ mathrm {Gyr} [\ mathbf {u}, \ mathbf {v}] = {\ begin {pmatrix} 1 & 0 \\ 0 & \ mathrm {gyr} [\ mathbf {u}, \ mathbf { v}] \ end {pmatrix}}}

\ mathrm {Gyr} [\ mathbf {u}, \ mathbf {v}] = \ begin {pmatrix} 1 & 0 \\ 0 & \ mathrm {gyr} [\ mathbf {u}, \ mathbf {v}] \ sfârșit {pmatrix}

Compoziția a două transformări Lorentz generice $L(\mathbf {u} ,U)$ ${\ displaystyle L (\ mathbf {u}, U)}$ $L (\ mathbf {u}, U)$ Și $L(\mathbf {u} ,V)$ ${\ displaystyle L (\ mathbf {u}, V)}$ $L (\ mathbf {u}, V)$ care include rotații $U$ ${\ displaystyle U}$ $U$ Și $V.$ ${\ displaystyle V}$ $V.$ este dat de:

L(\mathbf {u} ,U)L(\mathbf {u} ,V)=L(\mathbf {u} \oplus U\mathbf {v} ,\mathrm {gyr} [\mathbf {u} ,U\mathbf {v} ]UV)

{\ displaystyle L (\ mathbf {u}, U) L (\ mathbf {u}, V) = L (\ mathbf {u} \ oplus U \ mathbf {v}, \ mathrm {gyr} [\ mathbf {u }, U \ mathbf {v}] UV)}

L (\ mathbf {u}, U) L (\ mathbf {u}, V) = L (\ mathbf {u} \ oplus U \ mathbf {v}, \ mathrm {gyr} [\ mathbf {u}, U \ mathbf {v}] UV)

unde este $\mathrm {gyr}$ ${\ displaystyle \ mathrm {gyr}}$ $\ mathrm {gyr}$ este precesiunea giroscopică a lui Thomas , definită ca un operator de viteză $\mathbf {w}$ ${\ displaystyle \ mathbf {w}}$ $\ mathbf w$ În felul următor:

{\text{gyr}}[\mathbf {u} ,\mathbf {v} ]\mathbf {w} =\ominus (\mathbf {u} \oplus \mathbf {v} )\oplus (\mathbf {u} \oplus (\mathbf {v} \oplus \mathbf {w} ))\quad \forall \mathbf {w}

{\ displaystyle {\ text {gyr}} [\ mathbf {u}, \ mathbf {v}] \ mathbf {w} = \ ominus (\ mathbf {u} \ oplus \ mathbf {v}) \ oplus (\ mathbf {u} \ oplus (\ mathbf {v} \ oplus \ mathbf {w})) \ quad \ forall \ mathbf {w}}

\ text {gyr} [\ mathbf {u}, \ mathbf {v}] \ mathbf {w} = \ ominus (\ mathbf {u} \ oplus \ mathbf {v}) \ oplus (\ mathbf {u} \ oplus (\ mathbf {v} \ oplus \ mathbf {w})) \ quad \ forall \ mathbf w

Rapiditate

O transformare Lorentz poate fi expusă într-o formă echivalentă prin definirea parametrului $\phi$ ${\ displaystyle \ phi}$ $\ phi$ , numit rapiditate , astfel încât:

e^{\phi }=\gamma (1+\beta )=\gamma \left(1+{\frac {v}{c}}\right)={\sqrt {\frac {1+v/c}{1-v/c}}}

{\ displaystyle e ^ {\ phi} = \ gamma (1+ \ beta) = \ gamma \ left (1 + {\ frac {v} {c}} \ right) = {\ sqrt {\ frac {1 + v / c} {1-v / c}}}}

e ^ {\ phi} = \ gamma (1+ \ beta) = \ gamma \ left (1 + \ frac {v} {c} \ right) = \ sqrt \ frac {1 + v / c} {1 - v / c}

Avem:

e^{-\phi }=\gamma (1-\beta )=\gamma \left(1-{\frac {v}{c}}\right)={\sqrt {\frac {1-v/c}{1+v/c}}}

{\ displaystyle e ^ {- \ phi} = \ gamma (1- \ beta) = \ gamma \ left (1 - {\ frac {v} {c}} \ right) = {\ sqrt {\ frac {1- v / c} {1 + v / c}}}}

e ^ {- \ phi} = \ gamma (1- \ beta) = \ gamma \ left (1 - \ frac {v} {c} \ right) = \ sqrt \ frac {1 - v / c} {1 + v / c}

și echivalent:

\phi =\ln \left[\gamma (1+\beta )\right]=-\ln \left[\gamma (1-\beta )\right]

{\ displaystyle \ phi = \ ln \ left [\ gamma (1+ \ beta) \ right] = - \ ln \ left [\ gamma (1- \ beta) \ right]}

\ phi = \ ln \ left [\ gamma (1+ \ beta) \ right] = - \ ln \ left [\ gamma (1- \ beta) \ right]

Transformarea Lorentz în configurația standard devine, prin urmare, următoarea:

{\begin{aligned}&ct-x=e^{-\phi }(ct'-x')\\&ct+x=e^{\phi }(ct'+x')\\&y=y'\\&z=z'\end{aligned}}

{\ displaystyle {\ begin {align} & ct-x = e ^ {- \ phi} (ct'-x ') \\ & ct + x = e ^ {\ phi} (ct' + x ') \\ & y = y '\\ & z = z' \ end {align}}}

\ begin {align} & c tx = e ^ {- \ phi} (ct '- x') \\ & c t + x = e ^ {\ phi} (ct '+ x') \\ & y = y ' \\ & z = z '\ end {align}

sau echivalent:

{\begin{aligned}&ct={1 \over 2}(e^{\phi }(ct'+x')+e^{-\phi }(ct'-x'))\\&x={1 \over 2}(e^{\phi }(ct'+x')-e^{-\phi }(ct'-x'))\\&y=y'\\&z=z'\end{aligned}}

{\ displaystyle {\ begin {align} & ct = {1 \ over 2} (e ^ {\ phi} (ct '+ x') + e ^ {- \ phi} (ct'-x ')) \\ & x = {1 \ peste 2} (e ^ {\ phi} (ct '+ x') - e ^ {- \ phi} (ct'-x ')) \\ & y = y' \\ & z = z '\ end {align}}}

{\ displaystyle {\ begin {align} & ct = {1 \ over 2} (e ^ {\ phi} (ct '+ x') + e ^ {- \ phi} (ct'-x ')) \\ & x = {1 \ peste 2} (e ^ {\ phi} (ct '+ x') - e ^ {- \ phi} (ct'-x ')) \\ & y = y' \\ & z = z '\ end {align}}}

Expresii hiperbolice

Din expresiile lui $e^{\phi }$ ${\ displaystyle e ^ {\ phi}}$ $și ^ \ phi$ și $e^{-\phi }$ ${\ displaystyle e ^ {- \ phi}}$ $e ^ {- \ phi}$ avem:

\gamma =\cosh \phi ={e^{\phi }+e^{-\phi } \over 2}

{\ displaystyle \ gamma = \ cosh \ phi = {e ^ {\ phi} + e ^ {- \ phi} \ over 2}}

\ gamma = \ cosh \ phi = {e ^ {\ phi} + e ^ {- \ phi} \ over 2}

\beta \gamma =\sinh \phi ={e^{\phi }-e^{-\phi } \over 2}

\beta \gamma =\sinh \phi ={e^{\phi }-e^{-\phi } \over 2}

\beta \gamma = \sinh\phi = { e^{\phi} - e^{-\phi} \over 2 }

e quindi:

\beta =\tanh \phi ={e^{\phi }-e^{-\phi } \over e^{\phi }+e^{-\phi }}

\beta =\tanh \phi ={e^{\phi }-e^{-\phi } \over e^{\phi }+e^{-\phi }}

\beta = \tanh\phi = { e^{\phi} - e^{-\phi} \over e^{\phi} + e^{-\phi} }

Sostituendo nella forma matriciale della trasformazione:

{\begin{bmatrix}ct'\\x'\\y'\\z'\end{bmatrix}}={\begin{bmatrix}\cosh \phi &-\sinh \phi &0&0\\-\sinh \phi &\cosh \phi &0&0\\0&0&1&0\\0&0&0&1\\\end{bmatrix}}{\begin{bmatrix}ct\\x\\y\\z\end{bmatrix}}

{\begin{bmatrix}ct'\\x'\\y'\\z'\end{bmatrix}}={\begin{bmatrix}\cosh \phi &-\sinh \phi &0&0\\-\sinh \phi &\cosh \phi &0&0\\0&0&1&0\\0&0&0&1\\\end{bmatrix}}{\begin{bmatrix}ct\\x\\y\\z\end{bmatrix}}

\begin{bmatrix} c t' \\ x' \\ y' \\ z' \end{bmatrix} = \begin{bmatrix} \cosh\phi &-\sinh\phi & 0 & 0 \\ -\sinh\phi & \cosh\phi & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} c t \\ x \\ y \\ z \end{bmatrix}

Una trasformazione di Lorentz può essere pertanto vista come una rotazione iperbolica delle coordinate nello spazio di Minkowski , in cui il parametro $\phi$ $\phi$ $\phi$ rappresenta l'angolo iperbolico di rotazione.

Limite galileiano

Per velocità molto piccole rispetto a quella della luce, le trasformazioni di Lorentz si riconducono a quelle di Galileo :

{\begin{cases}t'=t\\x'=\left(x-vt\right)\\y'=y\\z'=z\end{cases}}

{\begin{cases}t'=t\\x'=\left(x-vt\right)\\y'=y\\z'=z\end{cases}}

\begin{cases} t' = t \\ x' = \left(x - v t \right) \\ y' = y \\ z' = z \end{cases}

infatti se $v\ll c$ $v\ll c$ $v \ll c$ allora $\left({\frac {v}{c}}\right)\approx 0$ $\left({\frac {v}{c}}\right)\approx 0$ $\left({\frac {v}{c}}\right)\approx 0$ .

In questo senso le trasformazioni galileiane rappresentano quindi un caso limite delle trasformazioni di Lorentz. Questo spiega perché effetti relativistici significativi di contrazione/dilatazione dei tempi e degli spazi non possono essere comunemente osservati.

Note

^ Michael N. Macrossan, A Note on Relativity Before Einstein , in Brit. Journal Philos. Science , vol. 37, 1986, pp. 232–34, DOI : 10.1093/bjps/37.2.232 . URL consultato l'8 marzo 2015 (archiviato dall' url originale il 29 ottobre 2013) .
^ Voigt .
^ Ricardo Heras, Voigt's transformations and the beginning of the relativistic revolution , 2014
^ A. Ernst e J.-P. Hsu, First proposal of the universal speed of light by Voigt 1887 , in Chinese Journal of Physics , vol. 39, n. 3, 2001, pp. 211–230.
^ Jackson , p. 527 .
^ Jackson , p. 540 .
^ Jackson , p. 525 .
^ Gravitation, JA Wheeler, C. Misner, KS Thorne, WH Freeman & Co, 1973, ISBN 0-7167-0344-0
^ Relativistic velocity space, Wigner rotation and Thomas precession , John A. Rhodes, Mark D. Semon (2005)
^ Ungar, A. A: The relativistic velocity composition paradox and the Thomas rotation. Found. Phys. 19, 1385–1396 (1989)
^ The relativistic composite-velocity reciprocity principle , AA Ungar - Foundations of Physics, 2000 - Springer

Bibliografia

( EN ) Albert Einstein , Relativity: The Special and the General Theory , New York, Three Rivers Press, 1995, ISBN 0-517-88441-0 .
( EN ) John D. Jackson, Classical Electrodynamics , 3ª ed., Wiley, 1999, ISBN 0-471-30932-X .
( FR ) Paul Langevin , L'évolution de l'éspace et du temps , in Scientia , vol. 10, 1911, pp. 31–54.
( EN ) Joseph Larmor , Upon a dynamical theory of the electric and luminiferous medium , in Philosophical Transactions of the Royal Society , vol. 190, 1897, pp. 205–300, DOI : 10.1098/rsta.1897.0020 .
( EN ) Joseph Larmor, Aether and matter , Cambridge, Cambridge University Press, 1900.
( EN ) Hendrik Lorentz , Simplified theory of electrical and optical phenomena in moving systems , in Proc. Acad. Science Amsterdam , vol. 1, 1899, pp. 427–443.
( EN ) Hendrik Lorentz, Electromagnetic phenomena in a system moving with any velocity smaller than that of light , in Proc. Acad. Science Amsterdam , vol. 4, 1904, pp. 669–678.
( EN ) Hendrik Lorentz, The theory of electrons and its applications to the phenomena of light and radiant heat; a course of lectures delivered in Columbia university, New York, in March and April 1906 , Lipsia; New York, NY, BG Teubner ; GE Stechert, 1909.
( FR ) Henri Poincaré , Sur la dynamique de l'électron ( PDF ), in Comptes Rendues , vol. 140, 1905, pp. 1504–1508.
( EN ) Stephen T. Thornton e Jerry B. Marion, Classical dynamics of particles and systems , 5ª ed., Belmont, CA, Brooks/Cole, 2004, pp. 546–579, ISBN 0-534-40896-6 .
( DE ) Woldemar Voigt , Über das Doppler'sche princip , in Nachrichten von der Königlicher Gesellschaft den Wissenschaft zu Göttingen , vol. 2, 1887, pp. 41–51.

Voci correlate

Altri progetti

Wikimedia Commons contiene immagini o altri file su Trasformazione di Lorentz

Collegamenti esterni

Derivation of the Lorentz transformations . This web page contains a more detailed derivation of the Lorentz transformation with special emphasis on group properties.
The Paradox of Special Relativity . This webpage poses a problem, the solution of which is the Lorentz transformation, which is presented graphically in its next page.
Relativity - a chapter from an online textbook
Special Relativity: The Lorentz Transformation, The Velocity Addition Law Archiviato il 14 maggio 2017 in Internet Archive . on Project PHYSNET
Warp Special Relativity Simulator . A computer program demonstrating the Lorentz transformations on everyday objects.
Animation clip visualizing the Lorentz transformation.
Lorentz Frames Animated from John de Pillis. Online Flash animations of Galilean and Lorentz frames, various paradoxes, EM wave phenomena, etc .
Vector Lorentz Transformations . Vector Lorentz Transformations of time, space, velocity and acceleration.

Controllo di autorità	LCCN ( EN ) sh85078398 · GND ( DE ) 4653925-6

Portale Matematica

Portale Relatività

[1] Michael N. Macrossan, A Note on Relativity Before Einstein , in Brit. Journal Philos. Science , vol. 37, 1986, pp. 232–34, DOI : 10.1093/bjps/37.2.232 . URL consultato l'8 marzo 2015 (archiviato dall' url originale il 29 ottobre 2013) .

[2] Voigt .

[3] Ricardo Heras, Voigt's transformations and the beginning of the relativistic revolution , 2014

[4] A. Ernst e J.-P. Hsu, First proposal of the universal speed of light by Voigt 1887 , in Chinese Journal of Physics , vol. 39, n. 3, 2001, pp. 211–230.

[5] Jackson , p. 527 .

[6] Jackson , p. 540 .

[7] Jackson , p. 525 .

[Gravitation,_J.A._Wheeler_1973-8] Gravitation, JA Wheeler, C. Misner, KS Thorne, WH Freeman & Co, 1973, ISBN 0-7167-0344-0

[9] Relativistic velocity space, Wigner rotation and Thomas precession , John A. Rhodes, Mark D. Semon (2005)

[relcompara-10] Ungar, A. A: The relativistic velocity composition paradox and the Thomas rotation. Found. Phys. 19, 1385–1396 (1989)

[11] The relativistic composite-velocity reciprocity principle , AA Ungar - Foundations of Physics, 2000 - Springer

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]