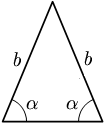
triunghi isoscel
În geometrie , un triunghi isoscel este definit ca un triunghi care are două laturi congruente.
Următoarea teoremă este valabilă: „Un triunghi este isoscel dacă și numai dacă are două unghiuri congruente”. Această teoremă constituie a cincea propunere din Cartea I a Elementelor a lui Euclid și este cunoscută sub numele de pons asinorum .
Într-un triunghi isoscel bisectoarea în raport cu unghiul vârfului coincide cu mediana , înălțimea și axa în raport cu baza.
Special triunghiuri isoscele sunt triunghiuri echilaterale și isoscel dreapta triunghiuri . Există, de asemenea, triunghiuri izoscele acute și obtuze .
Triunghiurile isoscel drepte sunt toate asemănătoare între ele, la fel ca triunghiurile echilaterale.
Simetriile
Un triunghi isoscel care nu este echilateral este invariant numai prin reflecție față de bisectoarea unghiului, altele decât cele două rămase. Grupul său de simetrie , pe lângă transformarea identității , include doar această reflecție și, prin urmare, este izomorf pentru grupul celor două elemente, adică pentru grupul multiplicativ în ansamblu {\ displaystyle \ {1, -1 \}}  .
.
Triunghiuri isoscele în geometrie analitică
Teorema 1: O condiție necesară și suficientă pentru ca un triunghi cu baza sa paralelă cu axele să fie isoscel este acela că are cele două laturi ale coeficientului unghiular opus.
Demonstrație.
Având în vedere cele trei linii
- {\ displaystyle y = k}

- {\ displaystyle y = mx}

- {\ displaystyle y = -mx}

calculăm intersecția.
- {\ displaystyle \ left \ {{\ begin {array} {rl} & y = k \\ & y = mx \ end {array}} \ right.}

- {\ displaystyle \ left \ {{\ begin {array} {rl} & x = {\ frac {k} {m}} \\ & y = k \ end {array}} \ right.}

- {\ displaystyle A \ left ({\ frac {k} {m}}, k \ right)}

- {\ displaystyle \ left \ {{\ begin {array} {rl} & y = k \\ & y = -mx \ end {array}} \ right.}

- {\ displaystyle \ left \ {{\ begin {array} {rl} & x = - {\ frac {k} {m}} \\ & y = k \ end {array}} \ right.}

- {\ displaystyle B \ left (- {\ frac {k} {m}}, k \ right)}

- {\ displaystyle \ left \ {{\ begin {array} {rl} & y = mx \\ & y = -mx \ end {array}} \ right.}

- {\ displaystyle \ left \ {{\ begin {array} {rl} & x = 0 \\ & y = 0 \ end {array}} \ right.}

- {\ displaystyle {\ rm {C}} (0,0)}

Acum să calculăm distanța segmentelor {\ displaystyle AC}  Și {\ displaystyle BC}
Și {\ displaystyle BC}  .
.
- {\ displaystyle AC = {\ sqrt {\ left ({\ frac {k} {m}} \ right) ^ {2} + k ^ {2}}}}

- {\ displaystyle BC = {\ sqrt {\ left (- {\ frac {k} {m}} \ right) ^ {2} + k ^ {2}}}}

Deci triunghiul este isoscel pe bază {\ displaystyle AB}  . În mod similar, este demonstrat cazul bazei paralele cu axa {\ displaystyle y}
. În mod similar, este demonstrat cazul bazei paralele cu axa {\ displaystyle y}  .
.
Viceversa construim un triunghi isoscel cu baza paralelă cu axa abscisei.
Având în vedere colonul:
- {\ displaystyle {\ rm {A}} (x_ {1}, k)}

- {\ displaystyle {\ rm {B}} (x_ {2}, k)}

întrucât vârful unui triunghi isoscel se află pe aceeași linie cu punctul de bază al bazei, găsim mai întâi {\ displaystyle M}  atunci {\ displaystyle C}
atunci {\ displaystyle C}  .
.
- {\ displaystyle M \ left ({\ frac {x_ {1} + x_ {2}} {2}}, k \ right)}

Așa că găsim {\ displaystyle C}  , care va avea aceeași abscisă ca {\ displaystyle M}
, care va avea aceeași abscisă ca {\ displaystyle M}  și diferit ordonat.
și diferit ordonat.
- {\ displaystyle C \ left ({\ frac {x_ {1} + x_ {2}} {2}}, h \ right)}

Verificăm dacă triunghiul este isoscel:
- {\ displaystyle AC = {\ sqrt {\ left ({\ frac {x_ {1} -x_ {2}} {2}} \ right) ^ {2} + (kh) ^ {2}}}}

- {\ displaystyle BC = {\ sqrt {\ left ({\ frac {x_ {2} -x_ {1}} {2}} \ right) ^ {2} + (kh) ^ {2}}}}

Acum să calculăm coeficientul unghiular al celor două laturi:
- {\ displaystyle mAC = (hk) \ cdot \ left ({\ frac {2} {x_ {2} -x_ {1}}} \ right) = {\ frac {2 (hk)} {x_ {2} - x_ {1}}}}

- {\ displaystyle mBC = (hk) \ cdot \ left ({\ frac {2} {x_ {1} -x_ {2}}} \ right) = {\ frac {2 (hk)} {x_ {1} - x_ {2}}}}

Teorema 2: O condiție necesară și suficientă pentru ca un triunghi cu baza paralelă cu bisectoarea a două cadrane să fie isoscel este acela că are cele două laturi cu un coeficient unghiular invers.
Demonstrație.
Având în vedere cele trei linii
- {\ displaystyle y = x + q}

- {\ displaystyle y = mx}

- {\ displaystyle y = {\ frac {1} {m}} x}

calculăm intersecția.
- {\ displaystyle \ left \ {{\ begin {array} {rl} & y = x + q \\ & y = mx \ end {array}} \ right.}

- {\ displaystyle \ left \ {{\ begin {array} {rl} & x (m-1) = q \\ & y = mx \ end {array}} \ right.}

- {\ displaystyle \ left \ {{\ begin {array} {rl} & x = {\ frac {q} {m-1}} \\ & y = {\ frac {mq} {m-1}} \ end {array}} \ right.}

- {\ displaystyle A \ left ({\ frac {q} {m-1}}, {\ frac {mq} {m-1}} \ right)}

- {\ displaystyle \ left \ {{\ begin {array} {rl} & y = x + q \\ & y = {\ frac {1} {m}} x \ end {array}} \ right.}

- {\ displaystyle \ left \ {{\ begin {array} {rl} & x (1-m) = mq \\ & y = {\ frac {1} {m}} x \ end {array}} \ right. }

- {\ displaystyle \ left \ {{\ begin {array} {rl} & x = {\ frac {mq} {1-m}} \\ & y = {\ frac {q} {1-m}} \ end {array}} \ right.}

- {\ displaystyle B \ left ({\ frac {mq} {1-m}}, {\ frac {q} {1-m}} \ right)}

- {\ displaystyle \ left \ {{\ begin {array} {rl} & y = {\ frac {1} {m}} x \ end {array}} \ right.}

- {\ displaystyle \ left \ {{\ begin {array} {rl} & x = 0 \\ & y = 0 \ end {array}} \ right.}

- {\ displaystyle {\ rm {C}} (0,0)}

Acum să calculăm distanța segmentelor {\ displaystyle AC}  Și {\ displaystyle BC}
Și {\ displaystyle BC}  .
.
- {\ displaystyle AC = {\ sqrt {\ left ({\ frac {q} {m-1}} \ right) ^ {2} + \ left ({\ frac {mq} {m-1}} \ right) ^ {2}}}}

- {\ displaystyle BC = {\ sqrt {\ left ({\ frac {mq} {1-m}} \ right) ^ {2} + \ left ({\ frac {q} {1-m}} \ right) ^ {2}}}}

Deci triunghiul este isoscel pe bază {\ displaystyle AB}  . În mod similar, este demonstrat cazul bazei paralele cu axa {\ displaystyle y}
. În mod similar, este demonstrat cazul bazei paralele cu axa {\ displaystyle y}  .
.
În schimb, construim un triunghi isoscel cu baza paralelă cu bisectoarea primului și celui de-al treilea cadran (același lucru este valabil și pentru cel paralel cu bisectoarea celui de-al doilea și al patrulea cadran).
Având în vedere colonul:
- {\ displaystyle {\ rm {A}} (0, q)}

- {\ displaystyle {\ rm {B}} (- q, 0)}

întrucât vârful unui triunghi isoscel se află pe aceeași linie cu punctul de bază al bazei, găsim mai întâi {\ displaystyle M}  atunci {\ displaystyle C}
atunci {\ displaystyle C}  .
.
- {\ displaystyle M \ left (- {\ frac {q} {2}}, {\ frac {q} {2}} \ right)}

Așa că găsim {\ displaystyle C}  , care se află pe linia ecuației {\ displaystyle y = -x}
, care se află pe linia ecuației {\ displaystyle y = -x}  perpendicular pe bază și trecând prin {\ displaystyle M}
perpendicular pe bază și trecând prin {\ displaystyle M}  .
.
- {\ displaystyle C (h, -h)}

unde este {\ displaystyle h}  este un număr real arbitrar, altul decât.
este un număr real arbitrar, altul decât.
Verificăm dacă triunghiul este isoscel:
- {\ displaystyle AC = {\ sqrt {h ^ {2} + (q + h) ^ {2}}}}

- {\ displaystyle BC = {\ sqrt {(-qh) ^ {2} + h ^ {2}}}}

Acum să calculăm coeficientul unghiular al celor două laturi:
- {\ displaystyle mAC = {\ frac {-hq} {h}} = - {\ frac {h + q} {h}}}

- {\ displaystyle mBC = {\ frac {-h} {h + q}} = - {\ frac {h} {h + q}}}

Elemente conexe
Alte proiecte
 Wikimedia Commons conține imagini sau alte fișiere pe triunghi isoscel
Wikimedia Commons conține imagini sau alte fișiere pe triunghi isoscel 




















































