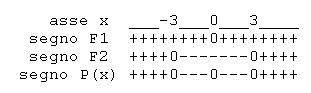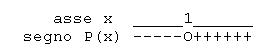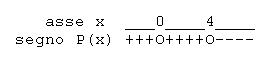Inegalitate întregi

O inegalitate se numește o inegalitate întreagă dacă, pusă în formă normală, se prezintă în formă

$P(x)\leq 0$ ${\ displaystyle P (x) \ leq 0}$ ${\ displaystyle P (x) \ leq 0}$ sau $P(x)<0$ ${\ displaystyle P (x) <0}$ ${\ displaystyle P (x) <0}$ sau $P(x)>0$ ${\ displaystyle P (x)> 0}$ ${\ displaystyle P (x)> 0}$ sau $P(x)\geq 0$ ${\ displaystyle P (x) \ geq 0}$ ${\ displaystyle P (x) \ geq 0}$

unde este $P(x)$ ${\ displaystyle P (x)}$ $P (x)$ este un polinom în litera x. Pe baza gradului polinomului, inegalitatea întregului va fi de gradul I, II, III, ...

Exemple

2x+1<0

{\ displaystyle 2x + 1 <0}

{\ displaystyle 2x + 1 <0}

este o inegalitate întregi de gradul I.

x^{2}-10x+9>0

{\ displaystyle x ^ {2} -10x + 9> 0}

{\ displaystyle x ^ {2} -10x + 9> 0}

este o inegalitate întregi de gradul doi.

x^{3}\leq 1

{\ displaystyle x ^ {3} \ leq 1}

{\ displaystyle x ^ {3} \ leq 1}

este o inegalitate întregi de gradul III, dar nu în formă normală.

{\frac {x+3}{x}}>x-2

{\ displaystyle {\ frac {x + 3} {x}}> x-2}

{\ displaystyle {\ frac {x + 3} {x}}> x-2}

este o inegalitate divizată, deoarece necunoscutul este prezent și în numitor.

Rezoluția inegalităților întregi de gradul I

Consultați articolul Inegalitate .

Rezolvarea inegalităților întregi de gradul II

Consultați articolul inegalitate de gradul II .

Rezoluția inegalităților întregi de un grad mai mare de o secundă

Există două metode de rezoluție.

Metoda descompunerii în factori și a studiului semnului produsului

Procedura include:

pune inegalitatea în formă normală;
luând în calcul polinomul $P(x)$ ${\ displaystyle P (x)}$ $P (x)$ la primul membru în factorii de gradul 1 și / sau 2;
studiază semnul fiecărui factor ( întotdeauna pentru $\geq 0$ ${\ displaystyle \ geq 0}$ ${\ displaystyle \ geq 0}$ sau pentru $>0$ ${\ displaystyle> 0}$ ${\ displaystyle> 0}$ în raport cu prezența egalului în inegalitate );
reprezintă grafic semnul tuturor factorilor și compune semnul produsului;
evidențiați acele valori pentru care factorii se anulează reciproc cu un anumit simbol (de exemplu O);
privind direcția inegalității în formă normală, identificați semnul lui pe grafic $P(x)$ ${\ displaystyle P (x)}$ $P (x)$ ansamblul soluțiilor, adică intervalul axei reale care satisface inegalitatea.

Exemplul 1

x^{3}\leq 1.

{\ displaystyle x ^ {3} \ leq 1.}

{\ displaystyle x ^ {3} \ leq 1.}

Inegalitatea nu este deci în formă normală

x^{3}-1\leq 0.

{\ displaystyle x ^ {3} -1 \ leq 0.}

{\ displaystyle x ^ {3} -1 \ leq 0.}

Factorizarea $P(x)$ ${\ displaystyle P (x)}$ $P (x)$ .

(x-1)(x^{2}+x+1)\leq 0.

{\ displaystyle (x-1) (x ^ {2} + x + 1) \ leq 0.}

{\ displaystyle (x-1) (x ^ {2} + x + 1) \ leq 0.}

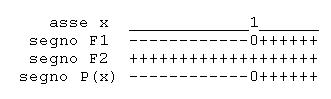
Studiul semnului factorilor ( întotdeauna pentru $\geq 0$ ${\ displaystyle \ geq 0}$ ${\ displaystyle \ geq 0}$ ):

F_{1}:x-1\geq 0\Rightarrow x\geq 1

{\ displaystyle F_ {1}: x-1 \ geq 0 \ Rightarrow x \ geq 1}

{\ displaystyle F_ {1}: x-1 \ geq 0 \ Rightarrow x \ geq 1}

;

F_{2}:x^{2}+x+1\geq 0

{\ displaystyle F_ {2}: x ^ {2} + x + 1 \ geq 0}

{\ displaystyle F_ {2}: x ^ {2} + x + 1 \ geq 0}

este o inegalitate de gradul II ;

\Rightarrow \Delta <0\Rightarrow

{\ displaystyle \ Rightarrow \ Delta <0 \ Rightarrow}

{\ displaystyle \ Rightarrow \ Delta <0 \ Rightarrow}

întotdeauna pozitiv în

\mathbb {R}

{\ displaystyle \ mathbb {R}}

\ R

.

Diagrama semnului $P(x)$ ${\ displaystyle P (x)}$ $P (x)$

Soluții.

Întrebă asta $P(x)$ ${\ displaystyle P (x)}$ $P (x)$ fie negativ, fie nul (priviți direcția inegalității în formă normală). Soluțiile inegalității sunt $x\leq 1$ ${\ displaystyle x \ leq 1}$ ${\ displaystyle x \ leq 1}$ .

Exemplul 2

x^{4}\geq 9x^{2}.

{\ displaystyle x ^ {4} \ geq 9x ^ {2}.}

{\ displaystyle x ^ {4} \ geq 9x ^ {2}.}

Inegalitatea nu este deci în formă normală

x^{4}-9x^{2}\geq 0.

{\ displaystyle x ^ {4} -9x ^ {2} \ geq 0.}

{\ displaystyle x ^ {4} -9x ^ {2} \ geq 0.}

Factorizarea $P(x)$ ${\ displaystyle P (x)}$ $P (x)$ .

x^{2}(x^{2}-9)\geq 0

{\ displaystyle x ^ {2} (x ^ {2} -9) \ geq 0}

{\ displaystyle x ^ {2} (x ^ {2} -9) \ geq 0}

.

Studiul semnului factorilor (întotdeauna pentru $\geq 0$ ${\ displaystyle \ geq 0}$ ${\ displaystyle \ geq 0}$ ).

F_{1}:x^{2}\geq 0

{\ displaystyle F_ {1}: x ^ {2} \ geq 0}

{\ displaystyle F_ {1}: x ^ {2} \ geq 0}

un pătrat este întotdeauna pozitiv, zero pentru x = 0, niciodată negativ.

F_{2}:x^{2}-9\geq 0

{\ displaystyle F_ {2}: x ^ {2} -9 \ geq 0}

{\ displaystyle F_ {2}: x ^ {2} -9 \ geq 0}

este o inegalitate de gradul 2 .

\Rightarrow

{\ displaystyle \ Rightarrow}

{\ displaystyle \ Rightarrow}

(ESTE LA)

x^{2}-9=0,\Delta >0,x_{1}=-3,x_{2}=+3\Rightarrow

{\ displaystyle x ^ {2} -9 = 0, \ Delta> 0, x_ {1} = - 3, x_ {2} = + 3 \ Rightarrow}

{\ displaystyle x ^ {2} -9 = 0, \ Delta> 0, x_ {1} = - 3, x_ {2} = + 3 \ Rightarrow}

pozitiv pentru

x<-3\vee x>+3

{\ displaystyle x <-3 \ vee x> +3}

{\ displaystyle x <-3 \ vee x> +3}

.

Diagrama semnului $P(x)$ ${\ displaystyle P (x)}$ $P (x)$

Soluții.

Întrebă asta $P(x)$ ${\ displaystyle P (x)}$ $P (x)$ fie pozitiv, fie nul (priviți direcția inegalității în formă normală). Soluțiile inegalității sunt $x\leq -3\vee x=0\vee x\geq +3$ ${\ displaystyle x \ leq -3 \ vee x = 0 \ vee x \ geq +3}$ ${\ displaystyle x \ leq -3 \ vee x = 0 \ vee x \ geq +3}$ .

Metoda de semnare rapidă P (x)

Procedura de reziliere prevede:

pune inegalitatea în formă normală;
rezolvați ecuația asociată (EA) $P(x)=0$ ${\ displaystyle P (x) = 0}$ ${\ displaystyle P (x) = 0}$ și găsiți soluțiile EA cu multiplicitatea lor;
reprezintă grafic semnul $P(x)$ ${\ displaystyle P (x)}$ $P (x)$ începând întotdeauna de la dreapta cu semnul coeficientului de $X$ ${\ displaystyle x}$ $X$ de grad maxim;
în schema grafică schimbați semnul numai atunci când se întâlnește o rădăcină (soluție) de EA cu multiplicitate impar ;
privind direcția inegalității în formă normală, identificați semnul de pe grafic $P(x)$ ${\ displaystyle P (x)}$ $P (x)$ ansamblul soluțiilor, adică intervalul axei reale care satisface inegalitatea.

Exemplul 3

x^{3}\leq 1.

{\ displaystyle x ^ {3} \ leq 1.}

{\ displaystyle x ^ {3} \ leq 1.}

Inegalitatea nu este în formă normală, prin urmare:

x^{3}-1\leq 0.

{\ displaystyle x ^ {3} -1 \ leq 0.}

{\ displaystyle x ^ {3} -1 \ leq 0.}

Ecuație asociată (EA) $P(x)=0$ ${\ displaystyle P (x) = 0}$ ${\ displaystyle P (x) = 0}$

x^{3}-1=0.

{\ displaystyle x ^ {3} -1 = 0.}

{\ displaystyle x ^ {3} -1 = 0.}

Este o ecuație binomială cu o singură soluție $x=1$ ${\ displaystyle x = 1}$ $x = 1$ cu multiplicitate 1. Coeficientul de $X$ ${\ displaystyle x}$ $X$ de grad maxim este 1 (pozitiv), prin urmare:

schema semnelor de $P(x)$ ${\ displaystyle P (x)}$ $P (x)$

Soluții.

Întrebă asta $P(x)$ ${\ displaystyle P (x)}$ $P (x)$ fie negativ, fie nul (priviți direcția inegalității în formă normală). Soluțiile inegalității sunt $x\leq 1$ ${\ displaystyle x \ leq 1}$ ${\ displaystyle x \ leq 1}$ .

Exemplul 4

-2x^{7}+8x^{6}\leq 0.

{\ displaystyle -2x ^ {7} + 8x ^ {6} \ leq 0.}

{\ displaystyle -2x ^ {7} + 8x ^ {6} \ leq 0.}

Inegalitatea este în formă normală.

Ecuație asociată (EA)

-2x^{7}+8x^{6}=0.

{\ displaystyle -2x ^ {7} + 8x ^ {6} = 0.}

{\ displaystyle -2x ^ {7} + 8x ^ {6} = 0.}

Este o ecuație generică care trebuie rezolvată prin descompunere

x^{6}(-2x+8)=0.

{\ displaystyle x ^ {6} (- 2x + 8) = 0.}

{\ displaystyle x ^ {6} (- 2x + 8) = 0.}

A cui soluții sunt $x=0$ ${\ displaystyle x = 0}$ $x = 0$ cu multiplicitate 6 și $x=4$ ${\ displaystyle x = 4}$ $x = 4$ cu multiplicitate 1. Coeficientul de $X$ ${\ displaystyle x}$ $X$ gradul maxim este -2 (negativ) prin urmare:

schema semnelor de $P(x)$ ${\ displaystyle P (x)}$ $P (x)$

Atenție: în $x=0$ ${\ displaystyle x = 0}$ $x = 0$ semnul nu se schimbă deoarece are multiplicitate 6 (pare).

Soluții.

Întrebă asta $P(x)$ ${\ displaystyle P (x)}$ $P (x)$ fie negativ, fie nul (priviți direcția inegalității în formă normală). Soluțiile inegalității sunt $x\geq 4\vee x=0$ ${\ displaystyle x \ geq 4 \ vee x = 0}$ ${\ displaystyle x \ geq 4 \ vee x = 0}$ .

Exemplul 5

x^{4}-9x^{2}\geq 0.

{\ displaystyle x ^ {4} -9x ^ {2} \ geq 0.}

{\ displaystyle x ^ {4} -9x ^ {2} \ geq 0.}

Inegalitatea este în formă normală.

Ecuație asociată (EA)

x^{4}-9x^{2}=0.

{\ displaystyle x ^ {4} -9x ^ {2} = 0.}

{\ displaystyle x ^ {4} -9x ^ {2} = 0.}

Este o ecuație generică care trebuie rezolvată prin descompunere

x^{2}(x^{2}-9)=0.

{\ displaystyle x ^ {2} (x ^ {2} -9) = 0.}

{\ displaystyle x ^ {2} (x ^ {2} -9) = 0.}

A cui soluții sunt $x=0$ ${\ displaystyle x = 0}$ $x = 0$ cu multiplicitate 2 și $x=-3$ ${\ displaystyle x = -3}$ ${\ displaystyle x = -3}$ Și $x=3$ ${\ displaystyle x = 3}$ $x = 3$ cu multiplicitate 1. Coeficientul de $X$ ${\ displaystyle x}$ $X$ de grad maxim este 1 (pozitiv), prin urmare:

schema semnelor de $P(x)$ ${\ displaystyle P (x)}$ $P (x)$

Atenție: în $x=0$ ${\ displaystyle x = 0}$ $x = 0$ semnul nu se schimbă deoarece are multiplicitate 2 (par).

Soluții.

Întrebă asta $P(x)$ ${\ displaystyle P (x)}$ $P (x)$ fie pozitiv, fie nul (priviți direcția inegalității în formă normală). Soluțiile inegalității sunt $x\leq -3\vee x=0\vee x\geq +3$ ${\ displaystyle x \ leq -3 \ vee x = 0 \ vee x \ geq +3}$ ${\ displaystyle x \ leq -3 \ vee x = 0 \ vee x \ geq +3}$ .

Cazuri speciale

Puteri cu exponent uniform

(x-3)^{4}<0.

{\ displaystyle (x-3) ^ {4} <0.}

{\ displaystyle (x-3) ^ {4} <0.}

Această inegalitate prezintă primului membru o putere cu exponent egal. O putere chiar exponentă este întotdeauna pozitivă sau nulă, niciodată negativă. Deci, chiar dacă inegalitatea nu este în formă normală, știm că nu va fi niciodată verificată.

S=\varnothing .

{\ displaystyle S = \ varnothing.}

{\ displaystyle S = \ varnothing.}

Puteri cu exponent ciudat

(2x+1)^{3}\geq 0.

{\ displaystyle (2x + 1) ^ {3} \ geq 0.}

{\ displaystyle (2x + 1) ^ {3} \ geq 0.}

Această inegalitate prezintă primului membru o putere cu exponent ciudat. O putere cu exponent impar urmează semnul bazei. Deci, chiar dacă inegalitatea nu este în formă normală, știm că va apărea când

2x+1\geq 0\Rightarrow x\geq -{\frac {1}{2}}.

{\ displaystyle 2x + 1 \ geq 0 \ Rightarrow x \ geq - {\ frac {1} {2}}.}

{\ displaystyle 2x + 1 \ geq 0 \ Rightarrow x \ geq - {\ frac {1} {2}}.}

Inegalități întregi cu polinom deja factorizat

(x-5)^{4}(x+1)^{3}(x^{4}-16)^{4}<0.

{\ displaystyle (x-5) ^ {4} (x + 1) ^ {3} (x ^ {4} -16) ^ {4} <0.}

{\ displaystyle (x-5) ^ {4} (x + 1) ^ {3} (x ^ {4} -16) ^ {4} <0.}

Această inegalitate prezintă deja un polinom factorizat primului membru. În acest caz, este recomandabil să utilizați metoda semnului factorilor

F_{1}:(x-5)^{2}\geq 0

{\ displaystyle F_ {1} :( x-5) ^ {2} \ geq 0}

{\ displaystyle F_ {1} :( x-5) ^ {2} \ geq 0}

este o putere cu exponent uniform, deci întotdeauna pozitiv cu excepția lui

x=5

{\ displaystyle x = 5}

{\ displaystyle x = 5}

unde este 0;

F_{2}:(x+1)^{3}\geq 0

{\ displaystyle F_ {2} :( x + 1) ^ {3} \ geq 0}

{\ displaystyle F_ {2} :( x + 1) ^ {3} \ geq 0}

este o putere cu exponent ciudat, deci urmează semnul bazei

x\geq -1

{\ displaystyle x \ geq -1}

{\ displaystyle x \ geq -1}

;

F_{3}:(x^{4}-16)^{4}\geq 0

{\ displaystyle F_ {3} :( x ^ {4} -16) ^ {4} \ geq 0}

{\ displaystyle F_ {3} :( x ^ {4} -16) ^ {4} \ geq 0}

este o putere cu exponent egal, deci întotdeauna pozitivă sau zero pentru

x^{4}-16=0\Rightarrow x^{4}=16\Rightarrow x=\pm 2

{\ displaystyle x ^ {4} -16 = 0 \ Rightarrow x ^ {4} = 16 \ Rightarrow x = \ pm 2}

{\ displaystyle x ^ {4} -16 = 0 \ Rightarrow x ^ {4} = 16 \ Rightarrow x = \ pm 2}

.

Schema semnului

Soluții.

$P(x)$ ${\ displaystyle P (x)}$ $P (x)$ trebuie să fie negativ, deci pentru $x<-1\land x\neq -2$ ${\ displaystyle x <-1 \ land x \ neq -2}$ ${\ displaystyle x <-1 \ land x \ neq -2}$ .

Inegalitățile de gradul al patrulea atribuite celui de-al doilea

Un caz particular de inegalitate de gradul patru este următorul:

ax^{4}+bx^{3}+cx^{2}+bx+a\leq 0\;\;\;

{\ displaystyle ax ^ {4} + bx ^ {3} + cx ^ {2} + bx + a \ leq 0 \; \; \;}

{\ displaystyle ax ^ {4} + bx ^ {3} + cx ^ {2} + bx + a \ leq 0 \; \; \;}

(sau

\geq 0

{\ displaystyle \ geq 0}

{\ displaystyle \ geq 0}

).

Acest tip de inegalitate se rezolvă prin efectuarea unei divizări membru cu membru prin $x^{2}\neq 0$ ${\ displaystyle x ^ {2} \ neq 0}$ ${\ displaystyle x ^ {2} \ neq 0}$ , sau:

{\frac {ax^{4}}{x^{2}}}+{\frac {bx^{3}}{x^{2}}}+{\frac {cx^{2}}{x^{2}}}+{\frac {bx}{x^{2}}}+{\frac {a}{x^{2}}}\leq 0,

{\ displaystyle {\ frac {ax ^ {4}} {x ^ {2}}} + {\ frac {bx ^ {3}} {x ^ {2}}} + {\ frac {cx ^ {2} } {x ^ {2}}} + {\ frac {bx} {x ^ {2}}} + {\ frac {a} {x ^ {2}}} \ leq 0,}

{\ displaystyle {\ frac {ax ^ {4}} {x ^ {2}}} + {\ frac {bx ^ {3}} {x ^ {2}}} + {\ frac {cx ^ {2} } {x ^ {2}}} + {\ frac {bx} {x ^ {2}}} + {\ frac {a} {x ^ {2}}} \ leq 0,}

și, prin urmare, prin simplificarea și colectarea factorilor comuni, obținem:

a(x^{2}+{\frac {1}{x^{2}}})+b(x+{\frac {1}{x}})+c\leq 0,

{\ displaystyle a (x ^ {2} + {\ frac {1} {x ^ {2}}}) + b (x + {\ frac {1} {x}}) + c \ leq 0,}

{\ displaystyle a (x ^ {2} + {\ frac {1} {x ^ {2}}}) + b (x + {\ frac {1} {x}}) + c \ leq 0,}

apoi continuați prin plasare $t$ ${\ displaystyle t}$ $t$ Și $t^{2}$ ${\ displaystyle t ^ {2}}$ ${\ displaystyle t ^ {2}}$ după cum urmează:

t=x+{\frac {1}{x}}\;\;\;

{\ displaystyle t = x + {\ frac {1} {x}} \; \; \;}

{\ displaystyle t = x + {\ frac {1} {x}} \; \; \;}

, din care (pătrând ambele părți) obținem:

x^{2}+{\frac {1}{x^{2}}}=t^{2}-2.

{\ displaystyle x ^ {2} + {\ frac {1} {x ^ {2}}} = t ^ {2} -2.}

{\ displaystyle x ^ {2} + {\ frac {1} {x ^ {2}}} = t ^ {2} -2.}

Prin înlocuire $t$ ${\ displaystyle t}$ $t$ Și $t^{2}$ ${\ displaystyle t ^ {2}}$ ${\ displaystyle t ^ {2}}$ în inegalitatea anterioară există oinegalitate comună degradul doi :

at^{2}+bt+c-2a\leq 0.

{\ displaystyle at ^ {2} + bt + c-2a \ leq 0.}

{\ displaystyle at ^ {2} + bt + c-2a \ leq 0.}

După rezolvarea inegalității de gradul al doilea efectuăm substituirea inversă a $t=x+{\frac {1}{x}}$ ${\ displaystyle t = x + {\ frac {1} {x}}}$ ${\ displaystyle t = x + {\ frac {1} {x}}}$ (este foarte important să acordați atenție domeniului rezoluției inegalității de gradul II).