Problemă de debit maxim

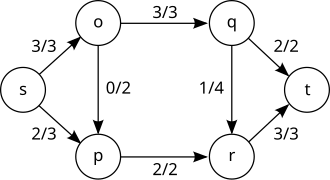
O rețea cu un exemplu de debit maxim. Sursa este s și fântâna este t . Numerele indică fluxul și capacitatea arcelor.

În teoria optimizării , problema debitului maxim constă în găsirea, într-o rețea de curgere cu o singură sursă și un puț, a unui debit admisibil care este maxim.

Problema debitului maxim poate fi văzută ca un caz particular de probleme mai complexe pe rețelele de curgere, cum ar fi problema circulației . Valoarea maximă a unui flux de st (adică un flux generat de o sursă s care se termină într-un puț t ) este echivalentă cu capacitatea minimă a unui st tăiat în aceeași rețea, așa cum este afirmat de debitul maxim și teorema de tăiere minimă .

Istorie

Problema debitului maxim a fost formulată pentru prima dată în 1954 de TE Harris și FS Ross pentru simplificarea modelului de debit al sistemului feroviar sovietic. ^[1] ^[2] ^[3] În 1955, Lester R. Ford, Jr. și Delbert R. Fulkerson au publicat primul algoritm cunoscut, algoritmul Ford-Fulkerson . ^[4] ^[5]

În anii următori, au fost concepute diverse soluții la această problemă, printre care cele mai cunoscute sunt cele ale americanilor Edmonds și Karp (1972) și Sovietul Dinitz (1970).

Definiție

O rețea de flux, cu sursă s și puț t . Numerele de lângă arce reprezintă capacitățile respective.

Este $N=(V,E)$ ${\ displaystyle N = (V, E)}$ ${\ displaystyle N = (V, E)}$ o rețea cu $s,t\in V$ ${\ displaystyle s, t \ in V}$ ${\ displaystyle s, t \ in V}$ respectiv sursă și fântână de $Nu.$ ${\ displaystyle N}$ $Nu.$ .

Capacitatea unui arc este o funcție $c:E\to \mathbb {R} ^{+}$ ${\ displaystyle c: E \ to \ mathbb {R} ^ {+}}$ ${\ displaystyle c: E \ to \ mathbb {R} ^ {+}}$ , indicat cu $c_{uv}$ ${\ displaystyle c_ {uv}}$ ${\ displaystyle c_ {uv}}$ sau $c(u,v)$ ${\ displaystyle c (u, v)}$ ${\ displaystyle c (u, v)}$ , care reprezintă debitul maxim care poate trece printr-un arc.

Un flux este o funcție $f:E\to \mathbb {R} ^{+}$ ${\ displaystyle f: E \ to \ mathbb {R} ^ {+}}$ ${\ displaystyle f: E \ to \ mathbb {R} ^ {+}}$ , indicat cu $f_{uv}$ ${\ displaystyle f_ {uv}}$ ${\ displaystyle f_ {uv}}$ sau $f(u,v)$ ${\ displaystyle f (u, v)}$ ${\ displaystyle f (u, v)}$ , sub rezerva următoarelor două constrângeri:

$f_{uv}\leq c_{uv}\forall (u,v)\in E$ ${\ displaystyle f_ {uv} \ leq c_ {uv} \ forall (u, v) \ în E}$ ${\ displaystyle f_ {uv} \ leq c_ {uv} \ forall (u, v) \ în E}$ (constrângerea capacității: fluxul printr-un arc nu poate fi mai mare decât capacitatea sa);
$\sum _{u:(u,v)\in E}f_{uv}=\sum _{u:(v,u)\in E}f_{vu}\forall v\in V\setminus \{s,t\}$ ${\ displaystyle \ sum _ {u: (u, v) \ in E} f_ {uv} = \ sum _ {u: (v, u) \ in E} f_ {vu} \ forall v \ in V \ setminus \ {s, t \}}$ ${\ displaystyle \ sum _ {u: (u, v) \ in E} f_ {uv} = \ sum _ {u: (v, u) \ in E} f_ {vu} \ forall v \ in V \ setminus \ {s, t \}}$ (constrângere de conservare a fluxului: suma fluxurilor care intră într-un nod trebuie să fie egală cu suma fluxurilor care ies din acesta, cu excepția sursei și a puțului).

Valoarea fluxului este definită de $|f|=\sum _{v:(s,v)\in E}f_{sv}$ ${\ displaystyle | f | = \ sum _ {v: (s, v) \ în E} f_ {sv}}$ ${\ displaystyle | f | = \ sum _ {v: (s, v) \ în E} f_ {sv}}$ , unde este $s$ ${\ displaystyle s}$ $s$ este sursa $Nu.$ ${\ displaystyle N}$ $Nu.$ . Reprezintă cantitatea de debit de la sursă la fântână.

Problema debitului maxim este de a maximiza $|f|$ ${\ displaystyle | f |}$ $| f |$ , adică să direcționeze cât mai mult flux posibil din $s$ ${\ displaystyle s}$ $s$ la $t$ ${\ displaystyle t}$ $t$ .

Soluții

Pentru a înțelege diferitele soluții ale problemei, este necesar să se introducă conceptul de rețea reziduală. Având în vedere o rețea de flux $G.$ ${\ displaystyle G}$ $G.$ și un flux $f$ ${\ displaystyle f}$ $f$ pe $G.$ ${\ displaystyle G}$ $G.$ , definim rețeaua reziduală $G_{f}$ ${\ displaystyle G_ {f}}$ ${\ displaystyle G_ {f}}$ pe $G.$ ${\ displaystyle G}$ $G.$ în comparație cu $f$ ${\ displaystyle f}$ $f$ după cum urmează:

Setul de noduri ale $G_{f}$ ${\ displaystyle G_ {f}}$ ${\ displaystyle G_ {f}}$ Este la fel ca $G.$ ${\ displaystyle G}$ $G.$ .
Fiecare arc $e=(u,v)$ ${\ displaystyle e = (u, v)}$ ${\ displaystyle e = (u, v)}$ din $G_{f}$ ${\ displaystyle G_ {f}}$ ${\ displaystyle G_ {f}}$ are o capacitate $c_{e}-f(e)$ ${\ displaystyle c_ {e} -f (e)}$ ${\ displaystyle c_ {e} -f (e)}$ .
Fiecare arc $e'=(v,u)$ ${\ displaystyle e '= (v, u)}$ ${\ displaystyle e '= (v, u)}$ din $G_{f}$ ${\ displaystyle G_ {f}}$ ${\ displaystyle G_ {f}}$ are o capacitate $f(e)$ ${\ displaystyle f (e)}$ ${\ displaystyle f (e)}$ .

Tabelul următor listează cei mai cunoscuți algoritmi pentru rezolvarea problemei debitului maxim.

Metodă	Complexitatea computațională	Notă
Algoritmul Ford-Fulkerson	$O(E\ max\|f\|)$ ${\ displaystyle O (E \ max \| f \|)}$ ${\ displaystyle O (E \ max \| f \|)}$	Încetarea algoritmului este garantată dacă toate greutățile sunt raționale , altfel este posibil ca algoritmul să nu convergă la valoarea maximă. În orice caz, dacă algoritmul se termină, corectitudinea rezultatului este garantată.
Algoritmul Edmonds-Karp	$O(VE^{2})$ ${\ displaystyle O (VE ^ {2})}$ ${\ displaystyle O (VE ^ {2})}$	O specializare a algoritmului Ford - Fulkerson care exploatează căutarea pe larg .
Algoritm dinic cu flux de blocare	$O(V^{2}E)$ ${\ displaystyle O (V ^ {2} E)}$ ${\ displaystyle O (V ^ {2} E)}$	În fiecare fază a algoritmului se construiește un grafic stratificat prin căutarea în amplitudine pe graficul rezidual. Debitul maxim pe un grafic stratificat poate fi calculat în timp $O(VE)$ ${\ displaystyle O (VE)}$ ${\ displaystyle O (VE)}$ iar numărul maxim de faze este $n-1$ ${\ displaystyle n-1}$ $n-1$ . În rețelele cu capacități unitare algoritmul se termină în timp $O(\min\{V^{2/3},E^{1/2}\}E)$ ${\ displaystyle O (\ min \ {V ^ {2/3}, E ^ {1/2} \} E)}$ ${\ displaystyle O (\ min \ {V ^ {2/3}, E ^ {1/2} \} E)}$ .
Algoritm MPM (Malhotra, Pramodh-Kumar și Maheshwari) ^[6]	$O(V^{3})$ ${\ displaystyle O (V ^ {3})}$ ${\ displaystyle O (V ^ {3})}$	Vă rugăm să consultați publicația originală .
Algoritmul lui Dinic	$O(VElog(V))$ ${\ displaystyle O (VElog (V))}$ ${\ displaystyle O (VElog (V))}$	Structura dinamică a arborelui accelerează calculul debitului maxim în graficul stratificat până la $O(Elog(V))$ ${\ displaystyle O (Elog (V))}$ ${\ displaystyle O (Elog (V))}$ .
Algoritm generic push-relabel	$O(V^{2}E)$ ${\ displaystyle O (V ^ {2} E)}$ ${\ displaystyle O (V ^ {2} E)}$
Algoritm push-relabel cu selecție FIFO	$O(V^{3})$ ${\ displaystyle O (V ^ {3})}$ ${\ displaystyle O (V ^ {3})}$
Algoritm push-relabel cu arbori dinamici	$O\left(VE\log {\frac {V^{2}}{E}}\right)$ ${\ displaystyle O \ left (VE \ log {\ frac {V ^ {2}} {E}} \ right)}$ ${\ displaystyle O \ left (VE \ log {\ frac {V ^ {2}} {E}} \ right)}$
Algoritmul KRT (King, Rao, Tarjan) ^[7]	$O(EV\log _{\frac {E}{V\log V}}V)$ ${\ displaystyle O (EV \ log _ {\ frac {E} {V \ log V}} V)}$ ${\ displaystyle O (EV \ log _ {\ frac {E} {V \ log V}} V)}$
Algoritm binar de blocare a fluxului ^[8]	$O\left(E\cdot \min(V^{\frac {2}{3}},{\sqrt {E}})\cdot \log {\frac {V^{2}}{E}}\log {U}\right)$ ${\ displaystyle O \ left (E \ cdot \ min (V ^ {\ frac {2} {3}}, {\ sqrt {E}}) \ cdot \ log {\ frac {V ^ {2}} {E }} \ log {U} \ right)}$ ${\ displaystyle O \ left (E \ cdot \ min (V ^ {\ frac {2} {3}}, {\ sqrt {E}}) \ cdot \ log {\ frac {V ^ {2}} {E }} \ log {U} \ right)}$	Valoarea $U$ ${\ displaystyle U}$ $U$ corespunde capacității maxime a rețelei.
James B Orlin + algoritmul KRT (King, Rao, Tarjan) ^[9]	$O(VE)$ ${\ displaystyle O (VE)}$ ${\ displaystyle O (VE)}$	Algoritmul lui Orlin găsește fluxul maxim în timp $O(VE)$ ${\ displaystyle O (VE)}$ ${\ displaystyle O (VE)}$ pentru $E\leq O(V^{{16 \over 15}-\epsilon })$ ${\ displaystyle E \ leq O (V ^ {{16 \ peste 15} - \ epsilon})}$ ${\ displaystyle E \ leq O (V ^ {{16 \ peste 15} - \ epsilon})}$ în timp ce KRT rezolvă problema în $O(VE)$ ${\ displaystyle O (VE)}$ ${\ displaystyle O (VE)}$ pentru $E>V^{1+\epsilon }$ ${\ displaystyle E> V ^ {1+ \ epsilon}}$ ${\ displaystyle E> V ^ {1+ \ epsilon}}$ .

Aplicații

Notă

^ (EN) A. Schrijver, Despre istoria transportului și problemele de debit maxim în programarea matematică, vol. 91, nr. 3, 2002, pp. 437-445, DOI : 10.1007 / s101070100259 .
^ (EN) Saul I. Gass și Arjang A. Assad, Dezvoltări matematice, algoritmice și profesionale ale cercetării operaționale din 1951 până în 1956, în An Annotated Timeline of Operations Research, International Series in Operations Research & Management Science, vol. 75, 2005, pp. 79-110, DOI : 10.1007 / 0-387-25837-X_5 , ISBN 1-4020-8116-2 .
^ (EN) TE Harris și FS Ross, Fundamentele unei metode pentru evaluarea capacităților feroviare nete (PDF), în Research Memorandum, Rand Corporation, 1955.
^ (EN) LR Ford și DR Fulkerson , Flux maxim printr-o rețea , în Canadian Journal of Mathematics , vol. 8, 1956, p. 399, DOI : 10.4153 / CJM-1956-045-5 .
^(RO) Ford, LR, Jr.; Fulkerson, DR, Flows in Networks , Princeton University Press (1962).
^ (EN) VM Malhotra, M.Pramodh Kumar și SN Maheshwari, An $O(|V|^{3})$ ${\ displaystyle O (| V | ^ {3})}$ ${\ displaystyle O (| V | ^ {3})}$ algoritm pentru găsirea fluxurilor maxime în rețele , în Scrisori de procesare a informațiilor , vol. 7, nr. 6, 1978, pp. 277-278, DOI : 10.1016 / 0020-0190 (78) 90016-9 .
^ (EN) V. King, S. Rao și R. Tarjan, Un algoritm de flux maxim determinist mai rapid , Journal of Algorithms, vol. 17, n. 3, 1994, pp. 447-474, DOI : 10.1006 / jagm.1994.1044 .
^ (EN) AV Goldberg și S. Rao, Dincolo de bariera de descompunere a fluxului , în Jurnalul ACM , vol. 45, n. 5, 1998, p. 783, DOI : 10.1145 / 290179.290181 .
^ (EN) James B. Orlin, Max curge în timp O (nm), sau mai bine , în STOC '13 Proceedings of the patruzeci și cincilea simpozion anual ACM on Theory of Computing, 2013, pp. 765-774, DOI : 10.1145 / 2488608.2488705 .

Bibliografie

( EN ) Joseph Cheriyan și Kurt Mehlhorn , O analiză a regulii de selecție la cel mai înalt nivel în algoritmul de debit maxim preflow-push , în Information Processing Letters , vol. 69, nr. 5, 1999, pp. 239-242, DOI : 10.1016 / S0020-0190 (99) 00019-8 .
( EN ) Daniel D. Sleator și Robert E. Tarjan , O structură de date pentru copaci dinamici ( PDF ), în Journal of Computer and System Sciences , vol. 26, n. 3, 1983, pp. 362-391, DOI : 10.1016 / 0022-0000 (83) 90006-5 , ISSN 0022-0000 ( WC ACNP ) .
( EN ) Eugene Lawler , 4. Fluxuri de rețea , în Combinatorial Optimization: Networks and Matroids , Dover, 2001, pp. 109-177, ISBN 0-486-41453-1 .

Elemente conexe

linkuri externe

Marco Di Summa, Problema fluxului maxim ( PDF ), pe math.unipd.it , Universitatea din Padova , Departamentul de Matematică. Adus la 31 august 2016 ( arhivat la 27 iunie 2013) .

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică

[1] (EN) A. Schrijver, Despre istoria transportului și problemele de debit maxim în programarea matematică, vol. 91, nr. 3, 2002, pp. 437-445, DOI : 10.1007 / s101070100259 .

[2] (EN) Saul I. Gass și Arjang A. Assad, Dezvoltări matematice, algoritmice și profesionale ale cercetării operaționale din 1951 până în 1956, în An Annotated Timeline of Operations Research, International Series in Operations Research & Management Science, vol. 75, 2005, pp. 79-110, DOI : 10.1007 / 0-387-25837-X_5 , ISBN 1-4020-8116-2 .

[3] (EN) TE Harris și FS Ross, Fundamentele unei metode pentru evaluarea capacităților feroviare nete (PDF), în Research Memorandum, Rand Corporation, 1955.

[4] (EN) LR Ford și DR Fulkerson , Flux maxim printr-o rețea , în Canadian Journal of Mathematics , vol. 8, 1956, p. 399, DOI : 10.4153 / CJM-1956-045-5 .

[5] (RO) Ford, LR, Jr.; Fulkerson, DR, Flows in Networks , Princeton University Press (1962).

[6] (EN) VM Malhotra, M.Pramodh Kumar și SN Maheshwari, An $O(|V|^{3})$ ${\ displaystyle O (| V | ^ {3})}$ ${\ displaystyle O (| V | ^ {3})}$ algoritm pentru găsirea fluxurilor maxime în rețele , în Scrisori de procesare a informațiilor , vol. 7, nr. 6, 1978, pp. 277-278, DOI : 10.1016 / 0020-0190 (78) 90016-9 .

[7] (EN) V. King, S. Rao și R. Tarjan, Un algoritm de flux maxim determinist mai rapid , Journal of Algorithms, vol. 17, n. 3, 1994, pp. 447-474, DOI : 10.1006 / jagm.1994.1044 .

[8] (EN) AV Goldberg și S. Rao, Dincolo de bariera de descompunere a fluxului , în Jurnalul ACM , vol. 45, n. 5, 1998, p. 783, DOI : 10.1145 / 290179.290181 .

[9] (EN) James B. Orlin, Max curge în timp O (nm), sau mai bine , în STOC '13 Proceedings of the patruzeci și cincilea simpozion anual ACM on Theory of Computing, 2013, pp. 765-774, DOI : 10.1145 / 2488608.2488705 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]