Axiome of Huzita-Hatori

Axiomele lui Huzita-Hatori sunt axiomele pe care se bazează matematica origami . Primele șase axiome au fost formulate de matematicianul italo - japonez Humiaki Huzita în 1992 și descriu operațiile care sunt permise atunci când pliați o bucată de hârtie, ca în arta origami . A șaptea axiomă a fost adăugată de matematicianul japonez Koshiro Hatori .

Cele șapte axiome

Axiomele se bazează pe ipotezele că fiecare operație este efectuată într-un plan și că toate îndoirile sunt în linie dreaptă. Axiomele sunt după cum urmează:

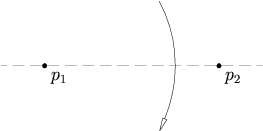
Având în vedere două puncte p ₁ și p ₂ , există o singură pliere care trece prin ambele.
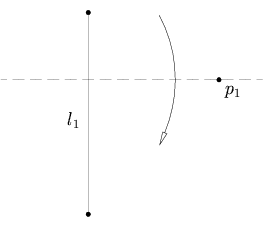
Având în vedere două puncte p ₁ și p ₂ , există o singură pliere care aduce p ₁ la p ₂ .
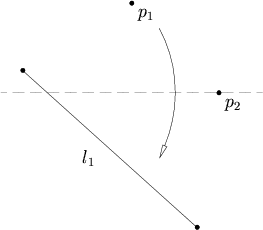
Având în vedere două linii drepte l ₁ și l ₂ , există întotdeauna un pli care aduce l ₁ peste l ₂ .
Având în vedere un punct p și o linie l , există o singură curbă perpendiculară pe l care trece prin punctul p .
Având în vedere două puncte p ₁ și p ₂ și o linie dreaptă l , dacă există o pliere prin p ₂ care aduce p ₁ peste l , atunci se poate construi o astfel de pliere.
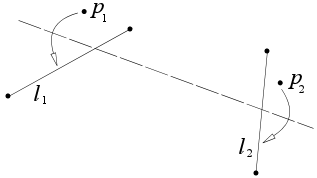
Având în vedere două puncte p ₁ și p ₂ și două linii l ₁ și l ₂ , dacă există un pli care aduce p ₁ la l ₁ și p ₂ la l ₂ . atunci se poate construi o astfel de pliere.
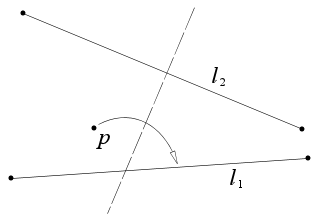
Având în vedere un punct p și două linii l ₁ și l ₂ , există întotdeauna un pli perpendicular pe l ₂ care aduce p la l ₁ .

Se poate vedea că axioma (5) poate avea zero, una sau două soluții, în timp ce axioma (6) poate avea zero, una, două sau trei. În acest fel, construcțiile geometrice rezultate sunt mai puternice decât construcțiile cu rigla și busola , unde numărul maxim de soluții ale unei axiome este de două. Din acest motiv, construcțiile cu rigla și busola pot rezolva cel mult ecuații de gradul doi, în timp ce construcțiile care utilizează origami pot rezolva și ecuații de gradul III.

Detalii

Axioma 1

Având în vedere două puncte p ₁ și p ₂ , există o singură pliere care trece prin ambele.

În formă parametrică , ecuația liniei care trece prin cele două puncte este:

F(s)=p_{1}+s(p_{2}-p_{1})

{\ displaystyle F (s) = p_ {1} + s (p_ {2} -p_ {1})}

{\ displaystyle F (s) = p_ {1} + s (p_ {2} -p_ {1})}

Axioma 2

Având în vedere două puncte p ₁ și p ₂ , există o singură pliere care aduce p ₁ la p ₂ .

Această axiomă este echivalentă cu găsirea axei segmentului p ₁ p ₂ . Acest lucru se poate face în patru pași:

Folosiți Axioma 1 pentru a găsi linia dintre p ₁ și p ₂ , dată de $P(s)=p_{1}+s(p_{2}-p_{1})$ ${\ displaystyle P (s) = p_ {1} + s (p_ {2} -p_ {1})}$ ${\ displaystyle P (s) = p_ {1} + s (p_ {2} -p_ {1})}$
Găsiți punctul mediu ( p _mijloc ) al lui P ( s )
Găsirea vectorului v ^făptașul perpendicular P (s)
Prin urmare, ecuația parametrică a îndoirii este:

F(s)=p_{\mathrm {mid} }+s\cdot \mathbf {v} ^{\mathrm {perp} }

{\ displaystyle F (s) = p _ {\ mathrm {mid}} + s \ cdot \ mathbf {v} ^ {\ mathrm {perp}}}

{\ displaystyle F (s) = p _ {\ mathrm {mid}} + s \ cdot \ mathbf {v} ^ {\ mathrm {perp}}}

Axioma 3

Având în vedere două linii drepte l ₁ și l ₂ , există întotdeauna un pli care aduce l ₁ peste l ₂ .

Această axiomă este echivalentă cu găsirea bisectoarei unghiului dintre l ₁ și l ₂ . Numim p ₁ și p ₂ oricare două puncte pe l ₁ și q ₁ și q ₂ orice două puncte pe l ₂ . Mai mult, noi numim u și V unitățile vectoriale care identifică direcțiile l ₁ și l ₂ , _respectiv. Prin urmare, avem:

\mathbf {u} =(p_{2}-p_{1})/\left|(p_{2}-p_{1})\right|

{\ displaystyle \ mathbf {u} = (p_ {2} -p_ {1}) / \ left | (p_ {2} -p_ {1}) \ right |}

{\ displaystyle \ mathbf {u} = (p_ {2} -p_ {1}) / \ left | (p_ {2} -p_ {1}) \ right |}

\mathbf {v} =(q_{2}-q_{1})/\left|(q_{2}-q_{1})\right|

{\ displaystyle \ mathbf {v} = (q_ {2} -q_ {1}) / \ left | (q_ {2} -q_ {1}) \ right |}

{\ displaystyle \ mathbf {v} = (q_ {2} -q_ {1}) / \ left | (q_ {2} -q_ {1}) \ right |}

Dacă cele două linii nu sunt paralele, punctul lor de intersecție este:

p_{\mathrm {int} }=p_{1}+s_{\mathrm {int} }\cdot \mathbf {u}

{\ displaystyle p _ {\ mathrm {int}} = p_ {1} + s _ {\ mathrm {int}} \ cdot \ mathbf {u}}

{\ displaystyle p _ {\ mathrm {int}} = p_ {1} + s _ {\ mathrm {int}} \ cdot \ mathbf {u}}

unde este

s_{int}={\frac {-v^{\perp }\cdot (p_{1}-q_{1})}{-\mathbf {v} \cdot \mathbf {u} }}

{\ displaystyle s_ {int} = {\ frac {-v ^ {\ perp} \ cdot (p_ {1} -q_ {1})} {- \ mathbf {v} \ cdot \ mathbf {u}}}}

{\ displaystyle s_ {int} = {\ frac {-v ^ {\ perp} \ cdot (p_ {1} -q_ {1})} {- \ mathbf {v} \ cdot \ mathbf {u}}}}

Bisectoarea uneia dintre bisectoare este dată de:

\mathbf {w} ={\frac {\left|\mathbf {u} \right|\mathbf {v} +\left|\mathbf {v} \right|\mathbf {u} }{\left|\mathbf {u} \right|+\left|\mathbf {v} \right|}}

{\ displaystyle \ mathbf {w} = {\ frac {\ left | \ mathbf {u} \ right | \ mathbf {v} + \ left | \ mathbf {v} \ right | \ mathbf {u}} {\ left | \ mathbf {u} \ right | + \ left | \ mathbf {v} \ right |}}}

{\ displaystyle \ mathbf {w} = {\ frac {\ left | \ mathbf {u} \ right | \ mathbf {v} + \ left | \ mathbf {v} \ right | \ mathbf {u}} {\ left | \ mathbf {u} \ right | + \ left | \ mathbf {v} \ right |}}}

Și ecuația parametrică a plierii este, prin urmare:

F(s)=p_{\mathrm {int} }+s\cdot \mathbf {w}

{\ displaystyle F (s) = p _ {\ mathrm {int}} + s \ cdot \ mathbf {w}}

{\ displaystyle F (s) = p _ {\ mathrm {int}} + s \ cdot \ mathbf {w}}

Există, de asemenea, o a doua bisectoare, perpendiculară pe prima și care trece prin p _int . Îndoirea de-a lungul acestei a doua bisectoare va duce în continuare la rezultatul dorit de a aduce l ₁ peste l ₂ . Este posibil să nu se poată face oricare dintre aceste pliuri, în funcție de locația punctului de intersecție

Dacă cele două linii sunt paralele, nu au intersecții. Pliul ar trebui să fie linia mediană între l ₁ și l ₂ , paralel cu ele.

Axioma 4

Având în vedere un punct p ₁ și o linie l ₁ , există o singură curbă perpendiculară pe l care trece prin punctul p .

Acest lucru este echivalent cu găsirea unei perpendiculare pe l ₁ care trece prin p ₁ . Dacă găsim un vector v perpendicular pe l ₁ , atunci [ecuația parametrică] a cotului va fi:

F(s)=p_{1}+s\cdot \mathbf {v}

{\ displaystyle F (s) = p_ {1} + s \ cdot \ mathbf {v}}

{\ displaystyle F (s) = p_ {1} + s \ cdot \ mathbf {v}}

Axioma 5

Având în vedere două puncte p ₁ și p ₂ și o linie dreaptă l , dacă există o pliere prin p ₂ care aduce p ₁ peste l , atunci se poate construi o astfel de pliere.

Exemplu în care nu există soluții: punctele p ₁ și p ₂ se află pe o linie perpendiculară pe l și distanța lui p _{2 de} la l este mai mare decât distanța lui p _{1 de} la l .

Axioma 6

Având în vedere două puncte p ₁ și p ₂ și două linii l ₁ și l ₂ , dacă există un pli care aduce p ₁ la l ₁ și p ₂ la l ₂ , atunci se poate construi un astfel de pli.

Exemplu în care nu există soluții: cele două linii l ₁ și l ₂ sunt paralele, punctele p ₁ și p ₂ se află pe o linie perpendiculară pe l ₁ și l ₂ , pe aceeași parte a planului față de cele două drepte și distanța lui p _{1 de} la l ₁ este egală cu distanța lui p _{2 de} la l ₂ .

Această axiomă este echivalentă cu găsirea unei linii care este simultan tangentă la două parabole și poate fi considerată echivalentă cu rezolvarea unei ecuații de gradul III. Cele două parabole au focare respectiv în p ₁ și p ₂ , cu linii definite de l ₁ și l ₂ .

Axioma 7

Având în vedere un punct p și două linii l ₁ și l ₂ , există întotdeauna un pli perpendicular pe l ₂ care aduce p la l ₁ .

Koshiro Hatori a descoperit această axiomă, iar Robert Lang a dovedit că completează lista axiomelor origami.

Alte proiecte

Wikimedia Commons conține imagini sau alte fișiere despre Axiomele Huzita-Hatori

linkuri externe

Construcții geometrice origami de Thomas Hull
O teorie matematică a construcțiilor și numerelor origami de Roger C. Alperin

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică