Automatul lui Büchi

Automat nedeterminist Büchi care recunoaște cuvinte infinite care conțin un număr finit de

la

{\ displaystyle a}

la

.

În informatică teoretică , un automat Büchi este un automat ω sau automat finit care operează pe cuvinte de lungime infinită, cu o condiție de acceptare particulară: o urmă are succes dacă și numai dacă trece de un număr infinit de ori pentru cel puțin o persoană care acceptă stare. Acest tip de automat este utilizat în mod obișnuit pentru verificarea modelului .

Acest tip de automat a fost definit de matematicianul Julius Richard Büchi ^[1] .

Definiție

Un automat Büchi pe un alfabet $LA$ ${\ displaystyle A}$ $LA$ este un automat ω ${\mathcal {A}}=(Q,{\mathcal {F}},I,T)$ ${\ displaystyle {\ mathcal {A}} = (Q, {\ mathcal {F}}, I, T)}$ ${\ displaystyle {\ mathcal {A}} = (Q, {\ mathcal {F}}, I, T)}$ , unde este

$Î$ ${\ displaystyle Q}$ $Î$ este un set finit de stări ;
${\mathcal {F}}\subset Q\times \Sigma \times Q$ ${\ displaystyle {\ mathcal {F}} \ subset Q \ times \ Sigma \ times Q}$ ${\ displaystyle {\ mathcal {F}} \ subset Q \ times \ Sigma \ times Q}$ este ansamblul tranzițiilor ;
$I\subseteq Q$ ${\ displaystyle I \ subseteq Q}$ ${\ displaystyle I \ subseteq Q}$ este ansamblul stărilor inițiale ;
$T\subseteq Q$ ${\ displaystyle T \ subseteq Q}$ ${\ displaystyle T \ subseteq Q}$ este un set de stări finale sau terminale sau de acceptare .

Se presupune adesea că setul de stări inițiale este compus dintr-un singur element. O tranziție $f=(p,a,q)\in {\mathcal {F}}$ ${\ displaystyle f = (p, a, q) \ în {\ mathcal {F}}}$ ${\ displaystyle f = (p, a, q) \ în {\ mathcal {F}}}$ este compus dintr-o stare de pornire $p$ ${\ displaystyle p}$ $p$ , o eticheta $la$ ${\ displaystyle a}$ $la$ și o stare de sosire $q$ ${\ displaystyle q}$ $q$ . Un calcul $c$ ${\ displaystyle c}$ $c$ (numită și cale sau pistă ) este o serie infinită de tranziții consecutive:

c=(p_{0},a_{1},p_{1})(p_{1},a_{2},p_{2})\cdots

{\ displaystyle c = (p_ {0}, a_ {1}, p_ {1}) (p_ {1}, a_ {2}, p_ {2}) \ cdots}

{\ displaystyle c = (p_ {0}, a_ {1}, p_ {1}) (p_ {1}, a_ {2}, p_ {2}) \ cdots}

Pentru $c$ ${\ displaystyle c}$ $c$ , starea inițială este $p_{0}$ ${\ displaystyle p_ {0}}$ $p_ {0}$ , eticheta sa este cuvântul infinit $a_{1}a_{2}\cdots a_{n}\cdots$ ${\ displaystyle a_ {1} a_ {2} \ cdots a_ {n} \ cdots}$ ${\ displaystyle a_ {1} a_ {2} \ cdots a_ {n} \ cdots}$ . Calculul are succes și cuvântul este acceptat (sau recunoscut de automat) dacă trece infinit de des printr-o stare terminală.

Se spune că un automat este determinist dacă îndeplinește următoarele două condiții:

are o singură stare inițială;
pentru fiecare stat $q$ ${\ displaystyle q}$ $q$ și pentru fiecare literă $la$ ${\ displaystyle a}$ $la$ , există cel mult o tranziție care începe de la $q$ ${\ displaystyle q}$ $q$ și purtând eticheta $la$ ${\ displaystyle a}$ $la$ .

Exemple

Exemplul 1

Automat Büchi care recunoaște cuvinte infinite care includ secvențe infinite de

la

{\ displaystyle a}

la

.

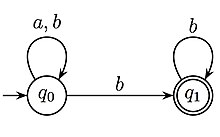
Automatul Büchi ${\mathcal {A}}=(\{q_{0},q_{1}\},{\mathcal {F}},q_{0},q_{1})$ ${\ displaystyle {\ mathcal {A}} = (\ {q_ {0}, q_ {1} \}, {\ mathcal {F}}, q_ {0}, q_ {1})}$ ${\ displaystyle {\ mathcal {A}} = (\ {q_ {0}, q_ {1} \}, {\ mathcal {F}}, q_ {0}, q_ {1})}$ al cărui set de tranziții ${\mathcal {F}}$ ${\ displaystyle {\ mathcal {F}}}$ ${\ mathcal {F}}$ este afișat în figura din stânga.

Cuvântul infinit $bbbb\cdots$ ${\ displaystyle bbbb \ cdots}$ ${\ displaystyle bbbb \ cdots}$ nu este acceptat deoarece singura piesă potrivită este $q_{0}q_{0}q_{0}\cdots$ ${\ displaystyle q_ {0} q_ {0} q_ {0} \ cdots}$ ${\ displaystyle q_ {0} q_ {0} q_ {0} \ cdots}$ iar singura stare care apare de un număr infinit de ori este $q_{0}$ ${\ displaystyle q_ {0}}$ $q_0$ , care nu acceptă. Pe de altă parte, cuvântul $aaaa\cdots$ ${\ displaystyle aaaa \ cdots}$ ${\ displaystyle aaaa \ cdots}$ este acceptat deoarece pista îi corespunde $q_{0}q_{1}q_{1}\cdots$ ${\ displaystyle q_ {0} q_ {1} q_ {1} \ cdots}$ ${\ displaystyle q_ {0} q_ {1} q_ {1} \ cdots}$ , Și $q_{1}$ ${\ displaystyle q_ {1}}$ $q_ {1}$ apare acolo de nenumărate ori și este o stare acceptantă. Mai general, automatul acceptă cuvinte infinite pe alfabetul din două litere $la$ ${\ displaystyle a}$ $la$ Și $b$ ${\ displaystyle b}$ $b$ , care conțin doar un număr finit de litere $la$ ${\ displaystyle a}$ $la$ , și anume expresia regulată $b^{*}a(a^{*}b^{+}a)^{\omega }$ ${\ displaystyle b ^ {*} a (a ^ {*} b ^ {+} a) ^ {\ omega}}$ ${\ displaystyle b ^ {*} a (a ^ {*} b ^ {+} a) ^ {\ omega}}$ .

Automat Büchi care recunoaște infinitele cuvinte în care fiecare apariție

b

{\ displaystyle b}

b

este precedat de un număr egal de zero

la

{\ displaystyle a}

la

.

Exemplul 2

Un alt exemplu este automatul Büchi determinist din figura din dreapta; automatul are trei stări: $q_{0}$ ${\ displaystyle q_ {0}}$ $q_0$ , $q_{1}$ ${\ displaystyle q_ {1}}$ $q_ {1}$ Și $q_{2}$ ${\ displaystyle q_ {2}}$ $q_ {2}$ . Acest automat recunoaște infinitele cuvinte în care fiecare apariție a $b$ ${\ displaystyle b}$ $b$ este precedat de un număr chiar nenul de apariții ale $la$ ${\ displaystyle a}$ $la$ . Calculul pe un cuvânt al limbii acceptate începe în starea inițială $q_{0}$ ${\ displaystyle q_ {0}}$ $q_0$ și citește un număr par de $la$ ${\ displaystyle a}$ $la$ (diferit de zero pentru că primul $la$ ${\ displaystyle a}$ $la$ determină tranziția în $q_{1}$ ${\ displaystyle q_ {1}}$ $q_ {1}$ ). Dacă un număr impar de $la$ ${\ displaystyle a}$ $la$ , automatul este în stare $q_{1}$ ${\ displaystyle q_ {1}}$ $q_ {1}$ altfel în stat $q_{2}$ ${\ displaystyle q_ {2}}$ $q_ {2}$ (care acceptă și, prin urmare, trebuie să apară de mai multe ori în pistă). Tranziția în $b$ ${\ displaystyle b}$ $b$ aduce din $q_{2}$ ${\ displaystyle q_ {2}}$ $q_ {2}$ La stat $q_{0}$ ${\ displaystyle q_ {0}}$ $q_0$ iar secvența începe din nou.

Automatele Büchi deterministe sunt strict mai puțin expresive decât automatele Büchi nedeterministe ^[2] ^[3] . Cu alte cuvinte, există limbaje recunoscute de automatele Büchi nedeterministe care nu pot fi recunoscute de automatele Büchi deterministe.

Limbi recunoscute

Seturile de cuvinte infinite recunoscute de automatele Büchi corespund limbajelor ω-regulate , adică seturilor formei

\bigcup _{1}^{m}U_{i}V_{i}^{\omega }

{\ displaystyle \ bigcup _ {1} ^ {m} U_ {i} V_ {i} ^ {\ omega}}

{\ displaystyle \ bigcup _ {1} ^ {m} U_ {i} V_ {i} ^ {\ omega}}

unde $U_{i}$ ${\ displaystyle U_ {i}}$ $U_ {i}$ Și $V_{i}$ ${\ displaystyle V_ {i}}$ $Tu$ sunt limbi regulate și i $V_{i}$ ${\ displaystyle V_ {i}}$ $Tu$ nu conțin cuvântul gol. Aceste limbi se mai numesc și Kleene ω- închiderea limbilor obișnuite ^[4] .

Pentru a obține formula generică pentru expresii regulate recunoscute de un automat Büchi, procedați după cum urmează. Având un automat Büchi, fie $W(p,q)$ ${\ displaystyle W (p, q)}$ ${\ displaystyle W (p, q)}$ ansamblul cuvintelor finite recunoscute având $p$ ${\ displaystyle p}$ $p$ ca stare inițială e $q$ ${\ displaystyle q}$ $q$ ca stare finală, adică toate cuvintele reprezentate de etichetele de pe o pistă din $p$ ${\ displaystyle p}$ $p$ la $q$ ${\ displaystyle q}$ $q$ . Aceste limbi finite sunt regulate. Un cuvânt infinit $X$ ${\ displaystyle x}$ $X$ este acceptat dacă există un calcul care trece de un număr infinit de ori printr-o stare terminală. Este $q$ ${\ displaystyle q}$ $q$ această stare terminală prin care urma trece de un număr infinit de ori. Acest lucru este echivalent cu a spune

x\in W(q_{0},q)W(q,q)^{\omega }

{\ displaystyle x \ în W (q_ {0}, q) W (q, q) ^ {\ omega}}

{\ displaystyle x \ în W (q_ {0}, q) W (q, q) ^ {\ omega}}

pentru o stare inițială $q_{0}$ ${\ displaystyle q_ {0}}$ $q_0$ . Luând mulțimile pe toate stările inițiale și terminale, obținem formula dată ^[4] . Pentru a demonstra că, reciproc, toate limbile ω-regulate sunt recunoscute de automatele Büchi, folosim operațiile de închidere ^[5] .

Descrierea limbilor recognized-regulate recunoscute arată că cuvântul problemă este decisiv pentru automatele Büchi, deoarece este suficient să verificăm dacă cel puțin una dintre limbile obișnuite date de $W(q_{0},q)W(q,q)$ ${\ displaystyle W (q_ {0}, q) W (q, q)}$ ${\ displaystyle W (q_ {0}, q) W (q, q)}$ nu este gol.

Proprietăți de închidere

Limbile recunoscute de automatele Büchi sunt închise pentru o serie de operațiuni.

Unire : Lasă-i să fie ${\mathcal {A}}=(Q_{A},{\mathcal {F}}_{A},I_{A},T_{A})$ ${\ displaystyle {\ mathcal {A}} = (Q_ {A}, {\ mathcal {F}} _ {A}, I_ {A}, T_ {A})}$ ${\ displaystyle {\ mathcal {A}} = (Q_ {A}, {\ mathcal {F}} _ {A}, I_ {A}, T_ {A})}$ Și ${\mathcal {B}}=(Q_{B},{\mathcal {F}}_{B},I_{B},T_{B})$ ${\ displaystyle {\ mathcal {B}} = (Q_ {B}, {\ mathcal {F}} _ {B}, I_ {B}, T_ {B})}$ ${\ displaystyle {\ mathcal {B}} = (Q_ {B}, {\ mathcal {F}} _ {B}, I_ {B}, T_ {B})}$ două automate care recunosc limbile $L_{A}$ ${\ displaystyle L_ {A}}$ $ACOLO$ Și $L_{B}$ ${\ displaystyle L_ {B}}$ $LIVRE$ . Un automat care recunoaște unirea $L_{A}\cup L_{B}$ ${\ displaystyle L_ {A} \ cup L_ {B}}$ ${\ displaystyle L_ {A} \ cup L_ {B}}$ se obține prin unirea celor două automate. Presupunând că mulțimile de stări $Q_{A}$ ${\ displaystyle Q_ {A}}$ ${\ displaystyle Q_ {A}}$ Și $Q_{B}$ ${\ displaystyle Q_ {B}}$ ${\ displaystyle Q_ {B}}$ sunt disjuncte: automatul ${\mathcal {C}}=(Q_{A}\cup Q_{B},{\mathcal {F}}_{A}\cup {\mathcal {F}}_{B},I_{A}\cup I_{B},T_{A}\cup T_{B})$ ${\ displaystyle {\ mathcal {C}} = (Q_ {A} \ cup Q_ {B}, {\ mathcal {F}} _ {A} \ cup {\ mathcal {F}} _ {B}, I_ { A} \ cup I_ {B}, T_ {A} \ cup T_ {B})}$ ${\ displaystyle {\ mathcal {C}} = (Q_ {A} \ cup Q_ {B}, {\ mathcal {F}} _ {A} \ cup {\ mathcal {F}} _ {B}, I_ { A} \ cup I_ {B}, T_ {A} \ cup T_ {B})}$ recunoaște unirea $L_{A}\cup L_{B}$ ${\ displaystyle L_ {A} \ cup L_ {B}}$ ${\ displaystyle L_ {A} \ cup L_ {B}}$ .

closure-închidere : pentru orice limbă obișnuită $L$ ${\ displaystyle L}$ $L$ care nu conține șirul gol, limba ω $L^{\omega }$ ${\ displaystyle L ^ {\ omega}}$ ${\ displaystyle L ^ {\ omega}}$ este recunoscută de un automat Büchi. Este ${\mathcal {A}}=(Q,{\mathcal {F}},i,T)$ ${\ displaystyle {\ mathcal {A}} = (Q, {\ mathcal {F}}, i, T)}$ ${\ displaystyle {\ mathcal {A}} = (Q, {\ mathcal {F}}, i, T)}$ un automat cu stare finită pe care îl recunoaște $L$ ${\ displaystyle L}$ $L$ . Dacă are o singură stare inițială $the$ ${\ displaystyle i}$ $the$ și fără tranziție (adică cel mai simplu automat care poate fi construit). Ele pot fi adăugate la ${\mathcal {A}}$ ${\ displaystyle {\ mathcal {A}}}$ ${\ mathcal {A}}$ tranzițiile $(q,a,i)$ ${\ displaystyle (q, a, i)}$ ${\ displaystyle (q, a, i)}$ pentru fiecare tranziție $(q,a,t)$ ${\ displaystyle (q, a, t)}$ ${\ displaystyle (q, a, t)}$ din ${\mathcal {F}}$ ${\ displaystyle {\ mathcal {F}}}$ ${\ mathcal {F}}$ cu $t\in T$ ${\ displaystyle t \ in T}$ $t \ in T$ . Automatul Büchi astfel construit, cu o singură stare inițială care este și terminală, recunoaște $L^{\omega }$ ${\ displaystyle L ^ {\ omega}}$ ${\ displaystyle L ^ {\ omega}}$ .

Concatenare : pentru orice limbă obișnuită $L$ ${\ displaystyle L}$ $L$ și orice limbă ω $M.$ ${\ displaystyle M}$ $M.$ recunoscută de un automat Büchi, produsul celor două limbi $L\circ M$ ${\ displaystyle L \ circ M}$ ${\ displaystyle L \ circ M}$ este un limbaj recognized recunoscut de un automat Büchi.

Cele trei proprietăți anterioare arată că fiecare limbaj regular obișnuit este recunoscut de un automat Büchi.

Intersecție : Let ${\mathcal {A}}=(Q_{A},{\mathcal {F}}_{A},I_{A},T_{A})$ ${\ displaystyle {\ mathcal {A}} = (Q_ {A}, {\ mathcal {F}} _ {A}, I_ {A}, T_ {A})}$ ${\ displaystyle {\ mathcal {A}} = (Q_ {A}, {\ mathcal {F}} _ {A}, I_ {A}, T_ {A})}$ Și ${\mathcal {B}}=(Q_{B},{\mathcal {F}}_{B},I_{B},T_{B})$ ${\ displaystyle {\ mathcal {B}} = (Q_ {B}, {\ mathcal {F}} _ {B}, I_ {B}, T_ {B})}$ ${\ displaystyle {\ mathcal {B}} = (Q_ {B}, {\ mathcal {F}} _ {B}, I_ {B}, T_ {B})}$ două automate care recunosc limbile $L_{A}$ ${\ displaystyle L_ {A}}$ $ACOLO$ Și $L_{B}$ ${\ displaystyle L_ {B}}$ $LIVRE$ . Un automat care recunoaște intersecția $L_{A}\cap L_{B}$ ${\ displaystyle L_ {A} \ cap L_ {B}}$ ${\ displaystyle L_ {A} \ cap L_ {B}}$ este construit după cum urmează:

{\mathcal {C}}=\{Q_{A}\times Q_{B}\times \{0,1,2\},Q_{A}\times Q_{b}\times \{0\},{\mathcal {F}},T\}

{\ displaystyle {\ mathcal {C}} = \ {Q_ {A} \ times Q_ {B} \ times \ {0,1,2 \}, Q_ {A} \ times Q_ {b} \ times \ {0 \}, {\ mathcal {F}}, T \}}

{\ displaystyle {\ mathcal {C}} = \ {Q_ {A} \ times Q_ {B} \ times \ {0,1,2 \}, Q_ {A} \ times Q_ {b} \ times \ {0 \}, {\ mathcal {F}}, T \}}

unde tranzițiile de ${\mathcal {F}}$ ${\ displaystyle {\ mathcal {F}}}$ ${\ mathcal {F}}$ copiați-le în ${\mathcal {F_{A}}}$ ${\ displaystyle {\ mathcal {F_ {A}}}}$ ${\ displaystyle {\ mathcal {F_ {A}}}}$ Și ${\mathcal {F_{B}}}$ ${\ displaystyle {\ mathcal {F_ {B}}}}$ ${\ displaystyle {\ mathcal {F_ {B}}}}$ pentru primele două componente și schimbați a treia componentă de la 0 la 1 când o stare de $T_{A}$ ${\ displaystyle T_ {A}}$ $T_ {A}$ apare în prima componentă, de la 1 la 2 când apare o stare de $T_{B}$ ${\ displaystyle T_ {B}}$ $T_ {B}$ apare în a doua componentă și revine la 0 imediat după aceea. Într-un calcul, un 2 apare infinit de des ca o a treia componentă dacă și numai dacă o stare de $T_{A}$ ${\ displaystyle T_ {A}}$ $T_ {A}$ și o stare de $T_{B}$ ${\ displaystyle T_ {B}}$ $T_ {B}$ apar infinit des în prima și a doua componentă. Prin urmare, alegerea ca terminal îi indică pe cei din ${\mathcal {T}}=Q_{A}\times Q_{b}\times \{2\}$ ${\ displaystyle {\ mathcal {T}} = Q_ {A} \ times Q_ {b} \ times \ {2 \}}$ ${\ displaystyle {\ mathcal {T}} = Q_ {A} \ times Q_ {b} \ times \ {2 \}}$ obținem un automat Büchi cu comportamentul dorit.

Limbile recunoscute de automatele Büchi sunt închise în ceea ce privește complementarea. Richard Büchi a demonstrat acest lucru în 1962 ^[1] . Mai târziu, alte construcții ale automatului au fost date recunoscând limbajul complementar al unui limbaj ω ^[6] ^[7] ^[8] ^[9] .

Conexiune cu alte automate

Automatele Büchi sunt echivalente cu automatele Muller , Rabin , Streett sau parity. Cu toate acestea, ele diferă prin concizie. De exemplu, automatele Büchi sunt exponențial mai concise decât automatele Rabin în următorul sens: există o familie de limbi $(L_{n})_{n=2\ldots }$ ${\ displaystyle (L_ {n}) _ {n = 2 \ ldots}}$ ${\ displaystyle (L_ {n}) _ {n = 2 \ ldots}}$ pe alfabetul {0, 1, #}, recunoscut prin automatele Büchi nedeterministe de dimensiune O (n), dar fiecare automat Rabin nedeterminist care recunoaște același limbaj trebuie să fie de dimensiune cel puțin n! ^[10] .

Automatele Büchi nedeterministe reprezintă exact proprietățile logicii monadice de ordinul doi cu un succesor (S1S), numite și „proprietăți ω-regulate”. Logica S1S este strict mai expresivă decât logica timpului liniar.

Automate Co-Büchi

Există o dublă condiție pentru acceptarea automatelor Büchi: acestea sunt automatele co-Büchi . Condiția de acceptare devine: o urmă (sau calcul sau cale infinită) are succes dacă și numai dacă o stare care apare de un număr fals de ori este o stare de acceptare ^[11] .

Algoritmic

Logica temporală liniară și verificarea modelului

Automatele Buchi sunt utilizate în verificarea modelului, unde apar întrebări cu privire la proprietățile algoritmilor. De exemplu, cunoașterea dacă limbajul acceptat de un automat Büchi nedeterminist este gol este o proprietate care se decide în timp liniar ^[12] . O formulă logică în timp liniar (LTL) poate fi recunoscută de un automat Büchi, dar dimensiunea sa va fi exponențială în dimensiunea formulei LTL ^[13] . Această transformare poate fi utilizată pentru:

Decideți problema de satisfacție LTL. Această problemă este completă PSPACE .
Verificați cu verificarea modelului . Acesta este motivul pentru care este construit automatul Büchi echivalent cu formula LTL și se realizează produsul cu sistemul de verificat. Produsul este un automat Büchi și verificarea constă în testarea dacă limba acceptată este goală.

Transformarea unui automat Büchi generalizat într-un automat Büchi clasic.

Transformarea unei formule LTL într-un automat Büchi este de obicei prezentată cu un pas intermediar, numit automat Büchi generalizat , pentru care condiția de acceptare este mai generală. Un automat Büchi generalizat este ca un automat Büchi, cu excepția faptului că setul de stări terminale $T\subseteq Q$ ${\ displaystyle T \ subseteq Q}$ ${\ displaystyle T \ subseteq Q}$ este înlocuit cu un set finit $\{T_{1},\dots ,T_{k}\}$ ${\ displaystyle \ {T_ {1}, \ dots, T_ {k} \}}$ ${\ displaystyle \ {T_ {1}, \ dots, T_ {k} \}}$ cu $T_{i}\subseteq Q$ ${\ displaystyle T_ {i} \ subseteq Q}$ ${\ displaystyle T_ {i} \ subseteq Q}$ . Condiția de acceptare devine următoarea: o urmă are succes dacă și numai dacă pentru fiecare i trece de un număr infinit de ori pentru cel puțin o stare acceptantă de $T_{i}$ ${\ displaystyle T_ {i}}$ $Tu}$ .

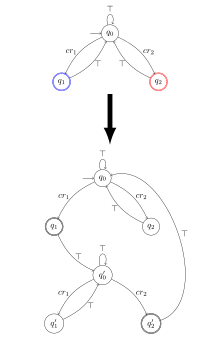
Exemplul verifică cuvintele alfabetului { $\top$ ${\ displaystyle \ top}$ $\top$ , cr1, cr2} proprietatea $\varphi$ ${\ displaystyle \ varphi}$ $\ varphi$ care apare „infinit de des în secțiunea critică 1 și infinit deseori în secțiunea critică 2”. Scrisoarea $\top$ ${\ displaystyle \ top}$ $\top$ corespunde unei secțiuni necritice, cr1 corespunde secțiunii critice 1 și cr2 secțiunii critice 2. $T\subseteq Q$ ${\ displaystyle T \ subseteq Q}$ ${\ displaystyle T \ subseteq Q}$ este egal cu {{q ₁ }, {q ₂ }}: o execuție acceptantă trebuie să treacă infinit de des pentru q1 și infinit de des pentru q2. Aceasta corespunde cu ceea ce este descris de proprietate $\varphi$ ${\ displaystyle \ varphi}$ $\ varphi$ .

Ca prim pas, formula LTL este transformată într-un automat Büchi generalizat (ideea este că stările automatului sunt subseturile maxime de subformule ale formulei LTL). De exemplu, pentru proprietate $\varphi$ ${\ displaystyle \ varphi}$ $\ varphi$ scris în LTL cu $GFcr_{1}\land GFcr_{2}$ ${\ displaystyle GFcr_ {1} \ land GFcr_ {2}}$ ${\ displaystyle GFcr_ {1} \ land GFcr_ {2}}$ (întotdeauna în viitorul cr1 și întotdeauna în viitorul cr2), automatul generalizat este dat de automatul din partea de sus a figurii. Acest automat se transformă într-un automat Büchi normal făcând o copie a automatului generalizat pentru fiecare subset $T_{i}$ ${\ displaystyle T_ {i}}$ $Tu}$ . În exemplul din lateral, este copiat de două ori: prima copie corespunde cu {q ₁ } și a doua cu {q ₂ }. Odată întâlnit q ₁ , trecem la a doua copie. Odată ce q ₂ este satisfăcut, reveniți la prima copie. Automatul obținut este un automat Büchi clasic și condiția de acceptare este de a trece de un număr infinit de ori pentru q ₁ sau q ₂ '. Prin construcție, această condiție este echivalentă cu trecerea unei infinități de ori în q ₁ și o infinitate de ori în q ₂ în automatul generalizat.

Există algoritmi eficienți pentru construirea unui automat Büchi echivalent dintr-o formulă LTL ^[14] .

S1S și WS1S

Richard Büchi ^{[1] a} arătat că există echivalență, pentru fiecare limbaj infinit L, între:

L este definibil de o proprietate S1S ( logică monadică de ordinul doi cu un succesor);
L este definibil prin proprietăți WS1S (logică monadică de ordinul doi cu un succesor, numită „slab” (slab), și anume că cuantificarea portului de ordinul doi pe mulțimi finite);
L este recunoscut de un automat Büchi.

Echivalențele sunt eficiente: o formulă S1S se transformă într-un automat Büchi. Prin urmare, logica S1S (și WS1S) este decisă. Logica S1S are o complexitate neelementară ^[15] .

Notă

^ ^a ^b ^c ( EN ) Julius R. Büchi , Despre o metodă de decizie în aritmetică limitată de ordinul doi , Proc. Congres internațional de logică, metodă și filozofie a științei (1960) , Stanford University Press, 3 ianuarie 1962, pp. 1-12.
^ Christel Baier și Joost-Pieter Katoen, Principiile verificării modelelor (seria de reprezentare și minte) , ediția MIT Pressª, 31 mai 2008, p. 191 și p. 975, ISBN 978-0-262-02649-9 .
^ Farwer
^ ^a ^b Farwer , p. 6 .
^ Thomas , pp. 138-139 .
^ (EN) Robert McNaughton , Testarea și generarea de secvențe infinite de un automat finit , în Informații și control, vol. 9, 1966, pp. 521-530, DOI : 10.1016 / s0019-9958 (66) 80013-x .
^ (EN) AP Sistla, MY Vardi și P. Wolper, Problema de complementare pentru automatele Büchi cu aplicații la logica temporală , în Theoretical Computer Science , vol. 49, 1987, pp. 217-237, DOI : 10.1016 / 0304-3975 (87) 90008-9 .
^ (EN) Shmuel Safra, Despre complexitatea ω-automatelor, în Proc. 29 Simpozion IEEE privind fundamentele de informatică , White Plains, New York, octombrie 1988, pp. 319-327.
^ (RO) O. Kupferman și MY Vardi, Automatele slabe alternante nu sunt atât de slabe, în ACM Transactions on Computational Logic , Vol. 2, nr. 2, iulie 2001, pp. 408-429.
^ Farwer , p. 18, Teorema 1.30.
^ (EN) Guillaume Sadegh, Complementarea Büchi Automata (PDF), în Raport tehnic, vol. 0903, révision 2073, Le Kremlin-Bicêtre, Laboratoire de Recherche et Développement de l'Epita, mai 2009.
^ Christel Baier și Joost-Pieter Katoen, Principiile verificării modelelor (seria de reprezentare și minte) , ediția MIT Pressª, 31 mai 2008, p. 185, Th. 4.42 și p. 975, ISBN 978-0-262-02649-9 .
^ Christel Baier și Joost-Pieter Katoen, Principiile verificării modelelor (seria de reprezentare și minte) , ediția MIT Pressª, 31 mai 2008, p. 975, ISBN 978-0-262-02649-9 .
^ (EN) Paul și Denis Gastin Oddoux, Fast LTL to Büchi Automata Translation in Computer Aided Verification, Lecture Notes in Computer Science, Berlin, Heidelberg, Springer, 18 iulie 2001, pp. 53-65, DOI : 10.1007 / 3-540-44585-4_6 , ISBN 3-540-44585-4 . Adus pe 7 februarie 2018 .
^ (RO) Luke Ong - Automate, logică și jocuri: teorie și aplicație 1. Büchi Automata și S1S (PDF) pe cs.ox.ac.uk.

Bibliografie

( EN ) Wolfgang Thomas, Automate on infinite objects , în Jan Van Leeuwen (ed.), Handbook of Theoretical Computer Science: Formal Models and Semantics , t. B, MIT Press, 1990, pp. 133-192, ISBN 0-262-72015-9 .
( EN ) Berndt Farwer, ω-Automata , în Erich Grädel, Wolfgang Thomas și Thomas Wilke (ed.), Automate logics, and infinite games: A guide to current research ,, Lecture Notes in Computer Science , n. 2500, Springer-Verlag New York, Inc., 1 ianuarie 2002, pp. 3-22, ISBN 978-3-540-00388-5 .
( EN ) Samuel Eilenberg, Cap. XIV. Comportamentul infinit al automatelor finite , în automate, limbi și mașini , matematică pură și aplicată , vol. A, Academic Press, 1974, pp. 379 -393, ISBN 978-0-12-234001-7 .

Alte proiecte

Wikimedia Commons conține imagini sau alte fișiere pe automatul lui Büchi

Portal IT

Portalul de matematică

[:0-1] ( EN ) Julius R. Büchi , Despre o metodă de decizie în aritmetică limitată de ordinul doi , Proc. Congres internațional de logică, metodă și filozofie a științei (1960) , Stanford University Press, 3 ianuarie 1962, pp. 1-12.

[2] Christel Baier și Joost-Pieter Katoen, Principiile verificării modelelor (seria de reprezentare și minte) , ediția MIT Pressª, 31 mai 2008, p. 191 și p. 975, ISBN 978-0-262-02649-9 .

[3] Farwer

[Farwer6-4] Farwer , p. 6 .

[5] Thomas , pp. 138-139 .

[6] (EN) Robert McNaughton , Testarea și generarea de secvențe infinite de un automat finit , în Informații și control, vol. 9, 1966, pp. 521-530, DOI : 10.1016 / s0019-9958 (66) 80013-x .

[7] (EN) AP Sistla, MY Vardi și P. Wolper, Problema de complementare pentru automatele Büchi cu aplicații la logica temporală , în Theoretical Computer Science , vol. 49, 1987, pp. 217-237, DOI : 10.1016 / 0304-3975 (87) 90008-9 .

[8] (EN) Shmuel Safra, Despre complexitatea ω-automatelor, în Proc. 29 Simpozion IEEE privind fundamentele de informatică , White Plains, New York, octombrie 1988, pp. 319-327.

[9] (RO) O. Kupferman și MY Vardi, Automatele slabe alternante nu sunt atât de slabe, în ACM Transactions on Computational Logic , Vol. 2, nr. 2, iulie 2001, pp. 408-429.

[10] Farwer , p. 18, Teorema 1.30.

[11] (EN) Guillaume Sadegh, Complementarea Büchi Automata (PDF), în Raport tehnic, vol. 0903, révision 2073, Le Kremlin-Bicêtre, Laboratoire de Recherche et Développement de l'Epita, mai 2009.

[12] Christel Baier și Joost-Pieter Katoen, Principiile verificării modelelor (seria de reprezentare și minte) , ediția MIT Pressª, 31 mai 2008, p. 185, Th. 4.42 și p. 975, ISBN 978-0-262-02649-9 .

[13] Christel Baier și Joost-Pieter Katoen, Principiile verificării modelelor (seria de reprezentare și minte) , ediția MIT Pressª, 31 mai 2008, p. 975, ISBN 978-0-262-02649-9 .

[14] (EN) Paul și Denis Gastin Oddoux, Fast LTL to Büchi Automata Translation in Computer Aided Verification, Lecture Notes in Computer Science, Berlin, Heidelberg, Springer, 18 iulie 2001, pp. 53-65, DOI : 10.1007 / 3-540-44585-4_6 , ISBN 3-540-44585-4 . Adus pe 7 februarie 2018 .

[15] (RO) Luke Ong - Automate, logică și jocuri: teorie și aplicație 1. Büchi Automata și S1S (PDF) pe cs.ox.ac.uk.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]