Teorema sferică a cochiliei

În mecanica clasică , teorema sferică a cochiliei (sau pur și simplu teorema cojii ) face posibilă simplificarea studiului gravitației în prezența corpurilor cu simetrie sferică.

Formulată de Isaac Newton , care a dezvoltat teoria gravitației universale , constă din două afirmații:

o carcasă sferică de masă M, având densitate uniformă, exercită asupra unei particule externe o forță gravitațională egală cu cea a unei particule punctuale de masă M plasată în centrul său;
forța gravitațională exercitată de o coajă sferică având densitate uniformă asupra unei particule plasate în interiorul acesteia este zero.

Dovada sa se datorează lui Carl Friedrich Gauss care și-a aplicat importanta teoremă a fluxului , cu toate acestea Newton însuși a dovedit-o și a folosit-o pentru a explica teoria gravitației lui Robert Hooke , fără a o pune vreodată în scris.

Deși teorema a fost dezvoltată pentru forța gravitațională, se aplică și forței electrostatice și oricărui fenomen în care forța depinde de inversul pătratului distanței.

Demonstrație

Prima afirmație

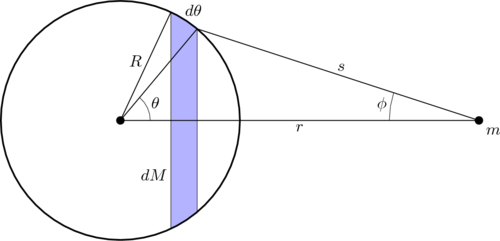
Să luăm în considerare o coajă sferică cu rază R și grosime infinitesimală și o particulă de masă m plasată la distanță $r$ ${\ displaystyle r}$ $r$ din centrul cochiliei. Putem considera învelișul ca fiind format dintr-o serie de inele cu rază $R\sin \theta$ ${\ displaystyle R \ sin \ theta}$ ${\ displaystyle R \ sin \ theta}$ , grosime $Rd\theta$ ${\ displaystyle Rd \ theta}$ ${\ displaystyle Rd \ theta}$ si masa $d M.$ ${\ displaystyle dM}$ ${\ displaystyle dM}$ , cu $0\leq \theta \leq \pi$ ${\ displaystyle 0 \ leq \ theta \ leq \ pi}$ ${\ displaystyle 0 \ leq \ theta \ leq \ pi}$ (figura din lateral prezintă o secțiune transversală).

Conform legii gravitației, forța de atracție exercitată de fiecare dintre aceste inele este

dF={\frac {Gm\;dM}{s^{2}}}\cos \phi

{\ displaystyle dF = {\ frac {Gm \; dM} {s ^ {2}}} \ cos \ phi}

{\ displaystyle dF = {\ frac {Gm \; dM} {s ^ {2}}} \ cos \ phi}

și este îndreptat de-a lungul $r$ ${\ displaystyle r}$ $r$ , deoarece pentru simetria inelului componentele forței perpendiculare pe $r$ ${\ displaystyle r}$ $r$ anulați-vă reciproc.

Forța totală exercitată de cochilie este dată de:

F=\int dF=Gm\int {\frac {dM\cos \phi }{s^{2}}}

{\ displaystyle F = \ int dF = Gm \ int {\ frac {dM \ cos \ phi} {s ^ {2}}}}

{\ displaystyle F = \ int dF = Gm \ int {\ frac {dM \ cos \ phi} {s ^ {2}}}}

acum este necesar să exprimăm $d M.$ ${\ displaystyle dM}$ ${\ displaystyle dM}$ Și $\cos \phi$ ${\ displaystyle \ cos \ phi}$ ${\ displaystyle \ cos \ phi}$ în funcție de s, pentru a calcula integralul, care va avea pentru extreme $s=r-R$ ${\ displaystyle s = rR}$ ${\ displaystyle s = r-R}$ Și $s=r+R$ ${\ displaystyle s = r + R}$ ${\ displaystyle s = r + R}$ .

Suprafața totală a unei cochilii sferice este

4\pi R^{2}

{\ displaystyle 4 \ pi R ^ {2}}

{\ displaystyle 4 \ pi R ^ {2}}

iar cea a inelului dintre θ și θ + dθ este

2\pi R^{2}\sin \theta \,d\theta

{\ displaystyle 2 \ pi R ^ {2} \ sin \ theta \, d \ theta}

{\ displaystyle 2 \ pi R ^ {2} \ sin \ theta \, d \ theta}

De sine $M.$ ${\ displaystyle M}$ $M.$ este masa totală a învelișului sferic, cea a inelului este deci:

dM={\frac {2\pi R^{2}\sin \theta }{4\pi R^{2}}}M\,d\theta =\textstyle {\frac {1}{2}}M\sin \theta \,d\theta

{\ displaystyle dM = {\ frac {2 \ pi R ^ {2} \ sin \ theta} {4 \ pi R ^ {2}}} M \, d \ theta = \ textstyle {\ frac {1} {2 }} M \ sin \ theta \, d \ theta}

{\ displaystyle dM = {\ frac {2 \ pi R ^ {2} \ sin \ theta} {4 \ pi R ^ {2}}} M \, d \ theta = \ textstyle {\ frac {1} {2 }} M \ sin \ theta \, d \ theta}

Pentru legea cosinusului (sau teorema lui Carnot) și alte considerații trigonometrice simple avem asta

\cos \phi ={\frac {r^{2}+s^{2}-R^{2}}{2rs}}

{\ displaystyle \ cos \ phi = {\ frac {r ^ {2} + s ^ {2} -R ^ {2}} {2rs}}}

{\ displaystyle \ cos \ phi = {\ frac {r ^ {2} + s ^ {2} -R ^ {2}} {2rs}}}

\cos \theta ={\frac {r^{2}+R^{2}-s^{2}}{2rR}}.

{\ displaystyle \ cos \ theta = {\ frac {r ^ {2} + R ^ {2} -s ^ {2}} {2rR}}.}

{\ displaystyle \ cos \ theta = {\ frac {r ^ {2} + R ^ {2} -s ^ {2}} {2rR}}.}

Prin diferențierea celei de-a doua ecuații față de $\theta$ ${\ displaystyle \ theta}$ $\ theta$ și s obținem și asta

\sin \theta \,d\theta ={\frac {s}{rR}}\,ds

{\ displaystyle \ sin \ theta \, d \ theta = {\ frac {s} {rR}} \, ds}

{\ displaystyle \ sin \ theta \, d \ theta = {\ frac {s} {rR}} \, ds}

Prin urmare, putem exprima integralul față de variabila s și obținem

F={\frac {GMm}{4r^{2}R}}\int _{r-R}^{r+R}\left(1+{\frac {r^{2}-R^{2}}{s^{2}}}\right)ds.

{\ displaystyle F = {\ frac {GMm} {4r ^ {2} R}} \ int _ {rR} ^ {r + R} \ left (1 + {\ frac {r ^ {2} -R ^ { 2}} {s ^ {2}}} \ right) ds.}

{\ displaystyle F = {\ frac {GMm} {4r ^ {2} R}} \ int _ {rR} ^ {r + R} \ left (1 + {\ frac {r ^ {2} -R ^ { 2}} {s ^ {2}}} \ right) ds.}

Valoarea integralei este 4R, deci obținem asta

F=G{\frac {Mm}{r^{2}}}

{\ displaystyle F = G {\ frac {Mm} {r ^ {2}}}}

{\ displaystyle F = G {\ frac {Mm} {r ^ {2}}}}

care este forța exercitată de o particulă de masă M plasată la o distanță r (adică la centrul învelișului) de particula m , așa cum am vrut să demonstrăm.

A doua afirmație

Arată în interiorul unei cochilii infinitesimale

Împărțim cochilia în cochilii cu grosime infinitesimală dS . Fie P o masă punctuală în interiorul învelișului infinitesimal. Dacă trecem prin P un con jumătate de deschidere (infinitesimal) α , axa sa se întâlnește cu coaja în punctele A și B. Aria suprafeței învelișului sferic conținută în conul de pe partea A va fi proporțională cu pătratul distanței PA. Același lucru este valabil și pentru B. Având în vedere densitatea σ, masa celor două volume va fi, respectiv

m_{A}=\sigma \pi \left(PA\,\operatorname {tan} \alpha \right)^{2}\times dS

{\ displaystyle m_ {A} = \ sigma \ pi \ left (PA \, \ operatorname {tan} \ alpha \ right) ^ {2} \ times dS}

{\ displaystyle m_ {A} = \ sigma \ pi \ left (PA \, \ operatorname {tan} \ alpha \ right) ^ {2} \ times dS}

m_{B}=\sigma \pi \left(PB\,\operatorname {tan} \alpha \right)^{2}\times dS

{\ displaystyle m_ {B} = \ sigma \ pi \ left (PB \, \ operatorname {tan} \ alpha \ right) ^ {2} \ times dS}

{\ displaystyle m_ {B} = \ sigma \ pi \ left (PB \, \ operatorname {tan} \ alpha \ right) ^ {2} \ times dS}

Dacă acum calculăm forța gravitațională exercitată de cele două volume pe P , se numește $m_{P}$ ${\ displaystyle m_ {P}}$ $m_ {P}$ masa sa, avem

F_{A}=G{\frac {m_{P}\times m_{A}}{PA^{2}}}=Gm_{P}\times \sigma \pi \operatorname {tan} ^{2}\alpha \times dS

{\ displaystyle F_ {A} = G {\ frac {m_ {P} \ times m_ {A}} {PA ^ {2}}} = Gm_ {P} \ times \ sigma \ pi \ operatorname {tan} ^ { 2} \ alpha \ times dS}

{\ displaystyle F_ {A} = G {\ frac {m_ {P} \ times m_ {A}} {PA ^ {2}}} = Gm_ {P} \ times \ sigma \ pi \ operatorname {tan} ^ { 2} \ alpha \ times dS}

F_{B}=G{\frac {m_{P}\times m_{B}}{PB^{2}}}=Gm_{P}\times \sigma \pi \operatorname {tan} ^{2}\alpha \times dS

{\ displaystyle F_ {B} = G {\ frac {m_ {P} \ times m_ {B}} {PB ^ {2}}} = Gm_ {P} \ times \ sigma \ pi \ operatorname {tan} ^ { 2} \ alpha \ times dS}

{\ displaystyle F_ {B} = G {\ frac {m_ {P} \ times m_ {B}} {PB ^ {2}}} = Gm_ {P} \ times \ sigma \ pi \ operatorname {tan} ^ { 2} \ alpha \ times dS}

Deoarece cele două forțe acționează în aceeași direcție, dar sunt în direcții opuse, fiind egale ca mărime, se anulează reciproc, anulând astfel influența cochiliei infinitesimale. Cu o operație simplă, extinzând integralul învelișului sferic, vedem că câmpul gravitațional, în interiorul învelișului sferic, este zero.

Potențialul câmpului gravitațional generat de o sferă omogenă

Extinderea discursului la o sferă omogenă cu centrul O , pentru un punct P situat în interior, datorită efectelor câmpului gravitațional, trebuie luată în considerare doar materia conținută în sfera cu centrul O și raza OP . Acest lucru este ușor de văzut considerând cea mai mare sferă de rază R ca fiind compusă dintr-o carcasă sferică de grosime R-OP și o sferă de rază OP .

Elemente conexe

Alte proiecte

Wikimedia Commons conține imagini sau alte fișiere pe teorema Shellical Shell

Portalul fizicii : accesați intrările Wikipedia care se ocupă cu fizica