Modelul Sommerfeld

In fizica stare solida, modelul electron liber este un model simplu care descrie comportamentul electronilor de valență în structura cristalină a unui metal. Acest model a fost dezvoltat de Arnold Sommerfeld , care a combinat modelul Drude (un model care consideră electronii ca un gaz ideal , care se supune statisticii clasice) cu statistica Fermi-Dirac , care este o statistică cuantică.

Modelul este foarte simplu, dar reușește să ofere o explicație satisfăcătoare a următoarelor lucruri:

conductivitate electrică ;
Legea Wiedemann-Franz , care se referă la o conductivitate termică conductivitate electrică;
dependența de temperatură a căldurii specifice electronice;
dependență energetică aproximativă de densitatea stărilor;
energia de coeziune a metalelor;
cale liberă medie

Îmbunătățirea directă a acestui model este cu modelul de electroni aproape liberi .

Ipoteză

Electronii de valență sunt considerați a fi complet liberi și constituie efectiv un gaz ideal de electroni. Ca și în cazul unui gaz ideal, interacțiunea electron-electron este complet neglijată.

Structura cristalină nu este luată în considerare. Singura limită a modelului este dată de cutia cubică pe lateral $L\$ ${\ displaystyle L \}$ $L \$ în care sunt conținuți electronii.

Statistica pe care aceasta se supune de gaze cuantice este statistica Fermi-Dirac . ^[1]

Model staționar

Să luăm în considerare o cutie cubică din lateral $L\$ ${\ displaystyle L \}$ $L \$ în cadrul căreia sunt cuprinse $N\$ ${\ displaystyle N \}$ $N \$ electroni care nu interacționează. Se poate arăta că forma casetei modifică rezultatele finale într-un mod irelevant. Să ne imaginăm că potențialul este infinit în afara cutiei, prin urmare funcția de undă trebuie să fie zero în afara cutiei în sine. Dacă alegem originea coordonatelor care coincid cu un vârf al cubului și axele carteziene orientate ca margini, funcția de undă va satisface ecuațiile din motive de continuitate:

\psi (0,y,z)=\psi (L,y,z)=0\

{\ displaystyle \ psi (0, y, z) = \ psi (L, y, z) = 0 \}

{\ displaystyle \ psi (0, y, z) = \ psi (L, y, z) = 0 \}

\psi (x,0,z)=\psi (x,L,z)=0\

{\ displaystyle \ psi (x, 0, z) = \ psi (x, L, z) = 0 \}

{\ displaystyle \ psi (x, 0, z) = \ psi (x, L, z) = 0 \}

\psi (x,y,0)=\psi (x,y,L)=0\

{\ displaystyle \ psi (x, y, 0) = \ psi (x, y, L) = 0 \}

{\ displaystyle \ psi (x, y, 0) = \ psi (x, y, L) = 0 \}

Soluția problemei este combinația liniară a undelor plane care călătoresc în direcții opuse:

$\psi (x,y,z)=A\left[e^{i{\vec {k}}\cdot {\vec {r}}}-e^{-i{\vec {k}}\cdot {\vec {r}}}\right]\$ ${\ displaystyle \ psi (x, y, z) = A \ left [e ^ {i {\ vec {k}} \ cdot {\ vec {r}}} - e ^ {- i {\ vec {k} } \ cdot {\ vec {r}}} \ right] \}$ ${\ displaystyle \ psi (x, y, z) = A \ left [e ^ {i {\ vec {k}} \ cdot {\ vec {r}}} - e ^ {- i {\ vec {k} } \ cdot {\ vec {r}}} \ right] \}$

Această ecuație poate fi rescrisă ca:

$\psi (x,y,z)=2iA\sin(k_{x}x)\sin(k_{y}y)\sin(k_{z}z)\$ ${\ displaystyle \ psi (x, y, z) = 2iA \ sin (k_ {x} x) \ sin (k_ {y} y) \ sin (k_ {z} z) \}$ ${\ displaystyle \ psi (x, y, z) = 2iA \ sin (k_ {x} x) \ sin (k_ {y} y) \ sin (k_ {z} z) \}$

Nevoia de a fi îndeplinite condițiile limită necesită ca componentele ${\vec {k}}\$ ${\ displaystyle {\ vec {k}} \}$ ${\ displaystyle {\ vec {k}} \}$ ei trebuie să ia doar valori discrete:

Opt soluții în spațiul k al unei cutii cubice tridimensionale cu latura L

$k_{x}=n_{x}{\frac {\pi }{L}}\$ ${\ displaystyle k_ {x} = n_ {x} {\ frac {\ pi} {L}} \}$ ${\ displaystyle k_ {x} = n_ {x} {\ frac {\ pi} {L}} \}$

$k_{y}=n_{y}{\frac {\pi }{L}}\$ ${\ displaystyle k_ {y} = n_ {y} {\ frac {\ pi} {L}} \}$ ${\ displaystyle k_ {y} = n_ {y} {\ frac {\ pi} {L}} \}$

$k_{z}=n_{z}{\frac {\pi }{L}}\$ ${\ displaystyle k_ {z} = n_ {z} {\ frac {\ pi} {L}} \}$ ${\ displaystyle k_ {z} = n_ {z} {\ frac {\ pi} {L}} \}$

Unde este $n_{x}\$ ${\ displaystyle n_ {x} \}$ ${\ displaystyle n_ {x} \}$ , $n_{y}\$ ${\ displaystyle n_ {y} \}$ ${\ displaystyle n_ {y} \}$ și $n_{z}\$ ${\ displaystyle n_ {z} \}$ ${\ displaystyle n_ {z} \}$ trebuie să fie numere pozitive și întregi. Chiar și acele soluții pentru care doar una dintre $n_{i}\$ ${\ displaystyle n_ {i} \}$ ${\ displaystyle n_ {i} \}$ este nul: de fapt, principiul incertitudinii ar fi încălcat în această direcție.

Dacă desenăm, în spațiu $k\$ ${\ displaystyle k \}$ $k \$ , setul de puncte care sunt soluții ale problemei $N\$ ${\ displaystyle N \}$ $N \$ particule din cutia cubului lateral $L\$ ${\ displaystyle L \}$ $L \$ , obținem o rețea cubică simplă de puncte într-un singur octant din acest spațiu.

La zero absolut mă aștept doar statele cu mai puțină energie care urmează să fie ocupat cu respectarea principiul de excluziune. Numărul de electroni din solidele macroscopice este foarte mare, deci dacă vom aranja al nostru $N\$ ${\ displaystyle N \}$ $N \$ electroni în stări posibile umplând mai întâi stările cu $|{\vec {k}}|\$ ${\ displaystyle | {\ vec {k}} | \}$ ${\ displaystyle | {\ vec {k}} | \}$ scăzut (energie scăzută) și apoi treptat cei cu $|{\vec {k}}|\$ ${\ displaystyle | {\ vec {k}} | \}$ ${\ displaystyle | {\ vec {k}} | \}$ mai mare (mare energie). Având în vedere că numărul $N\ \$ ${\ displaystyle N \ \}$ ${\ displaystyle N \ \}$ este foarte mare, discretizarea statelor poate fi neglijată. In spatiu $k\$ ${\ displaystyle k \}$ $k \$ stările posibile ocupă punctele unei simple rețele cubice. Distanța dintre punctele adiacente ale acestei rețele este evident: $a=\pi /L$ ${\ displaystyle a = \ pi / L}$ ${\ displaystyle a = \ pi / L}$ . În rețele cubice simple ale parametrului rețelei $a\$ ${\ displaystyle a \}$ ${\ displaystyle a \}$ , densitatea punctelor de rețea se menține în mod evident $n=a^{-3}\$ ${\ displaystyle n = a ^ {- 3} \}$ ${\ displaystyle n = a ^ {- 3} \}$ . Avem densitatea punctelor din spațiu $k\$ ${\ displaystyle k \}$ $k \$ este valabil:

$n({\vec {k}})=\left({\frac {L}{\pi }}\right)^{3}={\frac {V}{\pi ^{3}}}\$ ${\ displaystyle n ({\ vec {k}}) = \ left ({\ frac {L} {\ pi}} \ right) ^ {3} = {\ frac {V} {\ pi ^ {3}} } \}$ ${\ displaystyle n ({\ vec {k}}) = \ left ({\ frac {L} {\ pi}} \ right) ^ {3} = {\ frac {V} {\ pi ^ {3}} } \}$

unde este $V=L^{3}\$ ${\ displaystyle V = L ^ {3} \}$ ${\ displaystyle V = L ^ {3} \}$ este volumul cubului. Am calculat această densitate de puncte, dar fiecare stat poate fi ocupat de doar doi electroni din cauza principiului excluderii al lui Pauli , din moment ce electronii au un grad intern suplimentar de libertate din cauza spin semintere. Deci, pentru fiecare stare permisă funcției de undă a unui electron, există două stări electronice, care corespund celor două direcții posibile în care poate indica momentul unghiular al unui electron.

De aici și densitatea $g({\vec {k}})\$ ${\ displaystyle g ({\ vec {k}}) \}$ ${\ displaystyle g ({\ vec {k}}) \}$ a stărilor electronice în spațiu $k\$ ${\ displaystyle k \}$ $k \$ este valabil:

$g({\vec {k}})=2n({\vec {k}})=2{\frac {V}{(\pi )^{3}}}\$ ${\ displaystyle g ({\ vec {k}}) = 2n ({\ vec {k}}) = 2 {\ frac {V} {(\ pi) ^ {3}}} \}$ ${\ displaystyle g ({\ vec {k}}) = 2n ({\ vec {k}}) = 2 {\ frac {V} {(\ pi) ^ {3}}} \}$

Sensul fizic al $g({\vec {k}})\$ ${\ displaystyle g ({\ vec {k}}) \}$ ${\ displaystyle g ({\ vec {k}}) \}$ (extinderea definiției sale de la spațiul discret la cel continuu) este că există în volum $d^{3}k\$ ${\ displaystyle d ^ {3} k \}$ ${\ displaystyle d ^ {3} k \}$ de spațiu $k\$ ${\ displaystyle k \}$ $k \$ un număr $dn=g({\vec {k}})d^{3}k\$ ${\ displaystyle dn = g ({\ vec {k}}) d ^ {3} k \}$ ${\ displaystyle dn = g ({\ vec {k}}) d ^ {3} k \}$ electroni.

Putem determina raza $k_{F}\$ ${\ displaystyle k_ {F} \}$ ${\ displaystyle k_ {F} \}$ a optimei unei sfere care conține $N\$ ${\ displaystyle N \}$ $N \$ electroni metalici:

$N=g({\vec {k}}){\frac {1}{8}}{\frac {4}{3}}\pi k_{F}^{3}={\frac {Vk_{F}^{3}}{3\pi ^{2}}}\$ ${\ displaystyle N = g ({\ vec {k}}) {\ frac {1} {8}} {\ frac {4} {3}} \ pi k_ {F} ^ {3} = {\ frac { Vk_ {F} ^ {3}} {3 \ pi ^ {2}}} \}$ ${\ displaystyle N = g ({\ vec {k}}) {\ frac {1} {8}} {\ frac {4} {3}} \ pi k_ {F} ^ {3} = {\ frac { Vk_ {F} ^ {3}} {3 \ pi ^ {2}}} \}$

Observați cum se face o greșeală neglijabilă datorită includerii punctelor pe cele trei planuri carteziene. Din ecuație rezultă că:

$k_{F}=(3\pi ^{2}n)^{\frac {1}{3}}\$ ${\ displaystyle k_ {F} = (3 \ pi ^ {2} n) ^ {\ frac {1} {3}} \}$ ${\ displaystyle k_ {F} = (3 \ pi ^ {2} n) ^ {\ frac {1} {3}} \}$

Raza sectorului sferic $k_{F}\$ ${\ displaystyle k_ {F} \}$ ${\ displaystyle k_ {F} \}$ se numește vectorul undei Fermi. Spre deosebire de cazul clasic, prin urmare, electronii dintr-un metal, chiar și la temperaturi foarte scăzute, au o gamă largă de valori vectoriale de undă și, în consecință, de energii cinetice până la o anumită valoare maximă dependentă doar de densitatea electronilor.

Condiție periodică la graniță

Condiția dată funcției de undă, care a impus anularea acesteia pe suprafața cubului, este în practică nesatisfăcătoare, de fapt conduce ca o consecință că soluțiile problemei sunt unde staționare. În solidele macroscopice interacțiunea electronilor cu extremele solidului este adesea neglijabilă în fenomenele de transport al energiei și sarcinii: de aceea soluțiile de propagare descriu mai bine fenomenele fizice de interes, cu excepția ${\vec {k}}\$ ${\ displaystyle {\ vec {k}} \}$ ${\ displaystyle {\ vec {k}} \}$ la limita Brillouin zona I , dar în modelul periodicitatea rețeaua este neglijată. Proprietățile generale ale unui solid macroscopic (se poate demonstra riguros ^[2] ) nu depind de condițiile limită.

Condiție periodică la graniță

O alegere mai satisfăcătoare a condițiilor limită este cea a unei condiții limită periodice, numită și condiția limită Born-Von Karman : se imaginează că fiecare față a cubului este unită cu suprafața opusă, în așa fel încât fiecare electron care ajunge pe o suprafață nu este reflectată de suprafața însăși, ci lasă metalul să intre din nou de pe fața opusă. O astfel de condiție dictează faptul că densitatea electronilor nu variază de-a lungul solidului. În acești termeni, condiția funcției de undă este de tipul:

$\psi (x,y,z,t)=\psi (x+L,y,z,t)\$ ${\ displaystyle \ psi (x, y, z, t) = \ psi (x + L, y, z, t) \}$ ${\ displaystyle \ psi (x, y, z, t) = \ psi (x + L, y, z, t) \}$

$\psi (x,y,z,t)=\psi (x,y+L,z,t)\$ ${\ displaystyle \ psi (x, y, z, t) = \ psi (x, y + L, z, t) \}$ ${\ displaystyle \ psi (x, y, z, t) = \ psi (x, y + L, z, t) \}$

$\psi (x,y,z,t)=\psi (x,y,z+L,t)\$ ${\ displaystyle \ psi (x, y, z, t) = \ psi (x, y, z + L, t) \}$ ${\ displaystyle \ psi (x, y, z, t) = \ psi (x, y, z + L, t) \}$

Soluțiile problemei sunt în acest caz pur și simplu unde plane:

$\psi (x,y,z,t)=Ae^{i({\vec {k}}\cdot {\vec {r}}-\omega t)}\$ ${\ displaystyle \ psi (x, y, z, t) = Ae ^ {i ({\ vec {k}} \ cdot {\ vec {r}} - \ omega t)} \}$ ${\ displaystyle \ psi (x, y, z, t) = Ae ^ {i ({\ vec {k}} \ cdot {\ vec {r}} - \ omega t)} \}$

Nevoia de a fi îndeplinite condițiile limită necesită ca componentele ${\vec {k}}\$ ${\ displaystyle {\ vec {k}} \}$ ${\ displaystyle {\ vec {k}} \}$ poate presupune doar valori discrete:

$k_{x}=n_{x}{\frac {2\pi }{L}}\$ ${\ displaystyle k_ {x} = n_ {x} {\ frac {2 \ pi} {L}} \}$ ${\ displaystyle k_ {x} = n_ {x} {\ frac {2 \ pi} {L}} \}$

$k_{y}=n_{y}{\frac {2\pi }{L}}\$ ${\ displaystyle k_ {y} = n_ {y} {\ frac {2 \ pi} {L}} \}$ ${\ displaystyle k_ {y} = n_ {y} {\ frac {2 \ pi} {L}} \}$

$k_{z}=n_{z}{\frac {2\pi }{L}}\$ ${\ displaystyle k_ {z} = n_ {z} {\ frac {2 \ pi} {L}} \}$ ${\ displaystyle k_ {z} = n_ {z} {\ frac {2 \ pi} {L}} \}$

Unde este $n_{x}\$ ${\ displaystyle n_ {x} \}$ ${\ displaystyle n_ {x} \}$ , $n_{y}\$ ${\ displaystyle n_ {y} \}$ ${\ displaystyle n_ {y} \}$ și $n_{z}\$ ${\ displaystyle n_ {z} \}$ ${\ displaystyle n_ {z} \}$ trebuie să fie numere întregi pozitive sau negative, dar nu toate nule. În spațiul k aceste puncte formează o rețea cubică. Distanța dintre punctele rețelei cubice simple a stărilor permise este de două ori mai mare decât condiția limită anterioară. Deci în spațiu $k\$ ${\ displaystyle k \}$ $k \$ ansamblul de puncte care sunt soluții ale problemei $N\$ ${\ displaystyle N \}$ $N \$ particule din cutia periodică din lateral $L\$ ${\ displaystyle L \}$ $L \$ este o rețea cubică simplă de puncte în acel spațiu, dar dispuse simetric în jurul axelor de coordonate. Dar distanța dintre punctele rețelei în spațiu $k\$ ${\ displaystyle k \}$ $k \$ în mod normal, nu provoacă niciun efect măsurabil în solidele macroscopice.

Astfel de condiții conduc la aceeași soluție în ceea ce privește $k_{F}\$ ${\ displaystyle k_ {F} \}$ ${\ displaystyle k_ {F} \}$ . De fapt, repetarea raționamentului din caz $T=0\$ ${\ displaystyle T = 0 \}$ ${\ displaystyle T = 0 \}$ .

g({\vec {k}})=2n({\vec {k}})=2{\frac {V}{(2\pi )^{3}}}\

{\ displaystyle g ({\ vec {k}}) = 2n ({\ vec {k}}) = 2 {\ frac {V} {(2 \ pi) ^ {3}}} \}

{\ displaystyle g ({\ vec {k}}) = 2n ({\ vec {k}}) = 2 {\ frac {V} {(2 \ pi) ^ {3}}} \}

The $N\$ ${\ displaystyle N \}$ $N \$ electronii vor umple apoi o sferă cu o rază $k_{F}\$ ${\ displaystyle k_ {F} \}$ ${\ displaystyle k_ {F} \}$ (nu mai este o optime dintr-o sferă):

N=g({\vec {k}}){\frac {4}{3}}\pi k_{F}^{3}={\frac {Vk_{F}^{3}}{3\pi ^{2}}}\

{\ displaystyle N = g ({\ vec {k}}) {\ frac {4} {3}} \ pi k_ {F} ^ {3} = {\ frac {Vk_ {F} ^ {3}} { 3 \ pi ^ {2}}} \}

{\ displaystyle N = g ({\ vec {k}}) {\ frac {4} {3}} \ pi k_ {F} ^ {3} = {\ frac {Vk_ {F} ^ {3}} { 3 \ pi ^ {2}}} \}

care este aceeași ecuație ca cea obținută anterior. Prin urmare, vectorul undei Fermi este identic cu această condiție limită. Regiunea în spațiu $k\$ ${\ displaystyle k \}$ $k \$ permis stărilor unui electron este o sferă.

Energia Fermi

Deoarece electronii sunt liberi, relația de dispersie dintre $E\$ ${\ displaystyle E \}$ $ȘI\$ Și $k\$ ${\ displaystyle k \}$ $k \$ este valabil:

E={\frac {\hbar ^{2}k^{2}}{2m}}\

{\ displaystyle E = {\ frac {\ hbar ^ {2} k ^ {2}} {2m}} \}

{\ displaystyle E = {\ frac {\ hbar ^ {2} k ^ {2}} {2m}} \}

apoi la valoarea maximă $k_{F}\$ ${\ displaystyle k_ {F} \}$ ${\ displaystyle k_ {F} \}$ pentru $T=0\$ ${\ displaystyle T = 0 \}$ ${\ displaystyle T = 0 \}$ corespunde unei energii maxime, numită energie Fermi:

E_{F}={\frac {\hbar ^{2}k_{F}^{2}}{2m}}={\frac {\hbar ^{2}}{2m}}(3\pi ^{2}n)^{\frac {2}{3}}\

{\ displaystyle E_ {F} = {\ frac {\ hbar ^ {2} k_ {F} ^ {2}} {2m}} = {\ frac {\ hbar ^ {2}} {2m}} (3 \ pi ^ {2} n) ^ {\ frac {2} {3}} \}

{\ displaystyle E_ {F} = {\ frac {\ hbar ^ {2} k_ {F} ^ {2}} {2m}} = {\ frac {\ hbar ^ {2}} {2m}} (3 \ pi ^ {2} n) ^ {\ frac {2} {3}} \}

sau dacă doriți o viteză pătratică maximă $v_{F}={\sqrt {2E_{F}/m}}\$ ${\ displaystyle v_ {F} = {\ sqrt {2E_ {F} / m}} \}$ ${\ displaystyle v_ {F} = {\ sqrt {2E_ {F} / m}} \}$

v_{F}={\frac {\hbar }{m}}(3\pi ^{2}n)^{\frac {1}{3}}\

{\ displaystyle v_ {F} = {\ frac {\ hbar} {m}} (3 \ pi ^ {2} n) ^ {\ frac {1} {3}} \}

{\ displaystyle v_ {F} = {\ frac {\ hbar} {m}} (3 \ pi ^ {2} n) ^ {\ frac {1} {3}} \}

Temperatura Fermi este definită ca:

T_{F}={\frac {E_{F}}{k_{B}}}\

{\ displaystyle T_ {F} = {\ frac {E_ {F}} {k_ {B}}} \}

{\ displaystyle T_ {F} = {\ frac {E_ {F}} {k_ {B}}} \}

Viteza Fermi are o valoare similară pentru toate metalele și este aproximativ $1/100\$ ${\ displaystyle 1/100 \}$ ${\ displaystyle 1/100 \}$ a vitezei luminii. Existența acestei viteze explică de ce semnalele electrice din metale se propagă cu aceeași viteză, în jurul vitezei Fermi, indiferent de temperatură. Viteza Fermi joacă un rol analog în teoria metalelor față de viteza pătrată medie termică $v={\sqrt {3k_{B}T/m}}\$ ${\ displaystyle v = {\ sqrt {3k_ {B} T / m}} \}$ ${\ displaystyle v = {\ sqrt {3k_ {B} T / m}} \}$ a unui gaz clasic.

Modulul vectorului de undă Fermi are o valoare comparabilă cu cea a primei zone Brillouin. Sfera razei $k_{F}\$ ${\ displaystyle k_ {F} \}$ ${\ displaystyle k_ {F} \}$ , care conține nivelurile ocupate o singură dată se numește sferă Fermi. Suprafața sferei Fermi care separă starea ocupată de stările neocupate se numește suprafața Fermi.

Element	$E_{F}\ (eV)$ ${\ displaystyle E_ {F} \ (eV)}$ ${\ displaystyle E_ {F} \ (eV)}$	$T_{F}\ (10^{3}\ K)$ ${\ displaystyle T_ {F} \ (10 ^ {3} \ K)}$ ${\ displaystyle T_ {F} \ (10 ^ {3} \ K)}$	$v_{F}\ (10^{6}m/s)$ ${\ displaystyle v_ {F} \ (10 ^ {6} m / s)}$ ${\ displaystyle v_ {F} \ (10 ^ {6} m / s)}$
N / A	3.24	40	1.1
Cu	7	82	1.6
Pentru	12	136	2.0
Fe	11	130	2.0

Densitatea statelor

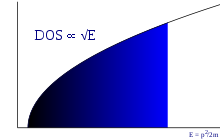
Densitatea statelor (DOS Abrevierea engleza) a unui gaz de liber fermioni este proporțională cu rădăcina pătrată din energia lor cinetică.

Densitatea statelor , adică numărul stărilor pe unitate de volum , cu un vector de undă mai mică sau egală cu $k_{i}$ ${\ displaystyle k_ {i}}$ $k_ {i}$ este valabil:

n_{i}=2{\frac {1}{(2\pi )^{3}}}{\frac {4}{3}}\pi k_{i}^{3}

{\ displaystyle n_ {i} = 2 {\ frac {1} {(2 \ pi) ^ {3}}} {\ frac {4} {3}} \ pi k_ {i} ^ {3}}

{\ displaystyle n_ {i} = 2 {\ frac {1} {(2 \ pi) ^ {3}}} {\ frac {4} {3}} \ pi k_ {i} ^ {3}}

Dar fiind $E_{i}={\frac {\hbar ^{2}k_{i}^{2}}{2m}}$ ${\ displaystyle E_ {i} = {\ frac {\ hbar ^ {2} k_ {i} ^ {2}} {2m}}}$ ${\ displaystyle E_ {i} = {\ frac {\ hbar ^ {2} k_ {i} ^ {2}} {2m}}}$ Pot scrie ecuația anterioară în funcție de $E_{i}$ ${\ displaystyle E_ {i}}$ $E_ {i}$ :

n(E_{i})={\frac {1}{3\pi ^{2}}}\left({\frac {2mE_{i}}{\hbar ^{2}}}\right)^{3/2}

{\ displaystyle n (E_ {i}) = {\ frac {1} {3 \ pi ^ {2}}} \ left ({\ frac {2mE_ {i}} {\ hbar ^ {2}}} \ right ) ^ {3/2}}

{\ displaystyle n (E_ {i}) = {\ frac {1} {3 \ pi ^ {2}}} \ left ({\ frac {2mE_ {i}} {\ hbar ^ {2}}} \ right ) ^ {3/2}}

Dar dacă definim $g(E)$ ${\ displaystyle g (E)}$ ${\ displaystyle g (E)}$ densitatea stărilor pe unitate de volum cu energie între $ȘI$ ${\ displaystyle E}$ $ȘI$ și $E+dE$ ${\ displaystyle E + dE}$ ${\ displaystyle E + dE}$ este legat de numărul de stări pe unitate de volum:

n(E)=\int _{0}^{E}g(E')dE'

{\ displaystyle n (E) = \ int _ {0} ^ {E} g (E ') dE'}

{\ displaystyle n (E) = \ int _ {0} ^ {E} g (E ') dE'}

De la care:

g(E)={\frac {dn}{dE}}={\frac {1}{2\pi ^{2}}}\left({\frac {2m}{\hbar ^{2}}}\right)^{3/2}{\sqrt {E}}

{\ displaystyle g (E) = {\ frac {dn} {dE}} = {\ frac {1} {2 \ pi ^ {2}}} \ left ({\ frac {2m} {\ hbar ^ {2 }}} \ right) ^ {3/2} {\ sqrt {E}}}

{\ displaystyle g (E) = {\ frac {dn} {dE}} = {\ frac {1} {2 \ pi ^ {2}}} \ left ({\ frac {2m} {\ hbar ^ {2 }}} \ right) ^ {3/2} {\ sqrt {E}}}

se preferă adesea eliminarea masei de electroni din expresie și rescrierea expresiei ca:

g(E)={\frac {3}{2}}{\frac {n}{E_{\rm {F}}^{3/2}}}{\sqrt {E}},

{\ displaystyle g (E) = {\ frac {3} {2}} {\ frac {n} {E _ {\ rm {F}} ^ {3/2}}} {\ sqrt {E}}, }

{\ displaystyle g (E) = {\ frac {3} {2}} {\ frac {n} {E _ {\ rm {F}} ^ {3/2}}} {\ sqrt {E}}, }

Potențialul chimic și temperatura

Aici încercăm să extindem ceea ce s-a spus la cazul altor temperaturi decât zero. De fapt, densitatea stărilor, ca primă aproximare, nu se modifică odată cu temperatura, precum și cu numărul stărilor.

La temperatura $T=0$ ${\ displaystyle T = 0}$ $T = 0$ am presupus că toți electronii erau în niveluri cu energie mai mică sau egală cu $E_{F}$ ${\ displaystyle E_ {F}}$ ${\ displaystyle E_ {F}}$ . Dacă mărim temperatura, unii dintre electronii din apropierea suprafeței Fermi vor putea ieși în afara suprafeței Fermi. Deci un $T>0$ ${\ displaystyle T> 0}$ $T> 0$ probabilitatea $f(E)$ ${\ displaystyle f (E)}$ ${\ displaystyle f (E)}$ de ocupare a stării energetice $ȘI$ ${\ displaystyle E}$ $ȘI$ nu mai devine:

f(E)=1\qquad E<E_{F}

{\ displaystyle f (E) = 1 \ qquad E <E_ {F}}

{\ displaystyle f (E) = 1 \ qquad E <E_ {F}}

f(E)=0\qquad E>E_{F}

{\ displaystyle f (E) = 0 \ qquad E> E_ {F}}

{\ displaystyle f (E) = 0 \ qquad E> E_ {F}}

așa cum ar trebui să facem $T=0$ ${\ displaystyle T = 0}$ $T = 0$ , Dar ia o altă formă , care ia în considerare principiul de excluziune al lui Pauli

Luând în considerare acest principiu, se arată că pentru fermioni probabilitatea de ocupație de stat $the$ ${\ displaystyle i}$ $the$ cu energie $ȘI$ ${\ displaystyle E}$ $ȘI$ este valabil:

f_{D}(E)={\frac {1}{e^{\frac {E-\mu }{K_{B}T}}+1}}

{\ displaystyle f_ {D} (E) = {\ frac {1} {e ^ {\ frac {E- \ mu} {K_ {B} T}} + 1}}}

{\ displaystyle f_ {D} (E) = {\ frac {1} {e ^ {\ frac {E- \ mu} {K_ {B} T}} + 1}}}

Unde este $\mu$ ${\ displaystyle \ mu}$ $\ mu$ , care este dimensiunea unei energii, se numește potențial chimic și reprezintă energia care trebuie furnizată sistemului pentru a adăuga un fermion, sau dacă doriți când $E=\mu$ ${\ displaystyle E = \ mu}$ ${\ displaystyle E = \ mu}$ probabilitatea angajării devine $1/2$ ${\ displaystyle 1/2}$ $1/2$ . Această distribuție de probabilitate se numește distribuția Fermi-Dirac . Orice fluid fermion are o distribuție de energie care urmează acestei distribuții.

Distribuția Fermi-Dirac pentru trei temperaturi diferite,

K_{B}T

{\ displaystyle K_ {B} T}

{\ displaystyle K_ {B} T}

este dat în eV, de asemenea

E-\mu

{\ displaystyle E- \ mu}

{\ displaystyle E- \ mu}

Puteți verifica cu ușurință conform $T\rightarrow 0$ ${\ displaystyle T \ rightarrow 0}$ ${\ displaystyle T \ rightarrow 0}$ distribuția Fermi-Dirac este:

\lim _{T\rightarrow 0}f_{D}(E)=1\qquad E<\mu

{\ displaystyle \ lim _ {T \ rightarrow 0} f_ {D} (E) = 1 \ qquad E <\ mu}

{\ displaystyle \ lim _ {T \ rightarrow 0} f_ {D} (E) = 1 \ qquad E <\ mu}

\lim _{T\rightarrow 0}f_{D}(E)=0\qquad E>\mu

{\ displaystyle \ lim _ {T \ rightarrow 0} f_ {D} (E) = 0 \ qquad E> \ mu}

{\ displaystyle \ lim _ {T \ rightarrow 0} f_ {D} (E) = 0 \ qquad E> \ mu}

Prin urmare, potențialul chimic coincide cu energia Fermi pentru $T\rightarrow 0$ ${\ displaystyle T \ rightarrow 0}$ ${\ displaystyle T \ rightarrow 0}$ :

\lim _{T\rightarrow 0}\mu =E_{F}

{\ displaystyle \ lim _ {T \ rightarrow 0} \ mu = E_ {F}}

{\ displaystyle \ lim _ {T \ rightarrow 0} \ mu = E_ {F}}

La orice temperatură $T.$ ${\ displaystyle T}$ $T.$ densitatea $d n$ ${\ displaystyle dn}$ ${\ displaystyle dn}$ de electroni cu energie între $ȘI$ ${\ displaystyle E}$ $ȘI$ și $E+dE$ ${\ displaystyle E + dE}$ ${\ displaystyle E + dE}$ devine egal cu:

dn=f_{D}(E)g(E)dE

{\ displaystyle dn = f_ {D} (E) g (E) dE}

{\ displaystyle dn = f_ {D} (E) g (E) dE}

Integrala din $d n$ ${\ displaystyle dn}$ ${\ displaystyle dn}$ pentru $0<E<\infty$ ${\ displaystyle 0 <E <\ infty}$ ${\ displaystyle 0 <E <\ infty}$ trebuie să fie densitatea totală $n$ ${\ displaystyle n}$ $n$ de electroni liberi ai metalului:

n=\int _{0}^{\infty }f_{D}(E)g(E)dE

{\ displaystyle n = \ int _ {0} ^ {\ infty} f_ {D} (E) g (E) dE}

{\ displaystyle n = \ int _ {0} ^ {\ infty} f_ {D} (E) g (E) dE}

Impunând asta $n$ ${\ displaystyle n}$ $n$ este independentă de temperatură rezultă, prin intermediul unor pasaje matematice nu explicite aici ^[3] , că:

\mu =E_{F}\left[1-{\frac {1}{3}}\left({\frac {\pi k_{B}T}{2E_{F}}}\right)^{2}\right]

{\ displaystyle \ mu = E_ {F} \ left [1 - {\ frac {1} {3}} \ left ({\ frac {\ pi k_ {B} T} {2E_ {F}}} \ right) ^ {2} \ dreapta]}

{\ displaystyle \ mu = E_ {F} \ left [1 - {\ frac {1} {3}} \ left ({\ frac {\ pi k_ {B} T} {2E_ {F}}} \ right) ^ {2} \ dreapta]}

Prin urmare, la temperatura camerei, potențialul chimic se abate de la energia Fermi într-un mod nesemnificativ pentru toate metalele. Din acest motiv, conceptul de potențial chimic este adesea confundat cu energia Fermi.

Căldură specifică electronică

Energia totală a gazului electron în funcție de temperatură este egală cu:

U=V\int _{0}^{\infty }Eg(E)f_{D}(E)dE

{\ displaystyle U = V \ int _ {0} ^ {\ infty} De exemplu (E) f_ {D} (E) dE}

{\ displaystyle U = V \ int _ {0} ^ {\ infty} De exemplu (E) f_ {D} (E) dE}

unde este $V.$ ${\ displaystyle V}$ $V.$ este volumul metalului. Dezvoltând distribuția Fermi-Dirac în jurul energiei Fermi din seria Taylor, constatăm că:

U=U_{0}+V{\frac {\pi ^{2}}{6}}(k_{B}T)^{2}g(E_{F})

{\ displaystyle U = U_ {0} + V {\ frac {\ pi ^ {2}} {6}} (k_ {B} T) ^ {2} g (E_ {F})}

{\ displaystyle U = U_ {0} + V {\ frac {\ pi ^ {2}} {6}} (k_ {B} T) ^ {2} g (E_ {F})}

Unde este $U_{0}=V\int _{0}^{E_{F}}Eg(E)dE$ ${\ displaystyle U_ {0} = V \ int _ {0} ^ {E_ {F}} De exemplu (E) dE}$ ${\ displaystyle U_ {0} = V \ int _ {0} ^ {E_ {F}} De exemplu (E) dE}$ este energia în sol starea , astfel încât căldura specifică este:

c_{v}={\frac {1}{V}}{\frac {\partial U}{\partial T}}={\frac {\pi ^{2}}{3}}k_{B}^{2}Tg(E_{F})

{\ displaystyle c_ {v} = {\ frac {1} {V}} {\ frac {\ partial U} {\ partial T}} = {\ frac {\ pi ^ {2}} {3}} k_ { B} ^ {2} Tg (E_ {F})}

{\ displaystyle c_ {v} = {\ frac {1} {V}} {\ frac {\ partial U} {\ partial T}} = {\ frac {\ pi ^ {2}} {3}} k_ { B} ^ {2} Tg (E_ {F})}

Observăm că această expresie nu este făcută în mod deliberat explicită $g(E_{F})$ ${\ displaystyle g (E_ {F})}$ ${\ displaystyle g (E_ {F})}$ , deoarece contul este valabil nu numai în cazul modelului de electroni liberi: oricare ar fi funcția de densitate a stărilor.

În cazul în care modelul de electroni liberi se aplică prin înlocuirea lui $g(E_{F})$ ${\ displaystyle g (E_ {F})}$ ${\ displaystyle g (E_ {F})}$ expresia sa explicită este obținută pentru un mol:

c_{v}={\frac {\pi ^{2}}{3}}{\frac {k_{B}T}{E_{F}}}\left({\frac {3}{2}}nk_{B}\right)

{\ displaystyle c_ {v} = {\ frac {\ pi ^ {2}} {3}} {\ frac {k_ {B} T} {E_ {F}}} \ left ({\ frac {3} { 2}} nk_ {B} \ dreapta)}

{\ displaystyle c_ {v} = {\ frac {\ pi ^ {2}} {3}} {\ frac {k_ {B} T} {E_ {F}}} \ left ({\ frac {3} { 2}} nk_ {B} \ dreapta)}

În paranteză, a fost evidențiat termenul care a fost derivat din ipoteza că gazul electronic este clasic. Deci efectul statisticii Fermi-Dirac este de a reduce căldura specifică a ${\frac {\pi ^{2}}{3}}{\frac {k_{B}T}{E_{F}}}$ ${\ displaystyle {\ frac {\ pi ^ {2}} {3}} {\ frac {k_ {B} T} {E_ {F}}}}$ ${\ displaystyle {\ frac {\ pi ^ {2}} {3}} {\ frac {k_ {B} T} {E_ {F}}}}$ , ceea ce înseamnă la temperatura camerei un factor de ordinul 100. Acest lucru explică absența la temperatura camerei a contribuției la căldura specifică datorată gazului electronic.

La temperaturi scăzute contribuția la căldură specifică din cauza fononi, modelul Debye , scade cu temperatura , cu o tendință de tip $T^{3}$ ${\ displaystyle T ^ {3}}$ $T ^ {3}$ , pentru care sub anumite temperaturi contribuția căldurii specifice datorită electronilor de conducere devine cel mai relevant termen; căldura specifică totală a metalelor, la temperaturi mai mici decât cea a lui Debye, are o expresie ca:

c_{v}=\gamma T+AT^{3}

{\ displaystyle c_ {v} = \ gamma T + AT ^ {3}}

{\ displaystyle c_ {v} = \ gamma T + AT ^ {3}}

cu $\gamma =\pi ^{2}k_{B}^{2}n/(2E_{F})$ ${\ displaystyle \ gamma = \ pi ^ {2} k_ {B} ^ {2} n / (2E_ {F})}$ ${\ displaystyle \ gamma = \ pi ^ {2} k_ {B} ^ {2} n / (2E_ {F})}$ . Experimental în toate metalele, căldura specifică datorată electronilor urmează o lege liniară cu temperatura. Constanta multiplicativă $\gamma$ ${\ displaystyle \ gamma}$ $\gamă$ este în acord cu valoarea tocmai dată doar pentru metalele alcaline, în alte metale există o constantă de multiplicare diferită de cea prezisă de modelul Sommerfield. Teoria benzilor elimină această inconsecvență datorită simplității modelului.

Conductibilitate electrică

Examinăm conductivitatea electrică folosind modelul de electroni liberi al mecanicii cuantice. La temperatura zero, electronii ocupă stări în sfera Fermi în spațiu $k$ ${\ displaystyle k}$ $k$ . Sfera Fermi fiind centrată în jurul său $k=0$ ${\ displaystyle k = 0}$ $k = 0$ pentru fiecare stat cu o anumită valoare ${\vec {k}}_{a}$ ${\ displaystyle {\ vec {k}} _ {a}}$ ${\ displaystyle {\ vec {k}} _ {a}}$ va fi alta $-{\vec {k}}_{a}$ ${\ displaystyle - {\ vec {k}} _ {a}}$ ${\ displaystyle - {\ vec {k}} _ {a}}$ în așa fel încât impulsul total al gazului electronic să fie zero.

Lucrul nu se schimbă a $T\neq 0$ ${\ displaystyle T \ neq 0}$ ${\ displaystyle T \ neq 0}$ de fapt, distribuția Fermi-Dirac face pur și simplu ocuparea statelor din zona apropiată sferei Fermi mai puțin clară, dar în mod egal există o compensare exactă a vectorilor de undă. De fapt, distribuția stărilor nu se modifică odată cu temperatura.

Aplicarea unui câmp electric ${\vec {\cal {E}}}$ ${\ displaystyle {\ vec {\ cal {E}}}}$ ${\ displaystyle {\ vec {\ cal {E}}}}$ modifică ecuația Schrödinger prin adăugarea unui termen constant aditiv în absența disipare. Dar dacă, cu considerații similare cu cele efectuate în cazul clasic, modelul Drude lui , interacțiunea cu imperfecțiuni este luată în considerare, efectul mediu al câmpului electric este doar o creștere a vitezelor posedat de fiecare electron de o viteză de drift ${\vec {v_{d}}}$ ${\ displaystyle {\ vec {v_ {d}}}}$ ${\ displaystyle {\ vec {v_ {d}}}}$ . Deci, vectorul de undă al fiecărui electron se va schimba prin:

\Delta {\vec {k}}={\frac {m}{\hbar }}{\vec {v}}_{d}

{\ displaystyle \ Delta {\ vec {k}} = {\ frac {m} {\ hbar}} {\ vec {v}} _ {d}}

{\ displaystyle \ Delta {\ vec {k}} = {\ frac {m} {\ hbar}} {\ vec {v}} _ {d}}

Apoi toți electronii se mută în noile stări deplasate ale $\Delta {\vec {k}}$ ${\ displaystyle \ Delta {\ vec {k}}}$ ${\ displaystyle \ Delta {\ vec {k}}}$ din vechi. Statele ocupate sunt încă într-o sferă, dar acum acea sferă este centrată în jur ${\vec {k}}=\Delta {\vec {k}}$ ${\ displaystyle {\ vec {k}} = \ Delta {\ vec {k}}}$ ${\ displaystyle {\ vec {k}} = \ Delta {\ vec {k}}}$ .

Am notat asta $\Delta {\vec {k}}$ ${\ displaystyle \ Delta {\ vec {k}}}$ ${\ displaystyle \ Delta {\ vec {k}}}$ este în direcția opusă ${\vec {\cal {E}}}$ ${\ displaystyle {\ vec {\ cal {E}}}}$ ${\ displaystyle {\ vec {\ cal {E}}}}$ datorită sarcinii negative a electronilor. Să vedem cum acum nu toți electronii sunt în perechi de ${\vec {k}}_{a}$ ${\ displaystyle {\ vec {k}} _ {a}}$ ${\ displaystyle {\ vec {k}} _ {a}}$ Și $-{\vec {k}}_{a}$ ${\ displaystyle - {\ vec {k}} _ {a}}$ ${\ displaystyle - {\ vec {k}} _ {a}}$ . Unele state pe o sferă nu sunt ocupate ca înainte și altele pe direcția opusă, care nu erau ocupate, sunt acum ocupate. Prin urmare, există un dezechilibru și valoarea medie a impulsului total nu mai este zero, deci există un curent electric.

Fiind $v_{d}\ll v_{F}$ ${\ displaystyle v_ {d} \ ll v_ {F}}$ ${\ displaystyle v_ {d} \ ll v_ {F}}$ , efectul este mic și aproape toți electronii sunt compensați în perechi. Electronii necompensați sunt doar într-o regiune foarte mică în jurul suprafeței Fermi. Toți ceilalți electroni sunt decalați și impulsul lor mediu este zero. Acești electroni nu contribuie în niciun fel la curentul electric. Curentul electric depinde doar de electronii necompensați de lângă suprafața Fermi. Deci, doar o fracțiune foarte mică din electroni participă la conducere. Deci, spre deosebire de cazul clasic în care toți electronii au participat la conducere cu o viteză medie $v_{d}$ ${\ displaystyle v_ {d}}$ ${\ displaystyle v_ {d}}$ , în cadrul cuantic numai electronii cu o viteză aproximativ egală cu cea a lui Fermi $v_{F}$ ${\ displaystyle v_ {F}}$ ${\ displaystyle v_ {F}}$ participă la management. Deci, numărul acestor electroni este de aproximativ:

\Delta n=n{\frac {v_{d}}{v_{F}}}

{\ displaystyle \ Delta n = n {\ frac {v_ {d}} {v_ {F}}}}

{\ displaystyle \ Delta n = n {\ frac {v_ {d}} {v_ {F}}}}

prin urmare, densitatea curentului va fi de aproximativ:

{\vec {J}}\cong {\frac {nv_{d}}{v_{F}}}e{\vec {v}}_{F}=ne{\vec {v}}_{d}

{\ displaystyle {\ vec {J}} \ cong {\ frac {nv_ {d}} {v_ {F}}} e {\ vec {v}} _ {F} = ne {\ vec {v}} _ {d}}

{\ displaystyle {\ vec {J}} \ cong {\ frac {nv_ {d}} {v_ {F}}} e {\ vec {v}} _ {F} = ne {\ vec {v}} _ {d}}

care este aceeași valoare găsită în cazul clasic, dar cu un număr extrem de mic de electroni de conducere.

În modelul cuantic, ${\vec {v}}_{d}$ ${\ displaystyle {\ vec {v}} _ {d}}$ ${\ displaystyle {\ vec {v}} _ {d}}$ are dimensiunile unei viteze, dar este legată de deplasarea suprafeței Fermi și nu de viteza medie de deriva ca în modelul Drude.

Folosind același raționament ca modelul lui Drude, rezultă că:

{\vec {v_{d}}}=-{\frac {e{\vec {\cal {E}}}\tau _{F}}{m}}

{\ displaystyle {\ vec {v_ {d}}} = - {\ frac {e {\ vec {\ cal {E}}} \ tau _ {F}} {m}}}

{\ displaystyle {\ vec {v_ {d}}} = - {\ frac {e {\ vec {\ cal {E}}} \ tau _ {F}} {m}}}

Acum $\tau _{F}$ ${\ displaystyle \ tau _ {F}}$ ${\ displaystyle \ tau _ {F}}$ este timpul mediu dintre o coliziune și următoarea pentru electronii de lângă suprafața Fermi.

Prin urmare, conductivitatea electrică devine egală cu:

\sigma ={\frac {ne^{2}\tau _{F}}{m}}

{\ displaystyle \ sigma = {\ frac {ne ^ {2} \ tau _ {F}} {m}}}

{\ displaystyle \ sigma = {\ frac {ne ^ {2} \ tau _ {F}} {m}}}

Prin urmare, deoarece forma distribuției vitezei electronilor nu influențează calculul conductivității în DC și AC sau în calculul coeficientului Hall, tratamentul acestor fenomene nu se modifică substanțial dacă se utilizează statisticile clasice sau Fermi-Dirac .

Calea liberă medie este:

\ell =v_{F}\tau _{F}

{\ displaystyle \ ell = v_ {F} \ tau _ {F}}

{\ displaystyle \ ell = v_ {F} \ tau _ {F}}

și reprezintă distanța medie parcursă doar de electroni în apropierea suprafeței Fermi. Modelul Drude lui consideră drum liber mediu conectat la distanța dintre ionii din material, aceasta implică o difuzivă mișcare a electronilor din cauza coliziunii cu ionii. În modelul Sommerfield calea liberă medie depinde de viteza Fermi și, prin urmare, este un ordin de mărime mai mare decât cazul clasic, așa cum este verificat și experimental. Prin urmare , Calea liberă nu este rezultatul coliziunii cu ionii, ci este legată de imperfecțiunile materialelor, defectele și fluctuațiile termice < ^[4] .

Conductivitate termică

Ca și în cazul modelului lui Drude, putem scrie că conductivitatea termică este dată de:

\kappa ={\frac {1}{3}}v^{2}\tau c_{v}

{\ displaystyle \ kappa = {\ frac {1} {3}} v ^ {2} \ tau c_ {v}}

{\ displaystyle \ kappa = {\ frac {1} {3}} v ^ {2} \ tau c_ {v}}

Dar cu semnificații diferite ale diferitelor cantități fizice enumerate mai jos: $v^{2}=v_{F}^{2}=2E_{F}/m$ ${\ displaystyle v ^ {2} = v_ {F} ^ {2} = 2E_ {F} / m}$ ${\ displaystyle v ^ {2} = v_ {F} ^ {2} = 2E_ {F} / m}$ , $\tau =\tau _{F}=\sigma m/(ne^{2})$ ${\ displaystyle \ tau = \ tau _ {F} = \ sigma m / (ne ^ {2})}$ ${\ displaystyle \ tau = \ tau _ {F} = \ sigma m / (ne ^ {2})}$ , $c_{v}=\pi ^{2}nk_{B}^{2}T/(2E_{F})$ $c_{v}=\pi ^{2}nk_{B}^{2}T/(2E_{F})$ $c_{v}=\pi ^{2}nk_{B}^{2}T/(2E_{F})$ quindi:

\kappa ={\frac {\pi ^{2}}{3}}\sigma T\left({\frac {k_{B}}{e}}\right)^{2}

\kappa ={\frac {\pi ^{2}}{3}}\sigma T\left({\frac {k_{B}}{e}}\right)^{2}

\kappa ={\frac {\pi ^{2}}{3}}\sigma T\left({\frac {k_{B}}{e}}\right)^{2}

{\frac {\kappa }{\sigma T}}={\frac {\pi ^{2}}{3}}\left({\frac {k_{B}}{e}}\right)^{2}=2.44\cdot 10^{-8}\ W\Omega /K^{2}

{\frac {\kappa }{\sigma T}}={\frac {\pi ^{2}}{3}}\left({\frac {k_{B}}{e}}\right)^{2}=2.44\cdot 10^{-8}\ W\Omega /K^{2}

{\frac {\kappa }{\sigma T}}={\frac {\pi ^{2}}{3}}\left({\frac {k_{B}}{e}}\right)^{2}=2.44\cdot 10^{-8}\ W\Omega /K^{2}

Questa costante detta di Lorentz è molto simile al valore sperimentale della maggior parte dei metalli ed è esattamente il valore previsto dalla legge di Wiedemann-Franz . Il valore previsto della costante di Lorentz dal modello di Drude è circa due volte più piccolo.

Effetto Seebeck

La costante di Seebeck può riscriversi come:

S=-{\frac {c_{v}}{3ne}}

S=-{\frac {c_{v}}{3ne}}

S=-{\frac {c_{v}}{3ne}}

sostituendo a $c_{v}=\pi ^{2}nk_{B}^{2}T/(2E_{F})$ $c_{v}=\pi ^{2}nk_{B}^{2}T/(2E_{F})$ $c_{v}=\pi ^{2}nk_{B}^{2}T/(2E_{F})$ si ha che:

S=-\pi ^{2}{\frac {k_{B}T}{2E_{F}}}\left({\frac {k_{B}}{3e}}\right)

S=-\pi ^{2}{\frac {k_{B}T}{2E_{F}}}\left({\frac {k_{B}}{3e}}\right)

S=-\pi ^{2}{\frac {k_{B}T}{2E_{F}}}\left({\frac {k_{B}}{3e}}\right)

Si è lasciato in parentesi il termine previsto dal modello di Drude. Quindi la differenza di potenziale prevista e trovata sperimentalmente per effetto del gradiente di temperatura sono di frazioni di microvolt a temperatura ambiente, il valore del modello di Drude è visibilmente errato per un paio di ordini di grandezza.

Note

^ NW Ashcroft and ND Mermin "Solid State Physics", 1976, pp 30-53, ISBN 978-0-03-083993-1
^ JL Lebowitz e EH Lieb, Phys. Rev. Lett. 1969; 22 631.
^ NW Ashcroft and ND Mermin "Solid State Physics", 1976, pp 41-47, ISBN 978-0-03-083993-1
^ Evgeny Tsymbal, Electronic Transport ( PDF ), su University of Nebraska-Lincoln , 2008.

Collegamenti esterni

( EN ) Modello di Sommerfeld / Modello di Sommerfeld (altra versione) , su Enciclopedia Britannica , Encyclopædia Britannica, Inc.

Portale Fisica : accedi alle voci di Wikipedia che trattano di Fisica

[1] NW Ashcroft and ND Mermin "Solid State Physics", 1976, pp 30-53, ISBN 978-0-03-083993-1

[Leb-2] JL Lebowitz e EH Lieb, Phys. Rev. Lett. 1969; 22 631.

[3] NW Ashcroft and ND Mermin "Solid State Physics", 1976, pp 41-47, ISBN 978-0-03-083993-1

[4] Evgeny Tsymbal, Electronic Transport ( PDF ), su University of Nebraska-Lincoln , 2008.

[1]

[2]

[3]

[4]