Mișcare parabolică

Mișcare parabolică descrisă de un jet de apă.

În cinematică , mișcarea parabolică este un tip de mișcare bidimensională care poate fi exprimată prin combinarea a două mișcări rectilinii simultane și independente:

Mișcarea parabolică poate fi descrisă prin relațiile cinematice care leagă poziția vectorilor, viteza și accelerația. Cea mai semnificativă realizare a acestei mișcări este asigurată de mișcarea proiectilului în care sunt utilizate următoarele simplificări (aproximări ale fizicii și geometriei problemei):

toată masa și geometria corpului sunt concentrate într-un singur punct ;
accelerația mișcării este verticală; modulul său este egal cu accelerația gravitației pe scoarța terestră: g = 9,81 m / s ² . Prin urmare, corpul se află într-un câmp gravitațional uniform și independent de timp;
orice forme de frecare legate de rezistența aerului sunt neglijabile.

Analiza mișcării parabolice: traiectorie

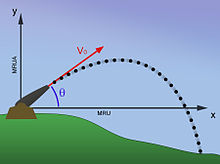
Mișcarea parabolică a unui baschet

Traiectorie balistică parabolică

Să presupunem că un corp este lansat la momentul t = 0 la originea O a unui sistem de coordonate cartezian Oxy și că viteza inițială are modulul v ₀ și formează un unghi θ cu axa orizontală x .

Traiectoria parabolică a punctului

Din legile mișcării accelerate uniform avem:

\mathbf {v} (t)=\mathbf {v} _{0}+\int _{0}^{t}\mathbf {a} (t)dt

{\ displaystyle \ mathbf {v} (t) = \ mathbf {v} _ {0} + \ int _ {0} ^ {t} \ mathbf {a} (t) dt}

{\ displaystyle \ mathbf {v} (t) = \ mathbf {v} _ {0} + \ int _ {0} ^ {t} \ mathbf {a} (t) dt}

Presupunând că corpul este aproape de pământ , este posibil să luăm în considerare funcția $\mathbf {a} (t)$ ${\ displaystyle \ mathbf {a} (t)}$ ${\ displaystyle \ mathbf {a} (t)}$ ca o constantă , cu o valoare egală cu $-\mathbf {g}$ ${\ displaystyle - \ mathbf {g}}$ ${\ displaystyle - \ mathbf {g}}$ direcționate de-a lungul perpendiculare pe sol (axa y), deci avem:

\mathbf {v} (t)=\mathbf {v} _{0}-g\cdot t\cdot {\hat {u}}_{y}

{\ displaystyle \ mathbf {v} (t) = \ mathbf {v} _ {0} -g \ cdot t \ cdot {\ hat {u}} _ {y}}

{\ displaystyle \ mathbf {v} (t) = \ mathbf {v} _ {0} -g \ cdot t \ cdot {\ hat {u}} _ {y}}

După cum se poate vedea din formulă, viteza se află întotdeauna în planul format de vectori constanți $\mathbf {v} _{0}$ ${\ displaystyle \ mathbf {v} _ {0}}$ ${\ displaystyle \ mathbf {v} _ {0}}$ Și $\mathbf {g}$ ${\ displaystyle \ mathbf {g}}$ ${\ mathbf {g}}$ , acesta este cel pe care are loc mișcarea.

Vectorul viteză poate fi descompus de-a lungul celor două componente x și y :

\mathbf {v} _{0}=v_{0}\cos {\theta }\cdot {\hat {u}}_{x}+v_{0}\sin {\theta }\cdot {\hat {u}}_{y}.

{\ displaystyle \ mathbf {v} _ {0} = v_ {0} \ cos {\ theta} \ cdot {\ hat {u}} _ {x} + v_ {0} \ sin {\ theta} \ cdot { \ hat {u}} _ {y}.}

{\ displaystyle \ mathbf {v} _ {0} = v_ {0} \ cos {\ theta} \ cdot {\ hat {u}} _ {x} + v_ {0} \ sin {\ theta} \ cdot { \ hat {u}} _ {y}.}

Din relația anterioară, obținem:

\mathbf {v} (t)=v_{0}\cos {\theta }\cdot {\hat {u}}_{x}+(v_{0}\sin {\theta }-gt)\cdot {\hat {u}}_{y}

{\ displaystyle \ mathbf {v} (t) = v_ {0} \ cos {\ theta} \ cdot {\ hat {u}} _ {x} + (v_ {0} \ sin {\ theta} -gt) \ cdot {\ hat {u}} _ {y}}

{\ displaystyle \ mathbf {v} (t) = v_ {0} \ cos {\ theta} \ cdot {\ hat {u}} _ {x} + (v_ {0} \ sin {\ theta} -gt) \ cdot {\ hat {u}} _ {y}}

Prin proiectarea vitezelor pe axe, se obțin următoarele componente:

v_{x}=v_{0}\,\cos {\theta },

{\ displaystyle v_ {x} = v_ {0} \, \ cos {\ theta},}

{\ displaystyle v_ {x} = v_ {0} \, \ cos {\ theta},}

constantă în timp, e

v_{y}=v_{0}\,\sin {\theta }-g\,t

{\ displaystyle v_ {y} = v_ {0} \, \ sin {\ theta} -g \, t}

{\ displaystyle v_ {y} = v_ {0} \, \ sin {\ theta} -g \, t}

,

din care, prin integrare, se obțin legile orare ale mișcărilor de-a lungul axelor x și y :

{\begin{cases}x(t)=v_{0}\cos {\theta }t\\y(t)=v_{0}\sin {\theta }t-{\dfrac {1}{2}}gt^{2}\end{cases}}

{\ displaystyle {\ begin {cases} x (t) = v_ {0} \ cos {\ theta} t \\ y (t) = v_ {0} \ sin {\ theta} t - {\ dfrac {1} {2}} gt ^ {2} \ end {cases}}}

{\ displaystyle {\ begin {cases} x (t) = v_ {0} \ cos {\ theta} t \\ y (t) = v_ {0} \ sin {\ theta} t - {\ dfrac {1} {2}} gt ^ {2} \ end {cases}}}

Traiectoria se obține prin eliminarea variabilei de timp, adică prin exprimarea raportului:

{\frac {y}{x}}={\frac {v_{0}\sin {\theta }t-{\frac {1}{2}}gt^{2}}{v_{0}\cos {\theta }t}}=\tan {\theta }-{\frac {gt}{2v_{0}\cos {\theta }}}

{\ displaystyle {\ frac {y} {x}} = {\ frac {v_ {0} \ sin {\ theta} t - {\ frac {1} {2}} gt ^ {2}} {v_ {0 } \ cos {\ theta} t}} = \ tan {\ theta} - {\ frac {gt} {2v_ {0} \ cos {\ theta}}}

{\ displaystyle {\ frac {y} {x}} = {\ frac {v_ {0} \ sin {\ theta} t - {\ frac {1} {2}} gt ^ {2}} {v_ {0 } \ cos {\ theta} t}} = \ tan {\ theta} - {\ frac {gt} {2v_ {0} \ cos {\ theta}}}

și făcând parametrul explicit $t$ ${\ displaystyle t}$ $t$ după legea orară $x(t)$ ${\ displaystyle x (t)}$ $x (t)$ :

t={\frac {x}{v_{0}\cos {\theta }}}

{\ displaystyle t = {\ frac {x} {v_ {0} \ cos {\ theta}}}}

{\ displaystyle t = {\ frac {x} {v_ {0} \ cos {\ theta}}}}

În acest fel ajungem la ecuația carteziană:

{\frac {y}{x}}=\tan {\theta }-{\frac {gt}{2v_{0}\cos {\theta }}}=\tan {\theta }-{\frac {g}{2v_{0}\cos {\theta }}}\cdot {\frac {x}{v_{0}\cos {\theta }}}

{\ displaystyle {\ frac {y} {x}} = \ tan {\ theta} - {\ frac {gt} {2v_ {0} \ cos {\ theta}}} = \ tan {\ theta} - {\ frac {g} {2v_ {0} \ cos {\ theta}}} \ cdot {\ frac {x} {v_ {0} \ cos {\ theta}}}}

{\ displaystyle {\ frac {y} {x}} = \ tan {\ theta} - {\ frac {gt} {2v_ {0} \ cos {\ theta}}} = \ tan {\ theta} - {\ frac {g} {2v_ {0} \ cos {\ theta}}} \ cdot {\ frac {x} {v_ {0} \ cos {\ theta}}}}

din care, înmulțind ambele părți cu x, obținem

\ y(x)=x\tan {\theta }-{\frac {g}{2v_{0}^{2}\cos ^{2}{\theta }}}\cdot x^{2}

{\ displaystyle \ y (x) = x \ tan {\ theta} - {\ frac {g} {2v_ {0} ^ {2} \ cos ^ {2} {\ theta}}} \ cdot x ^ {2 }}

{\ displaystyle \ y (x) = x \ tan {\ theta} - {\ frac {g} {2v_ {0} ^ {2} \ cos ^ {2} {\ theta}}} \ cdot x ^ {2 }}

care reprezintă o parabolă cu concavitatea orientată în jos, al cărei grafic este prezentat în figură. De asemenea, dacă poziția aruncării corpului nu este în origine, atunci de exemplu în punct $P=(x_{0},y_{0})$ ${\ displaystyle P = (x_ {0}, y_ {0})}$ ${\ displaystyle P = (x_ {0}, y_ {0})}$ curba poate fi aproximată cu o translație a axelor paralele cu axele carteziene cu originea în $P.$ ${\ displaystyle P}$ $P.$ (aproximarea se datorează faptului că luăm în considerare corpul lângă pământ, ergo g este constant)

Gamă

Raza de acțiune este distanța parcursă orizontal de corp înainte de a atinge solul. Dacă luăm în considerare traiectoria exprimată într-un plan cartezian Oxy, pentru a calcula intervalul putem folosi funcția y (x) văzută mai sus. Suntem interesați să știm la ce coordonată x coordonata y este egală cu zero, adică:

x\tan \theta -{\frac {g}{2v_{0}^{2}\cos ^{2}\theta }}\cdot x^{2}=0\quad \to \quad x\cdot \left(\tan \theta -{\frac {g}{2v_{0}^{2}\cos ^{2}\theta }}\cdot x\right)=0

{\ displaystyle x \ tan \ theta - {\ frac {g} {2v_ {0} ^ {2} \ cos ^ {2} \ theta}} \ cdot x ^ {2} = 0 \ quad \ to \ quad x \ cdot \ left (\ tan \ theta - {\ frac {g} {2v_ {0} ^ {2} \ cos ^ {2} \ theta}} \ cdot x \ right) = 0}

{\ displaystyle x \ tan \ theta - {\ frac {g} {2v_ {0} ^ {2} \ cos ^ {2} \ theta}} \ cdot x ^ {2} = 0 \ quad \ to \ quad x \ cdot \ left (\ tan \ theta - {\ frac {g} {2v_ {0} ^ {2} \ cos ^ {2} \ theta}} \ cdot x \ right) = 0}

Este o parabolă, așa că ne așteptăm la două soluții. Dacă corpul începe de la sol, una dintre cele două soluții va fi poziția de plecare și poate fi aruncată. Dacă corpul nu pornește de la sol, una dintre cele două soluții va fi „în spatele” poziției de plecare și nu are nicio semnificație fizică. Elaborăm ecuația de gradul doi pentru a obține domeniul x _G.

x_{G}={\frac {2v_{0}^{2}\sin \theta \cos \theta \ }{g}}={\frac {v_{0}^{2}\sin 2\theta }{g}}

{\ displaystyle x_ {G} = {\ frac {2v_ {0} ^ {2} \ sin \ theta \ cos \ theta \} {g}} = {\ frac {v_ {0} ^ {2} \ sin 2 \ theta} {g}}}

{\ displaystyle x_ {G} = {\ frac {2v_ {0} ^ {2} \ sin \ theta \ cos \ theta \} {g}} = {\ frac {v_ {0} ^ {2} \ sin 2 \ theta} {g}}}

Să studiem acum cazul în care înălțimea de pornire nu este zero. Tot ce trebuie să facem este să refolosim funcția y (x) prin adăugarea constantei $y_{0}\neq 0$ ${\ displaystyle y_ {0} \ neq 0}$ ${\ displaystyle y_ {0} \ neq 0}$ . Să elaborăm această altă ecuație de gradul doi pentru a obține:

$x_{G}={\frac {v_{0}^{2}\sin 2\theta }{2g}}\left(1+{\sqrt {1+{\frac {2g\ y_{0}}{v_{0}^{2}\sin ^{2}\theta }}\ }}\right)$ ${\ displaystyle x_ {G} = {\ frac {v_ {0} ^ {2} \ sin 2 \ theta} {2g}} \ left (1 + {\ sqrt {1 + {\ frac {2g \ y_ {0 }} {v_ {0} ^ {2} \ sin ^ {2} \ theta}} \}} \ right)}$ ${\ displaystyle x_ {G} = {\ frac {v_ {0} ^ {2} \ sin 2 \ theta} {2g}} \ left (1 + {\ sqrt {1 + {\ frac {2g \ y_ {0 }} {v_ {0} ^ {2} \ sin ^ {2} \ theta}} \}} \ right)}$

Sunt necesare diverse simplificări și transformări, dar în această formă este ușor de văzut cum acest rezultat se aplică atât unui corp aruncat de la sol, cât și unui corp aruncat de la o înălțime dată.

În acest moment este posibil să se obțină unghiul intervalului maxim. Reparați-vă $v_{0}$ ${\ displaystyle v_ {0}}$ $v_0$ pentru un punct lansat de la sol, ne întrebăm la ce unghi este maximă. $\sin {2\theta }$ ${\ displaystyle \ sin {2 \ theta}}$ ${\ displaystyle \ sin {2 \ theta}}$ are maxim relativ pentru argumentul sinus egal cu ${\frac {\pi }{2}}$ ${\ displaystyle {\ frac {\ pi} {2}}}$ ${\ frac {\ pi} {2}}$ prin urmare $\theta =45$ ${\ displaystyle \ theta = 45}$ ${\ displaystyle \ theta = 45}$ °

Înălțimea maximă

Deoarece mișcarea parabolică este simetrică față de axa care trece prin vârf și paralelă cu axa y ( proprietatea parabolei ), abscisa punctului de aterizare este de două ori abscisa vârfului parabolei, adică dubla abscisei a punctului de înălțime maximă. Prin urmare, această abscisă este:

x={\frac {v_{0}^{2}\sin(2\theta )}{2g}}={\frac {v_{0}^{2}\cos {\theta }\sin {\theta }}{g}}

{\ displaystyle x = {\ frac {v_ {0} ^ {2} \ sin (2 \ theta)} {2g}} = {\ frac {v_ {0} ^ {2} \ cos {\ theta} \ sin {\ theta}} {g}}}

{\ displaystyle x = {\ frac {v_ {0} ^ {2} \ sin (2 \ theta)} {2g}} = {\ frac {v_ {0} ^ {2} \ cos {\ theta} \ sin {\ theta}} {g}}}

Înlocuind în ecuația parabolei explicată anterior, avem că:

y_{M}={\frac {v_{0}^{2}\sin ^{2}{\theta }}{2g}}

{\ displaystyle y_ {M} = {\ frac {v_ {0} ^ {2} \ sin ^ {2} {\ theta}} {2g}}}

{\ displaystyle y_ {M} = {\ frac {v_ {0} ^ {2} \ sin ^ {2} {\ theta}} {2g}}}

Aceleași rezultate se obțin având în vedere faptul că punctul de înălțime maximă este un punct maxim al curbei traiectoriei și, prin urmare, punctul maxim al parabolei. Găsirea acestuia constă deci în stabilirea primei derivate a ecuației traiectoriei egală cu zero și obținerea abscisei punctului căutat din ecuația obținută. $X$ ${\ displaystyle x}$ $X$ (Care ar fi intervalul) înlocuirea ecuației traiectoriei obține, de asemenea, ordonata $y_{M}$ ${\ displaystyle y_ {M}}$ ${\ displaystyle y_ {M}}$ .

Timp de zbor

Timpul de zbor este timpul dintre momentul lansării și sosirea corpului, care coincide cu timpul necesar pentru a parcurge întinderea OG cu viteza v _x :

t_{G}={\frac {x_{G}}{v_{0}\cos \theta }}={\frac {2v_{0}\sin \theta }{g}}=2t_{M}

{\ displaystyle t_ {G} = {\ frac {x_ {G}} {v_ {0} \ cos \ theta}} = {\ frac {2v_ {0} \ sin \ theta} {g}} = 2t_ {M }}

{\ displaystyle t_ {G} = {\ frac {x_ {G}} {v_ {0} \ cos \ theta}} = {\ frac {2v_ {0} \ sin \ theta} {g}} = 2t_ {M }}

Dinamica mișcării proiectilului

Aparat pentru demonstrarea traiectoriei parabolice a proiectilelor (sfârșitul secolului al XVIII-lea, Museo Galileo din Florența).

Un exemplu tipic de mișcare parabolică este cel al glonțului , care este tratat de balistică . Un proiectil zburător este supus forței de greutate a Pământului. În ipoteza fricțiunii neglijabile a aerului, al doilea principiu al dinamicii conduce la o accelerație care poate fi descompusă după cum urmează:

{\begin{cases}a_{x}=0\\a_{y}=-g\end{cases}}

{\ displaystyle {\ begin {cases} a_ {x} = 0 \\ a_ {y} = - g \ end {cases}}}

{\ displaystyle {\ begin {cases} a_ {x} = 0 \\ a_ {y} = - g \ end {cases}}}

Dacă glonțul este tras cu viteza inițială v ₀ conform unui unghi θ, se obțin următoarele componente ale vitezei:

{\begin{cases}v_{x}=v_{0}\cos \theta \\v_{y}=v_{0}\sin {\theta }-gt\end{cases}}

{\ displaystyle {\ begin {cases} v_ {x} = v_ {0} \ cos \ theta \\ v_ {y} = v_ {0} \ sin {\ theta} -gt \ end {cases}}}

{\ displaystyle {\ begin {cases} v_ {x} = v_ {0} \ cos \ theta \\ v_ {y} = v_ {0} \ sin {\ theta} -gt \ end {cases}}}

Prin urmare, componentele poziției glonțului sunt:

{\begin{cases}x(t)=v_{0}\cos {\theta }t\\y(t)=v_{0}\sin {\theta }t-{\dfrac {1}{2}}gt^{2}\end{cases}}

{\ displaystyle {\ begin {cases} x (t) = v_ {0} \ cos {\ theta} t \\ y (t) = v_ {0} \ sin {\ theta} t - {\ dfrac {1} {2}} gt ^ {2} \ end {cases}}}

{\ displaystyle {\ begin {cases} x (t) = v_ {0} \ cos {\ theta} t \\ y (t) = v_ {0} \ sin {\ theta} t - {\ dfrac {1} {2}} gt ^ {2} \ end {cases}}}

De aceea, mișcarea de-a lungul axei x este uniformă și cea de-a lungul axei y accelerată. Dacă viteza inițială ar fi fost zero, mișcarea ar fi fost de cădere liberă.

Mișcare parabolică cu frecare vâscoasă

În primul rând, sunt luate în considerare toate forțele implicate: forța de greutate $F. p$ ${\ displaystyle Fp}$ ${\ displaystyle Fp}$ (datorită atracției gravitaționale a pământului, în ecuație este indicat cu un semn negativ deoarece se opune tracțiunii lui Arhimede), tracțiunea lui Arhimede $F. la$ ${\ displaystyle Fa}$ ${\ displaystyle Fa}$ (fiecare corp imersat într-un fluid suferă o împingere verticală de jos în sus egală cu greutatea lichidului deplasat, al cărui punct de aplicare coincide cu centrul de greutate al masei fluidului deplasat), forța de rezistență a mediului $F. r$ ${\ displaystyle Fr}$ ${\ displaystyle Fr}$ (datorită proprietăților fluidului în care se află proiectilul, în ecuație este indicat cu semn negativ deoarece se opune mișcării proiectilului) și în cele din urmă se consideră forța cu care este lansat proiectilul $F.$ ${\ displaystyle F}$ $F.$ . Datorită acestor forțe putem scrie ecuația forțelor care guvernează mișcarea:

$Fa-Fp-Fr=F$ ${\ displaystyle Fa-Fp-Fr = F}$ ${\ displaystyle Fa-Fp-Fr = F}$

Unde este $Fr=6\pi \eta {\sqrt[{3}]{abc}}v$ ${\ displaystyle Fr = 6 \ pi \ age {\ sqrt [{3}] {abc}} v}$ ${\ displaystyle Fr = 6 \ pi \ age {\ sqrt [{3}] {abc}} v}$ este legea generalizată a lui Stokes pentru sferoizi (oblate, prolate, scalene și pentru sfere). Dacă doriți să luați în considerare orice geometrie, aplicați doar formula: $Fr={\dfrac {1}{2}}Cd\rho Sv^{2}$ ${\ displaystyle Fr = {\ dfrac {1} {2}} Cd \ rho Sv ^ {2}}$ ${\ displaystyle Fr = {\ dfrac {1} {2}} Cd \ rho Sv ^ {2}}$ . Unde este dată forța de tracțiune: de coeficientul de frecare $C. d$ ${\ displaystyle Cd}$ ${\ displaystyle Cd}$ (care este adimensional și se schimbă în funcție de forma obiectului), de densitatea aerului $\rho$ ${\ displaystyle \ rho}$ $\ rho$ , din secțiunea sa transversală $S.$ ${\ displaystyle S}$ $S.$ , și în cele din urmă de viteza mare pătrat $v^{2}$ ${\ displaystyle v ^ {2}}$ ${\ displaystyle v ^ {2}}$ , toate înmulțite cu factorul convențional ${\dfrac {1}{2}}$ ${\ displaystyle {\ dfrac {1} {2}}}$ ${\ displaystyle {\ dfrac {1} {2}}}$ .

Având în vedere legea lui Stokes (deoarece glonțul este în general un sferoid prolat), ecuația inițială devine: $V\rho g-mg-6\pi \eta {\sqrt[{3}]{abc}}v=ma$ ${\ displaystyle V \ rho g-mg-6 \ pi \ eta {\ sqrt [{3}] {abc}} v = ma}$ ${\ displaystyle V \ rho g-mg-6 \ pi \ eta {\ sqrt [{3}] {abc}} v = ma}$

fiind volumul V cel al unui sferoid devine: $V={\dfrac {4}{3}}\pi abc$ ${\ displaystyle V = {\ dfrac {4} {3}} \ pi abc}$ ${\ displaystyle V = {\ dfrac {4} {3}} \ pi abc}$ unde a (este axa x), b (este axa y), c (este axa z).

atunci ecuația devine: $g({\dfrac {4}{3}}\pi \rho abc-m)-6\pi \eta {\sqrt[{3}]{abc}}v=m{\dfrac {dv}{dt}}$ ${\ displaystyle g ({\ dfrac {4} {3}} \ pi \ rho abc-m) -6 \ pi \ eta {\ sqrt [{3}] {abc}} v = m {\ dfrac {dv} {dt}}}$ ${\ displaystyle g ({\ dfrac {4} {3}} \ pi \ rho abc-m) -6 \ pi \ eta {\ sqrt [{3}] {abc}} v = m {\ dfrac {dv} {dt}}}$

Acum, descompunând accelerațiile de-a lungul axelor, obținem:

${\begin{cases}-6\pi \eta {\sqrt[{3}]{abc}}v_{x}=ma_{x}\\{\displaystyle g({\dfrac {4}{3}}\pi \rho abc-m)-6\pi \eta {\sqrt[{3}]{abc}}v_{y}=ma_{y}}\end{cases}}$ ${\ displaystyle {\ begin {cases} -6 \ pi \ eta {\ sqrt [{3}] {abc}} v_ {x} = ma_ {x} \\ {\ displaystyle g ({\ dfrac {4} { 3}} \ pi \ rho abc-m) -6 \ pi \ eta {\ sqrt [{3}] {abc}} v_ {y} = ma_ {y}} \ end {cases}}}$ ${\ displaystyle {\ begin {cases} -6 \ pi \ eta {\ sqrt [{3}] {abc}} v_ {x} = ma_ {x} \\ {\ displaystyle g ({\ dfrac {4} { 3}} \ pi \ rho abc-m) -6 \ pi \ eta {\ sqrt [{3}] {abc}} v_ {y} = ma_ {y}} \ end {cases}}}$

Apoi rescriem accelerația ca ( $a={\dfrac {dv}{dt}}$ ${\ displaystyle a = {\ dfrac {dv} {dt}}}$ ${\ displaystyle a = {\ dfrac {dv} {dt}}}$ ) obținerea:

${\begin{cases}-6\pi \eta {\sqrt[{3}]{abc}}v_{x}=m{\dfrac {dv_{x}}{dt}}\\{\displaystyle -g({\dfrac {4}{3}}\pi \rho abc-m)+6\pi \eta {\sqrt[{3}]{abc}}v_{y}=-m{\dfrac {dv_{y}}{dt}}}\end{cases}}$ ${\ displaystyle {\ begin {cases} -6 \ pi \ eta {\ sqrt [{3}] {abc}} v_ {x} = m {\ dfrac {dv_ {x}} {dt}} \\ {\ displaystyle -g ({\ dfrac {4} {3}} \ pi \ rho abc-m) +6 \ pi \ eta {\ sqrt [{3}] {abc}} v_ {y} = - m {\ dfrac {dv_ {y}} {dt}}} \ end {cases}}}$ ${\ displaystyle {\ begin {cases} -6 \ pi \ eta {\ sqrt [{3}] {abc}} v_ {x} = m {\ dfrac {dv_ {x}} {dt}} \\ {\ displaystyle -g ({\ dfrac {4} {3}} \ pi \ rho abc-m) +6 \ pi \ eta {\ sqrt [{3}] {abc}} v_ {y} = - m {\ dfrac {dv_ {y}} {dt}}} \ end {cases}}}$

V este izolat:

${\begin{cases}v_{x}=-{\dfrac {m}{6\pi \eta {\sqrt[{3}]{abc}}}}{\dfrac {dv_{x}}{dt}}\\{\displaystyle {\dfrac {g(m-{\dfrac {4}{3}}\pi \rho abc)}{6\pi \eta {\sqrt[{3}]{abc}}}}+v_{y}=-{\dfrac {m}{6\pi \eta {\sqrt[{3}]{abc}}}}{\dfrac {dv_{y}}{dt}}}\end{cases}}$ ${\ displaystyle {\ begin {cases} v_ {x} = - {\ dfrac {m} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}} {\ dfrac {dv_ {x}} {dt}} \\ {\ displaystyle {\ dfrac {g (m - {\ dfrac {4} {3}} \ pi \ rho abc)} {6 \ pi \ eta {\ sqrt [{3}] {abc }}}} + v_ {y} = - {\ dfrac {m} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}} {\ dfrac {dv_ {y}} {dt}} } \ end {cases}}}$ ${\ displaystyle {\ begin {cases} v_ {x} = - {\ dfrac {m} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}} {\ dfrac {dv_ {x}} {dt}} \\ {\ displaystyle {\ dfrac {g (m - {\ dfrac {4} {3}} \ pi \ rho abc)} {6 \ pi \ eta {\ sqrt [{3}] {abc }}}} + v_ {y} = - {\ dfrac {m} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}} {\ dfrac {dv_ {y}} {dt}} } \ end {cases}}}$

unde este $a={\dfrac {g(m-{\dfrac {4}{3}}\pi \rho abc)}{6\pi \eta {\sqrt[{3}]{abc}}}}$ ${\ displaystyle a = {\ dfrac {g (m - {\ dfrac {4} {3}} \ pi \ rho abc)} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}} }$ ${\ displaystyle a = {\ dfrac {g (m - {\ dfrac {4} {3}} \ pi \ rho abc)} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}} }$ Și $b={\dfrac {m}{6\pi \eta {\sqrt[{3}]{abc}}}}$ ${\ displaystyle b = {\ dfrac {m} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}}}$ ${\ displaystyle b = {\ dfrac {m} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}}}$

de aceea avem:

${\begin{cases}v_{x}=-b{\dfrac {dv_{x}}{dt}}\\{\displaystyle a+v_{y}=-b{\dfrac {dv_{y}}{dt}}}\end{cases}}$ ${\ displaystyle {\ begin {cases} v_ {x} = - b {\ dfrac {dv_ {x}} {dt}} \\ {\ displaystyle a + v_ {y} = - b {\ dfrac {dv_ {y }} {dt}}} \ end {cases}}}$ ${\ displaystyle {\ begin {cases} v_ {x} = - b {\ dfrac {dv_ {x}} {dt}} \\ {\ displaystyle a + v_ {y} = - b {\ dfrac {dv_ {y }} {dt}}} \ end {cases}}}$

rezolvând astfel ecuația diferențială: $a+v=-b{\dfrac {dv}{dt}}$ ${\ displaystyle a + v = -b {\ dfrac {dv} {dt}}}$ ${\ displaystyle a + v = -b {\ dfrac {dv} {dt}}}$ primesti: $\int {\dfrac {dv}{a+v}}=\int -{\dfrac {dt}{b}}$ ${\ displaystyle \ int {\ dfrac {dv} {a + v}} = \ int - {\ dfrac {dt} {b}}}$ ${\ displaystyle \ int {\ dfrac {dv} {a + v}} = \ int - {\ dfrac {dt} {b}}}$ al cărui rezultat este: $ln(a+v)=-{\dfrac {t}{b}}+c_{ostante}$ ${\ displaystyle ln (a + v) = - {\ dfrac {t} {b}} + c_ {constant}}$ ${\ displaystyle ln (a + v) = - {\ dfrac {t} {b}} + c_ {constant}}$

care atunci când este transformat în mod adecvat devine: $a+v=c_{ostante}e^{-{\dfrac {t}{b}}}$ ${\ displaystyle a + v = c_ {constant} e ^ {- {\ dfrac {t} {b}}}}$ ${\ displaystyle a + v = c_ {constant} e ^ {- {\ dfrac {t} {b}}}}$ unde constanta c pentru t = 0 devine: $c_{ostante}=a+v_{0}$ ${\ displaystyle c_ {constant} = a + v_ {0}}$ ${\ displaystyle c_ {constant} = a + v_ {0}}$ atunci ecuația diferențială finală devine: $a+v=(a+v_{0})e^{-{\dfrac {t}{b}}}$ ${\ displaystyle a + v = (a + v_ {0}) e ^ {- {\ dfrac {t} {b}}}}$ ${\ displaystyle a + v = (a + v_ {0}) e ^ {- {\ dfrac {t} {b}}}}$

prin urmare, deoarece nu există o accelerație de-a lungul mișcării pe axa x, vom avea că v pe axa x este:

$v_{x}=v_{0x}e^{-{\dfrac {t}{b}}}=v_{0x}e^{-{\dfrac {6\pi \eta {\sqrt[{3}]{abc}}t}{m}}}$ ${\ displaystyle v_ {x} = v_ {0x} e ^ {- {\ dfrac {t} {b}}} = v_ {0x} e ^ {- {\ dfrac {6 \ pi \ eta {\ sqrt [{ 3}] {abc}} t} {m}}}}$ ${\ displaystyle v_ {x} = v_ {0x} e ^ {- {\ dfrac {t} {b}}} = v_ {0x} e ^ {- {\ dfrac {6 \ pi \ eta {\ sqrt [{ 3}] {abc}} t} {m}}}}$ cu un egal cu 0;

în timp ce mișcarea de-a lungul axei y are caracteristica de a prezenta accelerația, v pe axa y este: $v_{y}=(a+v_{0y})e^{-{\dfrac {t}{b}}}-a=({\dfrac {g(m-{\dfrac {4}{3}}\pi \rho abc)}{6\pi \eta {\sqrt[{3}]{abc}}}}+v_{0y})e^{-{\dfrac {6\pi \eta {\sqrt[{3}]{abc}}t}{m}}}-{\dfrac {g(m-{\dfrac {4}{3}}\pi \rho abc)}{6\pi \eta {\sqrt[{3}]{abc}}}}$ ${\ displaystyle v_ {y} = (a + v_ {0y}) și ^ {- {\ dfrac {t} {b}}} - a = ({\ dfrac {g (m - {\ dfrac {4} { 3}} \ pi \ rho abc)} {6 \ pi \ age {\ sqrt [{3}] {abc}}}} + v_ {0y}) și ^ {- {\ dfrac {6 \ pi \ age { \ sqrt [{3}] {abc}} t} {m}}} - {\ dfrac {g (m - {\ dfrac {4} {3}} \ pi \ rho abc)} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}}}$ ${\ displaystyle v_ {y} = (a + v_ {0y}) și ^ {- {\ dfrac {t} {b}}} - a = ({\ dfrac {g (m - {\ dfrac {4} { 3}} \ pi \ rho abc)} {6 \ pi \ age {\ sqrt [{3}] {abc}}}} + v_ {0y}) și ^ {- {\ dfrac {6 \ pi \ age { \ sqrt [{3}] {abc}} t} {m}}} - {\ dfrac {g (m - {\ dfrac {4} {3}} \ pi \ rho abc)} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}}}$ cu un diferit de 0;

Acum, pentru a găsi ecuațiile carteziene ale mișcării parabolice, integrăm ecuațiile carteziene ale vitezei:

$\int v_{x}dt=\int v_{0x}e^{-{\dfrac {t}{b}}}dt$ ${\ displaystyle \ int v_ {x} dt = \ int v_ {0x} e ^ {- {\ dfrac {t} {b}}} dt}$ ${\ displaystyle \ int v_ {x} dt = \ int v_ {0x} e ^ {- {\ dfrac {t} {b}}} dt}$ a cărei soluție este: $x(t)=bv_{0x}(1-e^{-{\dfrac {t}{b}}})={\dfrac {m}{6\pi \eta {\sqrt[{3}]{abc}}}}v_{0x}(1-e^{-{\dfrac {6\pi \eta {\sqrt[{3}]{abc}}t}{m}}})$ ${\ displaystyle x (t) = bv_ {0x} (1-e ^ {- {\ dfrac {t} {b}}}) = {\ dfrac {m} {6 \ pi \ eta {\ sqrt [{3 }] {abc}}}} v_ {0x} (1-e ^ {- {\ dfrac {6 \ pi \ eta {\ sqrt [{3}] {abc}} t} {m}}})}$ ${\ displaystyle x (t) = bv_ {0x} (1-e ^ {- {\ dfrac {t} {b}}}) = {\ dfrac {m} {6 \ pi \ eta {\ sqrt [{3 }] {abc}}}} v_ {0x} (1-e ^ {- {\ dfrac {6 \ pi \ eta {\ sqrt [{3}] {abc}} t} {m}}})}$

$\int v_{y}dt=\int ((a+v_{0y})e^{-{\dfrac {t}{b}}}-a)dt$ ${\ displaystyle \ int v_ {y} dt = \ int ((a + v_ {0y}) e ^ {- {\ dfrac {t} {b}}} - a) dt}$ ${\ displaystyle \ int v_ {y} dt = \ int ((a + v_ {0y}) e ^ {- {\ dfrac {t} {b}}} - a) dt}$ a cărei soluție este: $y(t)=b(a+v_{0y})(1-e^{-{\dfrac {t}{b}}})-at={\dfrac {m}{6\pi \eta {\sqrt[{3}]{abc}}}}({\dfrac {g(m-{\dfrac {4}{3}}\pi \rho abc)}{6\pi \eta {\sqrt[{3}]{abc}}}}+v_{0y})(1-e^{-{\dfrac {6\pi \eta {\sqrt[{3}]{abc}}t}{m}}})-{\dfrac {g(m-{\dfrac {4}{3}}\pi \rho abc)}{6\pi \eta {\sqrt[{3}]{abc}}}}t$ ${\ displaystyle y (t) = b (a + v_ {0y}) (1-e ^ {- {\ dfrac {t} {b}}}) - at = {\ dfrac {m} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}} ({\ dfrac {g (m - {\ dfrac {4} {3}} \ pi \ rho abc)} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}} + v_ {0y}) (1-e ^ {- {\ dfrac {6 \ pi \ eta {\ sqrt [{3}] {abc}} t} {m} }}) - {\ dfrac {g (m - {\ dfrac {4} {3}} \ pi \ rho abc)} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}} t }$ ${\ displaystyle y (t) = b (a + v_ {0y}) (1-e ^ {- {\ dfrac {t} {b}}}) - at = {\ dfrac {m} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}} ({\ dfrac {g (m - {\ dfrac {4} {3}} \ pi \ rho abc)} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}} + v_ {0y}) (1-e ^ {- {\ dfrac {6 \ pi \ eta {\ sqrt [{3}] {abc}} t} {m} }}) - {\ dfrac {g (m - {\ dfrac {4} {3}} \ pi \ rho abc)} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}} t }$

Prin urmare, ecuația carteziană a parabolei este:

$y(x)=b(a+v_{0y})({-{\dfrac {x}{bv_{0x}}}})-abln(1-{\dfrac {x}{bv_{0x}}})$ ${\ displaystyle y (x) = b (a + v_ {0y}) ({- {\ dfrac {x} {bv_ {0x}}}}) - abln (1 - {\ dfrac {x} {bv_ {0x }}})}$ ${\ displaystyle y (x) = b (a + v_ {0y}) ({- {\ dfrac {x} {bv_ {0x}}}}) - abln (1 - {\ dfrac {x} {bv_ {0x }}})}$

Dacă vrei să fii și mai precis în traiectorie, poți considera forța de frecare ca. $Fr=k|v|v=6\pi \eta {\sqrt[{3}]{abc}}v^{2}$ ${\ displaystyle Fr = k | v | v = 6 \ pi \ age {\ sqrt [{3}] {abc}} v ^ {2}}$ ${\ displaystyle Fr = k | v | v = 6 \ pi \ age {\ sqrt [{3}] {abc}} v ^ {2}}$ prin urmare scriem întotdeauna ecuația inițială:

$Fa-Fp-Fr=F$ ${\ displaystyle Fa-Fp-Fr = F}$ ${\ displaystyle Fa-Fp-Fr = F}$ care devine: $V\rho g-mg-6\pi \eta {\sqrt[{3}]{abc}}v^{2}=ma$ ${\ displaystyle V \ rho g-mg-6 \ pi \ eta {\ sqrt [{3}] {abc}} v ^ {2} = ma}$ ${\ displaystyle V \ rho g-mg-6 \ pi \ eta {\ sqrt [{3}] {abc}} v ^ {2} = ma}$

Mișcarea de-a lungul axelor este descompusă:

${\begin{cases}-6\pi \eta {\sqrt[{3}]{abc}}v_{x}^{2}=ma_{x}\\{\displaystyle g({\dfrac {4}{3}}\pi \rho abc-m)-6\pi \eta {\sqrt[{3}]{abc}}v_{y}^{2}=ma_{y}}\end{cases}}$ ${\ displaystyle {\ begin {cases} -6 \ pi \ eta {\ sqrt [{3}] {abc}} v_ {x} ^ {2} = ma_ {x} \\ {\ displaystyle g ({\ dfrac {4} {3}} \ pi \ rho abc-m) -6 \ pi \ eta {\ sqrt [{3}] {abc}} v_ {y} ^ {2} = ma_ {y}} \ end { cazuri}}}$ ${\ displaystyle {\ begin {cases} -6 \ pi \ eta {\ sqrt [{3}] {abc}} v_ {x} ^ {2} = ma_ {x} \\ {\ displaystyle g ({\ dfrac {4} {3}} \ pi \ rho abc-m) -6 \ pi \ eta {\ sqrt [{3}] {abc}} v_ {y} ^ {2} = ma_ {y}} \ end { cazuri}}}$

Rescriem accelerația ca ( $a={\dfrac {dv}{dt}}$ ${\ displaystyle a = {\ dfrac {dv} {dt}}}$ ${\ displaystyle a = {\ dfrac {dv} {dt}}}$ ) obținerea:

${\begin{cases}6\pi \eta {\sqrt[{3}]{abc}}v_{x}^{2}=-m{\dfrac {dv_{x}}{dt}}\\{\displaystyle -g({\dfrac {4}{3}}\pi \rho abc-m)+6\pi \eta {\sqrt[{3}]{abc}}v_{y}^{2}=-m{\dfrac {dv_{y}}{dt}}}\end{cases}}$ ${\ displaystyle {\ begin {cases} 6 \ pi \ eta {\ sqrt [{3}] {abc}} v_ {x} ^ {2} = - m {\ dfrac {dv_ {x}} {dt}} \\ {\ displaystyle -g ({\ dfrac {4} {3}} \ pi \ rho abc-m) +6 \ pi \ eta {\ sqrt [{3}] {abc}} v_ {y} ^ { 2} = - m {\ dfrac {dv_ {y}} {dt}}} \ end {cases}}}$ ${\ displaystyle {\ begin {cases} 6 \ pi \ eta {\ sqrt [{3}] {abc}} v_ {x} ^ {2} = - m {\ dfrac {dv_ {x}} {dt}} \\ {\ displaystyle -g ({\ dfrac {4} {3}} \ pi \ rho abc-m) +6 \ pi \ eta {\ sqrt [{3}] {abc}} v_ {y} ^ { 2} = - m {\ dfrac {dv_ {y}} {dt}}} \ end {cases}}}$

izolăm v pătrat:

${\begin{cases}v_{x}^{2}=-{\dfrac {m}{6\pi \eta {\sqrt[{3}]{abc}}}}{\dfrac {dv_{x}}{dt}}\\{\displaystyle {\dfrac {g(m-{\dfrac {4}{3}}\pi \rho abc)}{6\pi \eta {\sqrt[{3}]{abc}}}}+v_{y}^{2}=-{\dfrac {m}{6\pi \eta {\sqrt[{3}]{abc}}}}{\dfrac {dv_{y}}{dt}}}\end{cases}}$ ${\ displaystyle {\ begin {cases} v_ {x} ^ {2} = - {\ dfrac {m} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}} {\ dfrac {dv_ {x}} {dt}} \\ {\ displaystyle {\ dfrac {g (m - {\ dfrac {4} {3}} \ pi \ rho abc)} {6 \ pi \ eta {\ sqrt [{3 }] {abc}}}} + v_ {y} ^ {2} = - {\ dfrac {m} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}} {\ dfrac {dv_ {y}} {dt}}} \ end {cases}}}$ ${\ displaystyle {\ begin {cases} v_ {x} ^ {2} = - {\ dfrac {m} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}} {\ dfrac {dv_ {x}} {dt}} \\ {\ displaystyle {\ dfrac {g (m - {\ dfrac {4} {3}} \ pi \ rho abc)} {6 \ pi \ eta {\ sqrt [{3 }] {abc}}}} + v_ {y} ^ {2} = - {\ dfrac {m} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}} {\ dfrac {dv_ {y}} {dt}}} \ end {cases}}}$

unde este $a={\dfrac {g(m-{\dfrac {4}{3}}\pi \rho abc)}{6\pi \eta {\sqrt[{3}]{abc}}}}$ ${\ displaystyle a = {\ dfrac {g (m - {\ dfrac {4} {3}} \ pi \ rho abc)} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}} }$ ${\ displaystyle a = {\ dfrac {g (m - {\ dfrac {4} {3}} \ pi \ rho abc)} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}} }$ Și $b={\dfrac {m}{6\pi \eta {\sqrt[{3}]{abc}}}}$ ${\ displaystyle b = {\ dfrac {m} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}}}$ ${\ displaystyle b = {\ dfrac {m} {6 \ pi \ eta {\ sqrt [{3}] {abc}}}}}$

de aceea avem:

${\begin{cases}v_{x}^{2}=-b{\dfrac {dv_{x}}{dt}}\\{\displaystyle a+v_{y}^{2}=-b{\dfrac {dv_{y}}{dt}}}\end{cases}}$ ${\ displaystyle {\ begin {cases} v_ {x} ^ {2} = - b {\ dfrac {dv_ {x}} {dt}} \\ {\ displaystyle a + v_ {y} ^ {2} = - b {\ dfrac {dv_ {y}} {dt}}} \ end {cases}}}$ ${\ displaystyle {\ begin {cases} v_ {x} ^ {2} = - b {\ dfrac {dv_ {x}} {dt}} \\ {\ displaystyle a + v_ {y} ^ {2} = - b {\ dfrac {dv_ {y}} {dt}}} \ end {cases}}}$

rezolvând astfel prima ecuație diferențială: $v^{2}=-b{\dfrac {dv}{dt}}$ ${\ displaystyle v ^ {2} = - b {\ dfrac {dv} {dt}}}$ ${\ displaystyle v ^ {2} = - b {\ dfrac {dv} {dt}}}$ primesti: $\int {\dfrac {dv}{v^{2}}}=\int -{\dfrac {dt}{b}}$ ${\ displaystyle \ int {\ dfrac {dv} {v ^ {2}}} = \ int - {\ dfrac {dt} {b}}}$ ${\ displaystyle \ int {\ dfrac {dv} {v ^ {2}}} = \ int - {\ dfrac {dt} {b}}}$ care duce la: ${\dfrac {1}{v}}={\dfrac {t}{b}}-c_{ostante}$ ${\ displaystyle {\ dfrac {1} {v}} = {\ dfrac {t} {b}} - c_ {constant}}$ ${\ displaystyle {\ dfrac {1} {v}} = {\ dfrac {t} {b}} - c_ {constant}}$ unde constanta c pentru t = 0 devine: $c_{ostante}=-{\dfrac {1}{v_{0}}}$ ${\ displaystyle c_ {constant} = - {\ dfrac {1} {v_ {0}}}}$ ${\ displaystyle c_ {constant} = - {\ dfrac {1} {v_ {0}}}}$ atunci ecuația diferențială finală devine: ${\dfrac {1}{v}}={\dfrac {t}{b}}+{\dfrac {1}{v_{0}}}$ ${\ displaystyle {\ dfrac {1} {v}} = {\ dfrac {t} {b}} + {\ dfrac {1} {v_ {0}}}}$ ${\ displaystyle {\ dfrac {1} {v}} = {\ dfrac {t} {b}} + {\ dfrac {1} {v_ {0}}}}$ unde evidențiind ve și proiectând mișcarea de-a lungul axei x obținem ecuația cartesiană a vitezei:

$v_{x}={\dfrac {1}{{\dfrac {t}{b}}+{\dfrac {1}{v_{0x}}}}}$ ${\ displaystyle v_ {x} = {\ dfrac {1} {{\ dfrac {t} {b}} + {\ dfrac {1} {v_ {0x}}}}}}$ ${\ displaystyle v_ {x} = {\ dfrac {1} {{\ dfrac {t} {b}} + {\ dfrac {1} {v_ {0x}}}}}}$ și integrând această ecuație obținem: $x(t)=bln(1+{\dfrac {v_{0x}t}{b}})$ ${\ displaystyle x (t) = bln (1 + {\ dfrac {v_ {0x} t} {b}})}$ ${\ displaystyle x (t) = bln (1 + {\ dfrac {v_ {0x} t} {b}})}$

rezolvând în schimb a doua ecuație diferențială: $(a+v^{2})=-b{\dfrac {dv}{dt}}$ ${\ displaystyle (a + v ^ {2}) = - b {\ dfrac {dv} {dt}}}$ ${\ displaystyle (a + v ^ {2}) = - b {\ dfrac {dv} {dt}}}$ primesti: $\int {\dfrac {dv}{a+v^{2}}}=\int -{\dfrac {dt}{b}}$ ${\ displaystyle \ int {\ dfrac {dv} {a + v ^ {2}}} = \ int - {\ dfrac {dt} {b}}}$ ${\ displaystyle \ int {\ dfrac {dv} {a + v ^ {2}}} = \ int - {\ dfrac {dt} {b}}}$ care duce la: $v={\sqrt {a}}tg({\dfrac {{\sqrt {a}}(bc-t)}{b}})$ ${\ displaystyle v = {\ sqrt {a}} tg ({\ dfrac {{\ sqrt {a}} (bc-t)} {b}})}$ ${\ displaystyle v = {\ sqrt {a}} tg ({\ dfrac {{\ sqrt {a}} (bc-t)} {b}})}$ unde constanta c pentru t = 0 devine: $c_{ostante}={\dfrac {arctg({\dfrac {v_{0}}{\sqrt {a}}})}{\sqrt {a}}}$ ${\ displaystyle c_ {constant} = {\ dfrac {arctg ({\ dfrac {v_ {0}} {\ sqrt {a}}})} {\ sqrt {a}}}}$ ${\ displaystyle c_ {constant} = {\ dfrac {arctg ({\ dfrac {v_ {0}} {\ sqrt {a}}})} {\ sqrt {a}}}}$ atunci ecuația diferențială finală devine: $v={\sqrt {a}}tg(arctg({\dfrac {v_{0}}{\sqrt {a}}})-{\dfrac {{\sqrt {a}}t}{b}})$ ${\ displaystyle v = {\ sqrt {a}} tg (arctg ({\ dfrac {v_ {0}} {\ sqrt {a}}}) - {\ dfrac {{\ sqrt {a}} t} {b }})}$ ${\ displaystyle v = {\ sqrt {a}} tg (arctg ({\ dfrac {v_ {0}} {\ sqrt {a}}}) - {\ dfrac {{\ sqrt {a}} t} {b }})}$ unde evidențiind ve și proiectând mișcarea de-a lungul axei x obținem ecuația cartesiană a vitezei:

$v_{y}={\sqrt {a}}tg(arctg({\dfrac {v_{0y}}{\sqrt {a}}})-{\dfrac {{\sqrt {a}}t}{b}})$ ${\ displaystyle v_ {y} = {\ sqrt {a}} tg (arctg ({\ dfrac {v_ {0y}} {\ sqrt {a}}}) - {\ dfrac {{\ sqrt {a}} t } {b}})}$ ${\ displaystyle v_ {y} = {\ sqrt {a}} tg (arctg ({\ dfrac {v_ {0y}} {\ sqrt {a}}}) - {\ dfrac {{\ sqrt {a}} t } {b}})}$ și integrând această ecuație obținem: $y(t)=y_{0}+b[ln(|cos({\dfrac {{\sqrt {a}}t}{b}}-arctg({\dfrac {v_{0y}}{\sqrt {a}}}))|)-ln(|cos(-arctg({\dfrac {v_{0y}}{\sqrt {a}}}))|)]$ ${\ displaystyle y (t) = y_ {0} + b [ln (| cos ({\ dfrac {{\ sqrt {a}} t} {b}} - arctg ({\ dfrac {v_ {0y}} { \ sqrt {a}}})) |) -ln (| cos (-arctg ({\ dfrac {v_ {0y}} {\ sqrt {a}}})) |)]}$ ${\ displaystyle y (t) = y_ {0} + b [ln (| cos ({\ dfrac {{\ sqrt {a}} t} {b}} - arctg ({\ dfrac {v_ {0y}} { \ sqrt {a}}})) |) -ln (| cos (-arctg ({\ dfrac {v_ {0y}} {\ sqrt {a}}})) |)]}$

Deci ecuația carteziană a parabolei este:

$y(x)=y_{0}+b[ln(|cos({\dfrac {{\sqrt {a}}(e^{\dfrac {x}{b}}-1)}{v_{0x}}}-arctg({\dfrac {v_{0y}}{\sqrt {a}}}))|)-ln(|cos(-arctg({\dfrac {v_{0y}}{\sqrt {a}}}))|)]$ ${\ displaystyle y (x) = y_ {0} + b [ln (| cos ({\ dfrac {{\ sqrt {a}} (e ^ {\ dfrac {x} {b}} - 1)} {v_ {0x}}} - arctg ({\ dfrac {v_ {0y}} {\ sqrt {a}}})) |) -ln (| cos (-arctg ({\ dfrac {v_ {0y}} {\ sqrt {a}}})) |))}$ ${\ displaystyle y (x) = y_ {0} + b [ln (| cos ({\ dfrac {{\ sqrt {a}} (e ^ {\ dfrac {x} {b}} - 1)} {v_ {0x}}} - arctg ({\ dfrac {v_ {0y}} {\ sqrt {a}}})) |) -ln (| cos (-arctg ({\ dfrac {v_ {0y}} {\ sqrt {a}}})) |))}$

Alte proiecte

Wikimedia Commons conține imagini sau alte fișiere despre mișcarea parabolică

linkuri externe

Aplicație Java a mișcării proiectilului , pe phy.hk.

Portalul mecanicii : accesați intrările Wikipedia care se ocupă de mecanică