Superellipse

Un exemplu de hipoelipse cu a = b = 1 și n = 1/2

În geometrie plană , cu super- elipsă sau matematicienilor Lamé curba înțelegem o figură geometrică care generalizează elipsei . Într-un sistem de coordonate cartezian este descris ca locusul punctelor (x, y) care satisfac ecuația

\left|{\frac {x}{a}}\right|^{n}\!+\left|{\frac {y}{b}}\right|^{n}\!=1

{\ displaystyle \ left | {\ frac {x} {a}} \ right | ^ {n} \! + \ left | {\ frac {y} {b}} \ right | ^ {n} \! = 1 }

\ left | {\ frac {x} {a}} \ right | ^ {n} \! + \ left | {\ frac {y} {b}} \ right | ^ {n} \! = 1

,

cu n , a și b real pozitiv.

Clasificare

În cazul n = 2 avem elipsa obișnuită; este, de asemenea, evident că acestea sunt seturi de puncte simetrice în ceea ce privește axele orizontale Ox și verticale Oy și, prin urmare, și în ceea ce privește punctul lor de intersecție, O, originea sistemului de referință. Pentru n = 1 avem un romb cu vârfuri (± a , 0) și (0, ± b ).

Aceste cifre pot fi urmărite înapoi la curbele familiei indexate numai de parametrul n care poate fi obținut prin setarea valorilor a = b = 1, adică la cifrele care satisfac ecuația normală

\left|x\right|^{n}\!+\left|y\right|^{n}\!=1

{\ displaystyle \ left | x \ right | ^ {n} \! + \ left | y \ right | ^ {n} \! = 1}

{\ displaystyle \ left | x \ right | ^ {n} \! + \ left | y \ right | ^ {n} \! = 1}

;

o superelipsă a formei generale se obține prin aplicarea omoteticii x → x / a și y → y / b la această ecuație.

Observând superelipsele canonice, vedem că sunt invariante și pentru reflecțiile cu privire la liniile pentru originea y = x și y = - x . Datorită invarianței pentru reflexiile față de cele două axe, punctele unei superelipse pot fi împărțite în 4 curbe parțiale, fiecare aparținând unui cadran. Prin urmare, pentru a studia super elipsele, este suficient să ne limităm la primul cadran al planului cartezian și să luăm în considerare curba dată de funcție

y\,=\,(1-x^{n})^{1/n}

{\ displaystyle y \, = \, (1-x ^ {n}) ^ {1 / n}}

{\ displaystyle y \, = \, (1-x ^ {n}) ^ {1 / n}}

.

Un exemplu de hipoelipse cu a = b = 1 și n = 3/2

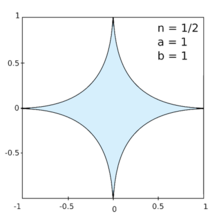
Un alt tip de super-elipsă este cea de la cuspidă sau „migdală”. Acest tip de elipsă posedă toate caracteristicile superelipsei clasice, dar este discontinuă la vârfuri și are forma caracteristică „ochi”. Elipsoidele ovoide cu forma lor caracteristică de ou, care pot fi reprezentate ca curbe quartice, aparțin, de asemenea, clasei superelipse. Pe de altă parte, acest ultim tip de super elipsă este discontinuu doar la un moment dat.

Cifrele familiei obținute cu n > 2 se numesc hiperelipse , cele referitoare la n <2 se numesc hipoelipse . Pe măsură ce n crește, curba canonică se apropie din ce în ce mai mult de dreptunghiul definit de vârfurile opuse (1,1) și (-1, -1); pe măsură ce n scade de la 2 la 1, curba cercului unitar se apropie de pătratul definit de vârfurile opuse (1,0) și (-1,0); pe măsură ce n scade de la 1 la 0 avem curbe care se apropie de crucea formată din cele două segmente de lungime 2 cu capete în (-1,0) și (1,0) și cu capete (0,1) și (0, - 1).

O superelipse cu n > 2 se mai numește și hiperelipse.

Bibliografie

( EN ) Martin Gardner , Superellipse-ul lui Piet Hein , în Carnavalul matematic , 1992, pp. 240-254.
Johan Gielis: Inventarea cercului. Geometria naturii . - Antwerpen: Geniaal Press, 2003. - ISBN 9080775614
Cresci Luciano: Curbele matematice dintre curiozitate și distracție - Hoepli 2005

Elemente conexe

Superformula

Alte proiecte

Wikimedia Commons conține imagini sau alte fișiere pe superelipse

linkuri externe

(EN) Eric W. Weisstein, Superellipse în MathWorld Wolfram Research.
Super Ellipse-ul lui Lamé (Java-Applet) , la activeart.de . Adus la 17 septembrie 2004 (arhivat din original la 27 februarie 2009) .
Super Ellipsoid (Java-Applet) , la activeart.de . Adus la 17 septembrie 2004 (arhivat din original la 24 mai 2005) .

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică