Fenomenul Gibbs

Fenomenul Gibbs apare atunci când este reconstruit un semnal din seria trunchiată Fourier . Acesta poartă numele fizicianului american Willard Gibbs .

Având o funcție periodică $f$ ${\ displaystyle f}$ $f$ care prezintă puncte de discontinuitate de primul fel, dezvoltarea sa prin seria Fourier este formată din termeni infiniti. Când semnalul este reconstruit, dacă această serie este trunchiată, depășirile valorii funcției reconstituite sunt obținute în jurul punctului de discontinuitate: pe măsură ce numărul componentelor seriei crește, valoarea de vârf a depășirii menționate rămâne constantă, în timp ce oscilațiile la care se referă aceste depășiri abordează punctul de discontinuitate.

Introducere

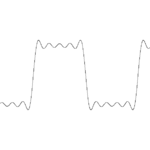
Unda pătrată aproximativă la termenul 5 din seria Fourier

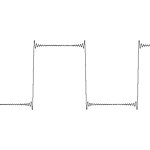
Unda pătrată aproximativă la termenul 25 din seria Fourier

Unda pătrată aproximativă la termenul 125 din seria Fourier

Cele trei figuri din dreapta descriu fenomenul pentru o undă pătrată , care sa extins în funcție de Fourier:

\sin(x)+{\frac {1}{3}}\sin(3x)+{\frac {1}{5}}\sin(5x)+\dots

{\ displaystyle \ sin (x) + {\ frac {1} {3}} \ sin (3x) + {\ frac {1} {5}} \ sin (5x) + \ dots}

\ sin (x) + {\ frac {1} {3}} \ sin (3x) + {\ frac {1} {5}} \ sin (5x) + \ dots

Mai exact aceasta este o funcție $f$ ${\ displaystyle f}$ $f$ care pentru fiecare n întreg își asumă valoarea $\pi /4$ ${\ displaystyle \ pi / 4}$ $\ pi / 4$ între $2n\pi$ ${\ displaystyle 2n \ pi}$ $2n \ pi$ Și $(2n+1)\pi$ ${\ displaystyle (2n + 1) \ pi}$ $(2n + 1) \ pi$ și valoarea $-\pi /4$ ${\ displaystyle - \ pi / 4}$ $- \ pi / 4$ între $(2n+1)\pi$ ${\ displaystyle (2n + 1) \ pi}$ $(2n + 1) \ pi$ Și $(2n+2)\pi$ ${\ displaystyle (2n + 2) \ pi}$ $(2n + 2) \ pi$ . Prin urmare, există o discontinuitate ridicată $\pi /2$ ${\ displaystyle \ pi / 2}$ $\ pi / 2$ orice multiplu de $\pi$ ${\ displaystyle \ pi}$ $\ pi$ , iar funcția are punct $2\pi$ ${\ displaystyle 2 \ pi}$ $2 \ pi$

Dacă sunt luați în considerare mai mulți termeni, eroarea de aproximare este redusă în amplitudine, dar converge la o înălțime fixă (care poate fi calculată printr-o formulă). Valoarea depășirii, în comparație cu înălțimea nominală a undei ( $\pi /4$ ${\ displaystyle \ pi / 4}$ $\ pi / 4$ ), este deci de:

{\frac {1}{2}}\int _{0}^{\pi }{\frac {\sin t}{t}}\,dt-{\frac {\pi }{4}}={\frac {\pi }{2}}\cdot 0.089490\dots

{\ displaystyle {\ frac {1} {2}} \ int _ {0} ^ {\ pi} {\ frac {\ sin t} {t}} \, dt - {\ frac {\ pi} {4} } = {\ frac {\ pi} {2}} \ cdot 0.089490 \ dots}

{\ frac {1} {2}} \ int _ {0} ^ {\ pi} {\ frac {\ sin t} {t}} \, dt - {\ frac {\ pi} {4}} = { \ frac {\ pi} {2}} \ cdot 0.089490 \ dots

Mai general, având o funcție periodică diferențiată , cu excepția cazului în care are un punct de discontinuitate în înălțime $la$ ${\ displaystyle a}$ $la$ , seria Fourier trunchiată are o depășire de aprox $a\cdot 0.089490$ ${\ displaystyle a \ cdot 0.089490}$ $a \ cdot 0.089490$ la fiecare capăt. Adică, funcția care derivă din seria Fourier trunchiată are o discontinuitate care este cu 18% mai mare decât funcția inițială.

Cantitatea:

\int _{0}^{\pi }{\frac {\sin t}{t}}\ dt={1.851937052\dots }={\frac {\pi }{2}}+\pi \cdot 0.089490\dots

{\ displaystyle \ int _ {0} ^ {\ pi} {\ frac {\ sin t} {t}} \ dt = {1.851937052 \ dots} = {\ frac {\ pi} {2}} + \ pi \ cdot 0,089490 \ dots}

\ int _ {0} ^ {\ pi} {\ frac {\ sin t} {t}} \ dt = {1.851937052 \ dots} = {\ frac {\ pi} {2}} + \ pi \ cdot 0.089490 \ puncte

este cunoscută sub numele de constanta Wilbraham-Gibbs .

Descriere

Având o funcție $f:{\mathbb {R} }\to {\mathbb {R} }$ ${\ displaystyle f: {\ mathbb {R}} \ to {\ mathbb {R}}}$ ${\ displaystyle f: {\ mathbb {R}} \ to {\ mathbb {R}}}$ continuu pe secțiuni, diferențiat și periodic cu punct $L>0$ ${\ displaystyle L> 0}$ $L> 0$ , să presupunem că la un moment dat $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ funcția este discontinuă și limita $f(x_{0}^{-})$ ${\ displaystyle f (x_ {0} ^ {-})}$ $f (x_ {0} ^ {-})$ pentru $X$ ${\ displaystyle x}$ $X$ care tinde spre $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ din stânga este diferit de limită $f(x_{0}^{+})$ ${\ displaystyle f (x_ {0} ^ {+})}$ $f (x_ {0} ^ {+})$ din dreapta. Mai exact, fie $la$ ${\ displaystyle a}$ $la$ diferența dintre limitele dreapta și stânga:

f(x_{0}^{+})-f(x_{0}^{-})=a\neq 0

{\ displaystyle f (x_ {0} ^ {+}) - f (x_ {0} ^ {-}) = a \ neq 0}

f (x_ {0} ^ {+}) - f (x_ {0} ^ {-}) = a \ neq 0

Pentru orice număr întreg pozitiv $N\geq 1$ ${\ displaystyle N \ geq 1}$ $N \ geq 1$ , este $S_{N}f$ ${\ displaystyle S_ {N} f}$ $S_ {N} f$ seria Fourier a $f$ ${\ displaystyle f}$ $f$ trunchiat la al N-lea termen:

S_{N}f(x):=\sum _{-N\leq n\leq N}{\hat {f}}(n)e^{2\pi inx/L}={\frac {1}{2}}a_{0}+\sum _{n=1}^{N}a_{n}\cos \left({\frac {2\pi nx}{L}}\right)+b_{n}\sin \left({\frac {2\pi nx}{L}}\right)

{\ displaystyle S_ {N} f (x): = \ sum _ {- N \ leq n \ leq N} {\ hat {f}} (n) e ^ {2 \ pi inx / L} = {\ frac {1} {2}} a_ {0} + \ sum _ {n = 1} ^ {N} a_ {n} \ cos \ left ({\ frac {2 \ pi nx} {L}} \ right) + b_ {n} \ sin \ left ({\ frac {2 \ pi nx} {L}} \ right)}

S_ {N} f (x): = \ sum _ {{- N \ leq n \ leq N}} {\ hat f} (n) e ^ {{2 \ pi inx / L}} = {\ frac { 1} {2}} a_ {0} + \ sum _ {{n = 1}} ^ {N} a_ {n} \ cos \ left ({\ frac {2 \ pi nx} {L}} \ right) + b_ {n} \ sin \ left ({\ frac {2 \ pi nx} {L}} \ right)

unde coeficienții Fourier ${\hat {f}}(n)$ ${\ displaystyle {\ hat {f}} (n)}$ ${\ hat f} (n)$ , $a_{n}$ ${\ displaystyle a_ {n}}$ $a_ {n}$ Și $b_{n}$ ${\ displaystyle b_ {n}}$ $b_ {n}$ sunt calculate folosind formulele uzuale:

{\hat {f}}(n):={\frac {1}{L}}\int _{0}^{L}f(x)e^{-2\pi inx/L}\ dx

{\ displaystyle {\ hat {f}} (n): = {\ frac {1} {L}} \ int _ {0} ^ {L} f (x) e ^ {- 2 \ pi inx / L} \ dx}

{\ hat f} (n): = {\ frac {1} {L}} \ int _ {0} ^ {L} f (x) e ^ {{- 2 \ pi inx / L}} \ dx

a_{n}:={\frac {2}{L}}\int _{0}^{L}f(x)\cos \left({\frac {2\pi nx}{L}}\right)\ dx

{\ displaystyle a_ {n}: = {\ frac {2} {L}} \ int _ {0} ^ {L} f (x) \ cos \ left ({\ frac {2 \ pi nx} {L} } \ dreapta) \ dx}

a_ {n}: = {\ frac {2} {L}} \ int _ {0} ^ {L} f (x) \ cos \ left ({\ frac {2 \ pi nx} {L}} \ right ) \ dx

b_{n}:={\frac {2}{L}}\int _{0}^{L}f(x)\sin \left({\frac {2\pi nx}{L}}\right)\ dx

{\ displaystyle b_ {n}: = {\ frac {2} {L}} \ int _ {0} ^ {L} f (x) \ sin \ left ({\ frac {2 \ pi nx} {L} } \ dreapta) \ dx}

b_ {n}: = {\ frac {2} {L}} \ int _ {0} ^ {L} f (x) \ sin \ left ({\ frac {2 \ pi nx} {L}} \ right ) \ dx

Avem asta:

\lim _{N\to \infty }S_{N}f\left(x_{0}+{\frac {L}{2N}}\right)=f(x_{0}^{+})+a\cdot 0.089490\dots

{\ displaystyle \ lim _ {N \ to \ infty} S_ {N} f \ left (x_ {0} + {\ frac {L} {2N}} \ right) = f (x_ {0} ^ {+} ) + a \ cdot 0.089490 \ dots}

\ lim _ {{N \ to \ infty}} S_ {N} f \ left (x_ {0} + {\ frac {L} {2N}} \ right) = f (x_ {0} ^ {+}) + a \ cdot 0.089490 \ dots

Și:

\lim _{N\to \infty }S_{N}f\left(x_{0}-{\frac {L}{2N}}\right)=f(x_{0}^{-})-a\cdot 0.089490\dots

{\ displaystyle \ lim _ {N \ to \ infty} S_ {N} f \ left (x_ {0} - {\ frac {L} {2N}} \ right) = f (x_ {0} ^ {-} ) -a \ cdot 0.089490 \ dots}

\ lim _ {{N \ to \ infty}} S_ {N} f \ left (x_ {0} - {\ frac {L} {2N}} \ right) = f (x_ {0} ^ {-}) -a \ cdot 0.089490 \ dots

dar:

\lim _{N\to \infty }S_{N}f(x_{0})={\frac {f(x_{0}^{-})+f(x_{0}^{+})}{2}}

{\ displaystyle \ lim _ {N \ to \ infty} S_ {N} f (x_ {0}) = {\ frac {f (x_ {0} ^ {-}) + f (x_ {0} ^ {+ })} {2}}}

\ lim _ {{N \ to \ infty}} S_ {N} f (x_ {0}) = {\ frac {f (x_ {0} ^ {-}) + f (x_ {0} ^ {+} )} {2}}

În general, dacă $x_{N}$ ${\ displaystyle x_ {N}}$ $x_ {N}$ este o succesiune de numere reale care converge la $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ pentru $N\to \infty$ ${\ displaystyle N \ to \ infty}$ $N \ to \ infty$ iar dacă saltul $la$ ${\ displaystyle a}$ $la$ este pozitiv, atunci:

\limsup _{N\to \infty }S_{N}f(x_{N})\leq f(x_{0}^{+})+a\cdot 0.089490\dots

{\ displaystyle \ limsup _ {N \ to \ infty} S_ {N} f (x_ {N}) \ leq f (x_ {0} ^ {+}) + a \ cdot 0.089490 \ dots}

\ limsup _ {{N \ to \ infty}} S_ {N} f (x_ {N}) \ leq f (x_ {0} ^ {+}) + a \ cdot 0.089490 \ dots

Și:

\liminf _{N\to \infty }S_{N}f(x_{N})\geq f(x_{0}^{-})-a\cdot 0.089490\dots

{\ displaystyle \ liminf _ {N \ to \ infty} S_ {N} f (x_ {N}) \ geq f (x_ {0} ^ {-}) - a \ cdot 0.089490 \ dots}

\ liminf _ {{N \ to \ infty}} S_ {N} f (x_ {N}) \ geq f (x_ {0} ^ {-}) - a \ cdot 0.089490 \ dots

Dacă în schimb săritura $la$ ${\ displaystyle a}$ $la$ este negativ, trebuie să schimbăm limita superioară cu limita inferioară și să schimbăm semnele inegalității ≤ cu ≥ și invers, adică:

\liminf _{N\to \infty }S_{N}f(x_{N})\geq f(x_{0}^{+})+a\cdot 0.089490\dots

{\ displaystyle \ liminf _ {N \ to \ infty} S_ {N} f (x_ {N}) \ geq f (x_ {0} ^ {+}) + a \ cdot 0.089490 \ dots}

\ liminf _ {{N \ to \ infty}} S_ {N} f (x_ {N}) \ geq f (x_ {0} ^ {+}) + a \ cdot 0.089490 \ dots

Și:

\limsup _{N\to \infty }S_{N}f(x_{N})\leq f(x_{0}^{-})-a\cdot 0.089490\dots

{\ displaystyle \ limsup _ {N \ to \ infty} S_ {N} f (x_ {N}) \ leq f (x_ {0} ^ {-}) - a \ cdot 0.089490 \ dots}

\ limsup _ {{N \ to \ infty}} S_ {N} f (x_ {N}) \ leq f (x_ {0} ^ {-}) - a \ cdot 0.089490 \ dots

Exemplu

În exemplul referitor la fenomenul din unda pătrată, descris mai sus, perioada $L$ ${\ displaystyle L}$ $L$ este egal cu $2\pi$ ${\ displaystyle 2 \ pi}$ $2 \ pi$ , discontinuitatea $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ este în 0 și în salt $la$ ${\ displaystyle a}$ $la$ Este egal cu $\pi /2$ ${\ displaystyle \ pi / 2}$ $\ pi / 2$ . Pentru simplitate, sunt luate în considerare doar cazurile cu N par (dacă N este ciudat, tratamentul este foarte similar). Avem:

S_{N}f(x)=\sin(x)+{\frac {1}{3}}\sin(3x)+\cdots +{\frac {1}{N-1}}\sin((N-1)x)

{\ displaystyle S_ {N} f (x) = \ sin (x) + {\ frac {1} {3}} \ sin (3x) + \ cdots + {\ frac {1} {N-1}} \ sin ((N-1) x)}

S_ {N} f (x) = \ sin (x) + {\ frac {1} {3}} \ sin (3x) + \ cdots + {\ frac {1} {N-1}} \ sin (( N-1) x)

înlocuind $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ primesti:

S_{N}f(0)=0={\frac {-{\frac {\pi }{4}}+{\frac {\pi }{4}}}{2}}={\frac {f(0^{-})+f(0^{+})}{2}}

{\ displaystyle S_ {N} f (0) = 0 = {\ frac {- {\ frac {\ pi} {4}} + {\ frac {\ pi} {4}}} {2}} = {\ frac {f (0 ^ {-}) + f (0 ^ {+})} {2}}}

S_ {N} f (0) = 0 = {\ frac {- {\ frac {\ pi} {4}} + {\ frac {\ pi} {4}}} {2}} = {\ frac {f (0 ^ {-}) + f (0 ^ {+})} {2}}

așa cum s-a văzut mai sus. Acum puteți calcula:

S_{N}f\left({\frac {2\pi }{2N}}\right)=\sin \left({\frac {\pi }{N}}\right)+{\frac {1}{3}}\sin \left({\frac {3\pi }{N}}\right)+\cdots +{\frac {1}{N-1}}\sin \left({\frac {(N-1)\pi }{N}}\right)

{\ displaystyle S_ {N} f \ left ({\ frac {2 \ pi} {2N}} \ right) = \ sin \ left ({\ frac {\ pi} {N}} \ right) + {\ frac {1} {3}} \ sin \ left ({\ frac {3 \ pi} {N}} \ right) + \ cdots + {\ frac {1} {N-1}} \ sin \ left ({\ frac {(N-1) \ pi} {N}} \ right)}

S_ {N} f \ left ({\ frac {2 \ pi} {2N}} \ right) = \ sin \ left ({\ frac {\ pi} {N}} \ right) + {\ frac {1} {3}} \ sin \ left ({\ frac {3 \ pi} {N}} \ right) + \ cdots + {\ frac {1} {N-1}} \ sin \ left ({\ frac {( N-1) \ pi} {N}} \ dreapta)

Dacă definiți funcția sinc $\operatorname {sinc} (x):=\sin(x)/x$ ${\ displaystyle \ operatorname {sinc} (x): = \ sin (x) / x}$ $\ operatorname {sinc} (x): = \ sin (x) / x$ puteți rescrie ecuația anterioară ca:

S_{N}f\left({\frac {2\pi }{2N}}\right)={\frac {1}{2}}\left[{\frac {2\pi }{N}}\operatorname {sinc} \left({\frac {\pi }{N}}\right)+{\frac {2\pi }{N}}\operatorname {sinc} \left({\frac {3\pi }{N}}\right)+\cdots +{\frac {2\pi }{N}}\operatorname {sinc} \left({\frac {(N-1)\pi }{N}}\right)\right]

{\ displaystyle S_ {N} f \ left ({\ frac {2 \ pi} {2N}} \ right) = {\ frac {1} {2}} \ left [{\ frac {2 \ pi} {N }} \ operatorname {sinc} \ left ({\ frac {\ pi} {N}} \ right) + {\ frac {2 \ pi} {N}} \ operatorname {sinc} \ left ({\ frac {3 \ pi} {N}} \ right) + \ cdots + {\ frac {2 \ pi} {N}} \ operatorname {sinc} \ left ({\ frac {(N-1) \ pi} {N}} \ corect corect]}

S_ {N} f \ left ({\ frac {2 \ pi} {2N}} \ right) = {\ frac {1} {2}} \ left [{\ frac {2 \ pi} {N}} \ operatorname {sinc} \ left ({\ frac {\ pi} {N}} \ right) + {\ frac {2 \ pi} {N}} \ operatorname {sinc} \ left ({\ frac {3 \ pi} {N}} \ right) + \ cdots + {\ frac {2 \ pi} {N}} \ operatorname {sinc} \ left ({\ frac {(N-1) \ pi} {N}} \ right) \ dreapta]

Dar expresia din paranteze este o aproximare a integralei $\int _{0}^{\pi }\operatorname {sinc} (t)\ dt$ ${\ displaystyle \ int _ {0} ^ {\ pi} \ operatorname {sinc} (t) \ dt}$ $\ int _ {0} ^ {\ pi} \ operatorname {sinc} (t) \ dt$ . Deoarece funcția sinc este continuă, aproximarea converge la integral cu $N\to \infty$ ${\ displaystyle N \ to \ infty}$ $N \ to \ infty$ . Deci avem:

\lim _{N\to \infty }S_{N}f\left({\frac {2\pi }{2N}}\right)={\frac {1}{2}}\int _{0}^{\pi }\operatorname {sinc} (t)\ dt={\frac {\pi }{4}}+{\frac {\pi }{2}}\cdot 0.089490\dots

{\ displaystyle \ lim _ {N \ to \ infty} S_ {N} f \ left ({\ frac {2 \ pi} {2N}} \ right) = {\ frac {1} {2}} \ int _ {0} ^ {\ pi} \ operatorname {sinc} (t) \ dt = {\ frac {\ pi} {4}} + {\ frac {\ pi} {2}} \ cdot 0.089490 \ dots}

\ lim _ {{N \ to \ infty}} S_ {N} f \ left ({\ frac {2 \ pi} {2N}} \ right) = {\ frac {1} {2}} \ int _ { 0} ^ {\ pi} \ operatorname {sinc} (t) \ dt = {\ frac {\ pi} {4}} + {\ frac {\ pi} {2}} \ cdot 0.089490 \ dots

ceea ce s-a constatat în paragraful anterior. În mod similar, găsim:

\lim _{N\to \infty }S_{N}f\left(-{\frac {2\pi }{2N}}\right)=-{\frac {1}{2}}\int _{0}^{\pi }\operatorname {sinc} (t)\ dt=-{\frac {\pi }{4}}-{\frac {\pi }{2}}\cdot 0.089490\dots

{\ displaystyle \ lim _ {N \ to \ infty} S_ {N} f \ left (- {\ frac {2 \ pi} {2N}} \ right) = - {\ frac {1} {2}} \ int _ {0} ^ {\ pi} \ operatorname {sinc} (t) \ dt = - {\ frac {\ pi} {4}} - {\ frac {\ pi} {2}} \ cdot 0.089490 \ dots }

\ lim _ {{N \ to \ infty}} S_ {N} f \ left (- {\ frac {2 \ pi} {2N}} \ right) = - {\ frac {1} {2}} \ int _ {0} ^ {\ pi} \ operatorname {sinc} (t) \ dt = - {\ frac {\ pi} {4}} - {\ frac {\ pi} {2}} \ cdot 0.089490 \ dots

Bibliografie

( EN ) JW Gibbs, Nature , 59 (1899) pp. 606
( EN ) HS Carslaw, Introducere în teoria seriei și a integralelor lui Fourier , Dover, reeditare (1930)
( EN ) Arfken, G. "Fenomenul Gibbs". §14.5 în Metode matematice pentru fizicieni, ed . A III-a . Orlando, FL: Academic Press, pp. 783-787, 1985.
( EN ) Foster, J. și Richards, FB Fenomenul Gibbs pentru aproximare liniară în bucăți. Amer. Matematica. Lunar 98, 47-49, 1991.

Elemente conexe

Alte proiecte

Wikimedia Commons conține imagini sau alte fișiere despre fenomenul Gibbs

linkuri externe

( EN ) PL Ul'yanov, fenomenul Gibbs , în Enciclopedia Matematicii , Springer și European Mathematical Society, 2002.

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică