Problema lui Monty Hall

După alegerea jucătorului, prezentatorul deschide o ușă (știe unde este mașina) care arată o capră. Orice se află în spatele alegerii inițiale a jucătorului, acesta are o șansă de 66,7% să câștige mașina schimbându-și alegerea, fără a o schimba ar avea 33,3%.

Problema Monty Hall (sau paradoxul lui Monty Hall ) este o faimoasă problemă a teoriei probabilității , legată de jocul cu premii SUA Let's Make a Deal . Își ia numele de la cel al gazdei spectacolului, Maurice Halprin, cunoscut sub pseudonimul de Monty Hall. Problema este cunoscută și sub numele de paradoxul Monty Hall , deoarece soluția poate părea contraintuitivă, dar nu este o adevărată antinomie , deoarece nu generează contradicții logice.

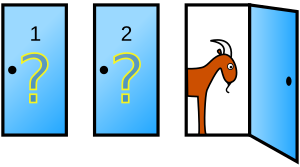
În joc, trei uși închise sunt prezentate concurentului; în spatele uneia este o mașină, în timp ce fiecare dintre celelalte două ascunde o capră . Jucătorul poate alege una dintre cele trei uși, câștigând premiul corespunzător. După ce jucătorul a selectat o ușă, dar nu a deschis-o încă, gazda spectacolului - cine știe ce se află în spatele fiecărei uși - deschide una dintre celelalte două, dezvăluind una dintre cele două capre și îi oferă jucătorului șansa de a-și schimba inițialul. alegere, trecând la singura ușă rămasă; schimbarea ușii îmbunătățește șansele jucătorului de a câștiga mașina, luându-le de la 1/3 la 2/3.

Istoria problemei și soluționarea ei

Problema

O formulare celebră a problemei este conținută într-o scrisoare din 1990 a lui Craig F. Whitaker, adresată coloanei Marilyn vos Savant din săptămâna Parade :

Să presupunem că participați la un joc premiat, în care puteți alege între trei uși: în spatele uneia dintre ele este o mașină, în spatele celorlalte, capre. Alegeți o ușă, să zicem numărul 1, iar gazda jocului premiat, care știe ce se ascunde în spatele fiecărei uși, deschide o altă ușă, să zicem 3, dezvăluind o capră. Așa că te întreabă: „Vrei să alegi numărul 2?” Ar trebui să vă schimbați alegerea inițială?

Cea propusă mai sus este o formulare a problemei dată de Steve Selvin, într-o scrisoare către statisticianul american (februarie 1975 ). Deci, configurat, problema este de fapt o variantă a temei originale a jocului premiat; Monty Hall a deschis de fapt o ușă pe care o capră stătea în spatele ei pentru a adăuga tensiunea, dar nu le-a permis jucătorilor să-și schimbe alegerea inițială. Așa cum Monty Hall însuși i-a scris lui Selvin:

Și dacă ea îmi va juca vreodată jocul, regulile ar fi aceleași pentru ea - fără schimb după alegerea inițială .
- (letsmakeadeal.com)

Marilyn vos Savant a rezolvat problema corect; episodul a provocat o anumită senzație, deoarece mai mulți academicieni nu au recunoscut corectitudinea soluției propuse de Savantul dvs. până când nu a explicat în detaliu într-un articol ulterior.

Scrisoarea ulterioară a lui Selvin către America Statistician (august 1975 ) botează problema ca fiind „problema Monty Hall”.

O problemă esențial identică apare în toate modurile în rubrica Jocuri matematice a lui Martin Gardner (în revista Scientific American ) din 1959 , sub numele de „Problema celor trei prizonieri”. ^[1] ^[2]

Această problemă a fost concepută de matematicianul francez Joseph Louis François Bertrand care a propus-o în cartea sa Calcul des Probabilités ( 1889 ) și a fost cunoscută sub numele de Paradoxul celor trei cutii ale lui Bertrand .

Următorul, în concluzie, este o formulare neechivocă a problemei, cu constrângeri explicite privind comportamentul conductorului, prezentată de Mueser și Granberg:

În spatele fiecăreia dintre cele trei uși se află o mașină sau o capră (două capre, o mașină în total); probabilitatea ca mașina să se afle în spatele unei uși date este identică pentru toate ușile;
Jucătorul alege una dintre uși; conținutul său nu este dezvăluit;
Dirijorul știe ce se ascunde în spatele fiecărei uși;
Manipulatorul trebuie să deschidă una dintre ușile neselectate și trebuie să ofere jucătorului posibilitatea de a-și schimba alegerea;
Manipulatorul va deschide întotdeauna o ușă care ascunde o capră;
- Adică, dacă jucătorul a ales o ușă care ascunde o capră, stăpânul va deschide ușa care ascunde cealaltă capră;
- Dacă, pe de altă parte, jucătorul a ales ușa care ascunde mașina, șoferul alege în mod aleatoriu una dintre cele două uși rămase;
Manipulatorul oferă jucătorului opțiunea de a revendica ceea ce se află în spatele obiectivului ales inițial sau de a schimba, revendicând ceea ce se află în spatele obiectivului rămas.

Șansele jucătorului de a câștiga cresc dacă își schimbă alegerea?

Soluţie

Răspunsul este da ; șansele de a găsi mașina se dublează. ^[3] ^[4]

Soluția poate fi ilustrată după cum urmează. Există trei scenarii posibile, fiecare cu probabilitate 1/3:

Jucătorul alege capra numărul 1. Șoferul alege cealaltă capră, numărul 2. Prin schimbare, jucătorul câștigă mașina.
Jucătorul alege capra numărul 2. Manipulatorul alege cealaltă capră, numărul 1. Prin schimbare, jucătorul câștigă mașina.
Jucătorul alege mașina. Manipulatorul alege o capră, indiferent care. Prin comutare, jucătorul găsește cealaltă capră.

În primele două scenarii, schimbarea jucătorului câștigă mașina; în al treilea scenariu jucătorul care se schimbă nu câștigă. Deoarece strategia „schimbării” duce la victorie în două din trei cazuri, șansele de a câștiga prin adoptarea strategiei sunt 2/3.

O strategie de soluție alternativă este de a considera că, dacă ar trebui să te schimbi, singurul caz în care pierzi este atunci când ai ales inițial mașina și, prin urmare, întrebarea șoferului poate fi considerată o invitație de a inversa șansele de succes cu cele de eșec.

Problema ar fi diferită dacă nu ar exista o alegere inițială sau dacă manipulatorul ar alege o ușă la întâmplare sau dacă manipulatorul ar putea oferi jucătorului să se schimbe în funcție de alegerea inițială a jucătorului. Unele formulări ale problemei și în mod semnificativ cea a Paradei săptămânale nu exclud în mod explicit aceste posibilități; mai multe texte de probabilitate elementare raportează variante ale problemei. De exemplu, dacă șoferul oferă opțiunea de a schimba numai dacă jucătorul a ales inițial mașina, șansele de câștig asociate cu strategia de „schimbare” sunt, desigur, 0%. În formularea propusă în secțiunea anterioară, jucătorul care se schimbă are o probabilitate de a câștiga egală cu 2/3 tocmai pentru că gestionarul trebuie să- i ofere posibilitatea de a se schimba și trebuie să dezvăluie o capră.

Ajutați la înțelegerea problemei

Cea mai comună obiecție la soluție este oferită de ideea că, din diverse motive, trecutul poate fi ignorat atunci când se evaluează probabilitățile. Prin urmare, alegerea primei uși și raționamentul conductorului cu privire la care ușă să se deschidă pot fi neglijate; deoarece puteți alege între două porturi, probabilitatea de a alege unul potrivit ar trebui să fie de 50%, indiferent dacă decideți să schimbați sau să păstrați portul ales.

Pentru a infirma acest lucru ne putem pune o întrebare. Să presupunem că un jucător adoptă strategia de a nu accepta niciodată oferta gazdei, oricare ar fi aceasta. Dacă șansele de a câștiga la început sunt de 33%, are sens să ne gândim că salt automat la 50% doar pentru că gazda a cerut ceva pe care jucătorul nici măcar nu îl ascultă? Evident nu.

Un scenariu care ar justifica estimarea jucătorului de 50% ar fi următorul: să presupunem că caprele și mașina sunt plasate de un operator ascuns nu la începutul jocului, ci după alegerea (aleatorie) a ușii de către conductor cu toate acestea, înainte ca aceasta să fie efectiv deschisă. Operatorul este însărcinat cu simularea jocului, așa că va pune neapărat o capră în spatele ușii pentru a se deschide în timp ce mașina și capra rămasă vor fi plasate aleatoriu în spatele celor două uși rămase. După deschiderea ușii, probabilitatea jucătorului de a câștiga devine efectiv cu 50%.

Deși ignoră lucrările din trecut în anumite jocuri, cum ar fi aruncarea unei monede, nu funcționează neapărat în toate jocurile. Un contraexemplu relevant este oferit de numărarea cărților în anumite jocuri de cărți, care le permite jucătorilor să folosească informații despre evenimentele din trecut în avantajul lor. Acest tip de informații este util în rezolvarea problemei Monty Hall, așa cum este ilustrat în următoarele exemple.

De fapt, este mai ușor (probabil) ca jucătorul să aleagă (prima alegere în trecut) o capră (avea o șansă de două din trei pentru o capră împotriva unei șanse din trei pentru o mașină).

Ceea ce face cu adevărat diferența este cunoașterea viitorului sau cel puțin restricționarea posibilelor evenimente viitoare. În timp ce în aruncarea cu monede șansele de capete sau cozi nu depind de aruncările din trecut, în exemplele de cărți (numărarea cărților) sau problema Monty Hall, posibilele evenimente viitoare sunt „reduse” după un anumit episod. În cazul numărării cărților, ieșirea unei cărți modifică posibilele cărți care mai pot ieși, modificându-le astfel probabilitatea. În cazul problemei Monty Hall, excluderea de către gazdă a unei alegeri cu siguranță „nepotrivite” face ca ușa rămasă să fie mai interesantă decât prima ușă aleasă când nu aveai cunoștințe.

În realitate, eroarea cognitivă de bază constă în luarea în considerare a posibilității de alegere oferită de prezentator concurentului, după ce a descoperit cartea cu capra, ca o joacă DIFERITĂ, de parcă jocul ar fi repornit EX NOVO și, prin urmare, probabilitățile au fost reduse la zero. în ceea ce privește primul joc; în realitate jocul CONTINUĂ, cu aceleași cote; în mod firesc, concurentul, după propunerea prezentatorului, ar trebui să schimbe cardul, deoarece, dacă nu l-ar schimba, nu ar putea profita de informațiile care i-au fost date de prezentator, descoperind cardul cu capra, o carte că concurentul NU are niciun mod de a ști pe care amândoi ÎNAINTE să îl afle prezentatorul; atunci când aceste informații ajung la concurent, acesta din urmă are o singură posibilitate de a profita de ea, adică să SCHIMBĂ cardul ales: în acest fel, în fața jocului, este ca și cum i s-ar oferi posibilitatea de a alege 2 cărți din 3 pentru a încerca să câștige mașina, de unde și probabilitatea de două treimi (66 la sută). Dacă nu ar face schimbarea, ar fi invariabil „blocat” de probabilitatea unei treimi (33 la sută) din jocul său inițial, care a avut loc fatal ÎNAINTE să aibă informații Sigur despre locul în care se afla una dintre cele două capre în joc.

Diagramele Euler-Venn

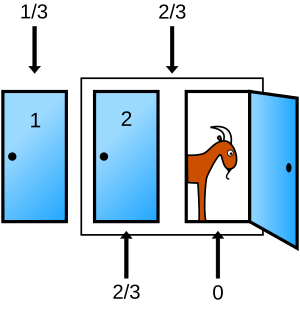
Probabilitatea ca mașina să se afle în spatele ușii rămase poate fi calculată cu ajutorul diagramei Venn prezentată mai jos. După alegerea ușii 1, de exemplu, jucătorul are o probabilitate de 1/3 de a fi selectat ușa cu mașina, care atribuie o probabilitate egală cu 2/3 celor două uși rămase. Rețineți că există o probabilitate de 1 pentru a găsi o capră în spatele cel puțin uneia dintre cele două uși care nu au fost selectate de jucător, deoarece există o singură mașină pentru apucat.

Să presupunem că manipulatorul deschide ușa 3. Deoarece poate deschide doar o ușă care ascunde o capră și nu deschide o ușă la întâmplare, aceste informații nu au niciun efect asupra probabilității ca mașina să se afle în spatele ușii selectate inițial, care rămâne egală cu 1/3. Dar mașina nu se află în spatele ușii 3, astfel încât întreaga probabilitate 2/3 a celor două uși neselectate de către jucător este acum atribuită doar ușii 2, așa cum se arată mai jos. O modalitate alternativă de a ajunge la această concluzie este să observați că, dacă mașina se află în spatele ușii 2 sau în spatele ușii 3, deschiderea ușii 3 implică faptul că mașina se află în spatele ușii 2 și invers.

Observăm că problema nu s-ar schimba dacă conductorul, în loc să deschidă o ușă, ar oferi jucătorului posibilitatea de a schimba ușa aleasă cu ambele celelalte. În acest caz, este evident că probabilitatea este de 2/3.

În schimb, situația s-ar schimba complet dacă prezentatorul, după excluderea ușii 3, a schimbat aleatoriu premiile ascunse în spatele ușilor 1 și 2. În acest caz, jucătorul ar avea o șansă de 1/2 de a câștiga atât dacă păstrează ușa 1, cât și dacă se schimbă aceasta. Fără acest amestec , șansele rămân 1/3 și 2/3.

Teorema lui Bayes

Același subiect în detaliu: teorema lui Bayes .

O analiză a problemei prin teorema lui Bayes explicită efectul ipotezelor de mai sus. Luați în considerare, fără a pierde generalitatea analizei, cazul în care ușa 3 a fost deschisă de către conducătorul care arată o capră și că concurentul a selectat ușa 1.

Probabilitatea ca mașina să fie în spatele ușii 2 (adică probabilitatea de a găsi mașina după schimbarea alegerii inițiale) este $\ 1-$ ${\ displaystyle \ 1-}$ $\ 1-$ $\ P(A1|C3)$ ${\ displaystyle \ P (A1 | C3)}$ $\ P (A1 | C3)$ unde A1 este evenimentul în care mașina se află în spatele ușii 1 și C3 este evenimentul în care șoferul selectează o capră în spatele ușii 3. Probabilitatea ( a priori , folosind jargonul Bayesian ) ca mașina să fie în spatele ușii 1, care este notată cu $\ P(A1)$ ${\ displaystyle \ P (A1)}$ $\ P (A1)$ , este în mod clar 1/3, deoarece mașina are a priori aceeași probabilitate de a fi în spatele fiecărei uși. Probabilitatea ca manipulantul să deschidă ușa 3 cu o capră în spatele ei, $\ P(C3)$ ${\ displaystyle \ P (C3)}$ $\ P (C3)$ , este la fel de clar 1/2 (din punctul de vedere al concurentului), deoarece șoferul trebuie să aleagă una dintre cele două uși care nu au fost alese de concurent. Probabilitatea ca manipulantul să selecteze o ușă cu capra în spatele ei, presupunând că mașina se află în spatele ușii 1, $\ P(C3|A1)$ ${\ displaystyle \ P (C3 | A1)}$ $\ P (C3 | A1)$ , este 1/2, deoarece dacă mașina se află în spatele ușii 1, aleasă inițial, șoferul poate alege să deschidă una dintre celelalte două uși 2 sau 3: din punctul de vedere al concurentului, șoferul are, prin urmare, două uși dintre care să aleagă, adică probabilitatea 1/2 pentru fiecare.

Prin urmare, folosind teorema lui Bayes:

Probabilitatea de a găsi mașina schimbând alegerea inițială, după ce conducătorul (atotștiutor) a arătat o ușă cu capra în spate este:

\ P(A2|C3)=1-

{\ displaystyle \ P (A2 | C3) = 1-}

\ P (A2 | C3) = 1-

\ P(A1|C3)=1-{\frac {P(C3|A1)P(A1)}{P(C3)}}=1-{\frac {{\frac {1}{2}}\times {\frac {1}{3}}}{\frac {1}{2}}}={\frac {2}{3}}

{\ displaystyle \ P (A1 | C3) = 1 - {\ frac {P (C3 | A1) P (A1)} {P (C3)}} = 1 - {\ frac {{\ frac {1} {2 }} \ times {\ frac {1} {3}}} {\ frac {1} {2}}} = {\ frac {2} {3}}}

\ P (A1 | C3) = 1 - {\ frac {P (C3 | A1) P (A1)} {P (C3)}} = 1 - {\ frac {{\ frac {1} {2}} \ ori {\ frac {1} {3}}} {\ frac {1} {2}}} = {\ frac {2} {3}}

Sau, având în vedere asta $\ P(C3|A2)=1$ ${\ displaystyle \ P (C3 | A2) = 1}$ $\ P (C3 | A2) = 1$ având în vedere că dirijorul trebuie să deschidă singura ușă nealeasă de concurent cu o capră în spate, este posibil să se calculeze direct:

\ P(A2|C3)=

{\ displaystyle \ P (A2 | C3) =}

\ P (A2 | C3) =

{\frac {P(C3|A2)P(A2)}{P(C3)}}={\frac {1\times {\frac {1}{3}}}{\frac {1}{2}}}={\frac {2}{3}}

{\ displaystyle {\ frac {P (C3 | A2) P (A2)} {P (C3)}} = {\ frac {1 \ times {\ frac {1} {3}}} {\ frac {1} {2}}} = {\ frac {2} {3}}}

{\ frac {P (C3 | A2) P (A2)} {P (C3)}} = {\ frac {1 \ times {\ frac {1} {3}}} {\ frac {1} {2} }} = {\ frac {2} {3}}

Teorema probabilității totale

Acum arătăm că, schimbând întotdeauna ultima alegere, probabilitatea de a câștiga mașina este $\ {\frac {2}{3}}$ ${\ displaystyle \ {\ frac {2} {3}}}$ $\ {\ frac {2} {3}}$ prin intermediul teoremei probabilității totale. Amintiți-vă că strategia noastră este să alegem mental două uși, să indicăm cealaltă ușă conductorului și apoi să ne schimbăm. Indicăm cu $\ V$ ${\ displaystyle \ V}$ $\ V$ evenimentul „victoria urmând această strategie”. Este $\ A$ ${\ displaystyle \ A}$ $\ LA$ evenimentul „sub cele două uși alese mental este mașina” e $\ B$ ${\ displaystyle \ B}$ $\ B$ evenimentul complementar. Clar $\ P(A)={\frac {2}{3}}$ ${\ displaystyle \ P (A) = {\ frac {2} {3}}}$ $\ P (A) = {\ frac {2} {3}}$ . De asemenea, rețineți că $\ P(V|A)=1$ ${\ displaystyle \ P (V | A) = 1}$ $\ P (V | A) = 1$ deoarece, datorită strategiei alese, dacă mașina se află în spatele celor două uși alese mental, șoferul ne va arăta apoi pe cel câștigător deschizând ușa care pierde. Prin teorema probabilității totale pe care o avem atunci

$\ P(V)=P(V|A)P(A)+P(V|B)P(B)=1\times {\frac {2}{3}}+0\times {\frac {1}{3}}={\frac {2}{3}}$ ${\ displaystyle \ P (V) = P (V | A) P (A) + P (V | B) P (B) = 1 \ times {\ frac {2} {3}} + 0 \ times {\ frac {1} {3}} = {\ frac {2} {3}}}$ $\ P (V) = P (V | A) P (A) + P (V | B) P (B) = 1 \ times {\ frac {2} {3}} + 0 \ times {\ frac {1 } {3}} = {\ frac {2} {3}}$

Variante

Conducătorul nu știe ce se află în spatele ușilor

După alegerea concurentului, manipulatorul deschide una dintre cele două uși rămase. Din moment ce nu știe ce se află în spatele ei, cu probabilitatea 1/3 găsește mașina și jocul s-a terminat. Cu probabilitatea 2/3 găsește capra și poate întreba concurentul dacă vrea să se schimbe cu ușa închisă. În acest caz, acceptarea tranzacției nu crește probabilitatea concurentului de a câștiga, care în acest moment este 1/2, indiferent de decizia sa. ^[5]

Doi jucători

Cu câteva minute înainte de sfârșitul jocului, dirijorul alege doi concurenți pentru a propune „marele pariu”. În spatele uneia dintre cele trei uși se află cel mai mare premiu. Fiecare jucător are voie să aleagă un gol (nu același).

În acest scenariu, o variantă a problemei poate fi investigată. Prezentatorul îl ucide pe jucătorul care a ales o ușă cu capra în spate (dacă amândoi au, una este aleasă la întâmplare), deschide ușa, dezvăluind capra și apoi oferă jucătorului rămas opțiunea de a-și schimba alegerea. Ar trebui jucătorul să facă schimbul?

Răspunsul este nu . Motivul: jucătorul care tranzacționează acest tip de joc ar câștiga dacă și numai dacă ambii jucători ar alege o ușă cu capra. care este probabilitatea ca această apariție? 1/3. Dacă ar păstra alegerea, ar mai exista o probabilitate de 2/3. Deci, cine păstrează alegerea făcută inițial, ar avea o șansă dublă de a câștiga.

Alternativ, există trei scenarii posibile, toate cu probabilitate egală (1/3):

Jucătorul 1 alege ușa care ascunde mașina. Manipulatorul trebuie să elimine jucătorul 2. Schimbarea alegerii implică pierderea.
Jucătorul 2 alege ușa care ascunde mașina. Manipulatorul trebuie să elimine jucătorul 1. Schimbarea alegerii implică pierderea.
Niciun jucător nu alege ușa care ascunde mașina. Handlerul elimină în mod aleatoriu unul dintre cei doi jucători. Schimbarea alegerii înseamnă câștig.

Jucătorul 1 este singurul rămas în primul caz și cu probabilitatea 1/2 în al treilea caz; în acest caz, schimbarea alegerii implică o probabilitate de a pierde (1/3) de două ori mai mare decât cea de a câștiga (1/6). În mod similar, în al doilea caz, jucătorul 2 este singurul rămas și este cu probabilitate 1/2 în al treilea caz; în acest caz, schimbarea alegerii implică o probabilitate de a pierde (1/3) de două ori mai mare decât cea de a câștiga (1/6). Deci , indiferent ce stă jucător, există o șansă de a câștiga 2/3 , dacă nu schimbi alegerea ta. Pentru a face mai evidentă diferența față de cazul precedent, se poate spune că aici nu putem argumenta ca înainte unde (singurul) jucător ajunge întotdeauna la runda a doua (cea a schimbului posibil) și probabilitatea că a selectat alegerea câștigătoare rămâne 1/3, față de 2/3 complementare ale alegerii alternative. În schimb, trebuie remarcat faptul că atunci când un jucător (unul dintre cei doi) ajunge la runda a doua trebuie să ia în considerare că probabilitatea ca inițial să facă alegerea corectă se schimbă și se ridică la 2/3. Practic, jucătorul rămas joacă în acest caz, din punct de vedere al probabilității, același rol care anterior (cazul unui jucător) acoperea ușa care nu era selectată de jucător și nici eliminată de dirijor.

n uși

Există o generalizare a problemei inițiale în care există n uși: în prima etapă a jocului, jucătorul alege o ușă. Apoi manipulatorul deschide o altă ușă, care ascunde o capră. Dacă jucătorul dorește, el își poate schimba alegerea și poate trece la o altă ușă. Manipulatorul va deschide apoi o altă ușă, care încă nu este deschisă, care ascunde o capră, diferită de cea aleasă în prezent de jucător. Jucătorul are apoi opțiunea de a-și schimba din nou alegerea și așa mai departe. Acest proces continuă până când rămân doar două uși nedeschise: alegerea actuală a jucătorului și o altă ușă. De câte ori ar trebui ca jucătorul să își schimbe alegerea și în ce moment al jocului (presupunând că se schimbă cel puțin o dată)?

Cea mai bună strategie este: rămâneți cu prima alegere până când mai sunt doar două uși și apoi comutați . Urmând această strategie, probabilitatea de a câștiga este $(n-1)/n$ ${\ displaystyle (n-1) / n}$ $(n-1) / n$ . Această variantă a paradoxului Monty Hall se datorează lui Bapeswara Rao și Rao.

Varianta în jocul podului

O variantă obișnuită a problemei a fost cunoscută jucătorilor de legătură , încă cu mult înainte de publicarea articolului Vos Savant. Această variantă este cunoscută sub numele de principiul alegerii restrânse . ^[6]

Versiunea cuantică

Există o versiune cuantică a paradoxului, care ilustrează unele aspecte ale relației dintre teoria informației clasice (non-cuantice) și „ informațiile cuantice , adică informațiile codificate în stările sistemelor mecanice cuantice. Cele trei uși sunt înlocuite de un sistem cuantic care constă din trei alternative, în care deschiderea unei uși și vizualizarea a ceea ce ascunde se traduce prin efectuarea unei măsurători speciale. Regulile jocului pot fi exprimate în acest limbaj și încă o dată jucătorul poate alege să rămână fidel alegerii inițiale sau să schimbe și să opteze pentru o alegere alternativă („ortogonală”). Această din urmă strategie are șansele de a câștiga dublu, la fel ca în cazul clasic. Cu toate acestea, dacă poziția premiului nu este pe deplin aleatorie în sens cuantic, jucătorul se poate descurca și mai bine și, în anumite cazuri, poate câștiga cu o cotă de unul. Un articol despre acest subiect este disponibil online, precum și un applet care ilustrează efectele descrise mai sus.

Explicație de la caz la caz

Deoarece nu există multe cazuri posibile în acest joc, vă puteți gândi să le schematizați după cum urmează, grupându-le în funcție de alegerea portului inițial:

Aleg portul A

1. G GC → (M deschide 2) → G XC → schimbare-pierdere, schimbare-câștigare

2. G CG → (M deschide 3) → G CX → schimbare-pierdere, schimbare-câștigare

3. C GG → (M se deschide al doilea sau al treilea) → C XG sau C GX → schimbare-câștig, schimbare-pierdere

Aleg portul B

1. G G C → (M deschide 1) → X G C → schimbare-pierdere, schimbare-câștigare

2. G C G → (M deschide 1 sau 3) → X C G sau G C X → schimbare-câștig, schimbare-pierdere

3. C G G → (M deschide 3) → C G X → schimbare-pierdere, schimbare-câștigare

Aleg portul C

1. GG C → (M deschide 1 sau 2) → XG C o GX C → schimb-câștig, schimb-pierd

2. GC G → (M deschide 1) → XC G → schimbare-pierdere, schimbare-câștigare

3. CG G → (M deschide 2) → CX G → schimbare-pierdere, schimbare-câștigare

Aranjamentele enumerate de la unu la trei sunt configurațiile în care cele două capre (G = Capră) și mașina (C = Mașină) din spatele fiecărei uși (A, B sau C) pot fi găsite la începutul jocului. Evident, acestea nu se schimbă atunci când se schimbă prima alegere a concurentului și îi sunt complet necunoscute. După această alegere inițială, manipulatorul (M = Monty) deschide una dintre cele două uși care ascund caprele, astfel încât să rămână două uși închise, adică cea aleasă inițial și ultima care se deschide: de exemplu, în cazul alegerii ușa A și în prezența dispoziției 1, vom avea cazul inițial G GC (în care boldul indică ușa aleasă), unde Monty va fi obligat să dezvăluie capra din spatele ușii B, adică prin indicarea cu X a ușă deschisă nu mai este în joc, vom găsi în cazul G XC. În acest caz, dacă concurentul rămâne la alegerea sa inițială (restul), el pierde.

După cum se poate vedea, numără doar cazurile câștigătoare legate de fiecare mod de joc, adică orice ușă pe care o alege inițial și luând în considerare cele trei aranjamente posibile, există două din trei în favoarea concurentului care corespund schimbării alegerii inițiale.

În divertisment

Această problemă este menționată, completată cu două dovezi (intuitive și matematice), în cartea lui Mark Haddon The Strange Case of the Dog Killed at Midnight , unde tânărul protagonist propune cititorilor întrebarea. ^[7]
O altă mențiune a problemei apare în emisiunea Numb3rs . ^[8]
În cel de-al optulea episod al celui de-al patrulea sezon al emisiunii TV Brooklyn Nine-Nine , căpitanul Ray Holt pune problema, care este rezolvată strălucit de detectivul Amy Santiago.
În filmul 21 , profesorul Mickey Rosa ( Kevin Spacey ) propune problema protagonistului filmului, studentul Ben Campbell ( Jim Sturgess ), care o rezolvă cu brio.
Scriitoarea Scarlett Thomas citează, de asemenea, această problemă în cartea sa PopCo , numind-o Dilema Monty Hall. ^[9]
În cartea „Iepurii lui Schrödinger” de Colin Bruce, este ilustrată problema lui Monty Hall. ^[10]
Problema este folosită ca element narativ în „Honey” a lui Ian McEwan. Protagonista romanului trebuie să explice problema (care prin natura sa este contraintuitivă) partenerului ei care dorește să o folosească într-o poveste.
În cartea „Fizica diavolului” a lui Jim Al-Khalili .
În jocul video „Zero time Dilemma”, jucătorul se confruntă cu o alegere care se referă la această problemă.
În carte Vrei să pariezi? de Gianfranco Preverino, problema este descrisă ca o modalitate de a câștiga un pariu.

Notă

^ Gardner, Martin (octombrie 1959a). „Jocuri matematice”. Scientific American: 180–182. Retipărit în A doua carte științifică americană de puzzle-uri și diversiuni matematice
^ Gardner, Martin (noiembrie 1959b). „Jocuri matematice”. Scientific American: 188.
^(EN) Grinstead, Charles M. și Snell, J. Laurie, Grinstead and Snell's Introduction to Probability (PDF), 4 iulie 2006, pp. 136-139. Adus pe 4 iulie 2012 .
^(EN) David Morin, Probabilitate , p. 49
^ (EN) Jeffrey S. Rosenthal, "Monty Hall, Monty Fall, Monty Crawl" (PDF), în Math Horizons, 2005a, pp. Numărul din septembrie, 5-7. Accesat la 12 iulie 2012 .
^ Alegerea îngustă
^ Mark Haddon, The Strange Case of the Dog Killed at Midnight , Einaudi (2003), pp. 77-80.
^ Numb3rs - Episodul 1.13, Manhunt
^ Scarlett Thomas, PopCo Newton Compton Publishers (2007)
^ p.75,76,77 Colin Bruce, Iepurii lui Schrödinger , Raffaello Cortina Editore (2006)

Bibliografie

( EN ) Bapeswara Rao, VV și Rao, M. Bhaskara (1992). Un joc cu trei uși și câteva dintre variantele sale. The Mathematical Scientist 17 (2), 89-94
( EN ) Bohl, Alan H.; Eliberator, Matthew J.; și Nydick, Robert L. (1995). O poveste despre două capre ... și o mașină sau importanța presupunerilor în soluțiile pentru probleme. Journal of Recreational Mathematics 1995, 1-9.
Joseph Bertrand (1889). Calcul des probabilités
(EN) Gardner, Martin (1959). Coloana „ Jocuri matematice ”, Scientific American , octombrie 1959, 180–182.
( EN ) Mueser, Peter R. și Granberg, Donald (1999). The Monty Hall Dilemma Revisited: Understanding the Interaction of Problem Definition and Making Making (Universitatea din Missouri Document de lucru 99-06). http://econwpa.wustl.edu:80/eps/exp/papers/9906/9906001.html Arhivat 10 decembrie 2004 la Internet Archive . (ultima accesare: 5 iulie 2005).
( EN ) Nahin, Paul J. (2000). Idiști dueliști și alți enigmi de probabilitate . Princeton University Press, Princeton, NJ, 192-193. ISBN 0-691-00979-1
( EN ) Selvin, Steve (1975a). O problemă de probabilitate (scrisoare către editor). American Statistician 29 (1): 67 (februarie 1975).
( EN ) Selvin, Steve (1975b). Despre problema Monty Hall (scrisoare către editor). American Statistician 29 (3): 134 (august 1975).
(EN) Tierney, John (1991). În spatele ușilor lui Monty Hall: puzzle, dezbatere și răspuns?, The New York Times 21 iulie 1991, duminică, secțiunea 1; Partea 1; Pagina 1; Coloana 5
vos Savant, Marilyn (1990). Coloana Ask Marilyn , Parade Magazine 12 (17 februarie 1990). [citat în Bohl și colab., 1995]
( EN ) Adams, Cecil (1990). În „Hai să facem o ofertă”, alegeți ușa nr. 1. Monty deschide ușa # 2 - fără premiu. Rămâi cu ușa # 1 sau treci la # 3?, The Straight Dope 2 noiembrie 1990. http://www.straightdope.com/classics/a3_189.html (accesat la 25 iulie 2005).
(EN) Tijms, Henk (2004). Înțelegerea probabilității, regulile șanselor în viața de zi cu zi . Cambridge University Press, New York, 213-215.
Haddon, Mark (2003). Ciudatul caz al câinelui ucis la miezul nopții Einaudi.
Rosenthal, Jeffrey S. (2006). Regulile cauzei, instrucțiuni de utilizare , Longanesi, Milano, ISBN 88-304-2370-X
(EN) Rosenhouse, Jason (2009). The Monty Hall Problem , Oxford University Press ISBN 978-0-19-536789-8

Elemente conexe

Paradoxul cu trei cărți

Alte proiecte

Wikimedia Commons conține imagini sau alte fișiere despre problema Monty Hall

linkuri externe

Simulare până la 100.000 de încercări , pe users.quipo.it .
Simulator de paradox redat , la math.ucsd.edu .

Portale Matematica : accedi alle voci di Wikipedia che trattano di matematica

[1] Gardner, Martin (octombrie 1959a). „Jocuri matematice”. Scientific American: 180–182. Retipărit în A doua carte științifică americană de puzzle-uri și diversiuni matematice

[2] Gardner, Martin (noiembrie 1959b). „Jocuri matematice”. Scientific American: 188.

[3] (EN) Grinstead, Charles M. și Snell, J. Laurie, Grinstead and Snell's Introduction to Probability (PDF), 4 iulie 2006, pp. 136-139. Adus pe 4 iulie 2012 .

[4] (EN) David Morin, Probabilitate , p. 49

[5] (EN) Jeffrey S. Rosenthal, "Monty Hall, Monty Fall, Monty Crawl" (PDF), în Math Horizons, 2005a, pp. Numărul din septembrie, 5-7. Accesat la 12 iulie 2012 .

[6] Alegerea îngustă

[7] Mark Haddon, The Strange Case of the Dog Killed at Midnight , Einaudi (2003), pp. 77-80.

[8] Numb3rs - Episodul 1.13, Manhunt

[9] Scarlett Thomas, PopCo Newton Compton Publishers (2007)

[10] .75,76,77 Colin Bruce, Iepurii lui Schrödinger , Raffaello Cortina Editore (2006)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]