Teorema lui Bayes

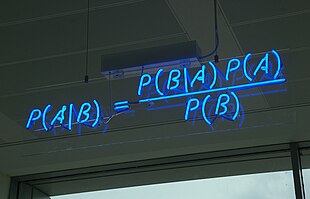
Formula teoremei lui Bayes reprodusă într-un semn cu tub fluorescent în birourile din Cambridge ale Autonomy Corporation

Teorema lui Bayes (cunoscută și ca formula lui Bayes sau teorema probabilității cauzelor ), propusă de Thomas Bayes (1702-1761), derivă din două teoreme fundamentale ale probabilității : teorema probabilității compuse și teorema probabilității absolute . Este folosit pentru a calcula probabilitatea unei cauze care a declanșat evenimentul verificat.

De exemplu, este posibil să se calculeze probabilitatea ca o anumită persoană să sufere de boala pentru care a efectuat testul de diagnostic (dacă acesta este negativ) sau invers nu este afectată de această boală (dacă testul este pozitiv), cunoscând frecvența cu care apare boala și procentul de eficacitate al testului de diagnostic. În mod formal, teorema lui Bayes este valabilă în toate interpretările probabilității. În orice caz, importanța acestei teoreme pentru statistici este de așa natură încât împărțirea dintre cele două școli ( statistici bayesiene și statistici frecventiste ) rezultă din interpretarea dată teoremei în sine.

Enunțarea teoremei lui Bayes

Luând în considerare un set de alternative $A_{1},\ldots ,A_{n}$ ${\ displaystyle A_ {1}, \ ldots, A_ {n}}$ $A_ {1}, \ ldots, A_ {n}$ care partiționează spațiul evenimentului $\Omega$ ${\ displaystyle \ Omega}$ $\Omega$ (sau $\ A_{i}\cap A_{j}=\varnothing \ \forall i\neq j$ ${\ displaystyle \ A_ {i} \ cap A_ {j} = \ varnothing \ \ forall i \ neq j}$ $\ A_ {i} \ cap A_ {j} = \ varnothing \ \ forall i \ neq j$ Și $\cup _{i=1}^{n}A_{i}=\Omega$ ${\ displaystyle \ cup _ {i = 1} ^ {n} A_ {i} = \ Omega}$ $\ cup _ {{i = 1}} ^ {n} A_ {i} = \ Omega$ ) găsim următoarea expresie pentru probabilitatea condițională :

P(A_{i}|E)={\frac {P(E|A_{i})P(A_{i})}{P(E)}}={\frac {P(E|A_{i})P(A_{i})}{\sum _{j=1}^{n}P(E|A_{j})P(A_{j})}}

{\ displaystyle P (A_ {i} | E) = {\ frac {P (E | A_ {i}) P (A_ {i})} {P (E)}} = {\ frac {P (E | A_ {i}) P (A_ {i})} {\ sum _ {j = 1} ^ {n} P (E | A_ {j}) P (A_ {j})}}}

P (A_ {i} | E) = {\ frac {P (E | A_ {i}) P (A_ {i})} {P (E)}} = {\ frac {P (E | A_ {i }) P (A_ {i})} {\ sum _ {{j = 1}} ^ {n} P (E | A_ {j}) P (A_ {j})}}

Unde este:

P (A) este probabilitatea a priori sau marginală a lui A. „A priori” înseamnă că nu ia în considerare nicio informație despre E.
P (A | E) este probabilitatea condițională a lui A, cunoscută E. Se mai numește probabilitate a posteriori, deoarece este derivată sau depinde de valoarea specifică a lui E.
P (E | A) este probabilitatea condițională a lui E, cunoscută A.
P (E) este probabilitatea a priori a lui E și servește drept constantă de normalizare .

Intuitiv, teorema descrie modul în care opiniile din observarea A sunt îmbogățite prin observarea evenimentului E.

Un exemplu

Luați în considerare o școală care are 60% bărbați și 40% femei.
Elevii poartă un număr egal de fuste sau pantaloni; elevii poartă toți pantaloni. Un observator, de la distanță, observă un student generic în pantaloni. Care este probabilitatea ca elevul respectiv să fie fată?

Problema poate fi rezolvată cu teorema lui Bayes, prin stabilirea evenimentului A că elevul observat este de sex feminin și al evenimentului B că studentul observat poartă pantaloni. Pentru a calcula P (A | B), va trebui să știm:

P (A) sau probabilitatea ca elevul să fie femeie fără alte informații. Deoarece observatorul vede un elev aleatoriu , aceasta înseamnă că toți elevii au șanse egale de a fi observați. Deoarece studentele reprezintă 40% din total, probabilitatea va fi de 2/5.
P (A ') sau probabilitatea ca elevul să fie bărbat fără alte informații. Deoarece A 'este evenimentul complementar al lui A, rezultă 3/5.
P (B | A) sau probabilitatea ca o studentă să poarte pantaloni (adică probabilitatea ca, odată cu evenimentul în care elevul este femeie, să se întâmple evenimentul în care ea poartă pantalonii). Deoarece poartă fuste și pantaloni în număr egal, probabilitatea va fi 1/2.
P (B | A '), sau probabilitatea ca un student să poarte pantaloni, observ că studentul este bărbat. Toți studenții de sex masculin poartă pantaloni, deci merită 1.
P (B) sau probabilitatea ca orice student (bărbat sau femeie) să poarte pantalonii. Deoarece numărul celor care poartă pantaloni este de 80 (60 bărbați + 20 femei) din 100 de bărbați și femei, probabilitatea P (B) este 80/100 = 4/5.

Acestea fiind spuse, putem aplica teorema:

P(A|B)={\frac {P(B|A)P(A)}{P(B)}}={\frac {{\frac {1}{2}}\times {\frac {2}{5}}}{\frac {4}{5}}}={\frac {1}{4}}.

{\ displaystyle P (A | B) = {\ frac {P (B | A) P (A)} {P (B)}} = {\ frac {{\ frac {1} {2}} \ times { \ frac {2} {5}}} {\ frac {4} {5}}} = {\ frac {1} {4}}.}

P (A | B) = {\ frac {P (B | A) P (A)} {P (B)}} = {\ frac {{\ frac {1} {2}} \ times {\ frac { 2} {5}}} {{\ frac {4} {5}}}} = {\ frac {1} {4}}.

Prin urmare, există 1/4 de probabilitate ca elevul să fie femeie, adică 25%. ^[1]

Derivarea teoremei

Teorema lui Bayes. Ω este spațiul măsurilor: A, nu A, B, nu B. Graficul evidențiază toate posibilitățile condiționate.

Teorema derivă din definiția probabilității condiționate . Probabilitatea unui eveniment A , odată cunoscut un eveniment B , este:

P(A|B)={\frac {P(A\cap B)}{P(B)}}

{\ displaystyle P (A | B) = {\ frac {P (A \ cap B)} {P (B)}}}

P (A | B) = {\ frac {P (A \ cap B)} {P (B)}}

În mod similar, probabilitatea evenimentului B observă evenimentul A :

P(B|A)={\frac {P(A\cap B)}{P(A)}}

{\ displaystyle P (B | A) = {\ frac {P (A \ cap B)} {P (A)}}}

P (B | A) = {\ frac {P (A \ cap B)} {P (A)}}

Prin urmare:

P(A\cap B)=P(B|A)\,P(A)

{\ displaystyle P (A \ cap B) = P (B | A) \, P (A)}

P (A \ cap B) = P (B | A) \, P (A)

Înlocuind în prima egalitate, găsim teorema lui Bayes:

P(A|B)={\frac {P(A\cap B)}{P(B)}}={\frac {P(B|A)\,P(A)}{P(B)}}.

{\ displaystyle P (A | B) = {\ frac {P (A \ cap B)} {P (B)}} = {\ frac {P (B | A) \, P (A)} {P ( B)}}.}

P (A | B) = {\ frac {P (A \ cap B)} {P (B)}} = {\ frac {P (B | A) \, P (A)} {P (B)} }.

Aplicații

Aplicarea la problema Monty Hall

Același subiect în detaliu: problema Monty Hall .

Să presupunem că participați la un joc premiat, în care puteți alege între trei uși: în spatele uneia dintre ele este o mașină, în spatele celorlalte, două capre. Se alege o ușă, să zicem numărul 1, iar dirijorul jocului premiat, care știe ce se ascunde în spatele fiecărei uși, deschide o altă ușă, să zicem 3, dezvăluind o capră. Apoi întreabă: „Ați vrea să alegeți numărul 2?” Ar trebui să vă schimbați alegerea inițială?

S-ar putea crede că, cu două uși închise, există o probabilitate de 50:50 pentru fiecare și, prin urmare, nu există niciun motiv pentru a schimba ușile. Nu este cazul. Numim evenimentul că mașina se află în spatele unei anumite uși A ₁ , A ₂ și _respectiv A ₃ .

La început, este evident că:

$P(A_{1})=P(A_{2})=P(A_{3})={\frac {1}{3}}$ ${\ displaystyle P (A_ {1}) = P (A_ {2}) = P (A_ {3}) = {\ frac {1} {3}}}$ $P (A_ {1}) = P (A_ {2}) = P (A_ {3}) = {\ frac 13}$

Așa cum am menționat anterior, ușa aleasă este numărul 1. Numim evenimentul „prezentatorul deschide ușa 3” B. Acum:

În cazul în care mașina se află în spatele ușii 1, prezentatorul va fi liber să aleagă în mod aleatoriu ușa 2 sau 3. Prin urmare, $P(B|A_{1})=1/2$ ${\ displaystyle P (B | A_ {1}) = 1/2}$ $P (B | A_ {1}) = 1/2$
În cazul în care mașina se află în spatele ușii 2, prezentatorul va fi obligat să deschidă ușa 3. Prin urmare $P(B|A_{2})=1$ ${\ displaystyle P (B | A_ {2}) = 1}$ $P (B | A_ {2}) = 1$
În cazul în care mașina se află în spatele ușii 3, prezentatorul va fi obligat să deschidă ușa 2. Prin urmare $P(B|A_{3})=0$ ${\ displaystyle P (B | A_ {3}) = 0}$ $P (B | A_ {3}) = 0$

Probabilitatea a priori pentru evenimentul B este de 50%, de fapt:

P(B)=\sum _{i=1}^{3}P(B|A_{i})P(A_{i})={\frac {1}{2}}\cdot {\frac {1}{3}}+1\cdot {\frac {1}{3}}+0\cdot {\frac {1}{3}}={\frac {1}{2}}

{\ displaystyle P (B) = \ sum _ {i = 1} ^ {3} P (B | A_ {i}) P (A_ {i}) = {\ frac {1} {2}} \ cdot { \ frac {1} {3}} + 1 \ cdot {\ frac {1} {3}} + 0 \ cdot {\ frac {1} {3}} = {\ frac {1} {2}}}

{\ displaystyle P (B) = \ sum _ {i = 1} ^ {3} P (B | A_ {i}) P (A_ {i}) = {\ frac {1} {2}} \ cdot { \ frac {1} {3}} + 1 \ cdot {\ frac {1} {3}} + 0 \ cdot {\ frac {1} {3}} = {\ frac {1} {2}}}

De la care:

{\begin{aligned}P(A_{1}|B)&={\frac {P(B|A_{1})P(A_{1})}{P(B)}}={\frac {{\frac {1}{2}}\cdot {\frac {1}{3}}}{\frac {1}{2}}}={\frac {1}{3}}\\P(A_{2}|B)&={\frac {P(B|A_{2})P(A_{2})}{P(B)}}={\frac {1\cdot {\frac {1}{3}}}{\frac {1}{2}}}={\frac {2}{3}}\\P(A_{3}|B)&={\frac {P(B|A_{3})P(A_{3})}{P(B)}}={\frac {0\cdot {\frac {1}{3}}}{\frac {1}{2}}}=0.\end{aligned}}

{\ displaystyle {\ begin {align} P (A_ {1} | B) & = {\ frac {P (B | A_ {1}) P (A_ {1})} {P (B)}} = { \ frac {{\ frac {1} {2}} \ cdot {\ frac {1} {3}}} {\ frac {1} {2}}} = {\ frac {1} {3}} \\ P (A_ {2} | B) & = {\ frac {P (B | A_ {2}) P (A_ {2})} {P (B)}} = {\ frac {1 \ cdot {\ frac {1} {3}}} {\ frac {1} {2}}} = {\ frac {2} {3}} \\ P (A_ {3} | B) & = {\ frac {P (B | A_ {3}) P (A_ {3})} {P (B)}} = {\ frac {0 \ cdot {\ frac {1} {3}}} {\ frac {1} {2}} } = 0. \ End {align}}}

{\ begin {align} P (A_ {1} | B) & = {\ frac {P (B | A_ {1}) P (A_ {1})} {P (B)}} = {\ frac { {\ frac 12} \ cdot {\ frac 13}} {{\ frac 12}}} = {\ frac 13} \\ P (A_ {2} | B) & = {\ frac {P (B | A_ { 2}) P (A_ {2})} {P (B)}} = {\ frac {1 \ cdot {\ frac 13}} {{\ frac 12}}} = {\ frac 23} \\ P ( A_ {3} | B) & = {\ frac {P (B | A_ {3}) P (A_ {3})} {P (B)}} = {\ frac {0 \ cdot {\ frac 13} } {{\ frac 12}}} = 0. \ end {align}}

Din aceasta este evident că trebuie să se schimbe întotdeauna cu portul 2.

Filtre bayesiene

Același subiect în detaliu: filtru bayesian .

Filtrele bayesiene sunt un instrument utilizat pentru combaterea spamului care își datorează funcționarea teoremei lui Bayes. Un filtru Bayesian folosește un clasificator Bayesian pentru a recunoaște dacă o anumită secvență de simboluri (cum ar fi un cuvânt) apare adesea în mesajele spam, apoi aplică inferența Bayesiană pentru a calcula probabilitatea ca un anumit mesaj să fie spam.

fundal

Teorema este numită în onoarea Reverendului Thomas Bayes (1702–1761), care a studiat cum se calculează o distribuție pentru parametrul unei distribuții binomiale . Un prieten de-al său, Richard Price, a publicat lucrarea în 1763 , după moartea lui Bayes, în articolul Essay Towards Solving a Problem in the Doctrine of Chances . Câțiva ani mai târziu (în 1774 ) a fost formulat de Pierre Simon Laplace, care probabil nu știa de munca lui Bayes.

Cercetările unui profesor de statistică (Stigler, 1982) par să sugereze că teorema lui Bayes a fost descoperită de Nicholas Saunderson cu ani înainte de Bayes.

Notă

^ Verificarea acurateței rezultatului, în acest exemplu simplu, este imediată dacă folosim definiția simplă a „probabilității unui eveniment” = „numărul de cazuri în favoarea evenimentului / numărul de cazuri posibile”. Numărul de cazuri posibile, purtând pantalonii studenți (sau studenți) observați, este de 80 (60 bărbați + 20 femei), în timp ce cel al cazurilor favorabile (adică femeile care poartă pantaloni) este de 20, deci probabilitatea ca aceasta să fie o femeie este de 20 / 80 adică 1/4 cvd

Bibliografie

Versiuni non-ficțiune

Thomas Bayes (1763), Un eseu către rezolvarea unei probleme din Doctrina șanselor. Până la sfârșitul reverendului dl Bayes, FRS a comunicat de dl Price, într-o scrisoare către John Canton, AMFRS , Philosophical Transactions , Dating some of the Present Entreprisesments , Studies and Labour of the Ingenious in Many Considerable Parts of the World, 53: 370-418.
Thomas Bayes (1763/1958), Studii de istorie a probabilității și statistici: IX. Eseul lui Thomas Bayes Către rezolvarea unei probleme în Doctrina șanselor , Biometrika 45: 296-315. ( Eseul lui Bayes în notație modernizată ).

Comentarii

GA Barnard , Studii în istoria probabilității și statisticii: IX. Eseul lui Thomas Bayes Către rezolvarea unei probleme în Doctrina șanselor , Biometrika 45: 293–295, 1958
Daniel Covarrubias, Un eseu către rezolvarea unei probleme în Doctrina șanselor
Stephen M. Stigler, Thomas Bayes 'Bayesian Inference , Journal of the Royal Statistical Society , Seria A, 145: 250–258, 1982
Isaac Todhunter , O istorie a teoriei matematice a probabilității de pe vremea lui Pascal până la cea a lui Laplace , Macmillan, 1865. Reeditat 1949, 1956 de Chelsea și 2001 de Thoemmes.