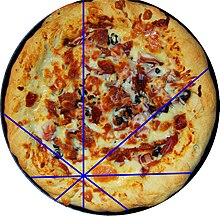
Teorema pizza

Exemplu de aplicare a teoremei pentru n = 8: prin tăierea pizza de-a lungul liniilor albastre și, luând alternativ câte o felie, procedând în sensul acelor de ceasornic sau în sens invers acelor de ceasornic, doi mese consumă aceeași cantitate de pizza.

Teorema pizza este o teoremă de geometrie elementară care dovedește egalitatea a două zone obținute prin partiționarea adecvată a unui cerc . Numele teoremei derivă din faptul că construcția imită felul în care este tăiată pizza .

Fie p un punct din interiorul discului și n un multiplu întreg de patru și mai mare sau egal cu opt. Discul este partiționat în n sectoare echiangulare, construite trasând o linie dreaptă prin p și rotind-o n / 2 - 1 ori în jurul valorii de p cu un unghi egal cu 2π / n . Dacă sunt numerotate progresiv în sensul acelor de ceasornic sau în sens invers acelor de ceasornic, atunci suma ariilor sectoarelor asociate cu un număr par este egală cu suma ariilor sectoarelor asociate cu un număr impar. ^[1]

Ca o consecință imediată, dacă două persoane taie o pizza în 4 m + 4 sectoare echiangulare (cu orice alt m natural decât zero), centrate în orice punct și alternează luând câte o felie fiecare, rulând pizza în sensul acelor de ceasornic sau în sens invers acelor de ceasornic. mâncați aceeași cantitate. ^[2]

Istorie

Dovadă fără cuvinte din 1994a , Carter & Wagon (1994a) pentru problema celor opt sectoare. Blocurile cu numerele corespunzătoare sunt congruente între ele.

Problema din care apare teorema a fost propusă de LJ Upton în mai 1968, publicată în revista Mathematical Magazine ^[1] și s-a limitat la luarea în considerare a opt sectoare cu unghiuri de 45 °. Textul original era:

( RO ) „Patru linii într-un plan sunt concurente la O. Unghiurile dintre linii sunt fiecare de 45 °. Un cerc este suprapus peste această configurație astfel încât O să se afle în cerc. (a) Arătați că sectoarele alternative acoperă jumătate din cerc. (b) Arătați acest rezultat fără a utiliza calculul. "	( IT ) «Patru linii drepte pe un plan trec toate prin același punct O. Unghiurile dintre linii sunt toate de 45 °. Un cerc este suprapus peste această configurație, astfel încât O să cadă în interiorul cercului. (a) Dovediți că sectoarele alternative acoperă jumătate din aria cercului. (b) Dovediți rezultatul fără a utiliza calcul infinitesimal. "
( Upton 1968, p. 46 )

Soluția publicată în jurnal, prezentată de Michael Goldberg ( Washington, DC ), ^[3] se bazează pe manipularea algebrică a expresiilor care exprimă zonele sectoarelor circulare. Pe lângă faptul că răspunde la întrebarea problemei (adică arată că subdiviziunea în opt sectoare este corectă), Goldberg subliniază că soluția este generalizată la cazul în care discul este împărțit, în mod similar, în 4 n + 4 sectoare echiangulare, permițându-l să îl împărțim în mod egal în n seturi de sectoare de echestezie ^[4] (formularea generală a teoremei anunțate anterior este o consecință imediată a acestui rezultat). ^[1]

O dovadă mai elegantă fără cuvinte pentru problema celor opt sectoare a fost dezvoltată de Larry Carter și Stan Wagon, arătând că pentru fiecare împărțire făcută conform ipotezelor teoremei există o partiție adecvată a sectoarelor, astfel încât fiecare bloc conținut într-un nivel egal sectorul este congruent cu un bloc corespunzător conținut într-un sector impar. ^[5] Greg Frederickson a formulat o familie de dovezi de acest tip care acoperă toate cazurile posibile ale teoremei în formularea generală. ^[6]

Generalizări

Condiția conform căreia numărul de sectoare este multiplu de patru și mai mare de patru este necesară: se arată cu ușurință că, dacă numărul de sectoare este egal cu patru, teorema nu este adevărată în general. Cu o dovadă elegantă care exploatează transcendența lui π , Don Coppersmith arată invaliditatea teoremei dacă numărul de sectoare nu este divizibil cu patru, fără a explica totuși care dintre cele două seturi este mai extins. ^[7] Rick Mabry și Paul Deiermann au rezolvat această problemă corelată, postată în revista Mathematical Magazine , ^[8] elaborând o versiune mai precisă a teoremei, care indică care dintre cele două domenii este mai mare decât cealaltă în cazul în care egalitatea nu există: ^[9]

dacă numărul de sectoare este congruent la 2 (mod 8) și nici o tăietură nu trece prin centrul discului, atunci setul de felii între care este prezentă cea care conține centrul are o zonă mai mică decât cealaltă;
dacă numărul de sectoare este congruent la 6 (mod 8) și nici o tăietură nu trece prin centrul discului, atunci setul de felii între care este prezentă cea care conține centrul are o suprafață mai mare decât cealaltă;
dacă o tăietură trece prin centru, construcția este simetrică și cele două seturi de felii au aceeași zonă indiferent de numărul de sectoare. ^[10]

În aceeași publicație observă, de asemenea, că, dacă crusta este definită ca perimetrul discului sau ca o coroană circulară între perimetru și o a doua circumferință concentrică cu o rază mai mică, atunci când pizza este împărțită în părți egale, la fel este și crusta . De fapt, deoarece zonele discurilor majore și minore sunt împărțite în mod egal între cele două seturi de felii, diferența lor, care este tocmai crusta, va fi împărțită în mod egal. Dacă, pe de altă parte, pizza este împărțită în diferite părți, oricine primește mai multă pizza primește și mai puțină crustă. ^[11]

Exemplu cu n = 12: zona verde este egală cu zona portocalie. Mai mult, conform hirschhorn , Hirschhorn et al. (1999) , alegând în mod corespunzător sectoarele, este posibil să împărțim discul în trei seturi de echestezie.

Dacă pizza este împărțită în părți egale, la fel sunt și toppingurile, dacă sunt distribuite pe un disc (nu neapărat concentric cu pizza) care conține punctul p în care este centrată divizarea sectoarelor. Mai mult, dacă un disc este împărțit în mod egal în funcție de condițiile teoremei (într-un număr n de sectoare echiangulare cu n multiplu de patru și mai mare sau egal cu opt) atunci sectoarele pot fi grupate și în n / 4 seturi de echestezie. De exemplu, o pizza tăiată în douăsprezece felii care respectă ipotezele teoremei poate fi împărțită în mod egal între trei mese, una împărțită în douăzeci de felii între cinci. ^[12]

Rezultate conexe

Din punctul de vedere al teoriei jocurilor , este posibil să se studieze strategia de alegere a feliilor pentru a obține cea mai mare cantitate de pizza. În acest scop, într-o versiune a problemei, pizza este tăiată radial (fără ipoteza sectoarelor echiangulare) și doi comensari iau câte o felie fiecare, atâta timp cât este adiacentă unei felii deja luate. Dacă cei doi mese aleg feliile pentru a încerca amândoi să maximizeze cantitatea de pizza luată, oricine ia prima felie poate asigura 4/9 din pizza și există o diviziune a acesteia astfel încât să nu poată lua mai mult. O problemă mai generală este aceea a partajării corecte (sau „tăierea tortului”), care are în vedere jocuri similare în care mai mulți jucători pot avea diverse reguli pentru măsurarea porțiilor luate (de exemplu, un restaurant poate prefera să maximizeze cantitatea de ardei, în timp ce altul poate încerca să ia cât mai multă brânză). ^[13] ^[14]

Alte rezultate matematice legate de tăierea pizza implică succesiunea numerelor poligonale centrale , care numără numărul de bucăți obținute prin tăierea pizza de-a lungul liniilor care nu trec toate prin același punct (pentru aplicațiile sale la tăierea alimentelor, se spune și această secvență al organizatorului leneș de banchet ). ^[15] Teorema Stone-Tukey (cunoscută sub numele de teorema sandvișului de șuncă) arată că pentru orice n obiecte dintr-un spațiu n-dimensional există un hiperplan adecvat (n -1) -dimensional care le împarte în două simultan: ^[16] aplicația sa în cazul bidimensional arată că există întotdeauna o linie dreaptă care împarte două pizza în două părți egale sau că există o tăietură dreaptă care împarte atât o pizza cât și crusta ei în părți egale.

Demonstrație

Schema demonstrativă.

Următoarea dovadă o urmează pe cea formulată de Goldberg și publicată ca soluție în revista Mathematical . ^[1] Să $P.$ ${\ displaystyle P}$ $P.$ centrul cercului de rază $r$ ${\ displaystyle r}$ $r$ și sunt $LA C.$ ${\ displaystyle AC}$ $B.C$ Și $B. D.$ ${\ displaystyle BD}$ $BD$ două șiruri perpendiculare una pe cealaltă trecând ambele printr-un punct $SAU$ ${\ displaystyle O}$ $SAU$ în interiorul cercului. Este $la$ ${\ displaystyle a}$ $la$ distanța dintre $P.$ ${\ displaystyle P}$ $P.$ Și $SAU$ ${\ displaystyle O}$ $SAU$ Și $\vartheta$ ${\ displaystyle \ vartheta}$ $\ vartheta$ unghiul dintre $B. D.$ ${\ displaystyle BD}$ $BD$ Și $SAU P.$ ${\ displaystyle OP}$ $OP$ . Se demonstrează algebric că suma lungimilor pătrate de $LA SAU$ ${\ displaystyle AO}$ $AO$ , $B. SAU$ ${\ displaystyle BO}$ $BO$ , $C. SAU$ ${\ displaystyle CO}$ $CO$ Și $D. SAU$ ${\ displaystyle DO}$ $DO$ nu depinde de alegerea $LA$ ${\ displaystyle A}$ $LA$ Și $\vartheta$ ${\ displaystyle \ vartheta}$ $\ vartheta$ . Din trigonometrie elementară avem:

{\begin{aligned}{\frac {AC}{2}}&={\sqrt {r^{2}-a^{2}\cos ^{2}{\vartheta }}}\\AO&={\sqrt {r^{2}-a^{2}\cos ^{2}{\vartheta }}}-a\sin {\vartheta }\\AO^{2}&=r^{2}-a^{2}\cos ^{2}{\vartheta }+a^{2}\sin ^{2}{\vartheta }-2a\sin {\vartheta }{\sqrt {r^{2}-a^{2}\cos ^{2}{\vartheta }}}.\end{aligned}}

{\ displaystyle {\ begin {align} {\ frac {AC} {2}} & = {\ sqrt {r ^ {2} -a ^ {2} \ cos ^ {2} {\ vartheta}}} \\ AO & = {\ sqrt {r ^ {2} -a ^ {2} \ cos ^ {2} {\ vartheta}}} - a \ sin {\ vartheta} \\ AO ^ {2} & = r ^ { 2} -a ^ {2} \ cos ^ {2} {\ vartheta} + a ^ {2} \ sin ^ {2} {\ vartheta} -2a \ sin {\ vartheta} {\ sqrt {r ^ {2 } -a ^ {2} \ cos ^ {2} {\ vartheta}}}. \ end {align}}}

{\ begin {align} {\ frac {AC} {2}} & = {\ sqrt {r ^ {2} -a ^ {2} \ cos ^ {2} {\ vartheta}}} \\ AO & = {\ sqrt {r ^ {2} -a ^ {2} \ cos ^ {2} {\ vartheta}}} - a \ sin {\ vartheta} \\ AO ^ {2} & = r ^ {2} - a ^ {2} \ cos ^ {2} {\ vartheta} + a ^ {2} \ sin ^ {2} {\ vartheta} -2a \ sin {\ vartheta} {\ sqrt {r ^ {2} -a ^ {2} \ cos ^ {2} {\ vartheta}}}. \ End {align}}

În mod similar:

{\begin{aligned}CO&={\sqrt {r^{2}-a^{2}\cos ^{2}{\vartheta }}}+a\sin {\vartheta }\\CO^{2}&=r^{2}-a^{2}\cos ^{2}{\vartheta }+a^{2}\sin ^{2}{\vartheta }+2a\sin {\vartheta }{\sqrt {r^{2}-a^{2}\cos ^{2}{\vartheta }}}.\end{aligned}}

{\ displaystyle {\ begin {align} CO & = {\ sqrt {r ^ {2} -a ^ {2} \ cos ^ {2} {\ vartheta}}} + a \ sin {\ vartheta} \\ CO ^ {2} & = r ^ {2} -a ^ {2} \ cos ^ {2} {\ vartheta} + a ^ {2} \ sin ^ {2} {\ vartheta} + 2a \ sin {\ vartheta } {\ sqrt {r ^ {2} -a ^ {2} \ cos ^ {2} {\ vartheta}}}. \ end {align}}}

{\ begin {align} CO & = {\ sqrt {r ^ {2} -a ^ {2} \ cos ^ {2} {\ vartheta}}} + a \ sin {\ vartheta} \\ CO ^ {2 } & = r ^ {2} -a ^ {2} \ cos ^ {2} {\ vartheta} + a ^ {2} \ sin ^ {2} {\ vartheta} + 2a \ sin {\ vartheta} {\ sqrt {r ^ {2} -a ^ {2} \ cos ^ {2} {\ vartheta}}}. \ end {align}}

Procedând în mod similar pentru frânghie $B. D.$ ${\ displaystyle BD}$ $BD$ și adunând avem:

{\begin{aligned}AO^{2}&+CO^{2}=2(r^{2}-a^{2}(\cos ^{2}{\vartheta }-\sin ^{2}{\vartheta }))\\BO^{2}&+DO^{2}=2(r^{2}+a^{2}(\cos ^{2}{\vartheta }-\sin ^{2}{\vartheta }))\\AO^{2}&+BO^{2}+CO^{2}+DO^{2}=4r^{2}.\end{aligned}}

{\ displaystyle {\ begin {align} AO ^ {2} & + CO ^ {2} = 2 (r ^ {2} -a ^ {2} (\ cos ^ {2} {\ vartheta} - \ sin ^ {2} {\ vartheta})) \\ BO ^ {2} & + DO ^ {2} = 2 (r ^ {2} + a ^ {2} (\ cos ^ {2} {\ vartheta} - \ sin ^ {2} {\ vartheta})) \\ AO ^ {2} & + BO ^ {2} + CO ^ {2} + DO ^ {2} = 4r ^ {2}. \ end {align}} }

{\ begin {align} AO ^ {2} & + CO ^ {2} = 2 (r ^ {2} -a ^ {2} (\ cos ^ {2} {\ vartheta} - \ sin ^ {2} {\ vartheta})) \\ BO ^ {2} & + DO ^ {2} = 2 (r ^ {2} + a ^ {2} (\ cos ^ {2} {\ vartheta} - \ sin ^ { 2} {\ vartheta})) \\ AO ^ {2} & + BO ^ {2} + CO ^ {2} + DO ^ {2} = 4r ^ {2}. \ End {align}}

Deci suma nu depinde de $\vartheta$ ${\ displaystyle \ vartheta}$ $\ vartheta$ . Zona $\mathrm {d} S$ ${\ displaystyle \ mathrm {d} S}$ ${\ mathrm {d}} S$ măturat de cele patru segmente pentru o rotație $\mathrm {d} \varphi$ ${\ displaystyle \ mathrm {d} \ varphi}$ ${\ mathrm {d}} \ varphi$ în jurul $SAU$ ${\ displaystyle O}$ $SAU$ va fi deci:

\mathrm {d} S={\frac {1}{2}}(AO^{2}+BO^{2}+CO^{2}+DO^{2})\mathrm {d} \varphi

{\ displaystyle \ mathrm {d} S = {\ frac {1} {2}} (AO ^ {2} + BO ^ {2} + CO ^ {2} + DO ^ {2}) \ mathrm {d} \ varphi}

{\ mathrm {d}} S = {\ frac {1} {2}} (AO ^ {2} + BO ^ {2} + CO ^ {2} + DO ^ {2}) {\ mathrm {d} } \ varphi

și întrucât suma pătratelor nu depinde de $\varphi$ ${\ displaystyle \ varphi}$ $\ varphi$ avem:

S={\frac {4r^{2}\varphi }{2}}.

{\ displaystyle S = {\ frac {4r ^ {2} \ varphi} {2}}.}

S = {\ frac {4r ^ {2} \ varphi} {2}}.

Prin plasare $\varphi ={\frac {\pi }{4}}$ ${\ displaystyle \ varphi = {\ frac {\ pi} {4}}}$ $\ varphi = {\ frac {\ pi} {4}}$ această zonă este echivalentă cu suma ariilor celor patru sectoare pare (sau impare) considerate în întrebare și este egală cu ${\frac {\pi r^{2}}{2}}$ ${\ displaystyle {\ frac {\ pi r ^ {2}} {2}}}$ ${\ frac {\ pi r ^ {2}} {2}}$ , adică jumătate din aria cercului, deci va fi egală cu aria rămasă, care este egală cu suma ariilor celorlalte patru sectoare.

Dovada este generalizată începând cu $2n$ ${\ displaystyle 2n}$ $2n$ frânghii echidistante și întorcându-le prin plasare $\varphi ={\frac {\pi }{2n}}$ ${\ displaystyle \ varphi = {\ frac {\ pi} {2n}}}$ $\ varphi = {\ frac {\ pi} {2n}}$ . În acest fel, pentru fiecare $p=1,...,n$ ${\ displaystyle p = 1, ..., n}$ $p = 1, ..., n$ suma ariilor din sectoarele aflate în poziție $\{p,p+n,p+2n,...\}$ ${\ displaystyle \ {p, p + n, p + 2n, ... \}}$ $\ {p, p + n, p + 2n, ... \}$ echivalentă cu ${\frac {\pi r^{2}}{n}}$ ${\ displaystyle {\ frac {\ pi r ^ {2}} {n}}}$ ${\ frac {\ pi r ^ {2}} {n}}$ iar discul este împărțit în $n$ ${\ displaystyle n}$ $n$ părti egale.

Notă

^ ^a ^b ^c ^d Upton 1968 , p. 46 .
^ Maurizio Codogno, The pizza teorema , pe ilpost.it , Il Post , 11 septembrie 2013. Accesat 30 octombrie 2013 .
^ Pe lângă soluția publicată, problema fusese rezolvată independent de Robert X. Brennan și Huseyin Demir ( Upton 1968 , p. 46 ).
^ Dacă sectoarele sunt numerotate progresiv de-a lungul pizza în sensul acelor de ceasornic sau în sens invers acelor de ceasornic, setul p este format din sectoarele într-o poziție congruentă cu p = 1, ..., n (mod n ).
^ Carter & Wagon 1994a , p. 267 .
^ Frederickson 2012 , pp. 26-33 .
^ Mabry & Deiermann 2009 , p. 424 .
^ Carter și Wagon 1994b , p. 304 .
^ Rețineți că congruențele cu numere impare nu sunt luate în considerare, deoarece cu tipul de construcție utilizat numărul de felii este întotdeauna par. Mai mult, congruențele la 4 (mod 8) și la 8≡0 (mod 8) se încadrează în formularea inițială a teoremei.
^ Mabry & Deiermann 2009 , p. 423 .
^ Mabry & Deiermann 2009 , p. 434 .
^ Hirschhorn și colab. 1999 , pp. 120-121 .
^ Cibulka și colab. 2010 , pp. 63-93 .
^ Knauer și colab. 2011 , pp. 1635-1645 .
^ Numere poligonale centrale , pe oeis.org , OEIS . Adus la 30 octombrie 2013 .
^ George Beck, Eric W. Weisstein,Ham Sandwich Theorem. , la mathworld.wolfram.com , MathWorld. Adus la 30 octombrie 2013 .

Bibliografie

Larry Carter, Stan Wagon, Dovadă fără cuvinte: Alocarea corectă a unei pizza , în revista Mathematics , vol. 67, nr. 4, 1994a, p. 267.
Larry Carter, Stan Wagon, Problema 1457 , în revista Mathematics , vol. 67, nr. 4, 1994b, p. 304.
Josef Cibulka, Jan Kynčl, Viola Mészáros, Rudolf Stolař, Pavel Valtr, Solution of Peter Winkler's pizza problem , în Fete of Combinatorics and Computer Science , Bolyai Society Mathematical Studies , vol. 20, Societatea matematică János Bolyai și Springer-Verlag, 2010, pp. 63 –93, DOI : 10.1007 / 978-3-642-13580-4_4 , arXiv : 0812.4322 .
Greg Frederickson, Dovada este în pizza , în revista Mathematics , vol. 85, nr. 1, 2012, pp. 26-33, DOI : 10.4169 / math.mag.85.1.26 .
J. Hirschhorn, MD Hirschhorn, JK Hirschhorn, AD Hirschhorn, PM Hirschhorn, The pizza teorema ( PDF ), în Australian Mathematical Society Gazette , vol. 26, 1999, pp. 120–121.
Kolja Knauer, Piotr Micek, Torsten Ueckerdt, How to eat 4/9 of a pizza , în Discrete Mathematics , vol. 311, n. 16, 2011, pp. 1635–1645, DOI : 10.1016 / j.disc.2011.03.015 , arXiv : 0812.2870 .
Rick Mabry, Paul Deiermann, Of Cheese and Crust: A Doved of the Pizza Conjecture and Other Tasty Results , în American Mathematical Monthly , vol. 116, nr. 5, 2009, pp. 423-438.
Stephen Ornes, Modul perfect de a felia o pizza , în NewScientist , 11 decembrie 2009.
LJ Upton, Problema 660 , în revista Mathematics , vol. 41, nr. 1, 1968, p. 46, JSTOR 2687962 . Soluția lui Michael Goldberg.

Alte proiecte

Wikimedia Commons conține imagini sau alte fișiere pe teorema pizza

linkuri externe

( EN ) Eric W. Weisstein, Pizza Theorem , în MathWorld , Wolfram Research.
( EN ) Torsten Sillke, Pizza Theorem , la math.uni-bielefeld.de . Adus la 24 noiembrie 2009 .

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică

[upton-1] Upton 1968 , p. 46 .

[2] Maurizio Codogno, The pizza teorema , pe ilpost.it , Il Post , 11 septembrie 2013. Accesat 30 octombrie 2013 .

[3] Pe lângă soluția publicată, problema fusese rezolvată independent de Robert X. Brennan și Huseyin Demir ( Upton 1968 , p. 46 ).

[4] Dacă sectoarele sunt numerotate progresiv de-a lungul pizza în sensul acelor de ceasornic sau în sens invers acelor de ceasornic, setul p este format din sectoarele într-o poziție congruentă cu p = 1, ..., n (mod n ).

[5] Carter & Wagon 1994a , p. 267 .

[6] Frederickson 2012 , pp. 26-33 .

[7] Mabry & Deiermann 2009 , p. 424 .

[8] Carter și Wagon 1994b , p. 304 .

[9] Rețineți că congruențele cu numere impare nu sunt luate în considerare, deoarece cu tipul de construcție utilizat numărul de felii este întotdeauna par. Mai mult, congruențele la 4 (mod 8) și la 8≡0 (mod 8) se încadrează în formularea inițială a teoremei.

[10] Mabry & Deiermann 2009 , p. 423 .

[11] Mabry & Deiermann 2009 , p. 434 .

[12] Hirschhorn și colab. 1999 , pp. 120-121 .

[13] Cibulka și colab. 2010 , pp. 63-93 .

[14] Knauer și colab. 2011 , pp. 1635-1645 .

[15] Numere poligonale centrale , pe oeis.org , OEIS . Adus la 30 octombrie 2013 .

[16] George Beck, Eric W. Weisstein,Ham Sandwich Theorem. , la mathworld.wolfram.com , MathWorld. Adus la 30 octombrie 2013 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]