Regula 68-95-99.7

Pentru un set de date aproximativ normal , valorile din cadrul unei abateri standard ale mediei reprezintă aproximativ 68% din set; în timp ce în cadrul a două abateri standard, acestea reprezintă aproximativ 95%; iar în cadrul a trei abateri standard, acestea reprezintă aproximativ 99,7%. Procentele prezentate sunt probabilități teoretice rotunjite, destinate numai aproximării datelor empirice derivate dintr-o populație normală.

Interval de predicție (pe axa y ) dat de scorul standard (pe axa x ). Axa

y

{\ displaystyle y}

y

este scalat logaritmic (dar valorile de pe acesta nu sunt modificate).

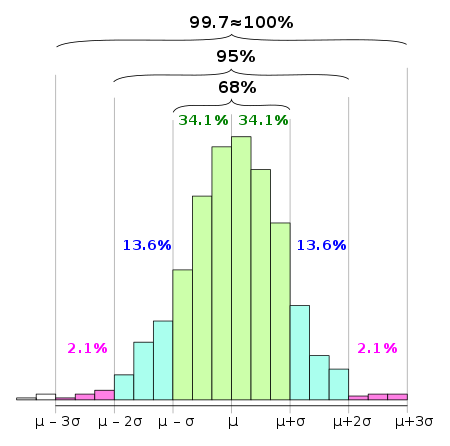
În statistici , regula 68-95-99.7 , cunoscută și sub numele de regula generală , este o abreviere utilizată pentru a aminti procentul de valori care se află într-o bandă în jurul mediei într-o distribuție normală cu o amplitudine de două, patru și, respectiv, șase deviații standard ; mai exact, 68,27%, 95,45% și 99,73% din valori se încadrează în una, două și trei abateri standard ale mediei.

În notația matematică, aceste concepte pot fi exprimate după cum urmează, unde Χ este o observație dintr-o variabilă aleatorie cu distribuție normală, μ este media distribuției și σ este abaterea standard:

{\begin{aligned}\Pr(\mu -1\sigma \leq X\leq \mu +1\sigma )&\approx 0,6827\\\Pr(\mu -2\sigma \leq X\leq \mu +2\sigma )&\approx 0,9545\\\Pr(\mu -3\sigma \leq X\leq \mu +3\sigma )&\approx 0,9973\end{aligned}}

{\ displaystyle {\ begin {align} \ Pr (\ mu -1 \ sigma \ leq X \ leq \ mu +1 \ sigma) & \ approx 0,6827 \\\ Pr (\ mu -2 \ sigma \ leq X \ leq \ mu +2 \ sigma) & \ approx 0.9545 \\\ Pr (\ mu -3 \ sigma \ leq X \ leq \ mu +3 \ sigma) & \ approx 0.9973 \ end {align}}}

{\ displaystyle {\ begin {align} \ Pr (\ mu -1 \ sigma \ leq X \ leq \ mu +1 \ sigma) & \ approx 0,6827 \\\ Pr (\ mu -2 \ sigma \ leq X \ leq \ mu +2 \ sigma) & \ approx 0.9545 \\\ Pr (\ mu -3 \ sigma \ leq X \ leq \ mu +3 \ sigma) & \ approx 0.9973 \ end {align}}}

În științele empirice așa-numita regulă generală de trei sigme exprimă o euristică convențională că aproape toate valorile sunt considerate a fi în cadrul a trei deviații standard ale mediei și, prin urmare, este empiric util să tratăm probabilitatea de 99,7% ca fiind aproape sigură. . ^[1]

Utilitatea acestei euristice depinde mai ales de întrebarea examinată. În științele sociale , un rezultat poate fi considerat semnificativ dacă nivelul său de încredere este de ordinul unui efect de două sigme (95%), în timp ce în fizica particulelor din motive teoretice este necesar un efect de cinci sigme (99,999994%). Nivelul de încredere) pentru a califica o descoperire.

O regulă mai slabă de trei sigme poate fi derivată din inegalitatea lui Chebyshev , afirmând că, chiar și pentru variabilele distribuite în mod normal, cel puțin 88,8% din cazuri ar trebui să se încadreze în intervale de trei sigme calculate corect. Pentru distribuțiile unimodale , probabilitatea de a se afla în interval este de cel puțin 95%, conform inegalității Vysochanskij-Petunin . Pot exista unele ipoteze pentru o distribuție care obligă această probabilitate să fie de cel puțin 98%. ^[2] ^[3]

Funcția de distribuție cumulativă

Diagrama care arată funcția de distribuție cumulativă pentru distribuția normală cu media ( μ ) 0 și varianța ( σ ² ) 1

Aceste valori numerice „68%, 95%, 99,7%” sunt derivate din funcția de distribuție cumulativă a distribuției normale .

Intervalul de predicție pentru orice scor standard $z$ ${\ displaystyle z}$ $z$ corespunde numeric la $(1-(1-\theta \mu ,\sigma ^{2}(z))\cdot 2)$ ${\ displaystyle (1- (1- \ theta \ mu, \ sigma ^ {2} (z)) \ cdot 2)}$ ${\ displaystyle (1- (1- \ theta \ mu, \ sigma ^ {2} (z)) \ cdot 2)}$ .

De exemplu, $\theta (2)\approx 0,9772$ ${\ displaystyle \ theta (2) \ approx 0.9772}$ ${\ displaystyle \ theta (2) \ approx 0.9772}$ sau $\Pr(\chi \leq \mu +2\sigma )\approx 0,9772$ ${\ displaystyle \ Pr (\ chi \ leq \ mu +2 \ sigma) \ approx 0,9772}$ ${\ displaystyle \ Pr (\ chi \ leq \ mu +2 \ sigma) \ approx 0,9772}$ , corespunzător unui interval de predicție de $(1-(1-0,97725)\cdot 2)=0,9545=95,45\%$ ${\ displaystyle (1- (1-0.97725) \ cdot 2) = 0,9545 = 95,45 \%}$ ${\ displaystyle (1- (1-0.97725) \ cdot 2) = 0,9545 = 95,45 \%}$ .

Acesta nu este un interval simetric - este pur și simplu probabilitatea ca o observație să fie mai mică de $\mu +2\sigma$ ${\ displaystyle \ mu +2 \ sigma}$ ${\ displaystyle \ mu +2 \ sigma}$ . Pentru a calcula probabilitatea ca o observație să se încadreze în două abateri standard ale mediei (mici diferențe datorate rotunjirii):

\Pr(\mu -2\sigma \leq X\leq \mu +2\sigma )=\Phi (2)-\Phi (-2)\approx 0,9772-(1-0,9772)\approx 0,9545.

{\ displaystyle \ Pr (\ mu -2 \ sigma \ leq X \ leq \ mu +2 \ sigma) = \ Phi (2) - \ Phi (-2) \ approx 0.9772- (1-0.9772) \ approx 0.9545. }

{\ displaystyle \ Pr (\ mu -2 \ sigma \ leq X \ leq \ mu +2 \ sigma) = \ Phi (2) - \ Phi (-2) \ approx 0.9772- (1-0.9772) \ approx 0.9545. }

Acest lucru este legat de intervalul de încredere utilizat în statistici: ${\bar {X}}\pm 2{\frac {\sigma }{\sqrt {n}}}$ ${\ displaystyle {\ bar {X}} \ pm 2 {\ frac {\ sigma} {\ sqrt {n}}}}$ ${\ displaystyle {\ bar {X}} \ pm 2 {\ frac {\ sigma} {\ sqrt {n}}}}$ este de aproximativ un interval de încredere de 95% în cazul în care ${\bar {X}}$ ${\ displaystyle {\ bar {X}}}$ ${\ displaystyle {\ bar {X}}}$ este media unui eșantion de dimensiuni $n$ ${\ displaystyle n}$ $n$ .

Test de normalitate

„Regula 68-95-99.7” este adesea utilizată pentru a obține rapid o estimare aproximativă a probabilității a ceva, dată fiind abaterea standard, dacă se presupune că populația este normală. De asemenea, este utilizat ca un test simplu pentru valori aberante dacă populația este considerată normală și ca test de normalitate dacă populația este potențial non-normală.

Pentru a trece de la un eșantion la un număr de abateri standard, calculați mai întâi abaterea, eroarea sau rezidualul, în funcție de dacă știți media populației sau doar o estimați. Următorul pas este standardizarea (împărțirea la abaterea standard a populației), dacă parametrii populației sunt cunoscuți, sau studențierea (împărțirea la o estimare a abaterii standard), dacă parametrii sunt necunoscuți și doar estimate.

Pentru a-l folosi ca test pentru valori aberante sau ca test de normalitate, dimensiunea abaterilor în termeni de abateri standard este calculată și comparată cu frecvența așteptată. Având în vedere un set de eșantioane, este posibil să se calculeze reziduurile studențiate și să le compare cu frecvența așteptată: punctele care scad mai mult de 3 abateri standard de la normă sunt probabil valori anormale (cu excepția cazului în care dimensiunea eșantionului este semnificativ extremă) și dacă există multe puncte cu mai mult de 3 abateri standard de la normă, este probabil să existe motive pentru a pune la îndoială presupusa normalitate a distribuției. Acest lucru este valabil mai ales pentru abaterile de 4 sau mai multe abateri standard.

Poate fi calculat mai precis prin aproximarea numărului de deviații extreme ale unei cantități date sau mai mari de la o distribuție Poisson : pur și simplu, dacă aveți mai mult de 4 deviații standard într-un eșantion de mărime 1 000 , există motive întemeiate pentru a lua în considerare aceste valori aberante sau pentru a pune sub semnul întrebării presupusa normalitate a distribuției.

De exemplu, un eveniment 6σ corespunde unei posibilități de aproximativ două părți pe miliard . Aceasta înseamnă că, dacă evenimentele obișnuite s-ar produce zilnic, ar exista un eveniment anormal previzibil la fiecare 1,4 milioane de ani. Din aceasta obținem un test simplu al normalității: dacă se observă un 6σ în datele zilnice și s-au scurs semnificativ mai puțin de 1 milion de ani, este foarte probabil ca amplitudinea sau frecvența abaterilor semnificative față de ceea ce a fost observat să nu poată fi explicată. din modelul considerat pentru o distribuție normală.

În eseul The Black Swan , Nassim Nicholas Taleb oferă exemplul modelelor de risc conform cărora prăbușirea Luni Negre din 1987 ar corespunde unui eveniment de 36 σ : apariția unui astfel de eveniment ar trebui să sugereze imediat că modelul este defect. procesul luat în considerare nu este modelat satisfăcător printr-o distribuție normală. Prin urmare, modelele rafinate ar trebui luate în considerare, de exemplu prin introducerea volatilității stocastice . În aceste studii este important să fim conștienți de problema erorilor jucătorilor , care afirmă că o singură observare a unui eveniment rar nu contrazice faptul că evenimentul este de fapt rar. Valabilitatea modelului presupus este observarea unei pluralități de evenimente presupuse rare. O modelare corectă a acestui proces de pierdere treptată a încrederii într-o ipoteză ar atrage necesitatea de a calcula probabilitatea a priori nu numai a ipotezei în sine, ci și a tuturor ipotezelor alternative posibile. Din acest motiv, testarea ipotezelor statistice funcționează nu atât prin confirmarea unei ipoteze considerate probabile, cât mai degrabă prin respingerea ipotezelor considerate improbabile .

Tabel cu valori numerice

Datorită cozilor exponențiale ale distribuției normale, probabilitățile abaterilor majore scad foarte rapid. Din regulile pentru datele distribuite în mod normal pentru un eveniment zilnic:

Gamă	Fracția estimată a populației în interval			Frecvența aproximativă pe eveniment zilnic
μ ± 0,5σ	0,382 924 922 548 026	Câte 3	5	De patru sau cinci ori pe săptămână
μ ± σ	0,682 689 492 137 086	1 fiecare	3	De două ori pe săptămână
μ ± 1,5σ	0,866 385 597 462 284	1 fiecare	7	săptămânal
μ ± 2σ	0,954 499 736 103 642	1 fiecare	22	La fiecare trei săptămâni
μ ± 2,5σ	0,987 580 669 348 448	1 fiecare	81	Trimestrial
μ ± 3σ	0,997 300 203 936 740	1 fiecare	370	Anual
μ ± 3,5σ	0,999 534 741 841 929	1 fiecare	2149	La fiecare 6 ani
μ ± 4σ	0,999 936 657 516 334	1 fiecare	15 787	La fiecare 43 de ani (de două ori în viață)
μ ± 4,5σ	0,999 993 204 653 751	1 fiecare	147 160	La fiecare 403 de ani (o dată în era modernă)
μ ± 5σ	0,999 999 426 696 856	1 fiecare	1 744 278	Fiecare 4 776 de ani (o dată în istoria înregistrată)
μ ± 5,5σ	0,999 999 962 020 875	1 fiecare	26 330 254	Fiecare 72 090 de ani (de trei ori în istoria umanității moderne)
μ ± 6σ	0,999 999 998 026 825	1 fiecare	506 797 346	La fiecare 1,38 milioane de ani ( de două ori în om istorie)
μ ± 6,5 σ	0,999 999 999 919 680	1 fiecare	12 450 197 393	La fiecare 34 de milioane de ani (de două ori de la dispariția dinozaurilor )
μ ± 7σ	0,999 999 999 997 440	1 fiecare	390 682 215 445	La fiecare 1,07 miliarde de ani (patru apariții în istoria Pământului )
μ ± x σ	$\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)$ ${\ displaystyle \ operatorname {erf} \ left ({\ frac {x} {\ sqrt {2}}} \ right)}$ ${\ displaystyle \ operatorname {erf} \ left ({\ frac {x} {\ sqrt {2}}} \ right)}$	1 fiecare	${\tfrac {1}{1-\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)}}$ ${\ displaystyle {\ tfrac {1} {1- \ operatorname {erf} \ left ({\ frac {x} {\ sqrt {2}}} \ right)}}}$ ${\ displaystyle {\ tfrac {1} {1- \ operatorname {erf} \ left ({\ frac {x} {\ sqrt {2}}} \ right)}}}$	Fiecare ${\tfrac {1}{1-\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)}}$ ${\ displaystyle {\ tfrac {1} {1- \ operatorname {erf} \ left ({\ frac {x} {\ sqrt {2}}} \ right)}}}$ ${\ displaystyle {\ tfrac {1} {1- \ operatorname {erf} \ left ({\ frac {x} {\ sqrt {2}}} \ right)}}}$ zile

Notă

^ Această utilizare a „regulii celor trei sigme” a intrat în uz comun în anii 2000, de exemplu citată în Schaum's Outline of Business Statistics , McGraw Hill Professional, 2003, p. 359.
^ (EN) Donald J. Wheeler și David Smith Chambers, Understanding Statistical Process Control , SPC Press, 1992, ISBN 978-0-945320-13-5 . Adus pe 29 noiembrie 2020 .
^ Friedrich Pukelsheim, The Three Sigma Rule , în The American Statistician , vol. 48, nr. 2, 1994-05, p. 88, DOI : 10.2307 / 2684253 . Adus pe 29 noiembrie 2020 .

Elemente conexe

Alte proiecte

Wikimedia Commons conține imagini sau alte fișiere din regula 68-95-99.7

linkuri externe

Distribuția normală de către Balasubramanian Narasimhan
Calculați proporția procentuală în cadrul x sigma pe WolframAlpha

Portal de statistici : accesați intrările de pe Wikipedia care se ocupă de statistici

[1] Această utilizare a „regulii celor trei sigme” a intrat în uz comun în anii 2000, de exemplu citată în Schaum's Outline of Business Statistics , McGraw Hill Professional, 2003, p. 359.

[2] (EN) Donald J. Wheeler și David Smith Chambers, Understanding Statistical Process Control , SPC Press, 1992, ISBN 978-0-945320-13-5 . Adus pe 29 noiembrie 2020 .

[3] Friedrich Pukelsheim, The Three Sigma Rule , în The American Statistician , vol. 48, nr. 2, 1994-05, p. 88, DOI : 10.2307 / 2684253 . Adus pe 29 noiembrie 2020 .

[1]

[2]

[3]