Problema Lambert

În mecanica cerească , problema Lambert privește determinarea unei orbite pornind de la doi vectori de poziție și timpul de zbor. A fost rezolvat de matematicianul elvețian Johann Heinrich Lambert . Are aplicații importante în domeniul întâlnirilor și manevrelor orbitale .

Să presupunem că un corp, sub influența unei forțe gravitaționale, este observat pe măsură ce se deplasează de la un punct P ₁ la un punct P ₂ , de-a lungul unei traiectorii conice date, într-un timp T. În această ipoteză, teorema lui Lambert afirmă că timpul de zbor depinde de unii parametri geometrici ai problemei. Mai precis, enunțul teoremei este următorul:

„Timpul necesar unui corp pentru a se deplasa între două puncte ale unei traiectorii conice este doar o funcție a sumei distanțelor celor două puncte de la originea forței, a distanței liniare dintre cele două puncte și axa semi-majoră a conicii. "

Exprimată într-un alt mod, problema Lambert poate fi formulată prin impunerea unor condiții limită asupra ecuației diferențiale a problemei cu doi corpuri

{\ddot {\bar {r}}}=-\mu \cdot {\frac {\hat {r}}{r^{2}}}

{\ displaystyle {\ ddot {\ bar {r}}} = - \ mu \ cdot {\ frac {\ hat {r}} {r ^ {2}}}}

{\ displaystyle {\ ddot {\ bar {r}}} = - \ mu \ cdot {\ frac {\ hat {r}} {r ^ {2}}}}

,

pentru care orbita Kepleriană este soluția generală.

Formulare exactă

Formularea precisă a problemei Lambert este următoarea.

Sunt date două momente diferite în timp $t_{1}$ ${\ displaystyle t_ {1}}$ ${\ displaystyle t_ {1}}$ Și $t_{2}$ ${\ displaystyle t_ {2}}$ ${\ displaystyle t_ {2}}$ și doi vectori de poziție ${\bar {r}}_{1}=r_{1}{\hat {r}}_{1}$ ${\ displaystyle {\ bar {r}} _ {1} = r_ {1} {\ hat {r}} _ {1}}$ ${\ displaystyle {\ bar {r}} _ {1} = r_ {1} {\ hat {r}} _ {1}}$ Și ${\bar {r}}_{2}=r_{2}{\hat {r}}_{2}$ ${\ displaystyle {\ bar {r}} _ {2} = r_ {2} {\ hat {r}} _ {2}}$ ${\ displaystyle {\ bar {r}} _ {2} = r_ {2} {\ hat {r}} _ {2}}$ .
Găsește soluția ${\bar {r}}(t)$ ${\ displaystyle {\ bar {r}} (t)}$ ${\ displaystyle {\ bar {r}} (t)}$ care satisface ecuația diferențială de mai sus deci

{\bar {r}}(t_{1})={\bar {r}}_{1}

{\ displaystyle {\ bar {r}} (t_ {1}) = {\ bar {r}} _ {1}}

{\ displaystyle {\ bar {r}} (t_ {1}) = {\ bar {r}} _ {1}}

{\bar {r}}(t_{2})={\bar {r}}_{2}

{\ displaystyle {\ bar {r}} (t_ {2}) = {\ bar {r}} _ {2}}

{\ displaystyle {\ bar {r}} (t_ {2}) = {\ bar {r}} _ {2}}

.

Analiza geometrică preliminară

Figura 1:

F_{1}

{\ displaystyle F_ {1}}

{\ displaystyle F_ {1}}

, originea forței gravitaționale;

P_{1}

{\ displaystyle P_ {1}}

{\ displaystyle P_ {1}}

, punctul corespunzător vectorului

{\bar {r}}_{1}

{\ displaystyle {\ bar {r}} _ {1}}

{\ displaystyle {\ bar {r}} _ {1}}

;

P_{1}

{\ displaystyle P_ {1}}

{\ displaystyle P_ {1}}

, punctul corespunzător vectorului

{\bar {r}}_{2}

{\ displaystyle {\ bar {r}} _ {2}}

{\ displaystyle {\ bar {r}} _ {2}}

.

Cele trei puncte
$F_{1}$ ${\ displaystyle F_ {1}}$ ${\ displaystyle F_ {1}}$ , originea forței gravitaționale,
$P_{1}$ ${\ displaystyle P_ {1}}$ ${\ displaystyle P_ {1}}$ , punct corespunzător vectorului ${\bar {r}}_{1}$ ${\ displaystyle {\ bar {r}} _ {1}}$ ${\ displaystyle {\ bar {r}} _ {1}}$ ,
$P_{1}$ ${\ displaystyle P_ {1}}$ ${\ displaystyle P_ {1}}$ , punct corespunzător vectorului ${\bar {r}}_{2}$ ${\ displaystyle {\ bar {r}} _ {2}}$ ${\ displaystyle {\ bar {r}} _ {2}}$ ,
formează un triunghi în planul definit de vectori ${\bar {r}}_{1}$ ${\ displaystyle {\ bar {r}} _ {1}}$ ${\ displaystyle {\ bar {r}} _ {1}}$ Și ${\bar {r}}_{2}$ ${\ displaystyle {\ bar {r}} _ {2}}$ ${\ displaystyle {\ bar {r}} _ {2}}$ și reprezentată în Figura 1. Distanța dintre puncte $P_{1}$ ${\ displaystyle P_ {1}}$ ${\ displaystyle P_ {1}}$ Și $P_{2}$ ${\ displaystyle P_ {2}}$ ${\ displaystyle P_ {2}}$ Și $2d$ ${\ displaystyle 2d}$ ${\ displaystyle 2d}$ , distanța dintre $P_{1}$ ${\ displaystyle P_ {1}}$ ${\ displaystyle P_ {1}}$ Și $F_{1}$ ${\ displaystyle F_ {1}}$ ${\ displaystyle F_ {1}}$ Și $r_{1}=r_{m}-A$ ${\ displaystyle r_ {1} = r_ {m} -A}$ ${\ displaystyle r_ {1} = r_ {m} -A}$ și distanța dintre $P_{2}$ ${\ displaystyle P_ {2}}$ ${\ displaystyle P_ {2}}$ Și $F_{1}$ ${\ displaystyle F_ {1}}$ ${\ displaystyle F_ {1}}$ Și $r_{2}=r_{m}+A$ ${\ displaystyle r_ {2} = r_ {m} + A}$ ${\ displaystyle r_ {2} = r_ {m} + A}$ . Valoarea a $LA$ ${\ displaystyle A}$ $LA$ este pozitiv sau negativ în funcție de care dintre puncte $P_{1}$ ${\ displaystyle P_ {1}}$ ${\ displaystyle P_ {1}}$ Și $P_{2}$ ${\ displaystyle P_ {2}}$ ${\ displaystyle P_ {2}}$ este mai departe de $F_{1}$ ${\ displaystyle F_ {1}}$ ${\ displaystyle F_ {1}}$ . Problema geometrică care trebuie rezolvată este găsirea unei elipse care traversează punctele $P_{1}$ ${\ displaystyle P_ {1}}$ ${\ displaystyle P_ {1}}$ Și $P_{2}$ ${\ displaystyle P_ {2}}$ ${\ displaystyle P_ {2}}$ și să ai un foc înăuntru $F_{1}$ ${\ displaystyle F_ {1}}$ ${\ displaystyle F_ {1}}$ .

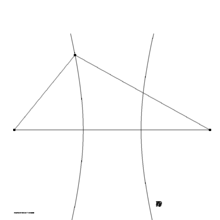
Figura 2: hiperbola cu focare în puncte

P_{1}

{\ displaystyle P_ {1}}

{\ displaystyle P_ {1}}

Și

P_{2}

{\ displaystyle P_ {2}}

{\ displaystyle P_ {2}}

și trecând prin punct

F_{1}

{\ displaystyle F_ {1}}

{\ displaystyle F_ {1}}

.

Punctele $F_{1}$ ${\ displaystyle F_ {1}}$ ${\ displaystyle F_ {1}}$ , $P_{1}$ ${\ displaystyle P_ {1}}$ ${\ displaystyle P_ {1}}$ Și $P_{2}$ ${\ displaystyle P_ {2}}$ ${\ displaystyle P_ {2}}$ definesc o hiperbolă care traversează punctul $F_{1}$ ${\ displaystyle F_ {1}}$ ${\ displaystyle F_ {1}}$ și are focare în puncte $P_{1}$ ${\ displaystyle P_ {1}}$ ${\ displaystyle P_ {1}}$ Și $P_{2}$ ${\ displaystyle P_ {2}}$ ${\ displaystyle P_ {2}}$ , așa cum se arată în figura 2. Punctul $F_{1}$ ${\ displaystyle F_ {1}}$ ${\ displaystyle F_ {1}}$ poate fi fie pe ramura dreaptă, fie pe cea stângă a hiperbolei, în funcție de semnul $LA$ ${\ displaystyle A}$ $LA$ . Axa semi-majoră a hiperbolei este $\left|A\right|$ ${\ displaystyle \ left | A \ right |}$ ${\ displaystyle \ left | A \ right |}$ și excentricitate $ȘI$ ${\ displaystyle E}$ $ȘI$ Și ${\frac {d}{\left|A\right|}}$ ${\ displaystyle {\ frac {d} {\ left | A \ right |}}}$ ${\ displaystyle {\ frac {d} {\ left | A \ right |}}}$ .

Ecuația hiperbolei , în coordonate carteziene, este

{\frac {x^{2}}{A^{2}}}-{\frac {y^{2}}{B^{2}}}=1\quad (1)

{\ displaystyle {\ frac {x ^ {2}} {A ^ {2}}} - {\ frac {y ^ {2}} {B ^ {2}}} = 1 \ quad (1)}

{\ displaystyle {\ frac {x ^ {2}} {A ^ {2}}} - {\ frac {y ^ {2}} {B ^ {2}}} = 1 \ quad (1)}

cu

B=\left|A\right|{\sqrt {E^{2}-1}}={\sqrt {d^{2}-A^{2}}}\quad (2)

{\ displaystyle B = \ left | A \ right | {\ sqrt {E ^ {2} -1}} = {\ sqrt {d ^ {2} -A ^ {2}}} \ quad (2)}

{\ displaystyle B = \ left | A \ right | {\ sqrt {E ^ {2} -1}} = {\ sqrt {d ^ {2} -A ^ {2}}} \ quad (2)}

Pentru orice punct de pe aceeași ramură a hiperbolei căreia îi aparține $F_{1}$ ${\ displaystyle F_ {1}}$ ${\ displaystyle F_ {1}}$ diferența dintre distanțele până la puncte $P_{1}$ ${\ displaystyle P_ {1}}$ ${\ displaystyle P_ {1}}$ Și $P_{2}$ ${\ displaystyle P_ {2}}$ ${\ displaystyle P_ {2}}$ Și

r_{2}-r_{1}=2A\quad (3)

{\ displaystyle r_ {2} -r_ {1} = 2A \ quad (3)}

{\ displaystyle r_ {2} -r_ {1} = 2A \ quad (3)}

Pentru fiecare punct $F_{2}$ ${\ displaystyle F_ {2}}$ ${\ displaystyle F_ {2}}$ pe cealaltă ramură a hiperbolei relația corespunzătoare este

s_{1}-s_{2}=2A\quad (4)

{\ displaystyle s_ {1} -s_ {2} = 2A \ quad (4)}

{\ displaystyle s_ {1} -s_ {2} = 2A \ quad (4)}

acesta este

r_{1}+s_{1}=r_{2}+s_{2}\quad (5)

{\ displaystyle r_ {1} + s_ {1} = r_ {2} + s_ {2} \ quad (5)}

{\ displaystyle r_ {1} + s_ {1} = r_ {2} + s_ {2} \ quad (5)}

Figura 3: elipsa cu focare în puncte

F_{1}

{\ displaystyle F_ {1}}

{\ displaystyle F_ {1}}

Și

F_{2}

{\ displaystyle F_ {2}}

{\ displaystyle F_ {2}}

și trecând prin puncte

P_{1}

{\ displaystyle P_ {1}}

{\ displaystyle P_ {1}}

Și

P_{2}

{\ displaystyle P_ {2}}

{\ displaystyle P_ {2}}

.

Aceasta înseamnă punctele $P_{1}$ ${\ displaystyle P_ {1}}$ ${\ displaystyle P_ {1}}$ Și $P_{2}$ ${\ displaystyle P_ {2}}$ ${\ displaystyle P_ {2}}$ ambii aparțin elipsei care are punctele ca focare $F_{1}$ ${\ displaystyle F_ {1}}$ ${\ displaystyle F_ {1}}$ Și $F_{2}$ ${\ displaystyle F_ {2}}$ ${\ displaystyle F_ {2}}$ și axa semi-majoră

a={\frac {r_{1}+s_{1}}{2}}={\frac {r_{2}+s_{2}}{2}}\quad (6)

{\ displaystyle a = {\ frac {r_ {1} + s_ {1}} {2}} = {\ frac {r_ {2} + s_ {2}} {2}} \ quad (6)}

{\ displaystyle a = {\ frac {r_ {1} + s_ {1}} {2}} = {\ frac {r_ {2} + s_ {2}} {2}} \ quad (6)}

Elipsa rezultată, a ales un punct $F_{2}$ ${\ displaystyle F_ {2}}$ ${\ displaystyle F_ {2}}$ arbitrar, este prezentat în Figura 3.

Soluția problemei Lambert pentru o orbită eliptică

În primul rând, luăm în considerare două cazuri separate, în funcție de faptul dacă polul orbital are direcție ${\bar {r}}_{1}\times {\bar {r}}_{2}$ ${\ displaystyle {\ bar {r}} _ {1} \ times {\ bar {r}} _ {2}}$ ${\ displaystyle {\ bar {r}} _ {1} \ times {\ bar {r}} _ {2}}$ sau $-{\bar {r}}_{1}\times {\bar {r}}_{2}$ ${\ displaystyle - {\ bar {r}} _ {1} \ times {\ bar {r}} _ {2}}$ ${\ displaystyle - {\ bar {r}} _ {1} \ times {\ bar {r}} _ {2}}$ . În primul caz unghiul de transfer $\alpha$ ${\ displaystyle \ alpha}$ $\ alfa$ pentru prima trecere prin ${\bar {r}}_{2}$ ${\ displaystyle {\ bar {r}} _ {2}}$ ${\ displaystyle {\ bar {r}} _ {2}}$ va fi în raza de acțiune $0<\alpha <180^{\circ }$ ${\ displaystyle 0 <\ alpha <180 ^ {\ circ}}$ ${\ displaystyle 0 <\ alpha <180 ^ {\ circ}}$ , în timp ce în al doilea caz va fi inclus în gamă $180^{\circ }<\alpha <360^{\circ }$ ${\ displaystyle 180 ^ {\ circ} <\ alpha <360 ^ {\ circ}}$ ${\ displaystyle 180 ^ {\ circ} <\ alpha <360 ^ {\ circ}}$ . Prin urmare ${\bar {r}}(t)$ ${\ displaystyle {\ bar {r}} (t)}$ ${\ displaystyle {\ bar {r}} (t)}$ va continua să treacă ${\bar {r}}_{2}$ ${\ displaystyle {\ bar {r}} _ {2}}$ ${\ displaystyle {\ bar {r}} _ {2}}$ cu fiecare revoluție orbitală.

În cazul în care ${\bar {r}}_{1}\times {\bar {r}}_{2}=0$ ${\ displaystyle {\ bar {r}} _ {1} \ times {\ bar {r}} _ {2} = 0}$ ${\ displaystyle {\ bar {r}} _ {1} \ times {\ bar {r}} _ {2} = 0}$ , cum ar fi în cazul ${\bar {r}}_{1}$ ${\ displaystyle {\ bar {r}} _ {1}}$ ${\ displaystyle {\ bar {r}} _ {1}}$ Și ${\bar {r}}_{2}$ ${\ displaystyle {\ bar {r}} _ {2}}$ ${\ displaystyle {\ bar {r}} _ {2}}$ au direcție opusă, toate planurile orbitale care conțin linia corespunzătoare sunt la fel de potrivite și unghiul de transfer $\alpha$ ${\ displaystyle \ alpha}$ $\ alfa$ pentru prima trecere prin ${\bar {r}}_{2}$ ${\ displaystyle {\ bar {r}} _ {2}}$ ${\ displaystyle {\ bar {r}} _ {2}}$ va fi de $180^{\circ }$ ${\ displaystyle 180 ^ {\ circ}}$ ${\ displaystyle 180 ^ {\ circ}}$ .

Pentru fiecare $\alpha$ ${\ displaystyle \ alpha}$ $\ alfa$ așa să fie $0<\alpha <\infty$ ${\ displaystyle 0 <\ alpha <\ infty}$ ${\ displaystyle 0 <\ alpha <\ infty}$ , în triunghiul format de puncte $P_{1}$ ${\ displaystyle P_ {1}}$ ${\ displaystyle P_ {1}}$ , $P_{2}$ ${\ displaystyle P_ {2}}$ ${\ displaystyle P_ {2}}$ Și $F_{1}$ ${\ displaystyle F_ {1}}$ ${\ displaystyle F_ {1}}$ , așa cum se arată în Figura 1, avem

d={\frac {\sqrt {{r_{1}}^{2}+{r_{2}}^{2}-2r_{1}r_{2}\cos \alpha }}{2}}\quad (7)

{\ displaystyle d = {\ frac {\ sqrt {{r_ {1}} ^ {2} + {r_ {2}} ^ {2} -2r_ {1} r_ {2} \ cos \ alpha}} {2 }} \ quad (7)}

{\ displaystyle d = {\ frac {\ sqrt {{r_ {1}} ^ {2} + {r_ {2}} ^ {2} -2r_ {1} r_ {2} \ cos \ alpha}} {2 }} \ quad (7)}

iar axa semi-majoră (semnată) a hiperbolei este

A={\frac {r_{2}-r_{1}}{2}}\quad (8)

{\ displaystyle A = {\ frac {r_ {2} -r_ {1}} {2}} \ quad (8)}

{\ displaystyle A = {\ frac {r_ {2} -r_ {1}} {2}} \ quad (8)}

Excentricitatea (cu semn) a hiperbolei este

E={\frac {d}{A}}\quad (9)

{\ displaystyle E = {\ frac {d} {A}} \ quad (9)}

{\ displaystyle E = {\ frac {d} {A}} \ quad (9)}

iar axa semi-minoră este

B=\left|A\right|{\sqrt {E^{2}-1}}={\sqrt {d^{2}-A^{2}}}\quad (10)

{\ displaystyle B = \ left | A \ right | {\ sqrt {E ^ {2} -1}} = {\ sqrt {d ^ {2} -A ^ {2}}} \ quad (10)}

{\ displaystyle B = \ left | A \ right | {\ sqrt {E ^ {2} -1}} = {\ sqrt {d ^ {2} -A ^ {2}}} \ quad (10)}

Coordonatele punctului $F_{1}$ ${\ displaystyle F_ {1}}$ ${\ displaystyle F_ {1}}$ relativ la sistemul de coordonate canonice pentru hiperbolă sunt

x_{0}=-{\frac {r_{m}}{E}}\quad (11)

{\ displaystyle x_ {0} = - {\ frac {r_ {m}} {E}} \ quad (11)}

{\ displaystyle x_ {0} = - {\ frac {r_ {m}} {E}} \ quad (11)}

(Rețineți că $ȘI$ ${\ displaystyle E}$ $ȘI$ are semnul de $r_{2}-r_{1}$ ${\ displaystyle r_ {2} -r_ {1}}$ ${\ displaystyle r_ {2} -r_ {1}}$ )

y_{0}=B{\sqrt {{\left({\frac {x_{0}}{A}}\right)}^{2}-1}}\quad (12)

{\ displaystyle y_ {0} = B {\ sqrt {{\ left ({\ frac {x_ {0}} {A}} \ right)} ^ {2} -1}} \ quad (12)}

{\ displaystyle y_ {0} = B {\ sqrt {{\ left ({\ frac {x_ {0}} {A}} \ right)} ^ {2} -1}} \ quad (12)}

unde este

r_{m}={\frac {r_{2}+r_{1}}{2}}\quad (13)

{\ displaystyle r_ {m} = {\ frac {r_ {2} + r_ {1}} {2}} \ quad (13)}

{\ displaystyle r_ {m} = {\ frac {r_ {2} + r_ {1}} {2}} \ quad (13)}

Alegând coordonata y a punctului $F_{2}$ ${\ displaystyle F_ {2}}$ ${\ displaystyle F_ {2}}$ pe cealaltă ramură a hiperbolei ca parametru liber, coordonata x a $F_{2}$ ${\ displaystyle F_ {2}}$ ${\ displaystyle F_ {2}}$ Și

x=A{\sqrt {1+{\left({\frac {y}{B}}\right)}^{2}}}\quad (14)

{\ displaystyle x = A {\ sqrt {1 + {\ left ({\ frac {y} {B}} \ right)} ^ {2}}} \ quad (14)}

{\ displaystyle x = A {\ sqrt {1 + {\ left ({\ frac {y} {B}} \ right)} ^ {2}}} \ quad (14)}

(Rețineți că $LA$ ${\ displaystyle A}$ $LA$ are semnul $r_{2}-r_{1}$ ${\ displaystyle r_ {2} -r_ {1}}$ ${\ displaystyle r_ {2} -r_ {1}}$ )

Axa semi-majoră a elipsei care trece prin puncte $P_{1}$ ${\ displaystyle P_ {1}}$ ${\ displaystyle P_ {1}}$ Și $P_{2}$ ${\ displaystyle P_ {2}}$ ${\ displaystyle P_ {2}}$ și având focarele în puncte $F_{1}$ ${\ displaystyle F_ {1}}$ ${\ displaystyle F_ {1}}$ Și $F_{2}$ ${\ displaystyle F_ {2}}$ ${\ displaystyle F_ {2}}$ Și

a={\frac {r_{1}+s_{1}}{2}}={\frac {r_{2}+s_{2}}{2}}={\frac {r_{m}+Ex}{2}}\quad (15)

{\ displaystyle a = {\ frac {r_ {1} + s_ {1}} {2}} = {\ frac {r_ {2} + s_ {2}} {2}} = {\ frac {r_ {m } + Ex} {2}} \ quad (15)}

{\ displaystyle a = {\ frac {r_ {1} + s_ {1}} {2}} = {\ frac {r_ {2} + s_ {2}} {2}} = {\ frac {r_ {m } + Ex} {2}} \ quad (15)}

Distanța dintre focare este

{\sqrt {(x_{0}-x)^{2}+(y_{0}-y)^{2}}}\quad (16)

{\ displaystyle {\ sqrt {(x_ {0} -x) ^ {2} + (y_ {0} -y) ^ {2}}} \ quad (16)}

{\ displaystyle {\ sqrt {(x_ {0} -x) ^ {2} + (y_ {0} -y) ^ {2}}} \ quad (16)}

iar excentricitatea este în consecință

e={\frac {\sqrt {(x_{0}-x)^{2}+(y_{0}-y)^{2}}}{2a}}\quad (17)

{\ displaystyle e = {\ frac {\ sqrt {(x_ {0} -x) ^ {2} + (y_ {0} -y) ^ {2}}} {2a}} \ quad (17)}

{\ displaystyle e = {\ frac {\ sqrt {(x_ {0} -x) ^ {2} + (y_ {0} -y) ^ {2}}} {2a}} \ quad (17)}

Adevarata anomalie $\theta _{1}$ ${\ displaystyle \ theta _ {1}}$ ${\ displaystyle \ theta _ {1}}$ în sens $P_{1}$ ${\ displaystyle P_ {1}}$ ${\ displaystyle P_ {1}}$ depinde de direcția mișcării, adică de semnul $\sin \alpha$ ${\ displaystyle \ sin \ alpha}$ ${\ displaystyle \ sin \ alpha}$ . În ambele cazuri avem asta

\cos \theta _{1}=-{\frac {(x_{0}+d)f_{x}+y_{0}f_{y}}{r_{1}}}\quad (18)

{\ displaystyle \ cos \ theta _ {1} = - {\ frac {(x_ {0} + d) f_ {x} + y_ {0} f_ {y}} {r_ {1}}} \ quad (18 )}}

{\ displaystyle \ cos \ theta _ {1} = - {\ frac {(x_ {0} + d) f_ {x} + y_ {0} f_ {y}} {r_ {1}}} \ quad (18 )}}

unde este

f_{x}={\frac {x_{0}-x}{\sqrt {(x_{0}-x)^{2}+(y_{0}-y)^{2}}}}\quad (19)

{\ displaystyle f_ {x} = {\ frac {x_ {0} -x} {\ sqrt {(x_ {0} -x) ^ {2} + (y_ {0} -y) ^ {2}}} } \ quad (19)}

{\ displaystyle f_ {x} = {\ frac {x_ {0} -x} {\ sqrt {(x_ {0} -x) ^ {2} + (y_ {0} -y) ^ {2}}} } \ quad (19)}

f_{y}={\frac {y_{0}-y}{\sqrt {(x_{0}-x)^{2}+(y_{0}-y)^{2}}}}\quad (20)

{\ displaystyle f_ {y} = {\ frac {y_ {0} -y} {\ sqrt {(x_ {0} -x) ^ {2} + (y_ {0} -y) ^ {2}}} } \ quad (20)}

{\ displaystyle f_ {y} = {\ frac {y_ {0} -y} {\ sqrt {(x_ {0} -x) ^ {2} + (y_ {0} -y) ^ {2}}} } \ quad (20)}

este vectorul unitar care reprezintă direcția de la $F_{2}$ ${\ displaystyle F_ {2}}$ ${\ displaystyle F_ {2}}$ la $F_{1}$ ${\ displaystyle F_ {1}}$ ${\ displaystyle F_ {1}}$ exprimată în coordonate canonice.

De sine $\sin \alpha$ ${\ displaystyle \ sin \ alpha}$ ${\ displaystyle \ sin \ alpha}$ atunci este pozitiv

\sin \theta _{1}={\frac {(x_{0}+d)f_{y}-y_{0}f_{x}}{r_{1}}}\quad (21)

{\ displaystyle \ sin \ theta _ {1} = {\ frac {(x_ {0} + d) f_ {y} -y_ {0} f_ {x}} {r_ {1}}} \ quad (21) }

{\ displaystyle \ sin \ theta _ {1} = {\ frac {(x_ {0} + d) f_ {y} -y_ {0} f_ {x}} {r_ {1}}} \ quad (21) }

De sine $\sin \alpha$ ${\ displaystyle \ sin \ alpha}$ ${\ displaystyle \ sin \ alpha}$ în schimb este negativ

\sin \theta _{1}=-{\frac {(x_{0}+d)f_{y}-y_{0}f_{x}}{r_{1}}}\quad (22)

{\ displaystyle \ sin \ theta _ {1} = - {\ frac {(x_ {0} + d) f_ {y} -y_ {0} f_ {x}} {r_ {1}}} \ quad (22 )}}

{\ displaystyle \ sin \ theta _ {1} = - {\ frac {(x_ {0} + d) f_ {y} -y_ {0} f_ {x}} {r_ {1}}} \ quad (22 )}}

Fiind

axa semi-majoră $la$ ${\ displaystyle a}$ $la$ ,
excentricitatea orbitală $Și$ ${\ displaystyle e}$ $Și$ ,
anomalia adevărată inițială $\theta$ ${\ displaystyle \ theta}$ $\ theta$

funcțiile cunoscute ale parametrului y, timpul necesar pentru ca adevărata anomalie să crească cu o valoare $\alpha$ ${\ displaystyle \ alpha}$ $\ alfa$ este, de asemenea, o funcție cunoscută a lui y. De sine $t_{2}-t_{1}$ ${\ displaystyle t_ {2} -t_ {1}}$ ${\ displaystyle t_ {2} -t_ {1}}$ este în intervalul care poate fi obținut cu o orbită Kepleriană eliptică, valoarea y corespunzătoare poate fi obținută cu un algoritm iterativ .

În cazul particular pe care îl aveți $r_{1}=r_{2}$ ${\ displaystyle r_ {1} = r_ {2}}$ ${\ displaystyle r_ {1} = r_ {2}}$ (sau foarte asemănător), avem asta $A=0$ ${\ displaystyle A = 0}$ ${\ displaystyle A = 0}$ iar hiperbola este redusă la o singură linie ortogonală la îmbinarea $P_{1}$ ${\ displaystyle P_ {1}}$ ${\ displaystyle P_ {1}}$ cu $P_{2}$ ${\ displaystyle P_ {2}}$ ${\ displaystyle P_ {2}}$ cu ecuație

x=0\quad (1')

{\ displaystyle x = 0 \ quad (1 ')}

{\ displaystyle x = 0 \ quad (1 ')}

Ecuațiile (11) și (12) sunt apoi înlocuite cu

x_{0}=0\quad (11')

{\ displaystyle x_ {0} = 0 \ quad (11 ')}

{\ displaystyle x_ {0} = 0 \ quad (11 ')}

y_{0}={\sqrt {{r_{m}}^{2}-d^{2}}}\quad (12')

{\ displaystyle y_ {0} = {\ sqrt {{r_ {m}} ^ {2} -d ^ {2}}} \ quad (12 ')}

{\ displaystyle y_ {0} = {\ sqrt {{r_ {m}} ^ {2} -d ^ {2}}} \ quad (12 ')}

(14) se înlocuiește cu

x=0\quad (14')

{\ displaystyle x = 0 \ quad (14 ')}

{\ displaystyle x = 0 \ quad (14 ')}

și (15) cu

a={\frac {r_{m}+{\sqrt {d^{2}+y^{2}}}}{2}}\quad (15')

{\ displaystyle a = {\ frac {r_ {m} + {\ sqrt {d ^ {2} + y ^ {2}}}} {2}} \ quad (15 ')}

{\ displaystyle a = {\ frac {r_ {m} + {\ sqrt {d ^ {2} + y ^ {2}}}} {2}} \ quad (15 ')}

Exemplu numeric

Să presupunem următoarele valori pentru o orbită kepleriană centrată pe Pământ:

r ₁ = 10 000 km
r ₂ = 10 000 km
α = 100 °

Alegând o valoare de y = 30 000 km, se obține un timp de transfer de 3072 secunde, presupunând constanta gravitațională egală cu μ = 398 603 km ³ / s ² . Parametrii orbitali corespunzători sunt:

axa semi-majoră = 23 001 km;
excentricitate = 0,566613;
anomalie adevărată la momentul t ₁ = -7,577 °;
anomalie adevărată la momentul t ₂ = 92,423 °.

Plasând în schimb:

r ₁ = 10 000 km
r ₂ = 10 000 km
α = 260 °

obținem aceeași orbită eliptică, dar rotația are loc în direcția opusă și avem:

anomalie adevărată la momentul t ₁ = 7,577 °;
anomalie adevărată la momentul t ₂ = 267,577 ° = 360 ° - 92,423 °

și un timp de transfer de 31 645 secunde.

Componentele radiale și tangențiale ale vitezei sunt date de:

V_{r}={\sqrt {\frac {\mu }{p}}}\cdot e\cdot \sin \theta

{\ displaystyle V_ {r} = {\ sqrt {\ frac {\ mu} {p}}} \ cdot și \ cdot \ sin \ theta}

{\ displaystyle V_ {r} = {\ sqrt {\ frac {\ mu} {p}}} \ cdot și \ cdot \ sin \ theta}

V_{t}={\sqrt {\frac {\mu }{p}}}\cdot (1+e\cdot \cos \theta )

{\ displaystyle V_ {t} = {\ sqrt {\ frac {\ mu} {p}}} \ cdot (1 + e \ cdot \ cos \ theta)}

{\ displaystyle V_ {t} = {\ sqrt {\ frac {\ mu} {p}}} \ cdot (1 + e \ cdot \ cos \ theta)}

Aplicații practice

În mod normal, acest algoritm este utilizat pentru a rezolva problema Lambert în proiectarea misiunilor interplanetare. De exemplu, o navă spațială care se deplasează de pe Pământ pe Marte poate fi considerată ca o primă aproximare într-o orbită Kepleriană eliptică eliocentrică de la poziția Pământului la lansare până la poziția lui Marte la sosire. Prin compararea vectorilor vitezei inițiale și finale pentru Pământ și Marte, se poate obține o estimare bună a energiei de lansare necesare și a manevrelor necesare pentru a intra pe orbita marțiană.

Elemente conexe

linkuri externe

( EN ) Cod MATLAB pentru rezolvarea problemei Lambert , la mathworks.com .

Portalul de astronautică

Portalul de matematică

Portalul mecanicii clasice