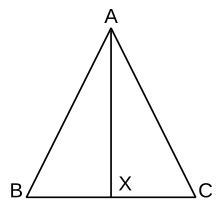
Teorema directă a triunghiurilor isosceli

În geometria euclidiană , teorema directă a triunghiurilor isosceli , cunoscută și sub numele de pons asinorum , afirmă că unghiurile opuse celor două laturi egale ale unui triunghi isoscel sunt congruente. Este, în esență, conținutul propunerii 5 din cartea I a Elementelor lui Euclid .

Pons asinorum

Teorema este uneori denumită pons asinorum ( latină pentru „puntea măgarului”). Există două explicații posibile pentru nume: cea mai simplă este că schema utilizată pentru demonstrație seamănă cu o punte reală. Dar cea mai populară explicație este că este primul test real din Elementele inteligenței cititorului și ca o punte către propunerile mai dificile care urmează. ^[1] Oricare ar fi originea, termenul pons asinorum este folosit ca metaforă pentru o problemă sau provocare care va separa încrezătorul de simplu, gânditorul agil de lent, determinat de ezitant: reprezintă un test critic de verificat abilitatea sau înțelegerea. ^[2] Un alt termen medieval pentru teoremă a fost Elefuga care, conform lui Roger Bacon , derivă din grecescul elegia miseria și din latina fugă , care înseamnă „evadarea mizerabilului”. Această etimologie este, de asemenea, îndoielnică, iar Chaucer se referă la termenul „zbor al nenorocitului” (în engleză „flemyng of wreches”) pentru teoremă. ^[3]

Utilizarea metaforică

Utilizările termenului sau teoremei ca metaforă includ:

Philobiblon de Richard Aungerville conține pasajul "Quot Euclidis discipulos retrojecit Elefuga quasi scopulos eminens et abruptus, qui nullo scalarum suffragio scandi posset! Durus, inquiunt, est hie sermo; quis potest eum audire?" în care teorema este comparată cu o stâncă abruptă pe care nicio scară nu poate ajuta la urcare și întreabă câți inspectori aspiranți au scăpat. ^[3]
Termenul pons asinorum , în ambele sensuri, ca punte și ca test este folosit ca metaforă pentru găsirea termenului mediu al unui silogism . ^[3]
În cartea Vita di Giovambattista Vico scrisă de el însuși, filosoful Giovambattista Vico spune că „a vrut să se aplice geometriei și să treacă la a cincea propunere a lui Euclid” cu următoarele rezultate: „cu prețul său, el a experimentat asta pentru minți deja universalizat prin metafizică că studiul minuțiozităților nu este ușor și a încetat să-l urmeze ".
În secolul al XVIII-lea, poetul Thomas Campbell a scris o poezie plină de umor intitulată The Pons asinorum în care o clasă de geometrie atacă teorema, precum o companie de soldați ar putea acuza o fortăreață; bătălia nu este lipsită de incidente. ^[4]
Economistul John Stuart Mill a numit Teoria chiriei lui Ricardo Pons Asinorum de economie. ^[5]
Pons Asinorum este numele dat unei anumite configurații a cubului Rubik . ^[6]

Demonstrații

Euclid și Proclus

Elementele lui Euclid Cartea 1 Propunerea 5; pons asinorum

Enunțul teoremei lui Euclid include o a doua concluzie, că dacă laturile egale ale triunghiului sunt extinse sub bază, atunci unghiurile dintre extensii și bază sunt egale. Dovada lui Euclid constă în definirea liniilor auxiliare pentru aceste extensii. Dar, comentând Euclid, Proclus subliniază că Euclid nu folosește niciodată a doua concluzie și că dovada sa poate fi simplificată oarecum prin trasarea liniilor auxiliare de pe laturile triunghiului, în timp ce restul probei se face în același mod. Au existat multe speculații și dezbateri cu privire la motivul pentru care Euclid a adăugat a doua concluzie la teoremă, deoarece aceasta face dovada mai complicată. O explicație plauzibilă, dată de Proclus, este că a doua concluzie poate fi utilizată în eventualele obiecții la dovezile ulterioare ale propozițiilor în care Euclid nu acoperă toate cazurile. ^[7] Dovada se bazează pe ceea ce se numește acum Side-Angle-Side , care este propoziția anterioară din Elements.

Dovada lui Proclus

Varianta lui Proclus a dovezii lui Euclid se desfășoară după cum urmează: ^{[8] let} $LA B. C.$ ${\ displaystyle ABC}$ $ABC$ un triunghi isoscel cu $LA B.$ ${\ displaystyle AB}$ $AB$ Și $LA C.$ ${\ displaystyle AC}$ $B.C$ laturi egale. Alegeți un punct arbitrar $D.$ ${\ displaystyle D}$ $D.$ pe partea de $LA B.$ ${\ displaystyle AB}$ $AB$ și ia ideea $ȘI$ ${\ displaystyle E}$ $ȘI$ pe $C. LA$ ${\ displaystyle CA}$ $CA$ astfel încât $AD\cong AE$ ${\ displaystyle AD \ cong AE}$ ${\ displaystyle AD \ cong AE}$ . Desenați liniile lui $B. ȘI$ ${\ displaystyle BE}$ ${\ displaystyle BE}$ , $D. C.$ ${\ displaystyle DC}$ $ANUNȚ$ Și $D. ȘI$ ${\ displaystyle DE}$ ${\ displaystyle DE}$ ia în considerare triunghiurile $B. LA ȘI$ ${\ displaystyle BAE}$ ${\ displaystyle BAE}$ Și $C. LA D.$ ${\ displaystyle CAD}$ ${\ displaystyle CAD}$ , aceste triunghiuri au $BA\cong AC$ ${\ displaystyle BA \ cong AC}$ ${\ displaystyle BA \ cong AC}$ , $AE\cong AD$ ${\ displaystyle AE \ cong AD}$ ${\ displaystyle AE \ cong AD}$ , și unghiul ${\hat {A}}$ ${\ displaystyle {\ hat {A}}}$ ${\ hat {A}}$ coincidentă, deci pentru criteriul de congruență lateral-unghi-lateral triunghiurile $B. LA ȘI$ ${\ displaystyle BAE}$ ${\ displaystyle BAE}$ Și $C. LA D.$ ${\ displaystyle CAD}$ ${\ displaystyle CAD}$ sunt congruente și, prin urmare, laturile și unghiurile corespunzătoare vor fi congruente: unghiul ${\widehat {ABE}}$ ${\ displaystyle {\ widehat {ABE}}}$ ${\ displaystyle {\ widehat {ABE}}}$ este egal cu unghiul ${\widehat {ACD}}$ ${\ displaystyle {\ widehat {ACD}}}$ $\ widehat {ACD}$ , coltul ${\widehat {ADC}}$ ${\ displaystyle {\ widehat {ADC}}}$ ${\ displaystyle {\ widehat {ADC}}}$ este egal cu unghiul ${\widehat {AEB}}$ ${\ displaystyle {\ widehat {AEB}}}$ ${\ displaystyle {\ widehat {AEB}}}$ , Și $BE\cong CD$ ${\ displaystyle BE \ cong CD}$ ${\ displaystyle BE \ cong CD}$ .

De cand $AC\cong AB$ ${\ displaystyle AC \ cong AB}$ ${\ displaystyle AC \ cong AB}$ Și $AD\cong AE$ ${\ displaystyle AD \ cong AE}$ ${\ displaystyle AD \ cong AE}$ , $BD\cong CE$ ${\ displaystyle BD \ cong CE}$ ${\ displaystyle BD \ cong CE}$ prin scăderea părților egale. Acum ia în considerare triunghiurile $D. B. ȘI$ ${\ displaystyle DBE}$ ${\ displaystyle DBE}$ Și $ȘI C. D.$ ${\ displaystyle ECD}$ ${\ displaystyle ECD}$ ; pentru ei $BD\cong CE$ ${\ displaystyle BD \ cong CE}$ ${\ displaystyle BD \ cong CE}$ , $BE\cong CD$ ${\ displaystyle BE \ cong CD}$ ${\ displaystyle BE \ cong CD}$ , și unghiul ${\widehat {DBE}}$ ${\ displaystyle {\ widehat {DBE}}}$ ${\ displaystyle {\ widehat {DBE}}}$ este egal cu unghiul ${\widehat {ECD}}$ ${\ displaystyle {\ widehat {ECD}}}$ ${\ displaystyle {\ widehat {ECD}}}$ așa cum tocmai s-a arătat, așa din nou pentru criteriul lateral-unghi-lateral, triunghiurile sunt congruente: unghiul ${\widehat {BDE}}$ ${\ displaystyle {\ widehat {BDE}}}$ ${\ displaystyle {\ widehat {BDE}}}$ este egal cu unghiul ${\widehat {CED}}$ ${\ displaystyle {\ widehat {CED}}}$ ${\ displaystyle {\ widehat {CED}}}$ . (Congruența implică, de asemenea $DE\cong ED$ ${\ displaystyle DE \ cong ED}$ ${\ displaystyle DE \ cong ED}$ , dar acest lucru este evident).

Din moment ce unghiul ${\widehat {BDE}}$ ${\ displaystyle {\ widehat {BDE}}}$ ${\ displaystyle {\ widehat {BDE}}}$ este egal cu unghiul ${\widehat {CED}}$ ${\ displaystyle {\ widehat {CED}}}$ ${\ displaystyle {\ widehat {CED}}}$ și unghiul ${\widehat {CDE}}$ ${\ displaystyle {\ widehat {CDE}}}$ ${\ displaystyle {\ widehat {CDE}}}$ este egal cu unghiul ${\widehat {BED}}$ ${\ displaystyle {\ widehat {BED}}}$ ${\ displaystyle {\ widehat {BED}}}$ , apoi unghiul ${\widehat {BDC}}$ ${\ displaystyle {\ widehat {BDC}}}$ ${\ displaystyle {\ widehat {BDC}}}$ va fi egal cu unghiul ${\widehat {CEB}}$ ${\ displaystyle {\ widehat {CEB}}}$ ${\ displaystyle {\ widehat {CEB}}}$ prin scăderea părților egale.

Să luăm în considerare o a treia pereche de triunghiuri, $B. D. C.$ ${\ displaystyle BDC}$ ${\ displaystyle BDC}$ Și $C. ȘI B.$ ${\ displaystyle CEB}$ ${\ displaystyle CEB}$ ; $DB\cong CE$ ${\ displaystyle DB \ cong CE}$ ${\ displaystyle DB \ cong CE}$ , $DC\cong EB$ ${\ displaystyle DC \ cong EB}$ ${\ displaystyle DC \ cong EB}$ , și unghiul ${\widehat {BDC}}$ ${\ displaystyle {\ widehat {BDC}}}$ ${\ displaystyle {\ widehat {BDC}}}$ egal cu unghiul ${\widehat {CEB}}$ ${\ displaystyle {\ widehat {CEB}}}$ ${\ displaystyle {\ widehat {CEB}}}$ , aplicând apoi unghiul lateral lateral pentru a treia oară, cele două triunghiuri se arată ca fiind congruente. În special, unghiul ${\widehat {CBD}}\cong {\widehat {BCE}}$ ${\ displaystyle {\ widehat {CBD}} \ cong {\ widehat {BCE}}}$ ${\ displaystyle {\ widehat {CBD}} \ cong {\ widehat {BCE}}}$ , așa cum au vrut să demonstreze.

Pappus

Proclus prezintă o dovadă mult mai scurtă atribuită lui Pappus din Alexandria . Nu este doar mai simplu, nu necesită nici o construcție suplimentară. Metoda de probă aplicată este criteriul lateral-unghi-lateral dintre un triunghi și imaginea sa în oglindă. Alți autori moderni descriu această metodă de demonstrație ca luând triunghiul, întorcându-l cu susul în jos și plasându-l pe sine. ^[9] Această metodă este subiectul satirei lui Charles Dodgson în Euclid și rivalii săi moderni , care îl numește „ taur irlandez ”, ceea ce este o prostie, deoarece se pare că triunghiul trebuie să fie în două locuri în același timp. ^[10]

Dovada este următoarea: ^[11] Let $LA B. C.$ ${\ displaystyle ABC}$ $ABC$ un triunghi isoscel cu $LA B.$ ${\ displaystyle AB}$ $AB$ Și $LA C.$ ${\ displaystyle AC}$ $B.C$ cele două laturi congruente ale acestuia. Luați în considerare triunghiurile $LA B. C.$ ${\ displaystyle ABC}$ $ABC$ Și $LA C. B.$ ${\ displaystyle ACB}$ $ACB$ , unde este $LA C. B.$ ${\ displaystyle ACB}$ $ACB$ este un al doilea triunghi cu vârfuri ${\hat {A}}$ ${\ displaystyle {\ hat {A}}}$ ${\ hat {A}}$ , ${\hat {C}}$ ${\ displaystyle {\ hat {C}}}$ ${\ hat {C}}$ Și ${\hat {B}}$ ${\ displaystyle {\ hat {B}}}$ ${\ hat {B}}$ corespunzând respectiv vârfurilor ${\hat {A}}$ ${\ displaystyle {\ hat {A}}}$ ${\ hat {A}}$ , ${\hat {B}}$ ${\ displaystyle {\ hat {B}}}$ ${\ hat {B}}$ Și ${\hat {C}}$ ${\ displaystyle {\ hat {C}}}$ ${\ hat {C}}$ în triunghiul original. Vei avea $AB\cong AC$ ${\ displaystyle AB \ cong AC}$ ${\ displaystyle AB \ cong AC}$ , $AC\cong AB$ ${\ displaystyle AC \ cong AB}$ ${\ displaystyle AC \ cong AB}$ și unghiul ${\hat {A}}$ ${\ displaystyle {\ hat {A}}}$ ${\ hat {A}}$ egală cu ea însăși, deci pentru criteriul lateral-unghi-lateral, triunghiurile $LA B. C.$ ${\ displaystyle ABC}$ $ABC$ Și $LA C. B.$ ${\ displaystyle ACB}$ $ACB$ sunt congruente. Mai ales unghiul ${\hat {B}}$ ${\ displaystyle {\ hat {B}}}$ ${\ hat {B}}$ este congruent cu unghiul ${\hat {C}}$ ${\ displaystyle {\ hat {C}}}$ ${\ hat {C}}$ . ^[12]

Alte

Demonstrarea manualelor

Dovada standard a manualelor constă în construirea bisectoarei unghiulare ${\hat {A}}$ ${\ displaystyle {\ hat {A}}}$ ${\ hat {A}}$ . ^[13] Aceasta este mai simplă decât dovada lui Euclid, dar Euclid nu prezintă construcția bisectoarei unui unghi înainte de propoziția 9. Astfel, ordinea de prezentare a propozițiilor lui Euclid trebuie modificată pentru a evita raționamentul circular.

Dovada se desfășoară după cum urmează: ^[14] ca înainte, luăm în considerare triunghiul $LA B. C.$ ${\ displaystyle ABC}$ $ABC$ cu $AB\cong AC$ ${\ displaystyle AB \ cong AC}$ ${\ displaystyle AB \ cong AC}$ . Construim bisectoarea unghiului ${\widehat {BAC}}$ ${\ displaystyle {\ widehat {BAC}}}$ ${\ displaystyle {\ widehat {BAC}}}$ și extindeți-l până când se întâlnește cu latura $B. C.$ ${\ displaystyle BC}$ $Î.Hr.$ în sens $X$ ${\ displaystyle X}$ $X$ . În triunghiuri $B. LA X$ ${\ displaystyle BAX}$ ${\ displaystyle BAX}$ Și $C. LA X$ ${\ displaystyle CAX}$ ${\ displaystyle CAX}$ da ai $AB\cong AC$ ${\ displaystyle AB \ cong AC}$ ${\ displaystyle AB \ cong AC}$ , $LA X$ ${\ displaystyle AX}$ ${\ displaystyle AX}$ coincidenta. Plus unghiul $B{\hat {A}}X\cong C{\hat {A}}X$ ${\ displaystyle B {\ hat {A}} X \ cong C {\ hat {A}} X}$ ${\ displaystyle B {\ hat {A}} X \ cong C {\ hat {A}} X}$ , astfel, pentru criteriul lateral-unghi-lateral, $B. LA X$ ${\ displaystyle BAX}$ ${\ displaystyle BAX}$ Și $C. LA X$ ${\ displaystyle CAX}$ ${\ displaystyle CAX}$ sunt congruente. Rezultă că colțurile ${\hat {B}}$ ${\ displaystyle {\ hat {B}}}$ ${\ hat {B}}$ Și ${\hat {C}}$ ${\ displaystyle {\ hat {C}}}$ ${\ hat {C}}$ sunt congruente.

Legendre folosește o construcție similară în Éléments de géométrie , dar considerând punctul X ca punct de mijloc al segmentului BD. ^[15] Dovada este similară, dar folosește criteriul Side-Side-Side în loc de side-corner-side, dar side-side-side nu este prezentat mult mai departe de Euclid în Elements .

Produs intern

Teorema directă a triunghiurilor isoscel este echivalentă cu produsul interior asupra numerelor reale sau complexe . În aceste spații este echivalent cu luarea vectorilor $X$ ${\ displaystyle x}$ $X$ , $y$ ${\ displaystyle y}$ $y$ Și $z$ ${\ displaystyle z}$ $z$ astfel încât ^[16]

x+y+z=0{\text{ and }}\|x\|=\|y\|,

{\ displaystyle x + y + z = 0 {\ text {și}} \ | x \ | = \ | y \ |,}

{\ displaystyle x + y + z = 0 {\ text {și}} \ | x \ | = \ | y \ |,}

asa de

\|x-z\|=\|y-z\|.

{\ displaystyle \ | xz \ | = \ | yz \ |.}

{\ displaystyle \ | x-z \ | = \ | y-z \ |.}

In timp ce

\|x-z\|^{2}=\|x\|^{2}-2x\cdot z+\|z\|^{2},

{\ displaystyle \ | xz \ | ^ {2} = \ | x \ | ^ {2} -2x \ cdot z + \ | z \ | ^ {2},}

{\ displaystyle \ | x-z \ | ^ {2} = \ | x \ | ^ {2} -2x \ cdot z + \ | z \ | ^ {2},}

Și

x\cdot z=\|x\|\|z\|\cos \theta ,

{\ displaystyle x \ cdot z = \ | x \ | \ | z \ | \ cos \ theta,}

{\ displaystyle x \ cdot z = \ | x \ | \ | z \ | \ cos \ theta,}

unde este $\theta$ ${\ displaystyle \ theta}$ $\ theta$ este unghiul dintre cei doi vectori, concluzia acestei forme a teoremei este echivalentă cu afirmarea egalității unghiurilor.

Notă

^ David Eugene Smith, History of Mathematics , New York, publicațiile Dover, 1958, p. 284 .
^ (EN) Merriam-Webster, Definiția Pons asinorum , pe merriam-webster.com. Accesat la 9 decembrie 2012 ( arhivat la 20 februarie 2010) .
^ ^a ^b ^c AF West, HD Thompson, On Dulcarnon, Elefuga și Pons Asinorum ca nume fanteziste pentru propuneri geometrice , în buletinul Universității Princeton , vol. 3, nr. 4, 1891, p. 84.
^ (EN) Thomas Campbell, William Edmondstoune Aytoun, Lucrările poetice ale lui Thomas Campbell , Little, Brown, 1864, p. 385.
^ (EN) Henry Dunning Macleod , Despre chirie , în The Elements of Economics, vol. 2, Londra, Longmans, 1886, p. 96. Accesat la 9 decembrie 2012 .
„Mills merge atât de departe încât să numească Teoria chiriei lui Ricardo„ pons asinorum de economie ”. .
^ Rubik's Cube pattern Arhivat 12 decembrie 2012 în Archive.is .
^ Heath pp. 251-255
^ După Proclus p. 53
^ Francis Cuthbertson, Primer of geometry , 1876, p. 7. Adus pe 9 decembrie 2012 .
^ Charles Lutwidge Dodgson, Euclid and His Modern Rivals Act I Scena II §6
^ După Proclus p. 54
^ Heath p. 254 pentru secțiune
^ De exemplu JM Wilson Elementary geometry (1878 Oxford) p. 20
^ În urma lui Wilson
^ AM Legendre Éléments de géométrie (1876 Libr. De Firmin-Didot et Cie) p. 14
^ JR Retherford, Hilbert Space , Cambridge University Press , 1993, pagina 27.

Bibliografie

Euclid, comentariu și trad. de TL Heath Elements Vol. 1 (1908 Cambridge) Google Books

Euclid, comentariu de Proclus, ed. și trans. de T. Taylor Elements Vol. 2 (1789) Google Books

Manual de geometrie - Standard IX , Consiliul de stat din Maharashtra pentru învățământul secundar și secundar superior , Pune - 411 005, India .
John Stillwell, Cei patru piloni ai geometriei , Springer , 2005, pagina 24.

Elemente conexe

Triunghi isoscel

linkuri externe

(EN) pons asinorum , în PlanetMath .

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică

[1] David Eugene Smith, History of Mathematics , New York, publicațiile Dover, 1958, p. 284 .

[2] (EN) Merriam-Webster, Definiția Pons asinorum , pe merriam-webster.com. Accesat la 9 decembrie 2012 ( arhivat la 20 februarie 2010) .

[PUb-3] AF West, HD Thompson, On Dulcarnon, Elefuga și Pons Asinorum ca nume fanteziste pentru propuneri geometrice , în buletinul Universității Princeton , vol. 3, nr. 4, 1891, p. 84.

[4] (EN) Thomas Campbell, William Edmondstoune Aytoun, Lucrările poetice ale lui Thomas Campbell , Little, Brown, 1864, p. 385.

[5] (EN) Henry Dunning Macleod , Despre chirie , în The Elements of Economics, vol. 2, Londra, Longmans, 1886, p. 96. Accesat la 9 decembrie 2012 .
„Mills merge atât de departe încât să numească Teoria chiriei lui Ricardo„ pons asinorum de economie ”. .

[6] Rubik's Cube pattern Arhivat 12 decembrie 2012 în Archive.is .

[7] Heath pp. 251-255

[8] După Proclus p. 53

[9] Francis Cuthbertson, Primer of geometry , 1876, p. 7. Adus pe 9 decembrie 2012 .

[10] Charles Lutwidge Dodgson, Euclid and His Modern Rivals Act I Scena II §6

[11] După Proclus p. 54

[12] Heath p. 254 pentru secțiune

[13] De exemplu JM Wilson Elementary geometry (1878 Oxford) p. 20

[14] În urma lui Wilson

[15] AM Legendre Éléments de géométrie (1876 Libr. De Firmin-Didot et Cie) p. 14

[16] JR Retherford, Hilbert Space , Cambridge University Press , 1993, pagina 27.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8] let

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]