Mecanica contactului cu frecare

Mecanica de contact este studiul deformării solidelor care se ating într-unul sau mai multe puncte. ^[1] ^[2] Aceasta poate fi împărțită în forțe de compresie și adezive într-o direcție perpendiculară pe interfață și forțe de frecare în direcția tangențială. Mecanica contactului de frecare cu (sau contactul de frecare) este studiul deformării corpurilor în prezența efectelor de frecare, în timp ce contactul mecanic fără frecare presupune absența unor astfel de efecte.

Mecanica de contact fără fricțiuni se ocupă de o gamă largă de scale diferite.

La scară macroscopică, se aplică investigației asupra mișcării corpurilor în contact (vezi Dinamica contactului ). De exemplu, săritura unei bile de cauciuc pe o suprafață depinde de interacțiunea de frecare pe interfața de contact. Forța totală în ceea ce privește indentarea și deplasarea laterală este de interes primordial aici.
La o scară intermediară, este interesat de tensiuni , de alungiri și deformări premise ale corpurilor în contact în și în apropierea zonei de contact. De exemplu, pentru a deriva sau valida modelele de contact pe o scară macroscopică sau pentru a investiga „ uzura și oboseala suprafețelor corpurilor în contact. Domeniile de aplicare ale acestei scări sunt interacțiunea pneu-trotuar, interacțiunea roată-cale ferată, analiza rulmentului cu role etc.
În cele din urmă, la scară microscopică și nanoscopică, mecanica de contact este utilizată pentru a ne spori înțelegerea sistemelor tribologice , de exemplu. investigați originea fricțiunii și a ingineriei dispozitivelor avansate, cum ar fi microscopii cu forță atomică și dispozitivele MEMS .

Acest articol se referă în primul rând la a doua scară: obținerea înțelegerii de bază a tensiunilor și deformărilor din și în apropierea zonei de contact, fără a acorda prea multă atenție mecanismelor detaliate prin care acestea apar.

Istorie

Mai mulți oameni de știință și ingineri celebri au contribuit la înțelegerea noastră a fricțiunii. ^[3] Acestea includ Leonardo da Vinci , Guillaume Amontons , John Theophilus Desaguliers , Leonhard Euler șiCharles-Augustin de Coulomb . Mai târziu, Nikolai Pavlovich Petrov , Osborne Reynolds și Richard Stribeck au completat aceste cunoștințe cu teoriile lubrifierii .

Deformarea materialelor solide a fost investigată în secolele al XVII-lea și al XVIII-lea de Robert Hooke , Joseph Louis Lagrange , iar în secolele al XIX-lea și al XX-lea de d'Alembert și Timoșenko . Comparativ cu mecanica de contact se desprinde contribuția clasică a lui Heinrich Hertz . ^[4] În plus, soluțiile fundamentale ale lui Boussinesq și Cerruti sunt de primă importanță pentru investigarea problemelor de contact cu frecare în regim (liniar) elastic .

În aplicațiile feroviare dorim să cunoaștem relația dintre alunecare (diferența de viteză)

\xi

{\ displaystyle \ xi}

\ xi

și forța de frecare

F_{w}

{\ displaystyle F_ {w}}

{\ displaystyle F_ {w}}

.

Rezultatele clasice ale unei adevărate probleme de contact prin frecare se referă la eseurile lui FW Carter (1926) și H. Fromm (1927). Au prezentat independent reacția de alunecare versus forță de alunecare pentru un cilindru pe un plan sau pentru doi cilindri în contact stabil de rulare folosind legea lui Coulomb a fricțiunii uscate (a se vedea mai jos). ^[5] Acestea se aplică tracțiunii locomotivelor feroviare și înțelegerii „ înfășurării oscilante a vehiculelor feroviare. Comparativ cu alunecarea, soluțiile clasice se datorează lui C. Cattaneo (1938) și RD Mindlin (1949), care considerau tangențialul unei sfere pe un plan de schimbare a vitezei (vezi mai jos). ^[1]

În anii 1950, interesul pentru contactul rulant al roților de cale ferată a crescut. În 1958 KL Johnson a prezentat o abordare aproximativă a problemei fricțiunii tridimensionale cu geometrie hertziană, cu alunecare laterală sau rotativă. Printre altele, el a constatat că alunecarea rotativă, care este simetrică în jurul centrului zonei de contact, duce la o forță laterală netă în condiții de rulare. Acest lucru se datorează diferențelor longitudinale în distribuția tracțiunii în zona de contact.

În 1967, Joost Kalker și-a publicat teza de doctorat referitoare la teoria liniară pentru contactul continuu. ^[6] Această teorie este corectă pentru situația unui coeficient de frecare infinit, caz în care zona de alunecare dispare și este aproximativă la alunecarea care nu dispare. Presupune legea fricțiunii lui Coulomb, care necesită suprafețe mai mult sau mai puțin (scrupulos) curate. Această teorie este pentru corpuri masive precum contactul feroviar roată-șină. Comparativ cu anvelopa de interacțiune-drum, o contribuție importantă se referă la așa-numita formulă magică a anvelopelor Hans Pacejka . ^[7]

În anii 1970, au fost dezvoltate multe modele numerice. În special abordările variaționale , cum ar fi cele care se bazează pe teoriile existenței și unicității lui Duvaut și Lion. De-a lungul timpului, acestea au fost dezvoltate în abordări ale elementelor finite pentru probleme de contact cu modelele și geometria generală a materialelor, și abordări bazate pe jumătăți de spații pentru așa-numitele probleme de contact cu margini lustruite pentru materiale liniar elastice. Modelele din prima categorie au fost prezentate de Laursen ^[8] și Wriggers. ^[9] Un exemplu al acestei din urmă categorii este modelul Kalker CONTACT. ^[10]

Un dezavantaj al abordărilor variaționale bine fundamentate este timpul lor mare de calcul. Prin urmare, au fost concepute și multe abordări aproximative diferite. Diferite teorii binecunoscute aproximative pentru problema contactului continuu sunt abordarea FASTSIM a lui Kalker, formula Shen-Hedrick-Elkins și abordarea Polach.

Mai multe informații despre istoria problemei contactului roată / șină sunt furnizate în eseul lui Knothe. ^[5] Mai mult, Johnson și-a ridicat cartea într-o cantitate enormă de informații despre mecanica de contact și subiecte conexe. ^[1] În comparație cu contactul mecanic de rulare, o prezentare generală a diferitelor teorii este prezentată și de Kalker. ^[11] În cele din urmă, este de interes procedurile unui curs de CISM, care oferă o introducere la aspecte mai avansate ale teoriei contactului continuu. ^[12]

Formularea problemei

Analiza centrală a problemelor de contact cu fricțiune este înțelegerea faptului că tensiunile de pe suprafața fiecărui corp sunt spațial variabile. În consecință, alungirile și deformările corpurilor sunt variabile în funcție de locație. Și mișcarea particulelor corpurilor în contact poate fi diferită în diferite puncte: într-o parte a zonei de contact particulele corpurilor opuse pot adera (se lipesc) una de cealaltă, în timp ce în alte părți ale zonei de contact se produce o mișcare relativă . Această deplasare relativă locală se numește micro- rezultat .

Această subdiviziune a zonei de contact în zonele suspendate (aderență) și a zonelor de derivare se manifestă printre altele prin „ uzură corozivă . Trebuie remarcat faptul că „ uzura are loc doar acolo unde este disipată puterea , care necesită o tensiune și o relativă locală de deplasare (deriva) între cele două suprafețe.

Mărimea și forma zonei de contact în sine și a zonelor sale de aderență și de derivare nu sunt, în general, cunoscute în prealabil. Dacă ar fi cunoscuți, atunci câmpurile elastice din cele două corpuri ar fi rezolvate independent unul de celălalt și aceasta nu ar mai fi o problemă de contact.

Într-o problemă de contact se pot distinge trei componente diferite.

În primul rând, există deformarea corpurilor separate ca reacție la sarcinile aplicate pe suprafețele lor. Acesta este obiectul mecanicii generale ale continuumului . Depinde în mare măsură de geometria corpurilor și de comportamentul materialelor acestora ( constituent ) (de exemplu. Răspuns elastic împotriva plasticului , structură omogenă împotriva stratificării etc.).
În al doilea rând, există o mișcare generală a corpurilor în raport unul cu celălalt. De exemplu, corpurile pot fi în repaus (statice) sau în apropiere rapidă între ele ( impact ) și pot fi deplasate (glisante) sau rotite ( rulate ) unul pe altul. Aceste mișcări agregate sunt studiate în mecanica clasică , a se vedea, de exemplu, dinamica multicorpului .
În cele din urmă, există procesele interfeței de contact: compresie și aderență în direcția perpendiculară pe interfață și frecare și micro-derivare în direcții tangențiale .

Ultimul aspect este obiectul principal al mecanicii de contact. Este descris în termenii așa-numitelor „condiții de contact”. Pentru direcția perpendiculară pe interfață, problema normală de contact, efectele de aderență sunt de obicei mici (pe scări spațiale mai mari) și sunt de obicei utilizate următoarele condiții:

Spărtura $e_{n}$ ${\ displaystyle e_ {n}}$ $e_n$ între cele două suprafețe trebuie să fie zero (contact) sau strict pozitiv (separare, $e_{n}>0$ ${\ displaystyle e_ {n}> 0}$ ${\ displaystyle e_ {n}> 0}$ );
Tensiune normală $p_{n}$ ${\ displaystyle p_ {n}}$ $p_n$ acționarea asupra fiecărui corp este zero (separare) sau compresivă ( $p_{n}>0$ ${\ displaystyle p_ {n}> 0}$ ${\ displaystyle p_ {n}> 0}$ în contact).

Matematic: $e_{n}\geq 0,p_{n}\geq 0,e_{n}\cdot p_{n}=0\,\!$ ${\ displaystyle e_ {n} \ geq 0, p_ {n} \ geq 0, e_ {n} \ cdot p_ {n} = 0 \, \!}$ ${\ displaystyle e_ {n} \ geq 0, p_ {n} \ geq 0, e_ {n} \ cdot p_ {n} = 0 \, \!}$ . Aici $e_{n},p_{n}$ ${\ displaystyle e_ {n}, p_ {n}}$ ${\ displaystyle e_ {n}, p_ {n}}$ sunt funcții care variază în funcție de poziția de-a lungul suprafețelor corpurilor.

În direcții tangențiale sunt adesea utilizate următoarele condiții:

Stresul de forfecare local (tangențial) ${\vec {p}}=(p_{x},p_{y})^{T}\,\!$ ${\ displaystyle {\ vec {p}} = (p_ {x}, p_ {y}) ^ {T} \, \!}$ ${\ displaystyle {\ vec {p}} = (p_ {x}, p_ {y}) ^ {T} \, \!}$ (presupunând direcția normală paralelă cu axa $z$ ${\ displaystyle z}$ $z$ ) nu poate depăși maximul în funcție de o anumită poziție, așa-numita limită de tracțiune $g$ ${\ displaystyle g}$ $g$ ;
În cazul în care amplitudinea tracțiunii tangențiale scade sub limita de tracțiune $\|{\vec {p}}\|<g\,\!$ ${\ displaystyle \ | {\ vec {p}} \ | <g \, \!}$ ${\ displaystyle \ | {\ vec {p}} \ | <g \, \!}$ , suprafețele opuse aderă împreună și microdrive dispare, ${\vec {s}}=(s_{x},s_{y})^{T}={\vec {0}}\,\!$ ${\ displaystyle {\ vec {s}} = (s_ {x}, s_ {y}) ^ {T} = {\ vec {0}} \, \!}$ ${\ displaystyle {\ vec {s}} = (s_ {x}, s_ {y}) ^ {T} = {\ vec {0}} \, \!}$ ;
Micro-deriva are loc în cazul în care tractiunile tangentiale sunt la limita de tractiune; direcția tracțiunii tangențiale este apoi opusă direcției micro-derivării ${\vec {p}}=-g{\vec {s}}/\|{\vec {s}}\|\,\!$ ${\ displaystyle {\ vec {p}} = - g {\ vec {s}} / \ | {\ vec {s}} \ | \, \!}$ ${\ displaystyle {\ vec {p}} = - g {\ vec {s}} / \ | {\ vec {s}} \ | \, \!}$ .

Forma exactă a limitei de tracțiune este așa-numita lege a fricțiunii locale. Din acest motiv, legea Coulomb a fricțiunii (globale) este adesea aplicată local: $\|{\vec {p}}\|\leq g=\mu p_{n}\,\!$ ${\ displaystyle \ | {\ vec {p}} \ | \ leq g = \ mu p_ {n} \, \!}$ ${\ displaystyle \ | {\ vec {p}} \ | \ leq g = \ mu p_ {n} \, \!}$ , cu $\mu$ ${\ displaystyle \ mu}$ $\ mu$ coeficientul de frecare. Sunt posibile și formule mai detaliate, de exemplu cu $\mu$ ${\ displaystyle \ mu}$ $\ mu$ in functie de temperatura $T.$ ${\ displaystyle T}$ $T.$ , viteza de derulare locală $\|{\vec {s}}\|$ ${\ displaystyle \ | {\ vec {s}} \ |}$ ${\ displaystyle \ | {\ vec {s}} \ |}$ , etc.

Soluții pentru cazuri statice

Coarda pe un bolard, ecuația cabestanului

Ilustrarea unui cablu bungee înfășurat în jurul unui element fix, cum ar fi un bolard. Zona de contact este împărțită în zone de aderență (lipire) și glisare (alunecare), în funcție de sarcinile exercitate pe ambele capete și de istoricul de încărcare.

Luați în considerare o coardă în care forțe egale (de ex. $F_{hold}=400N$ ${\ displaystyle F_ {hold} = 400N}$ ${\ displaystyle F_ {hold} = 400N}$ ) sunt exercitate de ambele părți. În acest fel coarda este ușor întinsă și induce o tensiune internă $T.$ ${\ displaystyle T}$ $T.$ ( $T=400N$ ${\ displaystyle T = 400N}$ ${\ displaystyle T = 400N}$ pe fiecare poziție de-a lungul șirului). Coarda este înfășurată în jurul unui element fix, cum ar fi o clemă ; este îndoit și este în contact cu suprafața elementului cu un unghi de contact (de ex. $180deg$ ${\ displaystyle 180deg}$ ${\ displaystyle 180deg}$ ). Presiunea normală este generată între frânghie și clemă, dar încă nu există frecare. Apoi, puterea pe o parte a bornei este crescută la o valoare mai mare (de ex $F_{load}=600N$ ${\ displaystyle F_ {load} = 600N}$ ${\ displaystyle F_ {load} = 600N}$ ). Acest lucru provoacă tensiuni de forfecare prin frecare în zona de contact. În situația finală, clema exercită o forță de frecare pe coardă, astfel încât să determine o situație statică.

Distribuția tensiunilor în frânghie în această situație finală este descrisă prin „ ecuația cabestanului , cu soluție:

{\begin{matrix}T(\phi )=T_{hold},&\phi \in [\phi _{hold},\phi _{intf}]\\T(\phi )=T_{load}\exp(-\mu \phi ),&\phi \in [\phi _{intf},\phi _{load}]\\\phi _{intf}=\log(T_{load}/T_{hold})/\mu &\end{matrix}}

{\ displaystyle {\ begin {matrix} T (\ phi) = T_ {hold}, & \ phi \ in [\ phi _ {hold}, \ phi _ {intf}] \\ T (\ phi) = T_ { load} \ exp (- \ mu \ phi), & \ phi \ in [\ phi _ {intf}, \ phi _ {load}] \\\ phi _ {intf} = \ log (T_ {load} / T_ {hold}) / \ mu & \ end {matrix}}}

{\ displaystyle {\ begin {matrix} T (\ phi) = T_ {hold}, & \ phi \ in [\ phi _ {hold}, \ phi _ {intf}] \\ T (\ phi) = T_ { load} \ exp (- \ mu \ phi), & \ phi \ in [\ phi _ {intf}, \ phi _ {load}] \\\ phi _ {intf} = \ log (T_ {load} / T_ {hold}) / \ mu & \ end {matrix}}}

Tensiunea crește din $T_{hold}$ ${\ displaystyle T_ {hold}}$ ${\ displaystyle T_ {hold}}$ pe partea lentă ( $\phi =\phi _{hold}$ ${\ displaystyle \ phi = \ phi _ {hold}}$ ${\ displaystyle \ phi = \ phi _ {hold}}$ ) la $T_{load}$ ${\ displaystyle T_ {load}}$ ${\ displaystyle T_ {load}}$ pe partea înaltă $\phi =\phi _{load}$ ${\ displaystyle \ phi = \ phi _ {load}}$ ${\ displaystyle \ phi = \ phi _ {load}}$ . Când privim din partea înaltă, tensiunea scade exponențial, până când atinge cea mai mică sarcină a $\phi =\phi _{intf}$ ${\ displaystyle \ phi = \ phi _ {intf}}$ ${\ displaystyle \ phi = \ phi _ {intf}}$ . După aceea, este constantă la această valoare. Punctul de tranziție $\phi _{intf}$ ${\ displaystyle \ phi _ {intf}}$ ${\ displaystyle \ phi _ {intf}}$ este determinată de relația dintre cele două sarcini și coeficientul de frecare. Aici tensiunile $T.$ ${\ displaystyle T}$ $T.$ sunt în newtoni și unghiuri $\phi$ ${\ displaystyle \ phi}$ $\ phi$ în radiani.

Tensiunea $T.$ ${\ displaystyle T}$ $T.$ în acordul în situația finală este crescut comparativ cu starea inițială. Prin urmare, frânghia s-a întins ușor. Aceasta înseamnă că nu toate particulele de suprafață ale corzii ar fi putut să-și fi menținut poziția inițială pe suprafața bornei. În timpul procesului de încărcare, coarda este ușor alunecată de-a lungul suprafeței în zona de alunecare (zona de alunecare) $\phi \in [\phi _{intf},\phi _{load}]$ ${\ displaystyle \ phi \ in [\ phi _ {intf}, \ phi _ {load}]}$ ${\ displaystyle \ phi \ in [\ phi _ {intf}, \ phi _ {load}]}$ . Această alunecare este exact suficient de mare pentru a ajunge la alungirea care apare în starea finală. Rețineți că nu există nici o alunecare care apare în starea finală; termenul de zonă de alunecare se referă la fluaj (alunecare) care a avut loc în timpul procesului de încărcare. Rețineți din nou că locația zonei de alunecare depinde de starea inițială și de procesul de încărcare. Dacă tensiunea inițială este $600N$ ${\ displaystyle 600N}$ ${\ displaystyle 600N}$ iar tensiunea este redusă la $400N$ ${\ displaystyle 400N}$ ${\ displaystyle 400N}$ în partea lentă, atunci zona de alunecare apare în partea lentă a zonei de contact. Pentru tensiunile inițiale dintre $400$ ${\ displaystyle 400}$ ${\ displaystyle 400}$ Și $600N$ ${\ displaystyle 600N}$ ${\ displaystyle 600N}$ , pot exista zone de alunecare pe ambele părți, cu o zonă de aderență între ele.

Sferă pe un plan, problema (tridimensională) a lui Cattaneo

Luați în considerare o sferă care este apăsată pe un plan (jumătate de spațiu) și apoi mutată pe suprafața planului. Dacă sfera și planul sunt privite în mod ideal ca corpuri rigide, atunci contactul s-ar produce exact într-un punct, iar sfera nu s-ar mișca până când forța tangențială aplicată atinge forța maximă de frecare. Apoi sfera începe să alunece pe suprafață până când forța aplicată este redusă din nou.

În realitate, având în vedere efectele elastice, situația este foarte diferită. Dacă o sferă elastică este presată pe un plan elastic din același material, atunci ambele corpuri se deformează, se creează o zonă circulară și apare o distribuție normală a presiunii (hertziene). De asemenea, centrul sferei este deplasat ușor pe o distanță $\delta _{n}$ ${\ displaystyle \ delta _ {n}}$ ${\ displaystyle \ delta _ {n}}$ care se numește abordare, care este, de asemenea, penetrarea maximă a suprafețelor nedeformate. Pentru o sferă de rază $R.$ ${\ displaystyle R}$ $R.$ și constante elastice $E,\nu$ ${\ displaystyle E, \ nu}$ ${\ displaystyle E, \ nu}$ soluția hertziană spune:

{\begin{array}{lll}p_{n}(x,y)=p_{0}{\sqrt {1-r^{2}/a^{2}}}&r={\sqrt {x^{2}+y^{2}}}\leq a&a={\sqrt {R\delta _{n}}}\\p_{0}={\frac {2}{\pi }}E^{*}\left(\delta _{n}/R\right)^{1/2}&F_{n}={\frac {4}{3}}E^{*}R^{1/2}\delta _{n}^{3/2}&E^{*}=E/2(1-\nu ^{2})\end{array}}

{\ displaystyle {\ begin {array} {lll} p_ {n} (x, y) = p_ {0} {\ sqrt {1-r ^ {2} / a ^ {2}}} & r = {\ sqrt {x ^ {2} + y ^ {2}}} \ leq a & a = {\ sqrt {R \ delta _ {n}}} \\ p_ {0} = {\ frac {2} {\ pi }} E ^ {*} \ left (\ delta _ {n} / R \ right) ^ {1/2} & F_ {n} = {\ frac {4} {3}} E ^ {*} R ^ {1/2} \ delta _ {n} ^ {3/2} & E ^ {*} = E / 2 (1- \ nu ^ {2}) \ end {array}}}

{\ displaystyle {\ begin {array} {lll} p_ {n} (x, y) = p_ {0} {\ sqrt {1-r ^ {2} / a ^ {2}}} & r = {\ sqrt {x ^ {2} + y ^ {2}}} \ leq a & a = {\ sqrt {R \ delta _ {n}}} \\ p_ {0} = {\ frac {2} {\ pi }} E ^ {*} \ left (\ delta _ {n} / R \ right) ^ {1/2} & F_ {n} = {\ frac {4} {3}} E ^ {*} R ^ {1/2} \ delta _ {n} ^ {3/2} & E ^ {*} = E / 2 (1- \ nu ^ {2}) \ end {array}}}

Acum considerați că se aplică o forță tangențială $F_{x}$ ${\ displaystyle F_ {x}}$ ${\ displaystyle F_ {x}}$ care este mai mică decât limita de frecare Coulomb $\mu F_{n}$ ${\ displaystyle \ mu F_ {n}}$ ${\ displaystyle \ mu F_ {n}}$ . Centrul sferei va fi apoi deplasat lateral pe o distanță mică $\delta _{x}$ ${\ displaystyle \ delta _ {x}}$ ${\ displaystyle \ delta _ {x}}$ care se numește deplasare. Se obține un echilibru static în care apar deformări elastice, precum și solicitări de frecare la forfecare la interfața de contact. În acest caz, dacă forța tangențială este redusă, atunci se reduc și deformările elastice și solicitările de forfecare. Mingea revine în mare măsură la poziția sa inițială, cu excepția pierderilor de frecare care apar din cauza alunecării locale în zona de contact.

Contact Această problemă a fost rezolvată în mod aproximativ de Cattaneo folosind o abordare analitică. Distribuția tensiunilor în starea de echilibru constă din două părți:

{\begin{array}{ll}p_{x}(x,y)=\mu p_{0}\left({\sqrt {1-r^{2}/a^{2}}}-{\frac {c}{a}}{\sqrt {1-r^{2}/c^{2}}}\right)&0\leq r\leq c\\p_{x}(x,y)=\mu p_{n}(x,y)&c\leq r\leq a\\p_{y}(x,y)=0&a\leq r\end{array}}

{\ displaystyle {\ begin {array} {ll} p_ {x} (x, y) = \ mu p_ {0} \ left ({\ sqrt {1-r ^ {2} / a ^ {2}}} - {\ frac {c} {a}} {\ sqrt {1-r ^ {2} / c ^ {2}}} \ right) & 0 \ leq r \ leq c \\ p_ {x} (x, y) = \ mu p_ {n} (x, y) & c \ leq r \ leq a \\ p_ {y} (x, y) = 0 & a \ leq r \ end {array}}}

{\ displaystyle {\ begin {array} {ll} p_ {x} (x, y) = \ mu p_ {0} \ left ({\ sqrt {1-r ^ {2} / a ^ {2}}} - {\ frac {c} {a}} {\ sqrt {1-r ^ {2} / c ^ {2}}} \ right) & 0 \ leq r \ leq c \\ p_ {x} (x, y) = \ mu p_ {n} (x, y) & c \ leq r \ leq a \\ p_ {y} (x, y) = 0 & a \ leq r \ end {array}}}

În regiunea centrală, adezivă, $0\leq r\leq c$ ${\ displaystyle 0 \ leq r \ leq c}$ ${\ displaystyle 0 \ leq r \ leq c}$ , particulele de suprafață ale planului se deplasează de-a lungul $u_{x}=\delta _{x}/2$ ${\ displaystyle u_ {x} = \ delta _ {x} / 2}$ ${\ displaystyle u_ {x} = \ delta _ {x} / 2}$ spre dreapta pe măsură ce particulele de suprafață ale sferei se deplasează de-a lungul $u_{x}=-\delta _{x}/2$ ${\ displaystyle u_ {x} = - \ delta _ {x} / 2}$ ${\ displaystyle u_ {x} = - \ delta _ {x} / 2}$ La stânga. Chiar dacă sfera în ansamblu se mișcă $\delta _{x}$ ${\ displaystyle \ delta _ {x}}$ ${\ displaystyle \ delta _ {x}}$ față de plan, aceste particule de suprafață nu s-au mișcat una față de cealaltă. În inelul circular exterior $a\leq r\leq c$ ${\ displaystyle a \ leq r \ leq c}$ ${\ displaystyle a \ leq r \ leq c}$ , particulele de suprafață s-au deplasat în schimb una față de cealaltă. Deplasarea lor locală se obține ca

s_{x}(x,y)=\delta _{x}+u_{x}^{sphere}(x,y)-u_{x}^{plane}(x,y)

{\ displaystyle s_ {x} (x, y) = \ delta _ {x} + u_ {x} ^ {sfera} (x, y) -u_ {x} ^ {plane} (x, y)}

{\ displaystyle s_ {x} (x, y) = \ delta _ {x} + u_ {x} ^ {sfera} (x, y) -u_ {x} ^ {plan} (x, y)}

Această schimbare $s_{x}(x,y)$ ${\ displaystyle s_ {x} (x, y)}$ ${\ displaystyle s_ {x} (x, y)}$ Are exact o astfel de magnitudine, încât obțineți un echilibru static cu solicitările de forfecare până la limita de tracțiune în această așa-numită zonă de alunecare (zona de alunecare).

Astfel, în timpul încărcării tangențiale a sferei, este o defilare parțială . Zona de contact este astfel împărțită într-o zonă de alunecare în care suprafețele se deplasează una față de cealaltă și o zonă de aderență în care nu se mișcă. În starea de echilibru, nu mai există alunecare.

Soluții pentru probleme de defilare dinamică

Soluția unei probleme de contact constă în starea de la interfață (unde este contactul, împărțirea zonei de contact în zone de aderență și alunecare și distribuțiile normale și de forță de forfecare) plus gama elastică din corpuri. Această soluție depinde de istoricul contactului. Acest lucru poate fi văzut printr-o extensie a problemei Cattaneo descrisă mai sus.

În problema lui Cattaneo, sfera este mai întâi apăsată pe plan și apoi mutată tangențial. Aceasta produce o alunecare parțială așa cum este descris mai sus.
Dacă sfera este mai întâi mutată tangențial și apoi apăsată pe plan, atunci nu există nicio diferență de deplasare între suprafețele opuse și, în consecință, nu există tensiune tangențială la interfața de contact.
Dacă abordarea în direcția normală și deplasarea tangențială sunt crescute simultan („compresie oblică”), atunci se poate obține o situație cu tensiune tangențială, dar fără alunecare locală. ^[2]

Acest lucru arată că starea din interfața de contact nu depinde doar de pozițiile relative ale celor două corpuri, ci și de istoricul mișcării lor. Un alt exemplu în acest sens apare dacă sfera este readusă la poziția sa inițială. Inițial nu a existat tensiune de forfecare la interfața de contact. Apoi a apărut micro-alunecarea inițială. Această micro-alunecare nu este complet anulată prin deplasarea înapoi. Prin urmare, în situația finală, tensiunile tangențiale rămân în interfață, în ceea ce pare a fi o configurație identică cu cea originală.

Soluția problemelor de contact cu rulare

Contact de rulare între un cilindru și un plan. Particulele se deplasează în zona de contact de la dreapta la stânga, fiind deformate din ce în ce mai mult până când începe fluirea locală.

Problemele de contact la rulare sunt probleme dinamice în care corpurile în contact se mișcă constant unul față de celălalt. O diferență cu problemele de contact din alunecare dinamică este că există mai multă varietate în starea diferitelor particule de suprafață. În timp ce zona de contact într-o problemă de alunecare constă din mai mult sau mai puțin din aceleași particule continuu, într-o problemă de contact cu rulare, particulele intră și ies din zona de contact neîncetat. Mai mult, într-o problemă de alunecare, particulele de suprafață sunt supuse peste tot mai mult sau mai puțin la aceeași deplasare tangențială, în timp ce într-o problemă de rulare, particulele de suprafață sunt stresate în moduri destul de diferite. Ele sunt lipsite de tensiuni atunci când intră în zona de contact, apoi aderă la o particulă a suprafeței opuse, sunt deformate de diferența de mișcare generală dintre cele două corpuri, până când se atinge limita de tracțiune locală și începe alunecarea locală. Acest proces se află în diferite etape pentru diferitele părți ale zonei de contact.

Dacă mișcarea generală a corpurilor este constantă, atunci se poate obține o stare staționară generală. Aici starea fiecărei particule de suprafață variază în timp, dar distribuția generală poate fi constantă. Acest lucru este formalizat folosind un sistem de coordonate care se deplasează de-a lungul zonei de contact.

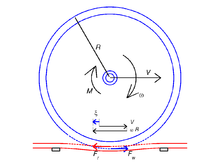
Rularea unui cilindru pe un plan, soluția (bidimensională) a Carter-Fromm

Luați în considerare un cilindru care rulează pe un plan (jumătate de spațiu) în condiții staționare, cu o alunecare longitudinală $\xi$ ${\ displaystyle \ xi}$ $\ xi$ independent de timp. (Relativ) departe de capetele cilindrilor apare o tensiune plană de situație și problema este bidimensională.

Dacă cilindrul și planul constau din aceleași materiale, atunci problema normală de contact este insensibilă la solicitări de forfecare. Zona de contact este o dungă $x\in [-a,a]$ ${\ displaystyle x \ în [-a, a]}$ ${\ displaystyle x \ în [-a, a]}$ , iar presiunea este descrisă de soluția bidimensională a lui Hertz.

{\begin{array}{lll}p_{n}(x)={\frac {p_{0}}{a}}{\sqrt {a^{2}-x^{2}}}&|x|\leq a&a^{2}=4F_{n}R/\pi E^{*}\\p_{0}=2F_{n}/\pi a&E^{*}=E/2(1-\nu ^{2})&\end{array}}

{\ displaystyle {\ begin {array} {lll} p_ {n} (x) = {\ frac {p_ {0}} {a}} {\ sqrt {a ^ {2} -x ^ {2}}} & | x | \ leq a & a ^ {2} = 4F_ {n} R / \ pi E ^ {*} \\ p_ {0} = 2F_ {n} / \ pi a & E ^ {*} = E / 2 (1 - \ nu ^ {2}) & \ end {array}}}

{\ displaystyle {\ begin {array} {lll} p_ {n} (x) = {\ frac {p_ {0}} {a}} {\ sqrt {a ^ {2} -x ^ {2}}} & | x | \ leq a & a ^ {2} = 4F_ {n} R / \ pi E ^ {*} \\ p_ {0} = 2F_ {n} / \ pi a & E ^ {*} = E / 2 (1 - \ nu ^ {2}) & \ end {array}}}

Distribuția tensiunii de forfecare din soluția Carter-Fromm. Se compune dintr-o zonă de aderență la marginea anterioară a zonei de contact și o zonă de alunecare la marginea din spate. Se notează lungimea zonei de aderență $2a'$ ${\ displaystyle 2a '}$ ${\ displaystyle 2a '}$ . În plus, coordonata de aderență este introdusă de $x'=x+a-a'$ ${\ displaystyle x '= x + a-a'}$ ${\ displaystyle x '= x + a-a'}$ . În cazul unei forțe pozitive $F_{x}>0$ ${\ displaystyle F_ {x}> 0}$ ${\ displaystyle F_ {x}> 0}$ (alunecare negativă $\xi <0$ ${\ displaystyle \ xi <0}$ ${\ displaystyle \ xi <0}$ ) Și:

{\begin{array}{ll}p_{x}(x)=0&|x|\geq a\\p_{x}(x)={\frac {\mu p_{0}}{a}}\left({\sqrt {a^{2}-x^{2}}}-{\sqrt {a'^{2}-x'^{2}}}\right)&a-2a'\leq x\leq a\\p_{x}(x)=\mu p_{n}(x)&x\leq a-2a'\end{array}}

{\ displaystyle {\ begin {array} {ll} p_ {x} (x) = 0 & | x | \ geq a \\ p_ {x} (x) = {\ frac {\ mu p_ {0}} { a}} \ left ({\ sqrt {a ^ {2} -x ^ {2}}} - {\ sqrt {a '^ {2} -x' ^ {2}}} \ right) & a-2a '\ leq x \ leq a \\ p_ {x} (x) = \ mu p_ {n} (x) & x \ leq a-2a' \ end {array}}}

{\ displaystyle {\ begin {array} {ll} p_ {x} (x) = 0 & | x | \ geq a \\ p_ {x} (x) = {\ frac {\ mu p_ {0}} { a}} \ left ({\ sqrt {a ^ {2} -x ^ {2}}} - {\ sqrt {a '^ {2} -x' ^ {2}}} \ right) & a-2a '\ leq x \ leq a \\ p_ {x} (x) = \ mu p_ {n} (x) & x \ leq a-2a' \ end {array}}}

Mărimea zonei de aderență depinde de alunecare, raza roții și coeficientul de frecare.

{\begin{array}{ll}a'=a{\sqrt {1-|F_{x}|/\mu F_{n}}},&{\mbox{per }}|F_{x}|\leq \mu F_{n}\\\xi =-sign(F_{x})\,\mu (a-a')/R,&{\mbox{cioè }}|\xi |\leq \mu a/R\\F_{x}=-sign(\xi )\,\mu F_{n}\left(1-\left(1+R|\xi |/\mu a\right)^{2}\right)\end{array}}

{\ displaystyle {\ begin {array} {ll} a '= a {\ sqrt {1- | F_ {x} | / \ mu F_ {n}}} și {\ mbox {per}} | F_ {x } | \ leq \ mu F_ {n} \\\ xi = -sign (F_ {x}) \, \ mu (aa ') / R, & {\ mbox {ie}} | \ xi | \ leq \ mu a / R \\ F_ {x} = - semn (\ xi) \, \ mu F_ {n} \ left (1- \ left (1 + R | \ xi | / \ mu a \ right) ^ {2} \ right) \ end {array}}}

{\ displaystyle {\ begin {array} {ll} a '= a {\ sqrt {1- | F_ {x} | / \ mu F_ {n}}} și {\ mbox {per}} | F_ {x } | \ leq \ mu F_ {n} \\\ xi = -sign (F_ {x}) \, \ mu (aa ') / R, & {\ mbox {ie}} | \ xi | \ leq \ mu a / R \\ F_ {x} = - semn (\ xi) \, \ mu F_ {n} \ left (1- \ left (1 + R | \ xi | / \ mu a \ right) ^ {2} \ right) \ end {array}}}

Pentru alunecări mai mari astfel încât $a'=0$ ${\ displaystyle a '= 0}$ $a '= 0$ apare o alunecare completă.

Abordări bazate pe jumătăți de spații

Când se iau în considerare problemele de contact pe scări spațiale intermediare, neomogenitățile materialelor și rugozitatea suprafețelor detectabile la scară mică sunt ignorate. Corpurile sunt considerate formate din suprafețe netede și materiale omogene. Se presupune o abordare continuă în care tensiunile, încordările și deplasările sunt descrise prin funcții (parțial) continue.

Abordarea demi-spațiilor este o soluție elegantă pentru așa-numitele probleme de contact cu „margini netede” sau „concentrate”.

Dacă un corp elastic masiv este încărcat pe o mică secțiune a suprafeței sale, atunci tensiunile elastice sunt atenuate proporțional cu $1/distanza^{2}$ ${\ displaystyle 1 / distance ^ {2}}$ ${\ displaystyle 1 / distance ^ {2}}$ iar deplasările elastice ale $1/distanza$ ${\ displaystyle 1 / distance}$ ${\ displaystyle 1 / distance}$ la îndepărtarea de această suprafață.
Dacă un corp nu are margini ascuțite în sau în apropierea regiunii de contact, atunci răspunsul său la o sarcină de suprafață poate fi bine aproximat prin răspunsul unui spațiu elastic (de exemplu, toate punctele $(x,y,z)^{T}\in \mathbb {R} ^{3}\,\!$ ${\ displaystyle (x, y, z) ^ {T} \ in \ mathbb {R} ^ {3} \, \!}$ ${\ displaystyle (x, y, z) ^ {T} \ in \ mathbb {R} ^ {3} \, \!}$ cu $z>0\,\!$ ${\ displaystyle z> 0 \, \!}$ ${\ displaystyle z> 0 \, \!}$ ).
Problema demi-spațiului elastic este rezolvată analitic, vezi soluția Boussinesq-Cerruti .
Datorită liniarității acestei abordări, mai multe soluții parțiale pot fi suprapuse.

Folosind soluția fundamentală pentru jumătate de spațiu, problema completă a contactului tridimensional este redusă la o problemă bidimensională pentru suprafețele de delimitare ale corpurilor.

O simplificare suplimentară apare dacă cele două corpuri sunt „asemănătoare din punct de vedere geometric și elastic”. În general, tensiunea într-un corp într-o anumită direcție induce deplasări chiar și în direcții perpendiculare. În consecință, în problema contactului există o interacțiune între stresul normal și deplasările tangențiale și o interacțiune între stresul de forfecare și deplasările normale. Ma se la tensione normale nell'interfaccia di contatto induce gli stessi spostamenti tangenziali in entrambi i corpi a contatto, allora non c'è nessuno spostamento tangenziale relativo delle due superfici. In quel caso, i problemi di contatto normale e tangenziale sono disaccoppiati. Se questo avviene, allora i due corpi sono chiamati quasi identici . Ciò accade ad esempio se i corpi sono simmetrici speculari rispetto al piano di contatto e hanno le stesse costanti elastiche.

Le soluzioni classiche basate sull'approccio dei semispazi sono:

Hertz risolse il problema del contatto in assenza di attrito, per una geometria semplice (superfici curve con raggi di curvatura costanti).
Carter considerò il contatto con rotolamento tra un cilindro e un piano, come descritto sopra. Una soluzione analitica completa è fornita per la trazione tangenziale.
Cattaneo considerò la compressione e lo spostamento di due sfere, come descritto sopra. Si noti che questa soluzione analitica è approssimata. In realtà si verificano piccole trazioni tangenziali $p_{y}$ $p_{y}$ $p_{y}$ che sono ignorate.

Note

^ ^a ^b ^c KL Johnson, Contact Mechanics , Cambridge, Cambridge University Press, 1985.
^ ^a ^b VL Popov, Contact Mechanics and Friction. Physical Principles and Applications , Berlino, Springer-Verlag, 2010.
^ Introduction to Tribology – Friction , su depts.washington.edu . URL consultato il 21 dicembre 2008 .
^ Heinrich Hertz , Contact between solid elastic bodies , in Journ. für reine und angewandte Math. , vol. 92, 1882.
^ ^a ^b K. Knothe, History of wheel/rail contact mechanics: from Redtenbacher to Kalker , in Vehicle System Dynamics , vol. 46, n. 1-2, 2008, pp. 9–26.
^ Joost J. Kalker, On the rolling contact of two elastic bodies in the presence of dry friction , Delft University of Technology, 1967.
^ Hans Pacejka, Tire and Vehicle Dynamics , Oxford, Butterworth-Heinemann, 2002.
^ TA Laursen, Computational Contact and Impact Mechanics, Fundamentals of Modeling Interfacial Phenomena in Nonlinear Finite Element Analysis , Berlino, Springer, 2002.
^ P. Wriggers, Computational Contact Mechanics, 2nd ed. , Heidelberg, Springer, 2006.
^ JJ Kalker, Three-Dimensional Elastic Bodies in Rolling Contact , Dordrecht, Kluwer Academic Publishers, 1990.
^ JJ Kalker, Three-Dimensional Elastic Bodies in Rolling Contact , Dordrecht, Kluwer Academic Publishers, 1990.
^ B. Jacobsen e JJ Kalker (a cura di), Rolling Contact Phenomena , Vienna-New York, Springer-Verlag, 2000.

Voci correlate

Collegamenti esterni

( EN ) [1] ^{[ collegamento interrotto ]} Biografia di JJ Kalker ( Università tecnica di Delft ).
( EN ) [2] Programma CONTACT hertziano/non hertziano di Kalker.

Portale Ingegneria

Portale Meccanica

[Johnson1985-1] KL Johnson, Contact Mechanics , Cambridge, Cambridge University Press, 1985.

[Popov2010-2] VL Popov, Contact Mechanics and Friction. Physical Principles and Applications , Berlino, Springer-Verlag, 2010.

[depts.washington.edu-3] Introduction to Tribology – Friction , su depts.washington.edu . URL consultato il 21 dicembre 2008 .

[Hertz1882-4] Heinrich Hertz , Contact between solid elastic bodies , in Journ. für reine und angewandte Math. , vol. 92, 1882.

[Knothe2008-5] K. Knothe, History of wheel/rail contact mechanics: from Redtenbacher to Kalker , in Vehicle System Dynamics , vol. 46, n. 1-2, 2008, pp. 9–26.

[Kalker1967-6] Joost J. Kalker, On the rolling contact of two elastic bodies in the presence of dry friction , Delft University of Technology, 1967.

[Pacejka2002-7] Hans Pacejka, Tire and Vehicle Dynamics , Oxford, Butterworth-Heinemann, 2002.

[Laursen2002-8] TA Laursen, Computational Contact and Impact Mechanics, Fundamentals of Modeling Interfacial Phenomena in Nonlinear Finite Element Analysis , Berlino, Springer, 2002.

[Wriggers2006-9] P. Wriggers, Computational Contact Mechanics, 2nd ed. , Heidelberg, Springer, 2006.

[10] JJ Kalker, Three-Dimensional Elastic Bodies in Rolling Contact , Dordrecht, Kluwer Academic Publishers, 1990.

[11] JJ Kalker, Three-Dimensional Elastic Bodies in Rolling Contact , Dordrecht, Kluwer Academic Publishers, 1990.

[Jacobsen2000-12] B. Jacobsen e JJ Kalker (a cura di), Rolling Contact Phenomena , Vienna-New York, Springer-Verlag, 2000.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]