Reprezentarea matricială a conicelor

În geometrie , o secțiune conică poate fi reprezentată sub formă de matrice , adică prin utilizarea matricilor .

Invarianții conicelor

Este posibil să se definească trei valori asociate fiecărei conice , care sunt definite ca invarianți . Având în vedere o ecuație conică :

$\Gamma \left(x,y\right):ax^{2}+2bxy+cy^{2}+2dx+2ey+f=0\;$ ${\ displaystyle \ Gamma \ left (x, y \ right): ax ^ {2} + 2bxy + cy ^ {2} + 2dx + 2ey + f = 0 \;}$ ${\ displaystyle \ Gamma \ left (x, y \ right): ax ^ {2} + 2bxy + cy ^ {2} + 2dx + 2ey + f = 0 \;}$

este posibil să se asocieze două matrice A și B :

$A={\begin{bmatrix}a&b&d\\b&c&e\\d&e&f\end{bmatrix}},B={\begin{bmatrix}a&b\\b&c\end{bmatrix}}$ ${\ displaystyle A = {\ begin {bmatrix} a & b & d \\ b & c & e \\ d & e & f \ end {bmatrix}}, B = {\ begin {bmatrix} a & b \\ b & c \ end {bmatrix}}}$ ${\ displaystyle A = {\ begin {bmatrix} a & b & d \\ b & c & e \\ d & e & f \ end {bmatrix}}, B = {\ begin {bmatrix} a & b \\ b & c \ end {bmatrix}}}$

din care se extrapolează trei numere:

invariantul cubic $I_{3}$ ${\ displaystyle I_ {3}}$ ${\ displaystyle I_ {3}}$ , determinant al matricei $LA$ ${\ displaystyle A}$ $LA$ :

I_{3}=\det(A)=\det {\begin{bmatrix}a&b&d\\b&c&e\\d&e&f\end{bmatrix}}

{\ displaystyle I_ {3} = \ det (A) = \ det {\ begin {bmatrix} a & b & d \\ b & c & e \\ d & e & f \ end {bmatrix}}}

{\ displaystyle I_ {3} = \ det (A) = \ det {\ begin {bmatrix} a & b & d \\ b & c & e \\ d & e & f \ end {bmatrix}}}

=

a(cf-e^{2})-b(bf-de)+d(be-cd)\;

{\ displaystyle a (cf-e ^ {2}) - b (bf-de) + d (be-cd) \;}

{\ displaystyle a (cf-e ^ {2}) - b (bf-de) + d (be-cd) \;}

invariantul pătratic $I_{2}$ ${\ displaystyle I_ {2}}$ $I_2$ , determinant al matricei $B.$ ${\ displaystyle B}$ $B.$ :

I_{2}=\det(B)=\det {\begin{bmatrix}a&b\\b&c\end{bmatrix}}

{\ displaystyle I_ {2} = \ det (B) = \ det {\ begin {bmatrix} a & b \\ b & c \ end {bmatrix}}}

{\ displaystyle I_ {2} = \ det (B) = \ det {\ begin {bmatrix} a & b \\ b & c \ end {bmatrix}}}

=

ac-b^{2}

{\ displaystyle ac-b ^ {2}}

{\ displaystyle ac-b ^ {2}}

invariantul liniar $I_{1}$ ${\ displaystyle I_ {1}}$ $I_1$ , urma matricei $B.$ ${\ displaystyle B}$ $B.$ :

I_{1}=\operatorname {tr} {\begin{bmatrix}a&b\\b&c\end{bmatrix}}

{\ displaystyle I_ {1} = \ operatorname {tr} {\ begin {bmatrix} a & b \\ b & c \ end {bmatrix}}}

{\ displaystyle I_ {1} = \ operatorname {tr} {\ begin {bmatrix} a & b \\ b & c \ end {bmatrix}}}

=

a+c

{\ displaystyle a + c}

{\ displaystyle a + c}

Denumirea de „invariant” derivă din faptul că prin aplicarea oricărei traduceri și / sau a oricărei rotații a conicii, aceste numere nu se modifică.

Denumirile „cubic”, „pătratic” și „liniar” derivă din faptul că înmulțind ambele fețe ale ecuației conice cu un număr real nenul p , invarianții sunt înmulțiți respectiv cu $p^{3}$ ${\ displaystyle p ^ {3}}$ $p ^ 3$ , $p^{2}$ ${\ displaystyle p ^ {2}}$ $p ^ 2$ Și $p$ ${\ displaystyle p}$ $p$ . Având în vedere ecuația conicii $\Gamma (x,y)=0$ ${\ displaystyle \ Gamma (x, y) = 0}$ ${\ displaystyle \ Gamma (x, y) = 0}$ , ziceri $I_{3}$ ${\ displaystyle I_ {3}}$ ${\ displaystyle I_ {3}}$ , $I_{2}$ ${\ displaystyle I_ {2}}$ $I_2$ Și $I_{1}$ ${\ displaystyle I_ {1}}$ $I_1$ invarianții acestei conici și ziceri $I_{3}'$ ${\ displaystyle I_ {3} '}$ ${\ displaystyle I_ {3} '}$ , $I_{2}'$ ${\ displaystyle I_ {2} '}$ ${\ displaystyle I_ {2} '}$ Și $I_{1}'$ ${\ displaystyle I_ {1} '}$ ${\ displaystyle I_ {1} '}$ invarianții conicii ecuației $p\cdot \Gamma (x,y)=0$ ${\ displaystyle p \ cdot \ Gamma (x, y) = 0}$ ${\ displaystyle p \ cdot \ Gamma (x, y) = 0}$ cu $p\neq 0$ ${\ displaystyle p \ neq 0}$ ${\ displaystyle p \ neq 0}$ , avem următoarele identități:

$I_{3}'=p^{3}I_{3}$ ${\ displaystyle I_ {3} '= p ^ {3} I_ {3}}$ ${\ displaystyle I_ {3} '= p ^ {3} I_ {3}}$ (invariant cub)

$I_{2}'=p^{2}I_{2}$ ${\ displaystyle I_ {2} '= p ^ {2} I_ {2}}$ ${\ displaystyle I_ {2} '= p ^ {2} I_ {2}}$ (invariant pătratic)

$I_{1}'=pI_{1}$ ${\ displaystyle I_ {1} '= pI_ {1}}$ ${\ displaystyle I_ {1} '= pI_ {1}}$ (invariant liniar)

Clasificarea metrică a conicelor

Pe baza invarianților este posibil să se clasifice conicele și, prin urmare, să se stabilească ce fel de obiect este, dacă:

$THE$ $3$ $=$ $0$ {\ displaystyle I_ {3} = 0} ${\ displaystyle I_ {3} = 0}$ conica este degenerată și, în special, dacă:
- $I_{2}<0$ ${\ displaystyle I_ {2} <0}$ ${\ displaystyle I_ {2} <0}$ , este redus la două linii reale distincte
- $THE$ $2$ $=$ $0$ {\ displaystyle I_ {2} = 0} ${\ displaystyle I_ {2} = 0}$ , se fierbe până
  - pereche de linii reale paralele sau complexe distincte conjugate fără puncte comune (rang matricial complet = 2)
  - pereche de linii reale coincidente (rang matricial complet = 1)
- $I_{2}>0$ ${\ displaystyle I_ {2}> 0}$ ${\ displaystyle I_ {2}> 0}$ , este redus la două linii imaginare conjugate.
$THE$ $3$ $\neq$ $0$ {\ displaystyle I_ {3} \ neq 0} ${\ displaystyle I_ {3} \ neq 0}$ conica nu este degenerată și, în special, dacă:
- $THE$ $2$ $<$ $0$ {\ displaystyle I_ {2} <0} ${\ displaystyle I_ {2} <0}$ este o hiperbolă
  - echilateral dacă $I_{1}=0$ ${\ displaystyle I_ {1} = 0}$ ${\ displaystyle I_ {1} = 0}$
  - nu echilaterală dacă $I_{1}\neq 0$ ${\ displaystyle I_ {1} \ neq 0}$ ${\ displaystyle I_ {1} \ neq 0}$
- $I_{2}=0$ ${\ displaystyle I_ {2} = 0}$ ${\ displaystyle I_ {2} = 0}$ este o parabolă
- $THE$ $2$ $>$ $0$ {\ displaystyle I_ {2}> 0} ${\ displaystyle I_ {2}> 0}$ este o elipsă
  - real dacă este $I_{1}I_{3}<0$ ${\ displaystyle I_ {1} I_ {3} <0}$ ${\ displaystyle I_ {1} I_ {3} <0}$
  - imaginar dacă este $I_{1}I_{3}>0$ ${\ displaystyle I_ {1} I_ {3}> 0}$ ${\ displaystyle I_ {1} I_ {3}> 0}$

De exemplu, ecuația conică : $x^{2}-x=0$ ${\ displaystyle x ^ {2} -x = 0}$ ${\ displaystyle x ^ {2} -x = 0}$ , având $I_{3}=0$ ${\ displaystyle I_ {3} = 0}$ ${\ displaystyle I_ {3} = 0}$ Și $I_{2}<0$ ${\ displaystyle I_ {2} <0}$ ${\ displaystyle I_ {2} <0}$ , este o conică degenerată în două linii reale distincte: $x=0$ ${\ displaystyle x = 0}$ $x = 0$ Și $x=1$ ${\ displaystyle x = 1}$ $x = 1$ .

Reducerea unei forme conice la canonice

Ecuația unei conici de tipul dat

ax^{2}+2bxy+cy^{2}+2dx+2ey+f=0\;

{\ displaystyle ax ^ {2} + 2bxy + cy ^ {2} + 2dx + 2ey + f = 0 \;}

ax ^ {2} + 2bxy + cy ^ {2} + 2dx + 2ey + f = 0 \;

este posibil să acționăm asupra coeficienților, prin invarianți, pentru a obține forma canonică a conicii. Prin formă canonică a unei conici , înțelegem:

pentru elipsă : trebuie să aibă ca centru originea axelor carteziene și focarele sale trebuie să fie pe axă $x\;$ ${\ displaystyle x \;}$ ${\ displaystyle x \;}$ sau pe axă $y\;$ ${\ displaystyle y \;}$ ${\ displaystyle y \;}$
pentru parabolă : trebuie să aibă un vârf la origine și una dintre axele carteziene ca axă
pentru hiperbolă : trebuie să aibă centru în originea axelor și focarele trebuie să aparțină axei $x\;$ ${\ displaystyle x \;}$ ${\ displaystyle x \;}$ sau la ax $y\;$ ${\ displaystyle y \;}$ ${\ displaystyle y \;}$ .

În general, o ecuație de tipul: $ax^{2}+2bxy+cy^{2}+2dx+2ey+f=0\;$ ${\ displaystyle ax ^ {2} + 2bxy + cy ^ {2} + 2dx + 2ey + f = 0 \;}$ $ax ^ {2} + 2bxy + cy ^ {2} + 2dx + 2ey + f = 0 \;$ , oferă o conică rototradusă în ceea ce privește originea axelor: este deci necesar să rotiți conica (primul pas) și apoi să o traduceți până când centrul sau vârful este adus la origine (al doilea pas).

Pasul 1: rotația conicii se obține prin anularea coeficientului de $xy\;$ ${\ displaystyle xy \;}$ ${\ displaystyle xy \;}$ , acesta este $2b\;$ ${\ displaystyle 2b \;}$ ${\ displaystyle 2b \;}$ .

După această operație, conica se micșorează în formă $\lambda _{1}x^{2}+\lambda _{2}y^{2}+2dx+2ey+f=0\;$ ${\ displaystyle \ lambda _ {1} x ^ {2} + \ lambda _ {2} y ^ {2} + 2dx + 2ey + f = 0 \;}$ ${\ displaystyle \ lambda _ {1} x ^ {2} + \ lambda _ {2} y ^ {2} + 2dx + 2ey + f = 0 \;}$ , in care $\lambda _{1}\;$ ${\ displaystyle \ lambda _ {1} \;}$ ${\ displaystyle \ lambda _ {1} \;}$ Și $\lambda _{2}\;$ ${\ displaystyle \ lambda _ {2} \;}$ ${\ displaystyle \ lambda _ {2} \;}$ se obțin în felul următor: matricea trebuie diagonalizată

B={\begin{bmatrix}a&b\\b&c\end{bmatrix}}

{\ displaystyle B = {\ begin {bmatrix} a & b \\ b & c \ end {bmatrix}}}

{\ displaystyle B = {\ begin {bmatrix} a & b \\ b & c \ end {bmatrix}}}

și veți obține matricea

B'={\begin{bmatrix}\lambda _{1}&0\\0&\lambda _{2}\end{bmatrix}}

{\ displaystyle B '= {\ begin {bmatrix} \ lambda _ {1} & 0 \\ 0 & \ lambda _ {2} \ end {bmatrix}}}

{\ displaystyle B '= {\ begin {bmatrix} \ lambda _ {1} & 0 \\ 0 & \ lambda _ {2} \ end {bmatrix}}}

cu $\lambda _{1}\;$ ${\ displaystyle \ lambda _ {1} \;}$ ${\ displaystyle \ lambda _ {1} \;}$ Și $\lambda _{2}\;$ ${\ displaystyle \ lambda _ {2} \;}$ ${\ displaystyle \ lambda _ {2} \;}$ valori proprii ale matricei diagonale .

$\lambda _{1}\;$ ${\ displaystyle \ lambda _ {1} \;}$ ${\ displaystyle \ lambda _ {1} \;}$ Și $\lambda _{2}\;$ ${\ displaystyle \ lambda _ {2} \;}$ ${\ displaystyle \ lambda _ {2} \;}$ sunt coeficienții termenilor pătratici ai ecuației conicii . În cazul pildei sau $\lambda _{1}\;$ ${\ displaystyle \ lambda _ {1} \;}$ ${\ displaystyle \ lambda _ {1} \;}$ sau $\lambda _{2}\;$ ${\ displaystyle \ lambda _ {2} \;}$ ${\ displaystyle \ lambda _ {2} \;}$ va fi nul, deoarece există un singur termen pătratic în ecuație .

Al doilea pas: cu traducerea, dacă conica este în centru (o elipsă sau o hiperbolă ), obținem o ecuație de tipul: $\lambda _{1}x^{2}+\lambda _{2}y^{2}+\lambda _{3}=0\;$ ${\ displaystyle \ lambda _ {1} x ^ {2} + \ lambda _ {2} y ^ {2} + \ lambda _ {3} = 0 \;}$ ${\ displaystyle \ lambda _ {1} x ^ {2} + \ lambda _ {2} y ^ {2} + \ lambda _ {3} = 0 \;}$ in care $\lambda _{1}\;$ ${\ displaystyle \ lambda _ {1} \;}$ ${\ displaystyle \ lambda _ {1} \;}$ Și $\lambda _{2}\;$ ${\ displaystyle \ lambda _ {2} \;}$ ${\ displaystyle \ lambda _ {2} \;}$ sunt valorile obținute cu pasul anterior, în timp ce $\lambda _{3}\;$ ${\ displaystyle \ lambda _ {3} \;}$ ${\ displaystyle \ lambda _ {3} \;}$ se obține în modul următor:

$\lambda _{3}={\frac {I_{3}}{I_{2}}}\;$ ${\ displaystyle \ lambda _ {3} = {\ frac {I_ {3}} {I_ {2}}} \;}$ ${\ displaystyle \ lambda _ {3} = {\ frac {I_ {3}} {I_ {2}}} \;}$ .

Dacă conica este o parabolă , obținem o ecuație ca: $\lambda _{1}x^{2}+2\lambda _{3}y=0\;$ ${\ displaystyle \ lambda _ {1} x ^ {2} +2 \ lambda _ {3} y = 0 \;}$ ${\ displaystyle \ lambda _ {1} x ^ {2} +2 \ lambda _ {3} y = 0 \;}$ in care: $\lambda _{1}\;$ ${\ displaystyle \ lambda _ {1} \;}$ ${\ displaystyle \ lambda _ {1} \;}$ este valoarea proprie diferită de zero e $\lambda _{3}=\pm {\sqrt {\left|{\frac {I_{3}}{\lambda _{1}}}\right|}}\;$ ${\ displaystyle \ lambda _ {3} = \ pm {\ sqrt {\ left | {\ frac {I_ {3}} {\ lambda _ {1}}} \ right |}} \;}$ ${\ displaystyle \ lambda _ {3} = \ pm {\ sqrt {\ left | {\ frac {I_ {3}} {\ lambda _ {1}}} \ right |}} \;}$ cu $I_{3}$ ${\ displaystyle I_ {3}}$ ${\ displaystyle I_ {3}}$ invariant cubic. Observăm în mod explicit că pentru pilde: $\lambda _{1}=I_{1}=a+c\;$ ${\ displaystyle \ lambda _ {1} = I_ {1} = a + c \;}$ ${\ displaystyle \ lambda _ {1} = I_ {1} = a + c \;}$

Exemple

Elipsă

Ecuația conică

9x^{2}-4xy+6y^{2}-3=0

{\ displaystyle 9x ^ {2} -4xy + 6y ^ {2} -3 = 0}

{\ displaystyle 9x ^ {2} -4xy + 6y ^ {2} -3 = 0}

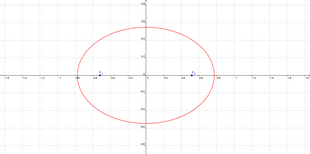
Rectoria conicii

9x^{2}-4xy+6y^{2}-3=0

{\ displaystyle 9x ^ {2} -4xy + 6y ^ {2} -3 = 0}

{\ displaystyle 9x ^ {2} -4xy + 6y ^ {2} -3 = 0}

Conica ecuației este dată $\Gamma (x,y)=9x^{2}-4xy+6y^{2}-3=0$ ${\ displaystyle \ Gamma (x, y) = 9x ^ {2} -4xy + 6y ^ {2} -3 = 0}$ ${\ displaystyle \ Gamma (x, y) = 9x ^ {2} -4xy + 6y ^ {2} -3 = 0}$ ; studiind determinanții $LA$ ${\ displaystyle A}$ $LA$ Și $B.$ ${\ displaystyle B}$ $B.$ constatăm că este o elipsă. Verificând derivatele parțiale ale ecuației, plasându-le într-un sistem și echivalându-le cu 0, obținem centrul curent al elipsei:

$\left\{{\begin{matrix}{\partial \Gamma \over \partial x}=18x-4y=0\\{\partial \Gamma \over \partial y}=-4x+12y=0\end{matrix}}\right.\Rightarrow C(0,0)$ ${\ displaystyle \ left \ {{\ begin {matrix} {\ partial \ Gamma \ over \ partial x} = 18x-4y = 0 \\ {\ partial \ Gamma \ over \ partial y} = - 4x + 12y = 0 \ end {matrix}} \ right. \ Rightarrow C (0,0)}$ ${\ displaystyle \ left \ {{\ begin {matrix} {\ partial \ Gamma \ over \ partial x} = 18x-4y = 0 \\ {\ partial \ Gamma \ over \ partial y} = - 4x + 12y = 0 \ end {matrix}} \ right. \ Rightarrow C (0,0)}$

Deoarece centrul este deja la origine, nu va fi nevoie să traducă conica. Pentru a obține forma canonică trebuie să rotim conica în diagonală $B.$ ${\ displaystyle B}$ $B.$ ; valorile proprii ale formei pătratice sunt 5 și 10 și vectorii proprii respectivi sunt (1,2) și (-2,1). Stivuind acești vectori proprii normalizați corespunzător într-o matrice $P.$ ${\ displaystyle P}$ $P.$ obținem o matrice de rotație (în sensul acelor de ceasornic, deoarece $det(P)=1$ ${\ displaystyle det (P) = 1}$ ${\ displaystyle det (P) = 1}$ ):

$P={\begin{bmatrix}{1 \over {\sqrt {5}}}&{-2 \over {\sqrt {5}}}\\{2 \over {\sqrt {5}}}&{1 \over {\sqrt {5}}}\end{bmatrix}}=\left({\frac {1}{\sqrt {5}}}\right){\begin{bmatrix}1&-2\\2&1\end{bmatrix}}$ ${\ displaystyle P = {\ begin {bmatrix} {1 \ over {\ sqrt {5}}} și {- 2 \ over {\ sqrt {5}}} \\ {2 \ over {\ sqrt {5}} } & {1 \ over {\ sqrt {5}}} \ end {bmatrix}} = \ left ({\ frac {1} {\ sqrt {5}}} \ right) {\ begin {bmatrix} 1 & - 2 \\ 2 & 1 \ end {bmatrix}}}$ ${\ displaystyle P = {\ begin {bmatrix} {1 \ over {\ sqrt {5}}} și {- 2 \ over {\ sqrt {5}}} \\ {2 \ over {\ sqrt {5}} } & {1 \ over {\ sqrt {5}}} \ end {bmatrix}} = \ left ({\ frac {1} {\ sqrt {5}}} \ right) {\ begin {bmatrix} 1 & - 2 \\ 2 & 1 \ end {bmatrix}}}$

Atâta timp cât $(x,y)^{T}=P({\tilde {x}},{\tilde {y}})^{T}$ ${\ displaystyle (x, y) ^ {T} = P ({\ tilde {x}}, {\ tilde {y}}) ^ {T}}$ ${\ displaystyle (x, y) ^ {T} = P ({\ tilde {x}}, {\ tilde {y}}) ^ {T}}$ , poti sa scrii:

$\left\{{\begin{matrix}x={\frac {1}{\sqrt {5}}}({\tilde {x}}-2{\tilde {y}})\\y={\frac {1}{\sqrt {5}}}(2{\tilde {x}}+{\tilde {y}})\end{matrix}}\right.$ ${\ displaystyle \ left \ {{\ begin {matrix} x = {\ frac {1} {\ sqrt {5}}} ({\ tilde {x}} - 2 {\ tilde {y}}) \\ y = {\ frac {1} {\ sqrt {5}}} (2 {\ tilde {x}} + {\ tilde {y}}) \ end {matrix}} \ right.}$ ${\ displaystyle \ left \ {{\ begin {matrix} x = {\ frac {1} {\ sqrt {5}}} ({\ tilde {x}} - 2 {\ tilde {y}}) \\ y = {\ frac {1} {\ sqrt {5}}} (2 {\ tilde {x}} + {\ tilde {y}}) \ end {matrix}} \ right.}$

Înlocuind conica în ecuația originală obținem noua ecuație $5{\tilde {x}}^{2}+10{\tilde {y}}^{2}-3=0$ ${\ displaystyle 5 {\ tilde {x}} ^ {2} +10 {\ tilde {y}} ^ {2} -3 = 0}$ ${\ displaystyle 5 {\ tilde {x}} ^ {2} +10 {\ tilde {y}} ^ {2} -3 = 0}$ , care este aceeași conică de pornire, dar rotită în așa fel încât să aibă focarele (în acest caz) pe axă $X$ ${\ displaystyle x}$ $X$ . Forma canonică a conicii noastre este ${5 \over 3}X^{2}+{10 \over 3}Y^{2}=1$ ${\ displaystyle {5 \ over 3} X ^ {2} + {10 \ over 3} Y ^ {2} = 1}$ ${\ displaystyle {5 \ over 3} X ^ {2} + {10 \ over 3} Y ^ {2} = 1}$ , cu focuri $F_{1}=\left(-{\sqrt {\frac {3}{10}}},0\right),F_{2}=\left({\sqrt {\frac {3}{10}}},0\right)$ ${\ displaystyle F_ {1} = \ left (- {\ sqrt {\ frac {3} {10}}}, 0 \ right), F_ {2} = \ left ({\ sqrt {\ frac {3} { 10}}}, 0 \ dreapta)}$ ${\ displaystyle F_ {1} = \ left (- {\ sqrt {\ frac {3} {10}}}, 0 \ right), F_ {2} = \ left ({\ sqrt {\ frac {3} { 10}}}, 0 \ dreapta)}$

Hiperbolă

Ecuația conică

4xy+3y^{2}+2x+4y=0

{\ displaystyle 4xy + 3y ^ {2} + 2x + 4y = 0}

{\ displaystyle 4xy + 3y ^ {2} + 2x + 4y = 0}

Rectoria conicii

4xy+3y^{2}+2x+4y=0

{\ displaystyle 4xy + 3y ^ {2} + 2x + 4y = 0}

{\ displaystyle 4xy + 3y ^ {2} + 2x + 4y = 0}

Conica ecuației este dată $\Gamma (x,y)=4xy+3y^{2}+2x+4y=0$ ${\ displaystyle \ Gamma (x, y) = 4xy + 3y ^ {2} + 2x + 4y = 0}$ ${\ displaystyle \ Gamma (x, y) = 4xy + 3y ^ {2} + 2x + 4y = 0}$ ; studiind determinanții $LA$ ${\ displaystyle A}$ $LA$ Și $B.$ ${\ displaystyle B}$ $B.$ descoperim că este hiperbolă. Verificând derivatele parțiale ale ecuației, plasându-le într-un sistem și echivalându-le cu 0, obținem centrul curent al hiperbolei:

$\left\{{\begin{matrix}{\partial \Gamma \over \partial x}=4y+2=0\\{\partial \Gamma \over \partial y}=4x+6y+4=0\end{matrix}}\right.\Rightarrow C\left(-{\frac {1}{4}},-{\frac {1}{2}}\right)$ ${\ displaystyle \ left \ {{\ begin {matrix} {\ partial \ Gamma \ over \ partial x} = 4y + 2 = 0 \\ {\ partial \ Gamma \ over \ partial y} = 4x + 6y + 4 = 0 \ end {matrix}} \ right. \ Rightarrow C \ left (- {\ frac {1} {4}}, - {\ frac {1} {2}} \ right)}$ ${\ displaystyle \ left \ {{\ begin {matrix} {\ partial \ Gamma \ over \ partial x} = 4y + 2 = 0 \\ {\ partial \ Gamma \ over \ partial y} = 4x + 6y + 4 = 0 \ end {matrix}} \ right. \ Rightarrow C \ left (- {\ frac {1} {4}}, - {\ frac {1} {2}} \ right)}$

Asimptotele sunt liniile drepte $C.$ ${\ displaystyle C}$ $C.$ paralele cu cele obținute prin descompunerea formei pătratice a conicii:

$4xy+3y^{2}=y(4x+3y)$ ${\ displaystyle 4xy + 3y ^ {2} = y (4x + 3y)}$ ${\ displaystyle 4xy + 3y ^ {2} = y (4x + 3y)}$
$\Rightarrow r_{1}:y=-{\frac {1}{2}}$ ${\ displaystyle \ Rightarrow r_ {1}: y = - {\ frac {1} {2}}}$ ${\ displaystyle \ Rightarrow r_ {1}: y = - {\ frac {1} {2}}}$
$\Rightarrow r_{2}:4x+3y=4\left(-{\frac {1}{4}}\right)+3\left(-{\frac {1}{2}}\right)=-{\frac {5}{2}}$ ${\ displaystyle \ Rightarrow r_ {2}: 4x + 3y = 4 \ left (- {\ frac {1} {4}} \ right) +3 \ left (- {\ frac {1} {2}} \ right ) = - {\ frac {5} {2}}}$ ${\ displaystyle \ Rightarrow r_ {2}: 4x + 3y = 4 \ left (- {\ frac {1} {4}} \ right) +3 \ left (- {\ frac {1} {2}} \ right ) = - {\ frac {5} {2}}}$

Formula poate fi utilizată pentru a obține forma canonică

$\lambda _{1}X^{2}+\lambda _{2}Y^{2}+\left({\frac {I_{3}}{I_{2}}}\right)=0$ ${\ displaystyle \ lambda _ {1} X ^ {2} + \ lambda _ {2} Y ^ {2} + \ left ({\ frac {I_ {3}} {I_ {2}}} \ right) = 0}$ ${\ displaystyle \ lambda _ {1} X ^ {2} + \ lambda _ {2} Y ^ {2} + \ left ({\ frac {I_ {3}} {I_ {2}}} \ right) = 0}$ ,

cu $\lambda _{1}=4,\lambda _{2}=-1$ ${\ displaystyle \ lambda _ {1} = 4, \ lambda _ {2} = - 1}$ ${\ displaystyle \ lambda _ {1} = 4, \ lambda _ {2} = - 1}$ valorile proprii ale $B.$ ${\ displaystyle B}$ $B.$ si este:

$4X^{2}-Y^{2}-{\frac {5}{4}}=0$ ${\ displaystyle 4X ^ {2} -Y ^ {2} - {\ frac {5} {4}} = 0}$ ${\ displaystyle 4X ^ {2} -Y ^ {2} - {\ frac {5} {4}} = 0}$

Noile asimptote sunt cele două linii drepte care au formă $x=y\left({\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}\right)$ ${\ displaystyle x = y \ left ({\ frac {-b \ pm {\ sqrt {b ^ {2} -4ac}}} {2a}} \ right)}$ ${\ displaystyle x = y \ left ({\ frac {-b \ pm {\ sqrt {b ^ {2} -4ac}}} {2a}} \ right)}$ și trecând prin origine:

$r'_{1}:x={\frac {y}{2}}$ ${\ displaystyle r '_ {1}: x = {\ frac {y} {2}}}$ ${\ displaystyle r '_ {1}: x = {\ frac {y} {2}}}$
$r'_{2}:x=-{\frac {y}{2}}$ ${\ displaystyle r '_ {2}: x = - {\ frac {y} {2}}}$ ${\ displaystyle r '_ {2}: x = - {\ frac {y} {2}}}$

Focurile formei canonice au formă $(\pm {\sqrt {a^{2}+b^{2}}},0)$ ${\ displaystyle (\ pm {\ sqrt {a ^ {2} + b ^ {2}}}, 0)}$ ${\ displaystyle (\ pm {\ sqrt {a ^ {2} + b ^ {2}}}, 0)}$ și sunt, prin urmare:

$F_{1}=\left(-{\frac {5}{4}},0\right)$ ${\ displaystyle F_ {1} = \ left (- {\ frac {5} {4}}, 0 \ right)}$ ${\ displaystyle F_ {1} = \ left (- {\ frac {5} {4}}, 0 \ right)}$
$F_{2}=\left({\frac {5}{4}},0\right)$ ${\ displaystyle F_ {2} = \ left ({\ frac {5} {4}}, 0 \ right)}$ ${\ displaystyle F_ {2} = \ left ({\ frac {5} {4}}, 0 \ right)}$

Parabolă

Ecuația conică

x^{2}+2xy+y^{2}-8x=0

{\ displaystyle x ^ {2} + 2xy + y ^ {2} -8x = 0}

{\ displaystyle x ^ {2} + 2xy + y ^ {2} -8x = 0}

Rectoria conicii

x^{2}+2xy+y^{2}-8x=0

{\ displaystyle x ^ {2} + 2xy + y ^ {2} -8x = 0}

{\ displaystyle x ^ {2} + 2xy + y ^ {2} -8x = 0}

Conica ecuației este dată $\Gamma (x,y)=x^{2}+2xy+y^{2}-8x=0$ ${\ displaystyle \ Gamma (x, y) = x ^ {2} + 2xy + y ^ {2} -8x = 0}$ ${\ displaystyle \ Gamma (x, y) = x ^ {2} + 2xy + y ^ {2} -8x = 0}$ ; studiu $I_{3}$ ${\ displaystyle I_ {3}}$ ${\ displaystyle I_ {3}}$ Și $I_{2}$ ${\ displaystyle I_ {2}}$ $I_2$ descoperim că este o parabolă. Diagonalizând $B.$ ${\ displaystyle B}$ $B.$ găsim ca valori proprii 0 și 2 și ca vectori proprii respectivi (1, -1) și (1,1). Pentru a găsi vârful $V.$ ${\ displaystyle V}$ $V.$ intersectăm parabola cu o linie ortogonală cu axa conicii: deoarece axa parabolei este o linie care trece prin vârf $V.$ ${\ displaystyle V}$ $V.$ direcție paralelă cu vectorul propriu relativ la valoarea proprie zero (în acest caz (1, -1)), o linie dreaptă paralelă cu acesta este cu siguranță $x=-y$ ${\ displaystyle x = -y}$ ${\ displaystyle x = -y}$ , deci o linie dreaptă ortogonală este $x=y$ ${\ displaystyle x = y}$ $x = y$ . De la intersecție găsești punctele $LA$ ${\ displaystyle A}$ $LA$ (0,0) și $B.$ ${\ displaystyle B}$ $B.$ (2.2); punctul lor de mijloc $M.$ ${\ displaystyle M}$ $M.$ (1,1) este pe axă. Axa este deci linia paralelă cu $x=-y$ ${\ displaystyle x = -y}$ ${\ displaystyle x = -y}$ trecând prin $M.$ ${\ displaystyle M}$ $M.$ si este $x+y=2$ ${\ displaystyle x + y = 2}$ ${\ displaystyle x + y = 2}$ . Acum intersectând axa cu parabola găsim vârful: $V(1/2,3/2)$ ${\ displaystyle V (1 / 2,3 / 2)}$ ${\ displaystyle V (1 / 2,3 / 2)}$ . Traducând astfel încât $V.$ ${\ displaystyle V}$ $V.$ este centrat pe origine:

$\left\{{\begin{matrix}{\tilde {x}}=x-{\frac {1}{2}}\\{\tilde {y}}=y-{\frac {3}{2}}\end{matrix}}\right.$ ${\ displaystyle \ left \ {{\ begin {matrix} {\ tilde {x}} = x - {\ frac {1} {2}} \\ {\ tilde {y}} = y - {\ frac {3 } {2}} \ end {matrix}} \ right.}$ ${\ displaystyle \ left \ {{\ begin {matrix} {\ tilde {x}} = x - {\ frac {1} {2}} \\ {\ tilde {y}} = y - {\ frac {3 } {2}} \ end {matrix}} \ right.}$

ecuația devine:

$({\tilde {x}}+{\tilde {y}})^{2}-4{\tilde {x}}+4{\tilde {y}}=0$ ${\ displaystyle ({\ tilde {x}} + {\ tilde {y}}) ^ {2} -4 {\ tilde {x}} + 4 {\ tilde {y}} = 0}$ ${\ displaystyle ({\ tilde {x}} + {\ tilde {y}}) ^ {2} -4 {\ tilde {x}} + 4 {\ tilde {y}} = 0}$

Matricea $P.$ ${\ displaystyle P}$ $P.$ este o matrice de rotație compusă din cei doi vectori proprii normalizați (auto-slăbitori):

$P={\begin{bmatrix}{1 \over {\sqrt {2}}}&{-1 \over {\sqrt {2}}}\\{1 \over {\sqrt {2}}}&{1 \over {\sqrt {2}}}\end{bmatrix}}=\left({\frac {1}{\sqrt {2}}}\right){\begin{bmatrix}1&-1\\1&1\end{bmatrix}}$ ${\ displaystyle P = {\ begin {bmatrix} {1 \ over {\ sqrt {2}}} și {- 1 \ over {\ sqrt {2}}} \\ {1 \ over {\ sqrt {2}} } & {1 \ over {\ sqrt {2}}} \ end {bmatrix}} = \ left ({\ frac {1} {\ sqrt {2}}} \ right) {\ begin {bmatrix} 1 & - 1 \\ 1 & 1 \ end {bmatrix}}}$ ${\ displaystyle P = {\ begin {bmatrix} {1 \ over {\ sqrt {2}}} și {- 1 \ over {\ sqrt {2}}} \\ {1 \ over {\ sqrt {2}} } & {1 \ over {\ sqrt {2}}} \ end {bmatrix}} = \ left ({\ frac {1} {\ sqrt {2}}} \ right) {\ begin {bmatrix} 1 & - 1 \\ 1 & 1 \ end {bmatrix}}}$

Atâta timp cât $(x,y)^{T}=P({\tilde {x}},{\tilde {y}})^{T}$ ${\ displaystyle (x, y) ^ {T} = P ({\ tilde {x}}, {\ tilde {y}}) ^ {T}}$ ${\ displaystyle (x, y) ^ {T} = P ({\ tilde {x}}, {\ tilde {y}}) ^ {T}}$ , poti sa scrii:

$\left\{{\begin{matrix}x={\frac {1}{\sqrt {2}}}({\tilde {x}}-{\tilde {y}})\\y={\frac {1}{\sqrt {2}}}({\tilde {x}}+{\tilde {y}})\end{matrix}}\right.$ ${\ displaystyle \ left \ {{\ begin {matrix} x = {\ frac {1} {\ sqrt {2}}} ({\ tilde {x}} - {\ tilde {y}}) \\ y = {\ frac {1} {\ sqrt {2}}} ({\ tilde {x}} + {\ tilde {y}}) \ end {matrix}} \ right.}$ ${\ displaystyle \ left \ {{\ begin {matrix} x = {\ frac {1} {\ sqrt {2}}} ({\ tilde {x}} - {\ tilde {y}}) \\ y = {\ frac {1} {\ sqrt {2}}} ({\ tilde {x}} + {\ tilde {y}}) \ end {matrix}} \ right.}$

Prin substituire obținem forma canonică $2{\sqrt {2}}X=Y^{2}$ ${\ displaystyle 2 {\ sqrt {2}} X = Y ^ {2}}$ ${\ displaystyle 2 {\ sqrt {2}} X = Y ^ {2}}$ , cu foc $F\left({\frac {\sqrt {2}}{2}},0\right)$ ${\ displaystyle F \ left ({\ frac {\ sqrt {2}} {2}}, 0 \ right)}$ ${\ displaystyle F \ left ({\ frac {\ sqrt {2}} {2}}, 0 \ right)}$ și director $d:x=-{\frac {\sqrt {2}}{2}}$ ${\ displaystyle d: x = - {\ frac {\ sqrt {2}} {2}}}$ ${\ displaystyle d: x = - {\ frac {\ sqrt {2}} {2}}}$

Elemente conexe

linkuri externe

Conics cu GeoGebra , la geogebratube.org .

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică