Matrice

Elementele unui tablou sunt de obicei indicate printr-o pereche de indici de indice.

În matematică , în special în algebra liniară , o matrice este un tabel ordonat de elemente.

De exemplu:

{\begin{pmatrix}1&0&5\\1&-2&0\end{pmatrix}}

{\ displaystyle {\ begin {pmatrix} 1 & 0 & 5 \\ 1 & -2 & 0 \ end {pmatrix}}}

{\ begin {pmatrix} 1 & 0 & 5 \\ 1 & -2 & 0 \ end {pmatrix}}

Matricile sunt utilizate pe scară largă în matematică și în toate științele pentru capacitatea lor de a reprezenta diverse obiecte matematice într-un mod util și concis, ca valori care depind de doi parametri sau chiar de sisteme liniare , ceea ce le face un instrument central pentru analiza matematică .

Istorie

Același subiect în detaliu: Istoria determinantului .

Urmele utilizării matricilor datează din primele secole î.Hr. De-a lungul istoriei s-a întâmplat de mai multe ori ca matematicienii care au trăit în timpuri și locuri diferite, în timpul studiului sistemelor liniare, să fi aranjat coeficienții sistemului sub formă de tabel , fapt care evidențiază modul în care matricile sunt o structură deosebit de intuitivă și convenabilă în aceste scopuri. ^[1] Descoperiri interesante sunt, de asemenea, pătratele latine și pătratele magice . Cu toate acestea, abia în secolul al XVII-lea ideea matricilor a fost reînviată și dezvoltată, mai întâi cu rezultate și idei obținute în contexte specifice de studiu, apoi cu generalizarea lor. Dezvoltarea a continuat în cele din urmă până când teoria matricii a primit forma pe care o cunoaștem astăzi. ^[1]

Primii care au exploatat matricile pentru a-și facilita propriile calcule au fost matematicienii chinezi, tocmai în tratarea sistemelor liniare. În Jiuzhang Suanshu ( Nouă capitole despre arte matematice ), scris în timpul dinastiei Han , capitolul opt este dedicat în întregime dezvoltării unei probleme matematice formulată sub forma unui sistem liniar. Autorul aranjează ingenios coeficienții fiecărei ecuații în paralel, deci diferit de notația de astăzi, care dorește ca acestea să fie aranjate orizontal, prin linii: o simplă diferență de notație. ^[1] ^[2] O serie de operații a fost aplicată numerelor astfel aranjate, aducându-le într-o formă astfel încât să clarifice care a fost soluția sistemului: este ceea ce știm astăzi ca metodă de eliminare gaussiană , descoperită în Occidentul abia la începutul secolului al XIX-lea cu studiile matematicianului german Carl Friedrich Gauss . ^[1] În cadrul Jiuzhang Suanshu a apărut și conceptul de determinant , înțeles ca o metodă pentru a determina dacă un sistem liniar admite o singură soluție. ^[2]

O idee mai modernă de determinant a apărut în 1683, la scurt timp atât în Japonia , cu Kōwa Seki ( Metodă de rezolvare a problemelor disimulate ), cât și în Europa , cu Leibniz . În prima jumătate a secolului al XVIII-lea, Maclaurin a scris Treatise of algebra (Tratatul de algebră) ^[3] , publicat postum în 1748 , care a arătat calculul determinanților pentru matricele pătrate de ordinul 2 și 3. Cramer și-a adus contribuția în 1750 prezentând algoritm pentru calcularea determinantului pentru matricile pătrate de orice ordine, utilizat în metoda cunoscută acum ca regula lui Cramer ( Introduction à l'analyse des lignes courbes algébriques ). Dezvoltări ulterioare asupra conceptului de determinant au fost făcute apoi de Bézout ( Sur le degré des équations résultantes de l'évanouissement des inconnues , 1764), Vandermonde ( Mémoire sur l'élimination , 1772) ^[4] , Laplace (1772), Lagrange ( 1773), Gauss (1801) care a introdus pentru prima dată termenul de determinant , Cauchy (1812) care a folosit determinantul pentru prima dată în concepția sa modernă, obținând rezultate importante și asupra minorilor și a matricelor adăugate și Jacobi . ^[1] La începutul secolului al XIX-lea, metoda de eliminare gaussiană de Gauss a fost utilizată pentru prima dată în Occident, pentru studiul orbitei asteroidului Pallas pe baza observațiilor obținute între 1803 și 1809. ^[1] Altele conceptele și ideile fundamentale ale teoriei matriciale au fost apoi studiate, din nou în contexte specifice, de Cauchy, Sturm , Jacobi, Kronecker , Weierstrass și Eisenstein .

În 1848, matematicianul și avocatul englez Sylvester a introdus pentru prima dată termenul de matrice . Colegul său avocat Cayley a introdus inversul unei matrice în 1853 . ^[1] , iar în 1858 a dat prima definiție abstractă a matricei, Memoir on the theory of matrices (Memorii despre teoria matricelor) ^[5] , arătând cum toate studiile anterioare nu erau altceva decât cazuri specifice ale conceptului său general. În cadrul textului, Cayley a furnizat, de asemenea, o algebră matricială, definind operațiile de bază ale adunării, înmulțirii între matrice, înmulțirii cu scalari și inversul unei matrice. ^[1] Încă necunoscând aceste lucrări, în 1878 Frobenius a publicat Ueber linear Substitutionen und bilineare Formen ( Despre substituții liniare și forme biliniare ), în care a raportat rezultate importante pe matrici, precum definiția rangului ^[1] . În 1888, geodezul Jordan, în cea de-a treia ediție a Handbuch der Vermessungskunde ( Manual de geodezie ), a extins metoda Gauss de eliminare în ceea ce este acum cunoscut sub numele de metoda Gauss-Jordan de eliminare . ^[6] Alte contribuții importante au fost făcute de Bôcher în 1907 cu Introducere în algebră superioară ; alte texte relevante au fost scrise de Turnbull și Aitken în anii treizeci ( Theory of Canonical Matrices and Determinants and Matrices ) și de Mirsky în 1955 ( The introduction of linear algebra ). ^[1]

Începând din a doua jumătate a secolului al XX-lea, apariția computerelor a dat o accelerație impresionantă răspândirii matricilor și a metodelor matriciale. De fapt, datorită computerelor a fost posibilă aplicarea eficientă a metodelor iterative considerate anterior prea scumpe, conducând în consecință la dezvoltarea de noi tehnici pentru rezolvarea problemelor importante ale algebrei liniare, cum ar fi calculul vectorilor proprii și al valorilor proprii , calculul inversului o matrice și rezoluția sistemelor liniare. ^[7] Acest lucru, la rândul său, a permis introducerea matricilor în alte discipline aplicate, cum ar fi matematica economică și probabilitatea , care datorită lor au putut reprezenta concepte complexe într-un mod mai simplu. Cu toate acestea, alte domenii relativ mai recente, cum ar fi cercetarea operațională , și-au bazat în mare măsură disciplina pe utilizarea matricelor. ^[7]

Definiții și notații

O matrice este un tabel dreptunghiular de numere. Din punct de vedere formal, poate fi definit ca o funcție

A:\{1,\ldots ,m\}\times \{1,\ldots ,n\}\to K

{\ displaystyle A: \ {1, \ ldots, m \} \ times \ {1, \ ldots, n \} \ to K}

{\ displaystyle A: \ {1, \ ldots, m \} \ times \ {1, \ ldots, n \} \ to K}

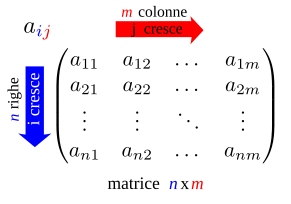
unde este $m$ ${\ displaystyle m}$ $m$ Și $n$ ${\ displaystyle n}$ $n$ sunt numere întregi pozitive fixe și $K.$ ${\ displaystyle K}$ $K.$ este orice set fix, cum ar fi cel al numerelor reale . Rândurile orizontale ale unei matrice se numesc rânduri , în timp ce cele verticale sunt coloane . De exemplu, matricea prezentată mai sus are două rânduri și trei coloane. O matrice $m\times n$ ${\ displaystyle m \ times n}$ $m \ ori n$ genericul este descris ca în figura de mai sus sau, de asemenea, în modul următor (care este considerat mai profitabil ca o notație datorită faptului că nu trebuie să diferențieze elementul de matricea însăși în operații):

A={\begin{pmatrix}\;[A]_{1,1}&[A]_{1,2}&\cdots &[A]_{1,n}\\\;[A]_{2,1}&[A]_{2,2}&\cdots &[A]_{2,n}\\\vdots &\vdots &\ddots &\vdots \\\;[A]_{m,1}&[A]_{m,2}&\cdots &[A]_{m,n}\end{pmatrix}}

{\ displaystyle A = {\ begin {pmatrix} \; [A] _ {1,1} & [A] _ {1,2} & \ cdots & [A] _ {1, n} \\\; [ A] _ {2,1} & [A] _ {2,2} & \ cdots & [A] _ {2, n} \\\ vdots & \ vdots & \ ddots & \ vdots \\\; [A ] _ {m, 1} & [A] _ {m, 2} & \ cdots & [A] _ {m, n} \ end {pmatrix}}}

A = {\ begin {pmatrix} \; [A] _ {{1,1}} & [A] _ {{1,2}} & \ cdots & [A] _ {{1, n}} \\ \; [A] _ {{2,1}} & [A] _ {{2,2}} & \ cdots & [A] _ {{2, n}} \\\ vdots & \ vdots & \ ddots & \ vdots \\\; [A] _ {{m, 1}} & [A] _ {{m, 2}} & \ cdots & [A] _ {{m, n}} \ end {pmatrix} }

indicând cu $[A]_{i,j}$ ${\ displaystyle [A] _ {i, j}}$ $[A] _ {{i, j}}$ elementul plasat pe rând $the$ ${\ displaystyle i}$ $the$ -alea și în coloană $j$ ${\ displaystyle j}$ $j$ -alea.

Linia $the$ ${\ displaystyle i}$ $the$ -alea este indicat cu $Row_{i}(A)$ ${\ displaystyle Row_ {i} (A)}$ $Rând_ {i} (A)$ , sau mai ambiguu $A_{i}$ ${\ displaystyle A_ {i}}$ $Către}$ , în timp ce coloana $j$ ${\ displaystyle j}$ $j$ -alea cu $Col_{j}(A)$ ${\ displaystyle Col_ {j} (A)}$ $Col_ {j} (A)$ , sau mai ambiguu $A^{j}$ ${\ displaystyle A ^ {j}}$ $A ^ {j}$ .

Elementele $[A]_{i,i}$ ${\ displaystyle [A] _ {i, i}}$ $[A] _ {{i, i}}$ constituie diagonala principală a matricei.

Vectorii pot fi considerați matrici având un singur rând sau o singură coloană. Un singur rând, matricea dimensionată $1\times n$ ${\ displaystyle 1 \ times n}$ $1 \ ori n$ , se numește matrice de rând sau vector de rând , în timp ce o matrice cu o singură coloană, de dimensiune $m\times 1$ ${\ displaystyle m \ times 1}$ $m \ ori 1$ , se numește matrice de coloane sau vector de coloană .

O matrice este prezentată în ordinea de mai jos $4\times 3$ ${\ displaystyle 4 \ times 3}$ $4 \ ori 3$ , o matrice de coloane și o matrice de rânduri;

{\begin{pmatrix}1&2&3\\1&-2&0\\4,5&0&2\\6&1&5\end{pmatrix}}\quad {\begin{pmatrix}7\\0\\\pi \end{pmatrix}}\quad {\begin{pmatrix}3&{\frac {7}{2}}&-9\end{pmatrix}}

{\ displaystyle {\ begin {pmatrix} 1 & 2 & 3 \\ 1 & -2 & 0 \\ 4,5 & 0 & 2 \\ 6 & 1 & 5 \ end {pmatrix}} \ quad {\ begin { pmatrix} 7 \\ 0 \\\ pi \ end {pmatrix}} \ quad {\ begin {pmatrix} 3 & {\ frac {7} {2}} & - 9 \ end {pmatrix}}}

{\ displaystyle {\ begin {pmatrix} 1 & 2 & 3 \\ 1 & -2 & 0 \\ 4,5 & 0 & 2 \\ 6 & 1 & 5 \ end {pmatrix}} \ quad {\ begin { pmatrix} 7 \\ 0 \\\ pi \ end {pmatrix}} \ quad {\ begin {pmatrix} 3 & {\ frac {7} {2}} & - 9 \ end {pmatrix}}}

După cum se arată în exemple, valorile prezente în matrice pot fi de diferite tipuri: întregi , reale sau chiar complexe . În multe cazuri, valorile sunt presupuse a fi elemente ale unui câmp $K.$ ${\ displaystyle K}$ $K.$ fix.

Algebra matricială

Numeroase operații pot fi definite pe matrici care adesea depind și de setul în care sunt alese valorile matricilor. În restul paragrafului presupunem că toate matricile au valori în același câmp $K.$ ${\ displaystyle K}$ $K.$ fix.

Sumă

Același subiect în detaliu: Suma matricilor .

Două matrice $LA$ ${\ displaystyle A}$ $LA$ Și $B.$ ${\ displaystyle B}$ $B.$ , ambele de tip $m\times n$ ${\ displaystyle m \ times n}$ $m \ ori n$ , pot fi adăugate împreună. Suma lor $A+B$ ${\ displaystyle A + B}$ $A + B$ este definit ca matricea $m\times n$ ${\ displaystyle m \ times n}$ $m \ ori n$ ale căror elemente se obțin prin adăugarea elementelor corespunzătoare ale $LA$ ${\ displaystyle A}$ $LA$ Și $B.$ ${\ displaystyle B}$ $B.$ . Oficial:

[A+B]_{i,j}:=[A]_{i,j}+[B]_{i,j}

{\ displaystyle [A + B] _ {i, j}: = [A] _ {i, j} + [B] _ {i, j}}

[A + B] _ {{i, j}}: = [A] _ {{i, j}} + [B] _ {{i, j}}

De exemplu:

{\begin{pmatrix}1&3&2\\1&0&0\\1&2&2\end{pmatrix}}+{\begin{pmatrix}0&0&5\\7&5&0\\2&1&1\end{pmatrix}}={\begin{pmatrix}1+0&3+0&2+5\\1+7&0+5&0+0\\1+2&2+1&2+1\end{pmatrix}}={\begin{pmatrix}1&3&7\\8&5&0\\3&3&3\end{pmatrix}}.

{\ displaystyle {\ begin {pmatrix} 1 & 3 & 2 \\ 1 & 0 & 0 \\ 1 & 2 & 2 \ end {pmatrix}} + {\ begin {pmatrix} 0 & 0 & 5 \\ 7 & 5 & ​​0 \\ 2 & 1 & 1 \ end {pmatrix}} = {\ begin {pmatrix} 1 + 0 & 3 + 0 & 2 + 5 \\ 1 + 7 & 0 + 5 & 0 + 0 \\ 1 + 2 & 2 + 1 & 2 + 1 \ end {pmatrix}} = {\ begin {pmatrix} 1 & 3 & 7 \\ 8 & 5 & 0 \\ 3 & 3 & 3 \ end {pmatrix}}.}

{\ begin {pmatrix} 1 & 3 & 2 \\ 1 & 0 & 0 \\ 1 & 2 & 2 \ end {pmatrix}} + {\ begin {pmatrix} 0 & 0 & 5 \\ 7 & 5 & 0 \\ 2 & 1 & 1 \ end {pmatrix}} = {\ begin {pmatrix} 1 + 0 & 3 + 0 & 2 + 5 \\ 1 + 7 & 0 + 5 & 0 + 0 \\ 1 + 2 & 2 + 1 & 2 + 1 \ end {pmatrix}} = {\ begin {pmatrix} 1 & 3 & 7 \\ 8 & 5 & 0 \\ 3 & 3 & 3 \ end {pmatrix}}.

Înmulțirea cu un scalar

Înmulțirea cu un scalar este o operație care, dată fiind o matrice $LA$ ${\ displaystyle A}$ $LA$ și un număr $c$ ${\ displaystyle c}$ $c$ (numit scalar ), construiește o nouă matrice $c\cdot A$ ${\ displaystyle c \ cdot A}$ $c \ cdot A$ , al cărui element se obține înmulțind elementul corespunzător al $LA$ ${\ displaystyle A}$ $LA$ pentru $c$ ${\ displaystyle c}$ $c$ ; elementele matricei și scalarul în cauză trebuie să aparțină aceluiași câmp . Oficial:

[cA]_{ij}:=c[A]_{i,j}

{\ displaystyle [cA] _ {ij}: = c [A] _ {i, j}}

[cA] _ {{ij}}: = c [A] _ {{i, j}}

De exemplu:

2{\begin{pmatrix}1&8&-3\\4&-2&5\end{pmatrix}}={\begin{pmatrix}2\times 1&2\times 8&2\times -3\\2\times 4&2\times -2&2\times 5\end{pmatrix}}={\begin{pmatrix}2&16&-6\\8&-4&10\end{pmatrix}}.

{\ displaystyle 2 {\ begin {pmatrix} 1 & 8 & -3 \\ 4 & -2 & 5 \ end {pmatrix}} = {\ begin {pmatrix} 2 \ times 1 & 2 \ times 8 & 2 \ times -3 \\ 2 \ times 4 & 2 \ times -2 & 2 \ times 5 \ end {pmatrix}} = {\ begin {pmatrix} 2 & 16 & -6 \\ 8 & -4 & 10 \ end {pmatrix }}.}

2 {\ begin {pmatrix} 1 & 8 & -3 \\ 4 & -2 & 5 \ end {pmatrix}} = {\ begin {pmatrix} 2 \ times 1 & 2 \ times 8 & 2 \ times -3 \ \ 2 \ times 4 & 2 \ times -2 & 2 \ times 5 \ end {pmatrix}} = {\ begin {pmatrix} 2 & 16 & -6 \\ 8 & -4 & 10 \ end {pmatrix}}.

Produs

Același subiect în detaliu: Înmulțirea matricilor .

Înmulțirea dintre două matrice $LA$ ${\ displaystyle A}$ $LA$ Și $B.$ ${\ displaystyle B}$ $B.$ este o operație mai complicată decât cele anterioare. Spre deosebire de sumă, nu se întâmplă prin simpla multiplicare a elementelor având același loc. Următoarea definiție a multiplicării este motivată de faptul că o matrice modelează o aplicație liniară , iar produsul matricelor corespunde compoziției aplicațiilor liniare.

Înmulțirea este, prin urmare, definită numai dacă matricile $LA$ ${\ displaystyle A}$ $LA$ Și $B.$ ${\ displaystyle B}$ $B.$ sunt respectiv de tip $m\times p$ ${\ displaystyle m \ times p}$ $m \ times p$ Și $p\times n$ ${\ displaystyle p \ times n}$ $p \ ori n$ : cu alte cuvinte, numărul $p$ ${\ displaystyle p}$ $p$ de coloane de $LA$ ${\ displaystyle A}$ $LA$ trebuie să se potrivească cu numărul $p$ ${\ displaystyle p}$ $p$ de rânduri de $B.$ ${\ displaystyle B}$ $B.$ . Rezultatul este o matrice $C.$ ${\ displaystyle C}$ $C.$ de tip $m\times n$ ${\ displaystyle m \ times n}$ $m \ ori n$ .

De exemplu, sunt $LA$ ${\ displaystyle A}$ $LA$ Și $B.$ ${\ displaystyle B}$ $B.$ respectiv două matrice $3\times 4$ ${\ displaystyle 3 \ times 4}$ $De 3 ori 4$ Și $4\times 2$ ${\ displaystyle 4 \ times 2}$ $4 \ ori 2$ : multiplicarea se poate efectua printre acestea $A\times B$ ${\ displaystyle A \ times B}$ $A \ ori B$ și obțineți o matrice $3\times 2$ ${\ displaystyle 3 \ times 2}$ $De 3 ori 2$ . Cu toate acestea, aceleași matrice nu pot fi multiplicate în felul acesta $B\times A$ ${\ displaystyle B \ times A}$ $B \ ori A$ , din moment ce coloanele din $B.$ ${\ displaystyle B}$ $B.$ nu sunt la fel de multe ca liniile de $LA$ ${\ displaystyle A}$ $LA$ .

Produsul $LA$ ${\ displaystyle A}$ $LA$ din $m$ ${\ displaystyle m}$ $m$ linii și $p$ ${\ displaystyle p}$ $p$ coloane e $B.$ ${\ displaystyle B}$ $B.$ din $p$ ${\ displaystyle p}$ $p$ linii și $n$ ${\ displaystyle n}$ $n$ coloane este matricea $C=A\times B$ ${\ displaystyle C = A \ ori B}$ $C = A \ ori B$ in marime $m\times n$ ${\ displaystyle m \ times n}$ $m \ ori n$ , al cărui element de poziție $(i,j)$ ${\ displaystyle (i, j)}$ $(i, j)$ este dat de suma:

[C]_{i,j}=Row_{i}(A)\times Col_{j}(B)=[A]_{i,1}[B]_{1,j}+[A]_{i,2}[B]_{2,j}+\cdots +[A]_{i,p}[B]_{p,j}

{\ displaystyle [C] _ {i, j} = Row_ {i} (A) \ times Col_ {j} (B) = [A] _ {i, 1} [B] _ {1, j} + [ A] _ {i, 2} [B] _ {2, j} + \ cdots + [A] _ {i, p} [B] _ {p, j}}

[C] _ {{i, j}} = Rând_ {i} (A) \ times Col_ {j} (B) = [A] _ {{i, 1}} [B] _ {{1, j} } + [A] _ {{i, 2}} [B] _ {{2, j}} + \ cdots + [A] _ {{i, p}} [B] _ {{p, j}}

Acesta din urmă se numește produs rând cu coloană . De exemplu:

A={\begin{pmatrix}1&1&2\\0&1&-3\\\end{pmatrix}}\qquad B={\begin{pmatrix}1&1&1\\2&5&1\\0&-2&1\end{pmatrix}}

{\ displaystyle A = {\ begin {pmatrix} 1 & 1 & 2 \\ 0 & 1 & -3 \\\ end {pmatrix}} \ qquad B = {\ begin {pmatrix} 1 & 1 & 1 \\ 2 & 5 & 1 \\ 0 & -2 & 1 \ end {pmatrix}}}

{\ displaystyle A = {\ begin {pmatrix} 1 & 1 & 2 \\ 0 & 1 & -3 \\\ end {pmatrix}} \ qquad B = {\ begin {pmatrix} 1 & 1 & 1 \\ 2 & 5 & 1 \\ 0 & -2 & 1 \ end {pmatrix}}}

C=A\times B={\begin{pmatrix}1&1&2\\0&1&-3\\\end{pmatrix}}\times {\begin{pmatrix}1&1&1\\2&5&1\\0&-2&1\end{pmatrix}}=

{\ displaystyle C = A \ times B = {\ begin {pmatrix} 1 & 1 & 2 \\ 0 & 1 & -3 \\\ end {pmatrix}} \ times {\ begin {pmatrix} 1 & 1 & 1 \\ 2 & 5 & 1 \\ 0 & -2 & 1 \ end {pmatrix}} =}

C = A \ times B = {\ begin {pmatrix} 1 & 1 & 2 \\ 0 & 1 & -3 \\\ end {pmatrix}} \ times {\ begin {pmatrix} 1 & 1 & 1 \\ 2 & 5 & 1 \\ 0 & -2 & 1 \ end {pmatrix}} =

Se observă că prin multiplicarea unei matrice $2\times 3$ ${\ displaystyle 2 \ times 3}$ $2 \ ori 3$ Pentru o $3\times 3$ ${\ displaystyle 3 \ times 3}$ $3 \ ori 3$ obții o matrice $2\times 3$ ${\ displaystyle 2 \ times 3}$ $2 \ ori 3$ .

Prima linie:

[C]_{1,1}=(1\times 1)+(1\times 2)+(2\times 0)=3

{\ displaystyle [C] _ {1,1} = (1 \ ori 1) + (1 \ ori 2) + (2 \ ori 0) = 3}

[C] _ {{1,1}} = (1 \ ori 1) + (1 \ ori 2) + (2 \ ori 0) = 3

[C]_{1,2}=(1\times 1)+(1\times 5)+(2\times (-2))=2

{\ displaystyle [C] _ {1,2} = (1 \ ori 1) + (1 \ ori 5) + (2 \ ori (-2)) = 2}

[C] _ {{1,2}} = (1 \ ori 1) + (1 \ ori 5) + (2 \ ori (-2)) = 2

[C]_{1,3}=(1\times 1)+(1\times 1)+(2\times 1)=4

{\ displaystyle [C] _ {1,3} = (1 \ ori 1) + (1 \ ori 1) + (2 \ ori 1) = 4}

[C] _ {{1,3}} = (1 \ ori 1) + (1 \ ori 1) + (2 \ ori 1) = 4

A doua linie:

[C]_{2,1}=(0\times 1)+(1\times 2)+(-3\times 0)=2

{\ displaystyle [C] _ {2,1} = (0 \ ori 1) + (1 \ ori 2) + (- 3 \ ori 0) = 2}

[C] _ {{2,1}} = (0 \ ori 1) + (1 \ ori 2) + (- 3 \ ori 0) = 2

[C]_{2,2}=(0\times 1)+(1\times 5)+(-3\times (-2))=11

{\ displaystyle [C] _ {2,2} = (0 \ ori 1) + (1 \ ori 5) + (- 3 \ ori (-2)) = 11}

[C] _ {{2,2}} = (0 \ ori 1) + (1 \ ori 5) + (- 3 \ ori (-2)) = 11

[C]_{2,3}=(0\times 1)+(1\times 1)+(-3\times 1)=-2

{\ displaystyle [C] _ {2,3} = (0 \ ori 1) + (1 \ ori 1) + (- 3 \ ori 1) = - 2}

[C] _ {{2,3}} = (0 \ ori 1) + (1 \ ori 1) + (- 3 \ ori 1) = - 2

C={\begin{pmatrix}\;[C]_{1,1}&[C]_{1,2}&[C]_{1,3}\\\;[C]_{2,1}&[C]_{2,2}&[C]_{2,3}\\\end{pmatrix}}={\begin{pmatrix}3&2&4\\2&11&-2\\\end{pmatrix}}

{\ displaystyle C = {\ begin {pmatrix} \; [C] _ {1,1} & [C] _ {1,2} & [C] _ {1,3} \\\; [C] _ {2,1} & [C] _ {2,2} & [C] _ {2,3} \\\ end {pmatrix}} = {\ begin {pmatrix} 3 & 2 & 4 \\ 2 & 11 & -2 \\\ end {pmatrix}}}

C = {\ begin {pmatrix} \; [C] _ {{1,1}} & [C] _ {{1,2}} & [C] _ {{1,3}} \\\; [ C] _ {{2,1}} & [C] _ {{2,2}} & [C] _ {{2,3}} \\\ end {pmatrix}} = {\ begin {pmatrix} 3 & 2 & 4 \\ 2 & 11 & -2 \\\ end {pmatrix}}

Spre deosebire de înmulțirea obișnuită a numerelor, aceasta nu este o operație comutativă , adică $LA B.$ ${\ displaystyle AB}$ $AB$ este în general diferită de $B. LA$ ${\ displaystyle BA}$ $BA$ , când puteți realiza ambele produse.

Un caz special, utilizat pe scară largă în algebra liniară pentru a reprezenta transformări liniare (cum ar fi rotații și reflexii ) este produsul unei matrice $m\times n$ ${\ displaystyle m \ times n}$ $m \ ori n$ și un vector coloană $n\times 1$ ${\ displaystyle n \ times 1}$ $n \ ori 1$ , care este numit și produsul matrice-vector .

Proprietate

Operațiile de adunare și produs de matrice satisfac toate proprietățile uzuale ale sumei și produsului numerelor, cu excepția, în cazul produsului matricilor, a proprietății comutative.

Este $0$ ${\ displaystyle 0}$ ${\ displaystyle 0}$ matricea nulă , formată doar din zerouri (și de aceeași dimensiune ca $LA$ ${\ displaystyle A}$ $LA$ ). De asemenea, să fie $-A=(-1)A$ ${\ displaystyle -A = (- 1) A}$ $-A = (- 1) A$ matricea obținută prin multiplicare $LA$ ${\ displaystyle A}$ $LA$ pentru alpinism $-1$ ${\ displaystyle -1}$ $-1$ . Următoarele relații sunt valabile pentru fiecare $LA, B., C.$ ${\ displaystyle A, B, C}$ $A, B, C$ matrici $m\times n$ ${\ displaystyle m \ times n}$ $m \ ori n$ și, pentru fiecare $la, b$ ${\ displaystyle a, b}$ $a, b$ numere reale.

Proprietățile sumei și ale produsului pentru un scalar

$A+0=0+A=A$ ${\ displaystyle A + 0 = 0 + A = A}$ $A + 0 = 0 + A = A$ (matricea nulă este elementul neutru al sumei)
$A+(-A)=0$ ${\ displaystyle A + (- A) = 0}$ $A + (- A) = 0$ (existența unui opus pentru suma)
$(A+B)+C=A+(B+C)$ ${\ displaystyle (A + B) + C = A + (B + C)}$ $(A + B) + C = A + (B + C)$ ( proprietatea asociativă a sumei)
$A+B=B+A$ ${\ displaystyle A + B = B + A}$ $A + B = B + A$ (proprietatea comutativă a sumei)
$1A=A$ ${\ displaystyle 1A = A}$ $1A = A$ (1 este elementul neutru al produsului pentru un scalar)
$(ab)A=a(bA)$ ${\ displaystyle (ab) A = a (bA)}$ $(ab) A = a (bA)$ (proprietate asociativă a produsului pentru un scalar)
$a(A+B)=aA+aB$ ${\ displaystyle a (A + B) = aA + aB}$ $a (A + B) = aA + aB$ (proprietatea distributivă a produsului pentru un scalar în raport cu suma)

Primele 4 proprietăți afirmă că matricile $m\times n$ ${\ displaystyle m \ times n}$ $m \ ori n$ formează un grup abelian în ceea ce privește operația de adăugare. După cum se arată mai sus, produsul nu este comutativ în general.

Proprietățile produsului între matrice

$(AB)C=A(BC)$ ${\ displaystyle (AB) C = A (BC)}$ $(AB) C = A (BC)$ (proprietatea asociativă a produsului)
$(A+B)C=AC+BC;$ ${\ displaystyle (A + B) C = AC + BC;}$ $(A + B) C = AC + BC;$ $C(A+B)=CA+CB$ ${\ displaystyle C (A + B) = CA + CB}$ $C (A + B) = CA + CB$ ( proprietatea distributivă a produsului în raport cu suma)

Alte operațiuni

Numeroase alte operații sunt definite pe matrice. Între acestea:

Transpunerea unei matrice
Suma directă
Produs direct (sau Kronecker )
Matricea exponențială
Inversia unei matrice inversabile
Diagonalizarea unei matrice diagonalizabile

Aplicații liniare

Același subiect în detaliu: Matricea de transformare .

Matricile permit să reprezinte transformările liniare dintre spațiile vectoriale . Pentru orice operator liniar $T:V\to W$ ${\ displaystyle T: V \ to W}$ $T: V \ to W$ dintr-un spațiu vectorial $V.$ ${\ displaystyle V}$ $V.$ ca dimensiune $m$ ${\ displaystyle m}$ $m$ la un spațiu vector $W$ ${\ displaystyle W}$ $W$ in marime $n$ ${\ displaystyle n}$ $n$ este asociat, pentru fiecare alegere posibilă, a unei perechi de baze $\{v_{1},v_{2},\ldots ,v_{m}\}$ ${\ displaystyle \ {v_ {1}, v_ {2}, \ ldots, v_ {m} \}}$ $\ {v_ {1}, v_ {2}, \ ldots, v_ {m} \}$ Și $\{w_{1},w_{2},\ldots ,w_{n}\}$ ${\ displaystyle \ {w_ {1}, w_ {2}, \ ldots, w_ {n} \}}$ $\ {w_ {1}, w_ {2}, \ ldots, w_ {n} \}$ , matricea $LA$ ${\ displaystyle A}$ $LA$ astfel încât:

T(v_{i})=\sum _{j=1}^{n}[A]_{i,j}w_{j}\quad \forall i\in \{1,2,\ldots ,m\}

{\ displaystyle T (v_ {i}) = \ sum _ {j = 1} ^ {n} [A] _ {i, j} w_ {j} \ quad \ forall i \ in \ {1,2, \ ldots, m \}}

T (v_ {i}) = \ sum _ {{j = 1}} ^ {n} [A] _ {{i, j}} w_ {j} \ quad \ forall i \ in \ {1,2, \ ldots, m \}

.

Această matrice reprezintă aplicația $T.$ ${\ displaystyle T}$ $T.$ în bazele alese. Multe operații între matrici duc la operații între aplicații liniare:

Imaginea $T(v)$ ${\ displaystyle T (v)}$ $TELEVIZOR)$ unui vector corespunde multiplicării matrice-vector.
Suma aplicațiilor (atunci când este posibil) corespunde sumei dintre matrici.
Compoziția aplicațiilor liniare (atunci când este posibil) corespunde produsului dintre matrice.

Sisteme liniare

Același subiect în detaliu: Sistem de ecuații liniare .

Matricile sunt utile în special pentru reprezentarea sistemelor de ecuații liniare. Sistemul:

\left\{{\begin{matrix}a_{11}x_{1}+a_{12}x_{2}+\cdots +a_{1n}x_{n}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+\cdots +a_{2n}x_{n}=b_{2}\\\vdots \\a_{m1}x_{1}+a_{m2}x_{2}+\cdots +a_{mn}x_{n}=b_{m}\end{matrix}}\right.

{\ displaystyle \ left \ {{\ begin {matrix} a_ {11} x_ {1} + a_ {12} x_ {2} + \ cdots + a_ {1n} x_ {n} = b_ {1} \\ a_ {21} x_ {1} + a_ {22} x_ {2} + \ cdots + a_ {2n} x_ {n} = b_ {2} \\\ vdots \\ a_ {m1} x_ {1} + a_ { m2} x_ {2} + \ cdots + a_ {mn} x_ {n} = b_ {m} \ end {matrix}} \ right.}

\ left \ {{\ begin {matrix} a _ {{11}} x_ {1} + a _ {{12}} x_ {2} + \ cdots + a _ {{1n}} x_ {n} = b_ {1} \\ a _ {{21}} x_ {1} + a _ {{22}} x_ {2} + \ cdots + a _ {{2n}} x_ {n} = b_ {2} \\ \ vdots \\ a_ {{m1}} x_ {1} + a _ {{m2}} x_ {2} + \ cdots + a _ {{mn}} x_ {n} = b_ {m} \ end {matrix }} \ dreapta.

poate fi reprezentat cu echivalentul său de matrice, prin produsul matrice-vector :

{\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{pmatrix}}{\begin{pmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{pmatrix}}={\begin{pmatrix}b_{1}\\b_{2}\\\vdots \\b_{m}\end{pmatrix}}

{\ displaystyle {\ begin {pmatrix} a_ {11} & a_ {12} & \ cdots & a_ {1n} \\ a_ {21} & a_ {22} & \ cdots & a_ {2n} \\\ vdots & \ vdots & \ ddots & \ vdots \\ a_ {m1} & a_ {m2} & \ cdots & a_ {mn} \ end {pmatrix}} {\ begin {pmatrix} x_ {1} \\ x_ {2} \ \\ vdots \\ x_ {n} \ end {pmatrix}} = {\ begin {pmatrix} b_ {1} \\ b_ {2} \\\ vdots \\ b_ {m} \ end {pmatrix}}}

{\ begin {pmatrix} a _ {{11}} & a _ {{12}} & \ cdots & a _ {{1n}} \\ a _ {{21}} & a _ {{22}} & \ cdots & a _ {{2n}} \\\ vdots & \ vdots & \ ddots & \ vdots \\ a _ {{m1}} & a _ {{m2}} & \ cdots & a _ {{mn} } \ end {pmatrix}} {\ begin {pmatrix} x_ {1} \\ x_ {2} \\\ vdots \\ x_ {n} \ end {pmatrix}} = {\ begin {pmatrix} b_ {1} \\ b_ {2} \\\ vdots \\ b_ {m} \ end {pmatrix}}

Matrici pătrate

Același subiect în detaliu: Matricea pătrată .

Dintre matrici, matricele pătrate, adică matricile, ocupă un loc proeminent $n\times n$ ${\ displaystyle n \ times n}$ $n \ ori n$ , care au același număr $n$ ${\ displaystyle n}$ $n$ de rânduri și coloane. O matrice pătrată are o diagonală principală , cea formată din toate elementele $a_{i,i}$ ${\ displaystyle a_ {i, i}}$ $a _ {{i, i}}$ cu indici egali. Suma acestor elemente se numește urmă . Operația de transpunere transformă o matrice pătrată $LA$ ${\ displaystyle A}$ $LA$ în matrice $A^{\mathrm {T} }$ ${\ displaystyle A ^ {\ mathrm {T}}}$ $A ^ {{\ mathrm {T}}}$ obținută prin schimbul fiecăruia $a_{i,j}$ ${\ displaystyle a_ {i, j}}$ $a _ {{i, j}}$ cu $a_{j,i}$ ${\ displaystyle a_ {j, i}}$ $a _ {{j, i}}$ , cu alte cuvinte prin răsturnarea matricei în jurul diagonalei sale principale.

O matrice astfel încât $a_{i,j}=a_{j,i}$ ${\ displaystyle a_ {i, j} = a_ {j, i}}$ $a _ {{i, j}} = a _ {{j, i}}$ este o matrice simetrică . Cu alte cuvinte, $LA$ ${\ displaystyle A}$ $LA$ este simetrică dacă $A=A^{\mathrm {T} }$ ${\ displaystyle A = A ^ {\ mathrm {T}}}$ $A = A ^ {{\ mathrm {T}}}$ . Dacă toate elementele care nu sunt în diagonala principală sunt nule, matricea se numește diagonală .

Produsul matricelor pătrate

Printre cele mai importante matrici $n\times n$ ${\ displaystyle n \ times n}$ $n \ ori n$ există matricea identității $I_{n}$ ${\ displaystyle I_ {n}}$ $În}$ : este o matrice care are 1 pe fiecare element al diagonalei și 0 în altă parte. Matricea este importantă deoarece reprezintă elementul neutru față de produs: de fapt matricile $n\times n$ ${\ displaystyle n \ times n}$ $n \ ori n$ ele pot fi înmulțite între ele și următoarele proprietăți sunt valabile pentru fiecare $LA$ ${\ displaystyle A}$ $LA$ :

AI_{n}=I_{n}A=A\qquad

{\ displaystyle AI_ {n} = I_ {n} A = A \ qquad}

AI_ {n} = I_ {n} A = A \ qquad

adică este elementul neutru al produsului. În spațiul matricilor $n\times n$ ${\ displaystyle n \ times n}$ $n \ ori n$ o sumă și un produs sunt, prin urmare, definite, iar proprietățile enumerate până acum afirmă că setul este un inel , similar cu inelul numerelor întregi , cu singura diferență că produsul matricilor nu este comutativ.

Determinant

Același subiect în detaliu: Determinant (algebră) .

O cantitate importantă definită pornind de la o matrice pătrată $LA$ ${\ displaystyle A}$ $LA$ este determinantul său. Indicat cu $\det A$ ${\ displaystyle \ det A}$ $\ det A$ , acest număr oferă o mulțime de informații esențiale despre matrice. De exemplu, determină dacă matricea este inversabilă , adică dacă există o matrice $B.$ ${\ displaystyle B}$ $B.$ astfel încât:

AB=BA=I_{n}

{\ displaystyle AB = BA = I_ {n}}

AB = BA = I_ {n}

Determinantul este ingredientul fundamental al regulii lui Cramer , util pentru rezolvarea unor sisteme liniare .

Polinom caracteristic, vectori proprii, diagonalizabilitate

Același subiect în detaliu: vector propriu și valoare proprie , polinom caracteristic și diagonalizabilitate .

Urma și determinantul pot fi închise într-un obiect și mai rafinat, de importanță fundamentală în studiul transformărilor liniare : polinomul caracteristic , un polinom ale cărui rădăcini sunt valorile proprii ale matricei. Cunoașterea valorilor proprii și a vectorilor proprii permite, de exemplu, să studieze asemănarea dintre matrice , în special asemănarea cu o matrice diagonală.

Clase de matrice reale și complexe

Același subiect în detaliu: Glosar Matrix .

Pe lângă matricile diagonale și simetrice deja introduse, există și alte categorii de matrice importante.

Matrici antisimetrice , în care valorile din casetele în poziții simetrice față de diagonala principală sunt opuse: $a_{i,j}=-a_{j,i}$ ${\ displaystyle a_ {i, j} = - a_ {j, i}}$ $a _ {{i, j}} = - a _ {{j, i}}$ .
Matrici hermitiene (sau auto-adăugate ), în care valorile din casetele pozițiilor simetrice față de diagonala principală sunt conjugate complexe : $a_{i,j}=a_{j,i}^{*}$ ${\ displaystyle a_ {i, j} = a_ {j, i} ^ {*}}$ $a _ {{i, j}} = a _ {{j, i}} ^ {*}$ .
Un pătrat magic este o matrice pătrată în care suma valorilor de pe fiecare rând, coloană sau diagonală este întotdeauna aceeași.
Matricile Toeplitz au valori constante pe diagonale paralele cu cea principală: $a_{i,j}=a_{i+1,j+1}$ ${\ displaystyle a_ {i, j} = a_ {i + 1, j + 1}}$ $a _ {{i, j}} = a _ {{i + 1, j + 1}}$
Matricile stochastice sunt matrice pătrate ale căror coloane sunt vectori de probabilitate , adică secvențe de reali între 0 și 1 cu o sumă egală cu 1; sunt folosite pentru a defini lanțurile Markov .

Spațiu matricial

Spațiul tuturor matricilor $m\times n$ ${\ displaystyle m \ times n}$ $m \ ori n$ la valori într-un interval fix $K.$ ${\ displaystyle K}$ $K.$ este indicat în general cu $K^{m\times n}$ ${\ displaystyle K ^ {m \ times n}}$ ${\ displaystyle K ^ {m \ times n}}$ sau $M(m,n,K)$ ${\ displaystyle M (m, n, K)}$ $M (m, n, K)$ . După cum am văzut deja, acest spațiu este un grup abelian cu suma. De asemenea, luată în considerare cu multiplicarea prin scalar, setul are o structură spațială vectorială pe $K.$ ${\ displaystyle K}$ $K.$ .

Acest spațiu are o bază canonică , alcătuită din toate matricile $e_{i,j}$ ${\ displaystyle e_ {i, j}}$ $și _ {{i, j}}$ având valoarea 1 pe cutia scaunului $(i,j)$ ${\ displaystyle (i, j)}$ $(i, j)$ și zero în toate celelalte. Baza constă din $m\times n$ ${\ displaystyle m \ times n}$ $m \ ori n$ elemente și, prin urmare, spațiul $K^{m\times n}$ ${\ displaystyle K ^ {m \ times n}}$ ${\ displaystyle K ^ {m \ times n}}$ are dimensiune $m\times n$ ${\ displaystyle m \ times n}$ $m \ ori n$ .

Algebra de câmp

In caz $m=n$ ${\ displaystyle m = n}$ $m = n$ de matrice pătrate, produsul este, de asemenea, definit. Cu această operațiune suplimentară, spațiul $K^{n\times n}$ ${\ displaystyle K ^ {n \ times n}}$ ${\ displaystyle K ^ {n \ times n}}$ , indicat și cu $M(n,K)$ ${\ displaystyle M (n, K)}$ $M (n, K)$ , moștenește o structură inelară cu unitate . Această structură este compatibilă cu cea a spațiului vectorial definit mai sus și, prin urmare, oferă un exemplu de bază al algebrei de câmp .

Generalizări

Una matrice infinita può essere definita come una successione di elementi $a_{i,j}$ $a_{i,j}$ $a_{{i,j}}$ , indicizzati da coppie di numeri naturali $(i,j)$ ${\displaystyle (i,j)}$ $(i,j)$ , senza nessun limite superiore per entrambi.

Più in generale, una generalizzazione del concetto di matrice è costruita prendendo due insiemi di indici $R, C$ ${\displaystyle R,C}$ $R,C$ qualsiasi (parametrizzanti le "righe" e le "colonne") e definendo una matrice come un'applicazione:

A:R\times C\rightarrow V

A:R\times C\rightarrow V

A:R\times C\rightarrow V

a valori in un altro dato insieme $V$ ${\displaystyle V}$ $V$ . La matrice usuale $m\times n$ $m\times n$ $m\times n$ corrisponde al caso in cui $R=\{1,2,\ldots ,m\}$ $R=\{1,2,\ldots ,m\}$ $R=\{1,2,\ldots ,m\}$ e $C=\{1,2,\ldots ,n\}$ $C=\{1,2,\ldots ,n\}$ $C=\{1,2,\ldots ,n\}$ , e $V$ ${\displaystyle V}$ $V$ è ad esempio l'insieme dei numeri reali o complessi.

Questa definizione generale si serve solo di nozioni insiemistiche e non ricorre a nozioni visive e intuitive come quella di schieramento rettangolare. Consente di trattare casi molto generali: ad esempio matrici le cui righe e colonne sono etichettate da indici in un qualunque sottoinsieme $I$ ${\displaystyle I}$ $I$ degli interi $\mathbb {Z}$ $\mathbb {Z}$ $\mathbb Z$ , matrici etichettate da coppie o in generale da $n$ ${\displaystyle n}$ $n$ -uple di interi come quelle che si incontrano nella meccanica quantistica o nella chimica molecolare, matrici infinite etichettate con gli insiemi $\mathbb {N}$ $\mathbb {N}$ $\mathbb N$ e $\mathbb {Z}$ $\mathbb {Z}$ $\mathbb Z$ come quelle che permettono di rappresentare successioni polinomiali o serie formali con due variabili.

Per poter definire somma, prodotto e altre operazioni sulle matrici, è opportuno che l'insieme $V$ ${\displaystyle V}$ $V$ sia dotato di tali operazioni, ad esempio che sia un anello .

Funzione di matrice

Lo stesso argomento in dettaglio: Funzione di matrice .

La teoria delle funzioni di matrice è di grande interesse per lo studio dei sistemi differenziali : in generale la funzione di una matrice non coincide con la matrice delle funzioni dei suoi elementi, ma si dimostra sfruttando il teorema di Hamilton-Cayley che ciascun suo elemento è una combinazione lineare di queste ultime.

Note

^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ( EN ) Storia dell'uso delle matrici e dei determinanti su MacTutor
^ ^a ^b ( EN ) Il Nove capitoli sulle arti matematiche su MacTutor
^ Il testo è consultabile on-line: Treatise of Algebra .
^ ( EN ) Biografia di Vandermonde su MacTutor
^ L' abstract del testo è consultabile on-line: Memoir on the theory of matrices in Proceedings of the Royal Society of London, Volume 9 .
^ SC Althoen and R. McLaughlin, "Gauss-Jordan Reduction: A Brief History," American Mathematical Monthly, 94:130–142 (1987).
^ ^a ^b Bronson 1989 , Preface .

Bibliografia

( EN ) Richard Bronson, Schaum's Outline of Theory and Problems of Matrix Operations , New York, McGraw-Hill, 1989, pp. 230 pagine., ISBN 0-07-007978-1 .

Altre letture

Fulvio Bisi, Francesco Bonsante e Sonia Brivio, 3 , in Lezioni di algebra lineare con applicazioni alla geometria analitica , Pavia, La Dotta, agosto 2013, ISBN 88-98648-02-2 .
( EN ) David M. Burton, The History of Mathematics: An Introduction , 6ª edizione, McGraw-Hill, 1º dicembre 2005, ISBN 978-0-07-110635-1 .
( EN ) Richard W. Jr. Feldmann, Arthur Cayley - Founder of Matrix Theory , The Mathematics Teacher, 55, 1962, Pagine 482-484..
( EN ) Gene H. Golub , Charles F. Van Loan, Matrix computations , 3ª edizione, Johns Hopkins University Press, 1996, ISBN 0-8018-5414-8 .

Voci correlate

Altri progetti

Wikizionario contiene il lemma di dizionario « matrice »
Wikiversità contiene risorse sulla matrice
Wikimedia Commons contiene immagini o altri file sulla matrice

Collegamenti esterni

( EN ) Matrice , su Enciclopedia Britannica , Encyclopædia Britannica, Inc.
( IT ) Calcolatrice per matrici e vettori online
( EN ) Storia dell'uso delle matrici e dei determinanti su MacTutor
( EN ) Matrice su MathWorld
( EN ) Matrice su PlanetMath

Controllo di autorità	Thesaurus BNCF 17734 · LCCN ( EN ) sh85082210 · GND ( DE ) 4037968-1 · BNF ( FR ) cb119324420 (data) · BNE ( ES ) XX529678 (data)

Portale Matematica : accedi alle voci di Wikipedia che trattano di matematica

[mactutor-1] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ( EN ) Storia dell'uso delle matrici e dei determinanti su MacTutor

[mactutor9-2] ( EN ) Il Nove capitoli sulle arti matematiche su MacTutor

[3] Il testo è consultabile on-line: Treatise of Algebra .

[mactutorv-4] ( EN ) Biografia di Vandermonde su MacTutor

[5] L' abstract del testo è consultabile on-line: Memoir on the theory of matrices in Proceedings of the Royal Society of London, Volume 9 .

[6] SC Althoen and R. McLaughlin, "Gauss-Jordan Reduction: A Brief History," American Mathematical Monthly, 94:130–142 (1987).

[bro89-1-7] Bronson 1989 , Preface .

[1]

[2]

[3]

[4]

[5]

[6]

[7]