Categoria monoidala

În matematică , o categorie monoidală sau o categorie tensorială este o categorie ${\mathcal {C}}$ ${\ displaystyle {\ mathcal {C}}}$ ${\ mathcal {C}}$ echipat cu o funcție duală

\otimes \colon {\mathcal {C}}\times {\mathcal {C}}\to {\mathcal {C}},

{\ displaystyle \ otimes \ colon {\ mathcal {C}} \ times {\ mathcal {C}} \ to {\ mathcal {C}},}

\ otimes \ colon \ mathcal {C} \ times \ mathcal {C} \ to \ mathcal {C},

care este asociativ, cu excepția cazului în izomorfisme naturale și a unui obiect $THE$ ${\ displaystyle I}$ $THE$ care este un element neutru atât în dreapta cât și în stânga pentru $\otimes$ ${\ displaystyle \ otimes}$ $\ otimes$ cu excepția cazului în izomorfisme naturale. Izomorfismul natural asociat este supus anumitor condiții care asigură că toate diagramele relevante sunt comutative. Într-o categorie monoidală, analogii monoizilor obișnuiți ai algebrei abstracte pot fi definiți folosind astfel de diagrame comutative. De fapt, monoizii clasici sunt exact obiectele monoide din categoria monoidală a seturilor cu produsul cartezian ca produs monoidal.

Un spațiu vector , un grup abelian , un $R.$ ${\ displaystyle R}$ $R.$ - modul sau a $R.$ ${\ displaystyle R}$ $R.$ - algebra cu produsul tensorial obișnuit este o categorie monoidală. Categoriile monoidale pot fi văzute ca o generalizare a acestor exemple.

În teoria categoriilor , categoriile monoidale pot fi utilizate pentru a defini conceptul de obiect monoidal și o acțiune asociată acestuia asupra altor obiecte din aceeași categorie. Ele sunt, de asemenea, utilizate în definirea unei categorii îmbogățite .

Categoriile monoidale au numeroase aplicații în afara teoriei categoriilor în sine. Ele sunt, de asemenea, utilizate pentru a defini modele pentru fragmentul multiplicativ al logicii liniare intuiționiste. De asemenea, formează baza matematică pentru ordinea topologică în materia condensată. Categoriile monoidale împletite au aplicații în teoria cuantică a câmpurilor și teoria șirurilor .

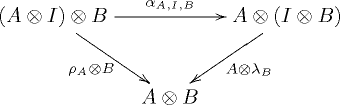
Definiție formală

O categorie monoidală este o categorie ${\mathcal {C}}$ ${\ displaystyle {\ mathcal {C}}}$ ${\ mathcal {C}}$ cu

un functor contravariant $\otimes \colon {\mathcal {C}}\times {\mathcal {C}}\to {\mathcal {C}}$ ${\ displaystyle \ otimes \ colon {\ mathcal {C}} \ times {\ mathcal {C}} \ to {\ mathcal {C}}}$ $\ otimes \ colon \ mathcal {C} \ times \ mathcal {C} \ to \ mathcal {C}$ denumit produs tensor sau produs monoidal ,
un obiect $THE$ ${\ displaystyle I}$ $THE$ numit obiect unitate sau obiect identitar ,
trei transformări naturale supuse anumitor condiții de coerență care exprimă faptul că operația tensorială
- este asociativ: există un izomorfism natural $\alpha$ ${\ displaystyle \ alpha}$ $\ alfa$ , numit asociator , indicat cu $\alpha _{A,B,C}\colon (A\otimes B)\otimes C\cong A\otimes (B\otimes C)$ ${\ displaystyle \ alpha _ {A, B, C} \ colon (A \ otimes B) \ otimes C \ cong A \ otimes (B \ otimes C)}$ $\ alpha_ {A, B, C} \ colon (A \ otimes B) \ otimes C \ cong A \ otimes (B \ otimes C)$ ,
- are $THE$ ${\ displaystyle I}$ $THE$ ca identitate stângă și dreaptă: există două izomofisme naturale $\lambda$ ${\ displaystyle \ lambda}$ $\ lambda$ Și $\rho$ ${\ displaystyle \ rho}$ $\ rho$ , respectiv numit reunificator dreapta și stânga , cu componentele $\lambda _{A}\colon I\otimes A\cong A$ ${\ displaystyle \ lambda _ {A} \ colon I \ otimes A \ cong A}$ $\ lambda_A \ colon I \ otimes A \ cong A$ Și $\rho _{A}\colon A\otimes I\cong A$ ${\ displaystyle \ rho _ {A} \ colon A \ otimes I \ cong A}$ $\ rho_A \ colon A \ otimes I \ cong A$ .

Condițiile pe care trebuie să le respecte aceste transformări naturale sunt:

pentru fiecare $LA$ ${\ displaystyle A}$ $LA$ , $B.$ ${\ displaystyle B}$ $B.$ , $C.$ ${\ displaystyle C}$ $C.$ Și $D.$ ${\ displaystyle D}$ $D.$ în ${\mathcal {C}}$ ${\ displaystyle {\ mathcal {C}}}$ ${\ mathcal {C}}$ , comuta următoarea diagramă :

comutatoare ;

pentru fiecare $LA$ ${\ displaystyle A}$ $LA$ Și $B.$ ${\ displaystyle B}$ $B.$ în ${\mathcal {C}}$ ${\ displaystyle {\ mathcal {C}}}$ ${\ mathcal {C}}$ , comuta următoarea diagramă :

Din aceste trei condiții rezultă că o clasă mare de diagrame de acest tip (adică diagrame construite folosind identități și produse tensoriale) $\alpha$ ${\ displaystyle \ alpha}$ $\ alfa$ , $\lambda$ ${\ displaystyle \ lambda}$ $\ lambda$ Și $\rho$ ${\ displaystyle \ rho}$ $\ rho$ ) naveta: aceasta este „teorema de coerență” a lui Mac Lane . Uneori se afirmă inexact că toate diagramele comută.

O categorie strict monoidală este o categorie pentru care izomorfismele naturale sunt identități $\alpha$ ${\ displaystyle \ alpha}$ $\ alfa$ , $\lambda$ ${\ displaystyle \ lambda}$ $\ lambda$ Și $\rho$ ${\ displaystyle \ rho}$ $\ rho$ . Fiecare categorie monoidală este echivalentă monoidal cu o categorie strict monoidală.

Exemple

Orice categorie cu produse finite poate fi văzută ca o categorie monoidală cu produsul ca un produs monoidal și obiectul terminal ca o identitate. Această categorie se numește uneori categoria monoidă carteziană . De exemplu:
- ${\mathcal {Set}}$ ${\ displaystyle {\ mathcal {Set}}}$ $\ mathcal {Set}$ , categoria seturilor cu produsul cartezian și singletele ca identitate;
- ${\mathcal {Cat}}$ ${\ displaystyle {\ mathcal {Cat}}}$ $\ mathcal {Cat}$ , bicategoria categoriilor mici cu produsul categoriilor și categoriile cu un singur obiect și morfismul său identitar ca unitate.
Orice categorie cu coproduse finite poate fi privită ca o categorie monoidală cu produsul ca un produs monoidal și obiectul inițial ca o identitate. Această categorie este uneori numită categoria cocarteziană monoidală .
$R.$ {\ displaystyle R} $R.$ - $M.$ $sau$ $d$ {\ displaystyle {\ mathcal {Mod}}} $\ mathcal {Mod}$ , categoria modulelor de pe un inel comutativ $R.$ {\ displaystyle R} $R.$ este o categorie monoidală cu produsul tensor al modulelor și inelului $R.$ {\ displaystyle R} $R.$ , vazut ca $R.$ {\ displaystyle R} $R.$ -modul, ca unitate. Ca cazuri speciale există:
- $K.$ ${\ displaystyle K}$ $K.$ - ${\mathcal {Vec}}$ ${\ displaystyle {\ mathcal {Vec}}}$ $\ mathcal {Vec}$ , categoria spațiilor vectoriale pe un câmp $K.$ ${\ displaystyle K}$ $K.$ cu spațiu vectorial $K.$ ${\ displaystyle K}$ $K.$ in marime $1$ ${\ displaystyle 1}$ $1$ ca identitate;
- ${\mathcal {Ab}}$ ${\ displaystyle {\ mathcal {Ab}}}$ $\ mathcal {Ab}$ , categoria grupurilor abeliene cu grup de numere întregi $\mathbb {Z}$ ${\ displaystyle \ mathbb {Z}}$ $\ mathbb {Z}$ ca unitate.
Pentru fiecare inel comutativ $R.$ ${\ displaystyle R}$ $R.$ categoria de $R.$ ${\ displaystyle R}$ $R.$ - algebrele sunt monoidale cu produsul tensor al algebrelor și $R.$ ${\ displaystyle R}$ $R.$ , vazut ca $R.$ ${\ displaystyle R}$ $R.$ -algebra, identitate.
Categoria spațiilor cu glonț este monoidală cu produsul smash și sfera 0 (un spațiu discret de două puncte) ca unitate.
Categoria tuturor endofuncționarilor dintr-o categorie ${\mathcal {C}}$ ${\ displaystyle {\ mathcal {C}}}$ ${\ mathcal {C}}$ este o categorie strict monoidală cu compoziția functorilor ca produs monoidal și identitatea functorului ca unitate.
La fel ca în orice categorie, subcategoria completă generată de orice obiect este un monoid. În cazul unei categorii 2 ${\mathcal {E}}$ ${\ displaystyle {\ mathcal {E}}}$ $\ mathcal {E}$ cu un obiect $C\in \mathrm {Ob} ({\mathcal {E}})$ ${\ displaystyle C \ in \ mathrm {Ob} ({\ mathcal {E}})}$ $C \ in \ mathrm {Ob} (\ mathcal {E})$ , 2-subcategoria completă a ${\mathcal {E}}$ ${\ displaystyle {\ mathcal {E}}}$ $\ mathcal {E}$ generat de $\{C\}$ ${\ displaystyle \ {C \}}$ $\ {C \}$ este o categorie monoidală. In caz ${\mathcal {E}}={\mathcal {Cat}}$ ${\ displaystyle {\ mathcal {E}} = {\ mathcal {Cat}}}$ $\ mathcal {E} = \ mathcal {Cat}$ se obține exemplul anterior de endofuncturisti.
O semi-rețea cu o minoritate și un maxim superior limitat este o categorie monoidală simetrică , produsul monoidal este operația de întâlnire a rețelei și elementul maxim este unitatea.

Categorii strict monoidale

Pentru fiecare categorie ${\mathcal {C}}$ ${\ displaystyle {\ mathcal {C}}}$ ${\ mathcal {C}}$ , categoria strict monoidală gratuită $\Sigma ({\mathcal {C}})$ ${\ displaystyle \ Sigma ({\ mathcal {C}})}$ $\ Sigma (\ mathcal {C})$ poate fi construit după cum urmează:

obiectele sale sunt secvențe finite $A_{1},\dots ,A_{n}$ ${\ displaystyle A_ {1}, \ dots, A_ {n}}$ $A_1, \ dots, A_n$ de obiecte de ${\mathcal {C}}$ ${\ displaystyle {\ mathcal {C}}}$ ${\ mathcal {C}}$ ;
există morfisme între două obiecte $A_{1},\dots ,A_{n}$ ${\ displaystyle A_ {1}, \ dots, A_ {n}}$ $A_1, \ dots, A_n$ Și $B_{1},\dots ,B_{m}$ ${\ displaystyle B_ {1}, \ dots, B_ {m}}$ $B_1, \ dots, B_m$ doar dacă $m=n$ ${\ displaystyle m = n}$ $m = n$ , în acest caz morfismele sunt secvențele finite ale morfismelor $f_{1},\dots ,f_{n}$ ${\ displaystyle f_ {1}, \ dots, f_ {n}}$ $f_1, \ dots, f_n$ cu $f_{i}\colon A_{i}\to B_{i}$ ${\ displaystyle f_ {i} \ colon A_ {i} \ to B_ {i}}$ $f_i \ colon A_i \ to B_i$ ;
produsul monoidal al două obiecte $A_{1},\dots ,A_{n}$ ${\ displaystyle A_ {1}, \ dots, A_ {n}}$ $A_1, \ dots, A_n$ Și $B_{1},\dots ,B_{m}$ ${\ displaystyle B_ {1}, \ dots, B_ {m}}$ $B_1, \ dots, B_m$ este concatenarea $A_{1},\dots ,A_{n},B_{1},\dots ,B_{m}$ ${\ displaystyle A_ {1}, \ dots, A_ {n}, B_ {1}, \ dots, B_ {m}}$ $A_1, \ dots, A_n, B_1, \ dots, B_m$ și în mod similar produsul a două morfisme este concatenarea celor două secvențe finite.