Poligon regulat necorespunzător
În geometrie, un poligon regulat necorespunzător este un poligon regulat care are mai puțin de trei laturi și mai puțin de trei vârfuri . Un poligon regulat necorespunzător devine o figură degenerată într-un plan euclidian , dar poate fi construit pe o sferă . Un digon nu este o figură degenerată dacă este construit între doi antipode pe un cerc sau sferă. [1]
Monogon
În geometrie, un monogon , numit și 1-gone , este un tip de poligon degenerat cu o margine și un vârf . Simbolul său Schläfli este {1} [2] și poate fi construit modificând un digon .
În geometria euclidiană, un monogon cu margini drepte este un obiect imposibil, deoarece capetele sale trebuie să coincidă, spre deosebire de orice linie dreaptă euclidiană. Din acest motiv, monogonul nu este un adevărat poligon în geometria euclidiană .
În geometria unui cerc , un monogon poate fi construit ca un vârf și o margine de 360 ° care se termină în același punct de plecare.
Pe o geometrie sferică, un monogon poate fi construit ca un vârf pe un cerc mare (ecuator). Aceasta formează un diedru, cu două fețe emisferice monogonale care împart o margine de 360 ° și un vârf. Poliedrul său dual este osoedrul , care are două vârfuri antipodale , o față a fusului de 360 ° și o margine formată dintr-un meridian care are ca vârfuri cele două vârfuri [2] . Un monogon trunchiat este un digon.
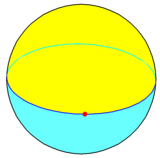 Diedro, {1,2} | 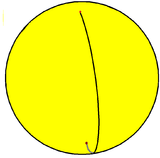 Osoedru, {2,1} |
Digono
În geometrie un digon , bigon sau 2-gone este un poligon cu două margini și două vârfuri și este reprezentat cu simbolul Schläfli {2}. În geometria euclidiană este un poligon degenerat, dar poate fi construit într-o geometrie sferică, cum ar fi două arcuri de 180 ° care leagă două puncte antipodale .
În geometria euclidiană
Un digon este un poligon regulat , deoarece cele două laturi ale sale au aceeași lungime și unghiurile sale sunt ambele de 0 °.
Unele definiții ale unui poligon nu consideră digonul ca un poligon real datorită degenerării sale în geometrie euclidiană
În geometria sferică
O sferă poate conține digoni nedegenerați (cu o zonă diferită de 0) dacă vârfurile sunt puncte antipodale . Unghiul intern al unui vârf poate avea orice valoare de la 0 ° la 360 °. Un astfel de poligon se mai numește și lună sferică.
În poliedre
Un digon este considerat o față degenerată a unui poliedru, deoarece nu are zonă și marginile sale sunt suprapuse. Dar uneori existența sa poate avea utilitate topologică în transformarea poliedrelor
Un poliedru poate fi modificat topologic prin înlocuirea unei fețe cu un digono. O astfel de operație adaugă o latură și o față poliedrului, chiar dacă rezultatul este identic din punct de vedere geometric. Această transformare nu are niciun efect asupra caracteristicii lui Euler ( χ = V - E + F ).
O față digonă poate fi creată și prin prăbușirea geometrică a unei fețe patrulatere prin mișcarea perechilor de vârfuri până când acestea coincid în spațiu. Acest digon poate fi înlocuit pe o singură parte. Pierde o față, două vârfuri și trei laturi, dar lasă totuși caracteristica Euler validă.
Clasele de poliedre pot fi derivate ca degenerări din poliedre primare, făcând să coincidă perechi sau grupuri de vârfuri. De exemplu, următorul poliedru uniform cu simetrie octaedrică (ultimul din tabel) se obține dintr-o degenerare a cuboctaedrului trunchiat .
| Poliedru | cub | Cub trunchiat | Otaedru trunchiat | Octaedru | Cuboctaedru | Rombicuboctaedru | Cuboctaedru trunchiat |
|---|---|---|---|---|---|---|---|
| Imagine |  | 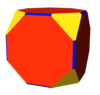 |  |  |  |  |  |
| Figura din partea de sus | ( 2 .4) 3 | 3.8. 2 .8 | 2 .6.4.6 | ( 2 .3) 4 | (3.4) 2 | 3.4.4.4 | 4.6.8 |
În aceste imagini marginile dintre fețele roșii din primele două poliedre și fețele de culoare galbenă din a treia și a patra pot fi văzute ca fețe digonale {2}. În cub , fețele galbene degenerează în puncte, în octaedru fețele roșii degenerează în puncte și în cuboctaedru fețele albastre degenerează în puncte. Acest principiu este utilizat în construcția Wythoff.
Notă
Bibliografie
- Herbert Busemann, Geometria geodeziei. New York, Academic Press, 1955
- Coxeter, Regular Polytopes (ediția a treia). Dover Publications Inc. ISBN 0-486-61480-8
linkuri externe
- (EN) Eric W. Weisstein, Digon în MathWorld Wolfram Research.
- ( EN ) AB Ivanov, Digon , în Enciclopedia Matematicii , Springer și European Mathematical Society, 2002.
