Teorema lui Morley

Teorema lui Morley afirmă că, dacă fiecare colț al triunghiului este împărțit în trei părți egale de doi trisectori, atunci triunghiul în violet este un triunghi echilateral.

În geometrie , teorema lui Morley stabilește că punctele de intersecție a perechilor de trisectori ale unghiurilor adiacente aceleiași părți a oricărui triunghi sunt vârfurile unui triunghi echilateral , ^[1] numit „primul triunghi Morley” sau mai simplu „triunghiul lui Morley ". Această teoremă a fost formulată pentru prima dată în 1899 de matematicianul anglo-american Frank Morley . Teorema, numită și „miracolul lui Morley”, datorită generalității și simplității sale, a făcut atunci obiectul diferitelor generalizări, dintre care una arată în special că, dacă toate trisecantele se intersectează, obținem alte patru triunghiuri echilaterale.
Teorema lui Morley este valabilă numai în contextul geometriei euclidiene și, prin urmare, nu există nici în geometria sferică, nici în cea hiperbolică . ^[2]

Demonstrații

Există multe dovezi ale teoremei lui Morley care utilizează tehnici care variază de la geometria elementară, ca în cazul dovezii date de John Conway , în care, pornind de la un triunghi echilateral, se construiește un alt triunghi care, în final, poate fi făcut similar la orice triunghi (iar triunghiul echilateral de pornire constituie triunghiul său Morley), ^[3] ^[4] la utilizarea trigonometriei , la utilizarea numerelor complexe . ^[5] ^[6]

Dovadă trigonometrică

Fig 1. Dovada elementară a teoremei lui Morley.

Una dintre dovezile care folosesc trigonometria pleacă de la următoarea identitate:

\sin(3\theta )=4\sin \theta \sin(60^{\circ }+\theta )\sin(120^{\circ }+\theta )

{\ displaystyle \ sin (3 \ theta) = 4 \ sin \ theta \ sin (60 ^ {\ circ} + \ theta) \ sin (120 ^ {\ circ} + \ theta)}

{\ displaystyle \ sin (3 \ theta) = 4 \ sin \ theta \ sin (60 ^ {\ circ} + \ theta) \ sin (120 ^ {\ circ} + \ theta)}

[1]

care, prin aplicarea formulei de adiție a sinusului , se poate dovedi a fi egală cu această altă identitate:

\sin(3\theta )=-4\sin ^{3}\theta +3\sin \theta .

{\ displaystyle \ sin (3 \ theta) = - 4 \ sin ^ {3} \ theta +3 \ sin \ theta.}

{\ displaystyle \ sin (3 \ theta) = - 4 \ sin ^ {3} \ theta +3 \ sin \ theta.}

Ceea ce la rândul său poate fi verificat aplicând de două ori formula de adăugare a sânilor la primul membru și apoi folosind formula: $\cos ^{2}\theta =1-\sin ^{2}\theta$ ${\ displaystyle \ cos ^ {2} \ theta = 1- \ sin ^ {2} \ theta}$ ${\ displaystyle \ cos ^ {2} \ theta = 1- \ sin ^ {2} \ theta}$ pentru a înlocui funcția de cosinus .

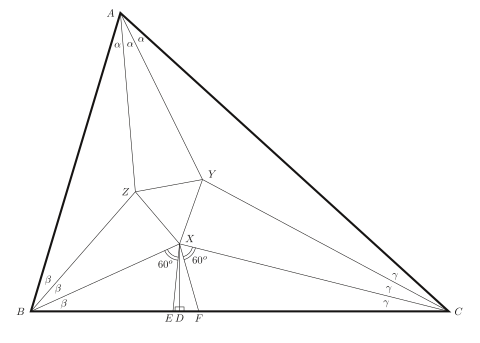
Privind Figura 1, vedem asta pe lateral ${\overline {BC}}$ ${\ displaystyle {\ overline {BC}}}$ $\ overline {BC}$ s-au luat puncte $D., ȘI, F.$ ${\ displaystyle D, E, F}$ ${\ displaystyle D, E, F}$ , și că, deoarece suma unghiurilor interne ale fiecărui triunghi este de 180 °, $3\alpha +3\beta +3\gamma =180^{\circ }$ ${\ displaystyle 3 \ alpha +3 \ beta +3 \ gamma = 180 ^ {\ circ}}$ ${\ displaystyle 3 \ alpha +3 \ beta +3 \ gamma = 180 ^ {\ circ}}$ , de la care $\alpha +\beta +\gamma =60^{\circ }.$ ${\ displaystyle \ alpha + \ beta + \ gamma = 60 ^ {\ circ}.}$ ${\ displaystyle \ alpha + \ beta + \ gamma = 60 ^ {\ circ}.}$ Din aceasta rezultă că unghiurile triunghiului $X ȘI F.$ ${\ displaystyle XEF}$ ${\ displaystyle XEF}$ Sunt $\alpha ,(60^{\circ }+\beta ),$ ${\ displaystyle \ alpha, (60 ^ {\ circ} + \ beta),}$ ${\ displaystyle \ alpha, (60 ^ {\ circ} + \ beta),}$ Și $(60^{\circ }+\gamma ).$ ${\ displaystyle (60 ^ {\ circ} + \ gamma).}$ ${\ displaystyle (60 ^ {\ circ} + \ gamma).}$

Din figura 1 se mai vede că:

\sin(60^{\circ }+\beta )={\frac {\overline {DX}}{\overline {XE}}}

{\ displaystyle \ sin (60 ^ {\ circ} + \ beta) = {\ frac {\ overline {DX}} {\ overline {XE}}}}

{\ displaystyle \ sin (60 ^ {\ circ} + \ beta) = {\ frac {\ overline {DX}} {\ overline {XE}}}}

[2]

Și

\sin(60^{\circ }+\gamma )={\frac {\overline {DX}}{\overline {XF}}}.

{\ displaystyle \ sin (60 ^ {\ circ} + \ gamma) = {\ frac {\ overline {DX}} {\ overline {XF}}}.}

{\ displaystyle \ sin (60 ^ {\ circ} + \ gamma) = {\ frac {\ overline {DX}} {\ overline {XF}}}.}

[3]

În plus,

{\hat {AYC}}=180^{\circ }-\alpha -\gamma =120^{\circ }+\beta

{\ displaystyle {\ hat {AYC}} = 180 ^ {\ circ} - \ alpha - \ gamma = 120 ^ {\ circ} + \ beta}

{\ displaystyle {\ hat {AYC}} = 180 ^ {\ circ} - \ alpha - \ gamma = 120 ^ {\ circ} + \ beta}

Și

{\hat {AZB}}=120^{\circ }+\gamma .

{\ displaystyle {\ hat {AZB}} = 120 ^ {\ circ} + \ gamma.}

{\ displaystyle {\ hat {AZB}} = 120 ^ {\ circ} + \ gamma.}

[4]

Aplicarea teoremei sinusurilor la triunghiuri $LA Da C.$ ${\ displaystyle AYC}$ ${\ displaystyle AYC}$ Și $LA Z B.$ ${\ displaystyle AZB}$ ${\ displaystyle AZB}$ primesti

\sin(120^{\circ }+\beta )={\frac {\overline {AC}}{\overline {AY}}}\sin \gamma

{\ displaystyle \ sin (120 ^ {\ circ} + \ beta) = {\ frac {\ overline {AC}} {\ overline {AY}}} \ sin \ gamma}

{\ displaystyle \ sin (120 ^ {\ circ} + \ beta) = {\ frac {\ overline {AC}} {\ overline {AY}}} \ sin \ gamma}

[5]

Și

\sin(120^{\circ }+\gamma )={\frac {\overline {AB}}{\overline {AZ}}}\sin \beta .

{\ displaystyle \ sin (120 ^ {\ circ} + \ gamma) = {\ frac {\ overline {AB}} {\ overline {AZ}}} \ sin \ beta.}

{\ displaystyle \ sin (120 ^ {\ circ} + \ gamma) = {\ frac {\ overline {AB}} {\ overline {AZ}}} \ sin \ beta.}

[6]

Înălțimea triunghiului $LA B. C.$ ${\ displaystyle ABC}$ $ABC$ poate fi exprimat, folosind ecuația [1] pentru a înlocui $\sin(3\beta )$ ${\ displaystyle \ sin (3 \ beta)}$ ${\ displaystyle \ sin (3 \ beta)}$ Și $\sin(3\gamma )$ ${\ displaystyle \ sin (3 \ gamma)}$ ${\ displaystyle \ sin (3 \ gamma)}$ , în două moduri:

h={\overline {AB}}\sin(3\beta )={\overline {AB}}\cdot 4\sin \beta \sin(60^{\circ }+\beta )\sin(120^{\circ }+\beta )

{\ displaystyle h = {\ overline {AB}} \ sin (3 \ beta) = {\ overline {AB}} \ cdot 4 \ sin \ beta \ sin (60 ^ {\ circ} + \ beta) \ sin ( 120 ^ {\ circ} + \ beta)}

{\ displaystyle h = {\ overline {AB}} \ sin (3 \ beta) = {\ overline {AB}} \ cdot 4 \ sin \ beta \ sin (60 ^ {\ circ} + \ beta) \ sin ( 120 ^ {\ circ} + \ beta)}

Și

h={\overline {AC}}\sin(3\gamma )={\overline {AC}}\cdot 4\sin \gamma \sin(60^{\circ }+\gamma )\sin(120^{\circ }+\gamma ).

{\ displaystyle h = {\ overline {AC}} \ sin (3 \ gamma) = {\ overline {AC}} \ cdot 4 \ sin \ gamma \ sin (60 ^ {\ circ} + \ gamma) \ sin ( 120 ^ {\ circ} + \ gamma).}

{\ displaystyle h = {\ overline {AC}} \ sin (3 \ gamma) = {\ overline {AC}} \ cdot 4 \ sin \ gamma \ sin (60 ^ {\ circ} + \ gamma) \ sin ( 120 ^ {\ circ} + \ gamma).}

Folosind acum ecuațiile [2] și [5] în ecuația lui $\beta$ ${\ displaystyle \ beta}$ $\ beta$ și ecuațiile [3] și [6] în cea a $\gamma$ ${\ displaystyle \ gamma}$ $\gamă$ , noi obținem:

h=4{\overline {AB}}\sin \beta \cdot {\frac {\overline {DX}}{\overline {XE}}}\cdot {\frac {\overline {AC}}{\overline {AY}}}\sin \gamma

{\ displaystyle h = 4 {\ overline {AB}} \ sin \ beta \ cdot {\ frac {\ overline {DX}} {\ overline {XE}}} \ cdot {\ frac {\ overline {AC}} { \ overline {AY}}} \ sin \ gamma}

{\ displaystyle h = 4 {\ overline {AB}} \ sin \ beta \ cdot {\ frac {\ overline {DX}} {\ overline {XE}}} \ cdot {\ frac {\ overline {AC}} { \ overline {AY}}} \ sin \ gamma}

Și

h=4{\overline {AC}}\sin \gamma \cdot {\frac {\overline {DX}}{\overline {XF}}}\cdot {\frac {\overline {AB}}{\overline {AZ}}}\sin \beta

{\ displaystyle h = 4 {\ overline {AC}} \ sin \ gamma \ cdot {\ frac {\ overline {DX}} {\ overline {XF}}} \ cdot {\ frac {\ overline {AB}} { \ overline {AZ}}} \ sin \ beta}

{\ displaystyle h = 4 {\ overline {AC}} \ sin \ gamma \ cdot {\ frac {\ overline {DX}} {\ overline {XF}}} \ cdot {\ frac {\ overline {AB}} { \ overline {AZ}}} \ sin \ beta}

Deoarece numeratorii sunt egali:

{\overline {XE}}\cdot {\overline {AY}}={\overline {XF}}\cdot {\overline {AZ}}

{\ displaystyle {\ overline {XE}} \ cdot {\ overline {AY}} = {\ overline {XF}} \ cdot {\ overline {AZ}}}

{\ displaystyle {\ overline {XE}} \ cdot {\ overline {AY}} = {\ overline {XF}} \ cdot {\ overline {AZ}}}

sau

{\frac {\overline {XE}}{\overline {XF}}}={\frac {\overline {AZ}}{\overline {AY}}}.

{\ displaystyle {\ frac {\ overline {XE}} {\ overline {XF}}} = {\ frac {\ overline {AZ}} {\ overline {AY}}}.}

{\ displaystyle {\ frac {\ overline {XE}} {\ overline {XF}}} = {\ frac {\ overline {AZ}} {\ overline {AY}}}.}

Din moment ce unghiul $ȘI X F.$ ${\ displaystyle EXF}$ ${\ displaystyle EXF}$ și unghiul $Z LA Da$ ${\ displaystyle ZAY}$ ${\ displaystyle ZAY}$ sunt congruente și laturile care formează aceste unghiuri sunt proporționale, apoi triunghiurile $X ȘI F.$ ${\ displaystyle XEF}$ ${\ displaystyle XEF}$ Și $LA Z Da$ ${\ displaystyle AZY}$ ${\ displaystyle AZY}$ sunt similare .

Prin urmare, rezultă că unghiurile $LA Da Z$ ${\ displaystyle AYZ}$ ${\ displaystyle AYZ}$ Și $X F. ȘI$ ${\ displaystyle XFE}$ ${\ displaystyle XFE}$ sunt congruente și egale cu $(60^{\circ }+\gamma )$ ${\ displaystyle (60 ^ {\ circ} + \ gamma)}$ ${\ displaystyle (60 ^ {\ circ} + \ gamma)}$ , în timp ce colțurile $LA Z Da$ ${\ displaystyle AZY}$ ${\ displaystyle AZY}$ Și $X ȘI F.$ ${\ displaystyle XEF}$ ${\ displaystyle XEF}$ sunt congruente și egale cu $(60^{\circ }+\beta ).$ ${\ displaystyle (60 ^ {\ circ} + \ beta).}$ ${\ displaystyle (60 ^ {\ circ} + \ beta).}$ În același mod puteți obține unghiurile de la bază pentru triunghiuri $B. X Z$ ${\ displaystyle BXZ}$ ${\ displaystyle BXZ}$ Și $C. Da X .$ ${\ displaystyle CYX.}$ ${\ displaystyle CYX.}$

În special, constatăm că unghiul $B. Z X$ ${\ displaystyle BZX}$ ${\ displaystyle BZX}$ este egal cu $(60^{\circ }+\alpha )$ ${\ displaystyle (60 ^ {\ circ} + \ alpha)}$ ${\ displaystyle (60 ^ {\ circ} + \ alpha)}$ și, din nou din figura 1, se poate observa că:

{\hat {AZY}}+{\hat {AZB}}+{\hat {BZX}}+{\hat {XZY}}=360^{\circ }.

{\ displaystyle {\ hat {AZY}} + {\ hat {AZB}} + {\ hat {BZX}} + {\ hat {XZY}} = 360 ^ {\ circ}.}

{\ displaystyle {\ hat {AZY}} + {\ hat {AZB}} + {\ hat {BZX}} + {\ hat {XZY}} = 360 ^ {\ circ}.}

Înlocuind unghiul pe baza celor de mai sus și folosind ecuația [4] $LA Z B.$ ${\ displaystyle AZB}$ ${\ displaystyle AZB}$ primesti:

(60^{\circ }+\beta )+(120^{\circ }+\gamma )+(60^{\circ }+\alpha )+{\hat {XZY}}=360^{\circ }

{\ displaystyle (60 ^ {\ circ} + \ beta) + (120 ^ {\ circ} + \ gamma) + (60 ^ {\ circ} + \ alpha) + {\ hat {XZY}} = 360 ^ { \ circ}}

{\ displaystyle (60 ^ {\ circ} + \ beta) + (120 ^ {\ circ} + \ gamma) + (60 ^ {\ circ} + \ alpha) + {\ hat {XZY}} = 360 ^ { \ circ}}

prin urmare:

{\hat {XZY}}=60^{\circ }.

{\ displaystyle {\ hat {XZY}} = 60 ^ {\ circ}.}

{\ displaystyle {\ hat {XZY}} = 60 ^ {\ circ}.}

În mod similar, constatăm că și celelalte două colțuri ale triunghiului $X Da Z$ ${\ displaystyle XYZ}$ ${\ displaystyle XYZ}$ au o valoare de $60^{\circ }$ ${\ displaystyle 60 ^ {\ circ}}$ ${\ displaystyle 60 ^ {\ circ}}$ și deci că triunghiul $X Da Z$ ${\ displaystyle XYZ}$ ${\ displaystyle XYZ}$ este un triunghi echilateral.

Partea și zona

Primul triunghi Morley are laturi de lungime egale cu: ^[7]

a^{\prime }=b^{\prime }=c^{\prime }=8R\sin(A/3)\sin(B/3)\sin(C/3),\,

{\ displaystyle a ^ {\ prime} = b ^ {\ prime} = c ^ {\ prime} = 8R \ sin (A / 3) \ sin (B / 3) \ sin (C / 3), \,}

{\ displaystyle a ^ {\ prime} = b ^ {\ prime} = c ^ {\ prime} = 8R \ sin (A / 3) \ sin (B / 3) \ sin (C / 3), \,}

unde R este circumradiusul triunghiului de pornire e ${\hat {A}},{\hat {B}}$ ${\ displaystyle {\ hat {A}}, {\ hat {B}}}$ ${\ displaystyle {\ hat {A}}, {\ hat {B}}}$ Și ${\hat {C}}$ ${\ displaystyle {\ hat {C}}}$ ${\ hat {C}}$ sunt unghiurile acestui triunghi. Deoarece aria unui triunghi echilateral este exprimată prin formula ${\tfrac {\sqrt {3}}{4}}a'^{2},$ ${\ displaystyle {\ tfrac {\ sqrt {3}} {4}} a '^ {2},}$ ${\ displaystyle {\ tfrac {\ sqrt {3}} {4}} a '^ {2},}$ aria triunghiului Morley poate fi exprimată ca:

{\text{Area}}=16{\sqrt {3}}R^{2}\sin ^{2}(A/3)\sin ^{2}(B/3)\sin ^{2}(C/3).

{\ displaystyle {\ text {Area}} = 16 {\ sqrt {3}} R ^ {2} \ sin ^ {2} (A / 3) \ sin ^ {2} (B / 3) \ sin ^ { 2} (C / 3).}

{\ displaystyle {\ text {Area}} = 16 {\ sqrt {3}} R ^ {2} \ sin ^ {2} (A / 3) \ sin ^ {2} (B / 3) \ sin ^ { 2} (C / 3).}

Triunghiuri Morley

Această figură arată cele 18 triunghiuri Morley ale unui triunghi ABC dat. Cele șase perechi de trisecante prezente la cele trei colțuri ale triunghiului sunt desenate și colorate în așa fel încât intersecțiile a două secante de aceeași culoare identifică 27 de puncte așezate pe 9 segmente diferite, fiecare dintre ele conținând 6 puncte de intersecție, cu aceste segmente fiind între ele sau paralele sau formând un unghi de 60 °.

Teorema lui Morley implică existența a 18 triunghiuri echilaterale. Triunghiul descris mai sus în teoremă, numit primul triunghi Morley , are vârfuri care, în coordonate triliniare în raport cu triunghiul ABC , sunt exprimate ca:

A- vârf = 1: 2 cos ( C / 3): 2 cos ( B / 3)

B- vârf = 2 cos ( C / 3): 1: 2 cos ( A / 3)

C- vârf = 2 cos ( B / 3): 2 cos ( A / 3): 1

Un alt triunghi echilateral al lui Morley, de asemenea un triunghi central, numit al doilea triunghi Morley, are în schimb vârfuri exprimate ca:

A- vârf = 1: 2 cos ( C / 3 - 2π / 3): 2 cos ( B / 3 - 2π / 3)

B- vârf = 2 cos ( C / 3 - 2π / 3): 1: 2 cos ( A / 3 - 2π / 3)

C- vârf = 2 cos ( B / 3 - 2π / 3): 2 cos ( A / 3 - 2π / 3): 1

Al treilea din cele 18 triunghiuri Morley echilaterale, de asemenea un triunghi central, numit al treilea triunghi Morley este dat de următoarele vârfuri:

A- vârf = 1: 2 cos ( C / 3 - 4π / 3): 2 cos ( B / 3 - 4π / 3)

B- vârf = 2 cos ( C / 3 - 4π / 3): 1: 2 cos ( A / 3 - 4π / 3)

C- vârf = 2 cos ( B / 3 - 4π / 3): 2 cos ( A / 3 - 4π / 3): 1

Cele trei triunghiuri descrise mai sus formează perechi omotetice între ele. Un alt triunghi homotetic pentru ei este format din trei puncte X prezente pe circumferința triunghiului ABC și astfel încât linia XX ⁻¹ este tangentă la circumferință , unde X ^-1 denotă conjugatul izogonal al lui X. Acest triunghi echilateral, numit triunghi circumtanțial , are următoarele vârfuri:

A- vertex = csc ( C / 3 - B / 3): csc ( B / 3 + 2 C / 3): −csc ( C / 3 + 2 B / 3)

B- vertex = −csc ( A / 3 + 2 C / 3): csc ( A / 3 - C / 3): csc ( C / 3 + 2 A / 3)

C- vertex = csc ( A / 3 + 2 B / 3): −csc ( B / 3 + 2 A / 3): csc ( B / 3 - A / 3)

Un al cincilea triunghi echilateral, de asemenea omotetic cu celelalte, este obținut prin rotirea triunghiului circumtangențial al lui? / 6 în jurul centrului său. Numit triunghi circular , vârfurile acestuia pot fi exprimate ca:

A- vârf = sec ( C / 3 - B / 3): −sec ( B / 3 + 2 C / 3): −sec ( C / 3 + 2 B / 3)

B- vertex = −sec ( A / 3 + 2 C / 3): sec ( A / 3 - C / 3): −sec ( C / 3 + 2 A / 3)

C- vertex = −sec ( A / 3 + 2 B / 3): −sec ( B / 3 + 2 A / 3): sec ( B / 3 - A / 3)

Printr-o operație numită „extraversiune”, fiecare dintre cele 18 triunghiuri Morley poate fi obținut din fiecare din celelalte 18. Mai mult, fiecare triunghi poate fi „extravertit” în trei moduri diferite, iar cele 18 triunghiuri Morley împreună cu cele 27 de perechi de triunghiuri extravertite , a format cele 18 vârfuri și 27 de fețe ale unui grafic Pappus . ^[8]

Centrele triunghiurilor

Centrul de greutate al primului triunghi Morley în coordonate triliniare este exprimat ca:

Centrul Morley = X (356) = cos ( A / 3) + 2 cos ( B / 3) cos ( C / 3): cos ( B / 3) + 2 cos ( C / 3) cos ( A / 3): cos ( C / 3) + 2 cos ( A / 3) cos ( B / 3).

Primul triunghi Morley este omolog triunghiului ABC : ^[9] liniile care leagă un vârf al triunghiului de pornire cu vârful opus al triunghiului Morley se întâlnesc în punctul:

Primul centru Morley - Taylor - Marr = X (357) = sec ( A / 3): sec ( B / 3): sec ( C / 3).

Notă

^ Teorema lui Morley , pe lorenzoroi.net , Lorenzo Roi. Adus de 13 mai 2020.
^ Teorema lui Morley în geometrie sferică , lienhard-wimmer.com , Lienhard Wimmer, 25 ianuarie 2008. Accesat la 13 mai 2020 .
^ Alexander Bogomolny, dovada lui J. Conway , cut-the-knot.org , Cut-the-nod. Adus de 13 mai 2020.
^ Renato Betti, miracolul lui Morley și alte regularități ale triunghiurilor , pe matematica.unibocconi.it , Universitatea Luigi Bocconi . Adus de 13 mai 2020.
^ Alexander Bogomolny, Miracolul lui Morley , la cut-the-knot.org , Cut-the-knot . Adus de 13 mai 2020.
^ Plan complex și teorema lui Morley ( PDF ), Universitatea din Padova . Adus de 13 mai 2020.
^ Eric W. Weisstein, First Morley Triangle , pe MathWorld . Adus de 13 mai 2020.
^ Richard K. Guy, The lighthouse theorem, Morley & Malfatti - a budget of paradoxes ( PDF ), în American Mathematical Monthly , vol. 114, nr. 2, 2007, pp. 97-141, JSTOR 27642143 . Adus la 14 mai 2020 (Arhivat din original la 1 aprilie 2010) .
^ MD Fox și JR Goggins, diagrama lui Morley generalizată , în Mathematical Gazette , n. 87, noiembrie 2003, pp. 453-467.

Alte proiecte

Wikimedia Commons conține imagini sau alte fișiere despre teorema lui Morley

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică

[1] Teorema lui Morley , pe lorenzoroi.net , Lorenzo Roi. Adus de 13 mai 2020.

[2] Teorema lui Morley în geometrie sferică , lienhard-wimmer.com , Lienhard Wimmer, 25 ianuarie 2008. Accesat la 13 mai 2020 .

[3] Alexander Bogomolny, dovada lui J. Conway , cut-the-knot.org , Cut-the-nod. Adus de 13 mai 2020.

[4] Renato Betti, miracolul lui Morley și alte regularități ale triunghiurilor , pe matematica.unibocconi.it , Universitatea Luigi Bocconi . Adus de 13 mai 2020.

[5] Alexander Bogomolny, Miracolul lui Morley , la cut-the-knot.org , Cut-the-knot . Adus de 13 mai 2020.

[6] Plan complex și teorema lui Morley ( PDF ), Universitatea din Padova . Adus de 13 mai 2020.

[7] Eric W. Weisstein, First Morley Triangle , pe MathWorld . Adus de 13 mai 2020.

[8] Richard K. Guy, The lighthouse theorem, Morley & Malfatti - a budget of paradoxes ( PDF ), în American Mathematical Monthly , vol. 114, nr. 2, 2007, pp. 97-141, JSTOR 27642143 . Adus la 14 mai 2020 (Arhivat din original la 1 aprilie 2010) .

[9] MD Fox și JR Goggins, diagrama lui Morley generalizată , în Mathematical Gazette , n. 87, noiembrie 2003, pp. 453-467.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]