Cosinus

Dat fiind un triunghi dreptunghic , cosinusul unui unghi acut este definit ca raportul dintre lungimile catetului adiacent unghiului și ale hipotenuzei

În matematică , în special în trigonometrie , având în vedere un triunghi dreptunghiular , cosinusul unuia dintre cele două unghiuri interne adiacente hipotenuzei este definit ca raportul dintre lungimile catetului adiacent unghiului și ale hipotenuzei .

Mai general, cosinusul unui unghi $\alpha$ ${\ displaystyle \ alpha}$ $\ alfa$ , exprimată în grade sau radiani , este o cantitate care depinde doar de $\alpha$ ${\ displaystyle \ alpha}$ $\ alfa$ , construită folosind circumferința unității .

Definirea modului $\cos(x)$ ${\ displaystyle \ cos (x)}$ $\ cos (x)$ valoarea cosinusului în unghi $X$ ${\ displaystyle x}$ $X$ , obținem funcția cosinus, o funcție trigonometrică de importanță fundamentală în analiza matematică .

S-ar putea afirma în continuare că cosinusul este abscisa extremului $P.$ ${\ displaystyle P}$ $P.$ calculat în raport cu raza sa unitară (a circumferinței goniometrice ) Din aceasta se poate deduce că:

pentru valori cuprinse între 0º și 90º cosinusul punctului $P.$ ${\ displaystyle P}$ $P.$ scade;
pentru valori cuprinse între 90º și 180º cosinusul punctului $P.$ ${\ displaystyle P}$ $P.$ scade;
pentru valori cuprinse între 180º și 270º cosinusul punctului $P.$ ${\ displaystyle P}$ $P.$ crește;
pentru valori cuprinse între 270º și 360º cosinusul punctului $P.$ ${\ displaystyle P}$ $P.$ crește.

Definiție

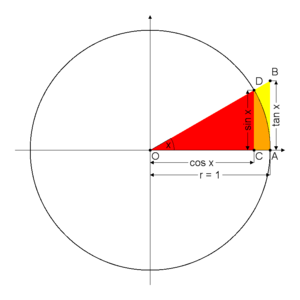
În triunghiul roșu din figură, cosinusul lui $X$ ${\ displaystyle x}$ $X$ este dat de

\cos x={\overline {OC}}.

{\ displaystyle \ cos x = {\ overline {OC}}.}

{\ displaystyle \ cos x = {\ overline {OC}}.}

Mai general, cosinusul este definit prin luarea unei circumferințe a razei unitare și a razei care iese din origine care formează un unghi $X$ ${\ displaystyle x}$ $X$ cu axa absciselor ca în figură. Cosinusul unghiului $X$ ${\ displaystyle x}$ $X$ prin urmare, este definită ca valoarea coordonatei $X$ ${\ displaystyle x}$ $X$ a punctului de intersecție între prima rază și circumferința (în figură, este lungimea segmentului $SAU C.$ ${\ displaystyle OC}$ $OC$ ).

Următorul tabel listează principalele valori notabile asumate de funcția cosinus: ^[1] ^[2]

$X$ ${\ displaystyle x}$ $X$ în radiani	0	${\frac {\pi }{12}}$ ${\ displaystyle {\ frac {\ pi} {12}}}$ ${\ displaystyle {\ frac {\ pi} {12}}}$	${\frac {\pi }{10}}$ ${\ displaystyle {\ frac {\ pi} {10}}}$ ${\ displaystyle {\ frac {\ pi} {10}}}$	${\frac {\pi }{6}}$ ${\ displaystyle {\ frac {\ pi} {6}}}$ ${\ frac {\ pi} {6}}$	${\frac {\pi }{4}}$ ${\ displaystyle {\ frac {\ pi} {4}}}$ ${\ frac {\ pi} {4}}$	${\frac {\pi }{3}}$ ${\ displaystyle {\ frac {\ pi} {3}}}$ ${\ frac {\ pi} {3}}$	${\frac {5}{12}}\pi$ ${\ displaystyle {\ frac {5} {12}} \ pi}$ ${\ displaystyle {\ frac {5} {12}} \ pi}$	${\frac {\pi }{2}}$ ${\ displaystyle {\ frac {\ pi} {2}}}$ ${\ frac {\ pi} {2}}$	$\pi$ ${\ displaystyle \ pi}$ $\ pi$	${\frac {3\pi }{2}}$ ${\ displaystyle {\ frac {3 \ pi} {2}}}$ ${\ frac {3 \ pi} {2}}$	$2\pi$ ${\ displaystyle 2 \ pi}$ $2 \ pi$
$X$ ${\ displaystyle x}$ $X$ în grade	0 °	15 °	18 °	30 °	45 °	60 °	75 °	90 °	180 °	270 °	360 °
$\cos(x)$ ${\ displaystyle \ cos (x)}$ $\ cos (x)$	$1$ ${\ displaystyle 1}$ $1$	${\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}$ ${\ displaystyle {\ frac {{\ sqrt {6}} + {\ sqrt {2}}} {4}}}$ ${\ displaystyle {\ frac {{\ sqrt {6}} + {\ sqrt {2}}} {4}}}$	${\frac {\sqrt {10+2{\sqrt {5}}}}{4}}$ ${\ displaystyle {\ frac {\ sqrt {10 + 2 {\ sqrt {5}}}} {4}}}$ ${\ displaystyle {\ frac {\ sqrt {10 + 2 {\ sqrt {5}}}} {4}}}$	${\frac {\sqrt {3}}{2}}$ ${\ displaystyle {\ frac {\ sqrt {3}} {2}}}$ ${\ frac {\ sqrt {3}} {2}}$	${\frac {\sqrt {2}}{2}}$ ${\ displaystyle {\ frac {\ sqrt {2}} {2}}}$ ${\ frac {\ sqrt {2}} {2}}$	${\frac {1}{2}}$ ${\ displaystyle {\ frac {1} {2}}}$ ${\ frac {1} {2}}$	${\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}$ ${\ displaystyle {\ frac {{\ sqrt {6}} - {\ sqrt {2}}} {4}}}$ ${\ displaystyle {\ frac {{\ sqrt {6}} - {\ sqrt {2}}} {4}}}$		$-1$ ${\ displaystyle -1}$ $-1$		$1$ ${\ displaystyle 1}$ $1$

Există o altă definiție a cosinusului în raport cu rotațiile: cosinusul unui unghi $X$ ${\ displaystyle x}$ $X$ este componenta de-a lungul axei abscisei unității vectoriale $the$ ${\ displaystyle i}$ $the$ , vector unitate de axă $X$ ${\ displaystyle x}$ $X$ , rotit de $X$ ${\ displaystyle x}$ $X$ .

Funcția cosinusului

Funcția cosinusului este definită prin asocierea cu $X$ ${\ displaystyle x}$ $X$ cosinusul unghiului $X$ ${\ displaystyle x}$ $X$ (reprezentat în radiani), și este indicat cu $f(x)=\cos x$ ${\ displaystyle f (x) = \ cos x}$ ${\ displaystyle f (x) = \ cos x}$ . Atâta timp cât $X$ ${\ displaystyle x}$ $X$ Și $x+2k\pi$ ${\ displaystyle x + 2k \ pi}$ $x + 2k \ pi$ definiți același unghi pentru orice $k$ ${\ displaystyle k}$ $k$ întreg , funcția cosinusului este o funcție periodică a perioadei $2\pi .$ ${\ displaystyle 2 \ pi.}$ ${\ displaystyle 2 \ pi.}$ Curba graficului acestei funcții se numește cosinusoid . ^[3] Ansamblul variabilității funcției cosinusului este $[-1,1]$ ${\ displaystyle [-1,1]}$ $[-1,1]$ , adică, aplicând această funcție oricărui număr real obținem întotdeauna un număr real între $-1$ ${\ displaystyle -1}$ $-1$ Și $1$ ${\ displaystyle 1}$ $1$ , extreme incluse.

Reprezentarea grafică a unei unde cosinus.

Cosinus și sinus

Valori principale (cosinus, sinus)

Între sinus și cosinus există relația fundamentală, numită prima relație fundamentală (sau lege) a trigonometriei: ^[4]

\sin ^{2}x+\cos ^{2}x=1,

{\ displaystyle \ sin ^ {2} x + \ cos ^ {2} x = 1,}

{\ displaystyle \ sin ^ {2} x + \ cos ^ {2} x = 1,}

ceea ce este o consecință a teoremei lui Pitagora .

Proprietăți analitice ale cosinusului

Derivata funcției cosinus este opusul funcției sinus. ^[5] ^[6] . Adică avem:

(\cos x)^{\prime }=-\sin x.

{\ displaystyle (\ cos x) ^ {\ prime} = - \ sin x.}

(\ cos x) ^ {{\ prime}} = - \ sin x.

Acest lucru poate fi demonstrat prin aplicarea unei formule de prostoafereză pentru a calcula limita raportului incremental al cosinusului:

{\frac {\cos(x+h)-\cos x}{h}}={\frac {-2\sin {\frac {2x+h}{2}}\sin {\frac {h}{2}}}{h}}=-{\frac {\sin {\frac {h}{2}}}{\frac {h}{2}}}\sin \left(x+{\frac {h}{2}}\right){\underset {h\rightarrow 0}{\longrightarrow }}-\sin x

{\ displaystyle {\ frac {\ cos (x + h) - \ cos x} {h}} = {\ frac {-2 \ sin {\ frac {2x + h} {2}} \ sin {\ frac { h} {2}}} {h}} = - {\ frac {\ sin {\ frac {h} {2}}} {\ frac {h} {2}}} \ sin \ left (x + {\ frac {h} {2}} \ right) {\ underset {h \ rightarrow 0} {\ longrightarrow}} - \ sin x}

{\ frac {\ cos (x + h) - \ cos x} {h}} = {\ frac {-2 \ sin {\ frac {2x + h} {2}} \ sin {\ frac {h} { 2}}} {h}} = - {\ frac {\ sin {\ frac {h} {2}}} {{\ frac {h} {2}}}} \ sin \ left (x + {\ frac {h} {2}} \ right) {\ underset {h \ rightarrow 0} {\ longrightarrow}} - \ sin x

^[7] .

A doua derivată a cosinusului este funcția în sine schimbată în semn:

(\cos x)^{\prime \prime }=-\cos x,

{\ displaystyle (\ cos x) ^ {\ prime \ prime} = - \ cos x,}

(\ cos x) ^ {{\ prime \ prime}} = - \ cos x,

prin urmare, funcția cosinusului (precum și funcția sinus ) rezolvă ecuația diferențială

y^{\prime \prime }+y=0

{\ displaystyle y ^ {\ prime \ prime} + y = 0}

y ^ {{\ prime \ prime}} + y = 0

,

care descrie mișcarea unui oscilator armonic liber ideal.

Funcția cosinusului este o funcție derivată echilimitată (de fapt avem $|y^{(k)}|\leq 1$ ${\ displaystyle | y ^ {(k)} | \ leq 1}$ $| y ^ {{(k)}} | \ leq 1$ pentru fiecare $k$ ${\ displaystyle k}$ $k$ ) și, prin urmare, este analitică ; expansiunea sa din seria Taylor este: ^[8]

\cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots

{\ displaystyle \ cos x = 1 - {\ frac {x ^ {2}} {2!}} + {\ frac {x ^ {4}} {4!}} - {\ frac {x ^ {6} } {6!}} + \ Cdots}

\ cos x = 1 - {\ frac {x ^ {2}} {2!}} + {\ frac {x ^ {4}} {4!}} - {\ frac {x ^ {6}} {6 !}} + \ cdots

=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}

{\ displaystyle = \ sum _ {n = 0} ^ {\ infty} {\ frac {(-1) ^ {n} x ^ {2n}} {(2n)!}}}

= \ sum _ {{n = 0}} ^ {\ infty} {\ frac {(-1) ^ {n} x ^ {{2n}}} {(2n)!}}

pentru fiecare $X$ ${\ displaystyle x}$ $X$ real.

În analiza matematică, această egalitate este adesea utilizată pentru a defini cosinusul. Aceeași serie definește cosinusul ca o funcție holomorfă pe întregul plan complex .

Primitivul cosinusului este sinusul, adică:

\int \cos xdx=\sin x+c.

{\ displaystyle \ int \ cos xdx = \ sin x + c.}

{\ displaystyle \ int \ cos xdx = \ sin x + c.}

Ecuații fundamentale relative la cosinus

Următorul arc plus (și scădere) formulă se aplică:

\cos(x\pm y)=\cos x\cos y\mp \sin x\sin y,

{\ displaystyle \ cos (x \ pm y) = \ cos x \ cos y \ mp \ sin x \ sin y,}

\ cos (x \ pm y) = \ cos x \ cos y \ mp \ sin x \ sin y,

și în special formula de duplicare

\cos {(2x)}=\cos ^{2}x-\sin ^{2}x=1-2\sin ^{2}x=2\cos ^{2}x-1.

{\ displaystyle \ cos {(2x)} = \ cos ^ {2} x- \ sin ^ {2} x = 1-2 \ sin ^ {2} x = 2 \ cos ^ {2} x-1.}

\ cos {(2x)} = \ cos ^ {2} x- \ sin ^ {2} x = 1-2 \ sin ^ {2} x = 2 \ cos ^ {2} x-1.

Formula de bisecție pentru cosinus este: ^[9]

\cos \left({\frac {\alpha }{2}}\right)=\pm {\sqrt {\frac {1+\cos \alpha }{2}}}.

{\ displaystyle \ cos \ left ({\ frac {\ alpha} {2}} \ right) = \ pm {\ sqrt {\ frac {1+ \ cos \ alpha} {2}}}.}

{\ displaystyle \ cos \ left ({\ frac {\ alpha} {2}} \ right) = \ pm {\ sqrt {\ frac {1+ \ cos \ alpha} {2}}}.}

Următoarele sunt formulele de prosterafere legate de cosinus :

\cos x+\cos y=2\cos {\frac {x+y}{2}}\cos {\frac {x-y}{2}},

{\ displaystyle \ cos x + \ cos y = 2 \ cos {\ frac {x + y} {2}} \ cos {\ frac {xy} {2}},}

{\ displaystyle \ cos x + \ cos y = 2 \ cos {\ frac {x + y} {2}} \ cos {\ frac {x-y} {2}},}

\cos x-\cos y=-2\sin {\frac {x+y}{2}}\sin {\frac {x-y}{2}}.

{\ displaystyle \ cos x- \ cos y = -2 \ sin {\ frac {x + y} {2}} \ sin {\ frac {xy} {2}}.}

{\ displaystyle \ cos x- \ cos y = -2 \ sin {\ frac {x + y} {2}} \ sin {\ frac {x-y} {2}}.}

Lanțul inegalităților se aplică și:

0<x\cos x<\sin x<x\quad {\text{ per }}\quad 0<x<{\frac {\pi }{2}}.

{\ displaystyle 0 <x \ cos x <\ sin x <x \ quad {\ text {per}} \ quad 0 <x <{\ frac {\ pi} {2}}.}

0 <x \ cos x <\ sin x <x \ quad {\ text {per}} \ quad 0 <x <{\ frac {\ pi} {2}}.

Demonstrație

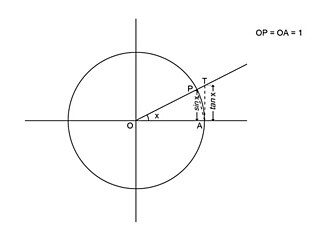
Luați în considerare circumferința unității și lăsați-o să fie $0<x<\pi /2$ ${\ displaystyle 0 <x <\ pi / 2}$ $0 <x <\ pi / 2$ , așa cum se arată în figură.

Desenați raza care iese din originea care formează un unghi $X$ ${\ displaystyle x}$ $X$ (în sens invers acelor de ceasornic) în ceea ce privește semiaxa pozitivă a absciselor. Apoi coordonatele punctului de intersecție $P.$ ${\ displaystyle P}$ $P.$ ale razei cu circumferința sunt $(\cos x,\sin x)$ ${\ displaystyle (\ cos x, \ sin x)}$ $(\ cos x, \ sin x)$ . Desenați segmentul care se unește $P.$ ${\ displaystyle P}$ $P.$ până la punctul $A=(1,0)$ ${\ displaystyle A = (1,0)}$ $A = (1,0)$ . De asemenea, să fie $T.$ ${\ displaystyle T}$ $T.$ punctul de intersecție dintre rază și linia abscisei $1$ ${\ displaystyle 1}$ $1$ (axa tangentelor). $T.$ ${\ displaystyle T}$ $T.$ are coordonate $(1,\tan x)$ ${\ displaystyle (1, \ tan x)}$ $(1, \ tan x)$ .

Observăm că triunghiul $P. SAU LA$ ${\ displaystyle POA}$ $POA$ este strict încadrat în sectorul circular $P. SAU LA$ ${\ displaystyle POA}$ $POA$ , care la rândul său este strâns închis în triunghi $T. SAU LA$ ${\ displaystyle TOA}$ $TOA$ . Atunci se aplică inegalitatea zonelor respective (amintiți-vă că $X$ ${\ displaystyle x}$ $X$ este unghiul, exprimat în radiani ):

0<{\frac {1}{2}}\sin x<{\frac {1}{2}}x<{\frac {1}{2}}{\frac {\sin x}{\cos x}},

{\ displaystyle 0 <{\ frac {1} {2}} \ sin x <{\ frac {1} {2}} x <{\ frac {1} {2}} {\ frac {\ sin x} { \ cos x}},}

0 <{\ frac {1} {2}} \ sin x <{\ frac {1} {2}} x <{\ frac {1} {2}} {\ frac {\ sin x} {\ cos x }},

sau

0<\sin x<x<{\frac {\sin x}{\cos x}}.

{\ displaystyle 0 <\ sin x <x <{\ frac {\ sin x} {\ cos x}}.}

0 <\ sin x <x <{\ frac {\ sin x} {\ cos x}}.

Din prima parte a inegalității rezultă că $0<\sin x<x$ ${\ displaystyle 0 <\ sin x <x}$ $0 <\ sin x <x$ , în timp ce îl manipulați pe al doilea, adică împărțind la $\sin x$ ${\ displaystyle \ sin x}$ $\ sin x$ (ceea ce este posibil pentru că $\sin x>0$ ${\ displaystyle \ sin x> 0}$ $\ sin x> 0$ ), avem că:

1<{\frac {x}{\sin x}}<{\frac {1}{\cos x}},

{\ displaystyle 1 <{\ frac {x} {\ sin x}} <{\ frac {1} {\ cos x}},}

1 <{\ frac {x} {\ sin x}} <{\ frac {1} {\ cos x}},

sau

\sin x\cos x<x\cos x<\sin x,

{\ displaystyle \ sin x \ cos x <x \ cos x <\ sin x,}

\ sin x \ cos x <x \ cos x <\ sin x,

unde s-a înmulțit în cele din urmă cu $\sin x$ ${\ displaystyle \ sin x}$ $\ sin x$ si pentru $\cos x$ ${\ displaystyle \ cos x}$ $\ cos x$ , care păstrează direcția inegalității, deoarece ambele sunt pozitive. Rezumând rezultatele,

$0<x\cos x<\sin x<x.$ ${\ displaystyle 0 <x \ cos x <\ sin x <x.}$ $0 <x \ cos x <\ sin x <x.$

QED .

Există, de asemenea, o identitate trigonometrică care leagă funcția cosinus de funcția tangentă :

\cos x={\frac {1-\tau ^{2}}{1+\tau ^{2}}},\quad {\text{ con }}\quad \tau =\tan {\frac {x}{2}}

{\ displaystyle \ cos x = {\ frac {1- \ tau ^ {2}} {1+ \ tau ^ {2}}}, \ quad {\ text {cu}} \ quad \ tau = \ tan {\ frac {x} {2}}}

{\ displaystyle \ cos x = {\ frac {1- \ tau ^ {2}} {1+ \ tau ^ {2}}}, \ quad {\ text {cu}} \ quad \ tau = \ tan {\ frac {x} {2}}}

^[10] .

Această identitate, numită formula parametrică , are o importanță fundamentală în rezolvarea ecuațiilor goniometrice în care necunoscutul apare ca argument atât al unui sinus, cât și al unui cosinus (sau al funcțiilor derivate din acestea). Există, de fapt, o identitate analogă în ceea ce privește sânul, care permite rezolvarea ecuației în necunoscut $\tau$ ${\ displaystyle \ tau}$ $\ tau$ . În mod similar, această relație poate fi exploatată pentru calculul primitivelor funcțiilor goniometrice.

Definiții conexe

Reciprocul cosinusului (definit unde cosinusul este diferit de zero) este secanta : ^[11]

\sec x={\frac {1}{\cos x}}.

{\ displaystyle \ sec x = {\ frac {1} {\ cos x}}.}

\ sec x = {\ frac 1 {\ cos x}}.

Funcția cosinusului este injectivă pe parcursul intervalului $[0,\pi ]$ ${\ displaystyle [0, \ pi]}$ $[0, \ pi]$ și, prin urmare, are un invers , numit arccosine (notat cu $\arccos$ ${\ displaystyle \ arccos}$ $\ arccos$ sau cu $\cos ^{-1}$ ${\ displaystyle \ cos ^ {- 1}}$ $\ cos ^ {{- 1}}$ care preia notația funcției inverse ). ^[12]

Alte proprietăți

Din formula lui Euler se poate deduce că funcția cosinusului este legată de funcția exponențială și de funcția cosinusului hiperbolic . De fapt, pentru orice număr real $X$ ${\ displaystyle x}$ $X$ da ai

\cos x={\frac {e^{ix}+e^{-ix}}{2}}=\cosh(ix).

{\ displaystyle \ cos x = {\ frac {e ^ {ix} + e ^ {- ix}} {2}} = \ cosh (ix).}

{\ displaystyle \ cos x = {\ frac {e ^ {ix} + e ^ {- ix}} {2}} = \ cosh (ix).}

În analiza complexă , aplicândteorema factorizării Weierstrass funcției cosinusului, aceasta poate fi exprimată ca un produs infinit , folosind următoarea formulă care se aplică pentru orice număr complex $z$ ${\ displaystyle z}$ $z$

\cos z=\prod _{n=1}^{\infty }\left[1-{\frac {4z^{2}}{\pi ^{2}(2n-1)^{2}}}\right].

{\ displaystyle \ cos z = \ prod _ {n = 1} ^ {\ infty} \ left [1 - {\ frac {4z ^ {2}} {\ pi ^ {2} (2n-1) ^ {2 }}} \ dreapta].}

{\ displaystyle \ cos z = \ prod _ {n = 1} ^ {\ infty} \ left [1 - {\ frac {4z ^ {2}} {\ pi ^ {2} (2n-1) ^ {2 }}} \ dreapta].}

Un alt produs infinit raportează sinusul și cosinusul:

\sin z=z\cdot \prod _{n=1}^{\infty }\cos \left({\frac {z}{2^{n}}}\right).

{\ displaystyle \ sin z = z \ cdot \ prod _ {n = 1} ^ {\ infty} \ cos \ left ({\ frac {z} {2 ^ {n}}} \ right).}

{\ displaystyle \ sin z = z \ cdot \ prod _ {n = 1} ^ {\ infty} \ cos \ left ({\ frac {z} {2 ^ {n}}} \ right).}

Există, de asemenea, o relație între funcția cosinus și funcția Gamma dată de următoarea integrală definită, valabilă pentru $n>1$ ${\ displaystyle n> 1}$ $n> 1$ : ^[13]

\int _{0}^{\infty }\cos(x^{n})dx=\Gamma \left(1+{\frac {1}{n}}\right)\cos \left({\frac {\pi }{2n}}\right).

{\ displaystyle \ int _ {0} ^ {\ infty} \ cos (x ^ {n}) dx = \ Gamma \ left (1 + {\ frac {1} {n}} \ right) \ cos \ left ( {\ frac {\ pi} {2n}} \ right).}

{\ displaystyle \ int _ {0} ^ {\ infty} \ cos (x ^ {n}) dx = \ Gamma \ left (1 + {\ frac {1} {n}} \ right) \ cos \ left ( {\ frac {\ pi} {2n}} \ right).}

În cele din urmă, folosind formula fracției continue a lui Euler, este posibil să se exprime funcția cosinusului sub forma unei fracții continue : ^[14]

\cos x=1-{\cfrac {x^{2}}{1\cdot 2+{\cfrac {1\cdot 2\ x^{2}}{(3\cdot 4-x^{2})+{\cfrac {3\cdot 4\ x^{2}}{(5\cdot 6-x^{2})+{\cfrac {5\cdot 6\ x^{2}}{(7\cdot 8-x^{2})+\ddots }}}}}}}}.

{\ displaystyle \ cos x = 1 - {\ cfrac {x ^ {2}} {1 \ cdot 2 + {\ cfrac {1 \ cdot 2 \ x ^ {2}} {(3 \ cdot 4-x ^ { 2}) + {\ cfrac {3 \ cdot 4 \ x ^ {2}} {(5 \ cdot 6-x ^ {2}) + {\ cfrac {5 \ cdot 6 \ x ^ {2}} {( 7 \ cdot 8-x ^ {2}) + \ ddots}}}}}}}}.}

{\ displaystyle \ cos x = 1 - {\ cfrac {x ^ {2}} {1 \ cdot 2 + {\ cfrac {1 \ cdot 2 \ x ^ {2}} {(3 \ cdot 4-x ^ { 2}) + {\ cfrac {3 \ cdot 4 \ x ^ {2}} {(5 \ cdot 6-x ^ {2}) + {\ cfrac {5 \ cdot 6 \ x ^ {2}} {( 7 \ cdot 8-x ^ {2}) + \ ddots}}}}}}}}.}

Originea numelui

Termenul cosinus provine din latinescul complementi sinus „sinusul complementarului (unghiului)”. ^[15] Într-adevăr, pentru unghiurile dintre și $\pi /2$ ${\ displaystyle \ pi / 2}$ $\ pi / 2$ , cosinusul unui unghi este sinusul unghiului complementar , adică

\cos x=\sin \left({\frac {\pi }{2}}\pm x\right).

{\ displaystyle \ cos x = \ sin \ left ({\ frac {\ pi} {2}} \ pm x \ right).}

{\ displaystyle \ cos x = \ sin \ left ({\ frac {\ pi} {2}} \ pm x \ right).}

Această relație, care se obține din suma formulelor arcurilor, este valabilă pentru fiecare $X$ ${\ displaystyle x}$ $X$ ; totuși noțiunea geometrică de unghi complementar se aplică doar unghiurilor pozitive și, prin urmare, inclusă între și $\pi /2$ ${\ displaystyle \ pi / 2}$ $\ pi / 2$ .

Originea numelui sine (înțeles în sensul de golf ) se întoarce la rândul său la o traducere incorectă a unui termen arab.

Notă

^ Valorile funcțiilor goniometrice , pe youmath.it , YouMath. Accesat 19 octombrie 2016.
^ ExerciseMatica.com , https://www.esercizimatematica.com/tabella-seno-coseno-con-tutti-gli-angoli/ .
^ cosinusoide , în Dicționar de științe fizice , Treccani, 1996. Adus 19 octombrie 2016 .
^ Formule trigonometrice , pe youmath.it , YouMath. Accesat 19 octombrie 2016.
^ Derivat al cosinusului , pe youmath.it , YouMath. Accesat 19 octombrie 2016.
^ Paolo Baroncini, Roberto Manfredi, Ilaria Fragni, Lineamenti.Math Blu-Volumul 5 , Ghisetti și Corvi, 2012, ISBN 978-88-538-0433-4 . p.283
^ . Ultimul pas folosește limita notabilă :
$\lim _{x\to 0}{\frac {\sin x}{x}}=1,$ ${\ displaystyle \ lim _ {x \ to 0} {\ frac {\ sin x} {x}} = 1,}$ $\ lim _ {{x \ to 0}} {{\ frac {\ sin x} {x}}} = 1,$
care poate fi dovedit geometric.
^ Carla Maderna și Paolo Maurizio Soardi, Lecții de analiză matematică , CittàStudi Edizioni - Milano, 1995, ISBN 88-251-7090-4 . p.238
^ Paolo Baroncini, Roberto Manfredi, Ilaria Fragni, Lineamenti.Math Blu-Volumul 4 , Ghisetti și Corvi, 2012, ISBN 978-88-538-0432-7 . p.245
^ De fapt avem, în virtutea unității goniometrice și împărțirea la $\cos x$ ${\ displaystyle \ cos x}$ $\ cos x$ (atâta timp cât nu este nulă), identitatea
$\cos {(2x)}=\cos ^{2}x-\sin ^{2}x={\frac {\cos ^{2}x-\sin ^{2}x}{\cos ^{2}x+\sin ^{2}x}}={\frac {1-\tan ^{2}x}{1+\tan ^{2}x}}$ ${\ displaystyle \ cos {(2x)} = \ cos ^ {2} x- \ sin ^ {2} x = {\ frac {\ cos ^ {2} x- \ sin ^ {2} x} {\ cos ^ {2} x + \ sin ^ {2} x}} = {\ frac {1- \ tan ^ {2} x} {1+ \ tan ^ {2} x}}}$ ${\ displaystyle \ cos {(2x)} = \ cos ^ {2} x- \ sin ^ {2} x = {\ frac {\ cos ^ {2} x- \ sin ^ {2} x} {\ cos ^ {2} x + \ sin ^ {2} x}} = {\ frac {1- \ tan ^ {2} x} {1+ \ tan ^ {2} x}}}$ .
^ secante , în Enciclopedie online , Treccani. Accesat 19 octombrie 2016.
^ arcocoséno , în Enciclopedie online , Treccani. Accesat 19 octombrie 2016.
^ Wolfram Mathworld - Cosinus , la mathworld.wolfram.com . Adus 9 aprilie 2020.
^ Mauro Fiorentini - Funcții exprimate prin fracții continue , pe bitman.name . Adus pe 10 aprilie 2020 .
^ cosinus în „Dicționar de științe fizice”

Bibliografie

C. Maderna și Soardi PM, lecții de matematică, Ediții CittàStudi - Milano, 1995, ISBN 88-251-7090-4 .
Paolo Baroncini, Roberto Manfredi, Ilaria Fragni, Lineamenti.Math Blu-Volumul 5 , Ghisetti și Corvi, 2012, ISBN 978-88-538-0433-4 .
Paolo Baroncini, Roberto Manfredi, Ilaria Fragni, Lineamenti.Math Blu-Volumul 4 , Ghisetti și Corvi, 2012, ISBN 978-88-538-0432-7 .

Elemente conexe

Alte proiecte

Wikționarul conține dicționarul lema „ cosinus ”
Wikimedia Commons conține imagini sau alte fișiere pe cosinus

linkuri externe

Cosinus - de la Wolfram MathWorld

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică

[1] Valorile funcțiilor goniometrice , pe youmath.it , YouMath. Accesat 19 octombrie 2016.

[2] ExerciseMatica.com , https://www.esercizimatematica.com/tabella-seno-coseno-con-tutti-gli-angoli/ .

[3] sinusoide , în Dicționar de științe fizice , Treccani, 1996. Adus 19 octombrie 2016 .

[4] Formule trigonometrice , pe youmath.it , YouMath. Accesat 19 octombrie 2016.

[5] Derivat al cosinusului , pe youmath.it , YouMath. Accesat 19 octombrie 2016.

[6] Paolo Baroncini, Roberto Manfredi, Ilaria Fragni, Lineamenti.Math Blu-Volumul 5 , Ghisetti și Corvi, 2012, ISBN 978-88-538-0433-4 . p.283

[7] . Ultimul pas folosește limita notabilă :
$\lim _{x\to 0}{\frac {\sin x}{x}}=1,$ ${\ displaystyle \ lim _ {x \ to 0} {\ frac {\ sin x} {x}} = 1,}$ $\ lim _ {{x \ to 0}} {{\ frac {\ sin x} {x}}} = 1,$
care poate fi dovedit geometric.

[8] Carla Maderna și Paolo Maurizio Soardi, Lecții de analiză matematică , CittàStudi Edizioni - Milano, 1995, ISBN 88-251-7090-4 . p.238

[9] Paolo Baroncini, Roberto Manfredi, Ilaria Fragni, Lineamenti.Math Blu-Volumul 4 , Ghisetti și Corvi, 2012, ISBN 978-88-538-0432-7 . p.245

[10] De fapt avem, în virtutea unității goniometrice și împărțirea la $\cos x$ ${\ displaystyle \ cos x}$ $\ cos x$ (atâta timp cât nu este nulă), identitatea
$\cos {(2x)}=\cos ^{2}x-\sin ^{2}x={\frac {\cos ^{2}x-\sin ^{2}x}{\cos ^{2}x+\sin ^{2}x}}={\frac {1-\tan ^{2}x}{1+\tan ^{2}x}}$ ${\ displaystyle \ cos {(2x)} = \ cos ^ {2} x- \ sin ^ {2} x = {\ frac {\ cos ^ {2} x- \ sin ^ {2} x} {\ cos ^ {2} x + \ sin ^ {2} x}} = {\ frac {1- \ tan ^ {2} x} {1+ \ tan ^ {2} x}}}$ ${\ displaystyle \ cos {(2x)} = \ cos ^ {2} x- \ sin ^ {2} x = {\ frac {\ cos ^ {2} x- \ sin ^ {2} x} {\ cos ^ {2} x + \ sin ^ {2} x}} = {\ frac {1- \ tan ^ {2} x} {1+ \ tan ^ {2} x}}}$ .

[11] secante , în Enciclopedie online , Treccani. Accesat 19 octombrie 2016.

[12] rcocoséno , în Enciclopedie online , Treccani. Accesat 19 octombrie 2016.

[mathworld-13] Wolfram Mathworld - Cosinus , la mathworld.wolfram.com . Adus 9 aprilie 2020.

[14] Mauro Fiorentini - Funcții exprimate prin fracții continue , pe bitman.name . Adus pe 10 aprilie 2020 .

[15] sinus în „Dicționar de științe fizice”

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

V · D · M Trigonometrie
Funcția trigonometrică · Funcția trigonometrică inversă
Funcții	Sân · versin · cosinus · Cosenoverso · Tangent · Cotangent · Secant · Secante externe · Cosecant · Cosecant extern
Funcții inverse	Arc sinus · Arc cosinus · Arctangent · cotangent invers · Arcosecante · Arcocosecante
Teoreme și formule	Rope Teorema · sani Teorema · cosinus teorema · drept de tangentele · cotangents Teorema · Pitagora · Formulele Prosthaphaeresis · Formulele Werner
Alte	Tabel trigonometric · tabel de integrale nedefinite ale funcțiilor trigonometrice · tabel de integrale nedefinite ale funcțiilor arc · Funcții hiperbolice · identități trigonometrice · Constante trigonometrice exacte · Istoricul funcțiilor trigonometrice