Funcția trigonometrică

Funcțiile trigonometrice ale unghiului θ pot fi construite geometric în funcție de un cerc circular centrat în O.

Graficele funcțiilor trigonometrice cosinus ( verde ), sinus ( albastru ), tangent ( roșu ), cosecant ( galben ), secant ( magenta ), cotangent ( cian ).

În matematică , funcțiile trigonometrice sau funcțiile goniometrice sau funcțiile circulare sunt funcții ale unui unghi ; acestea sunt importante în studiul triunghiurilor și în modelarea fenomenelor periodice, precum și un număr mare de alte aplicații.

Ele sunt adesea definite ca raporturile dintre laturile unui triunghi dreptunghiular care conține unghiul și, în mod echivalent, pot fi definite ca lungimile mai multor segmente construite din cercul unitar . Definiții mai moderne le exprimă ca serii infinite sau ca soluții ale anumitor ecuații diferențiale , obținându-se extinderea lor la valori pozitive sau negative și, de asemenea, la numere complexe . Toate aceste abordări diferite sunt prezentate mai jos.

Studiul funcțiilor trigonometrice datează de pe vremea babilonienilor și o cantitate considerabilă din munca fundamentală a fost făcută de matematicieni greci , indieni și persani .

În utilizarea curentă, există șase funcții trigonometrice de bază, care sunt listate mai jos împreună cu identitățile care le raportează. În special pentru ultimele patru, aceste relații sunt adesea luate ca definiții ale acelor funcții, deși este la fel de posibil să le definim geometric sau în alte moduri și numai mai târziu să derivăm aceste relații. Puține alte funcții erau comune în trecut (și au apărut în tabelele vechi), dar sunt puțin folosite astăzi, cum ar fi inversul (1 - cos θ) și exsecante (sec θ - 1). Multe alte relații notabile dintre aceste funcții sunt listate în intrarea privind identitățile trigonometrice .

Funcţie	Abreviere	Relație
In caz contrar	sin (sau sen, nomenclatura italiană)	$\sin \theta =\cos \left({\frac {\pi }{2}}-\theta \right)$ ${\ displaystyle \ sin \ theta = \ cos \ left ({\ frac {\ pi} {2}} - \ theta \ right)}$ $\ sin \ theta = \ cos \ left (\ frac {\ pi} {2} - \ theta \ right)$
Cosinus	cos	$\cos \theta =\sin \left({\frac {\pi }{2}}-\theta \right)$ ${\ displaystyle \ cos \ theta = \ sin \ left ({\ frac {\ pi} {2}} - \ theta \ right)}$ $\ cos \ theta = \ sin \ left (\ frac {\ pi} {2} - \ theta \ right)$
Tangentă	bronz (sau tg)	$\tan \theta ={\frac {1}{\cot \theta }}={\frac {\sin \theta }{\cos \theta }}=\cot \left({\frac {\pi }{2}}-\theta \right)$ ${\ displaystyle \ tan \ theta = {\ frac {1} {\ cot \ theta}} = {\ frac {\ sin \ theta} {\ cos \ theta}} = \ cot \ left ({\ frac {\ pi } {2}} - \ theta \ right)}$ $\ tan \ theta = \ frac {1} {\ cot \ theta} = \ frac {\ sin \ theta} {\ cos \ theta} = \ cot \ left (\ frac {\ pi} {2} - \ theta \ dreapta)$
Cotangentă	pătuț (sau ctg)	$\cot \theta ={\frac {1}{\tan \theta }}={\frac {\cos \theta }{\sin \theta }}=\tan \left({\frac {\pi }{2}}-\theta \right)$ ${\ displaystyle \ cot \ theta = {\ frac {1} {\ tan \ theta}} = {\ frac {\ cos \ theta} {\ sin \ theta}} = \ tan \ left ({\ frac {\ pi } {2}} - \ theta \ right)}$ $\ cot \ theta = \ frac {1} {\ tan \ theta} = \ frac {\ cos \ theta} {\ sin \ theta} = \ tan \ left (\ frac {\ pi} {2} - \ theta \ dreapta)$
Secantă	sec	$\sec \theta ={\frac {1}{\cos \theta }}=\csc \left({\frac {\pi }{2}}-\theta \right)$ ${\ displaystyle \ sec \ theta = {\ frac {1} {\ cos \ theta}} = \ csc \ left ({\ frac {\ pi} {2}} - \ theta \ right)}$ $\ sec \ theta = \ frac {1} {\ cos \ theta} = \ csc \ left (\ frac {\ pi} {2} - \ theta \ right)$
Cosecant	csc (sau cosec)	$\csc \theta ={\frac {1}{\sin \theta }}=\sec \left({\frac {\pi }{2}}-\theta \right)$ ${\ displaystyle \ csc \ theta = {\ frac {1} {\ sin \ theta}} = \ sec \ left ({\ frac {\ pi} {2}} - \ theta \ right)}$ $\ csc \ theta = \ frac {1} {\ sin \ theta} = \ sec \ left (\ frac {\ pi} {2} - \ theta \ right)$

Istorie

Același subiect în detaliu:Istoria funcțiilor trigonometrice .

Cea mai veche referire la funcția sinusoidală datează din Sulba Sutras , scrisă în India antică din secolele VIII-VI î.Hr. Mai târziu, funcțiile trigonometrice au fost studiate de Hipparhus din Niceea (180-125 î.Hr.), Aryabhata (476 - 550), Varāhamihira , Brahmagupta , Muḥammad ibn Mūsā al-Ḵwārizmī , Abu'l-Wafa , Omar Khayyam , Bhaskara II , Nasir al-Din Tusi , Regiomontano (1464), Ghiyath al-Kashi ( sec. XIV ), Ulugh Beg (sec. XIV), Madhava (c. 1400), retez , discipolul său Valentin Otho . În Introducuctio in analysin infinitorum ( 1748 ) al lui Leonardo Euler recunoaștem meritul de a fi stabilit tratamentul analitic al funcțiilor trigonometrice în Europa, definindu-le ca serii infinite și prezentând „ formula Euler ”.

Noțiunea că trebuie să existe o corespondență între lungimile laturilor unui triunghi și unghiurile triunghiului apare imediat ce se înțelege că triunghiuri similare mențin aceleași relații între laturile corespunzătoare. Cu alte cuvinte, pentru orice triunghi similar, relația dintre ipotenuză (de exemplu) și o altă latură rămâne aceeași. Dacă hipotenuza este de două ori mai lungă, laturile sunt, de asemenea, de două ori mai lungi. Funcțiile trigonometrice exprimă exact aceste relații.

Definiții prin intermediul triunghiurilor unghiulare

Un triunghi dreptunghiular include întotdeauna un unghi de 90 ° (π / 2 radiani), numit aici C. Unghiurile A și B pot varia. Funcțiile trigonometrice specifică relațiile dintre lungimile laturilor și unghiurile interioare ale unui triunghi dreptunghiular.

Pentru a defini funcțiile trigonometrice ale unghiului A , luați în considerare un triunghi dreptunghiular care conține unghiul A :

Folosim următoarele nume pentru laturile triunghiului:

Hipotenuza este latura opusă unghiului drept sau, în mod echivalent, cea mai lungă parte a unui triunghi dreptunghiular, în acest caz i .
Partea opusă este partea opusă unghiului pe care îl luăm în considerare, în acest caz a .
Partea adiacentă este partea în contact cu unghiul pe care îl luăm în considerare și cu unghiul drept. În acest caz, partea adiacentă este b .

Se consideră că toate triunghiurile aparțin planului euclidian, astfel încât suma unghiurilor interne este π radiani (sau 180 ° ); în consecință, pentru un triunghi dreptunghiular, cele două unghiuri non-drepte sunt cuprinse între 0 și π / 2 radiani. Strict vorbind, următoarele definiții vă permit să definiți funcții trigonometrice numai pentru unghiurile din acest interval. Cu toate acestea, putem extinde definițiile la setul de numere reale utilizând cercul unitar sau impunând că aceste funcții posedă anumite simetrii sau sunt periodice .

1) Sinusul unui unghi este raportul dintre lungimea laturii opuse și lungimea hipotenuzei. Eu sunt cazul nostru

\sin A={\frac {{\textrm {lato}}\ {\textrm {opposto}}}{\textrm {ipotenusa}}}={\frac {a}{i}}

{\ displaystyle \ sin A = {\ frac {{\ textrm {side}} \ {\ textrm {adverse}}} {\ textrm {hypotenuse}}} = {\ frac {a} {i}}}

{\ displaystyle \ sin A = {\ frac {{\ textrm {side}} \ {\ textrm {adverse}}} {\ textrm {hypotenuse}}} = {\ frac {a} {i}}}

Este important de reținut că acest raport nu depinde de triunghiul dreptunghiular ales, atâta timp cât conține unghiul A, deoarece toate aceste triunghiuri sunt similare .

Setul de zerouri sinusoidale este

\left\{n\pi {\big |}n\in \mathbb {Z} \right\}

{\ displaystyle \ left \ {n \ pi {\ big |} n \ in \ mathbb {Z} \ right \}}

\ left \ {n \ pi \ big | n \ isin \ mathbb {Z} \ right \}

2) Cosinusul unui unghi este raportul dintre lungimea laturii adiacente și lungimea hipotenuzei. Eu sunt cazul nostru

\cos A={\frac {{\textrm {lato}}\ {\textrm {adiacente}}}{\textrm {ipotenusa}}}={\frac {b}{i}}

{\ displaystyle \ cos A = {\ frac {{\ textrm {side}} \ {\ textrm {adjacent}}} {\ textrm {hypotenuse}}} = {\ frac {b} {i}}}

{\ displaystyle \ cos A = {\ frac {{\ textrm {side}} \ {\ textrm {adjacent}}} {\ textrm {hypotenuse}}} = {\ frac {b} {i}}}

Setul de zerouri ale cosinusului este

\left\{{\frac {\pi }{2}}+n\pi {\bigg |}n\in \mathbb {Z} \right\}

{\ displaystyle \ left \ {{\ frac {\ pi} {2}} + n \ pi {\ bigg |} n \ in \ mathbb {Z} \ right \}}

\ left \ {\ frac {\ pi} {2} + n \ pi \ bigg | n \ isin \ mathbb {Z} \ right \}

3) Tangenta unui unghi este raportul dintre lungimea laturii opuse și lungimea laturii adiacente. Eu sunt cazul nostru

\tan A={\frac {{\textrm {lato}}\ {\textrm {opposto}}}{{\textrm {lato}}\ {\textrm {adiacente}}}}={\frac {a}{b}}

{\ displaystyle \ tan A = {\ frac {{\ textrm {side}} \ {\ textrm {adverse}}} {{\ textrm {side}} \ {\ textrm {adjacent}}}} = {\ frac { a} {b}}}

{\ displaystyle \ tan A = {\ frac {{\ textrm {side}} \ {\ textrm {adverse}}} {{\ textrm {side}} \ {\ textrm {adjacent}}}} = {\ frac { a} {b}}}

Setul de zerouri ale tangentei este

\left\{n\pi {\big |}n\in \mathbb {Z} \right\}

{\ displaystyle \ left \ {n \ pi {\ big |} n \ in \ mathbb {Z} \ right \}}

\ left \ {n \ pi \ big | n \ isin \ mathbb {Z} \ right \}

Coincide cu setul de zerouri ale sinusului din moment ce

\tan A={\frac {\mathrm {sen\,} A}{\cos A}}

{\ displaystyle \ tan A = {\ frac {\ mathrm {sen \,} A} {\ cos A}}}

\ tan A = \ frac {\ mathrm {sen \,} A} {\ cos A}

Funcțiile rămase sunt definite în mod convenabil folosind cele trei definiții deja furnizate.

4) Csc cosecant ( A ) este inversul multiplicativ al păcatului ( A ), adică raportul dintre lungimea hipotenuzei și cea a laturii opuse:

\csc A={\frac {\textrm {ipotenusa}}{{\textrm {lato}}\ {\textrm {opposto}}}}={\frac {i}{a}}

{\ displaystyle \ csc A = {\ frac {\ textrm {hypotenuse}} {{\ textrm {side}} \ {\ textrm {adverse}}}} = {\ frac {i} {a}}}

{\ displaystyle \ csc A = {\ frac {\ textrm {hypotenuse}} {{\ textrm {side}} \ {\ textrm {adverse}}}} = {\ frac {i} {a}}}

5) Secanta secantă ( A ) este inversul multiplicativ al cos ( A ), adică raportul dintre lungimea hipotenuzei și cea a laturii adiacente:

\sec A={\frac {\textrm {ipotenusa}}{{\textrm {lato}}\ {\textrm {adiacente}}}}={\frac {i}{b}}

{\ displaystyle \ sec A = {\ frac {\ textrm {hypotenuse}} {{\ textrm {side}} \ {\ textrm {adjacent}}}} = {\ frac {i} {b}}}

{\ displaystyle \ sec A = {\ frac {\ textrm {hypotenuse}} {{\ textrm {side}} \ {\ textrm {adjacent}}}} = {\ frac {i} {b}}}

6) Patul cotangent ( A ) este inversul multiplicativ al tanului ( A ), adică raportul dintre lungimea laturii adiacente și cea a laturii opuse:

\cot A={\frac {{\textrm {lato}}\ {\textrm {adiacente}}}{{\textrm {lato}}\ {\textrm {opposto}}}}={\frac {b}{a}}

{\ displaystyle \ cot A = {\ frac {{\ textrm {side}} \ {\ textrm {adjacent}}} {{\ textrm {side}} \ {\ textrm {adverse}}}} = {\ frac { b} {a}}}

{\ displaystyle \ cot A = {\ frac {{\ textrm {side}} \ {\ textrm {adjacent}}} {{\ textrm {side}} \ {\ textrm {adverse}}}} = {\ frac { b} {a}}}

Definiții în circumferința goniometrică

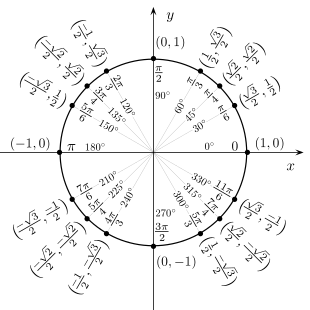
Circumferința goniometrică și unele unghiuri notabile

Este posibil să se definească cele șase funcții trigonometrice pornind de la circumferința unității sau circumferința goniometrică, centrată la origine și cu raza egală cu 1. Definiția prin circumferința goniometrică nu ajută la calculul practic al valorilor funcții; de fapt se bazează pe triunghiuri dreptunghiulare pentru multe unghiuri. Cu toate acestea, permite definirea funcțiilor trigonometrice pentru toate argumentele reale, pozitive și negative, nu doar pentru cele limitate la intervalul dintre 0 și π / 2. De asemenea, vă permite să afișați grafic toate funcțiile trigonometrice într-o singură figură. Ecuația circumferinței goniometrice este:

x^{2}+y^{2}=1

{\ displaystyle x ^ {2} + y ^ {2} = 1}

x ^ 2 + y ^ 2 = 1

Unele unghiuri comune sunt prezentate în imagine, măsurate în radiani. Măsurătorile în sens invers acelor de ceasornic sunt unghiuri pozitive, măsurătorile în sensul acelor de ceasornic sunt negative. Să luăm în considerare intersecția cu circumferința goniometrică a unei drepte care formează un unghi θ cu jumătatea pozitivă a axei x . X abscisa și ordonata y ale acestui punct sunt egale cu cos θ și respectiv sin θ. Triunghiul din desen demonstrează echivalența cu definiția anterioară: raza circumferinței este hipotenuza triunghiului și are o lungime egală cu 1, prin urmare sin θ = y / 1 și cos θ = x / 1. Ne putem gândi la circumferința goniometrică ca la o modalitate de a considera un număr infinit de triunghiuri dreptunghiulare în care lungimea picioarelor variază, în timp ce hipotenuza rămâne egală cu 1.

Graficele funcțiilor f ( x ) = sin ( x ) și f ( x ) = cos ( x ) pe plan cartezian.

Animația pentru funcția sin (x) arată corelația dintre cerc și sinus.

Pentru unghiurile mai mari de 2π sau mai mici de −2π, ne putem imagina făcând mai multe rotații în jurul cercului. În acest fel, sinusul și cosinusul devin funcții periodice ale perioadei 2π.

\sin \theta =\sin \left(\theta +2\pi k\right)

{\ displaystyle \ sin \ theta = \ sin \ left (\ theta +2 \ pi k \ right)}

\ sin \ theta = \ sin \ left (\ theta + 2 \ pi k \ right)

\cos \theta =\cos \left(\theta +2\pi k\right)

{\ displaystyle \ cos \ theta = \ cos \ left (\ theta +2 \ pi k \ right)}

\ cos \ theta = \ cos \ left (\ theta + 2 \ pi k \ right)

pentru fiecare unghi θ și fiecare număr întreg k .

Cea mai mică perioadă pozitivă a unei funcții periodice se numește perioada primitivă a funcției. Perioada primitivă a sinusului, cosinusului, secantei și cosecantei este întreaga circumferință, adică 2π radiani sau 360 de grade; perioada primitivă a tangentei și cotangentei este doar jumătate din circumferință, adică π radiani sau 180 de grade. Mai sus, numai funcțiile sinus și cosinus au fost definite pe cercul unitar, dar celelalte patru funcții trigonometrice pot fi definite prin:

\tan \theta ={\frac {\sin \theta }{\cos \theta }}\quad \sec \theta ={\frac {1}{\cos \theta }}

{\ displaystyle \ tan \ theta = {\ frac {\ sin \ theta} {\ cos \ theta}} \ quad \ sec \ theta = {\ frac {1} {\ cos \ theta}}}

\ tan \ theta = \ frac {\ sin \ theta} {\ cos \ theta} \ quad \ sec \ theta = \ frac {1} {\ cos \ theta}

\csc \theta ={\frac {1}{\sin \theta }}\quad \cot \theta ={\frac {\cos \theta }{\mathrm {sen\,} \theta }}

{\ displaystyle \ csc \ theta = {\ frac {1} {\ sin \ theta}} \ quad \ cot \ theta = {\ frac {\ cos \ theta} {\ mathrm {sen \,} \ theta}}}

\ csc \ theta = \ frac {1} {\ sin \ theta} \ quad \ cot \ theta = \ frac {\ cos \ theta} {\ mathrm {sen \,} \ theta}

Graficul funcției f (x) = tan (x) pe plan cartezian.

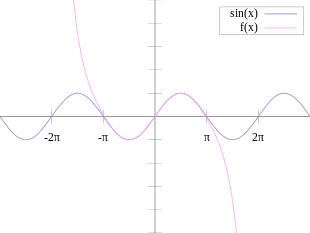
Imaginea din dreapta arată graficul pe plan cartezian al funcției f (θ) = tan (θ), considerabil diferite de cele văzute anterior pentru sinus și cosinus. Punctele de intersecție cu axa x coincid cu sinul corespunzător (θ), în timp ce funcția nu este definită la intersecțiile funcției cos (θ) cu axa x . Valorile funcției se schimbă lent în vecinătatea unghiurilor egale cu k π, în timp ce se schimbă rapid pentru unghiurile din vecinătatea ( k / 2) π. Graficul tangentei are și o asimptotă verticală pentru θ = k π / 2: de fapt funcția tinde spre infinit dacă unghiul θ tinde spre k / π din stânga și minus infinit dacă θ tinde spre k / π din dreapta .

Toate funcțiile trigonometrice pot fi construite geometric pornind de la circumferința goniometrică.

Alternativ, este posibil să se definească toate funcțiile trigonometrice de bază pornind de la circumferința goniometrică (prezentată în dreapta); astfel de definiții au fost utilizate istoric. În special, având în vedere o coardă AB a circumferinței, unde θ este jumătate din unghiul subtensionat, sin (θ) este AC (jumătate din lungimea coardei), adică piciorul triunghiului dreptunghi având coarda ca hipotenuză și un picior întins pe rază, definiție introdusă în India (vezi mai sus). cos (θ) este distanța orizontală OC , adică cealaltă parte, iar versin (θ) = 1 - cos (θ) este CD, adică distanța dintre cosinus și punctul circumferinței care atinge raza pe care se află . tan (θ) este lungimea segmentului AE pe linia tangentă pentru A , de unde și denumirea de tangentă , dată de intersecția acesteia cu extensia razei . cot (θ) este un alt segment tangent, AF, care este extensia tangentei care se întâlnește cu cea a razei perpendiculare pe cea pe care se află cosinusul . sec (θ) = OE și csc (θ) = OF sunt segmente de linii secante (care intersectează circumferința în două puncte), adică suma sinusului, cosenoversului și seclului extern OA aglital. DE se numește exsec (θ) = sec (θ) - 1 (porțiunea secantei din exterior care intersectează cotangenta de cerc). Din aceste construcții, este ușor de văzut că funcțiile secante și tangente diverg dacă θ tinde la π / 2 (90 de grade) și că cosecanta și cotangenta diverg dacă θ tinde la zero. (Se pot realiza multe construcții similare, iar identitățile trig de bază pot fi demonstrate grafic.)

Definiții după dezvoltarea seriei

Funcția sinusoidală (în albastru) este foarte bine aproximată de gradul său 7 polinomul Taylor (în roz) pentru valori cuprinse între -π și π.

Folosind doar noțiunile de geometrie și proprietățile limitelor , se poate arăta că derivata sinusului este cosinusul și derivata cosinusului este opusul sinusului. (Aici și, în general, în calcul , toate unghiurile sunt măsurate în radiani ; vezi și importanța radianilor de mai jos.) Teoria seriei lui Taylor poate fi utilizată pentru a demonstra că următoarele identități sunt valabile pentru orice număr real $X$ ${\ displaystyle x}$ $X$ :

\sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {{(-1)}^{n}x^{2n+1}}{(2n+1)!}}

{\ displaystyle \ sin x = x - {\ frac {x ^ {3}} {3!}} + {\ frac {x ^ {5}} {5!}} - {\ frac {x ^ {7} } {7!}} + \ Cdots = \ sum _ {n = 0} ^ {\ infty} {\ frac {{(-1)} ^ {n} x ^ {2n + 1}} {(2n + 1 )!}}}

\ sin x = x - \ frac {x ^ 3} {3!} + \ frac {x ^ 5} {5!} - \ frac {x ^ 7} {7!} + \ cdots = \ sum_ {n = 0} ^ \ infty \ frac {{(- 1)} ^ nx ^ {2n + 1}} {(2n + 1)!}

\cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {{(-1)}^{n}x^{2n}}{(2n)!}}

{\ displaystyle \ cos x = 1 - {\ frac {x ^ {2}} {2!}} + {\ frac {x ^ {4}} {4!}} - {\ frac {x ^ {6} } {6!}} + \ Cdots = \ sum _ {n = 0} ^ {\ infty} {\ frac {{(-1)} ^ {n} x ^ {2n}} {(2n)!}} }

\ cos x = 1 - \ frac {x ^ 2} {2!} + \ frac {x ^ 4} {4!} - \ frac {x ^ 6} {6!} + \ cdots = \ sum_ {n = 0} ^ \ infty \ frac {{(- 1)} ^ nx ^ {2n}} {(2n)!}

Aceste identități sunt adesea luate ca definiții ale funcțiilor sinus și cosinus. Ele sunt adesea folosite ca punct de plecare pentru un tratament riguros al funcțiilor trigonometrice și al aplicațiilor acestora, deoarece teoria seriilor infinite poate fi dezvoltată pornind de la fundamentele sistemului numerelor reale, indiferent de orice considerație geometrică. Diferențialitatea și continuitatea acestor funcții sunt apoi obținute pornind doar de la definiția din seria de putere.

Alte evoluții pot fi obținute în serie: ^[1]

$\tan x\,$ ${\ displaystyle \ tan x \,}$ $\ tan x \,$	${}=\sum _{n=0}^{\infty }{\frac {U_{2n+1}x^{2n+1}}{(2n+1)!}}$ ${\ displaystyle {} = \ sum _ {n = 0} ^ {\ infty} {\ frac {U_ {2n + 1} x ^ {2n + 1}} {(2n + 1)!}}}$ ${} = \ sum_ {n = 0} ^ \ infty \ frac {U_ {2n + 1} x ^ {2n + 1}} {(2n + 1)!}$
	${}=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}}$ ${\ displaystyle {} = \ sum _ {n = 1} ^ {\ infty} {\ frac {(-1) ^ {n-1} 2 ^ {2n} (2 ^ {2n} -1) B_ {2n } x ^ {2n-1}} {(2n)!}}}$ ${} = \ sum_ {n = 1} ^ \ infty \ frac {(- 1) ^ {n-1} 2 ^ {2n} (2 ^ {2n} -1) B_ {2n} x ^ {2n-1 }} {(2n)!}$
	${}=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+{\frac {17x^{7}}{315}}+\cdots ,\qquad {\mbox{for }}\|x\|<{\frac {\pi }{2}}$ ${\ displaystyle {} = x + {\ frac {x ^ {3}} {3}} + {\ frac {2x ^ {5}} {15}} + {\ frac {17x ^ {7}} {315 }} + \ cdots, \ qquad {\ mbox {for}} \| x \| <{\ frac {\ pi} {2}}}$ ${} = x + \ frac {x ^ 3} {3} + \ frac {2 x ^ 5} {15} + \ frac {17 x ^ 7} {315} + \ cdots, \ qquad \ mbox {for} \| x \| <\ frac {\ pi} {2}$

unde este

U_{n}

{\ displaystyle U_ {n}}

A

este numărul de permutări alternative , adică permutări ale

\{1,2,\ldots ,n\}

{\ displaystyle \ {1,2, \ ldots, n \}}

\ {1, 2, \ ldots, n \}

astfel încât primul element este mai mic decât al doilea, al doilea este mai mare decât al treilea, al treilea este mai mic decât al patrulea și așa mai departe.

B_{n}

{\ displaystyle B_ {n}}

B_ {n}

este

n

{\ displaystyle n}

n

-al număr Bernoulli , e

E_{n}

{\ displaystyle E_ {n}}

E_ {n}

(mai jos) este

n

{\ displaystyle n}

n

-numărul lui Euler .

Coeficientul $U_{2n+1}$ ${\ displaystyle U_ {2n + 1}}$ $U_ {2n + 1}$ Numeratorul are o interpretare combinatorie : indică numărul permutațiilor alternante ale seturilor finite de cardinalitate impară.

\csc x\,

{\ displaystyle \ csc x \,}

\ csc x \,

{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n+1}2(2^{2n-1}-1)B_{2n}x^{2n-1}}{(2n)!}}

{\ displaystyle {} = \ sum _ {n = 0} ^ {\ infty} {\ frac {(-1) ^ {n + 1} 2 (2 ^ {2n-1} -1) B_ {2n} x ^ {2n-1}} {(2n)!}}}

{\ displaystyle {} = \ sum _ {n = 0} ^ {\ infty} {\ frac {(-1) ^ {n + 1} 2 (2 ^ {2n-1} -1) B_ {2n} x ^ {2n-1}} {(2n)!}}}

{}={\frac {1}{x}}+{\frac {x}{6}}+{\frac {7x^{3}}{360}}+{\frac {31x^{5}}{15120}}+\cdots ,\qquad {\mbox{for }}0<|x|<\pi

{\ displaystyle {} = {\ frac {1} {x}} + {\ frac {x} {6}} + {\ frac {7x ^ {3}} {360}} + {\ frac {31x ^ { 5}} {15120}} + \ cdots, \ qquad {\ mbox {for}} 0 <| x | <\ pi}

{} = \ frac {1} {x} + \ frac {x} {6} + \ frac {7 x ^ 3} {360} + \ frac {31 x ^ 5} {15120} + \ cdots, \ qquad \ mbox {for} 0 <| x | <\ pi

\sec x\,

{\ displaystyle \ sec x \,}

\ sec x \,

{}=\sum _{n=0}^{\infty }{\frac {U_{2n}x^{2n}}{(2n)!}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{n}x^{2n}}{(2n)!}}

{\ displaystyle {} = \ sum _ {n = 0} ^ {\ infty} {\ frac {U_ {2n} x ^ {2n}} {(2n)!}} = \ sum _ {n = 0} ^ {\ infty} {\ frac {(-1) ^ {n} E_ {n} x ^ {2n}} {(2n)!}}}

{} = \ sum_ {n = 0} ^ \ infty \ frac {U_ {2n} x ^ {2n}} {(2n)!} = \ sum_ {n = 0} ^ \ infty \ frac {(- 1) ^ n E_n x ^ {2n}} {(2n)!}

{}=1+{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}+{\frac {61x^{6}}{720}}+\cdots ,\qquad {\mbox{for }}|x|<{\frac {\pi }{2}}

{\ displaystyle {} = 1 + {\ frac {x ^ {2}} {2}} + {\ frac {5x ^ {4}} {24}} + {\ frac {61x ^ {6}} {720 }} + \ cdots, \ qquad {\ mbox {for}} | x | <{\ frac {\ pi} {2}}}

{} = 1 + \ frac {x ^ 2} {2} + \ frac {5 x ^ 4} {24} + \ frac {61 x ^ 6} {720} + \ cdots, \ qquad \ mbox {for} | x | <\ frac {\ pi} {2}

Coeficientul $U_{2n}$ ${\ displaystyle U_ {2n}}$ $U _ {{2n}}$ un numărător poate fi interpretat, din punct de vedere combinatoriu, ca număr de permutații alternante de mulțimi finite de cardinalitate pare.

\cot x\,

{\ displaystyle \ cot x \,}

\ cot x \,

{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}2^{2n}B_{2n}x^{2n-1}}{(2n)!}}

{\ displaystyle {} = \ sum _ {n = 0} ^ {\ infty} {\ frac {(-1) ^ {n} 2 ^ {2n} B_ {2n} x ^ {2n-1}} {( 2n)!}}}

{} = \ sum_ {n = 0} ^ \ infty \ frac {(- 1) ^ n 2 ^ {2n} B_ {2n} x ^ {2n-1}} {(2n)!}

{}={\frac {1}{x}}-{\frac {x}{3}}-{\frac {x^{3}}{45}}-{\frac {2x^{5}}{945}}-\cdots ,\qquad {\mbox{for }}0<|x|<\pi

{\ displaystyle {} = {\ frac {1} {x}} - {\ frac {x} {3}} - {\ frac {x ^ {3}} {45}} - {\ frac {2x ^ { 5}} {945}} - \ cdots, \ qquad {\ mbox {for}} 0 <| x | <\ pi}

{} = \ frac {1} {x} - \ frac {x} {3} - \ frac {x ^ 3} {45} - \ frac {2 x ^ 5} {945} - \ cdots, \ qquad \ mbox {pentru} 0 <| x | <\ pi

Pentru o teoremă de analiză complexă , există o singură extensie analitică a acestei funcții la numere complexe. Funcțiile trigonometrice sunt definite pe numere complexe utilizând seria Taylor văzută mai sus.

Relația cu funcția exponențială și numerele complexe

Se poate arăta, din definițiile seriei, că funcțiile sinus și cosinus sunt respectiv imaginarul și partea reală a funcției exponențiale complexe atunci când argumentul său este un număr imaginar:

e^{i\theta }=\cos \theta +i\sin \theta .

{\ displaystyle e ^ {i \ theta} = \ cos \ theta + i \ sin \ theta.}

e ^ {i \ theta} = \ cos \ theta + i \ sin \ theta.

Această relație a fost observată pentru prima dată de Euler și, din acest motiv, identitatea este cunoscută sub numele de formula lui Euler . În acest fel, funcțiile trigonometrice devin esențiale în interpretarea geometrică a analizei complexe . De exemplu, dacă luăm în considerare circumferința unității în planul complex (din punct de vedere algebric, cu înmulțirea obișnuită între numere complexe, este un grup multiplicativ abelian , cunoscut sub numele de grup circular ), definit de $e^{ix}=1$ ${\ displaystyle e ^ {ix} = 1}$ $și ^ {ix} = 1$ , această circumferință poate fi parametrizată în termeni de cosinus și sinus, făcând evidentă relația dintre funcțiile trigonometrice și exponențialul complex .

Acest lucru ne permite, de asemenea, să extindem definiția funcțiilor trigonometrice la un subiect complex $z$ ${\ displaystyle z}$ $z$ :

\sin z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}z^{2n+1}={e^{\imath z}-e^{-\imath z} \over 2\imath }=-\imath \,\sinh \left(\imath z\right)

{\ displaystyle \ sin z = \ sum _ {n = 0} ^ {\ infty} {\ frac {(-1) ^ {n}} {(2n + 1)!}} z ^ {2n + 1} = {e ^ {\ imath z} -e ^ {- \ imath z} \ over 2 \ imath} = - \ imath \, \ sinh \ left (\ imath z \ right)}

\ sin z = \ sum_ {n = 0} ^ {\ infty} \ frac {(- 1) ^ {n}} {(2n + 1)!} z ^ {2n + 1} = {e ^ {\ imath z} - e ^ {- \ imath z} \ over 2 \ imath} = - \ imath \, \ sinh \ left (\ imath z \ right)

\cos z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}z^{2n}={e^{\imath z}+e^{-\imath z} \over 2}=\cosh \left(\imath z\right)

{\ displaystyle \ cos z = \ sum _ {n = 0} ^ {\ infty} {\ frac {(-1) ^ {n}} {(2n)!}} z ^ {2n} = {e ^ { \ imath z} + e ^ {- \ imath z} \ over 2} = \ cosh \ left (\ imath z \ right)}

\ cos z = \ sum_ {n = 0} ^ {\ infty} \ frac {(- 1) ^ {n}} {(2n)!} z ^ {2n} = {e ^ {\ imath z} + e ^ {- \ imath z} \ over 2} = \ cosh \ left (\ imath z \ right)

unde este $i^{2}=-1$ ${\ displaystyle i ^ {2} = - 1}$ $i ^ 2 = -1$ . Mai mult, pentru $X$ ${\ displaystyle x}$ $X$ real,

\cos x={\mbox{Re }}(e^{\imath x})

{\ displaystyle \ cos x = {\ mbox {Re}} (e ^ {\ imath x})}

\ cos x = \ mbox {Re} (e ^ {\ imath x})

\sin x={\mbox{Im }}(e^{\imath x})

{\ displaystyle \ sin x = {\ mbox {Im}} (e ^ {\ imath x})}

\ sin x = \ mbox {Im} (e ^ {\ imath x})

Se știe, de asemenea, că procesele exponențiale sunt strâns legate de mișcarea circulară și de comportamentele periodice.

Definiții prin ecuații diferențiale

Ambele funcții sinus și cosinus satisfac ecuația diferențială

y\,''=-y.

{\ displaystyle y \, '' = - y.}

y \, '' = - y.

Adică, fiecare este opusul celei de-a doua derivate. În spațiul vectorial bidimensional V format din toate soluțiile acestei ecuații, funcția sinusoidală este singura soluție care îndeplinește condițiile inițiale y (0) = 0 și y ′ (0) = 1, iar funcția cosinusului este doar una care îndeplinește condițiile inițiale y (0) = 1 și y ′ (0) = 0. Deoarece funcțiile sinus și cosinus sunt liniar independente, împreună formează o bază a lui V. Această metodă de definire a funcțiilor sinus și cosinus este în esență echivalentă cu utilizarea formulei lui Euler. (A se vedea ecuația diferențială liniară ) Această ecuație diferențială poate fi utilizată nu numai pentru a defini funcțiile sinus și cosinus, ci și pentru a dovedi identitățile trigonometrice pentru funcțiile sinus și cosinus.

Tangenta este singura soluție a ecuației diferențiale neliniare

y\,'=1+y^{2}

{\ displaystyle y \, '= 1 + y ^ {2}}

y \, '= 1 + y ^ 2

care satisface condiția inițială y (0) = 0. Există o demonstrație grafică foarte interesantă că funcția tangentă satisface această ecuație diferențială; vezi Analiza complexului vizual al lui Needham. ^[2]

Importanța radianilor

Radianii specifică un unghi măsurând lungimea arcului corespunzător al circumferinței goniometrice. Există alte unități de măsură pentru unghiuri, cum ar fi gradele sexagesimale comune. Cu toate acestea, numai dacă unghiul este măsurat în radiani, funcțiile sinus și cosinus satisfac ecuația diferențială care este utilizată în mod clasic pentru a le descrie. Dacă argumentul sinus sau cosinus este înmulțit cu o constantă de conversie adecvată,

f(x)=\mathrm {sen} (kx);k\neq 0,k\neq 1

{\ displaystyle f (x) = \ mathrm {sen} (kx); k \ neq 0, k \ neq 1}

f (x) = \ mathrm {sen} (kx); k \ ne 0, k \ ne 1

atunci derivata va fi egală cu

f'(x)=k\cos(kx)

{\ displaystyle f '(x) = k \ cos (kx)}

f '(x) = k \ cos (kx)

.

Dacă x este în grade, atunci

k={\frac {\pi }{180^{\circ }}}.

{\ displaystyle k = {\ frac {\ pi} {180 ^ {\ circ}}}.}

k = \ frac {\ pi} {180 ^ \ circ}.

Aceasta înseamnă că a doua derivată a sinusului în grade nu satisface ecuația diferențială

y''=-y

{\ displaystyle y '' = - y}

y '' = -y

,

dar

y''=-k^{2}y

{\ displaystyle y '' = - k ^ {2} y}

y '' = -k ^ 2y

;

și același lucru este valabil și pentru cosinus.

Aceasta înseamnă că aceste funcții sinus și cosinus au un comportament diferit și, de exemplu, a patra derivată a sinusului este egală cu sinusul numai dacă argumentul este măsurat în radiani.

Identitate

Același subiect în detaliu: identitatea Trig .

Există multe identități care leagă diferitele funcții trig. Printre cele mai frecvent utilizate este identitatea fundamentală a trigonometriei , numită și identitatea pitagorică , care afirmă că, pentru fiecare unghi, suma dintre pătratul sinusului și pătratul cosinusului este $1$ ${\ displaystyle 1}$ $1$ . Acest lucru este ușor verificat prin aplicarea teoremei lui Pitagora pe un triunghi dreptunghiular de hipotenuză $1$ ${\ displaystyle 1}$ $1$ . Simbolic poate fi scris

(\sin x)^{2}+(\cos x)^{2}=1

{\ displaystyle (\ sin x) ^ {2} + (\ cos x) ^ {2} = 1}

(\ sin x) ^ 2 + (\ cos x) ^ 2 = 1

.

Alte relații de importanță primară sunt formulele de adunare și scădere , care furnizează sinusul și cosinusul sumei și diferenței a două unghiuri în funcție de sinusul și cosinusul unghiurilor în sine.

\sin(x\pm y)=\sin(x)\cos(y)\pm \cos(x)\sin(y)

{\ displaystyle \ sin (x \ pm y) = \ sin (x) \ cos (y) \ pm \ cos (x) \ sin (y)}

\ sin (x \ pm y) = \ sin (x) \ cos (y) \ pm \ cos (x) \ sin (y)

\cos(x\pm y)=\cos(x)\cos(y)\mp \sin(x)\sin(y)

{\ displaystyle \ cos (x \ pm y) = \ cos (x) \ cos (y) \ mp \ sin (x) \ sin (y)}

\ cos (x \ pm y) = \ cos (x) \ cos (y) \ mp \ sin (x) \ sin (y)

Dacă cele două unghiuri sunt egale, formulele de adunare se reduc la identități mai simple cunoscute sub numele de formule de duplicare .

Pentru integralele și derivatele funcțiilor trigonometrice, consultați secțiunile relevante din tabelul derivatelor , tabelul integralelor cele mai comune și tabelul integralelor nedefinite ale funcțiilor trigonometrice .

Definirea prin ecuații funcționale

În analiza matematică , funcțiile trigonometrice pot fi definite folosind ecuații funcționale bazate pe proprietăți, cum ar fi formule de adunare și scădere. Impunând validitatea acestor formule și a identității fundamentale, de exemplu, se poate arăta că există doar două funcții reale care îndeplinesc aceste condiții. În simboluri, există doar câteva funcții reale $s$ ${\ displaystyle s}$ $s$ Și $c$ ${\ displaystyle c}$ $c$ astfel încât, pentru toate numerele reale $X$ ${\ displaystyle x}$ $X$ Și $y$ ${\ displaystyle y}$ $y$ , sunt îndeplinite următoarele egalități:

{\begin{cases}s(x)^{2}+c(x)^{2}=1\\s(x+y)=s(x)c(y)+c(x)s(y)\\c(x+y)=c(x)c(y)-s(x)s(y)\end{cases}}

{\ displaystyle {\ begin {cases} s (x) ^ {2} + c (x) ^ {2} = 1 \\ s (x + y) = s (x) c (y) + c (x) s (y) \\ c (x + y) = c (x) c (y) -s (x) s (y) \ end {cases}}}

\ begin {cases} s (x) ^ 2 + c (x) ^ 2 = 1 \\ s (x + y) = s (x) c (y) + c (x) s (y) \\ c ( x + y) = c (x) c (y) - s (x) s (y) \ end {cases}

cu, în plus, condiția ca.

0<x<1\Rightarrow 0<xc(x)<s(x)<x

{\ displaystyle 0 <x <1 \ Rightarrow 0 <xc (x) <s (x) <x}

0 <x <1 \ Rightarrow 0 <xc (x) <s (x) <x

Pornind de la ecuații funcționale, sunt posibile și alte derivări, care pot fi extinse la numere complexe. De exemplu, o metodă similară vă permite să definiți trigonometria în câmpurile Galois .

Calcul practic

Il calcolo delle funzioni trigonometriche è un argomento complicato, che oggi può essere evitato dalla maggior parte delle persone a causa della grande disponibilità di computer e calcolatrici scientifiche che consentono di calcolare le funzioni trigonometriche per qualsiasi angolo. In questa sezione, comunque, descriviamo i dettagli del loro calcolo in tre contesti differenti: l'uso storico delle tavole trigonometriche, le tecniche moderne usate dai computer e alcuni angoli "importanti" per cui si trovano facilmente i valori esatti. (È sufficiente considerare un intervallo relativamente piccolo di angoli, ad esempio da 0 a π/2, dal momento che tutti gli altri angoli si possono ricondurre a questo intervallo sfruttando la periodicità e le simmetrie delle funzioni trigonometriche.)

Lo stesso argomento in dettaglio: Tavola trigonometrica .

Prima dell'avvento dei computer, il metodo più usato per approssimare le funzioni trigonometriche era quello di interpolare da una tavola dei loro valori, calcolate con una precisione di molte cifre significative . Queste tavole sono state utilizzate fin da quando le funzioni trigonometriche sono state descritte (vedi Storia sopra), ed erano tipicamente generate tramite ripetute applicazioni delle identità di bisezione e di addizione di angoli, partendo da angoli noti.

I computer moderni usano una grande varietà di tecniche. ^[3] Un metodo comune, specialmente sui processori di fascia alta dotati di unità floating point (a virgola mobile), è quello di combinare un'approssimazione polinomiale (come le serie di Taylor o una funzione razionale ) con una tabella precalcolata — in altri termini, questi algoritmi cercano prima nella tabella l'angolo più vicino disponibile, quindi utilizzano il polinomio per calcolare la correzione. Su dispositivi semplici che sono privi di moltiplicatore hardware , vi è un algoritmo chiamato CORDIC (insieme ad altre tecniche correlate) che risulta più efficiente, dal momento che utilizza solo operazioni di shift e addizioni . Tutte queste tecniche sono solitamente implementate a livello hardware per motivi di prestazioni.

Lo stesso argomento in dettaglio: Costanti trigonometriche esatte .

Infine, per alcuni angoli semplici, i valori delle funzioni trigonometriche possono essere calcolati esplicitamente a mano usando il teorema di Pitagora , come nei seguenti esempi. In effetti, il seno, il coseno e la tangente dei multipli di π/60 radianti (3 gradi) si possono determinare esattamente a mano.

Si consideri un triangolo rettangolo con i due angoli acuti uguali, e quindi pari a π/4 radianti (45 gradi). Allora la lunghezza del lato b e del lato a sono uguali; possiamo scegliere a = b = 1. I valori del seno, del coseno e della tangente di un angolo di 45 gradi si possono quindi determinare con il teorema di Pitagora:

c={\sqrt {a^{2}+b^{2}}}={\sqrt {2}}.

c={\sqrt {a^{2}+b^{2}}}={\sqrt {2}}.

c = \sqrt { a^2+b^2 } = \sqrt2.

Quindi:

\mathrm {sen} \left(\pi /4\right)=\mathrm {sen} \left(45^{\circ }\right)=\cos \left(\pi /4\right)=\cos \left(45^{\circ }\right)={1 \over {\sqrt {2}}},

\mathrm {sen} \left(\pi /4\right)=\mathrm {sen} \left(45^{\circ }\right)=\cos \left(\pi /4\right)=\cos \left(45^{\circ }\right)={1 \over {\sqrt {2}}},

\mathrm{sen} \left(\pi / 4 \right) = \mathrm{sen} \left(45^\circ\right) = \cos \left(\pi / 4 \right) = \cos \left(45^\circ\right) = {1 \over \sqrt2},

\tan \left(\pi /4\right)=\tan \left(45^{\circ }\right)={{\sqrt {2}} \over {\sqrt {2}}}=1.

\tan \left(\pi /4\right)=\tan \left(45^{\circ }\right)={{\sqrt {2}} \over {\sqrt {2}}}=1.

\tan \left(\pi / 4 \right) = \tan \left(45^\circ\right) = {\sqrt2 \over \sqrt2} = 1.

Per determinare le funzioni trigonometriche degli angoli di π/3 radianti (60 gradi) e π/6 radianti (30 gradi), iniziamo con un triangolo equilatero di lato 1. Tutti i suoi angoli sono pari a π/3 radianti. Dividendo il triangolo in due parti tramite un'altezza, otteniamo un triangolo rettangolo con angoli di π/6 e π/3 radianti, ossia 30 e 60 gradi. Per questo triangolo, i due cateti valgono 1/2 e (√3)/2 e l'ipotenusa 1. Ciò implica:

\mathrm {sen} \left(\pi /6\right)=\mathrm {sen} \left(30^{\circ }\right)=\cos \left(\pi /3\right)=\cos \left(60^{\circ }\right)={1 \over 2},

\mathrm {sen} \left(\pi /6\right)=\mathrm {sen} \left(30^{\circ }\right)=\cos \left(\pi /3\right)=\cos \left(60^{\circ }\right)={1 \over 2},

\mathrm{sen} \left(\pi / 6 \right) = \mathrm{sen} \left(30^\circ\right) = \cos \left(\pi / 3 \right) = \cos \left(60^\circ\right) = {1 \over 2},

\cos \left(\pi /6\right)=\cos \left(30^{\circ }\right)=\mathrm {sen} \left(\pi /3\right)=\mathrm {sen} \left(60^{\circ }\right)={{\sqrt {3}} \over 2},

\cos \left(\pi /6\right)=\cos \left(30^{\circ }\right)=\mathrm {sen} \left(\pi /3\right)=\mathrm {sen} \left(60^{\circ }\right)={{\sqrt {3}} \over 2},

\cos \left(\pi / 6 \right) = \cos \left(30^\circ\right) = \mathrm{sen} \left(\pi / 3 \right) = \mathrm{sen} \left(60^\circ\right) = {\sqrt3 \over 2},

\tan \left(\pi /6\right)=\tan \left(30^{\circ }\right)=\cot \left(\pi /3\right)=\cot \left(60^{\circ }\right)={1 \over {\sqrt {3}}}.

\tan \left(\pi /6\right)=\tan \left(30^{\circ }\right)=\cot \left(\pi /3\right)=\cot \left(60^{\circ }\right)={1 \over {\sqrt {3}}}.

\tan \left(\pi / 6 \right) = \tan \left(30^\circ\right) = \cot \left(\pi / 3 \right) = \cot \left(60^\circ\right) = {1 \over \sqrt3}.

Nel triangolo possono essere calcolate esattamente le funzioni trigonometriche degli angoli, mediante i lati, a titolo esemplificativo si usa soltanto l'angolo α relativo al vertici A e opposto al lato a

\cos {\alpha }={\frac {b^{2}+c^{2}-a^{2}}{2bc}}

\cos {\alpha }={\frac {b^{2}+c^{2}-a^{2}}{2bc}}

\cos{\alpha} = \frac{b^2 + c^2 - a^2}{2bc}

\sin {\alpha }={\frac {2\Delta }{bc}}

\sin {\alpha }={\frac {2\Delta }{bc}}

\sin{\alpha} = \frac{2\Delta}{bc}

\tan {\alpha }={\frac {4\Delta }{b^{2}+c^{2}-a^{2}}}

\tan {\alpha }={\frac {4\Delta }{b^{2}+c^{2}-a^{2}}}

\tan{\alpha} = \frac{4\Delta}{b^2 + c^2 - a^2}

dove Δ rappresenta l'area del triangolo.

Funzioni inverse

Lo stesso argomento in dettaglio: Funzioni trigonometriche inverse .

Poiché le funzioni trigonometriche sono periodiche, è necessario restringere il loro dominio per non avere ambiguità nella definizione dell'inverso. Di seguito presentiamo le definizioni usuali per le funzioni inverse:

{\begin{matrix}{\mbox{per}}&-{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}},&y=\mathrm {arcsen} (x)&{\mbox{se e solo se}}&x=\mathrm {sen\,} (y)\\\\{\mbox{per}}&0\leq y\leq \pi ,&y=\arccos(x)&{\mbox{se e solo se}}&x=\cos(y)\\\\{\mbox{per}}&-{\frac {\pi }{2}}<y<{\frac {\pi }{2}},&y=\arctan(x)&{\mbox{se e solo se}}&x=\tan(y)\\\\{\mbox{per}}&-{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}},y\neq 0,&y=\operatorname {arccsc}(x)&{\mbox{se e solo se}}&x=\csc(y)\\\\{\mbox{per}}&0\leq y\leq \pi ,y\neq {\frac {\pi }{2}},&y=\operatorname {arcsec}(x)&{\mbox{se e solo se}}&x=\sec(y)\\\\{\mbox{per}}&-{\frac {\pi }{2}}<y<{\frac {\pi }{2}},y\neq 0,&y=\operatorname {arccot}(x)&{\mbox{se e solo se}}&x=\cot(y)\end{matrix}}

{\begin{matrix}{\mbox{per}}&-{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}},&y=\mathrm {arcsen} (x)&{\mbox{se e solo se}}&x=\mathrm {sen\,} (y)\\\\{\mbox{per}}&0\leq y\leq \pi ,&y=\arccos(x)&{\mbox{se e solo se}}&x=\cos(y)\\\\{\mbox{per}}&-{\frac {\pi }{2}}<y<{\frac {\pi }{2}},&y=\arctan(x)&{\mbox{se e solo se}}&x=\tan(y)\\\\{\mbox{per}}&-{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}},y\neq 0,&y=\operatorname {arccsc}(x)&{\mbox{se e solo se}}&x=\csc(y)\\\\{\mbox{per}}&0\leq y\leq \pi ,y\neq {\frac {\pi }{2}},&y=\operatorname {arcsec}(x)&{\mbox{se e solo se}}&x=\sec(y)\\\\{\mbox{per}}&-{\frac {\pi }{2}}<y<{\frac {\pi }{2}},y\neq 0,&y=\operatorname {arccot}(x)&{\mbox{se e solo se}}&x=\cot(y)\end{matrix}}

\begin{matrix} \mbox{per} & -\frac{\pi}{2} \le y \le \frac{\pi}{2}, & y = \mathrm{arcsen}(x) & \mbox{se e solo se} & x = \mathrm{sen\,}(y) \\ \\ \mbox{per} & 0 \le y \le \pi, & y = \arccos(x) & \mbox{se e solo se} & x = \cos(y) \\ \\ \mbox{per} & -\frac{\pi}{2} < y < \frac{\pi}{2}, & y = \arctan(x) & \mbox{se e solo se} & x = \tan(y) \\ \\ \mbox{per} & -\frac{\pi}{2} \le y \le \frac{\pi}{2}, y \ne 0, & y = \arccsc(x) & \mbox{se e solo se} & x = \csc(y) \\ \\ \mbox{per} & 0 \le y \le \pi, y \ne \frac{\pi}{2}, & y = \arcsec(x) & \mbox{se e solo se} & x = \sec(y) \\ \\ \mbox{per} & -\frac{\pi}{2} < y < \frac{\pi}{2}, y \ne 0, & y = \arccot(x) & \mbox{se e solo se} & x = \cot(y) \end{matrix}

Per le funzioni trigonometriche inverse, viene spesso usata anche la notazione sin ⁻¹ , cos ⁻¹ , ecc. in luogo di arcsin e arccos. Con questa notazione, però, corre il rischio di confondere le funzioni inverse con l' inverso moltiplicativo delle funzioni.

Analogamente al seno e al coseno, anche le funzioni trigonometriche inverse si possono definire tramite serie infinite. Ad esempio,

\arcsin z=z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots

\arcsin z=z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots

\arcsin z = z + \left( \frac {1} {2} \right) \frac {z^3} {3} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {z^5} {5} + \left( \frac{1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6 } \right) \frac{z^7} {7} + \cdots

Queste funzioni si possono definire anche dimostrando che sono gli integrali indefiniti di altre funzioni. L'arcoseno, per esempio, si può scrivere tramite il seguente integrale:

\arcsin \left(x\right)=\int _{0}^{x}{\frac {1}{\sqrt {1-z^{2}}}}\,\mathrm {d} z,\quad |x|<1

\arcsin \left(x\right)=\int _{0}^{x}{\frac {1}{\sqrt {1-z^{2}}}}\,\mathrm {d} z,\quad |x|<1

\arcsin\left(x\right) = \int_0^x \frac 1 {\sqrt{1 - z^2}}\,\mathrm{d}z, \quad |x| < 1

Formule analoghe per le altre funzioni si possono trovare nella voce sulle funzioni trigonometriche inverse . Usando il logaritmo complesso , è possibile generalizzare tutte queste funzioni ad argomenti complessi:

\arcsin(z)=-i\log \left(iz+{\sqrt {1-z^{2}}}\right)

\arcsin(z)=-i\log \left(iz+{\sqrt {1-z^{2}}}\right)

\arcsin (z) = -i \log \left( i z + \sqrt{1 - z^2} \right)

\arccos(z)=-i\log \left(z+{\sqrt {z^{2}-1}}\right)

\arccos(z)=-i\log \left(z+{\sqrt {z^{2}-1}}\right)

\arccos (z) = -i \log \left( z + \sqrt{z^2 - 1}\right)

\arctan(z)={\frac {i}{2}}\log \left({\frac {1-iz}{1+iz}}\right)

\arctan(z)={\frac {i}{2}}\log \left({\frac {1-iz}{1+iz}}\right)

\arctan (z) = \frac{i}{2} \log\left(\frac{1-iz}{1+iz}\right)

Proprietà e applicazioni

Lo stesso argomento in dettaglio: Applicazioni della trigonometria .

Le funzioni trigonometriche, come dice il nome, sono di importanza cruciale nella trigonometria , principalmente per i due seguenti risultati.

Teorema dei seni

Il teorema dei seni afferma che per ogni triangolo vale:

{\frac {\mathrm {sen\,} A}{a}}={\frac {\mathrm {sen\,} B}{b}}={\frac {\mathrm {sen\,} C}{c}}

{\frac {\mathrm {sen\,} A}{a}}={\frac {\mathrm {sen\,} B}{b}}={\frac {\mathrm {sen\,} C}{c}}

\frac{\mathrm{sen\,} A}{a} = \frac{\mathrm{sen\,} B}{b} = \frac{\mathrm{sen\,} C}{c}

scritto spesso come:

{\frac {a}{\mathrm {sen\,} A}}={\frac {b}{\mathrm {sen\,} B}}={\frac {c}{\mathrm {sen\,} C}}=2R

{\frac {a}{\mathrm {sen\,} A}}={\frac {b}{\mathrm {sen\,} B}}={\frac {c}{\mathrm {sen\,} C}}=2R

\frac{a}{\mathrm{sen\,} A} = \frac{b}{\mathrm{sen\,} B} = \frac{c}{\mathrm{sen\,} C} = 2R

Una curva di Lissajous , una curva basata sulle funzioni trigonometriche.

Questo teorema si può dimostrare dividendo il triangolo in due triangoli rettangoli (tracciando l'altezza) e usando la definizione di seno. Il numero comune a /(sin A ) è uguale al diametro della circonferenza circoscritta al triangolo, ossia quella passante per i tre punti A , B e C . Il teorema dei seni è utile per calcolare la lunghezza di lati ignoti di un triangolo se sono noti due angoli e un lato. Questa situazione è comune nella triangolazione , una tecnica per determinare le distanze misurando due angoli e la distanza fra i due punti in cui è effettuata la misurazione.

Teorema dei coseni o di Carnot

Il teorema del coseno o di Carnot è una generalizzazione a qualunque triangolo del teorema di Pitagora :

c^{2}=a^{2}+b^{2}-2ab\cos C

c^{2}=a^{2}+b^{2}-2ab\cos C

c^2=a^2+b^2-2ab\cos C

ossia:

\cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}

\cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}

\cos C=\frac{a^2+b^2-c^2}{2ab}

Anche questo teorema si può dimostrare dividendo il triangolo in due triangoli rettangoli. Il teorema di Carnot è utile per la risoluzione di un triangolo di cui siano noti due lati e l'angolo compreso fra di essi.

Se l'angolo noto non è quello compreso fra i due lati, il triangolo potrebbe non essere unico. È necessario prestare la dovuta attenzione a questo caso ambiguo del teorema.

Altre proprietà utili

Esiste anche un teorema delle tangenti o teorema di Nepero :

{\frac {a+b}{a-b}}={\frac {\tan[{\frac {1}{2}}(A+B)]}{\tan[{\frac {1}{2}}(A-B)]}}

{\frac {a+b}{ab}}={\frac {\tan[{\frac {1}{2}}(A+B)]}{\tan[{\frac {1}{2}}(AB)]}}

\frac{a+b}{a-b} = \frac{\tan[\frac{1}{2}(A+B)]}{\tan[\frac{1}{2}(A-B)]}

Funzioni periodiche

Rappresentazione animata della sintesi additiva di un' onda quadra con un numero crescente di armoniche (da 1 a 24)

La funzione seno (e di conseguenza la funzione coseno, che altro non è se non la funzione seno sfasata di π/2) è essenziale per la descrizione del moto armonico semplice , un concetto molto importante in fisica. In questo contesto, il seno e il coseno sono usati per descrivere la proiezione in una dimensione del moto circolare uniforme , il moto di una massa soggetta ad una forza elastica o piccole oscillazioni di un pendolo . Esse sono funzioni periodiche il cui grafico è il tipico schema di un' onda , e sono utili per la modellizzazione di fenomeni periodici come le onde acustiche o elettromagnetiche . Qualsiasi segnale si può rappresentare come una somma (tipicamente infinita) di funzioni seno e coseno di frequenza differente; questa è l'idea di base dell' analisi di Fourier , in cui le serie trigonometriche sono utilizzate per risolvere molti problemi con condizioni al contorno nelle equazioni differenziali alle derivate parziali . Per esempio, l' onda quadra si può scrivere attraverso la serie di Fourier

x_{\mathrm {quadra} }(t)={\frac {4}{\pi }}\sum _{k=1}^{\infty }{\mathrm {sen} \,{\left((2k-1)t\right)} \over (2k-1)}.

x_{\mathrm {quadra} }(t)={\frac {4}{\pi }}\sum _{k=1}^{\infty }{\mathrm {sen} \,{\left((2k-1)t\right)} \over (2k-1)}.

x_{\mathrm{quadra}}(t) = \frac{4}{\pi} \sum_{k=1}^\infty {\mathrm{sen} \, {\left( (2k-1)t \right)} \over (2k-1)}.

Note

^ Abramowitz; Weisstein.
^ Needham, p. ix.
^ Kantabutra.

Bibliografia

Abramowitz, Milton and Irene A. Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables , Dover, New York. (1964). ISBN 0-486-61272-4 .
Boyer, Carl B. , A History of Mathematics , John Wiley & Sons, Inc., 2nd edition. (1991). ISBN 0-471-54397-7 .
Joseph, George G., The Crest of the Peacock: Non-European Roots of Mathematics , 2nd ed. Penguin Books , London. (2000). ISBN 0-691-00659-8 .
Kantabutra, Vitit, "On hardware for computing exponential and trigonometric functions," IEEE Trans. Computers 45 (3), 328-339 (1996).
Maor, Eli, Trigonometric Delights , Princeton University Press. (1998). Reprint edition (February 25, 2002): ISBN 0-691-09541-8 .
Needham, Tristan, "Preface" " to Visual Complex Analysis . Oxford University Press, (1999). ISBN 0-19-853446-9 .
O'Connor, JJ, and EF Robertson, "Trigonometric functions" , MacTutor History of Mathematics Archive . (1996).
O'Connor, JJ, and EF Robertson, "Madhava of Sangamagramma" , MacTutor History of Mathematics Archive . (2000).
Pearce, Ian G., "Madhava of Sangamagramma" , MacTutor History of Mathematics Archive . (2002).
Weisstein, Eric W., "Tangent" da MathWorld .

Voci correlate

Altri progetti

Wikibooks contiene testi o manuali sulla funzione trigonometrica
Wikiversità contiene risorse sulla funzione trigonometrica
Wikimedia Commons contiene immagini o altri file sulla funzione trigonometrica

Collegamenti esterni

( EN ) Funzione trigonometrica , su Enciclopedia Britannica , Encyclopædia Britannica, Inc.
( EN ) In questa pagina si può vedere la rappresentazione grafica interattiva delle tre funzioni trigonometriche principali (seno, coseno e tangente).
( EN ) JavaScript function grapher usa una libreria din JavaScript per visualizzare il grafico delle funzioni. Funziona nella maggior parte dei browser moderni.
( EN ) Funzioni seno e coseno , su geocities.com . URL consultato il 28 settembre 2006 (archiviato dall' url originale il 31 maggio 2002; seconda copia archiviata ) . con un'implementazione in Rexx.

Controllo di autorità	Thesaurus BNCF 32484 · LCCN ( EN ) sh85137518 · GND ( DE ) 4186137-1 · BNF ( FR ) cb12168469v (data) · NDL ( EN , JA ) 00570156

Portale Matematica : accedi alle voci di Wikipedia che trattano di matematica

[1] Abramowitz; Weisstein.

[2] Needham, p. ix.

[3] Kantabutra.

[1]

[2]

[3]

V · D · M Trigonometria
Funzione trigonometrica · Funzione trigonometrica inversa
Funzioni	Seno · Senoverso · Coseno · Cosenoverso · Tangente · Cotangente · Secante · Secante esterna · Cosecante · Cosecante esterna
Funzioni inverse	Arcoseno · Arcocoseno · Arcotangente · Arcocotangente · Arcosecante · Arcocosecante
Teoremi e formule	Teorema della corda · Teorema dei seni · Teorema del coseno · Teorema di Nepero · Teorema delle cotangenti · Teorema di Pitagora · Formule di prostaferesi · Formule di Werner
Altro	Tavola trigonometrica · Tavola degli integrali indefiniti di funzioni trigonometriche · Tavola degli integrali indefiniti di funzioni d'arco · Funzioni iperboliche · Identità trigonometrica · Costanti trigonometriche esatte ·Storia delle funzioni trigonometriche