Ecuația de gradul III

Graficul funcției de gradul III:

f(x)=x^{3}-15x-4

{\ displaystyle f (x) = x ^ {3} -15x-4}

f (x) = x ^ 3-15x-4

. Zerourile funcției sunt marcate cu roșu.

În matematică , o ecuație care se prezintă sau poate fi transformată într- o formă polinomială în care gradul maxim al necunoscutului este al treilea se numește ecuație de gradul trei sau ecuație cubică . Prin urmare, forma sa canonică este

ax^{3}+bx^{2}+cx+d=0\qquad {\mbox{con }}a\neq 0

{\ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0 \ qquad {\ mbox {con}} a \ neq 0}

ax ^ 3 + bx ^ 2 + cx + d = 0 \ qquad \ mbox {con} a \ n și 0

Prima metodă de soluție generală pentru această clasă de ecuații se datorează lui Scipione del Ferro . Cu toate acestea, numele lui Gerolamo Cardano și Niccolò Fontana cunoscute sub numele de Tartaglia sunt în mod normal asociate cu formula soluției, care a adus o serie de îmbunătățiri ale metodei datorate diferiților autori ai școlii algebrice italiene.

fundal

De pe vremea matematicii babiloniene, au fost cunoscute metode de rezolvare pentru anumite ecuații de gradul al treilea, în esență cele care pot fi urmărite înapoi la o ecuație de gradul al doilea . Grecii au reușit să rezolve câteva ecuații de gradul trei cu metoda conică , metodă făcută celebră prin anecdota duplicării altarului lui Apollo . În epoca matematicii persane , ʿUmar Khayyām credea că, în afară de cazurile reductibile, nu exista o metodă generală de soluție pentru ecuațiile de gradul III, o părere pe care Luca Pacioli a raportat-o din nou în lucrarea sa din 1494 Summa de arithmetica, geometria, proportioni et proportionality .

O primă procedură de rezolvare de bună generalitate a fost descoperită de Scipione del Ferro ; data exactă a acestei descoperiri rămâne necunoscută, dar el a comunicat-o la sfârșitul vieții sale (aprox. 1526 ) unuia dintre elevii săi, Antonio Maria del Fiore , numit în latină Floridus .

Niccolò Fontana , cunoscut sub numele de Tartaglia, deja în 1541 știa cum să rezolve problemele care implicau ecuații de gradul al treilea: când s-a răspândit cuvântul, Floridus și Tartaglia s-au provocat reciproc, fiecare supunându-se celorlalte treizeci de „întrebări” pentru a fi rezolvate la o anumită dată. . Când a sosit ziua stabilită, Tartaglia rezolvase toate problemele lui Floridus și nici măcar una dintre ele. La acea vreme, de fapt, nu se foloseau numere negative și s-au folosit diverse metode de soluție cu numere pozitive doar: Floridus cunoștea o singură metodă pentru coeficienții pozitivi, adică pentru ecuațiile formei

x^{3}+px=q

{\ displaystyle x ^ {3} + px = q}

x ^ 3 + px = q

în timp ce Tartaglia a prezentat toate problemele cu coeficienți negativi și în formă

x^{3}+px^{2}=q

{\ displaystyle x ^ {3} + px ^ {2} = q}

x ^ 3 + px ^ 2 = q

aducând probabil acest caz înapoi la cel precedent. De fapt, se știa că, dacă coeficientul de gradul al treilea este unitatea, atunci coeficientul de gradul al doilea schimbat în semn este suma rădăcinilor.

Niccolò Tartaglia , al treilea răspuns dat lui Messer Hieronimo Cardano și Messer Lodovico Ferraro , 1547

Apoi a apărut o controversă amară în 1545 între Tartaglia , Gerolamo Cardano și Lodovico Ferrari , cărora le datorăm soluția generală a ecuației de gradul patru , despre autoritatea soluției. La auzul victoriei asupra lui Floridus, Cardano îl invitase pe Tartaglia să-l viziteze în orașul Milano , cu promisiunea vagă de a-l găsi patron. Tartaglia nu avea surse stabile de venit, probabil din cauza bâlbâielii , cauzată de o sabie pe care a primit-o de băiat în timpul asaltului de la Brescia de către trupele franceze în 1512 . Defectul, căruia i se datorează și porecla autoimpusă a lui Tartaglia, l-a făcut nepotrivit pentru predare, așa că oferta a fost acceptată. Prin urmare, Tartaglia i-a dezvăluit lui Cardano procedura sub formă de poezie (notația actuală între paranteze):

Girolamo Cardano

„Când acel cub cu lucrurile de mai jos [ $x^{3}+px$ ${\ displaystyle x ^ {3} + px}$ $x ^ 3 + px$ ]
Dacă se potrivește cu un număr discret [ $=q$ ${\ displaystyle = q}$ $= q$ ]
Vor găsi alți doi diferiți în el. [ $u-v=q$ ${\ displaystyle uv = q}$ $u -v = q$ ]

Apoi, veți păstra acest lucru ca de obicei
Produsul respectiv va fi întotdeauna egal [ $uv=$ ${\ displaystyle uv =}$ $uv =$ ]
La al treilea cub de neto lucruri, [ $(p/3)^{3}$ ${\ displaystyle (p / 3) ^ {3}}$ $(p / 3) ^ 3$ ]

El a rămas apoi generalul său
Din laturile lor cubice bine scăzute [ ${\sqrt[{3}]{u}}-{\sqrt[{3}]{v}}$ ${\ displaystyle {\ sqrt [{3}] {u}} - {\ sqrt [{3}] {v}}}$ $\ sqrt [3] {u} - \ sqrt [3] {v}$ ]
Principalul tău lucru va merita. [ $=x$ ${\ displaystyle = x}$ $= x$ ] "

( Umberto Bottazzini, „Marea artă”: algebră în Renaștere , editat de Paolo Rossi , Istoria științei Vol. 1. )

Mai târziu, Tartaglia va susține că l-a făcut pe Cardano să jure că nu l-ar fi făcut niciodată public, dar faptul este contestat de Cardano însuși. Cardano și Ferrari au lucrat apoi la materialul furnizat de Tartaglia, depășind descoperirile sale și reușind să ofere o demonstrație riguroasă a soluției; tocmai în această perioadă Ferrari rezolvă ecuația de gradul patru. Procedura de soluție identificată de matematicianul bologonez a necesitat totuși soluția ecuației de gradul III descoperită de Tartaglia și care nu a putut fi publicată datorită promisiunii făcute de Cardano. După ceva timp, însă, acesta din urmă a aflat de deducțiile anterioare ale lui Scipione del Ferro și apoi a mers la Annibale della Nave , ginerele lui del Ferro și succesorul său la catedra de matematică a Universității din Bologna, în speranța că de a putea înțelege informațiile de care avea nevoie. Della Nave i-a arătat lui Cardano manuscrisul pe care socrul său notase soluția ecuației, aceeași găsită de Tartaglia; așa că Cardano, simțindu-se liber de promisiunea făcută, a publicat rezultatul cunoscut sub numele de formula lui Cardano . Ținând cont de poezia care $x={\sqrt[{3}]{u}}-{\sqrt[{3}]{v}}$ ${\ displaystyle x = {\ sqrt [{3}] {u}} - {\ sqrt [{3}] {v}}}$ $x = \ sqrt [3] {u} - \ sqrt [3] {v}$ exprimând procedura într-o singură formulă, se obțin formulele cardan cunoscute:

x^{3}+px+q=0\ \quad \Rightarrow \quad x={\sqrt[{3}]{-{q \over 2}+{\sqrt[{2}]{{q^{2} \over 4}+{p^{3} \over 27}}}}}+{\sqrt[{3}]{-{q \over 2}-{\sqrt[{2}]{{q^{2} \over 4}+{p^{3} \over 27}}}}}

{\ displaystyle x ^ {3} + px + q = 0 \ \ quad \ Rightarrow \ quad x = {\ sqrt [{3}] {- {q \ over 2} + {\ sqrt [{2}] {{ q ^ {2} \ over 4} + {p ^ {3} \ over 27}}}}} + {\ sqrt [{3}] {- {q \ over 2} - {\ sqrt [{2}] {{q ^ {2} \ peste 4} + {p ^ {3} \ peste 27}}}}}}

x ^ 3 + px + q = 0 \ \ quad \ Rightarrow \ quad x = \ sqrt [3] {- {q \ over 2} + \ sqrt [2] {{q ^ {2} \ over 4} + { p ^ {3} \ over 27}}} + \ sqrt [3] {- {q \ over 2} - \ sqrt [2] {{q ^ {2} \ over 4} + {p ^ {3} \ peste 27}}}

Deși fiu nelegitim, astrolog, eretic și jucător inveterat, Cardano a fost un profesor respectabil la Bologna și Milano, atât de mult încât a primit o pensie de la Papa. A fost un scriitor prolific în domeniile medicinei, științelor naturii și matematicii. Odată cu lansarea Artis Magnae sive de regulis algebraicis în 1545 , în care au fost publicate soluțiile pentru ecuațiile de gradul III și IV, recunoscând în același timp autorul descoperirilor respective din Ferrari și Tartaglia, controversa cu Tartaglia a luat naștere. De fapt, acest lucru nu a fost suficient pentru a evita mânia lui Tartaglia, care l-a jignit public pe Cardano numindu-l „om cu sos mic” ^[1] . Ferrari a apărat cu înverșunare maestrul și a urmat o lungă dispută (de la care, însă, Cardano a rămas mereu neutru). Provocat public de Ferrari, Tartaglia a fost umilit și învins și, la scurt timp, a văzut retragerea postului său de profesor .

Cardano și Ferrari au devenit brusc celebri, totuși norocul lor nu a durat mult: fiul lui Cardano a fost condamnat la moarte pentru uciderea soției sale, în timp ce celălalt fiu al său l-a jefuit pentru a-și achita datoriile de jocuri de noroc. Mai târziu, el însuși a fost închis pentru calculul horoscopului lui Iisus Hristos ; Ferrari, pe de altă parte, după ce a pierdut degetele unei mâini într-o luptă, a fost probabil otrăvit de sora sa.

În anii următori, François Viète a găsit o altă metodă de rezoluție: odată ce coeficientul de gradul doi a fost eliminat, se aplică substituția $x=y-{\tfrac {p}{3y}}$ ${\ displaystyle x = y - {\ tfrac {p} {3y}}}$ $x = y - \ tfrac {p} {3y}$ ceea ce duce la o ecuație de gradul doi în variabilă $y^{3}$ ${\ displaystyle y ^ {3}}$ $y ^ 3$ . ^[2]

Metoda soluției

Cardano , Tartaglia și alți algebri italieni ai Renașterii și-au publicat propriile metode pentru rezolvarea ecuațiilor de gradul III. Ceva mai târziu, François Viète , în urma introducerii coeficienților literali, a publicat în Isagoge în artem analyticam o metodă foarte liniară, care implică soluția unei ecuații complete de gradul al treilea prin reducerea acesteia, printr-o substituție multiplă a variabilelor, la o anumită ecuație pătratică. Procedura este următoarea.

O ecuație de tipul

ax^{3}+bx^{2}+cx+d=0

{\ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}

ax ^ 3 + bx ^ 2 + cx + d = 0

duce înapoi, aplicând următoarea substituție

$x=y-{\frac {b}{3a}}$ ${\ displaystyle x = y - {\ frac {b} {3a}}}$ $x = y- \ frac {b} {3a}$

(din punct de vedere geometric această translație poziționează cubul astfel încât să aibă inflexiunea pe axa ordonată; în general, ecuațiile de acest tip sunt simetrice în raport cu punctul lor de inflexiune)

a forma

y^{3}+py+q=0

{\ displaystyle y ^ {3} + py + q = 0}

y ^ 3 + py + q = 0

unde este

p={\frac {c}{a}}-{\frac {b^{2}}{3a^{2}}}

{\ displaystyle p = {\ frac {c} {a}} - {\ frac {b ^ {2}} {3a ^ {2}}}}

p = \ frac {c} {a} - \ frac {b ^ 2} {3a ^ 2}

Și

q={\frac {d}{a}}-{\frac {bc}{3a^{2}}}+{\frac {2b^{3}}{27a^{3}}}

{\ displaystyle q = {\ frac {d} {a}} - {\ frac {bc} {3a ^ {2}}} + {\ frac {2b ^ {3}} {27a ^ {3}}}}

q = \ frac {d} {a} - \ frac {bc} {3a ^ 2} + \ frac {2b ^ 3} {27a ^ 3}

Obținem astfel o ecuație în forma descrisă anterior ale cărei soluții sunt $y=u+v$ ${\ displaystyle y = u + v}$ $y = u + v$ unde este $tu$ ${\ displaystyle u}$ $tu$ Și $v$ ${\ displaystyle v}$ $v$ sunt rădăcinile:

u={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}};\quad v={\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}

{\ displaystyle u = {\ sqrt [{3}] {- {\ frac {q} {2}} + {\ sqrt {{\ frac {q ^ {2}} {4}} + {\ frac {p ^ {3}} {27}}}}}}; \ quad v = {\ sqrt [{3}] {- {\ frac {q} {2}} - {\ sqrt {{\ frac {q ^ { 2}} {4}} + {\ frac {p ^ {3}} {27}}}}}}}

{\ displaystyle u = {\ sqrt [{3}] {- {\ frac {q} {2}} + {\ sqrt {{\ frac {q ^ {2}} {4}} + {\ frac {p ^ {3}} {27}}}}}}; \ quad v = {\ sqrt [{3}] {- {\ frac {q} {2}} - {\ sqrt {{\ frac {q ^ { 2}} {4}} + {\ frac {p ^ {3}} {27}}}}}}}

Din care deducem că

y={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}+{\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}

{\ displaystyle y = {\ sqrt [{3}] {- {\ frac {q} {2}} + {\ sqrt {{\ frac {q ^ {2}} {4}} + {\ frac {p ^ {3}} {27}}}}}} + {\ sqrt [{3}] {- {\ frac {q} {2}} - {\ sqrt {{\ frac {q ^ {2}} { 4}} + {\ frac {p ^ {3}} {27}}}}}}}

y = \ sqrt [3] {- \ frac {q} {2} + \ sqrt {\ frac {q ^ 2} {4} + \ frac {p ^ 3} {27}}} + \ sqrt [3] {- \ frac {q} {2} - \ sqrt {\ frac {q ^ 2} {4} + \ frac {p ^ 3} {27}}}

Formula pentru calcularea soluțiilor ecuației de gradul al treilea este deci:

x=-{\frac {b}{3a}}+{\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}+{\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}

{\ displaystyle x = - {\ frac {b} {3a}} + {\ sqrt [{3}] {- {\ frac {q} {2}} + {\ sqrt {{\ frac {q ^ {2 }} {4}} + {\ frac {p ^ {3}} {27}}}}}} + {\ sqrt [{3}] {- {\ frac {q} {2}} - {\ sqrt {{\ frac {q ^ {2}} {4}} + {\ frac {p ^ {3}} {27}}}}}}}

{\ displaystyle x = - {\ frac {b} {3a}} + {\ sqrt [{3}] {- {\ frac {q} {2}} + {\ sqrt {{\ frac {q ^ {2 }} {4}} + {\ frac {p ^ {3}} {27}}}}}} + {\ sqrt [{3}] {- {\ frac {q} {2}} - {\ sqrt {{\ frac {q ^ {2}} {4}} + {\ frac {p ^ {3}} {27}}}}}}}

Trebuie să ne amintim că pentru teorema fundamentală a algebrei o ecuație de gradul trei trebuie să aibă 3 soluții, de aceea trebuie să evaluăm și rezultatele complexe ale rădăcinilor.

Acum este necesar să calculăm dacă cantitatea care se află sub rădăcinile pătrate, pe care o vom numi $\Delta _{\text{III}}$ ${\ displaystyle \ Delta _ {\ text {III}}}$ ${\ displaystyle \ Delta _ {\ text {III}}}$ , este pozitiv sau negativ.

De sine $\Delta _{\text{III}}$ ${\ displaystyle \ Delta _ {\ text {III}}}$ ${\ displaystyle \ Delta _ {\ text {III}}}$ este mai mare decât 0, se calculează cele două numere reale $tu$ ${\ displaystyle u}$ $tu$ Și $v$ ${\ displaystyle v}$ $v$ La fel ca
$u={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {\Delta _{\text{III}}}}}};\quad v={\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {\Delta _{\text{III}}}}}}$ ${\ displaystyle u = {\ sqrt [{3}] {- {\ frac {q} {2}} + {\ sqrt {\ Delta _ {\ text {III}}}}}}; \ quad v = { \ sqrt [{3}] {- {\ frac {q} {2}} - {\ sqrt {\ Delta _ {\ text {III}}}}}}}$ ${\ displaystyle u = {\ sqrt [{3}] {- {\ frac {q} {2}} + {\ sqrt {\ Delta _ {\ text {III}}}}}}; \ quad v = { \ sqrt [{3}] {- {\ frac {q} {2}} - {\ sqrt {\ Delta _ {\ text {III}}}}}}}$
iar soluțiile ecuației vor fi:
$y_{1}=u+v$ ${\ displaystyle y_ {1} = u + v}$ $y_1 = u + v$
$y_{2}=u\cdot \left(-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\right)+v\cdot \left(-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\right)$ ${\ displaystyle y_ {2} = u \ cdot \ left (- {\ frac {1} {2}} + i {\ frac {\ sqrt {3}} {2}} \ right) + v \ cdot \ left (- {\ frac {1} {2}} - i {\ frac {\ sqrt {3}} {2}} \ right)}$ $y_2 = u \ cdot \ left (- \ frac {1} {2} + i \ frac {\ sqrt {3}} {2} \ right) + v \ cdot \ left (- \ frac {1} {2} -i \ frac {\ sqrt {3}} {2} \ dreapta)$
$y_{3}=u\cdot \left(-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\right)+v\cdot \left(-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\right)$ ${\ displaystyle y_ {3} = u \ cdot \ left (- {\ frac {1} {2}} - i {\ frac {\ sqrt {3}} {2}} \ right) + v \ cdot \ left (- {\ frac {1} {2}} + i {\ frac {\ sqrt {3}} {2}} \ right)}$ $y_3 = u \ cdot \ left (- \ frac {1} {2} -i \ frac {\ sqrt {3}} {2} \ right) + v \ cdot \ left (- \ frac {1} {2} + i \ frac {\ sqrt {3}} {2} \ right)$
De sine $\Delta _{\text{III}}$ ${\ displaystyle \ Delta _ {\ text {III}}}$ ${\ displaystyle \ Delta _ {\ text {III}}}$ este mai mic decât 0, numărul complex trebuie convertit
$-{\frac {q}{2}}+i{\sqrt {-\Delta _{\text{III}}}}$ ${\ displaystyle - {\ frac {q} {2}} + i {\ sqrt {- \ Delta _ {\ text {III}}}}}$ ${\ displaystyle - {\ frac {q} {2}} + i {\ sqrt {- \ Delta _ {\ text {III}}}}}$
sub forma trigonometrică $\rho (\cos \theta +i\sin \theta )$ ${\ displaystyle \ rho (\ cos \ theta + i \ sin \ theta)}$ $\ rho (\ cos \ theta + i \ sin \ theta)$ iar cele trei soluții vor fi rezultatele formulelor:
$y_{1}=2{\sqrt {-{\frac {p}{3}}}}\cdot \cos {\frac {\theta }{3}}$ ${\ displaystyle y_ {1} = 2 {\ sqrt {- {\ frac {p} {3}}}} \ cdot \ cos {\ frac {\ theta} {3}}}$ $y_1 = 2 \ sqrt {- \ frac {p} {3}} \ cdot \ cos \ frac {\ theta} {3}$
$y_{2}=2{\sqrt {-{\frac {p}{3}}}}\cdot \cos {\frac {\theta +2\pi }{3}}$ ${\ displaystyle y_ {2} = 2 {\ sqrt {- {\ frac {p} {3}}}} \ cdot \ cos {\ frac {\ theta +2 \ pi} {3}}}$ $y_2 = 2 \ sqrt {- \ frac {p} {3}} \ cdot \ cos \ frac {\ theta + 2 \ pi} {3}$
$y_{3}=2{\sqrt {-{\frac {p}{3}}}}\cdot \cos {\frac {\theta +4\pi }{3}}$ ${\ displaystyle y_ {3} = 2 {\ sqrt {- {\ frac {p} {3}}}} \ cdot \ cos {\ frac {\ theta +4 \ pi} {3}}}$ $y_3 = 2 \ sqrt {- \ frac {p} {3}} \ cdot \ cos \ frac {\ theta + 4 \ pi} {3}$
De sine $\Delta _{\text{III}}$ ${\ displaystyle \ Delta _ {\ text {III}}}$ ${\ displaystyle \ Delta _ {\ text {III}}}$ este egal cu 0 soluțiile ecuației vor fi:
$y_{1}=-2{\sqrt[{3}]{\frac {q}{2}}}$ ${\ displaystyle y_ {1} = - 2 {\ sqrt [{3}] {\ frac {q} {2}}}}$ $y_1 = -2 \ sqrt [3] {\ frac {q} {2}}$
$y_{2}=y_{3}={\sqrt[{3}]{\frac {q}{2}}}$ ${\ displaystyle y_ {2} = y_ {3} = {\ sqrt [{3}] {\ frac {q} {2}}}}$ $y_2 = y_3 = \ sqrt [3] {\ frac {q} {2}}$

Probleme legate de soluții

Cardano, însă, a întâmpinat unele dificultăți, date fiind metodele vremii, în tratarea cazurilor precum

x^{3}=15x+4

{\ displaystyle x ^ {3} = 15x + 4}

x ^ 3 = 15x + 4

De fapt, aplicând formula soluției se găsește

x={\sqrt[{3}]{2+11{\sqrt {-1}}}}+{\sqrt[{3}]{2-11{\sqrt {-1}}}}

{\ displaystyle x = {\ sqrt [{3}] {2 + 11 {\ sqrt {-1}}}} + {\ sqrt [{3}] {2-11 {\ sqrt {-1}}}} }

x = \ sqrt [3] {2 +11 \ sqrt {-1}} + \ sqrt [3] {2-11 \ sqrt {-1}}

iar rădăcina unui număr negativ nu a putut fi tratată. Cu toate acestea, în căutarea unei soluții cu metodele geometrice ale lui marUmar Khayyām , găsim că o soluție este $x=4$ ${\ displaystyle x = 4}$ $x = 4$ și în consecință alte două soluții sunt obținute prin rezolvarea ecuației

x^{2}+4x+1=0

{\ displaystyle x ^ {2} + 4x + 1 = 0}

x ^ 2 + 4x + 1 = 0

Deci ecuația are trei rădăcini reale, adică există factorizare

x^{3}-15x-4=(x-4)\cdot (x+2-{\sqrt {3}})\cdot (x+2+{\sqrt {3}})

{\ displaystyle x ^ {3} -15x-4 = (x-4) \ cdot (x + 2 - {\ sqrt {3}}) \ cdot (x + 2 + {\ sqrt {3}})}

x ^ 3-15x-4 = (x-4) \ cdot (x + 2- \ sqrt {3}) \ cdot (x + 2 + \ sqrt {3})

în timp ce formula soluției duce la numere non-reale.

În general, avem un număr nereal cu ecuații de formă $y^{3}+py+q$ ${\ displaystyle y ^ {3} + py + q}$ $y ^ 3 + py + q$ pentru care

\left({p \over 3}\right)^{3}<-\left({q \over 2}\right)^{2}

{\ displaystyle \ left ({p \ over 3} \ right) ^ {3} <- \ left ({q \ over 2} \ right) ^ {2}}

\ left ({p \ over 3} \ right) ^ 3 <- \ left ({q \ over 2} \ right) ^ 2

Această inegalitate caracterizează ceea ce s-a numit cazul ireductibil, caz considerat de nerezolvat. Autorii ulteriori (în primul rând Rafael Bombelli ) vor prelua aceste rezultate introducând numere complexe , entități indispensabile pentru a avea o procedură generală pentru rezolvarea ecuațiilor de gradul III cu coeficienți reali. Numerele complexe s-au dovedit a fi fundamentale pentru multe alte dezvoltări matematice, în special pentru teorema fundamentală a algebrei .

Demonstrație

Transformarea formulei generale într-o formulă cu soluții cunoscute

Tehnica utilizată pentru a găsi formula soluției unei ecuații de gradul al treilea este de a o transforma într-o ecuație cu soluții cunoscute. Dacă luăm identitatea:

y=u+v

{\ displaystyle y = u + v}

y = u + v

și ridicăm totul la cub pe care îl obținem:

y^{3}=(u+v)^{3}

{\ displaystyle y ^ {3} = (u + v) ^ {3}}

y ^ 3 = (u + v) ^ 3

y^{3}=u^{3}+3u^{2}v+3uv^{2}+v^{3}

{\ displaystyle y ^ {3} = u ^ {3} + 3u ^ {2} v + 3uv ^ {2} + v ^ {3}}

y ^ 3 = u ^ 3 + 3u ^ 2 v + 3uv ^ 2 + v ^ 3

y^{3}=u^{3}+v^{3}+3uv(u+v)

{\ displaystyle y ^ {3} = u ^ {3} + v ^ {3} + 3uv (u + v)}

y ^ 3 = u ^ 3 + v ^ 3 + 3uv (u + v)

y^{3}=u^{3}+v^{3}+3uvy

{\ displaystyle y ^ {3} = u ^ {3} + v ^ {3} + 3uvy}

y ^ 3 = u ^ 3 + v ^ 3 + 3uvy

y^{3}-3uvy-(u^{3}+v^{3})=0

{\ displaystyle y ^ {3} -3uvy- (u ^ {3} + v ^ {3}) = 0}

y ^ 3-3uvy- (u ^ 3 + v ^ 3) = 0

Am construit astfel o ecuație de gradul trei din care cunoaștem soluția ( $y=u+v$ ${\ displaystyle y = u + v}$ $y = u + v$ ). Putem observa că ecuația obținută nu are termenul de gradul doi e $y^{3}$ ${\ displaystyle y ^ {3}}$ $y ^ 3$ are coeficientul 1. Următorii pași vor avea ca obiectiv transformarea unei ecuații clasice de gradul III într-o ecuație similară cu cea care tocmai a fost construită.

Luăm apoi ecuația de gradul trei și împărțim toți termenii la constantă $la$ ${\ displaystyle a}$ $la$ :

x^{3}+{\frac {b}{a}}x^{2}+{\frac {c}{a}}x+{\frac {d}{a}}=0

{\ displaystyle x ^ {3} + {\ frac {b} {a}} x ^ {2} + {\ frac {c} {a}} x + {\ frac {d} {a}} = 0}

x ^ 3 + \ frac {b} {a} x ^ 2 + \ frac {c} {a} x + \ frac {d} {a} = 0

Am adus astfel coeficientul de $x^{3}$ ${\ displaystyle x ^ {3}}$ $x ^ {3}$ egal cu 1. Acum trebuie să anulăm termenul de gradul doi, efectuând o traducere de tipul $x=y-k$ ${\ displaystyle x = yk}$ $x = y-k$ noi obținem:

(y-k)^{3}+{\frac {b}{a}}(y-k)^{2}+{\frac {c}{a}}(y-k)+{\frac {d}{a}}=0

{\ displaystyle (yk) ^ {3} + {\ frac {b} {a}} (yk) ^ {2} + {\ frac {c} {a}} (yk) + {\ frac {d} { a}} = 0}

(y-k) ^ 3 + \ frac {b} {a} (y-k) ^ 2 + \ frac {c} {a} (y-k) + \ frac {d} {a} = 0

dezvoltând puterile binomiale se poate observa că coeficientul termenului de gradul doi este egal cu: $(-3k+{\tfrac {b}{a}})$ ${\ displaystyle (-3k + {\ tfrac {b} {a}})}$ $(-3k + \ tfrac {b} {a})$ pentru a-l anula îl putem egaliza cu zero și pentru a obține:

-3k+{\frac {b}{a}}=0\Longleftrightarrow k={\frac {b}{3a}}

{\ displaystyle -3k + {\ frac {b} {a}} = 0 \ Longleftrightarrow k = {\ frac {b} {3a}}}

-3k + \ frac {b} {a} = 0 \ Longleftrightarrow k = \ frac {b} {3a}

Prin urmare, înlocuirea pe care ar trebui să o facem va fi:

x=y-{\frac {b}{3a}}

{\ displaystyle x = y - {\ frac {b} {3a}}}

x = y- \ frac {b} {3a}

Prin efectuarea calculelor obținem o ecuație a formei:

y^{3}+py+q=0

{\ displaystyle y ^ {3} + py + q = 0}

y ^ 3 + py + q = 0

Unde:

{\begin{cases}p=-{\frac {b^{2}}{3a^{2}}}+{\frac {c}{a}}\\q={\frac {2b^{3}}{27a^{3}}}-{\frac {bc}{3a^{2}}}+{\frac {d}{a}}\end{cases}}

{\ displaystyle {\ begin {cases} p = - {\ frac {b ^ {2}} {3a ^ {2}}} + {\ frac {c} {a}} \\ q = {\ frac {2b ^ {3}} {27a ^ {3}}} - {\ frac {bc} {3a ^ {2}}} + {\ frac {d} {a}} \ end {cases}}}

\ begin {cases} p = - \ frac {b ^ 2} {3a ^ 2} + \ frac {c} {a} \\ q = \ frac {2b ^ 3} {27a ^ 3} - \ frac {bc } {3a ^ 2} + \ frac {d} {a} \ end {cases}

Am transformat astfel o ecuație clasică de gradul trei într-o ecuație cu un termen de gradul doi zero și un coeficient al termenului de gradul trei egal cu 1 . Acum trebuie să facem ecuația pe care tocmai am obținut-o complet identică cu ecuația inițială despre care știam soluția. Pentru a face acest lucru, trebuie să corespundem condițiilor primului grad $-3uv$ ${\ displaystyle -3uv}$ $-3uv$ la $p$ ${\ displaystyle p}$ $p$ și termeni cunoscuți $-(u^{3}+v^{3})$ ${\ displaystyle - (u ^ {3} + v ^ {3})}$ $- (u ^ 3 + v ^ 3)$ la $q$ ${\ displaystyle q}$ $q$ rezolvarea sistemului:

{\begin{cases}-3uv=p\\-(u^{3}+v^{3})=q\end{cases}}\Rightarrow {\begin{cases}uv=-{\frac {p}{3}}\\u^{3}+v^{3}=-q\end{cases}}

{\ displaystyle {\ begin {cases} -3uv = p \\ - (u ^ {3} + v ^ {3}) = q \ end {cases}} \ Rightarrow {\ begin {cases} uv = - {\ frac {p} {3}} \\ u ^ {3} + v ^ {3} = - q \ end {cases}}}

\ begin {cases} -3uv = p \\ - (u ^ 3 + v ^ 3) = q \ end {cases} \ Rightarrow \ begin {cases} uv = - \ frac {p} {3} \\ u ^ 3 + v ^ 3 = -q \ end {cases}

Dacă am tăiat prima ecuație a sistemului, vom obține:

{\begin{cases}u^{3}v^{3}=-{\frac {p^{3}}{27}}\\u^{3}+v^{3}=-q\end{cases}}

{\ displaystyle {\ begin {cases} u ^ {3} v ^ {3} = - {\ frac {p ^ {3}} {27}} \\ u ^ {3} + v ^ {3} = - q \ end {cases}}}

\ begin {cases} u ^ 3v ^ 3 = - \ frac {p ^ 3} {27} \\ u ^ 3 + v ^ 3 = -q \ end {cases}

Sistemul ne cere să găsim două necunoscute a căror sumă este $-q$ ${\ displaystyle -q}$ $-q$ iar produsul este $-{\frac {p^{3}}{27}}$ ${\ displaystyle - {\ frac {p ^ {3}} {27}}}$ $- {\ frac {p ^ {3}} {27}}$ . Pentru a rezolva un astfel de sistem putem folosi ecuația de gradul doi :

z^{2}-rz+s=0

{\ displaystyle z ^ {2} -rz + s = 0}

z ^ 2-rz + s = 0

Unde $r$ ${\ displaystyle r}$ $r$ Și $s$ ${\ displaystyle s}$ $s$ reprezintă respectiv suma și produsul celor două necunoscute ale noastre, deci să rezolvăm ecuația:

z^{2}+qz-{\frac {p^{3}}{27}}=0

{\ displaystyle z ^ {2} + qz - {\ frac {p ^ {3}} {27}} = 0}

z ^ 2 + qz- \ frac {p ^ 3} {27} = 0

u^{3}={\frac {-q+{\sqrt {q^{2}+{\frac {4p^{3}}{27}}}}}{2}}=-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}\ \Rightarrow \ u={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}

{\ displaystyle u ^ {3} = {\ frac {-q + {\ sqrt {q ^ {2} + {\ frac {4p ^ {3}} {27}}}}} {2}} = - { \ frac {q} {2}} + {\ sqrt {{\ frac {q ^ {2}} {4}} + {\ frac {p ^ {3}} {27}}}} \ \ Rightarrow \ u = {\ sqrt [{3}] {- {\ frac {q} {2}} + {\ sqrt {{\ frac {q ^ {2}} {4}} + {\ frac {p ^ {3} } {27}}}}}}}

u ^ 3 = \ frac {-q + \ sqrt {q ^ 2 + \ frac {4p ^ 3} {27}}} {2} = - \ frac {q} {2} + \ sqrt {\ frac {q ^ 2} {4} + \ frac {p ^ 3} {27}} \ \ Rightarrow \ u = \ sqrt [3] {- \ frac {q} {2} + \ sqrt {\ frac {q ^ 2} {4} + \ frac {p ^ 3} {27}}}

v^{3}={\frac {-q-{\sqrt {q^{2}+{\frac {4p^{3}}{27}}}}}{2}}=-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}\ \Rightarrow \ v={\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}

{\ displaystyle v ^ {3} = {\ frac {-q - {\ sqrt {q ^ {2} + {\ frac {4p ^ {3}} {27}}}}} {2}} = - { \ frac {q} {2}} - {\ sqrt {{\ frac {q ^ {2}} {4}} + {\ frac {p ^ {3}} {27}}}} \ \ Rightarrow \ v = {\ sqrt [{3}] {- {\ frac {q} {2}} - {\ sqrt {{\ frac {q ^ {2}} {4}} + {\ frac {p ^ {3} } {27}}}}}}}

v ^ 3 = \ frac {-q- \ sqrt {q ^ 2 + \ frac {4p ^ 3} {27}}} {2} = - \ frac {q} {2} - \ sqrt {\ frac {q ^ 2} {4} + \ frac {p ^ 3} {27}} \ \ Rightarrow \ v = \ sqrt [3] {- \ frac {q} {2} - \ sqrt {\ frac {q ^ 2} {4} + \ frac {p ^ 3} {27}}}

Întrucât soluția ecuației noastre este $y=u+v$ ${\ displaystyle y = u + v}$ $y = u + v$ putem scrie:

y={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}+{\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}

{\ displaystyle y = {\ sqrt [{3}] {- {\ frac {q} {2}} + {\ sqrt {{\ frac {q ^ {2}} {4}} + {\ frac {p ^ {3}} {27}}}}}} + {\ sqrt [{3}] {- {\ frac {q} {2}} - {\ sqrt {{\ frac {q ^ {2}} { 4}} + {\ frac {p ^ {3}} {27}}}}}}}

y = \ sqrt [3] {- \ frac {q} {2} + \ sqrt {\ frac {q ^ 2} {4} + \ frac {p ^ 3} {27}}} + \ sqrt [3] {- \ frac {q} {2} - \ sqrt {\ frac {q ^ 2} {4} + \ frac {p ^ 3} {27}}}

Folosirea numerelor complexe pentru a găsi soluțiile ecuației

Formula soluției găsite are două rădăcini cubice care în câmpul real au o singură soluție, dar în câmpul complex au câte 3 fiecare. Prin urmare, oferă un total de 9 rezultate, dintre care doar 3 dintre ele vor fi o soluție a ecuației de gradul III, aceasta deoarece teorema fundamentală a algebrei afirmă că o ecuație de grad $n$ ${\ displaystyle n}$ $n$ recunoaște cu precizie $n$ ${\ displaystyle n}$ $n$ soluții.

Problema apare din faptul că am cubuit prima ecuație a sistemului

{\begin{cases}uv=-{\frac {p}{3}}\\u^{3}+v^{3}=-q\end{cases}}

{\ displaystyle {\ begin {cases} uv = - {\ frac {p} {3}} \\ u ^ {3} + v ^ {3} = - q \ end {cases}}}

\ begin {cases} uv = - \ frac {p} {3} \\ u ^ 3 + v ^ 3 = -q \ end {cases}

și, prin urmare, întrucât rezonăm într-un domeniu complex, soluțiile sistemului anterior sunt acele soluții ale

{\begin{cases}u^{3}v^{3}=-{\frac {p^{3}}{27}}\\u^{3}+v^{3}=-q\end{cases}}

{\ displaystyle {\ begin {cases} u ^ {3} v ^ {3} = - {\ frac {p ^ {3}} {27}} \\ u ^ {3} + v ^ {3} = - q \ end {cases}}}

\ begin {cases} u ^ 3v ^ 3 = - \ frac {p ^ 3} {27} \\ u ^ 3 + v ^ 3 = -q \ end {cases}

care rezolvă $uv=-{\tfrac {p}{3}}$ ${\ displaystyle uv = - {\ tfrac {p} {3}}}$ $uv = - \ tfrac {p} {3}$ și în special având în vedere că $-{\tfrac {p}{3}}$ ${\ displaystyle - {\ tfrac {p} {3}}}$ $- \ tfrac {p} {3}$ este un număr real pe care trebuie să îl verificăm când $tu v$ ${\ displaystyle uv}$ $uv$ este, de asemenea, real.

De asemenea, trebuie remarcat faptul că formula soluției are și rădăcini pătrate care în câmpul complex au întotdeauna 2 soluții pe care ar trebui să le luăm întotdeauna în considerare.

Atunci sunăm ${\tfrac {q^{2}}{4}}+{\tfrac {p^{3}}{27}}$ ${\ displaystyle {\ tfrac {q ^ {2}} {4}} + {\ tfrac {p ^ {3}} {27}}}$ $\ tfrac {q ^ 2} {4} + \ tfrac {p ^ 3} {27}$ cu simbolul $\Delta _{\text{III}}$ ${\ displaystyle \ Delta _ {\ text {III}}}$ ${\ displaystyle \ Delta _ {\ text {III}}}$ și să studiem cele două cazuri: $\Delta _{\text{III}}$ ${\ displaystyle \ Delta _ {\ text {III}}}$ ${\ displaystyle \ Delta _ {\ text {III}}}$ pozitiv și $\Delta _{\text{III}}$ ${\ displaystyle \ Delta _ {\ text {III}}}$ ${\ displaystyle \ Delta _ {\ text {III}}}$ negativ și cazul special în care $\Delta _{\text{III}}$ ${\ displaystyle \ Delta _ {\ text {III}}}$ ${\ displaystyle \ Delta _ {\ text {III}}}$ este nul.

Primul caz $\Delta _{\text{III}}<0$ ${\ displaystyle \ Delta _ {\ text {III}} <0}$ ${\ displaystyle \ Delta _ {\ text {III}} <0}$

Putem rescrie formula soluției după cum urmează:

y={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {\Delta _{\text{III}}}}}}+{\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {\Delta _{\text{III}}}}}}

{\ displaystyle y = {\ sqrt [{3}] {- {\ frac {q} {2}} + {\ sqrt {\ Delta _ {\ text {III}}}}}} + {\ sqrt [{ 3}] {- {\ frac {q} {2}} - {\ sqrt {\ Delta _ {\ text {III}}}}}}}

{\ displaystyle y = {\ sqrt [{3}] {- {\ frac {q} {2}} + {\ sqrt {\ Delta _ {\ text {III}}}}}} + {\ sqrt [{ 3}] {- {\ frac {q} {2}} - {\ sqrt {\ Delta _ {\ text {III}}}}}}}

y={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {-1(-\Delta _{\text{III}})}}}}+{\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {-1(-\Delta _{\text{III}})}}}}

{\ displaystyle y = {\ sqrt [{3}] {- {\ frac {q} {2}} + {\ sqrt {-1 (- \ Delta _ {\ text {III}})}}}} + {\ sqrt [{3}] {- {\ frac {q} {2}} - {\ sqrt {-1 (- \ Delta _ {\ text {III}})}}}}

{\ displaystyle y = {\ sqrt [{3}] {- {\ frac {q} {2}} + {\ sqrt {-1 (- \ Delta _ {\ text {III}})}}}} + {\ sqrt [{3}] {- {\ frac {q} {2}} - {\ sqrt {-1 (- \ Delta _ {\ text {III}})}}}}

y={\sqrt[{3}]{-{\frac {q}{2}}+i{\sqrt {-\Delta _{\text{III}}}}}}+{\sqrt[{3}]{-{\frac {q}{2}}-i{\sqrt {-\Delta _{\text{III}}}}}}

{\ displaystyle y = {\ sqrt [{3}] {- {\ frac {q} {2}} + i {\ sqrt {- \ Delta _ {\ text {III}}}}}} + {\ sqrt [{3}] {- {\ frac {q} {2}} - i {\ sqrt {- \ Delta _ {\ text {III}}}}}}}

{\ displaystyle y = {\ sqrt [{3}] {- {\ frac {q} {2}} + i {\ sqrt {- \ Delta _ {\ text {III}}}}}} + {\ sqrt [{3}] {- {\ frac {q} {2}} - i {\ sqrt {- \ Delta _ {\ text {III}}}}}}}

Pentru a calcula rădăcinile cubului putem converti numere complexe $-{\tfrac {q}{2}}+i{\sqrt {-\Delta _{\text{III}}}}$ ${\ displaystyle - {\ tfrac {q} {2}} + i {\ sqrt {- \ Delta _ {\ text {III}}}}}$ ${\ displaystyle - {\ tfrac {q} {2}} + i {\ sqrt {- \ Delta _ {\ text {III}}}}}$ Și $-{\tfrac {q}{2}}-i{\sqrt {-\Delta _{\text{III}}}}$ ${\ displaystyle - {\ tfrac {q} {2}} - i {\ sqrt {- \ Delta _ {\ text {III}}}}}$ ${\ displaystyle - {\ tfrac {q} {2}} - i {\ sqrt {- \ Delta _ {\ text {III}}}}}$ sub formă trigonometrică. Prin urmare, cele două module vor fi egale cu:

\rho ={\sqrt {\left(-{\frac {q}{2}}\right)^{2}+{\big (}{\sqrt {-\Delta _{\text{III}}}}{\big )}^{2}}}={\sqrt {{\frac {q^{2}}{4}}-{\frac {q^{2}}{4}}-{\frac {p^{3}}{27}}}}={\sqrt {-{\frac {p^{3}}{27}}}}

{\ displaystyle \ rho = {\ sqrt {\ left (- {\ frac {q} {2}} \ right) ^ {2} + {\ big (} {\ sqrt {- \ Delta _ {\ text {III }}}} {\ big)} ^ {2}}} = {\ sqrt {{\ frac {q ^ {2}} {4}} - {\ frac {q ^ {2}} {4}} - {\ frac {p ^ {3}} {27}}}} = {\ sqrt {- {\ frac {p ^ {3}} {27}}}}}

{\ displaystyle \ rho = {\ sqrt {\ left (- {\ frac {q} {2}} \ right) ^ {2} + {\ big (} {\ sqrt {- \ Delta _ {\ text {III }}}} {\ big)} ^ {2}}} = {\ sqrt {{\ frac {q ^ {2}} {4}} - {\ frac {q ^ {2}} {4}} - {\ frac {p ^ {3}} {27}}}} = {\ sqrt {- {\ frac {p ^ {3}} {27}}}}}

unghiurile vor avea aceeași amplitudine, dar semn opus, deoarece părțile imaginare ale celor două numere complexe sunt opuse, așa că le vom numi $\theta$ ${\ displaystyle \ theta}$ $\ theta$ Și $-\theta$ ${\ displaystyle - \ theta}$ $- \ theta$ .

Să calculăm acum rădăcinile cubice ale numerelor $(\rho ,\theta )$ ${\ displaystyle (\ rho, \ theta)}$ $(\ rho, \ theta)$ Și $(\rho ,-\theta )$ ${\ displaystyle (\ rho, - \ theta)}$ $(\ rho, - \ theta)$ . Forma lor va fi egală cu:

{\sqrt[{3}]{\rho }}={\sqrt[{3}]{\sqrt {-{\frac {p^{3}}{27}}}}}={\sqrt[{3}]{\left({\sqrt {-{\frac {p}{3}}}}\right)^{3}}}={\sqrt {-{\frac {p}{3}}}}

{\ displaystyle {\ sqrt [{3}] {\ rho}} = {\ sqrt [{3}] {\ sqrt {- {\ frac {p ^ {3}} {27}}}}} = {\ sqrt [{3}] {\ left ({\ sqrt {- {\ frac {p} {3}}}} \ right) ^ {3}}} = {\ sqrt {- {\ frac {p} {3 }}}}}

\ sqrt [3] {\ rho} = \ sqrt [3] {\ sqrt {- \ frac {p ^ 3} {27}}} = \ sqrt [3] {\ left (\ sqrt {- \ frac {p } {3}} \ right) ^ 3} = \ sqrt {- \ frac {p} {3}}

iar rădăcinile vor fi:

{\sqrt[{3}]{-{\frac {q}{2}}+i{\sqrt {-\Delta _{\text{III}}}}}}={\begin{cases}{\sqrt {-{\frac {p}{3}}}}\cdot \left(\cos {\frac {\theta }{3}}+i\sin {\frac {\theta }{3}}\right)&(u_{1})\\{\sqrt {-{\frac {p}{3}}}}\cdot \left(\cos {\frac {\theta +2\pi }{3}}+i\sin {\frac {\theta +2\pi }{3}}\right)&(u_{2})\\{\sqrt {-{\frac {p}{3}}}}\cdot \left(\cos {\frac {\theta +4\pi }{3}}+i\sin {\frac {\theta +4\pi }{3}}\right)&(u_{3})\\\end{cases}}

{\ displaystyle {\ sqrt [{3}] {- {\ frac {q} {2}} + i {\ sqrt {- \ Delta _ {\ text {III}}}}}} = {\ begin {cases } {\ sqrt {- {\ frac {p} {3}}}} \ cdot \ left (\ cos {\ frac {\ theta} {3}} + i \ sin {\ frac {\ theta} {3} } \ right) & (u_ {1}) \\ {\ sqrt {- {\ frac {p} {3}}}} \ cdot \ left (\ cos {\ frac {\ theta +2 \ pi} {3 }} + i \ sin {\ frac {\ theta +2 \ pi} {3}} \ right) & (u_ {2}) \\ {\ sqrt {- {\ frac {p} {3}}}} \ cdot \ left (\ cos {\ frac {\ theta +4 \ pi} {3}} + i \ sin {\ frac {\ theta +4 \ pi} {3}} \ right) & (u_ {3} ) \\\ end {cases}}}

{\ displaystyle {\ sqrt [{3}] {- {\ frac {q} {2}} + i {\ sqrt {- \ Delta _ {\ text {III}}}}}} = {\ begin {cases } {\ sqrt {- {\ frac {p} {3}}}} \ cdot \ left (\ cos {\ frac {\ theta} {3}} + i \ sin {\ frac {\ theta} {3} } \ right) & (u_ {1}) \\ {\ sqrt {- {\ frac {p} {3}}}} \ cdot \ left (\ cos {\ frac {\ theta +2 \ pi} {3 }} + i \ sin {\ frac {\ theta +2 \ pi} {3}} \ right) & (u_ {2}) \\ {\ sqrt {- {\ frac {p} {3}}}} \ cdot \ left (\ cos {\ frac {\ theta +4 \ pi} {3}} + i \ sin {\ frac {\ theta +4 \ pi} {3}} \ right) & (u_ {3} ) \\\ end {cases}}}

{\sqrt[{3}]{-{\frac {q}{2}}-i{\sqrt {-\Delta _{\text{III}}}}}}={\begin{cases}{\sqrt {-{\frac {p}{3}}}}\cdot \left(\cos {\frac {-\theta }{3}}+i\sin {\frac {-\theta }{3}}\right)&(v_{1})\\{\sqrt {-{\frac {p}{3}}}}\cdot \left(\cos {\frac {-\theta +2\pi }{3}}+i\sin {\frac {-\theta +2\pi }{3}}\right)&(v_{2})\\{\sqrt {-{\frac {p}{3}}}}\cdot \left(\cos {\frac {-\theta +4\pi }{3}}+i\sin {\frac {-\theta +4\pi }{3}}\right)&(v_{3})\\\end{cases}}

{\ displaystyle {\ sqrt [{3}] {- {\ frac {q} {2}} - i {\ sqrt {- \ Delta _ {\ text {III}}}}}} = {\ begin {cases } {\ sqrt {- {\ frac {p} {3}}}} \ cdot \ left (\ cos {\ frac {- \ theta} {3}} + i \ sin {\ frac {- \ theta} { 3}} \ right) & (v_ {1}) \\ {\ sqrt {- {\ frac {p} {3}}}} \ cdot \ left (\ cos {\ frac {- \ theta +2 \ pi } {3}} + i \ sin {\ frac {- \ theta +2 \ pi} {3}} \ right) & (v_ {2}) \\ {\ sqrt {- {\ frac {p} {3 }}}} \ cdot \ left (\ cos {\ frac {- \ theta +4 \ pi} {3}} + i \ sin {\ frac {- \ theta +4 \ pi} {3}} \ right) & (v_ {3}) \\\ end {cases}}}

{\ displaystyle {\ sqrt [{3}] {- {\ frac {q} {2}} - i {\ sqrt {- \ Delta _ {\ text {III}}}}}} = {\ begin {cases } {\ sqrt {- {\ frac {p} {3}}}} \ cdot \ left (\ cos {\ frac {- \ theta} {3}} + i \ sin {\ frac {- \ theta} { 3}} \ right) & (v_ {1}) \\ {\ sqrt {- {\ frac {p} {3}}}} \ cdot \ left (\ cos {\ frac {- \ theta +2 \ pi } {3}} + i \ sin {\ frac {- \ theta +2 \ pi} {3}} \ right) & (v_ {2}) \\ {\ sqrt {- {\ frac {p} {3 }}}} \ cdot \ left (\ cos {\ frac {- \ theta +4 \ pi} {3}} + i \ sin {\ frac {- \ theta +4 \ pi} {3}} \ right) & (v_ {3}) \\\ end {cases}}}

Soluțiile vor fi deci de formă $y=u_{i}+v_{j}$ ${\ displaystyle y = u_ {i} + v_ {j}}$ $y = u_i + v_j$ dar în realitate doar în trei cazuri produsul $u_{i}\cdot v_{j}$ ${\ displaystyle u_ {i} \ cdot v_ {j}}$ $u_i \ cdot v_j$ ne dă un număr real (și, prin urmare, rezolvă $uv=-{\tfrac {p}{3}}$ ${\ displaystyle uv = - {\ tfrac {p} {3}}}$ $uv = - \ tfrac {p} {3}$ ). De fapt numai în cazuri $u_{1}\cdot v_{1}$ ${\ displaystyle u_ {1} \ cdot v_ {1}}$ $u_1 \ cdot v_1$ , $u_{2}\cdot v_{3}$ ${\ displaystyle u_ {2} \ cdot v_ {3}}$ $u_2 \ cdot v_3$ și $u_{3}\cdot v_{2}$ ${\ displaystyle u_ {3} \ cdot v_ {2}}$ $u_3 \ cdot v_2$ partea imaginară dispare.

Deci, soluțiile ecuației vor fi:

y_{1}=u_{1}+v_{1}=2{\sqrt {-{\frac {p}{3}}}}\cdot \cos {\frac {\theta }{3}}

{\ displaystyle y_ {1} = u_ {1} + v_ {1} = 2 {\ sqrt {- {\ frac {p} {3}}}} \ cdot \ cos {\ frac {\ theta} {3} }}

y_1 = u_1 + v_1 = 2 \ sqrt {- \ frac {p} {3}} \ cdot \ cos \ frac {\ theta} {3}

y_{2}=u_{2}+v_{3}=2{\sqrt {-{\frac {p}{3}}}}\cdot \cos {\frac {\theta +2\pi }{3}}

{\ displaystyle y_ {2} = u_ {2} + v_ {3} = 2 {\ sqrt {- {\ frac {p} {3}}}} \ cdot \ cos {\ frac {\ theta +2 \ pi } {3}}}

y_2 = u_2 + v_3 = 2 \ sqrt {- \ frac {p} {3}} \ cdot \ cos \ frac {\ theta + 2 \ pi} {3}

y_{3}=u_{3}+v_{2}=2{\sqrt {-{\frac {p}{3}}}}\cdot \cos {\frac {\theta +4\pi }{3}}

{\ displaystyle y_ {3} = u_ {3} + v_ {2} = 2 {\ sqrt {- {\ frac {p} {3}}}} \ cdot \ cos {\ frac {\ theta +4 \ pi } {3}}}

y_3 = u_3 + v_2 = 2 \ sqrt {- \ frac {p} {3}} \ cdot \ cos \ frac {\ theta + 4 \ pi} {3}

Al doilea caz $\Delta _{\text{III}}>0$ ${\ displaystyle \ Delta _ {\ text {III}}> 0}$ ${\ displaystyle \ Delta _ {\ text {III}}> 0}$

În cazul în care $\Delta _{\text{III}}$ ${\ displaystyle \ Delta _ {\ text {III}}}$ ${\ displaystyle \ Delta _ {\ text {III}}}$ este mai mare decât 0 va avea o rădăcină pătrată reală și, prin urmare, vor exista două numere reale $u_{1}$ ${\ displaystyle u_ {1}}$ $u_1$ Și $v_{1}$ ${\ displaystyle v_ {1}}$ $v_1$ La fel ca

u_{1}={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {\Delta _{\text{III}}}}}}

{\ displaystyle u_ {1} = {\ sqrt [{3}] {- {\ frac {q} {2}} + {\ sqrt {\ Delta _ {\ text {III}}}}}}

u_{1}={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {\Delta _{\text{III}}}}}}

v_{1}={\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {\Delta _{\text{III}}}}}}

v_{1}={\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {\Delta _{\text{III}}}}}}

v_{1}={\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {\Delta _{\text{III}}}}}}

Come nel caso precedente non bisogna soffermarsi sulle radici reali ma bisogna analizzare anche cosa avviene quando il risultato delle radici cubiche è complesso. Per trovare anche i risultati complessi basterà moltiplicare i risultati reali $u_{1}$ $u_{1}$ $u_1$ e $v_{1}$ $v_{1}$ $v_1$ per le radici cubiche dell'unità; abbiamo quindi i 6 risultati:

u_{1}={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {\Delta _{\text{III}}}}}},\quad u_{2}=u_{1}\cdot \left(-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\right),\quad u_{3}=u_{1}\cdot \left(-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\right)

u_{1}={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {\Delta _{\text{III}}}}}},\quad u_{2}=u_{1}\cdot \left(-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\right),\quad u_{3}=u_{1}\cdot \left(-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\right)

u_{1}={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {\Delta _{\text{III}}}}}},\quad u_{2}=u_{1}\cdot \left(-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\right),\quad u_{3}=u_{1}\cdot \left(-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\right)

v_{1}={\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {\Delta _{\text{III}}}}}},\quad v_{2}=v_{1}\cdot \left(-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\right),\quad v_{3}=v_{1}\cdot \left(-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\right)

v_{1}={\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {\Delta _{\text{III}}}}}},\quad v_{2}=v_{1}\cdot \left(-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\right),\quad v_{3}=v_{1}\cdot \left(-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\right)

v_{1}={\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {\Delta _{\text{III}}}}}},\quad v_{2}=v_{1}\cdot \left(-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\right),\quad v_{3}=v_{1}\cdot \left(-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\right)

Anche questa volta, per controllare quando $u_{i}\cdot v_{j}=-{\tfrac {p}{3}}$ $u_{i}\cdot v_{j}=-{\tfrac {p}{3}}$ $u_i\cdot v_j=-\tfrac{p}{3}$ , ci basta vedere quando $u_{i}\cdot v_{j}$ $u_{i}\cdot v_{j}$ $u_i\cdot v_j$ è un numero reale. Svolgendo i conti otteniamo quindi che le soluzioni dell'equazione di terzo grado sono

y_{1}=u_{1}+v_{1}

y_{1}=u_{1}+v_{1}

y_1=u_1+v_1

y_{2}=u_{2}+v_{3}=u_{1}\cdot \left(-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\right)+v_{1}\cdot \left(-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\right)

y_{2}=u_{2}+v_{3}=u_{1}\cdot \left(-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\right)+v_{1}\cdot \left(-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\right)

y_2=u_2+v_3=u_1\cdot\left(-\frac{1}{2}+i\frac{\sqrt{3}}{2}\right)+v_1\cdot\left(-\frac{1}{2}-i\frac{\sqrt{3}}{2}\right)

y_{3}=u_{3}+v_{2}=u_{1}\cdot \left(-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\right)+v_{1}\cdot \left(-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\right)

y_{3}=u_{3}+v_{2}=u_{1}\cdot \left(-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\right)+v_{1}\cdot \left(-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\right)

y_3=u_3+v_2=u_1\cdot\left(-\frac{1}{2}-i\frac{\sqrt{3}}{2}\right)+v_1\cdot\left(-\frac{1}{2}+i\frac{\sqrt{3}}{2}\right)

Caso $\Delta _{\text{III}}=0$ $\Delta _{\text{III}}=0$ $\Delta _{\text{III}}=0$

Nel caso particolare in cui $\Delta _{\text{III}}$ $\Delta _{\text{III}}$ $\Delta _{\text{III}}$ sia uguale a 0 si può ricavare dalle formule trovate che le soluzioni sono:

y_{1}=-2{\sqrt[{3}]{\frac {q}{2}}}

y_{1}=-2{\sqrt[{3}]{\frac {q}{2}}}

y_1=-2\sqrt[3]{\frac{q}{2}}

y_{2}=y_{3}={\sqrt[{3}]{\frac {q}{2}}}

y_{2}=y_{3}={\sqrt[{3}]{\frac {q}{2}}}

y_2=y_3=\sqrt[3]{\frac{q}{2}}

Soluzione in forma non depressa

Si consideri una generica cubica della forma:

P(x)=ax^{3}+bx^{2}+cx+d=a(x-x_{1})(x-x_{2})(x-x_{3}).

P(x)=ax^{3}+bx^{2}+cx+d=a(x-x_{1})(x-x_{2})(x-x_{3}).

P(x)=ax^{3}+bx^{2}+cx+d=a(x-x_{1})(x-x_{2})(x-x_{3}).

Si calcolino

q={\frac {3ac-b^{2}}{3a^{2}}}

q={\frac {3ac-b^{2}}{3a^{2}}}

q = \frac{3ac-b^2}{3a^2}

p={\frac {9abc-27a^{2}d-2b^{3}}{27a^{3}}}

p={\frac {9abc-27a^{2}d-2b^{3}}{27a^{3}}}

p={\frac {9abc-27a^{2}d-2b^{3}}{27a^{3}}}

s={\sqrt[{3}]{{\frac {p}{2}}+{\sqrt {{\frac {q^{3}}{27}}+{\frac {p^{2}}{4}}}}}}

s={\sqrt[{3}]{{\frac {p}{2}}+{\sqrt {{\frac {q^{3}}{27}}+{\frac {p^{2}}{4}}}}}}

s={\sqrt[{3}]{{\frac {p}{2}}+{\sqrt {{\frac {q^{3}}{27}}+{\frac {p^{2}}{4}}}}}}

t={\sqrt[{3}]{{\frac {p}{2}}-{\sqrt {{\frac {q^{3}}{27}}+{\frac {p^{2}}{4}}}}}}

t={\sqrt[{3}]{{\frac {p}{2}}-{\sqrt {{\frac {q^{3}}{27}}+{\frac {p^{2}}{4}}}}}}

t={\sqrt[{3}]{{\frac {p}{2}}-{\sqrt {{\frac {q^{3}}{27}}+{\frac {p^{2}}{4}}}}}}

Le soluzioni dell'equazione $P(x)=0$ ${\displaystyle P(x)=0}$ $P(x)=0$ sono date da

x_{1}=s+t-{\frac {b}{3a}}

x_{1}=s+t-{\frac {b}{3a}}

x_1 = s+t-\frac{{b}}{{3a}}

x_{2}=-{\frac {1}{2}}(s+t)-{\frac {b}{3a}}+{\frac {\sqrt {3}}{2}}(s-t)i

x_{2}=-{\frac {1}{2}}(s+t)-{\frac {b}{3a}}+{\frac {\sqrt {3}}{2}}(st)i

x_2=-\frac{1}{2}(s+t)-\frac{b}{3a}+\frac{\sqrt{3}}{2}(s-t)i

x_{3}=-{\frac {1}{2}}(s+t)-{\frac {b}{3a}}-{\frac {\sqrt {3}}{2}}(s-t)i

x_{3}=-{\frac {1}{2}}(s+t)-{\frac {b}{3a}}-{\frac {\sqrt {3}}{2}}(st)i

x_3=-\frac{1}{2}(s+t)-\frac{b}{3a}-\frac{\sqrt{3}}{2}(s-t)i

Alternativamente, la soluzione generale dell'equazione di terzo grado in termini dei coefficienti può essere scritta in forma compatta nel seguente modo:

x_{k}=-{\frac {b}{3a}}-{\frac {q}{3tu_{k}}}+tu_{k}\ ,\qquad k\in \{1,2,3\}

x_{k}=-{\frac {b}{3a}}-{\frac {q}{3tu_{k}}}+tu_{k}\ ,\qquad k\in \{1,2,3\}

x_k = - \frac{b}{3a}-\frac{q}{3tu_k}+tu_k \ , \qquad k \in \{1,2, 3\}

dove

u_{1}=1\ ,\qquad u_{2}={-1-i{\sqrt {3}} \over 2}\ ,\qquad u_{3}={-1+i{\sqrt {3}} \over 2}

u_{1}=1\ ,\qquad u_{2}={-1-i{\sqrt {3}} \over 2}\ ,\qquad u_{3}={-1+i{\sqrt {3}} \over 2}

u_1 = 1\ ,\qquad u_2 = {-1 - i\sqrt{3} \over 2}\ ,\qquad u_3 = {-1 + i\sqrt{3} \over 2}

sono le tre radici cubiche dell'unità nel campo complesso . Essa può essere riscritta anche come

x_{k}=-{\frac {1}{3a}}\left(b\ +\ u_{k}C\ +\ {\frac {\Delta _{0}}{u_{k}C}}\right)\ ,\qquad k\in \{1,2,3\}

x_{k}=-{\frac {1}{3a}}\left(b\ +\ u_{k}C\ +\ {\frac {\Delta _{0}}{u_{k}C}}\right)\ ,\qquad k\in \{1,2,3\}

x_k = - \frac{1}{3a}\left(b\ +\ u_k C\ +\ \frac{\Delta_0}{u_kC}\right)\ , \qquad k \in \{1,2, 3\}

dove

C={\sqrt[{3}]{\frac {\Delta _{1}+{\sqrt {\Delta _{1}^{2}-4\Delta _{0}^{3}}}}{2}}}=-3at

C={\sqrt[{3}]{\frac {\Delta _{1}+{\sqrt {\Delta _{1}^{2}-4\Delta _{0}^{3}}}}{2}}}=-3at

C = \sqrt[3]{\frac{\Delta_1 + \sqrt{\Delta_1^2 - 4 \Delta_0^3}}{2}}=-3at

con

\Delta _{0}=b^{2}-3ac=-3a^{2}q

\Delta _{0}=b^{2}-3ac=-3a^{2}q

\Delta_0 = b^2-3 a c=-3a^2 q

\Delta _{1}=2b^{3}-9abc+27a^{2}d=-27a^{3}r

\Delta _{1}=2b^{3}-9abc+27a^{2}d=-27a^{3}r

\Delta_1 = 2 b^3-9 a b c+27 a^2 d= -27a^3 r

Casi particolari

Caso 1: $x^{3}+x=c$ $x^{3}+x=c$ $x^{3}+x=c$

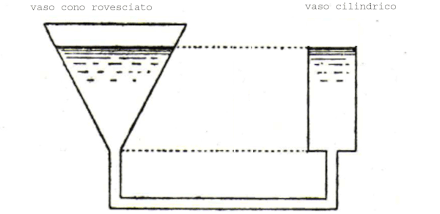
Uno schizzo del sistema di vasi comunicanti

Un metodo di soluzione di tipo idraulico è stato trovato da A. Demanet nel 1898 e tratta il caso particolare ^[3] ^[4]

ax^{3}+bx^{2}+cx+d=0

ax^{3}+bx^{2}+cx+d=0

ax^3+bx^2+cx+d=0

in cui

a=1,\ b=0,\ c=1,\ d<0

a=1,\ b=0,\ c=1,\ d<0

a=1,\ b=0,\ c=1,\ d<0

L'equazione può essere, quindi, riscritta in modo semplificato eguagliando $k=-d$ ${\displaystyle k=-d}$ $k=-d$

x^{3}+x=k

x^{3}+x=k

x^3 + x = k

La soluzione si basa sulla teoria dei vasi comunicanti , mediante lo studio di un sistema formato da un vaso a cono rovesciato collegato ad uno cilindrico di eguale altezza, problemi di tensione superficiale possono rendere meno accurata la precisione della soluzione.

Ipotizziamo di avere il sistema descritto sopra, che l'area della base del cilindro sia pari a 1 e che il rapporto tra il raggio $r$ ${\displaystyle r}$ $r$ del cono e la sua altezza $a$ ${\displaystyle a}$ $a$ sia:

{\frac {r}{a}}={\sqrt {\frac {3}{\pi }}}

{\frac {r}{a}}={\sqrt {\frac {3}{\pi }}}

\frac{r}{a}=\sqrt{\frac{3}{\pi}}

Ora se indichiamo con $V_{cono}$ $V_{cono}$ $V_{cono}$ e $V_{cilindro}$ $V_{cilindro}$ $V_{cilindro}$ rispettivamente il volume dell'acqua ^[5] presente nel cono e nel cilindro, e con $h$ ${\displaystyle h}$ $h$ l'altezza dell'acqua nei due recipienti ^[6] avremmo che:

V_{cilindro}=h\cdot area_{base}=h\cdot 1=h

V_{cilindro}=h\cdot area_{base}=h\cdot 1=h

V_{cilindro}=h \cdot area_{base}=h \cdot 1=h

e che

V_{cono}=\pi \cdot r^{2}\cdot {\frac {h}{3}}

V_{cono}=\pi \cdot r^{2}\cdot {\frac {h}{3}}

V_{cono}=\pi \cdot r^2 \cdot \frac{h}{3}

tenendo conto della relazione tra l'altezza e il raggio del cono si ha che:

V_{cono}=\pi \cdot \left(h{\sqrt {\frac {3}{\pi }}}\right)^{2}\cdot {\frac {h}{3}}=h^{3}

V_{cono}=\pi \cdot \left(h{\sqrt {\frac {3}{\pi }}}\right)^{2}\cdot {\frac {h}{3}}=h^{3}

V_{{cono}}=\pi \cdot \left(h{\sqrt {{\frac {3}{\pi }}}}\right)^{2}\cdot {\frac {h}{3}}=h^{3}

Se indichiamo con $V_{tubo}$ $V_{tubo}$ $V_{tubo}$ il volume dell'acqua presente nel tubo che collega i due vasi e con $V_{acqua}$ $V_{acqua}$ $V_{acqua}$ il volume dell'acqua versata nei due vasi risulterà che:

V_{acqua}=V_{cilindro}+V_{cono}+V_{tubo}

V_{acqua}=V_{cilindro}+V_{cono}+V_{tubo}

V_{acqua}=V_{cilindro}+V_{cono}+V_{tubo}

V_{acqua}=h+h^{3}+V_{tubo}

V_{acqua}=h+h^{3}+V_{tubo}

V_{acqua}=h+h^3+V_{tubo}

h^{3}+h=V_{acqua}-V_{tubo}

h^{3}+h=V_{acqua}-V_{tubo}

h^3+h=V_{acqua}-V_{tubo}

se chiamiamo $k=V_{acqua}-V_{tubo}$ $k=V_{acqua}-V_{tubo}$ $k=V_{acqua}-V_{tubo}$ otteniamo

h^{3}+h=k

h^{3}+h=k

h^3+h=k

Abbiamo così ottenuto un'equazione di terzo grado la cui soluzione sarà l'altezza, misurabile, dell'acqua in uno dei due vasi comunicanti.

Più in generale, se chiamiamo con $r_{cono}$ $r_{cono}$ $r_{cono}$ ed $r_{cilindro}$ $r_{cilindro}$ $r_{cilindro}$ rispettivamente il raggio del cono e del cilindro, $h$ ${\displaystyle h}$ $h$ l'altezza del cono e $x$ ${\displaystyle x}$ $x$ l'altezza raggiunta dall'acqua si può ottenere l'equazione:

{\frac {1}{3}}\pi {\frac {(r_{cono})^{2}}{h^{2}}}x^{3}+\pi (r_{cilindro})^{2}x=k

{\frac {1}{3}}\pi {\frac {(r_{cono})^{2}}{h^{2}}}x^{3}+\pi (r_{cilindro})^{2}x=k

\frac{1}{3}\pi\frac{(r_{cono})^2}{h^2}x^3+\pi (r_{cilindro})^2 x=k

quindi scegliendo opportunamente i due recipienti possiamo risolvere anche un'equazione del tipo:

ax^{3}+bx=c\qquad {\mbox{con }}c>0

ax^{3}+bx=c\qquad {\mbox{con }}c>0

ax^3+bx=c \qquad \mbox{con } c>0

Caso 2: $d={\frac {bc}{a}}$ $d={\frac {bc}{a}}$ $d={\frac {bc}{a}}$

Se l'equazione di terzo grado possiede la particolare caratteristica di avere il termine noto uguale a ${\tfrac {bc}{a}}$ ${\tfrac {bc}{a}}$ $\tfrac{bc}{a}$ l'equazione si presenta nella formula:

ax^{3}+bx^{2}+cx+{\frac {bc}{a}}=0

ax^{3}+bx^{2}+cx+{\frac {bc}{a}}=0

ax^3 + bx^2 + cx + \frac{bc}{a} = 0

in questo caso abbiamo immediatamente almeno una soluzione reale dato che la formula può essere vista come:

ax^{3}+bx^{2}+cx+{\frac {bc}{a}}=a\cdot \left(x+{\frac {b}{a}}\right)\cdot \left(x^{2}+{\frac {c}{a}}\right)

ax^{3}+bx^{2}+cx+{\frac {bc}{a}}=a\cdot \left(x+{\frac {b}{a}}\right)\cdot \left(x^{2}+{\frac {c}{a}}\right)

ax^3 + bx^2 + cx + \frac{bc}{a} = a\cdot\left(x + \frac{b}{a}\right)\cdot\left(x^2 + \frac{c}{a}\right)

Una soluzione, quindi, sarà sicuramente $x=-{\tfrac {b}{a}}$ $x=-{\tfrac {b}{a}}$ $x=-\tfrac{b}{a}$ ; le altre 2 saranno reali o no in base al segno di ${\tfrac {c}{a}}$ ${\tfrac {c}{a}}$ $\tfrac{c}{a}$ .

Note

^ Umberto Bottazzini, La "grande arte": l'algebra del rinascimento , in Storia della scienza moderna e contemporanea , diretto da Paolo Rossi , Vol. 1: Dalla rivoluzione scientifica all'età dei lumi, p. 72, ISBN 88-02-04152-0 .
^ ( EN ) Eric W. Weisstein,Vieta's Substitution , in MathWorld , Wolfram Research.
^ Francesco Daddi, Strategie didattiche per promuovere un atteggiamento positivo verso la Matematica e la Fisica - Risolutore di equazioni ad acqua ( PDF ), su dm.unipi.it , Università di Pisa . URL consultato il 28 dicembre 2012 (archiviato dall'url originale l'11 marzo 2014) .
^ Italo Ghersi, Metodi fisici per la soluzione di equazioni algebriche , in Matematica dilettevole e curiosa , appendice di R. Leonardi, 5ª ed., Milano, Ulrico Hoepli Editore , 2004 [1913] , p. 253, ISBN 88-203-0469-4 .
^ L'unità di misura del volume dovrà appartenere allo stesso sistema di misura utilizzato per l'altezza, il raggio e l'area, quindi se, per esempio, l'altezza è misurata in centimetri l'area dovrà essere misurata in centimetri quadrati e il volume in centimetri cubi.
^ L'altezza dell'acqua nei due vasi sarà la stessa dato che non contengono due liquidi diversi.

Bibliografia

Carl Boyer , Storia della matematica , Milano, Arnoldo Mondadori Editore , 1976, ISBN 88-04-33431-2 .

Voci correlate

Altri progetti

Wikimedia Commons contiene immagini o altri file su equazione di terzo grado

Collegamenti esterni

( EN ) Equazione di terzo grado , su Enciclopedia Britannica , Encyclopædia Britannica, Inc.
( EN ) Eric W. Weisstein, Cubic Equation , in MathWorld , Wolfram Research.
( EN ) Eric W. Weisstein, Cubic Formula , in MathWorld , Wolfram Research.
( EN ) cubic formula , in PlanetMath .
( EN ) Cardano's derivation of the cubic formula , in PlanetMath .
( EN ) IV Proskuryakov, Cubic equation , in Encyclopaedia of Mathematics , Springer e European Mathematical Society, 2002.
( EN ) IV Proskuryakov, Cardano formula , in Encyclopaedia of Mathematics , Springer e European Mathematical Society, 2002.

Controllo di autorità	Thesaurus BNCF 32448 · LCCN ( EN ) sh85044516 · BNF ( FR ) cb122693768 (data)

Portale Matematica : accedi alle voci di Wikipedia che trattano di matematica

[1] Umberto Bottazzini, La "grande arte": l'algebra del rinascimento , in Storia della scienza moderna e contemporanea , diretto da Paolo Rossi , Vol. 1: Dalla rivoluzione scientifica all'età dei lumi, p. 72, ISBN 88-02-04152-0 .

[2] ( EN ) Eric W. Weisstein,Vieta's Substitution , in MathWorld , Wolfram Research.

[3] Francesco Daddi, Strategie didattiche per promuovere un atteggiamento positivo verso la Matematica e la Fisica - Risolutore di equazioni ad acqua ( PDF ), su dm.unipi.it , Università di Pisa . URL consultato il 28 dicembre 2012 (archiviato dall'url originale l'11 marzo 2014) .

[4] Italo Ghersi, Metodi fisici per la soluzione di equazioni algebriche , in Matematica dilettevole e curiosa , appendice di R. Leonardi, 5ª ed., Milano, Ulrico Hoepli Editore , 2004 [1913] , p. 253, ISBN 88-203-0469-4 .

[5] L'unità di misura del volume dovrà appartenere allo stesso sistema di misura utilizzato per l'altezza, il raggio e l'area, quindi se, per esempio, l'altezza è misurata in centimetri l'area dovrà essere misurata in centimetri quadrati e il volume in centimetri cubi.

[6] L'altezza dell'acqua nei due vasi sarà la stessa dato che non contengono due liquidi diversi.

[1]

[2]

[3]

[4]

[5]

[6]